澄清经典文献中洛匈棱镜分束角公式的问题

李东风; 李如意; 杨春旺; 周珺; 陆守香

doi:10.37188/CO.2025-0036

澄清经典文献中洛匈棱镜分束角公式的问题

doi: 10.37188/CO.2025-0036

cstr: 32171.14.CO.2025-0036

李东风^{1, 2,},
李如意²,
杨春旺²,
周珺³,
陆守香^1, ,

1.
火灾科学国家重点实验室, 安徽合肥230037
2.
安徽芯核防务装备技术股份有限公司, 安徽合肥230088
3.
公安部第一研究所, 北京 100048

基金项目: 公安部科技计划项目（No. 2022ZB12）

详细信息

作者简介:
李东风，河南濉溪人，正高级工程师，中国科学技术大学火灾火灾安全全国重点实验室博士研究生在读，现任公司董事长、总经理、党支部书记，入选第二批合肥市学术和技术带头人后备人选、安徽省国资委第五批538英才工程人才计划、安徽军工集团第三批学术带头人；主持研究国家重点研发项目、高新工程2项、公安部科技计划重点项目2项、公安部科技强警及成果引导计划项目各1项，上述参与的科研计划项目均已通过验收；获得安徽省科学技术三等奖1项，获得公安部科技技术进步奖2项，另获得发明专利5项，实用新型专利15项，论文在国家级刊物上发表并收录。E-mail：lidf@ahxhfw.corn

陆守香，安徽合肥人，中国科学技术大学火灾安全全国重点实验室教授，博士生导师，主要从事应急技术理论，火灾科学与消防技术应用研究；先进火灾探测技术研究与开发，高效环保灭火装备及核心部件研究；智慧消防物联网系统开发。先后发表SCI学术论文200余篇，合著《火灾风险评估方法学》，获授权专利13项、软件著作权6项。E-mail：sxlu@ustc.edu.cn

中图分类号: O436.3;O439;
计量
- 文章访问数: 82
- HTML全文浏览量: 38
- PDF下载量: 3
- 被引次数: 0
出版历程
- 网络出版日期: 2025-08-21

Clarify the problem of the beam deviation angle formula of a Rochon Prism in classical literatures

1.
State Key Laboratory of Fire Science, Hefei 230037, China
2.
Anhui Core Defense Equipment Technology Co., Ltd, Hefei 230088, China
3.
The First Research Institute of the Ministry of Public Security, Beijing 100048, China

Funds: Supported by the Science and Technology Program Project of the Ministry of Public Security (No. 2022ZB12)

More Information

Corresponding author: sxlu@ustc.edu.cn

摘要

摘要:
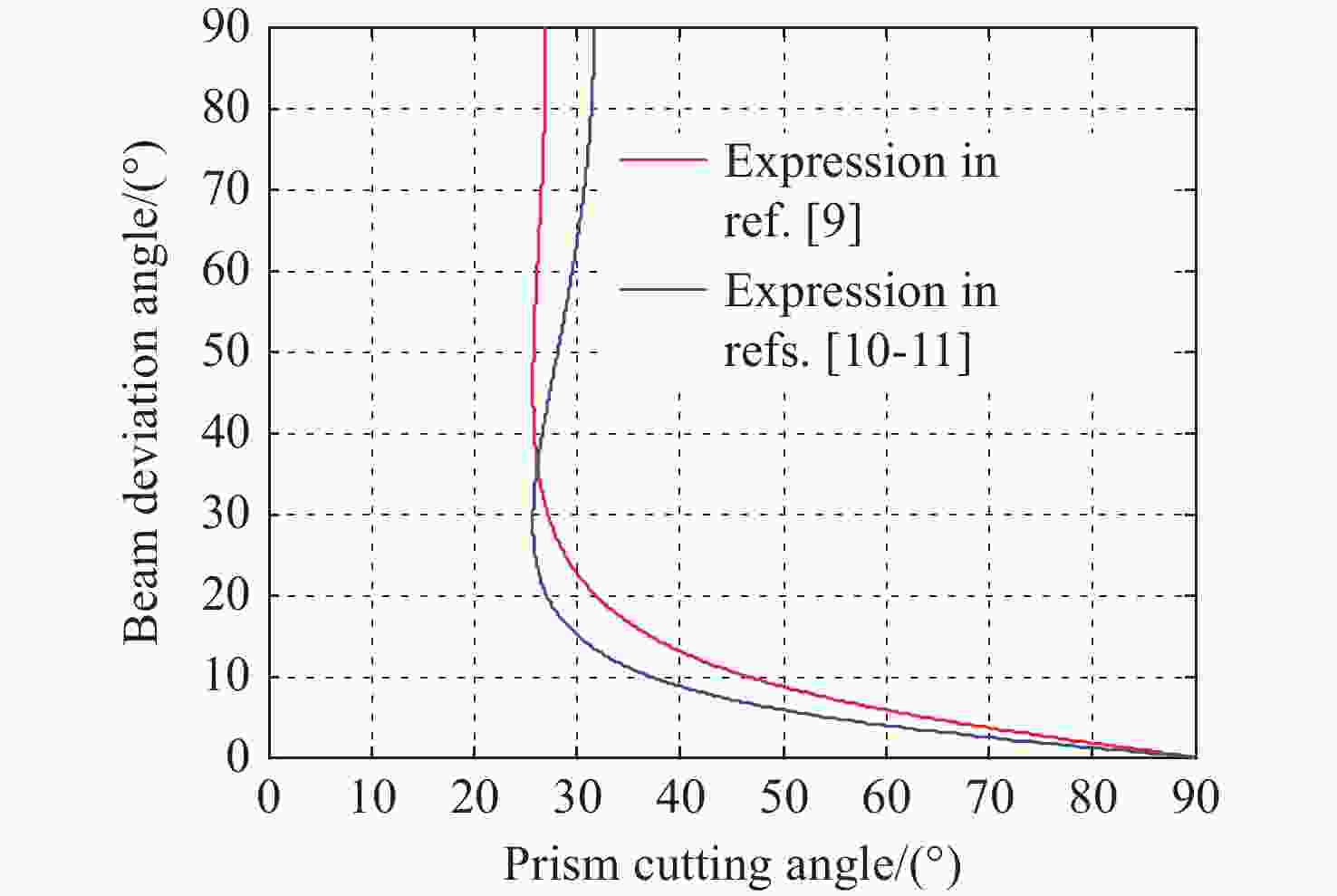
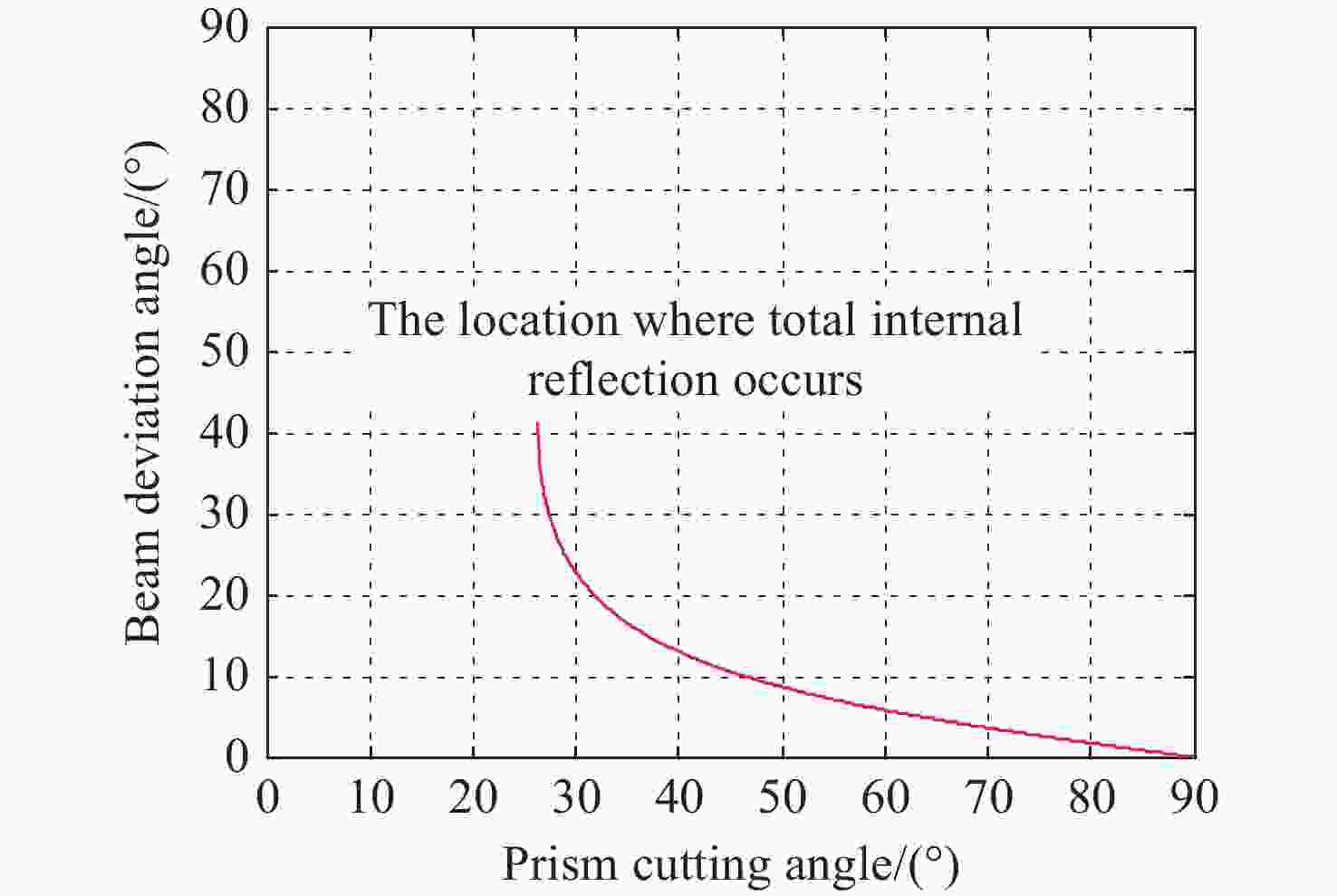
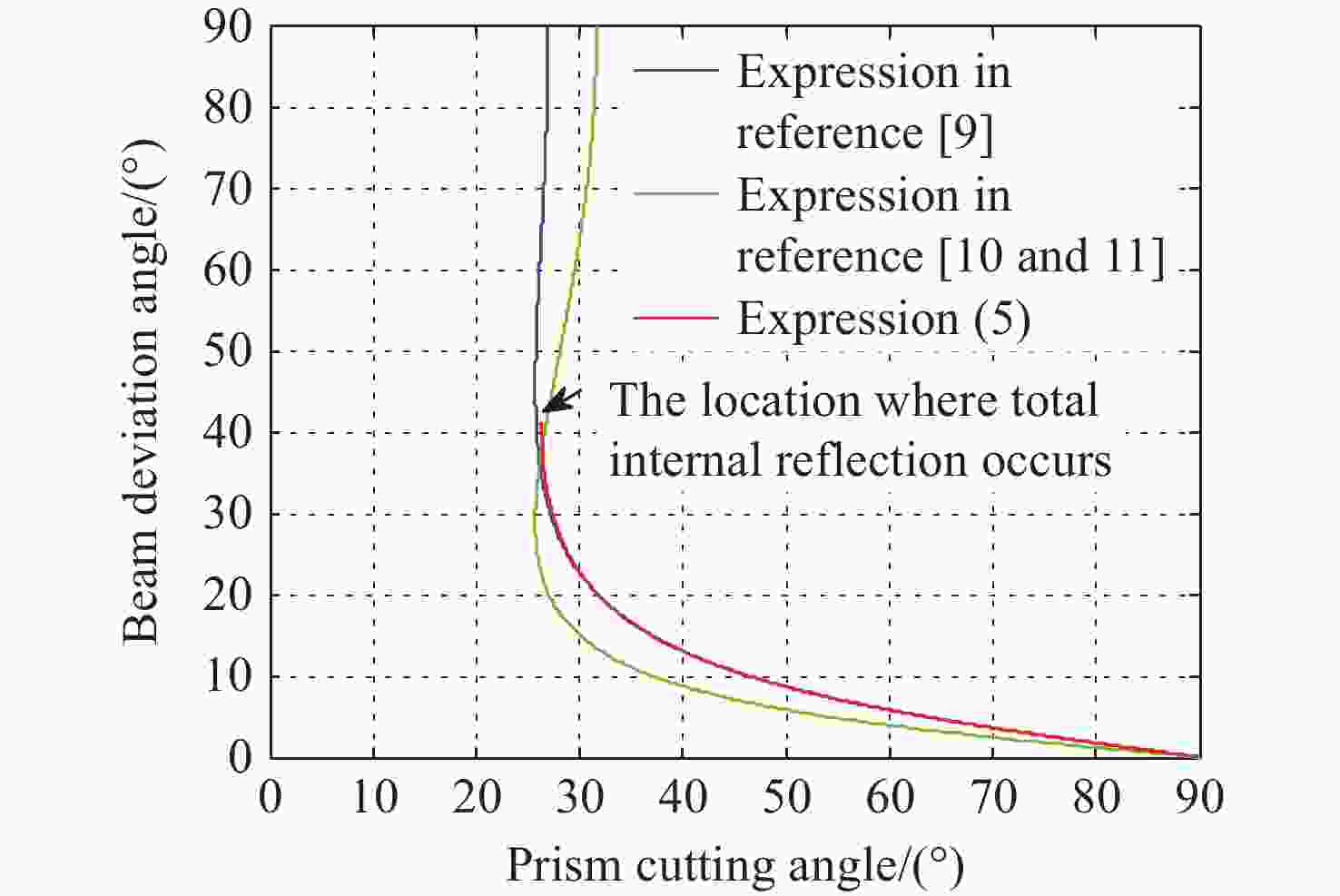
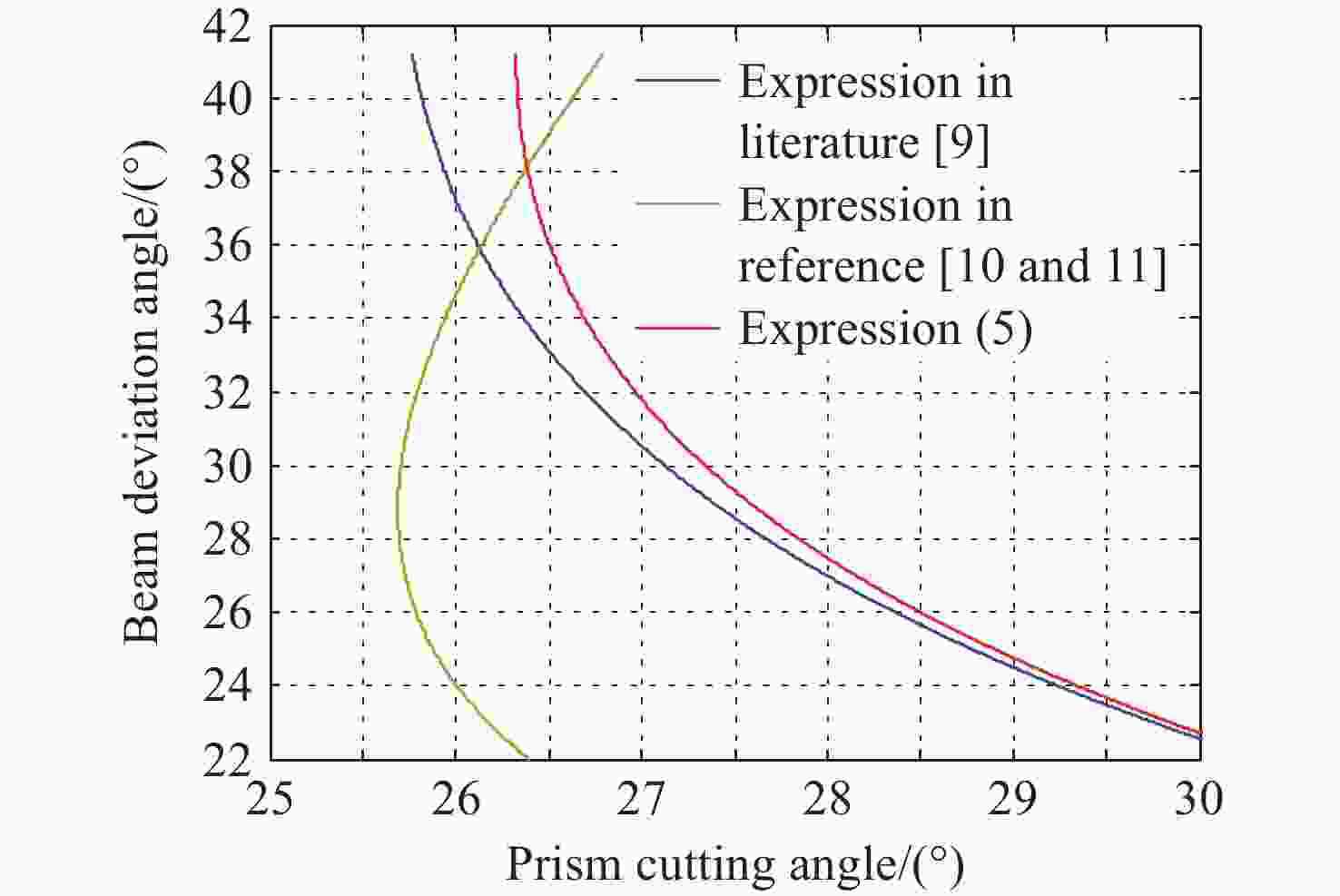
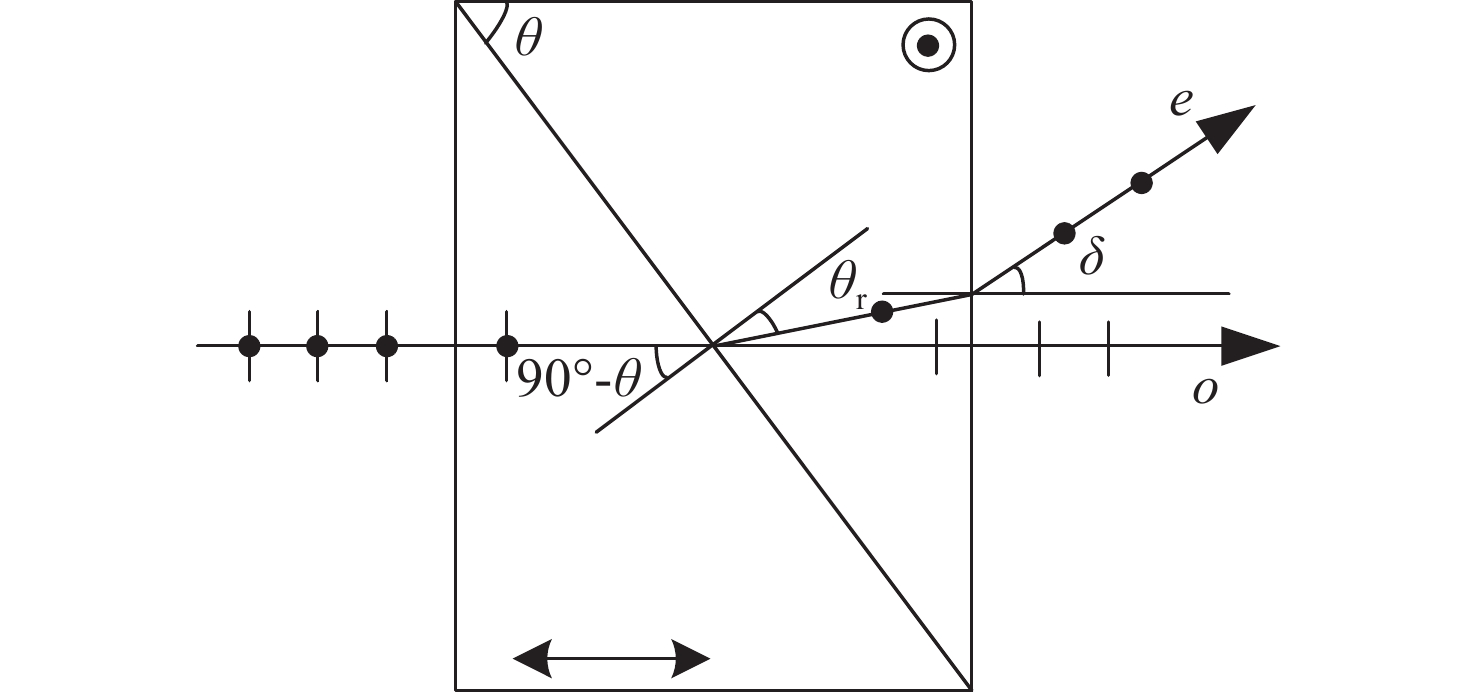
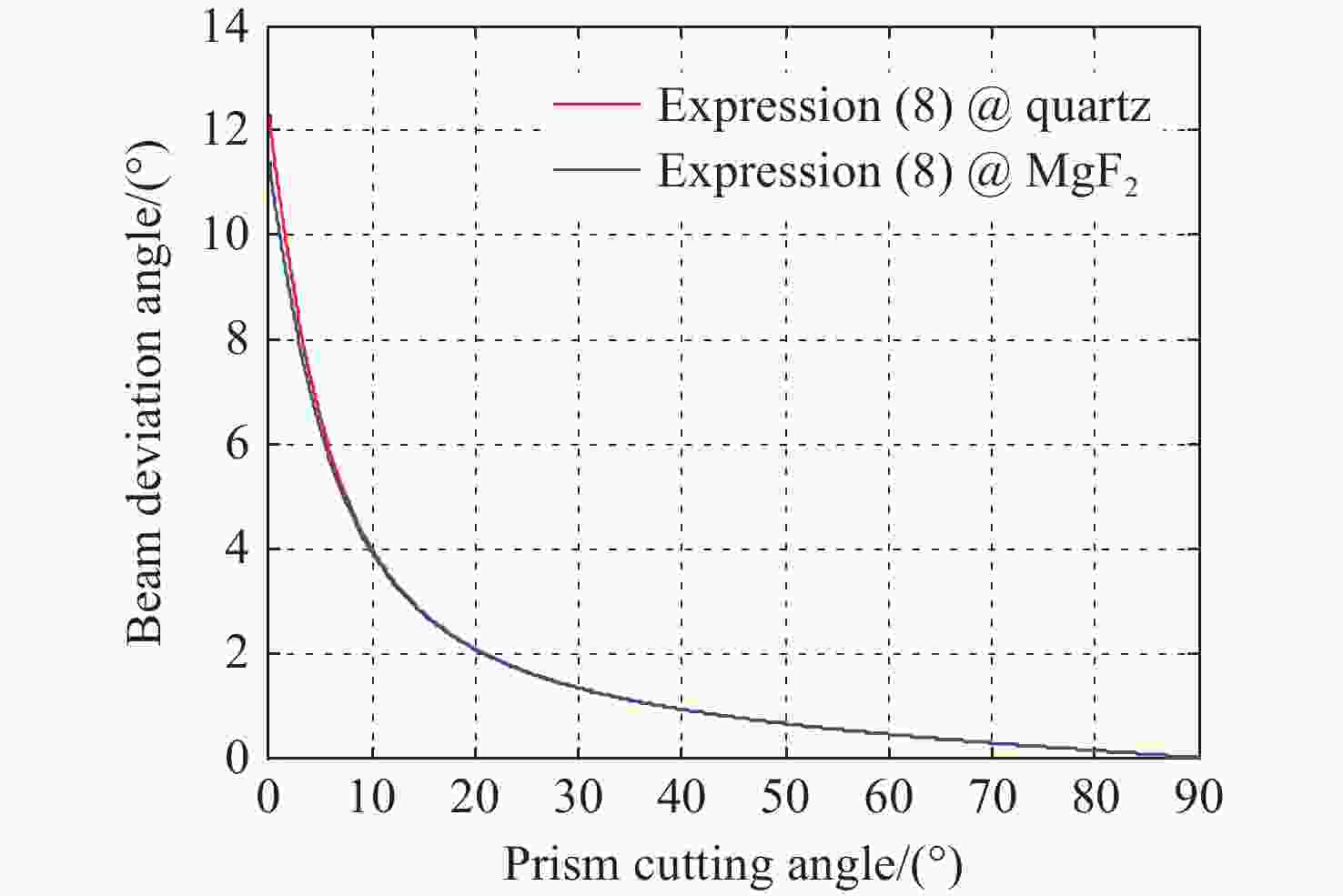
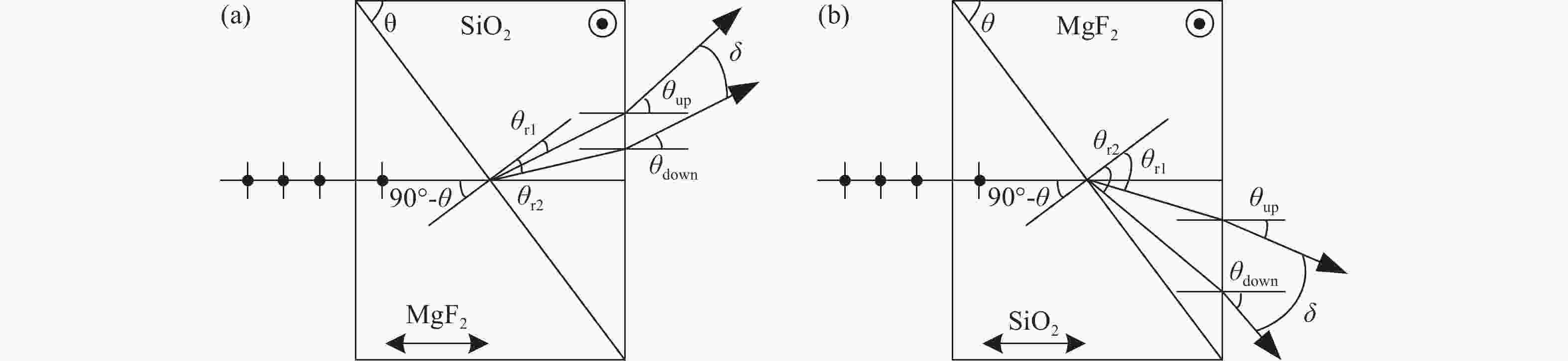
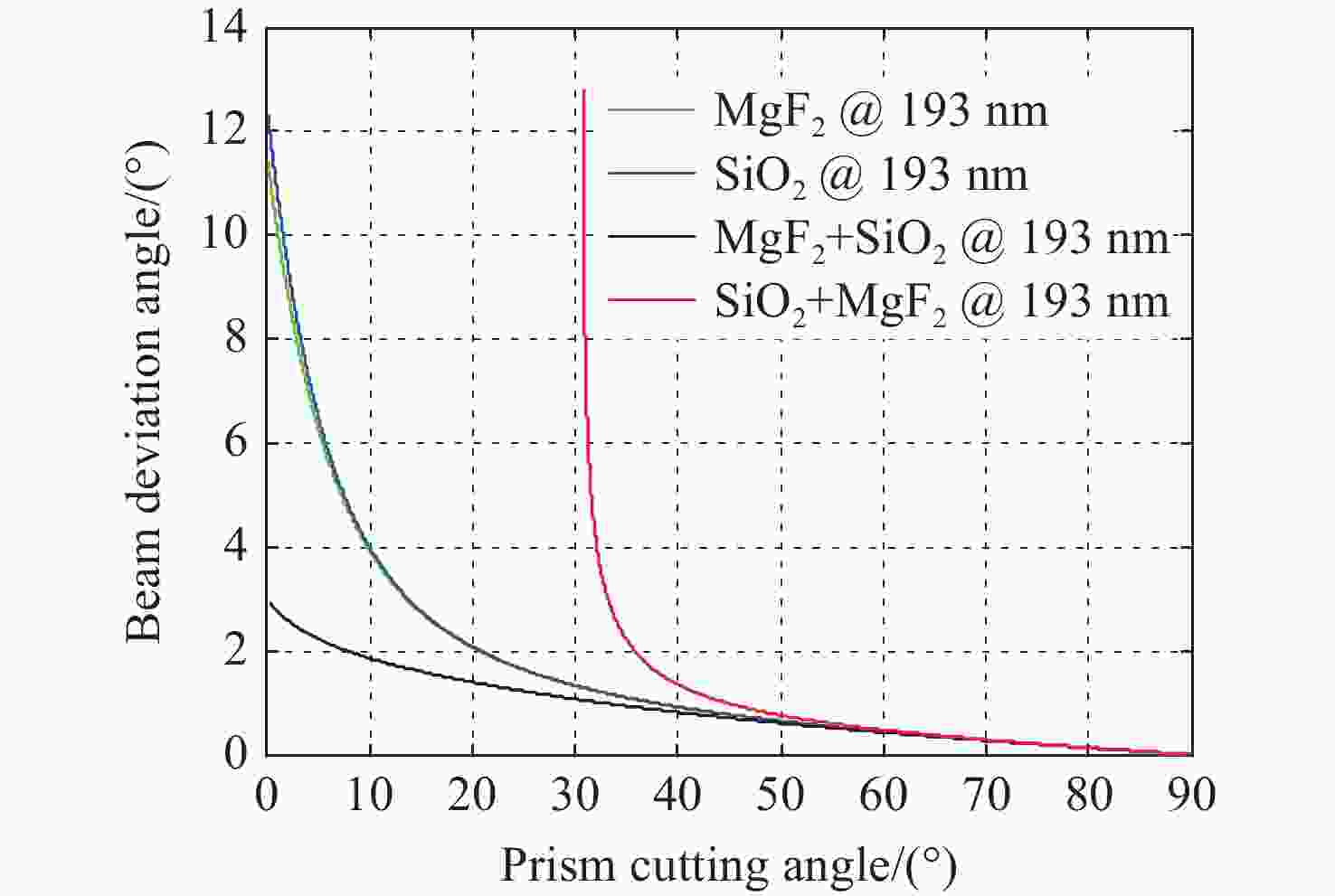
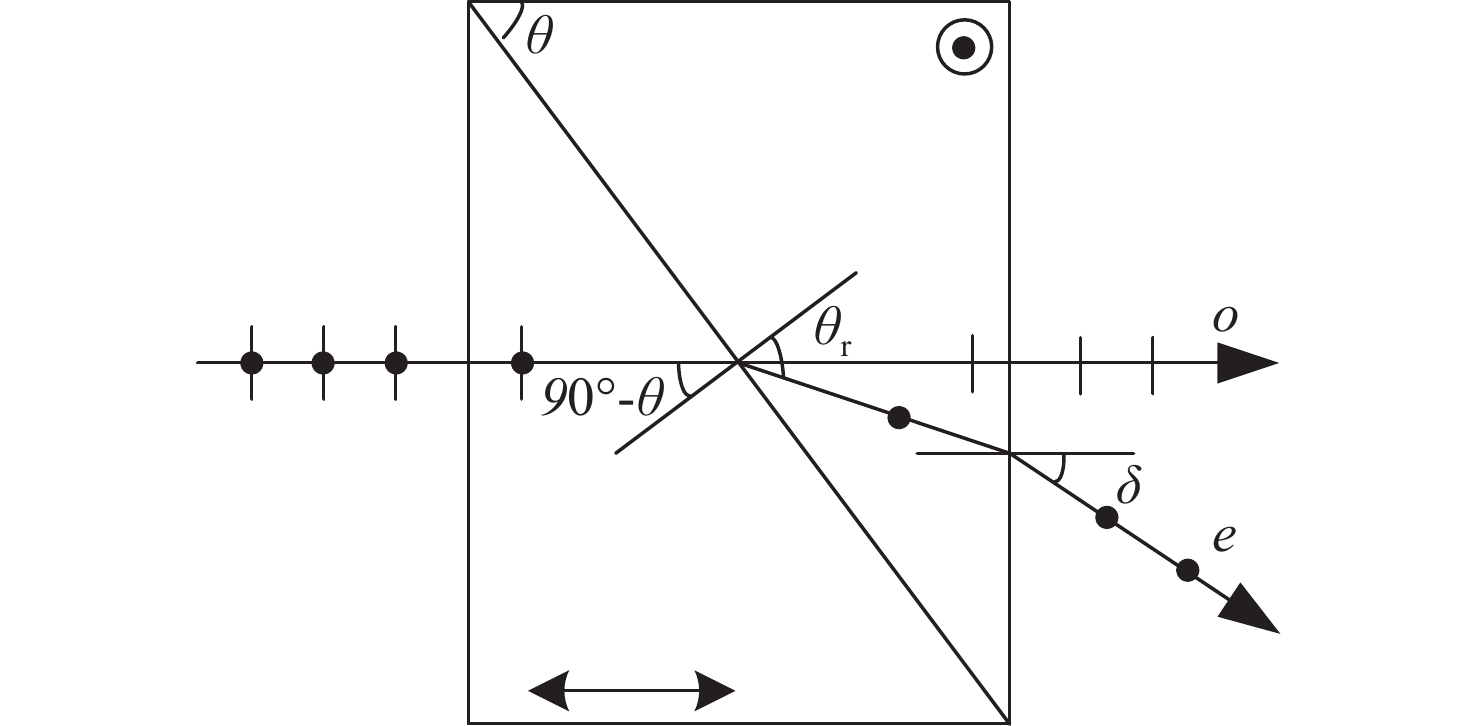
在科研项目研发过程中发现经典光学文献中的洛匈棱镜（Rochon Prism）的分束角公式（针对负晶体）是错误的，为此推导了准确的洛匈棱镜分束角表达式（分别针对负晶体、正晶体），并解决了科研项目中包含洛匈棱镜的光学系统设计错误问题。针对一般洛匈棱镜产品输出的2束光的夹角较小的问题，推导了分别由负晶体、正晶体构成的洛匈棱镜的分束角表达式。另外，对由异种晶体材料构成的洛匈棱镜的分束角进行了分析并推导出表达式。通过用实际数据计算和比较知道，由异种晶体材料构成洛匈棱镜的分束角比由同种晶体材料构成洛匈棱镜的分束角有很大的提高。对于在紫外波段的应用，具体给出一种由异种晶体材料构成洛匈棱镜的较大分束角的设计实例。这种由异种晶体材料构成洛匈棱镜，按照合适的晶体排列顺序，可以在合理的晶体厚度的限制下获得相对较大的分束角度，这显然是有利于偏振仪器设备的结构设计。
- 洛匈棱镜 /
- 石英晶体 /
- 氟化镁晶体 /
- o光 /
- e光
Abstract:
During the research and development process of the scientific research project, it was found that the beam deviation angle formula of a Rochon Prism in classical optical literatures (for negative crystals) was incorrect. Therefore, an accurate expression for the beam deviation angle of a Rochon Prism was derived (distributed for negative and positive crystals), and the problem of design in the optical systems containing a Rochon Prism in the scientific research projects was solved. In response to the problem of small angles between the two output beams of light in general a Rochon Prism products, the expressions for the deviation angles of a Rochon Prism composed of negative and positive crystals, respectively, were analyzed and derived. In addition, the deviation angles of a Rochon Prism composed of different crystal materials were analyzed and the expression was derived. By calculating and comparing with actual data, it is known that the beam deviation angle of a Rochon Prism made of different crystal materials is significantly higher than that of a Rochon Prism made of the same crystal material. For applications in the ultraviolet band, provide a specific design example of a large beam deviation angle for a Rochon Prism composed of heterogeneous crystal materials. This type of a Rochon Prism is composed of heterogeneous crystal materials, and according to the appropriate crystal arrangement order, a relatively large beam deviation angle can be obtained under the limitation of reasonable crystal thickness, which is obviously beneficial for the structural design of the polarization instruments and equipments.
- Rochon prism /
- quartz /
- MgF₂ crystal /
- o ray /
- e ray

HTML全文

图 1 由负单轴晶体构成的洛匈棱镜的原理

Figure 1. Principle of Rochon prism composed of negative uniaxial crystal

下载: 全尺寸图片幻灯片

图 2 文献[9]及文献[10-11]推导的切割角和分束角之间的关系

Figure 2. Relationship between cutting angle and beam deviation angle in Ref. [9] and Refs. [10-11]

下载: 全尺寸图片幻灯片

图 3 本文推导的切割角和分束角之间的关系@方解石晶体

Figure 3. Relationship between cutting angle and beam deviation angle in this paper

下载: 全尺寸图片幻灯片

图 4 切割角和分束角之间的关系（全部）

Figure 4. Relationship between cutting angle and beam deviation angle

下载: 全尺寸图片幻灯片

图 5 切割角和分束角之间的关系（局部）

Figure 5. Relationship between cutting angle and beam deviation angle

下载: 全尺寸图片幻灯片

图 6 由正单轴晶体构成的洛匈棱镜的原理

Figure 6. Principle of a Rochon prism composed of positive uniaxial crystals

下载: 全尺寸图片幻灯片

图 7 由式（8）得到的由正晶体构成的洛匈棱镜的切割角和分束角之间的关系（193 nm波长）

Figure 7. Relationship between cutting angle and beam deviation angle of a Rochon prism composed of positive crystals, derived from equation 8 at 193 nm wavelength

下载: 全尺寸图片幻灯片

图 8 两种正晶体构成的洛匈棱镜光路。(a)氟化镁+石英；(b)石英+氟化镁

Figure 8. Optical path of the Rochon prism made of two types of positive crystal: (a) magnesium fluoride and quartz; (b) Quartz and magnesium fluoride

下载: 全尺寸图片幻灯片

图 9 几种正晶体洛匈棱镜的分束角

Figure 9. Beam deviation angles of a Rochon prism composed of several types of positive uniaxial crystals

下载: 全尺寸图片幻灯片

图 10 由石英和氟化镁晶体构成的洛匈棱镜

Figure 10. A Rochon prism made of Quartz and magnesium fluoride crystals

下载: 全尺寸图片幻灯片

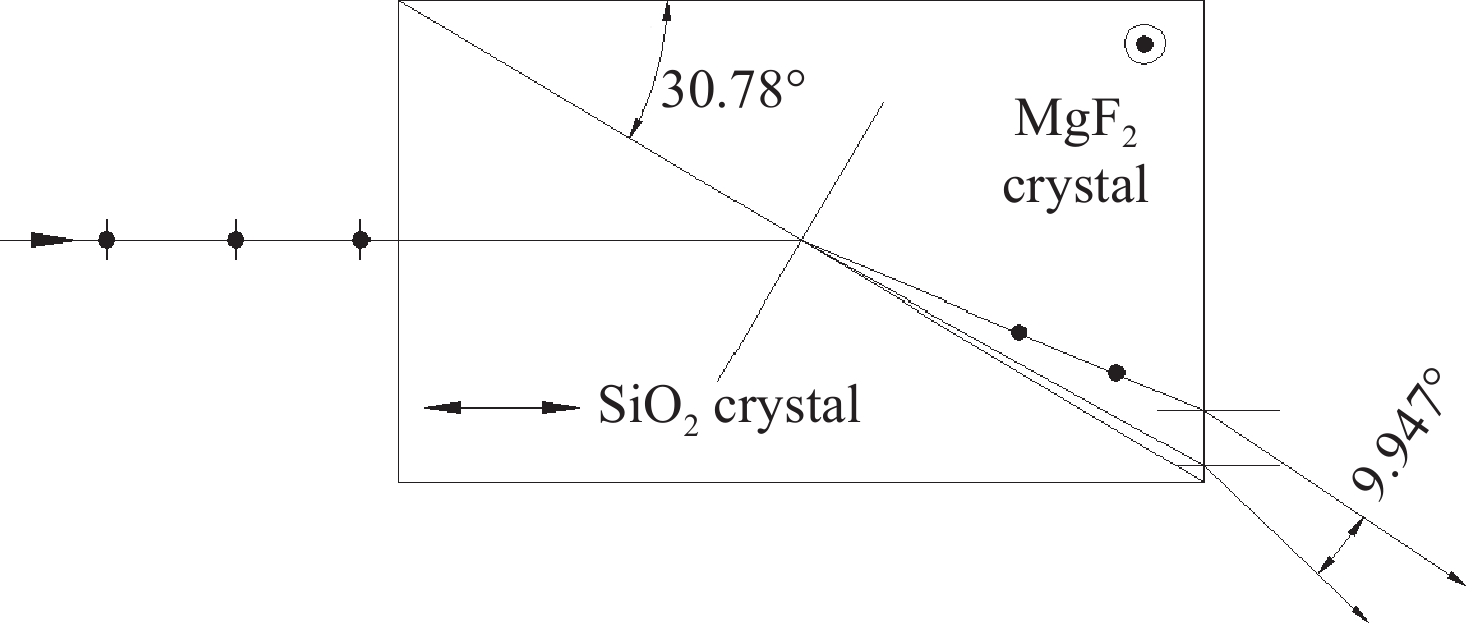
表 1 各种洛匈棱镜分束角的比较

Table 1. Comparison beam deviation angles of several kinds of a Rochon Prisms (RP)

Rochon prisms (RP)	Prism cutting angle/(°)	RP made of Quartz and MgF₂	RP made of MgF₂	RP made of Quartz	RP made of MgF₂ and Quartz
Beam deviation angle/(°)	30.78	9.9474	1.2914	1.2974	1.0550
	32	4.1185	1.2324	1.2380	1.0213
	37	1.7548	1.0257	1.0298	0.8925
	42	1.1850	0.8605	0.8637	0.7767
	47	0.8897	0.7237	0.7262	0.6717

下载: 导出CSV

参考文献(20)

[1]	朱化凤, 南玉杰, 云茂金, 等. 双沃拉斯顿棱镜光强分束比精确分析[J]. 光学学报, 2012, 32(6): 0623002. doi: 10.3788/AOS201232.0623002 ZHU H F, NAN Y J, YUN M J, et al. Precise analysis of the intensity splitting ratio of double wollaston prism[J]. Acta Optica Sinica, 2012, 32(6): 0623002. (in Chinese). doi: 10.3788/AOS201232.0623002
[2]	史萌, 吴福全. 双向分束角对称的偏光分束镜设计与性能分析[J]. 光子学报, 2006, 35(3): 439-442. SHI M, WU F Q. The principle design and performance analysis of two-way symmetric splitting angle beam splitting prism[J]. Acta Photonica Sinica, 2006, 35(3): 439-442. (in Chinese).
[3]	薛林, 吴福全, 蒋琳琳. Wollaston棱镜对发散光束的分束特性分析[J]. 激光技术, 2011, 35(6): 833-836. XUE L, WU F Q, JIANG L L. Effect of Wollaston prism on splitting properties of divergent beam[J]. Laser Technology, 2011, 35(6): 833-836. (in Chinese).
[4]	蔡燕民, 王向朝, 黄惠杰. 用于ArF光刻机偏振照明系统的沃拉斯顿棱镜的设计[J]. 中国激光, 2014, 41(6): 0616002. doi: 10.3788/CJL201441.0616002 CAI Y M, WANG X ZH, HUANG H J. Design of Wollaston prism used for polarization illumination system in ArF lithography tool[J]. Chinese Journal of Lasers, 2014, 41(6): 0616002. (in Chinese). doi: 10.3788/CJL201441.0616002
[5]	罗云瀚, 王芳, 葛菁华, 等. 基于洛匈棱镜的偏振度测量与空间退偏度分析方法研究[J]. 光子学报, 2014, 43(9): 0912002. doi: 10.3788/gzxb20144309.0912002 LUO Y H, WANG F, GE J H, et al. Simultaneous measurement of the degree of polarization and spatial analysis of depolarization based on a Rochon prism[J]. Acta Photonica Sinica, 2014, 43(9): 0912002. (in Chinese). doi: 10.3788/gzxb20144309.0912002
[6]	侯影, 石广立, 冯彤, 等. 洛匈棱镜分束角的光谱效应及入射角效应[J]. 曲阜师范大学学报(自然科学版), 2012, 38(2): 73-76. HOU Y, SHI G L, FENG T, et al. The spectral and the incident angle’s effections of the los Austro-Hungarian prism’s splitting angle[J]. Journal of Qufu Normal University (Natural Science), 2012, 38(2): 73-76. (in Chinese).
[7]	陈西园, 单明. 洛匈棱镜的正反向特性[J]. 光学技术, 2006, 32(2): 280-283. doi: 10.3321/j.issn:1002-1582.2006.02.017 CHEN X Y, SHAN M. Characteristics of the Rochan prism in forward-use and backward-use[J]. Optical Technique, 2006, 32(2): 280-283. (in Chinese). doi: 10.3321/j.issn:1002-1582.2006.02.017
[8]	吴许强. 利用惠更斯原理作图解释罗雄棱镜的工作原理[J]. 合肥师范学院学报, 2023, 41(3): 59-62. (查阅网上资料, 未找到对应的英文翻译, 请确认并补充).
[9]	STEINRNETZ D L, PHILLIPS W G, WIRICK M, et al. A polarizer for the vacuum ultraviolet[J]. Applied Optics, 1967, 6(6): 1001-1004. doi: 10.1364/AO.6.001001
[10]	廖延彪. 偏振光学[M]. 北京: 科学出版社, 2003: 206-207. LIAO Y B. Polarization Optics[M]. Beijing: Science Press, 2003: 206-207. (in Chinese).
[11]	李景镇. 光学手册[M]. 西安: 陕西科学技术出版社, 1986: 526-527. LI J ZH. Optical Handbook[M]. Xi'an: Shaanxi Science and Technology Press, 1986: 526-527. (in Chinese).
[12]	LV M B, WANG P. Ray tracing in Rochon prisms with absorption[J]. Optics Express, 2017, 25(13): 14676-14690. doi: 10.1364/OE.25.014676
[13]	WANG B, DONG F L, FENG H, et al. Rochon-prism-like planar circularly polarized beam splitters based on dielectric metasurfaces[J]. ACS Photonics, 2018, 5(5): 1660-1664. doi: 10.1021/acsphotonics.7b01191
[14]	WANG X, GAO Z, GAO C J, et al. Digital shearing speckle pattern interferometry based on Rochon prism and its application[J]. Applied Sciences, 2019, 9(12): 2554. doi: 10.3390/app9122554
[15]	KHALID A U R, ULLAH N, HAN Y, et al. Metasurface based spin-selective wollaston-and-Rochon-prism-like circularly polarized beam splitter[J]. Advanced Theory and Simulations, 2023, 6(1): 2200574. doi: 10.1002/adts.202200574
[16]	张郁文, 刘丙才, 王红军, 等. 同步相移横向剪切干涉中偏振器件的误差建模[J]. 中国光学(中英文), 2024, 17(3): 640-647. doi: 10.37188/CO.2023-0152 ZHANG Y W, LIU B C, WANG H J, et al. Error modeling of polarization devices in simultaneous phase-shifted lateral shearing interferometry[J]. Chinese Optics, 2024, 17(3): 640-647. (in Chinese). doi: 10.37188/CO.2023-0152
[17]	张智淼, 王承邈, 谢冕, 等. 基于超构透镜的微型头戴式荧光显微镜设计[J]. 中国光学(中英文), 2024, 17(3): 512-520. doi: 10.37188/CO.2023-0237 ZHANG ZH M, WANG CH M, XIE M, et al. Design of miniature head-mounted fluorescence microscope based on metalens[J]. Chinese Optics, 2024, 17(3): 512-520. (in Chinese). doi: 10.37188/CO.2023-0237
[18]	张旭, 李世杰, 刘丙才, 等. 凹非球面的非零位干涉检测技术[J]. 中国光学(中英文), 2024, 17(1): 140-149. doi: 10.37188/CO.2023-0042 ZHANG X, LI SH J, LIU B C, et al. A non-null interferometry for concave aspheric surface[J]. Chinese Optics, 2024, 17(1): 140-149. (in Chinese). doi: 10.37188/CO.2023-0042
[19]	王同盟, 高芬, 李兵. 基于空洞空间卷积网络的点衍射干涉图像相位解包技术[J]. 光学精密工程, 2024, 32(2): 208-220. doi: 10.37188/OPE.20243202.0208 WANG T M, GAO F, LI B. Phase unwrapping technology about point diffraction interference fringe based on atrous spatial convolutional networks[J]. Optics and Precision Engineering, 2024, 32(2): 208-220. (in Chinese). doi: 10.37188/OPE.20243202.0208
[20]	周志鹏, 楼盈天, 王升帆, 等. 基于卡尔曼滤波的激光外差干涉位移测量误差补偿[J]. 光学精密工程, 2024, 32(3): 357-365. doi: 10.37188/OPE.20243203.0357 ZHOU ZH P, LOU Y T, WANG SH F, et al. Error compensation for laser heterodyne interferometric displacement measurement based on Kalman filter[J]. Optics and Precision Engineering, 2024, 32(3): 357-365. (in Chinese). doi: 10.37188/OPE.20243203.0357