Monocular camera-based relative position and orientation estimation system for space targets
-
摘要:
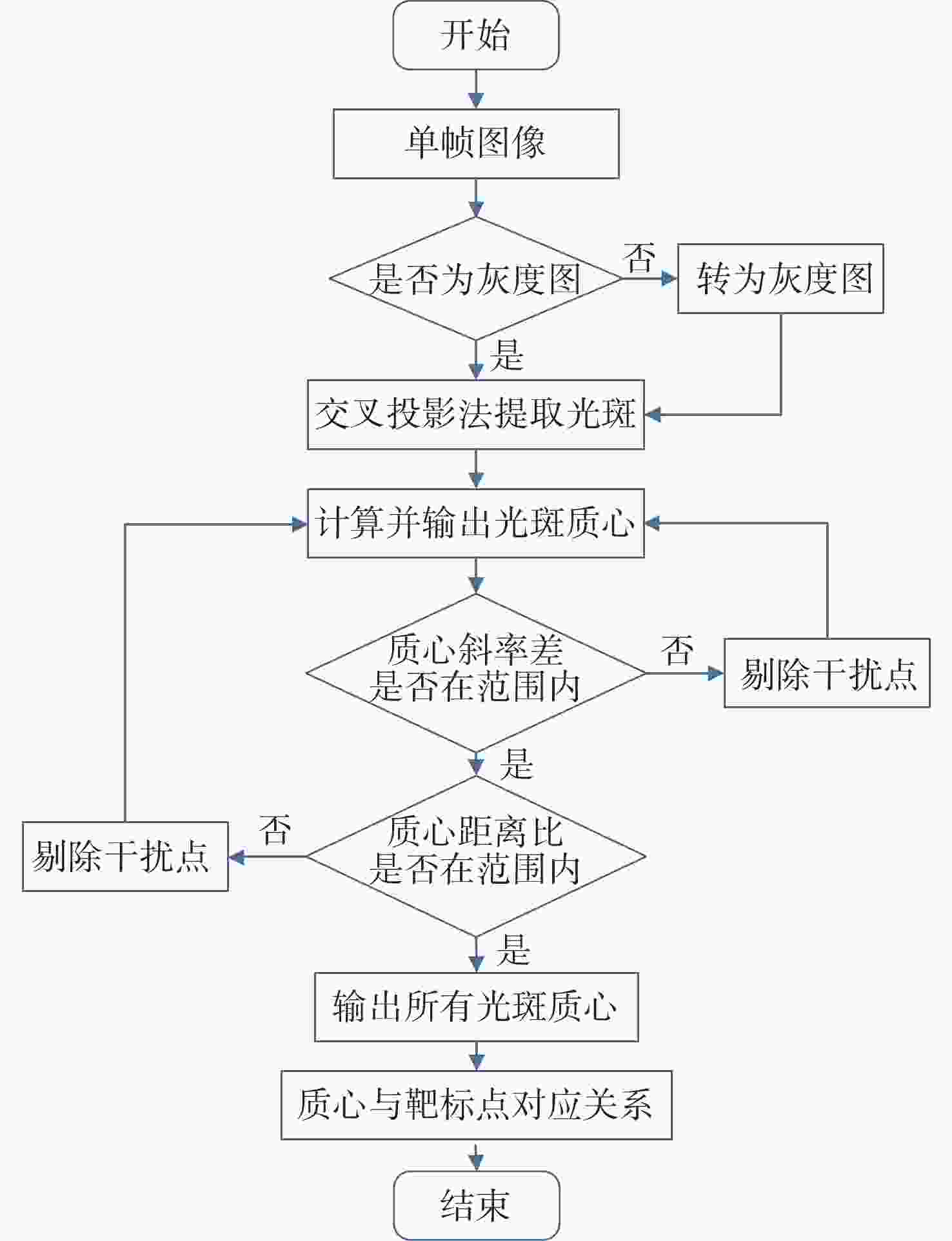
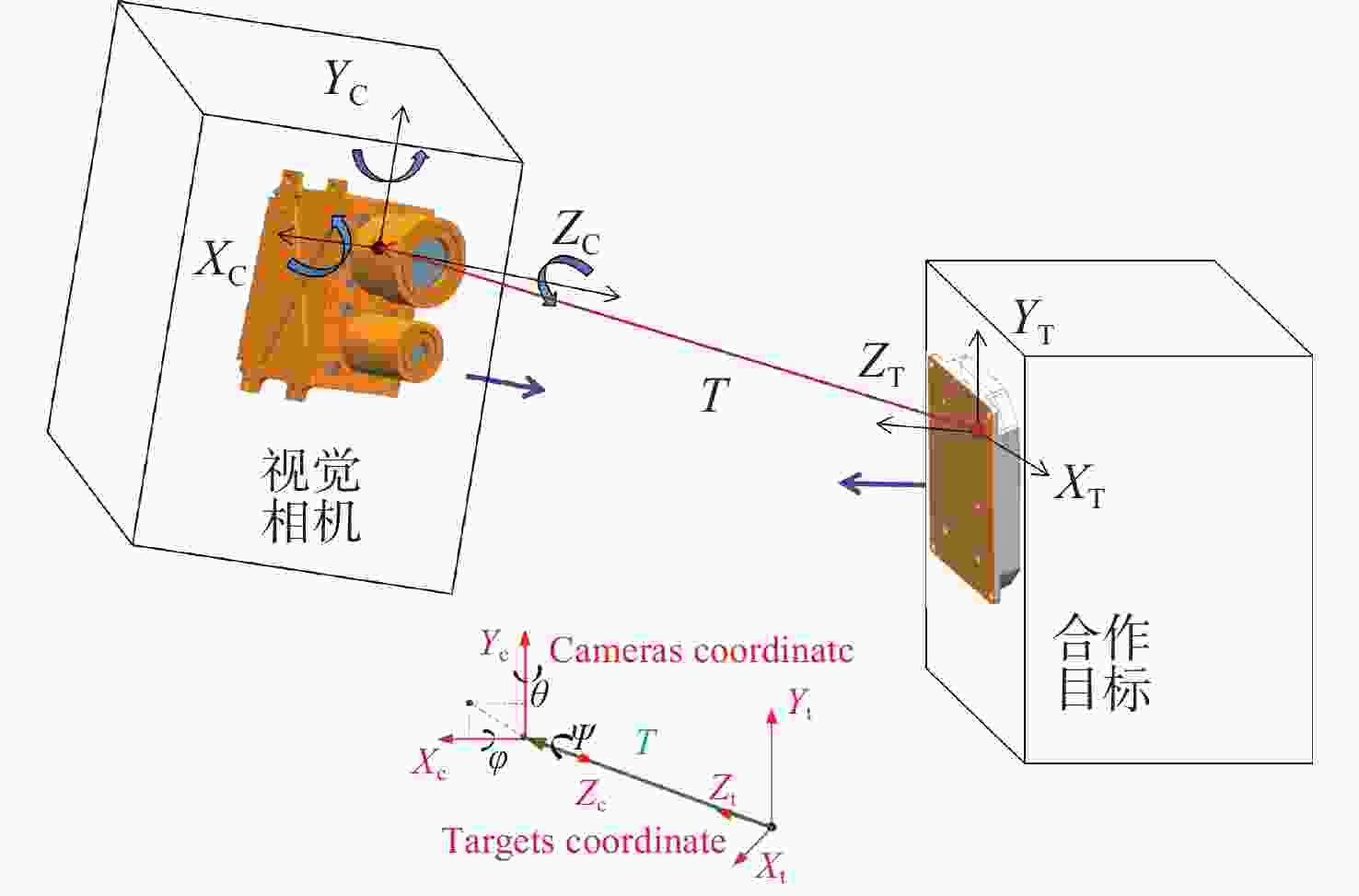
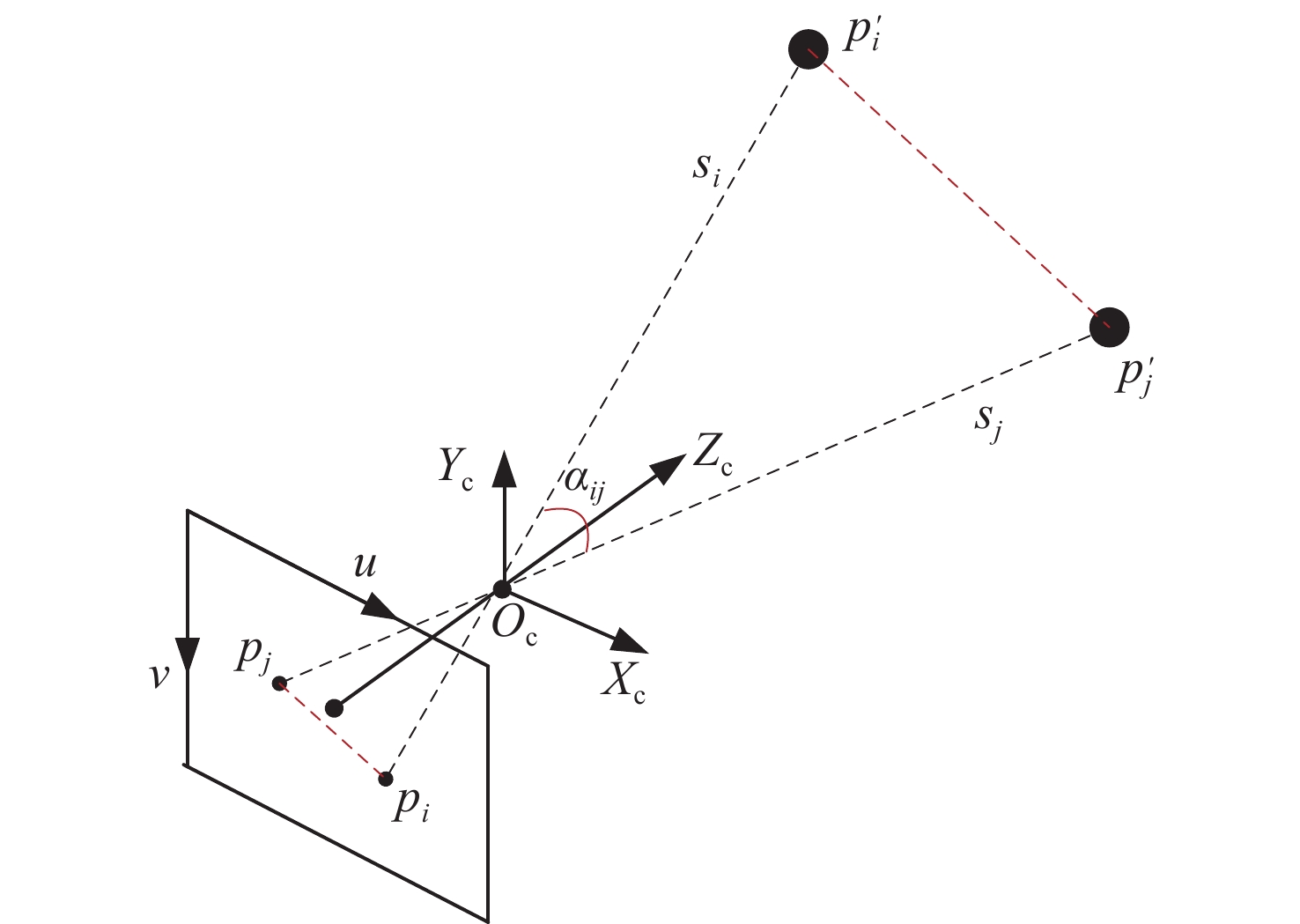
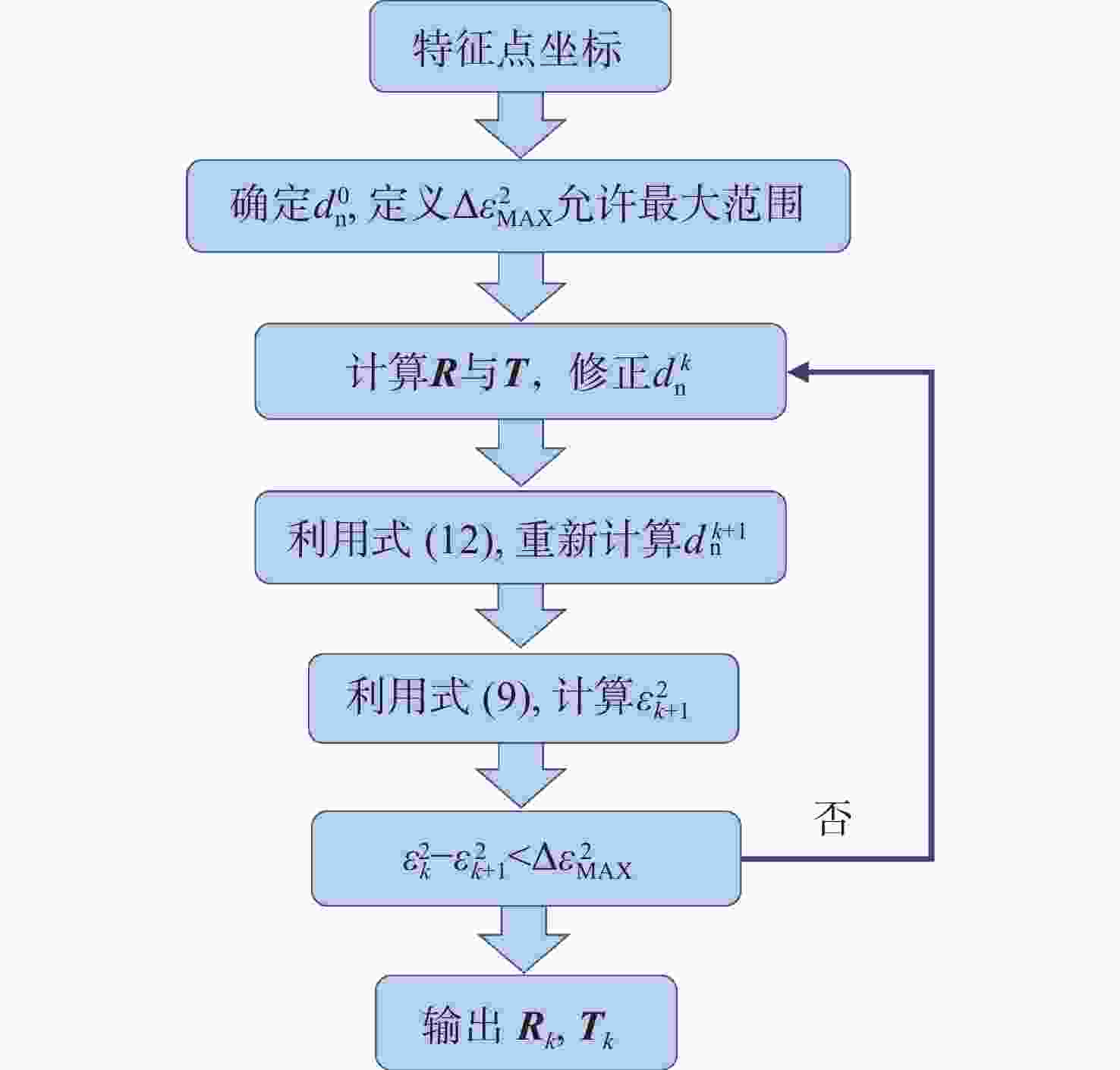
为提高测量系统的稳定性及精度，实现航天器超近距离高精度对接，本文提出了一种基于单相机及合作靶标的相对位姿测量系统，用于双星间相对位置及姿态的高精度测量。通过设计追踪星视觉相机及目标星LED合作靶标，在双星距离为50米到0.4米的范围内，实现了高精度的相对位姿测量。通过设计远近场LED靶标，实现了相机与靶标间的协同工作，保证在50米到0.4米的距离均能清晰成像；根据设计的靶标特性，提出了多尺度质心提取算法，利用斜率一致性约束与间距比筛选，在复杂光照下能稳定获取特征目标；最后，结合靶标几何约束的初值估计，实现了目标星相对于追踪星的位姿解算，为进一步提高测量精度，引入非线性优化方法对位姿结果进行迭代优化，有效降低了测量误差。试验结果表明，系统测量精度由远及近逐渐提高，在距离为0.4 m时，位置测量精度优于1 mm，姿态测量精度优于0.2°，满足超近距离对接任务需求。本方案为空间在轨目标相对位姿测量提供了高精度、高稳定性的技术支撑，具有重要的工程应用价值。
Abstract:To enhance the stability and accuracy of estimation systems for ultra-close high-precision docking of spacecrafts, this article proposes a system for high-precision estimation of relative position and orientation between two satellites. Through vision cameras on the chaser satellite and co-designed LED targets on the target satellite, precise relative pose measurement is achieved within 0.4−50 meters. To ensure clear imaging within the effective range, both far-field and near-field LED targets were designed. A multi-scale centroid extraction algorithm was proposed based on target characteristics, while slope consistency constraints and spacing ratio screening were employed to guarantee target feature acquisition under complex illumination conditions. Pose estimation utilizes target geometric constraints as initial values, employing iterative nonlinear optimization to refine results and effectively reduce measurement errors. Test results demonstrate progressively improving measurement accuracy from far to near distances. At 0.4 meters, position estimation achieves sub-millimeter precision while orientation estimation maintains sub-degree accuracy, meeting ultra-close-range docking requirements. This solution provides high-precision, high-stability technical support for relative position and orientation estimation between on-orbit space targets, demonstrating significant engineering application value.
-
图 12 光学成像组件与靶标组件装星图
Figure 12. Flight integration diagram of optical imaging assembly and cooperative target assembly
图 14 双星距离50 m时的相对位置与姿态数据分布图
Figure 14. Relative position and orientation distribution map at 50 meters between two satellites
图 15 双星距离20 m时的相对位置与姿态数据分布图
Figure 15. Relative position and orientation distribution map at 20 m between two satellites
图 16 双星距离5.6 m时的相对位置与姿态数据分布图
Figure 16. Relative position and orientation distribution map at 5.6 m between two satellites
图 17 双星距离1.7 m时的相对位置与姿态数据分布图
Figure 17. Relative position and orientation distribution map at 1.7 m between two satellites
图 18 双星距离0.4 m时的相对位置与姿态数据分布图
Figure 18. Relative position and orientation distribution map at 0.4 m between two satellites
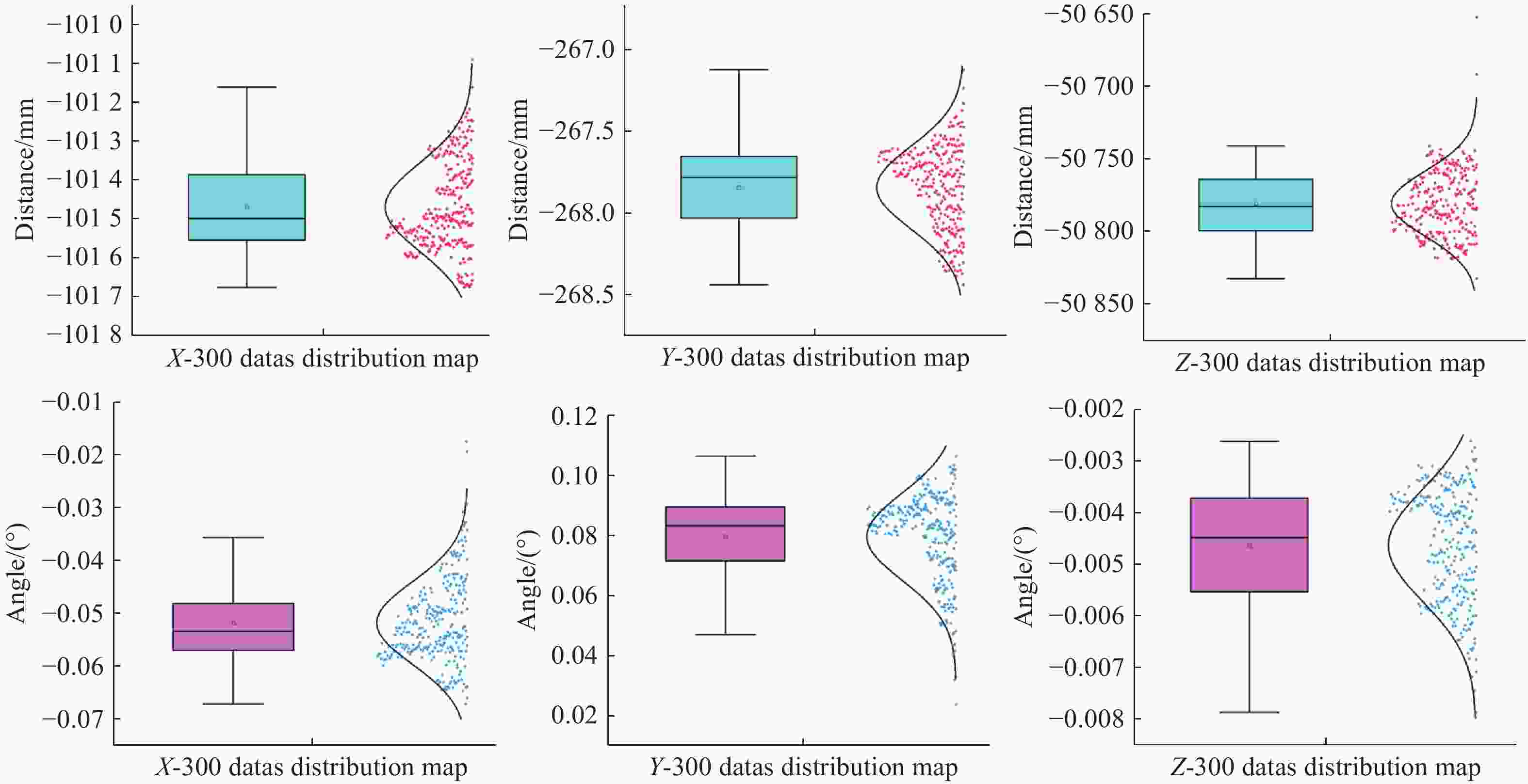
表 1 双星距离50 m时的相对位置与姿态测量结果
Table 1. Relative position and orientation estimation results at a distance of 50 m between two satellites
Parameters Std Mean-value Max-value Min-value Tx/mm 1.2015 − 1013.5044 − 1010.9075 − 1016.7402 Ty/mm 3.9683 − 276.5156 − 267.5542 − 285.0395 Tz/mm 52.8736 − 50780.0293 − 50652.7305 − 50832.2031 $\varphi $/(°) 0.081 − 0.05188 − 0.0176 − 0.0672 $\theta $/(°) 0.0154 0.07840 0.1064 0.0238 $\psi $/(°) 0.0010 − 0.0046 − 0.0027 − 0.0079 
下载: 导出CSV
表 2 双星距离20 m时的相对位置与姿态测量结果
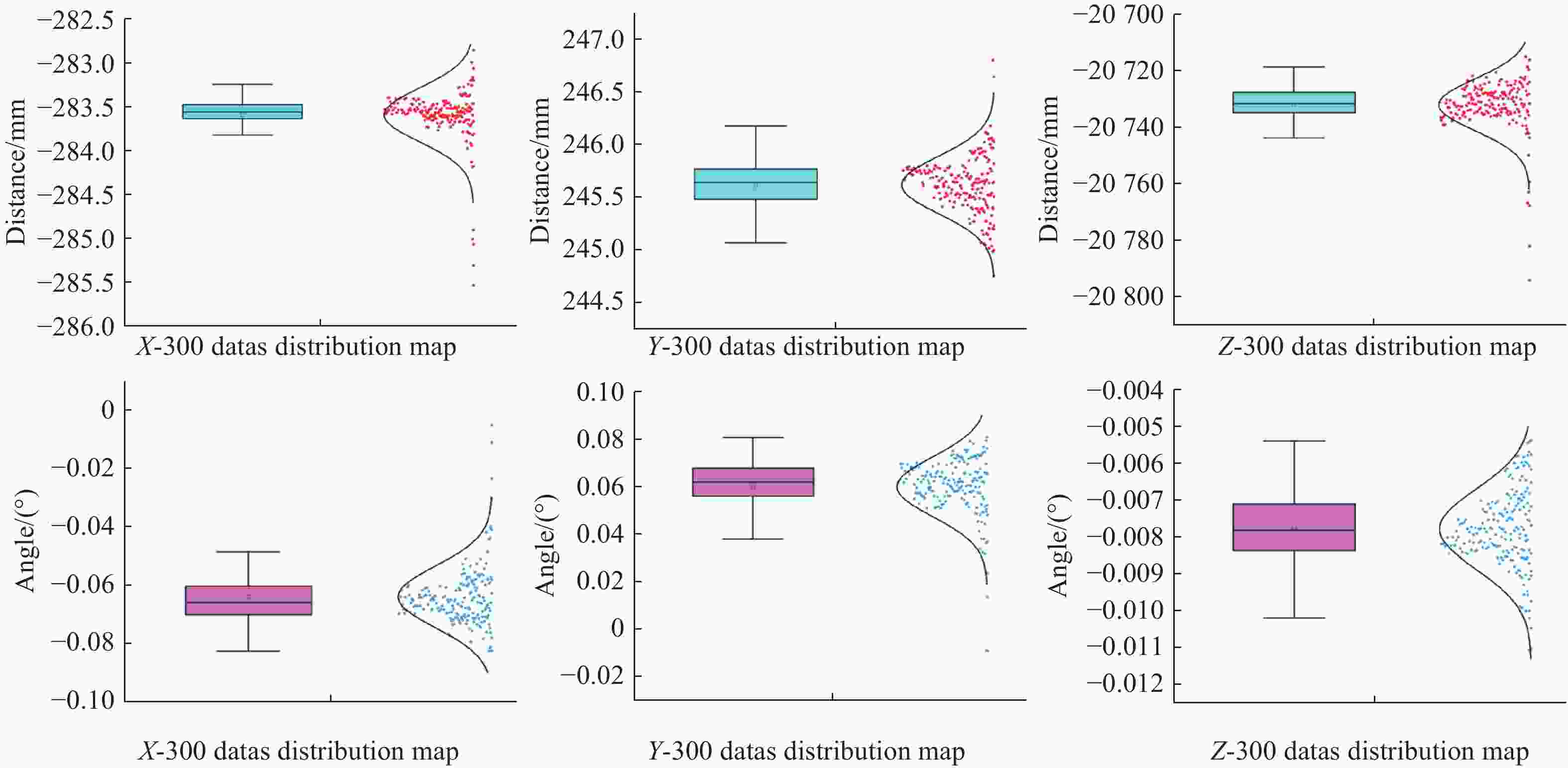
Table 2. Relative position and orientation estimation at a distance of 20 m between two satellites
Parameters Std Mean-value Max-vaule Min-vaule Tx/mm 0.3180 − 283.5990 − 283.2110 − 285.5420 Ty/mm 0.2050 245.5650 246.7930 244.7530 Tz/mm 4.3640 − 20730.6000 − 20715.2000 − 20742.5000 $\varphi $/(°) 0.0107 − 0.0645 − 0.0052 − 0.0827 $\theta $/(°) 0.0108 0.0595 0.0807 − 0.0091 $\psi $/(°) 0.0011 − 0.0079 − 0.0054 − 0.0111
下载: 导出CSV
表 3 双星距离5.6 m时的相对位置与姿态测量结果
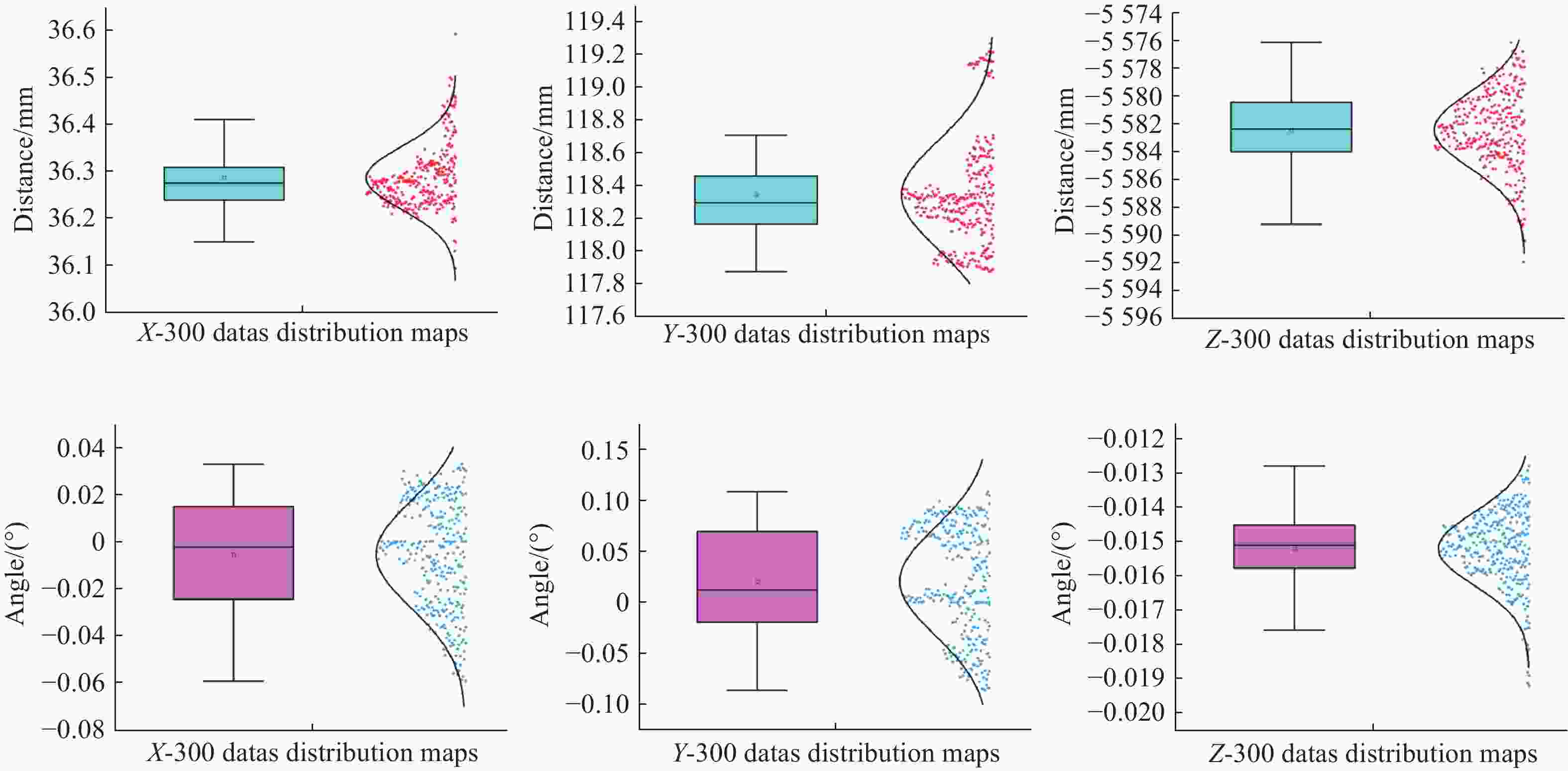
Table 3. Relative position and orientation estimation at a distance of 5.6 m between two satellites
Parameters Std Mean-value Max-v Min-v Tx/mm 0.1450 36.2800 36.5910 36.0940 Ty/mm 0.9140 118.6200 119.2630 117.8860 Tz/mm 1.6290 − 5583.1500 − 5576.1830 − 5591.8940 $\varphi $/(°) 0.0230 − 0.0080 0.0716 − 0.0676 $\theta $/(°) 0.0250 − 0.0020 0.1047 − 0.0843 $\psi $/(°) 0.0011 − 0.0149 − 0.0128 − 0.0192
下载: 导出CSV
表 4 双星距离1.7 m时的相对位置与姿态测量结果
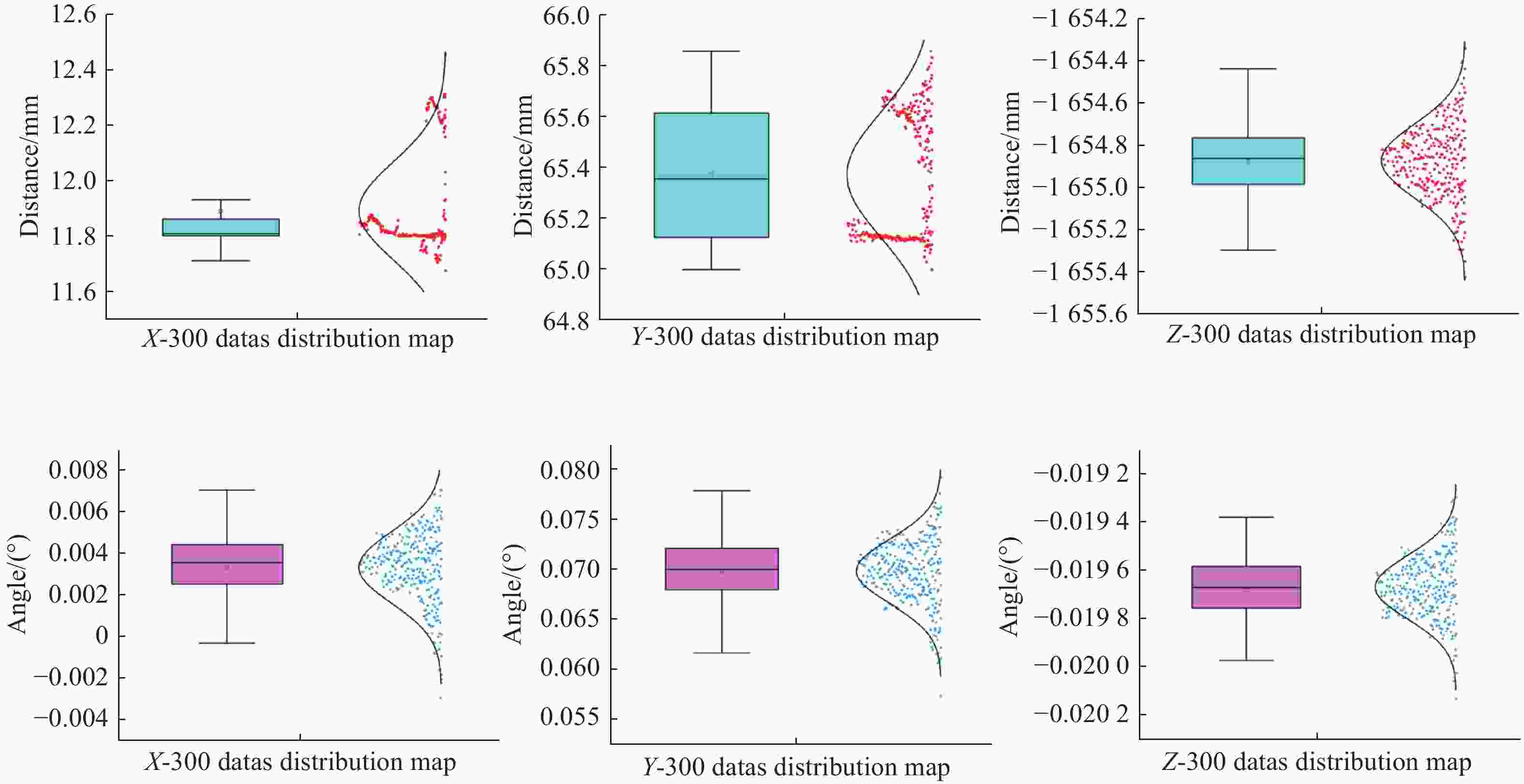
Table 4. Relative position and orientation estimation at a distance of 1.7 m between two satellites
Parameters Std Mean-value Max-v Min-v Tx/mm 0.2270 11.8730 12.4530 11.6760 Ty/mm 0.2810 65.3370 65.7950 64.9990 Tz/mm 0.1870 − 1654.8800 − 1654.3430 − 1655.4240 $\varphi $/(°) 0.0020 − 0.0032 0.0078 − 0.0029 $\theta $/(°) 0.0036 − 0.0691 − 0.0792 − 0.0574 $\psi $/(°) 0.0002 − 0.0197 − 0.0192 − 0.0201
下载: 导出CSV
表 5 双星距离0.4 m时的相对位置与姿态测量结果
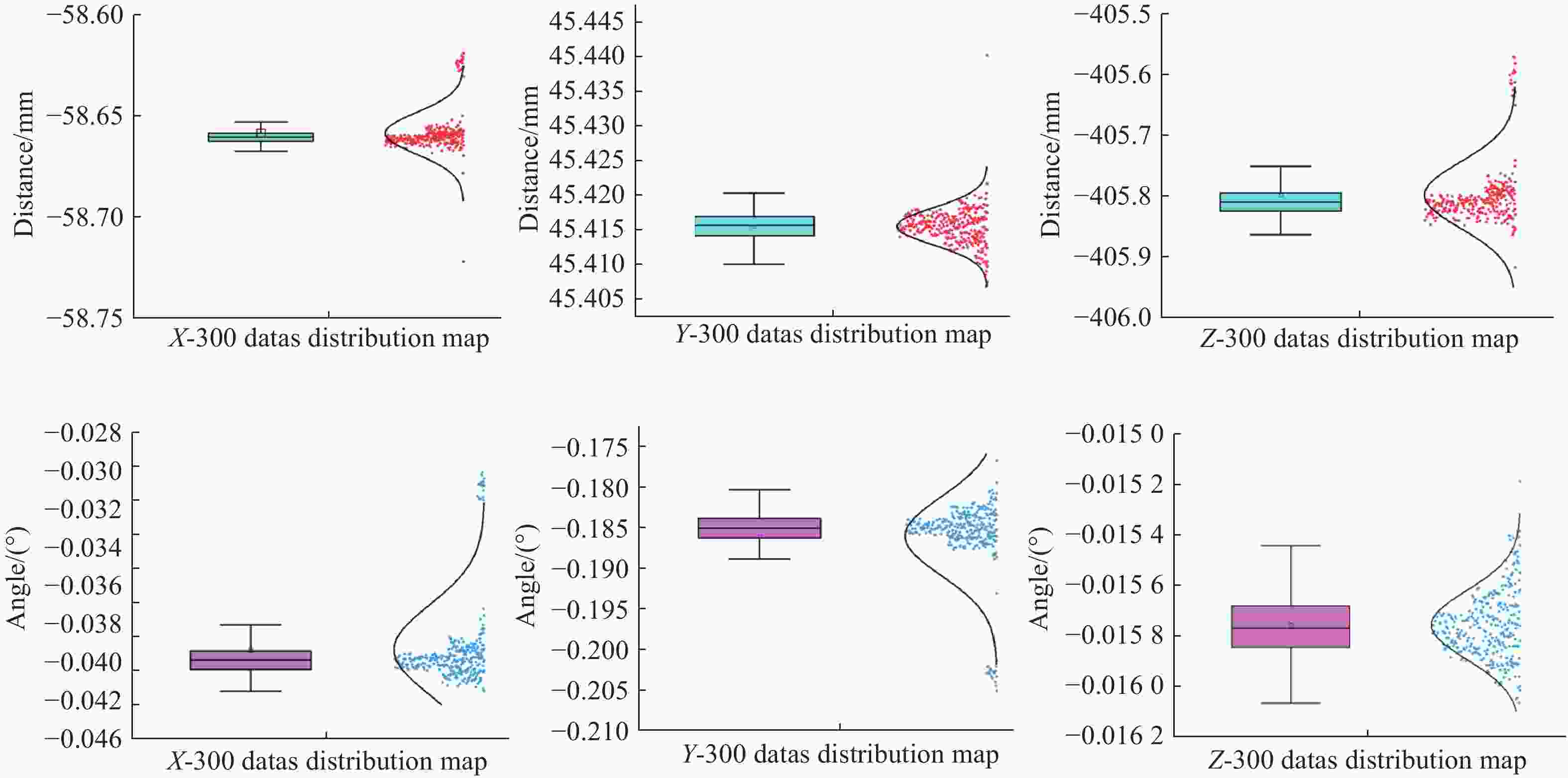
Table 5. Relative position and orientation estimation at a distance of 0.4 m between two satellites
Parameters Std Mean-value Max-v Min-v Tx/mm 0.08 −58.63 − 58.3670 −58.72 Ty/mm 0.003 45.41 45.478 45.40 Tz/mm 0.10 −405.79 −402.922 −405.89 $\varphi $/(°) 0.003 −0.041 0.0009 −0.043 $\theta $/(°) 0.006 −0.184 −0.046 −0.07 $\psi $/(°) 0.0003 − 0.0157 −0.007 − 0.0161
下载: 导出CSV
-
[1] ZHANG H F, WU J X, LIU D L, et al. Research on rocket engine pose measurement technology based on monocular vision[J]. Proceedings of SPIE, 2023, 12934: 129340I. [2] SEO C T, KANG S W, CHO M. Three-dimensional free view reconstruction in axially distributed image sensing[J]. Chinese Optics Letters, 2017, 15(8): 081102. doi: 10.3788/COL201715.081102 [3] HEATON A F, HOWARD R T, PINSON R M. Orbital express AVGS validation and calibration for automated rendezvous[C]. AIAA/AAS Astrodynamics Specialist Conference and Exhibit, AIAA, 2008. [4] KAWANO I, MOKUNO M, KASAI T, et al. Result of autonomous rendezvous docking experiment of engineering test Satellite-VII[J]. Journal of Spacecraft and Rockets, 2001, 38(1): 105-111. doi: 10.2514/2.3661 [5] YAN K, XIONG ZH, LAO D B, et al. Attitude measurement method based on 2DPSD and monocular vision[J]. Proceedings of SPIE, 2019, 11338: 113382L. [6] MAO J F, HUANG W, SHENG W G. Target distance measurement method using monocular vision[J]. IET Image Processing, 2020, 14(13): 3181-3187. doi: 10.1049/iet-ipr.2019.1293 [7] 屈也频, 刘坚强, 侯旺. 单目视觉高精度测量中的合作目标图形设计[J]. 光学学报, 2020, 40(13): 1315001. doi: 10.3788/AOS202040.1315001QU Y P, LIU J Q, HOU W. Graphics design of cooperative targets on monocular vision high precision measurement[J]. Acta Optica Sinica, 2020, 40(13): 1315001. (in Chinese). doi: 10.3788/AOS202040.1315001 [8] 董永英, 张高鹏, 常三三, 等. 一种基于单目视觉的空间目标位姿测量算法及其精度定量分析[J]. 光子学报, 2021, 50(11): 1112003. doi: 10.3788/gzxb20215011.1112003DONG Y Y, ZHANG G P, CHANG S S, et al. A pose measurement algorithm of space target based on monocular vision and accuracy analysis[J]. Acta Photonica Sinica, 2021, 50(11): 1112003. (in Chinese). doi: 10.3788/gzxb20215011.1112003 [9] RONDAO D, HE L, AOUF N. AI-based monocular pose estimation for autonomous space refuelling[J]. Acta Astronautica, 2024, 220: 126-140. doi: 10.1016/j.actaastro.2024.04.003 [10] 高豆豆, 董登峰, 邱启帆, 等. 面向激光跟踪测量的大范围高精度姿态测量[J]. 光学精密工程, 2024, 32(07): 976-986.GAO Doudou, DONG Dengfeng, QIU Qifan, et al. Large range automatic attitude measurement method for laser tracking measurement[J]. Optics and Precision Engineering, 2024, 32(07): 976-986. [11] SANSONE F, FRANCESCONI A, OLIVIERI L, et al. Low-cost relative navigation sensors for miniature spacecraft and drones[C]. 2015 IEEE Metrology for Aerospace (MetroAeroSpace), IEEE, 2015: 389-394. [12] PIRAT C, ANKERSEN F, WALKER R, et al. Vision based navigation for autonomous cooperative docking of CubeSats[J]. Acta Astronautica, 2018, 146: 418-434. doi: 10.1016/j.actaastro.2018.01.059 [13] BUI M T, DOSKOCIL R, KRIVANEK V. Distance and angle measurement using monocular vision[C]. 2018 18th International Conference on Mechatronics, IEEE, 2018: 1-6. [14] 路荣, 张高鹏, 曹剑中, 等. 基于单目视觉的火箭回收高度测量技术研究[J]. 光学精密工程, 2024, 32(14): 2166-2188.LU Rong, ZHANG Gaopeng, CAO Jianzhong, et al. Research on measurement technology of rocket recovery height based on monocular vision[J]. Optics and Precision Engineering, 2024, 32(14): 2166-2188. [15] 宋力夺, 姚凯男, 徐志强等. 全天时中高轨目标探测系统恒星移除[J]. 光学精密工程, 2024, 32(23): 3436-3445.SONG Liduo, YAO Kainan, XU Zhiqiang, et al. Stars removal of all day time mid-high orbit target detection system[J]. Optics and Precision Engineering, 2024, 32(23): 3436-3445. [16] 陈天择, 葛宝臻, 罗其俊. 重投影优化的自由双目相机位姿估计方法[J]. 中国光学, 2021, 14(6): 1400-1409. doi: 10.37188/CO.2021-0105CHEN T Z, GE B ZH, LUO Q J. Pose estimation for free binocular cameras based on reprojection error optimization[J]. Chinese Optics, 2021, 14(6): 1400-1409. (in Chinese). doi: 10.37188/CO.2021-0105 [17] CAPUANO V, KIM K, HARVARD A, et al. Monocular-based pose determination of uncooperative space objects[J]. Acta Astronautica, 2020, 166: 493-506. doi: 10.1016/j.actaastro.2019.09.027 [18] ZHANG ZH, BIN W, KANG J H, et al. Dynamic pose estimation of uncooperative space targets based on monocular vision[J]. Applied Optics, 2020, 59(26): 7876-7882. doi: 10.1364/AO.395081 [19] PIAZZA M, MAESTRINI M, DI LIZIA P. Monocular relative pose estimation pipeline for uncooperative resident space objects[J]. Journal of Aerospace Information Systems, 2022, 19(9): 613-632. doi: 10.2514/1.I011064 -
下载:
计量
- 文章访问数: 107
- HTML全文浏览量: 45
- PDF下载量: 12
- 被引次数: 0
