Spatial correlation singularities and orbital angular momentum spectra of partially coherent beams with noncanonical vortex pairs
doi: 10.37188/CO.EN-2025-0001
-
摘要:
将非正则涡旋对引入部分相干光领域，利用Fraunhofer衍射积分公式研究了该光束在远场的空间相关奇点（SCS）和轨道角动量（OAM），详细探讨了非正则因子、离轴距离和涡旋符号对空间相关奇点的影响，研究了远场OAM谱、密度、检测与串扰几率。结果表明：不论是正则还是非正则涡旋对，SCS的位错数量总是等于拓扑荷的绝对值之和。尽管OAM模式与其功率权重的乘积之和等于拓扑荷的代数和，但是该关系对于非正则情况却不再成立。离轴距离、非正则因子或相干长度的变化会导致毗邻模相比于探测模具有更大功率，这也意味着串扰几率会大于中心探测几率。本文结果对基于OAM的光通信、光成像、光传感、光计算具有潜在的应用价值。
Abstract:By introducing noncanonical vortex pairs to partially coherent beams, spatial correlation singularity (SCS) and orbital angular momenta (OAM) of the resulting beams are studied using the Fraunhofer diffraction integral, where the effect of noncanonical strength, off-axis distance and vortex sign on spatial correlation singularities in far field is stressed. Furthermore, far-field OAM spectra and densities are also investigated, where the OAM detection and crosstalk probabilities are discussed. The results show that the number of dislocations of SCS always equals the sum of absolute values of topological charges for canonical or noncanonical vortex pairs. Although the sum of the product of each OAM mode and its power weight equals the algebraic sum of topological charges for canonical vortex pairs, the relationship no longer holds in the noncanonical case except for opposite-charge vortex pairs. The change of off-axis distance, noncanonical strength or coherence length can lead to a more dominant power of adjacent mode than the center detection mode, which also indicates that crosstalk probabilities of adjacent modes exceed the center detection probability. This work may provide potential applications in OAM-based optical communication, imaging, sensing and computing.
-
Figure 1. Far-field spatial correlation singularities (a)-(c) partially coherent beams with canonical vortex pairs and their corresponding theoretical interferograms (d)-(f) at z=50z0, σ=w0, Q=1. (a), (d): d=0, l1=l2=+1; (b), (e): d=0, l1=+1, l2=+2; (c), (f): d=0.7w0, l1=l2=+1.
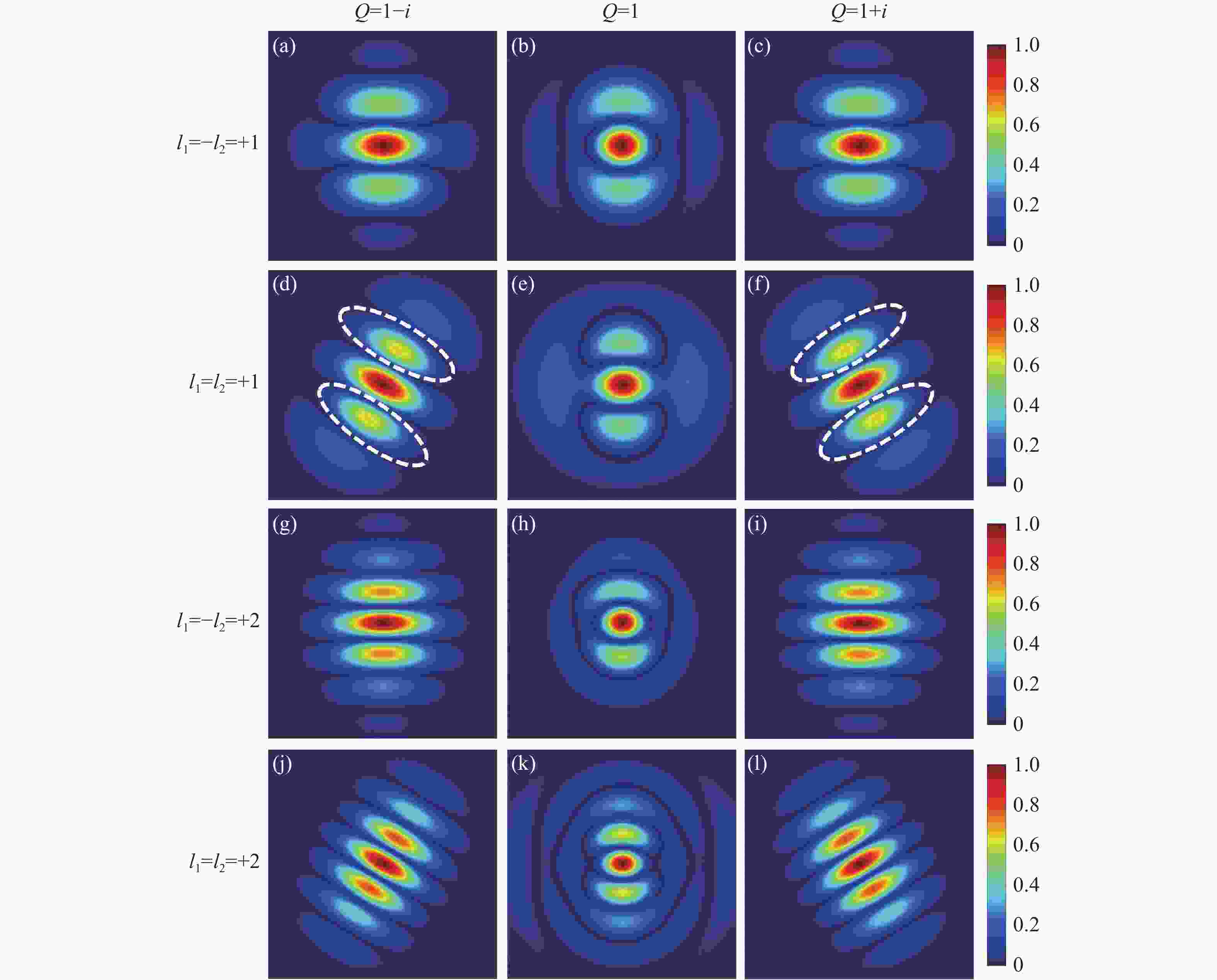
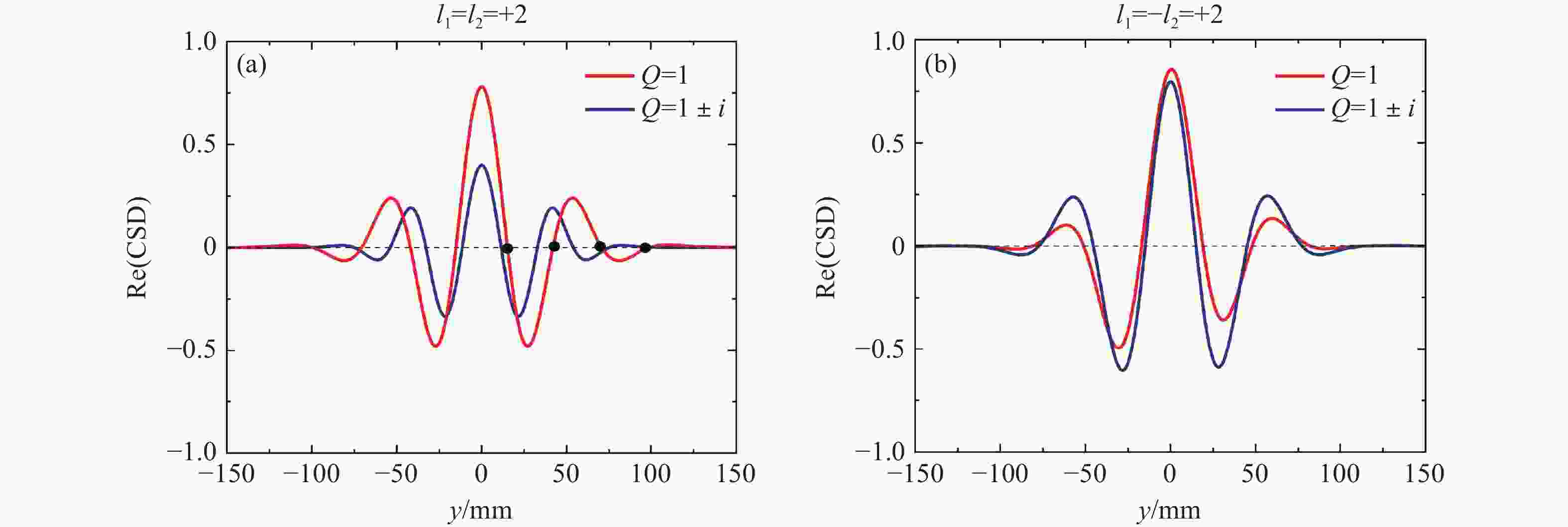
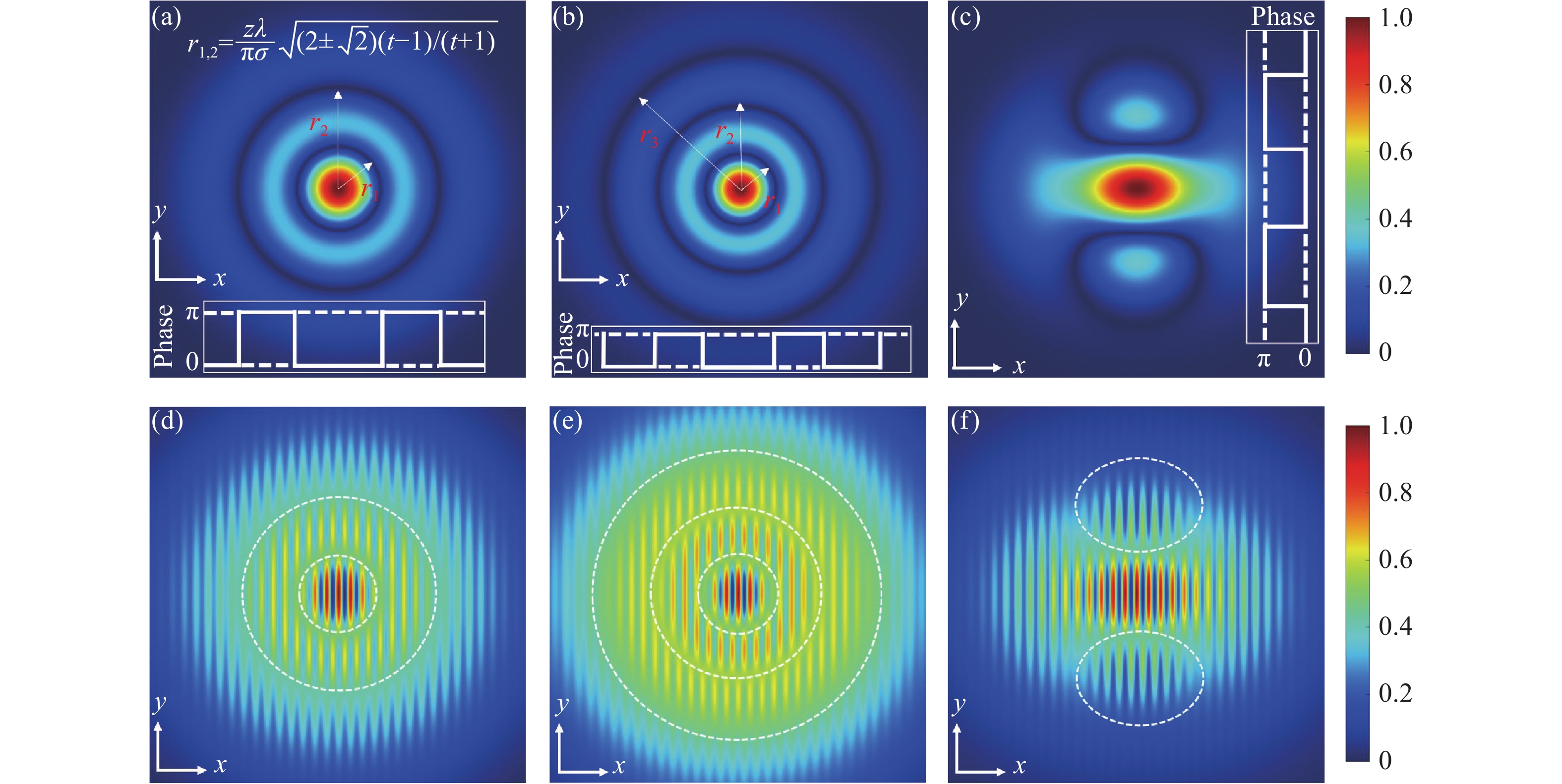
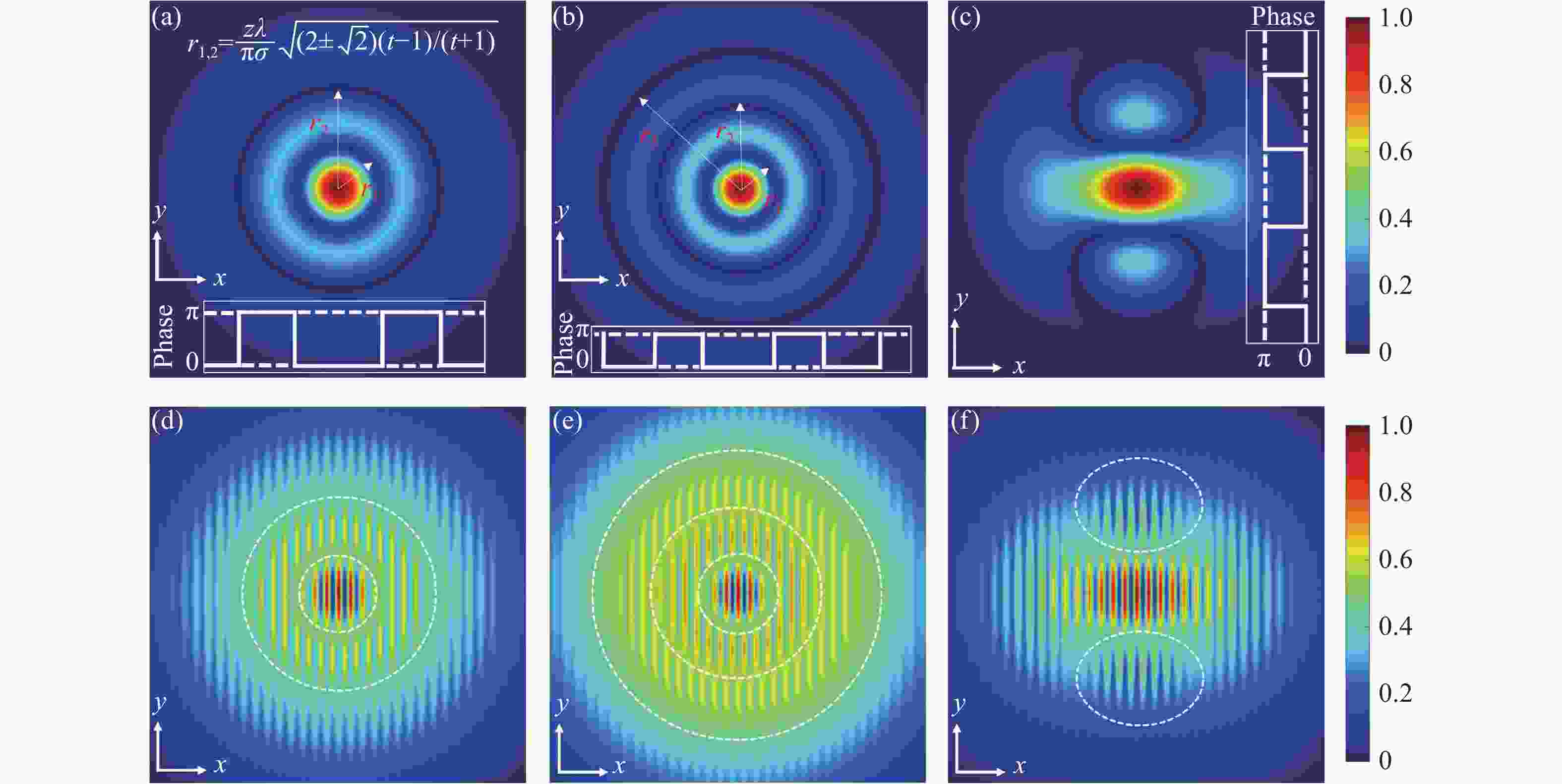
Figure 2. Far-field spatial correlation singularities of partially coherent beams with off-axis noncanonical vortex pairs for same-charge and opposite-charge vortices at z=50z0, σ=1 and d=0.5w0, where the canonical cases are also compared. (a)-(c): l1=−l2=+1; (d)-(f): l1=l2=+1; (g)-(i): l1=−l2=+2; (j)-(l): l1=l2=+2.
Figure 3. The real part of cross-spectral density versus the distance in y-axis direction, where the parameters are the same as Fig. 2
Figure 4. Far-field OAM spectra and longitudinal OAM densities of partially coherent beam with canonical vortex pairs at Q=1. The other parameters are the same as those in Fig. 2.
Figure 5. Far-field OAM spectra and longitudinal OAM densities of partially coherent beam with noncanonical vortex pairs at Q=1+i. The other parameters are the same as those in Fig. 2.
Figure 6. Far-field OAM spectra of partially coherent beam for different off-axis distance, noncanonical strength and coherence length at z=50z0. The same-charge vortex pairs are l1=l2=+2. (a): σ=w0, Q=1+0.5i; (b): σ=2w0, d=0.3w0; (c): Q=1+0.6i, d=0.4w0.
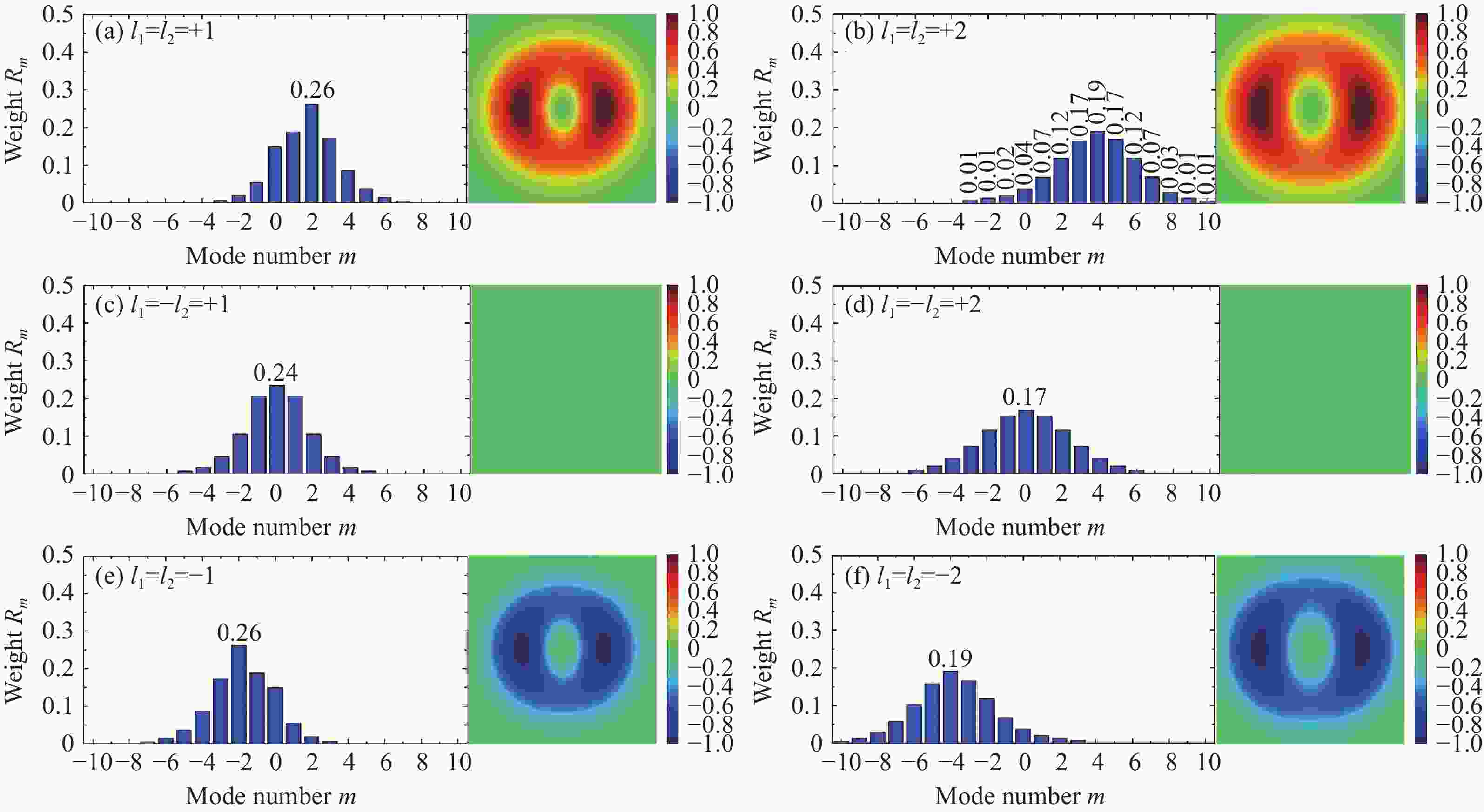
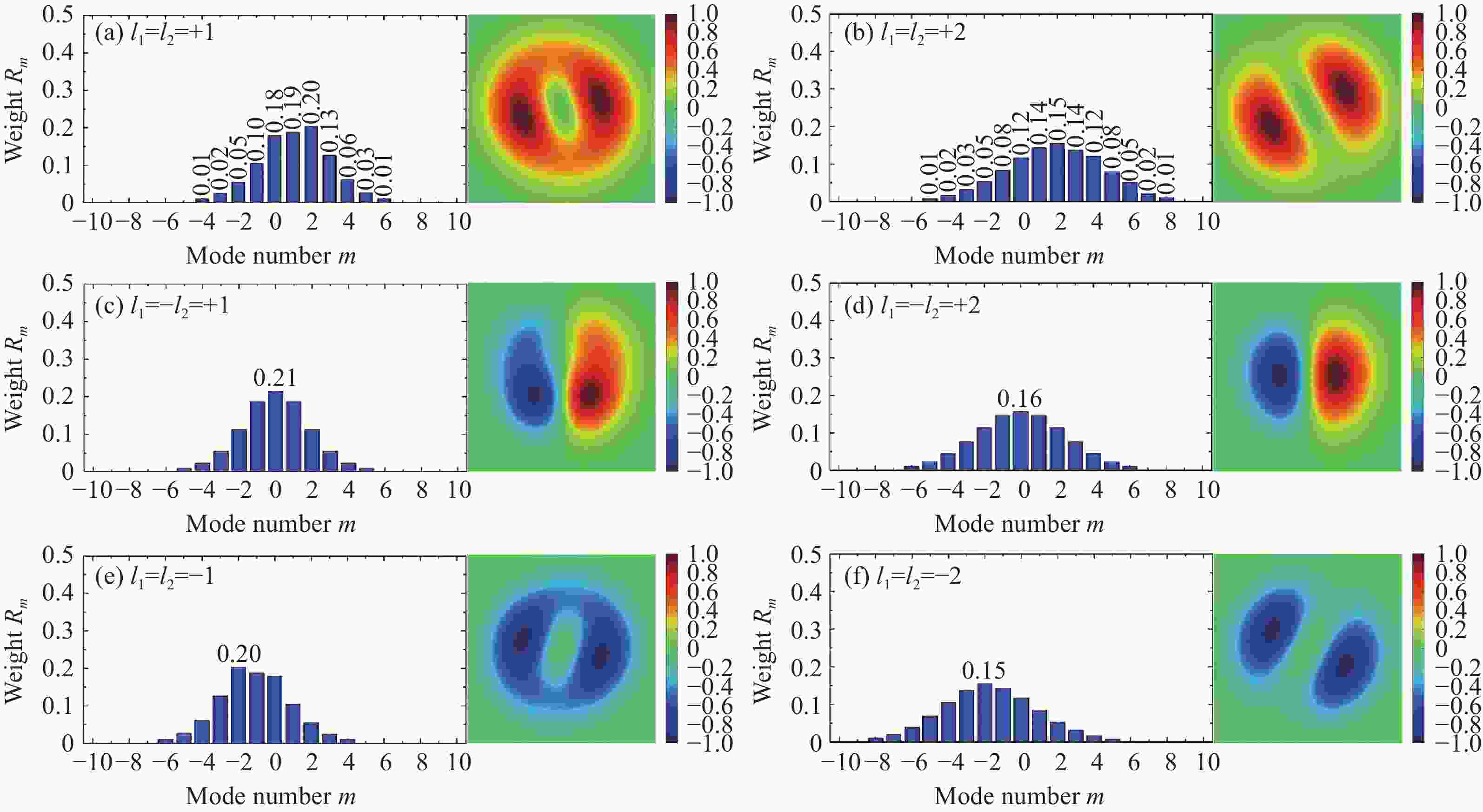
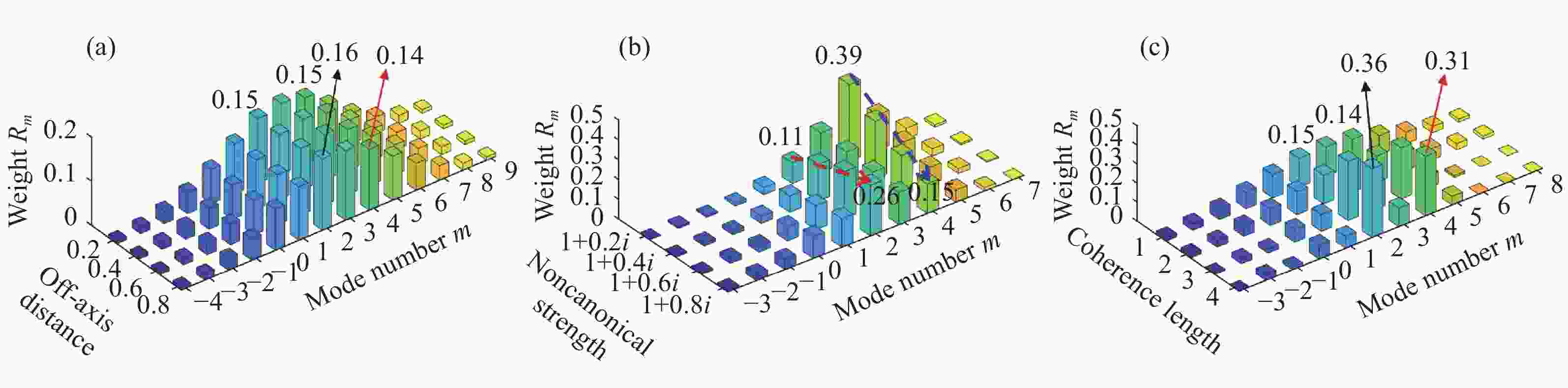
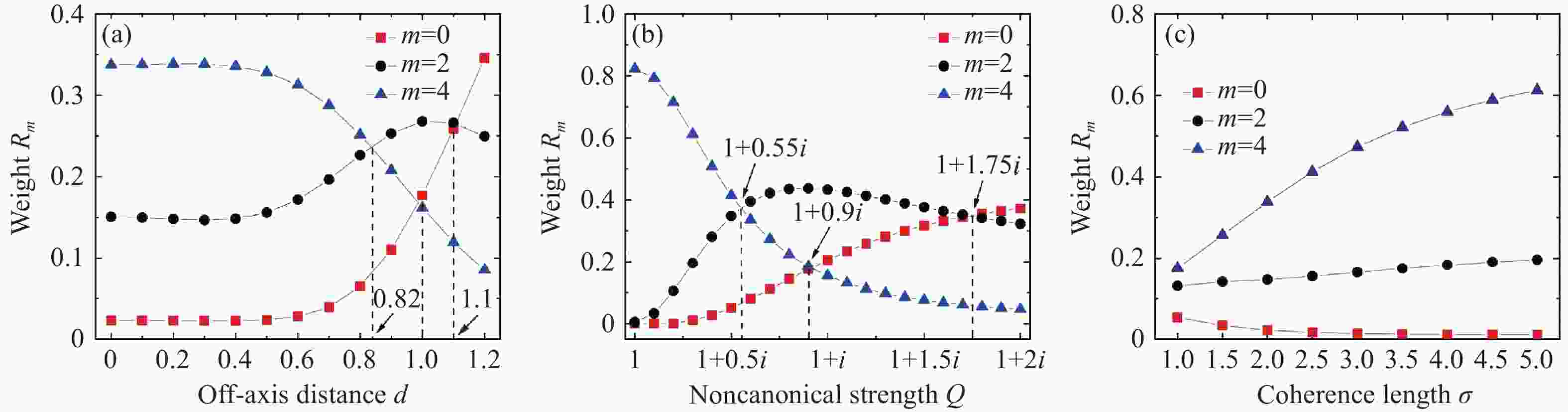
Figure 7. Variation of far-field OAM detection and crosstalk probabilities Rm=4 and Rm=0, 2 of partially coherent beam for different off-axis distance, noncanonical strength and coherence length at z=50z0. The same-charge vortex pairs are l1=l2=+2. (a): σ=2w0, Q=1+0.3i; (b): σ=5w0, d=0.3w0; (c): Q=1+0.3i, d=0.3w0.
-
[1] SOSKIN M S, VASNETSOV M V. Singular optics[J]. Progress in Optics, 2001, 42: 219-276. [2] SHEN Y J, WANG X J, XIE ZH W, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities[J]. Light: Science & Applications, 2019, 8(1): 90. [3] BAI Y H, LV H R, FU X, et al. Vortex beam: generation and detection of orbital angular momentum [Invited][J]. Chinese Optics Letters, 2022, 20(1): 012601. doi: 10.3788/COL202220.012601 [4] GBUR G, VISSER T D. Coherence vortices in partially coherent beams[J]. Optics Communications, 2003, 222(1-6): 117-125. doi: 10.1016/S0030-4018(03)01606-7 [5] GBUR G, VISSER T D, WOLF E. 'Hidden' singularities in partially coherent wavefields[J]. Journal of Optics A: Pure and Applied Optics, 2004, 6(5): S239-S242. doi: 10.1088/1464-4258/6/5/017 [6] GBUR G, VISSER T D, WOLF E. Complete destructive interference of partially coherent fields[J]. Optics Communications, 2004, 239(1-3): 15-23. doi: 10.1016/j.optcom.2004.05.027 [7] PALACIOS D M, MALEEV I D, MARATHAY A S, et al. Spatial correlation singularity of a vortex field[J]. Physical Review Letters, 2004, 92(14): 143905. doi: 10.1103/PhysRevLett.92.143905 [8] MALEEV I D, PALACIOS D M, MARATHAY A S, et al. Spatial correlation vortices in partially coherent light: theory[J]. Journal of the Optical Society of America B, 2004, 21(11): 1895-1900. doi: 10.1364/JOSAB.21.001895 [9] GBUR G, VISSER T D. Phase singularities and coherence vortices in linear optical systems[J]. Optics Communications, 2006, 259(2): 428-435. doi: 10.1016/j.optcom.2005.08.074 [10] MALEEV I D, SWARTZLANDER JR G A. Propagation of spatial correlation vortices[J]. Journal of the Optical Society of America B, 2008, 25(6): 915-922. doi: 10.1364/JOSAB.25.000915 [11] CHENG K, LÜ B D. Composite coherence vortices in coherent and incoherent superpositions of two off-axis partially coherent vortex beams[J]. Journal of Modern Optics, 2008, 55(17): 2751-2764. doi: 10.1080/09500340802167524 [12] GBUR G, VISSER T D. The structure of partially coherent fields[J]. Progress in Optics, 2010, 55: 285-341. [13] YANG Y J, MAZILU M, DHOLAKIA K. Measuring the orbital angular momentum of partially coherent optical vortices through singularities in their cross-spectral density functions[J]. Optics Letters, 2012, 37(23): 4949-4951. doi: 10.1364/OL.37.004949 [14] YANG Y J, CHEN M ZH, MAZILU M, et al. Effect of the radial and azimuthal mode indices of a partially coherent vortex field upon a spatial correlation singularity[J]. New Journal of Physics, 2013, 15(11): 113053. doi: 10.1088/1367-2630/15/11/113053 [15] LIU X L, ZENG J, CAI Y J. Review on vortex beams with low spatial coherence[J]. Advances in Physics: X, 2019, 4(1): 1626766. doi: 10.1080/23746149.2019.1626766 [16] DONG M, ZHAO CH L, CAI Y J, et al. Partially coherent vortex beams: fundamentals and applications[J]. Science China Physics, Mechanics & Astronomy, 2021, 64(2): 224201. [17] LI X F, BASHIRI S, MA Y, et al. Perfect correlation vortices[J]. Optics Letters, 2024, 49(16): 4717-4720. doi: 10.1364/OL.529970 [18] VANITHA P, NA Y, KO D K. Characterizing the fractional coherence vortices through the area of the intensity cross-correlation function[J]. Journal of the Optical Society of America A, 2024, 41(7): 1397-1402. doi: 10.1364/JOSAA.527925 [19] GAUTAM A, AGARWAL A K, SINGH R K. Coherence vortices by binary pinholes[J]. Nanophotonics, 2024, 13(24): 4397-4407. doi: 10.1515/nanoph-2024-0380 [20] ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185-8189. doi: 10.1103/PhysRevA.45.8185 [21] YANG Y J, ZHAO Q, LIU L L, et al. Manipulation of orbital-angular-momentum spectrum using pinhole plates[J]. Physical Review Applied, 2019, 12(6): 064007. doi: 10.1103/PhysRevApplied.12.064007 [22] ZHAO Q, DONG M, BAI Y H, et al. Measuring high orbital angular momentum of vortex beams with an improved multipoint interferometer[J]. Photonics Research, 2020, 8(5): 745-749. doi: 10.1364/PRJ.384925 [23] SHU L Y, CHENG K, LIAO S, et al. Asymmetrical spiral spectra and orbital angular momentum density of non-uniformly polarized vortex beams in uniaxial crystals[J]. Chinese Physics B, 2023, 32(2): 024211. doi: 10.1088/1674-1056/ac7860 [24] YANG C H, CHENG K, HUANG H W, et al. Orbital-angular-momentum spectra in coherent optical vortex beam arrays with hybrid states of polarization[J]. Chinese Optics, 2023, 16(6): 1501-1511. doi: 10.37188/CO.EN-2023-0010 [25] WILLNER A E, HUANG H, YAN Y, et al. Optical communications using orbital angular momentum beams[J]. Advances in Optics and Photonics, 2015, 7(1): 66-106. doi: 10.1364/AOP.7.000066 [26] PADGETT M J. Orbital angular momentum 25 years on [Invited][J]. Optics Express, 2017, 25(10): 11265-11274. doi: 10.1364/OE.25.011265 [27] WENG Y, PAN ZH Q. Orbital angular momentum based sensing and their applications: a review[J]. Journal of Lightwave Technology, 2023, 41(7): 2007-2016. doi: 10.1109/JLT.2022.3202184 [28] LI X F, LIU X, WU Q Y, et al. Prime number factorization with light beams carrying orbital angular momentum[J]. APL Photonics, 2024, 9(4): 046107. doi: 10.1063/5.0192223 [29] FORBES A, MKHUMBUZA L, FENG L. Orbital angular momentum lasers[J]. Nature Reviews Physics, 2024, 6(6): 352-364. doi: 10.1038/s42254-024-00715-2 [30] YI X, ZHENG R Q, YUE P, et al. Propagation properties of OAM modes carried by partially coherent LG beams in turbulent ocean based on an oceanic power-law spectrum[J]. Optics Communications, 2019, 443: 238-244. doi: 10.1016/j.optcom.2019.03.038 [31] LI Y X, HAN Y P, CUI ZH W, et al. Performance analysis of the OAM based optical wireless communication systems with partially coherent elegant Laguerre-Gaussian beams in oceanic turbulence[J]. Journal of Optics, 2019, 21(3): 035702. doi: 10.1088/2040-8986/ab0270 [32] LV H, REN CH CH, LIU X D. Orbital angular momentum spectrum of partially coherent vortex beams in slant atmospheric turbulence[J]. Infrared Physics & Technology, 2020, 105: 103181. [33] WANG Y K, BAI L, XIE J Y, et al. Spiral spectrum of high-order elliptic Gaussian vortex beams in a non-Kolmogorov turbulent atmosphere[J]. Optics Express, 2021, 29(11): 16056-16072. doi: 10.1364/OE.416324 [34] WANG H Y, YANG ZH H, LIU L, et al. Orbital angular momentum spectra of twisted Laguerre-Gaussian Schell-model beams propagating in weak-to-strong Kolmogorov atmospheric turbulence[J]. Optics Express, 2023, 31(2): 916-928. doi: 10.1364/OE.477029 [35] ZHANG Y T, CAI Y J, GBUR G. Switch of orbital angular momentum flux density of partially coherent vortex beams[J]. Optics Express, 2023, 31(23): 38004-38012. doi: 10.1364/OE.503442 [36] ZHAO Z Y, HAO P Q, LIU J H, et al. Conservation and non-conservation of photonic angular momentum in a gradient-index fiber[J]. Optics Communications, 2024, 554: 130211. doi: 10.1016/j.optcom.2023.130211 [37] SHIRI A, GBUR G. Orbital angular momentum spectrum of model partially coherent beams in turbulence[J]. Optics Express, 2024, 32(10): 18175-18192. doi: 10.1364/OE.523635 [38] GUO M X, LE W, WANG CH, et al. Generation, topological charge, and orbital angular momentum of off-axis double vortex beams[J]. Photonics, 2023, 10(4): 368. doi: 10.3390/photonics10040368 [39] CHEN L L, WANG G Q, YIN Y, et al. Partially coherent off-axis double vortex beam and its properties in oceanic turbulence[J]. Photonics, 2023, 11(1): 20. doi: 10.3390/photonics11010020 [40] MOLINA-TERRIZA G, WRIGHT E M, TORNER L. Propagation and control of noncanonical optical vortices[J]. Optics Letters, 2001, 26(3): 163-165. doi: 10.1364/OL.26.000163 [41] MANDEL L, WOLF E. Optical Coherence and Quantum Optics[M]. Cambridge: Cambridge University Press, 1995. [42] YIN CH, KAN X F, DAI H L, et al. Propagation dynamics of off-axis noncanonical vortices in a collimated Gaussian beam[J]. Chinese Physics B, 2019, 28(3): 034205. doi: 10.1088/1674-1056/28/3/034205 [43] KOTLYAR V V, KOVALEV A A. Optical vortex beams with a symmetric and almost symmetric OAM spectrum[J]. Journal of the Optical Society of America A, 2021, 38(9): 1276-1283. doi: 10.1364/JOSAA.432623 -
下载:
计量
- 文章访问数: 124
- HTML全文浏览量: 38
- PDF下载量: 8
- 被引次数: 0
