旋转对称幂指数涡旋光束在生物组织中的传输特性

高俊; 张明明; 刘俊; 胡友友; 朱志宇

doi:10.37188/CO.EN-2025-0042

旋转对称幂指数涡旋光束在生物组织中的传输特性

高俊^1,,
张明明^1, ,,
刘俊¹,
胡友友¹,
朱志宇²

1.
江苏科技大学理学院, 江苏镇江 212100
2.
江苏科技大学自动化学院, 江苏镇江 212100

详细信息

中图分类号: O482.31
计量
- 文章访问数: 50
- HTML全文浏览量: 14
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2020-01-03
- 修回日期: 2020-01-05
- 录用日期: 2025-12-11
- 网络出版日期: 2025-12-30

The transmission characteristics of rotationally-symmetric power-exponent-phase vortex beams in biological tissue

doi: 10.37188/CO.EN-2025-0042

1.
School of Science, Jiangsu University of Science and Technology, Zhenjiang 212100, China
2.
School of Automation, Jiangsu University of Science and Technology, Zhenjiang 212100, China

Funds: Supported by National Natural Science Foundation of China (No. 62476113); General Project of Natural Science research in Colleges and Universities of Jiangsu Province (No. 20KJB14008); Jiangsu Province Industry University Research Cooperation Project (No. BY2020680)

More Information

Author Bio:
GAO Jun (2001—), male, born in Huaian, Jiangsu Province, master degree candidate, received his bachelor's degree from Jiangsu University of Science and Technology in 2023. His research focuses on beam propagation and light field modulation. E-mail: 192210505209@stu.just.edu.cn

ZHANG Ming-ming (1988—), male, born in Bozhou, Anhui Province, Ph.D., Associate Professor, graduate student supervisor, received his Ph.D. degree from Xiamen University in 2019. His research interests include beam propagation, light field modulation, and the preparation of solid-state lasers. E-mail: zhangmingming@just.edu.cn

Corresponding author: zhangmingming@just.edu.cn

摘要

摘要:
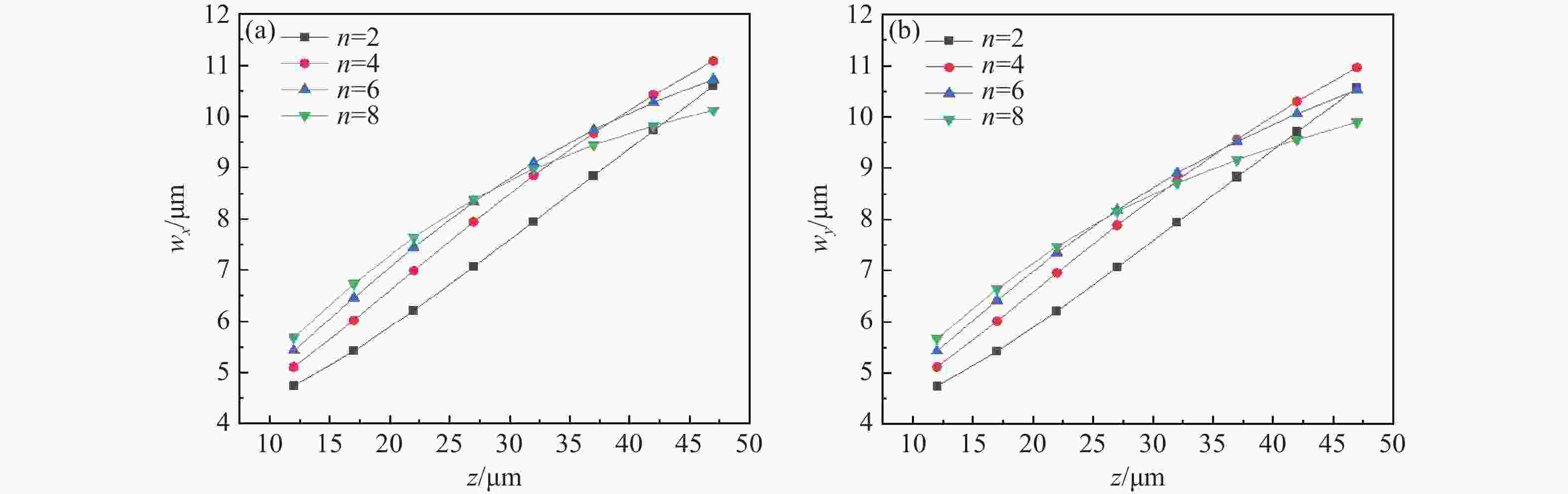
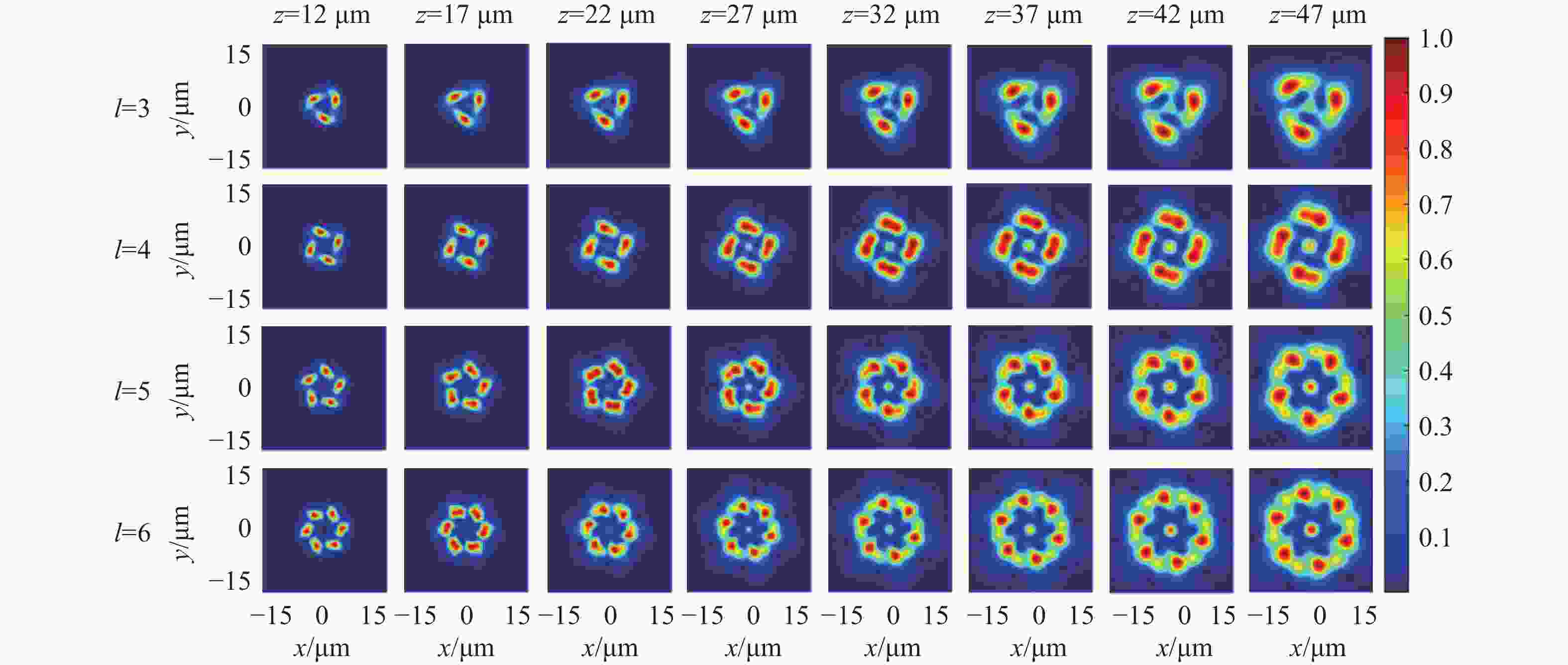
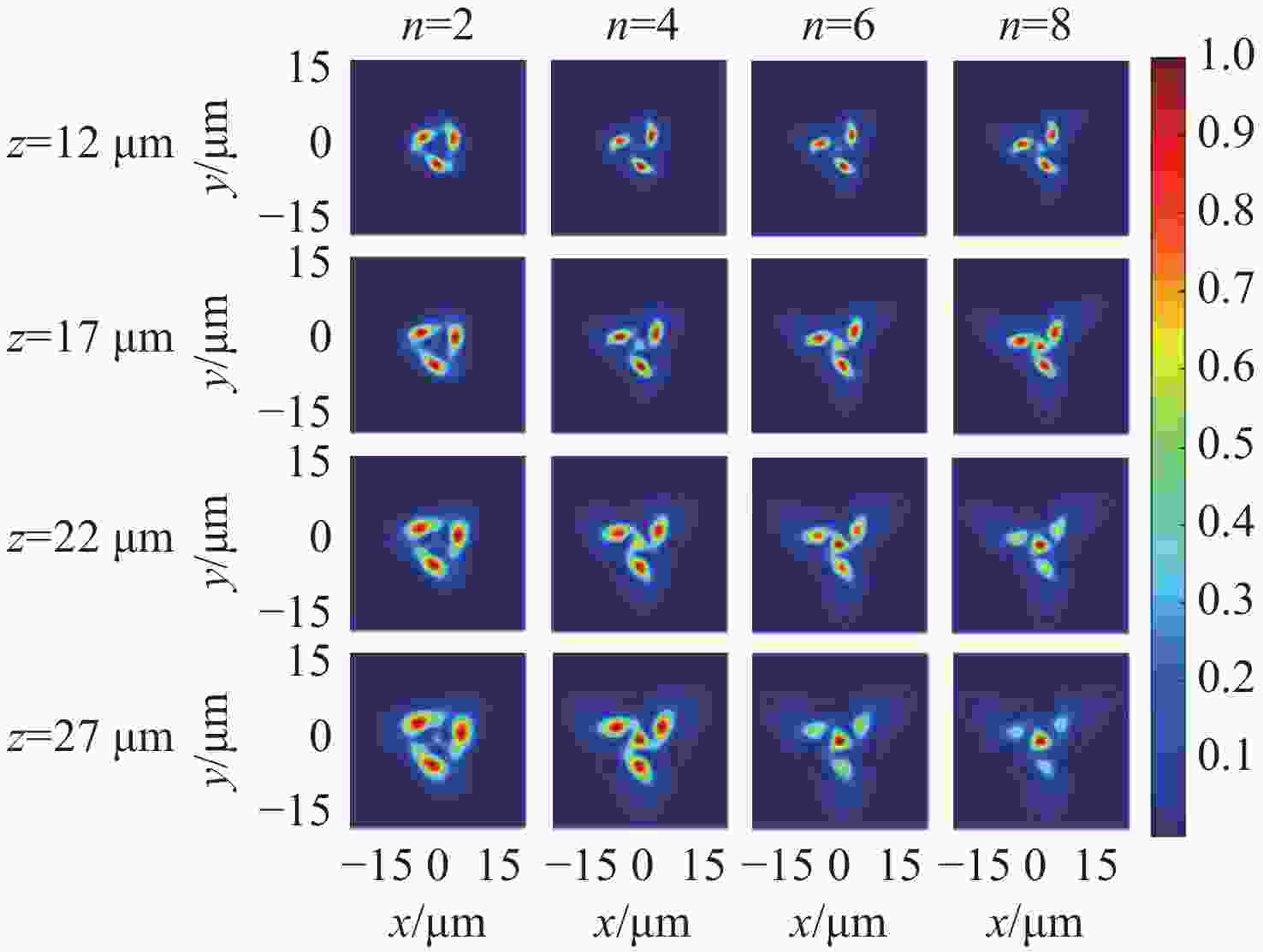
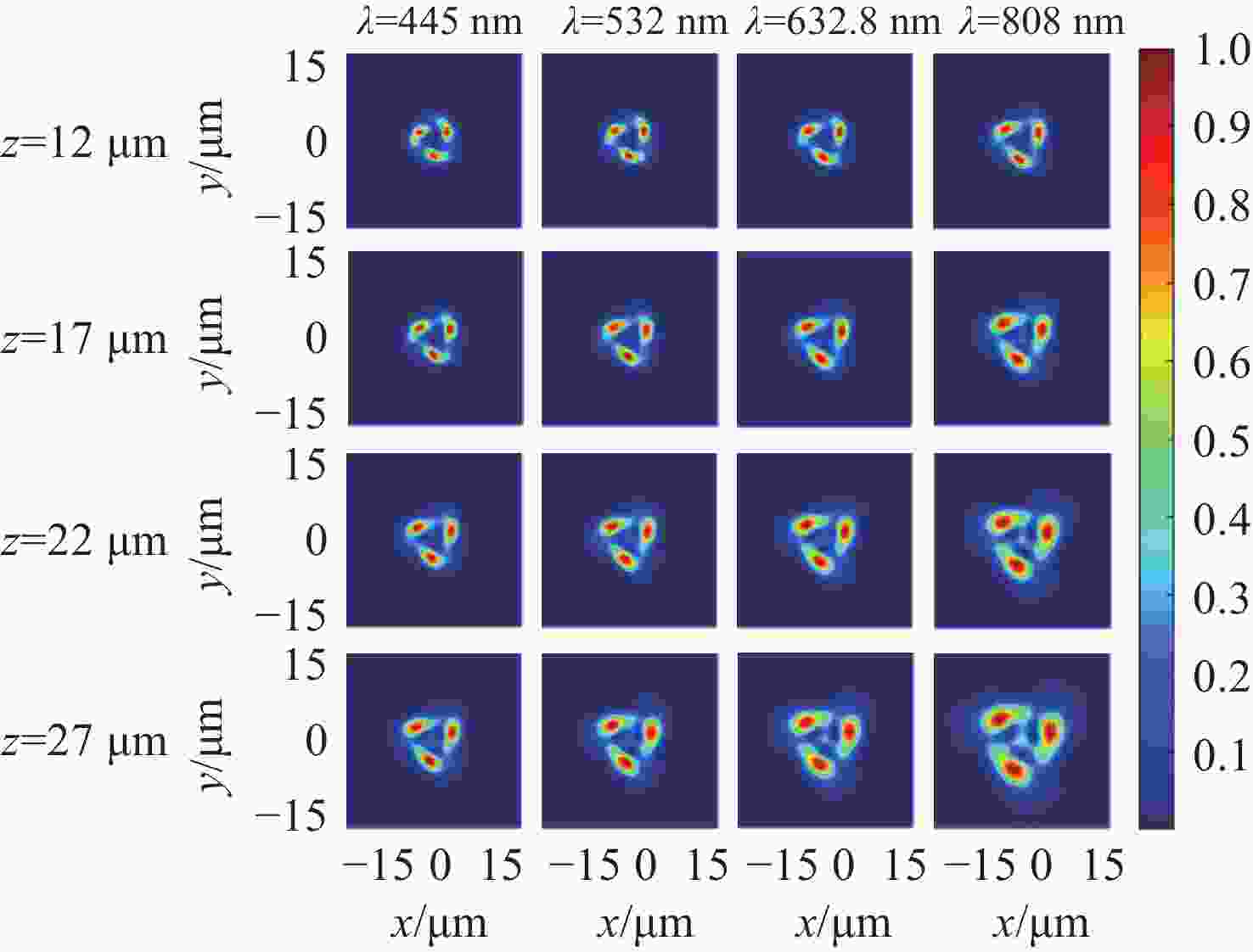
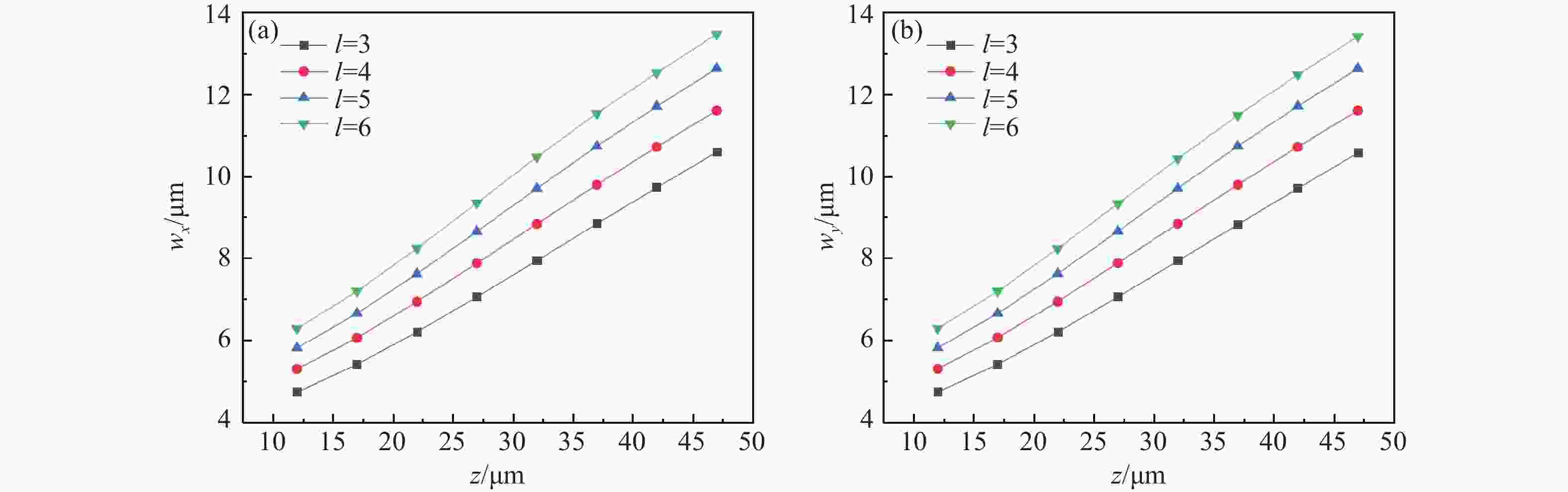
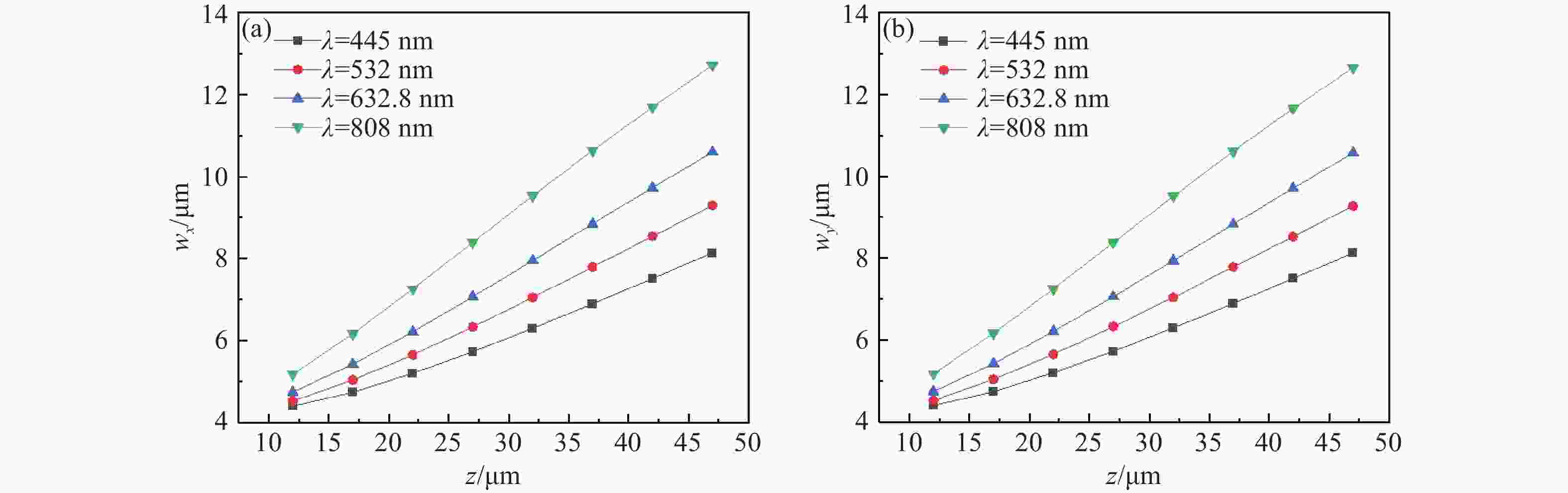
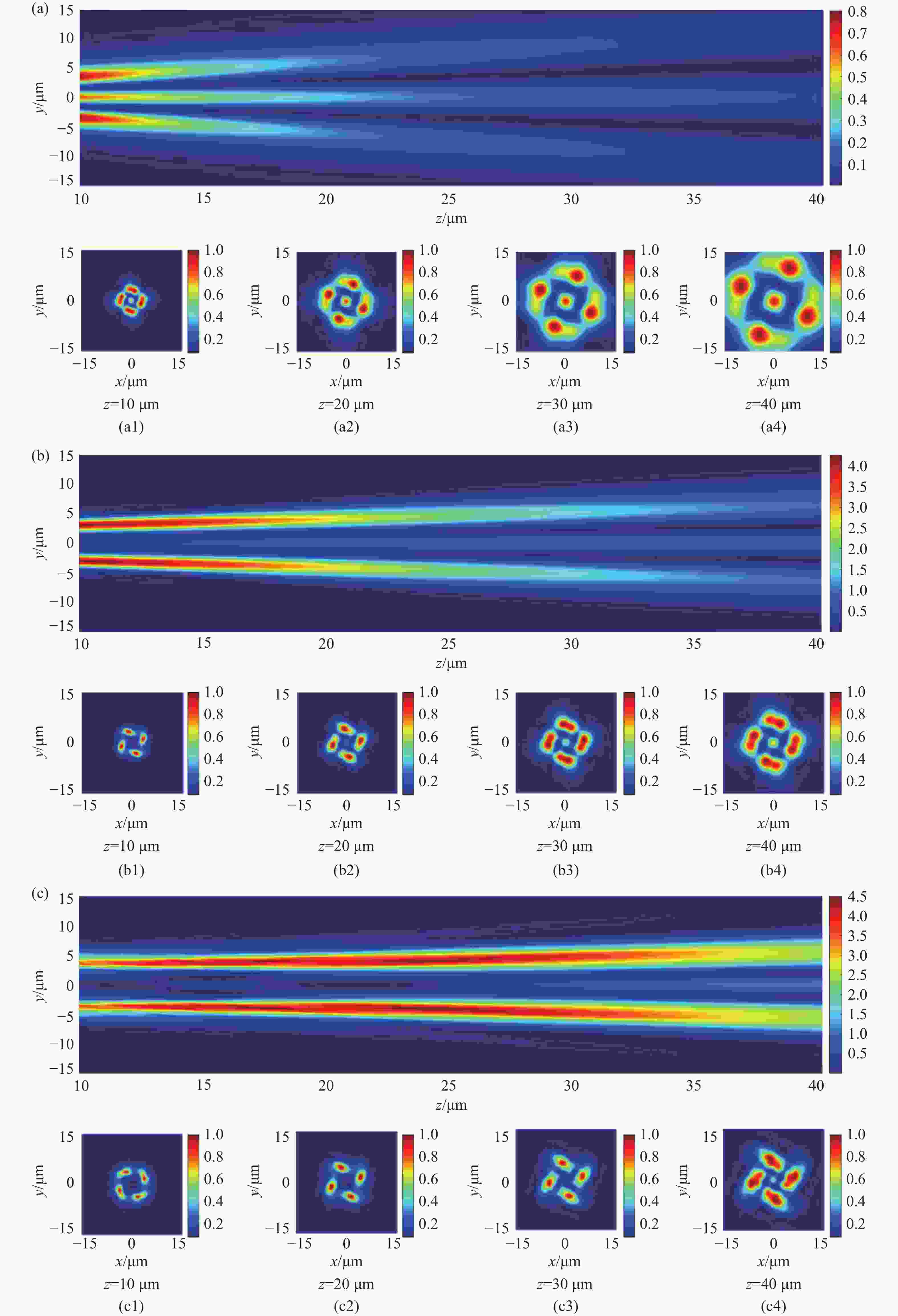
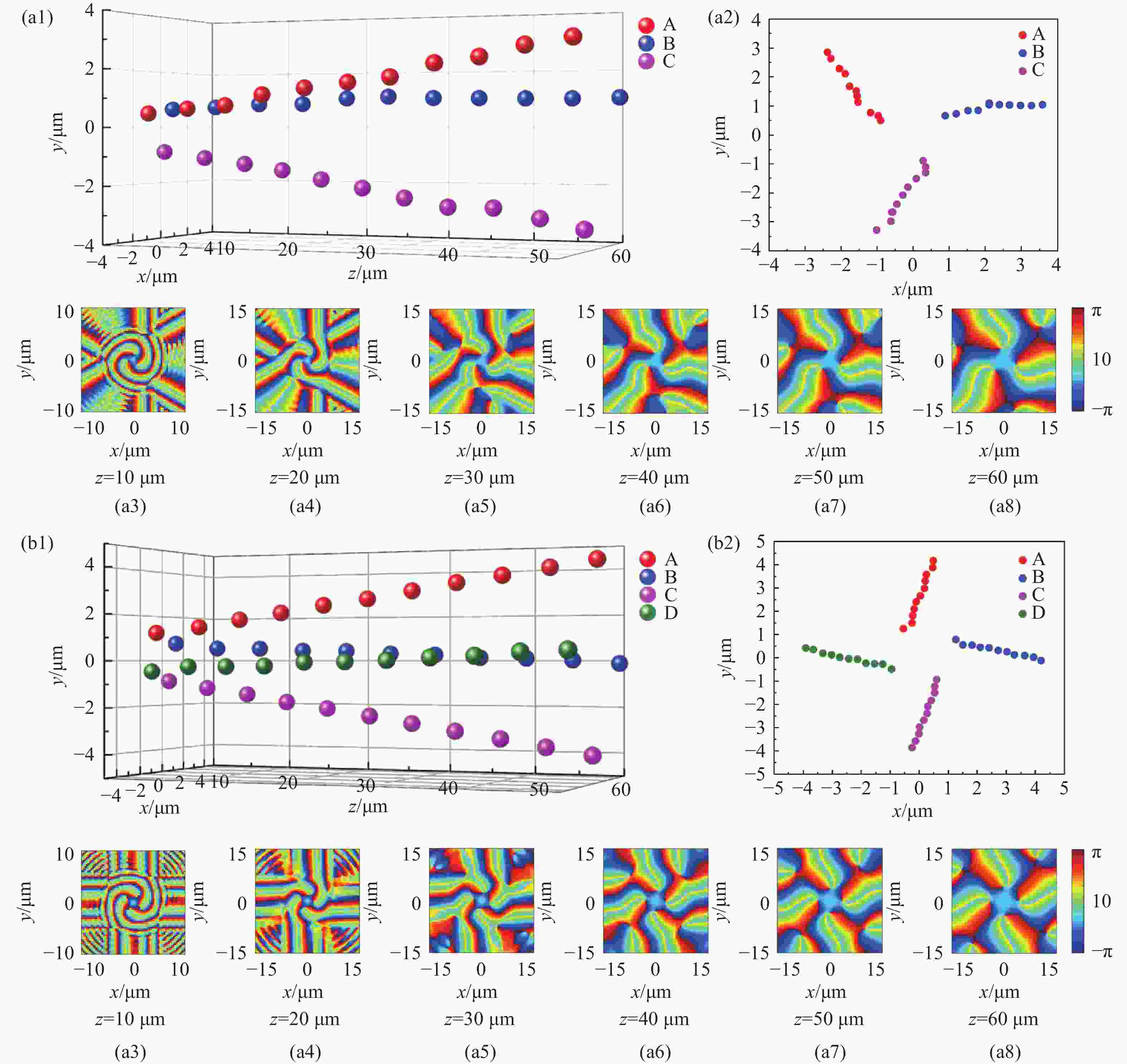
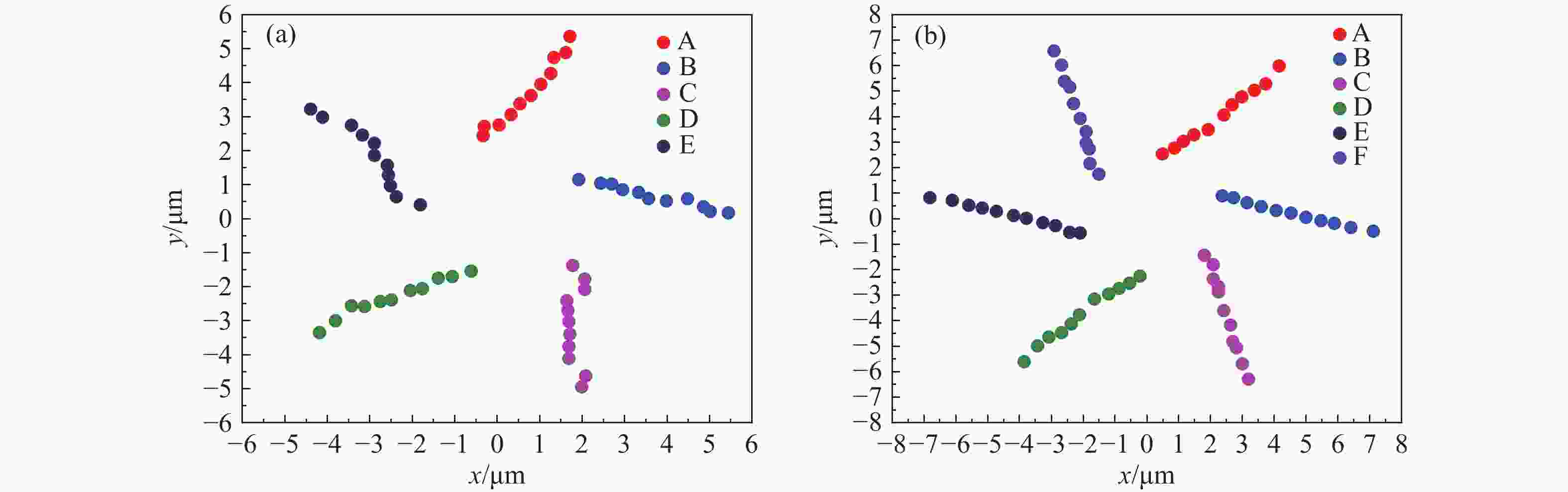
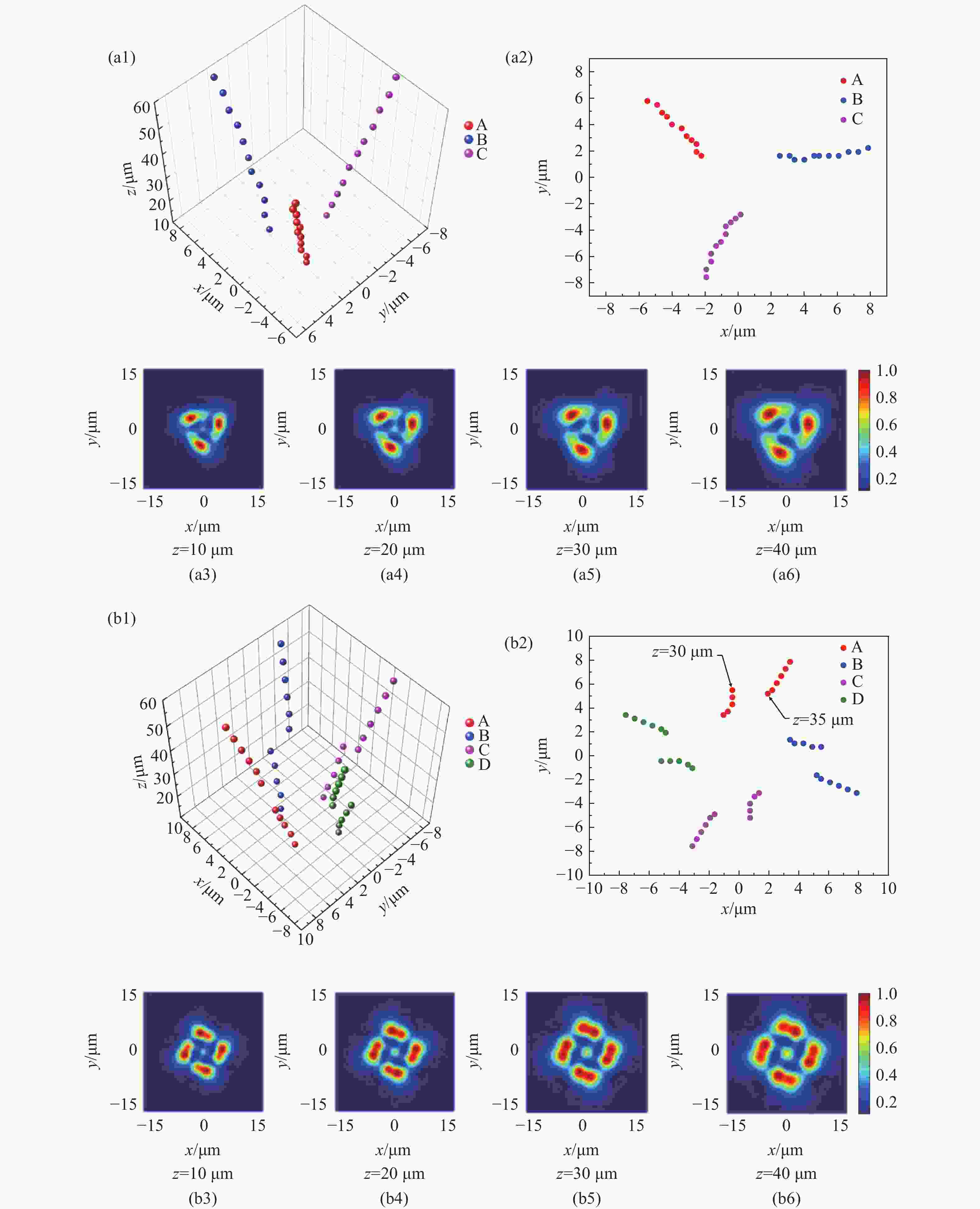
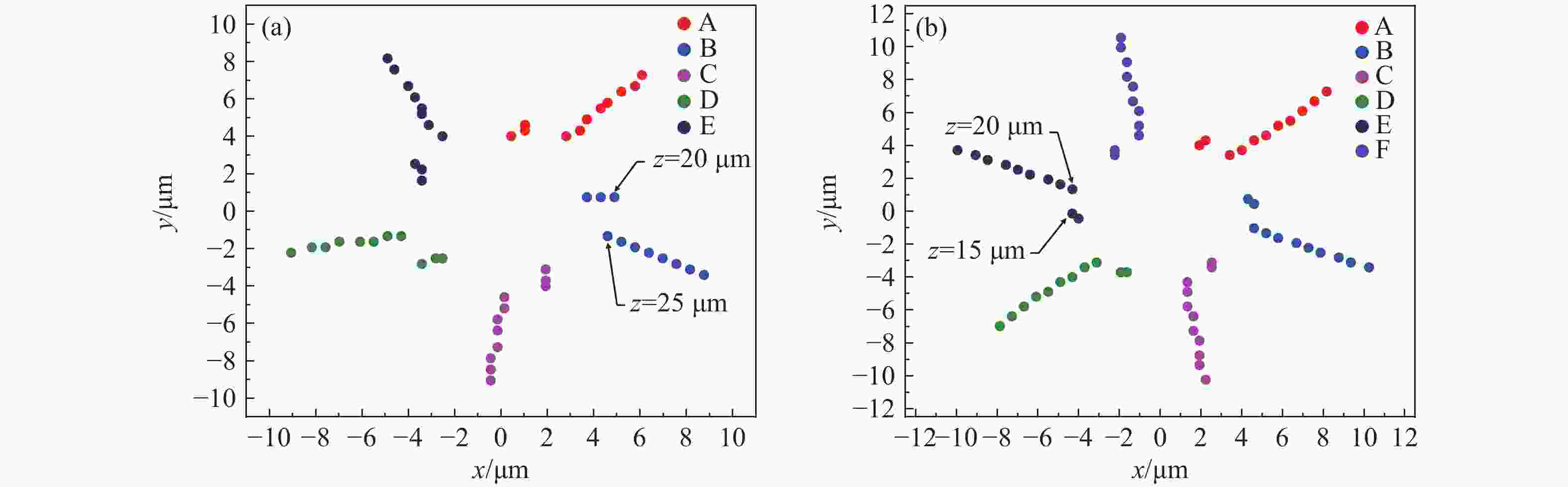
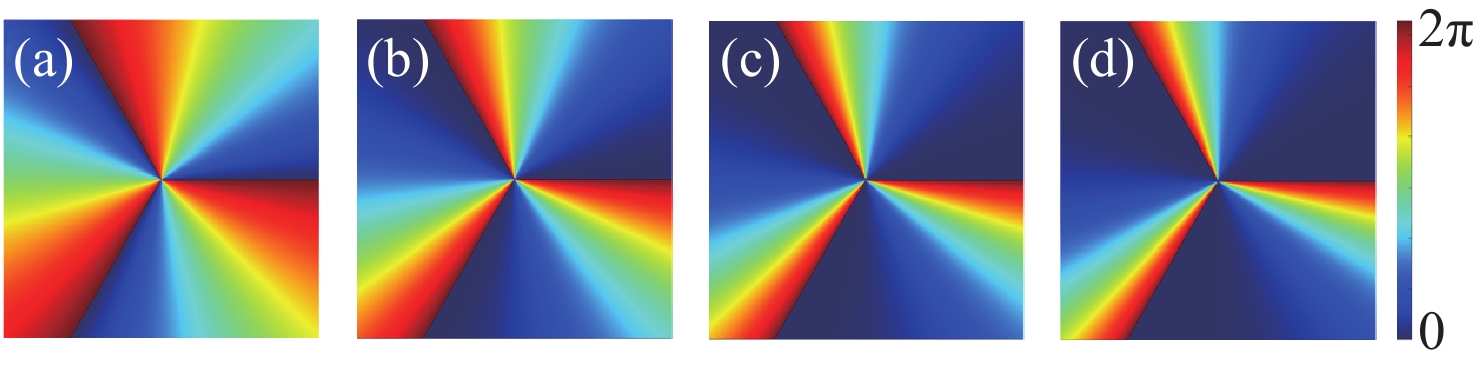
本研究探讨了旋转对称幂指数涡旋光束（RSPEPVBs）在生物组织中的传输特性。根据广义惠更斯-菲涅耳原理，建立了描述RSPEPVBs通过生物组织传输的一般表达式。通过数值模拟，研究了传播距离z、幂指数n、波长$ \lambda $和束腰宽度w对光强、光束宽度和光束发散角的影响。研究结果表明，增加传播距离和波长会导致更大的光束扩散和光束宽度增大。相反，较高的幂指数会使光强向中心集中，并减缓光束宽度的扩展。此外，较长的波长和较小的束腰宽度会导致更大的光束发散角。还分析了相干涡旋和强度峰值位置随传播距离增加的演变情况，结果显示它们逐渐从光束中心向外偏移，并伴随着角度偏差和位置变化。特别是当拓扑荷l ≥ 4时，峰值点的位置在传输过程中会发生跃变。作为一种高阶模式光束，RSPEPVB在生物组织中的传输表现出多样性和可控性，为生物医学领域的微操作技术开辟了新的可能性。
- 涡旋光束 /
- 生物组织 /
- 幂指数相位 /
- 相干涡旋和峰值点
Abstract:
The transmission characteristics of rotationally symmetric power-exponent-phase vortex beams (RSPEPVBs) in biological tissues are explored in this study. Based on the extended Huygens-Fresnel principle, a general expression describing the transmission of RSPEPVBs through biological tissues is established. Numerical simulations are performed to explore the influence of the propagation distance z, power exponent n, wavelength λ, and beam waist width w on light intensity, beam width, and beam divergence. The findings reveal that increasing the propagation distance and wavelength results in greater beam diffusion and an enlarged beam width. Conversely, a higher power exponent concentrates the light intensity toward the center and mitigates the broadening of the beam width. Additionally, a longer wavelength and smaller beam waist width lead to a larger beam divergence angle. The evolution of coherence vortices and intensity peak positions with increasing propagation distance is also analyzed, revealing a gradual outward displacement from the beam center, accompanied by angular deviations and positional shifts. Notably, when the topological charge l ≥ 4, the position of the peak point undergo an abrupt shift during the transmission process. As a high-order mode beam, the transmission of RSPEPVBs in biological tissues exhibits diversity and controllability, opening up new possibilities for micro-manipulation technologies in the biomedical field.
- vortex beam /
- biological tissue /
- power-exponent-phase /
- coherent vortices and peak points

HTML全文

Figure 1. The phase distributions of RSPEPVB with different mode orders, (a) l=3, n=1; (b) l=3, n=2; (c) l=3, n=3; (d) l=3, n=4

下载: 全尺寸图片幻灯片

Figure 2. The normalized intensity distribution of RSPEPVBs propagating through mouse deep dermal tissue.

下载: 全尺寸图片幻灯片

Figure 3. The normalized intensity distributions corresponding to different power exponents at varying propagation distances.

下载: 全尺寸图片幻灯片

Figure 4. The normalized intensity distributions corresponding to different wavelengths at varying propagation distances.

下载: 全尺寸图片幻灯片

Figure 5. The mean-squared beam width under different topological charges(a) x-direction (b) y-direction.

下载: 全尺寸图片幻灯片

Figure 6. The mean-squared beam width under different power exponents (a) x-direction (b) y-direction.

下载: 全尺寸图片幻灯片

Figure 7. The mean-squared beam width under different wavelengths (a) x-direction (b) y-direction.

下载: 全尺寸图片幻灯片

Figure 8. The intensity distributions of RSPEPVB with different waist widths propagating in biological tissue, (a) w=1 µm, (b) w=2 µm, (c) w=3 µm, where (a1)−(a4), (b1)−(b4), (c1)−(c4) is the normalized intensity distribution in the x-y plane at several fixed transmission distances, respectively.

下载: 全尺寸图片幻灯片

Figure 9. The propagation trajectory diagram of coherent vortex positions, (a1)−(a8) l=3, (b1)−(b8) l=4, where (a3)−(a8), (b3)−(b8) is the phase distribution at several fixed transmission distances, respectively.

下载: 全尺寸图片幻灯片

Figure 10. Coherent vortex projections onto the xy-plane (a) l=5 (b) l=6.

下载: 全尺寸图片幻灯片

Figure 11. The propagation trajectory diagram of peak point, (a1)−(a8) l=3, (b1)−(b8) l=4, where (a3)−(a8), (b3)−(b8) is the normalized intensity distribution at several fixed transmission distances, respectively.

下载: 全尺寸图片幻灯片

Figure 12. Peak point projections onto the xy-plane (a) l=5 (b) l=6.

下载: 全尺寸图片幻灯片

参考文献(36)

[1]	KONYSHEV I V, BYVALOV A A. The bacterial flagellum as an object for optical trapping[J]. Biophysical Reviews, 2024, 16(4): 403-415. doi: 10.1007/s12551-024-01212-7
[2]	FAVRE-BULLE I A, SCOTT E K. Optical tweezers across scales in cell biology[J]. Trends in Cell Biology, 2022, 32(11): 932-946. doi: 10.1016/j.tcb.2022.05.001
[3]	GE G R, ROLLAND J P, PARKER K J. Speckle statistics of biological tissues in optical coherence tomography[J]. Biomedical Optics Express, 2021, 12(7): 4179-4191. doi: 10.1364/BOE.422765
[4]	DOBLE P A, DE VEGA R G, BISHOP D P, et al. Laser ablation–inductively coupled plasma–mass spectrometry imaging in biology[J]. Chemical Reviews, 2021, 121(19): 11769-11822. doi: 10.1021/acs.chemrev.0c01219
[5]	CATALÀ-CASTRO F, SCHÄFFER E, KRIEG M. Exploring cell and tissue mechanics with optical tweezers[J]. Journal of Cell Science, 2022, 135(15): jcs259355. doi: 10.1242/jcs.259355
[6]	PAN T, LU D Y, XIN H B, et al. Biophotonic probes for bio-detection and imaging[J]. Light: Science & Applications, 2021, 10(1): 124.
[7]	BITON N, KUPFERMAN J, ARNON S. OAM light propagation through tissue[J]. Scientific Reports, 2021, 11(1): 2407. doi: 10.1038/s41598-021-82033-6
[8]	LUO M L, CHEN Q, HUA L M, et al. Propagation of stochastic electromagnetic vortex beams through the turbulent biological tissues[J]. Physics Letters A, 2014, 378(3): 308-314. doi: 10.1016/j.physleta.2013.11.022
[9]	BAYRAKTAR M, ELMABRUK K, DUNCAN J C M, et al. Propagation of hollow higher-order cosh-Gaussian beam in human upper dermis[J]. Physica Scripta, 2023, 98(11): 115538. doi: 10.1088/1402-4896/ad0340
[10]	JIN H, ZHENG W, MA H T, et al. Average intensity and scintillation of light in a turbulent biological tissue[J]. Optik, 2016, 127(20): 9813-9820. doi: 10.1016/j.ijleo.2016.07.077
[11]	CHIB S, DALIL-ESSAKALI L, BELAFHAL A. Partially coherent beam propagation in turbid tissue-like scattering medium[J]. Optical and Quantum Electronics, 2023, 55(7): 602. doi: 10.1007/s11082-023-04874-x
[12]	DUAN M L, WU Y G, SU N N. Changes in the polarization states of random electromagnetic vortex beams propagating in biological tissues[J]. Optica Applicata, 2018, 48(2): 297-309. doi: 10.1016/j.ijleo.2017.09.020
[13]	WU Y G, DUAN M L, LI Y J. Changes in the degree of polarization of random electromagnetic GSM vortex beams in biological tissues[J]. Optik, 2017, 149: 95-103. doi: 10.1016/j.ijleo.2017.09.020
[14]	CHIB S, BELAFHAL A. Analyzing the spreading properties of vortex beam in turbulent biological tissues[J]. Optical and Quantum Electronics, 2023, 55(1): 98. doi: 10.1007/s11082-022-04367-3
[15]	SATO S, ISHIGURE M, INABA H. Optical trapping and rotational manipulation of microscopic particles and biological cells using higher-order mode Nd: YAG laser beams[J]. Electronics Letters, 1991, 27(20): 1831-1832.
[16]	DASGUPTA R, AHLAWAT S, VERMA R S, et al. Optical trapping of spermatozoa using Laguerre-Gaussian laser modes[J]. Journal of Biomedical Optics, 2010, 15(6): 065010. doi: 10.1117/1.3526362
[17]	DASGUPTA R, AHLAWAT S, VERMA R S, et al. Optical orientation and rotation of trapped red blood cells with Laguerre-Gaussian mode[J]. Optics Express, 2011, 19(8): 7680-7688. doi: 10.1364/OE.19.007680
[18]	SHI L Y, LINDWASSER L, WANG W B, et al. Propagation of Gaussian and Laguerre-Gaussian vortex beams through mouse brain tissue[J]. Journal of Biophotonics, 2017, 10(12): 1756-1760. doi: 10.1002/jbio.201700022
[19]	YU M P, HAN Y P, CUI ZH W, et al. Scattering of a Laguerre-Gaussian beam by complicated shaped biological cells[J]. Journal of the Optical Society of America A, 2018, 35(9): 1504-1510. doi: 10.1364/JOSAA.35.001504
[20]	LIU D J, YIN H M, WANG G Q, et al. Spreading properties of a Lorentz-Gauss vortex beam propagating in biological tissues[J]. Progress in Electromagnetics Research Letters, 2019, 84: 83-89. doi: 10.2528/pierl19031801
[21]	ZHANG H H, CUI ZH W, HAN Y P, et al. Average intensity and beam quality of Hermite-Gaussian correlated Schell-model beams propagating in turbulent biological tissue[J]. Frontiers in Physics, 2021, 9: 650537. doi: 10.3389/fphy.2021.650537
[22]	HU Y Y, ZHANG M, DOU J T, et al. Influences of salinity and temperature on propagation of radially polarized rotationally-symmetric power-exponent-phase vortex beams in oceanic turbulence[J]. Optics Express, 2022, 30(23): 42772-42783. doi: 10.1364/OE.477398
[23]	MA ZH Y, PAN Y Q, DOU J T, et al. Statistical properties of partially coherent higher-order Laguerre-Gaussian power-exponent phase vortex beams[J]. Photonics, 2023, 10(4): 461. doi: 10.3390/photonics10040461
[24]	ZHANG M, DOU J T, XU J Q, et al. Generation of rotationally symmetric power-exponent-phase vortex beams based on digital micromirror devices[J]. Optics Express, 2023, 31(21): 34954-34962. doi: 10.1364/OE.500141
[25]	ZHOU T, HONG Y CH, DOU J T, et al. Generation of multiple rotationally-symmetric power-exponent-phase vortex beams on a spatial arbitrary distribution by using holographic phase control techniques[J]. Results in Physics, 2024, 61: 107773. doi: 10.1016/j.rinp.2024.107773
[26]	ZHANG F, HOU ZH CH, ZHANG M M, et al. Thermal blooming effect of power-exponent-phase vortex beams propagating through the atmosphere[J]. Photonics, 2023, 10(12): 1343. doi: 10.3390/photonics10121343
[27]	LI J S, SUN P J, MA H J, et al. Focus properties of cosh-Gaussian beams with the power-exponent-phase vortex[J]. Journal of the Optical Society of America A, 2020, 37(3): 483-490. doi: 10.1364/JOSAA.381192
[28]	WOLF E. Unified theory of coherence and polarization of random electromagnetic beams[J]. Physics Letters A, 2003, 312(5-6): 263-267. doi: 10.1016/S0375-9601(03)00684-4
[29]	PAN Y Q, ZHAO M L, ZHANG M M, et al. Propagation properties of rotationally-symmetric power-exponent-phase vortex beam through oceanic turbulence[J]. Optics & Laser Technology, 2023, 159: 109024. doi: 10.1016/j.optlastec.2022.109024
[30]	DUAN M L, TIAN Y N, LI J H. Propagation of Gaussian Schell-model vortex beams in biological tissues[J]. Optica Applicata, 2019, 49(2): 203-215.
[31]	DUAN M L, TIAN Y N, ZHANG Y M, et al. Influence of biological tissue and spatial correlation on spectral changes of Gaussian-Schell model vortex beam[J]. Optics and Lasers in Engineering, 2020, 134: 106224. doi: 10.1016/j.optlaseng.2020.106224
[32]	WANG S C H, PLONUS M A. Optical beam propagation for a partially coherent source in the turbulent atmosphere[J]. Journal of the Optical Society of America, 1979, 69(9): 1297-1304. doi: 10.1364/JOSA.69.001297
[33]	LIU D J, ZHONG H Y, WANG Y CH. Intensity properties of anomalous hollow vortex beam propagating in biological tissues[J]. Optik, 2018, 170: 61-69. doi: 10.1016/j.ijleo.2018.05.098
[34]	ZHANG Y Q, JI X L, LI X Q, et al. Thermal blooming effect of laser beams propagating through seawater[J]. Optics Express, 2017, 25(6): 5861-5875. doi: 10.1364/OE.25.005861
[35]	DUAN M L, DU J, ZHAO H F, et al. The singularity of the partially coherent beam in biological tissue[J]. Results in Physics, 2022, 43: 106097. doi: 10.1016/j.rinp.2022.106097
[36]	CHENG K, ZHU B Y, SHU L Y, et al. Averaged intensity and spectral shift of partially coherent chirped optical coherence vortex lattices in biological tissue turbulence[J]. Chinese Optics, 2022, 15(2): 364-372. (in Chinese).