-
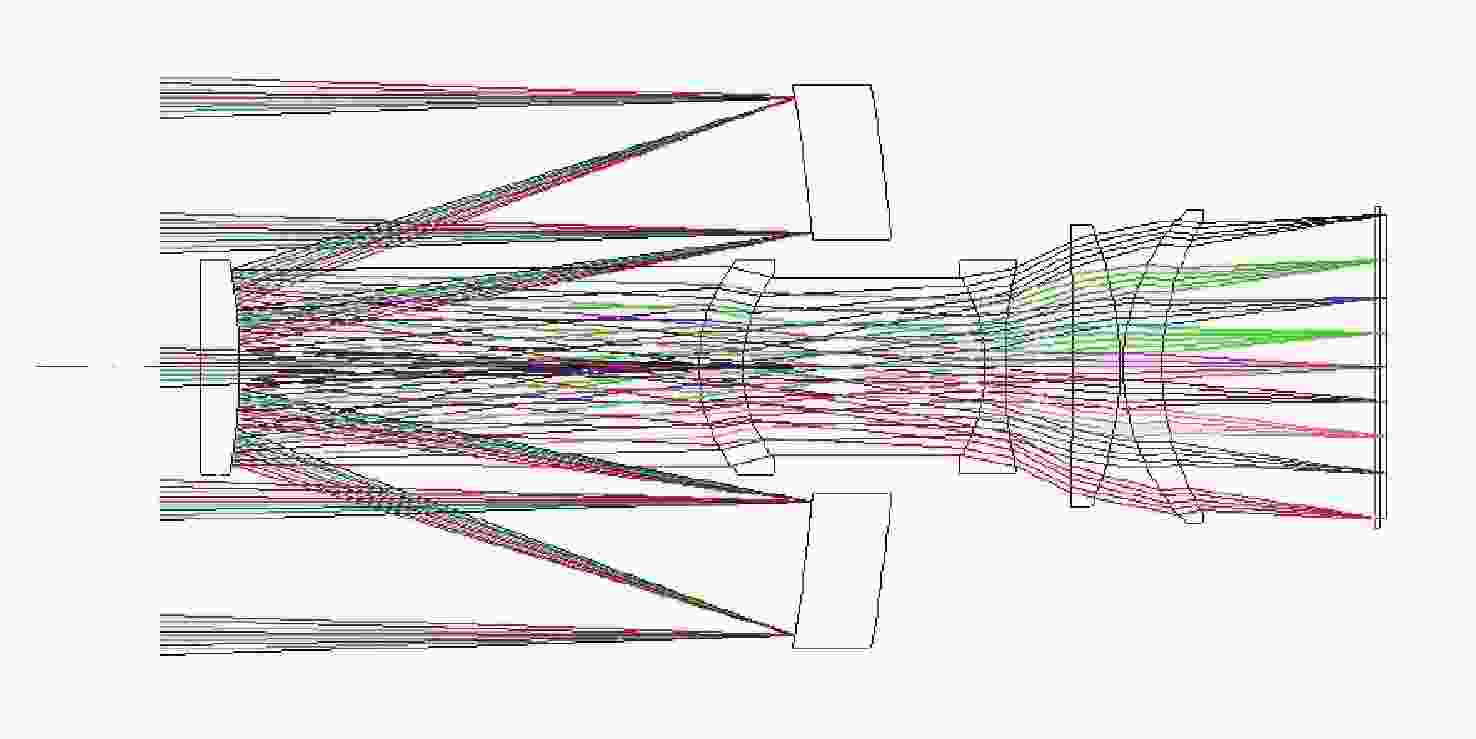
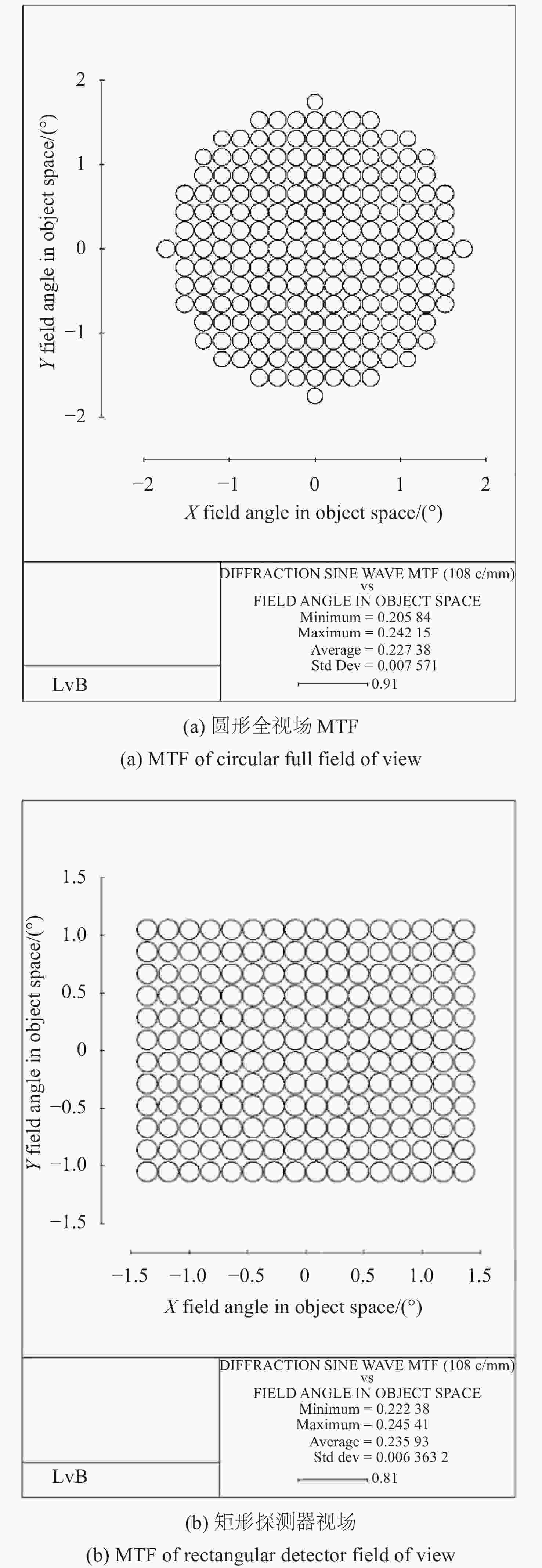
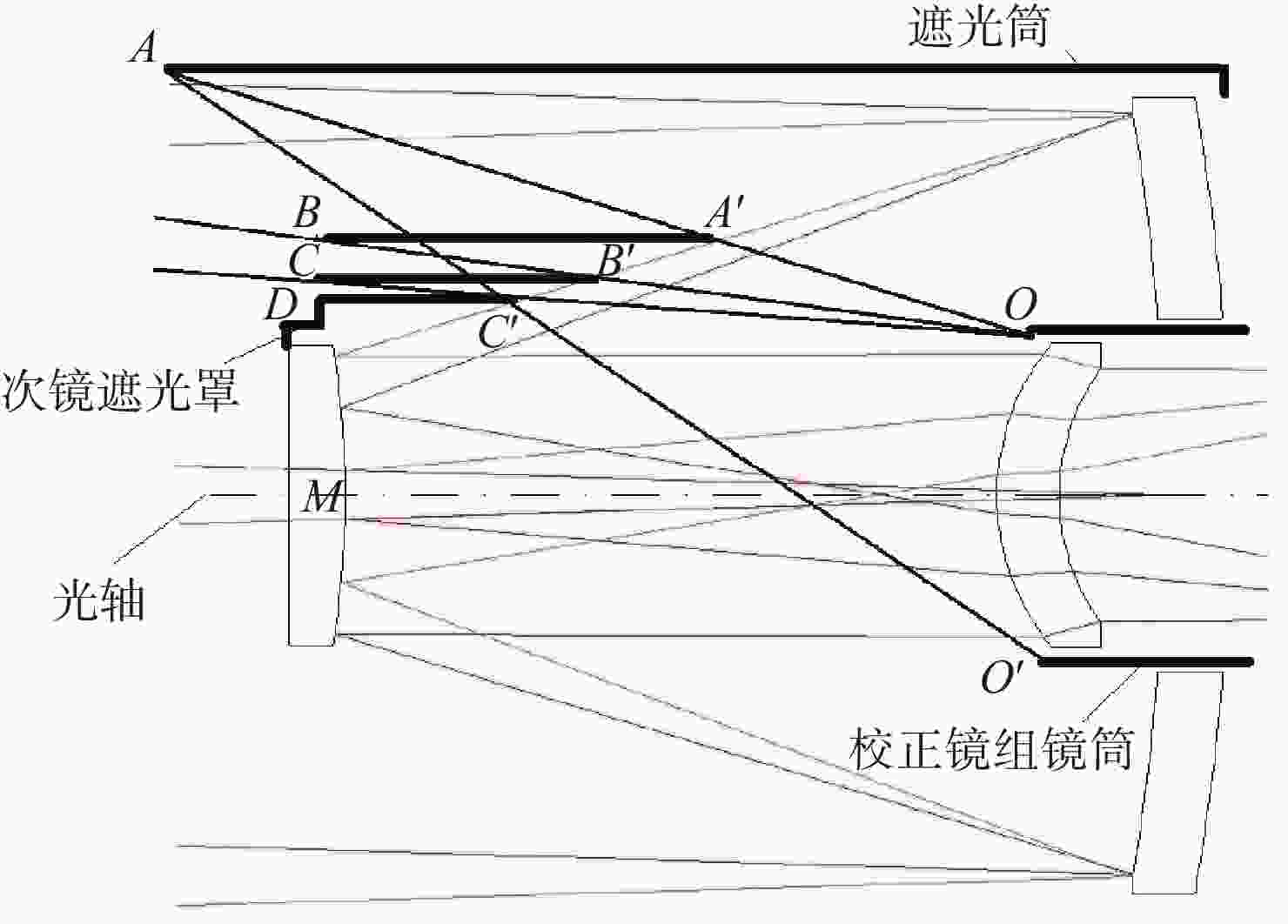
摘要: 针对同轴两反射镜光学成像视场角受限、大视场角下成像对比度较低的问题,采用透镜组作为像差校正组,合理分配光学系统的光焦度及间距,来扩大两反射结构的成像视场角,提升相机全视场内的成像质量。以某一工程应用需要为例,设计并研制了焦距为750 mm、视场角2ω=3.45°、全视场平均传递函数在108 lp/mm处优于0.2的相机光学系统,且在未使用主镜筒外遮光罩的前提下,优化设计了次镜遮光罩以实现杂散光抑制。采用TracePro软件进行相机杂散光环境建模仿真,结果表明:在非成像视场角内的杂散光点源透过率(PST)的量值范围为10−3~10−6。系统满足传统地面目标探测成像要求,验证了紧凑型大视场折反射光学杂散光抑制结构的可行性,并为商用同轴折反射光学系统设计及优化提供了一定的参考。
-
关键词:
- 光学设计 /
- 折反射 /
- 杂散光抑制 /
- 点源透过率(PST)
Abstract: A lens group is used as an aberration correction group to solve the limited field of view angle and low imaging contrast at a large field of view in the coaxial two-mirror optical system. The lens group adopts reasonable optical power and pitch, it expands the field of view of two-reflection mirrors and improves imaging quality in the camera's full field of view. Taking an engineering application as an example, we design and develop an optical system with a 750 mm focal length, a field of view of 2ω=3.45°, an average transfer function better than 0.2 at 108 lp/mm, and an optimized design for its secondary mirror hood that suppresses stray light without a main mirror barrel hood. Simulation stray light was optimized by using TracePro software. The results show that the stray light Point Source Transmittance (PST) in the non-imaging field of view ranges from 10−3 to 10−6. The system meets the requirements for traditional ground target detection and imaging, the feasibility of a compact large-field refracting optical stray light suppression structure is verified, and a certain reference for the design and optimization of commercial coaxial refracting optical systems is provided. -
表 1 光学系统设计参数
Table 1. Design parameters of optical system
光学参数 数值 焦距/mm 750 视场角2ω/(°) 3.45 像方F数 10 工作波段/nm 420~700 畸变 <1% 探测器像元 8 K×6 K@4.65 μm×4.65 μm 相对照度 ≥95% 体积/mm ≤$\varnothing $95×200 -
[1] 孙俊, 张世杰, 李葆华. 利用地球紫外和恒星可见光的卫星自主导航[J]. 光学 精密工程,2013,21(5):1192-1198. doi: 10.3788/OPE.20132105.1192SUN J, ZHANG SH J, LI B H. Autonomous navigation based on star light and ultraviolet earth sensors[J]. Optics and Precision Engineering, 2013, 21(5): 1192-1198. (in Chinese) doi: 10.3788/OPE.20132105.1192 [2] 颜昌翔, 许杰, 彭岩. 离轴三反空间光学望远系统的杂散光抑制[J]. 光学 精密工程,2010,18(2):289-293.YAN CH X, XU J, PENG Y. Stray light suppression of three-mirror off-axis space optical telescope[J]. Optics and Precision Engineering, 2010, 18(2): 289-293. (in Chinese) [3] 廖志波, 伏瑞敏, 宗肖颖. 星敏感器反射式遮光罩设计[J]. 红外与激光工程,2011,40(1):66-69. doi: 10.3969/j.issn.1007-2276.2011.01.014LIAO ZH B, FU R M, ZONG X Y. Design of specular baffle of star sensor[J]. Infrared and Laser Engineering, 2011, 40(1): 66-69. (in Chinese) doi: 10.3969/j.issn.1007-2276.2011.01.014 [4] 王威, 陈凡胜. 静止轨道对地观测成像系统外遮光罩设计[J]. 中国激光,2014,41(9):0916001. doi: 10.3788/CJL201441.0916001WANG W, CHEN F SH. Design of baffle of imaging system for earth observation on geostationary earth orbit[J]. Chinese Journal of Lasers, 2014, 41(9): 0916001. (in Chinese) doi: 10.3788/CJL201441.0916001 [5] 钟兴, 张雷, 金光. 反射光学系统杂散光的消除[J]. 红外与激光工程,2008,37(2):316-318. doi: 10.3969/j.issn.1007-2276.2008.02.031ZHONG X, ZHANG L, JIN G. Stray light removing of reflective optical system[J]. Infrared and Laser Engineering, 2008, 37(2): 316-318. (in Chinese) doi: 10.3969/j.issn.1007-2276.2008.02.031 [6] 史光辉. 消除卡塞格林系统杂光的措施[J]. 光学 精密工程,1997,5(5):10-16.SHI G H. Mathods preventing stray light emergenced in cassegrain systems[J]. Optics and Precision Engineering, 1997, 5(5): 10-16. (in Chinese) [7] 黄强. 空间光学系统的杂散光分析[J]. 红外,2006,27(1):26-33. doi: 10.3969/j.issn.1672-8785.2006.01.006HUANG Q. Analysis of stray light in space optical system[J]. Infrared, 2006, 27(1): 26-33. (in Chinese) doi: 10.3969/j.issn.1672-8785.2006.01.006 [8] 吴峰, 沈为民. 折反式大视场星敏感器光学系统设计[J]. 光学技术,2004,30(2):142-145. doi: 10.3321/j.issn:1002-1582.2004.02.015WU F, SHEN W M. Design of a catadioptric system for star sensors with wide field of view[J]. Optical Technique, 2004, 30(2): 142-145. (in Chinese) doi: 10.3321/j.issn:1002-1582.2004.02.015 [9] 潘君骅. 光学非球面的设计、加工与检验[M]. 苏州: 苏州大学出版社, 2004: 24-32.PAN J H. The Design, Manufacture and Test of the Aspherical Optical Surfaces[M]. Suzhou: Soochow University Press, 2004: 24-32. (in Chinese) [10] SCHLICK C. A survey of shading and reflectance models[J]. Computer Graphics Forum, 1994, 13(2): 121-131. doi: 10.1111/1467-8659.1320121 [11] 赵阳. 新型反射式星敏感器光学系统设计[D]. 哈尔滨: 哈尔滨工业大学, 2007.ZHAO Y. New type reflective optical system design for a star sensor[D]. Harbin: Harbin Institute of Technology, 2007. (in Chinese) [12] YOUNG A T. Design of cassegrain light shields[J]. Applied Optics, 1967, 6(6): 1063-1067. doi: 10.1364/AO.6.001063 [13] HARVEY J E, THOMPSON A K. Scattering effects from residual optical fabrication errors[J]. Proceedings of SPIE, 1995, 2576: 155-174. doi: 10.1117/12.215588 [14] VAN BEZOOIJEN R W H. SIRTF autonomous star tracker[J]. Proceedings of SPIE, 2003, 4850: 108-121. doi: 10.1117/12.461606 [15] 梅超, 周泗忠, 闫佩佩, 等. 基于散射模型设计外遮光罩[J]. 光学学报,2013,33(1):0122005. doi: 10.3788/AOS201333.0122005MEI CH, ZHOU S ZH, YAN P P, et al. Design of an outer baffle based on scattering model[J]. Acta Optica Sinica, 2013, 33(1): 0122005. (in Chinese) doi: 10.3788/AOS201333.0122005 -






 下载:
下载: