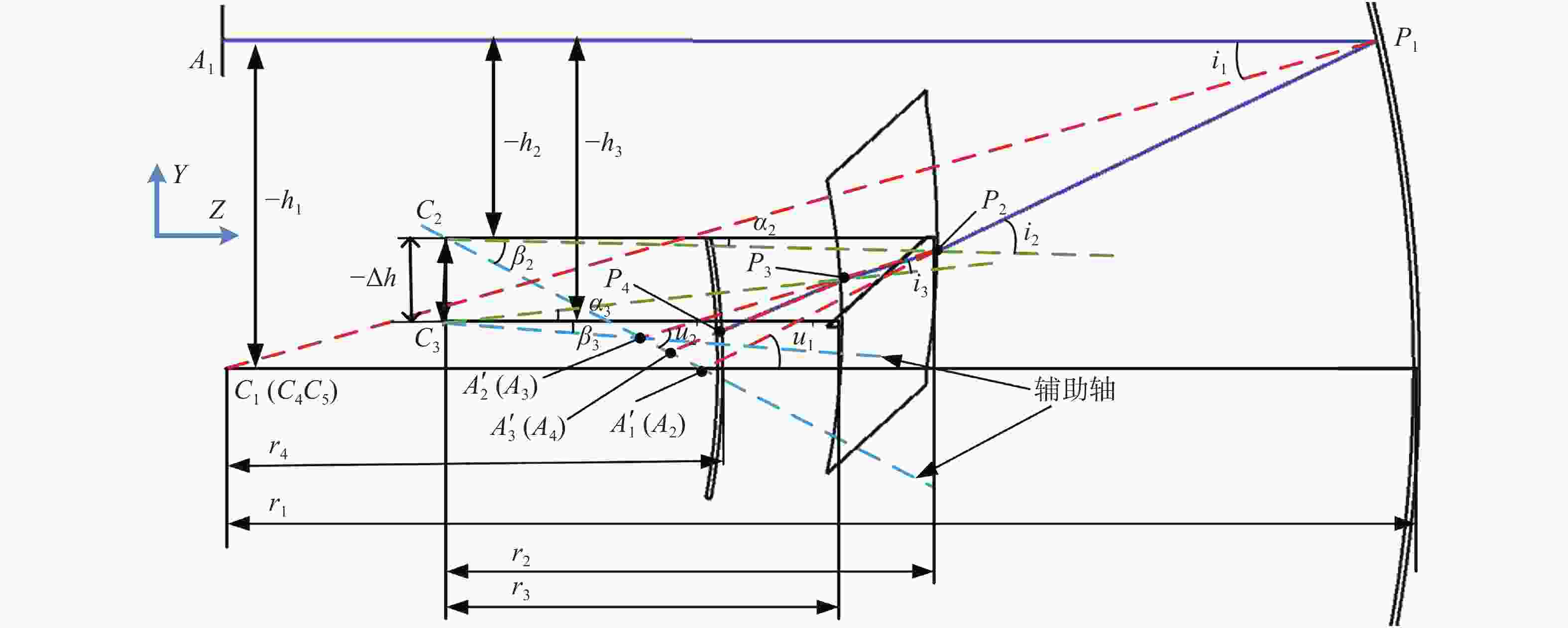
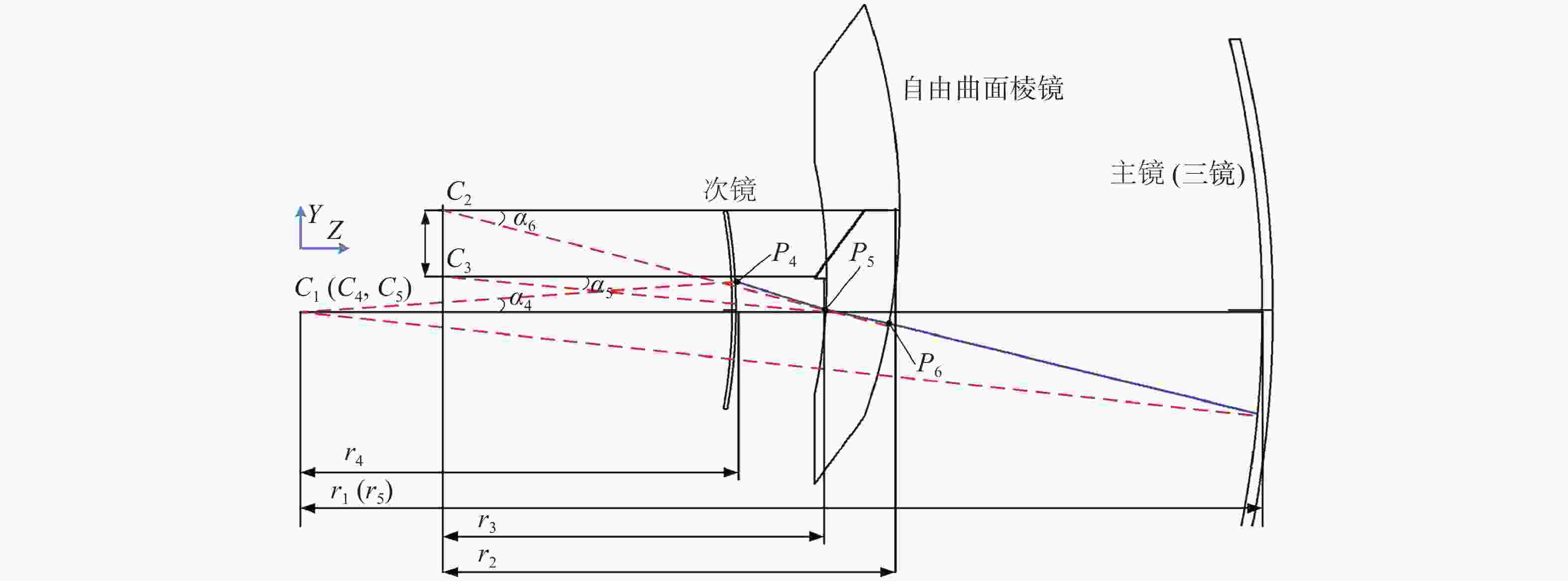
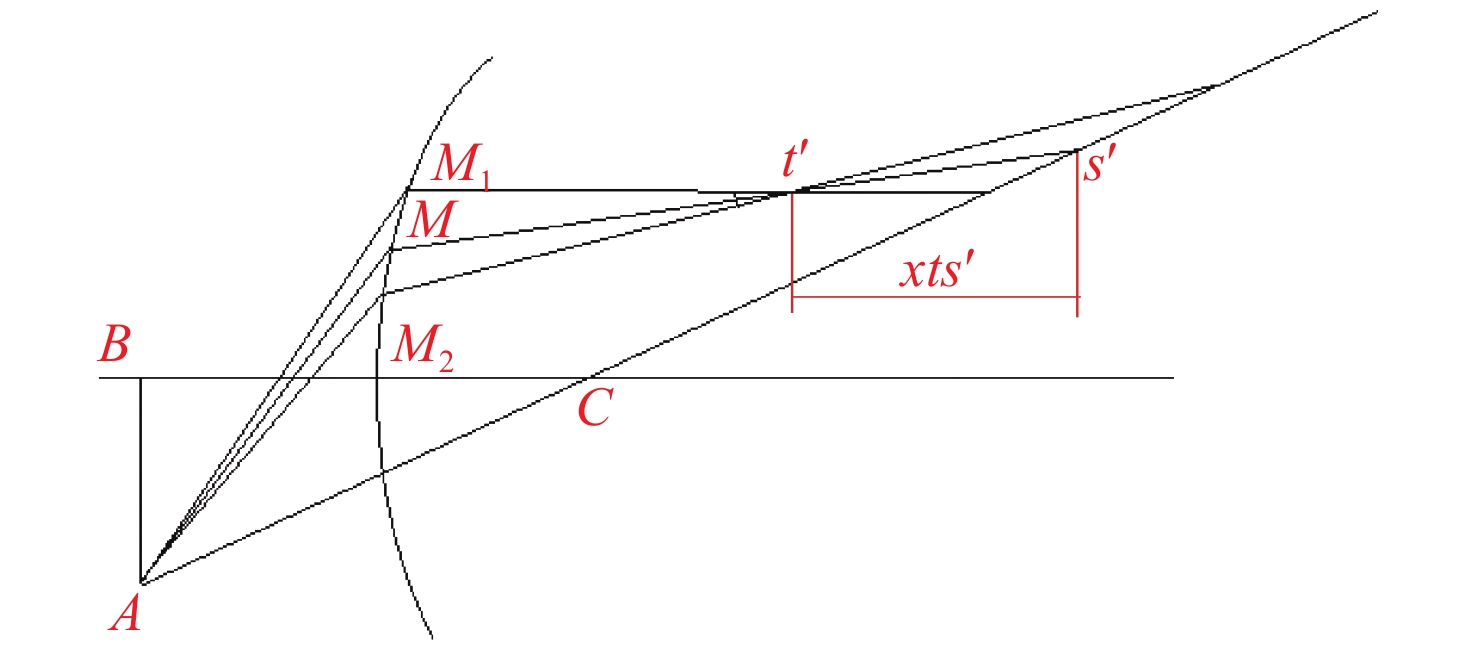
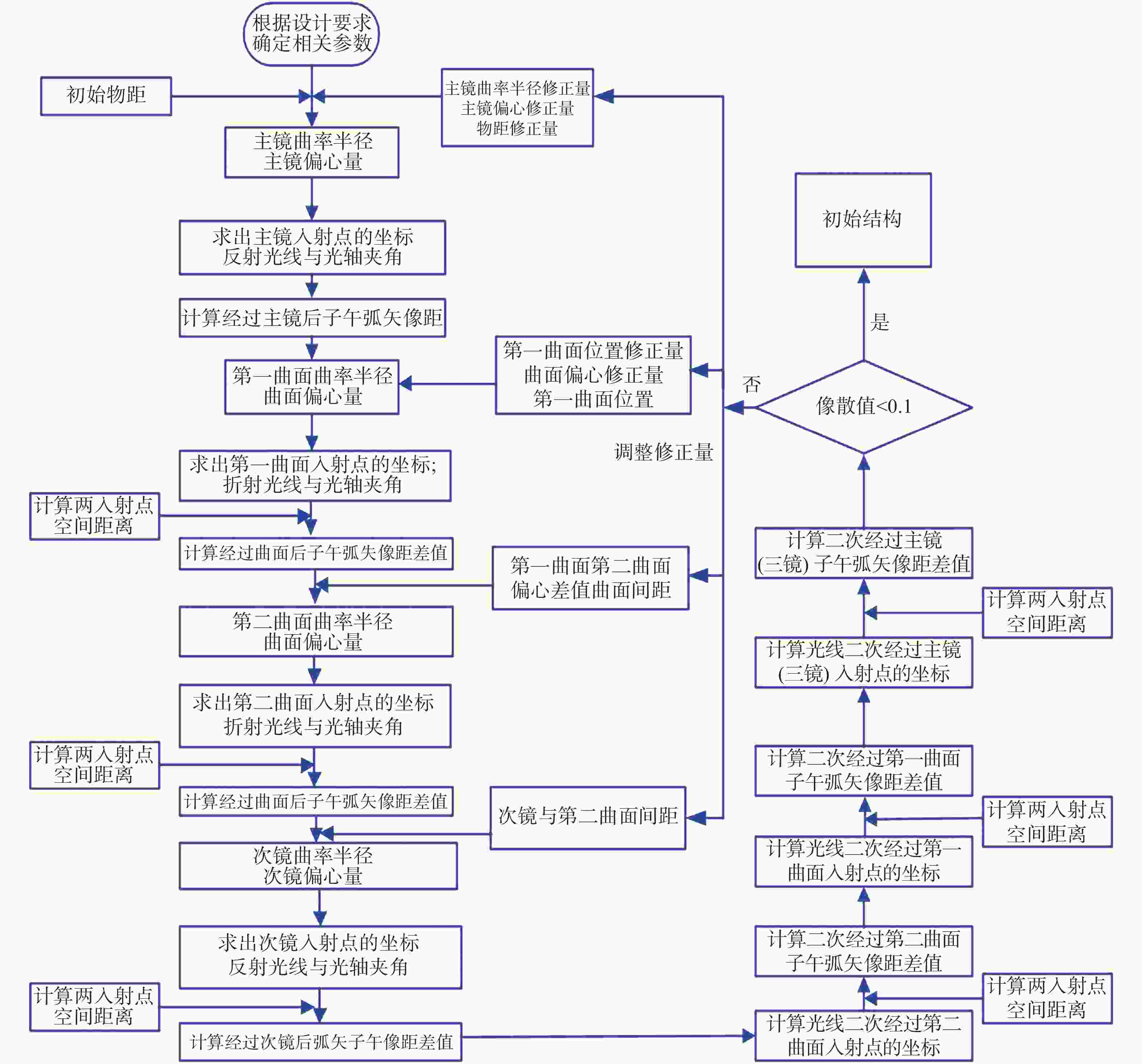
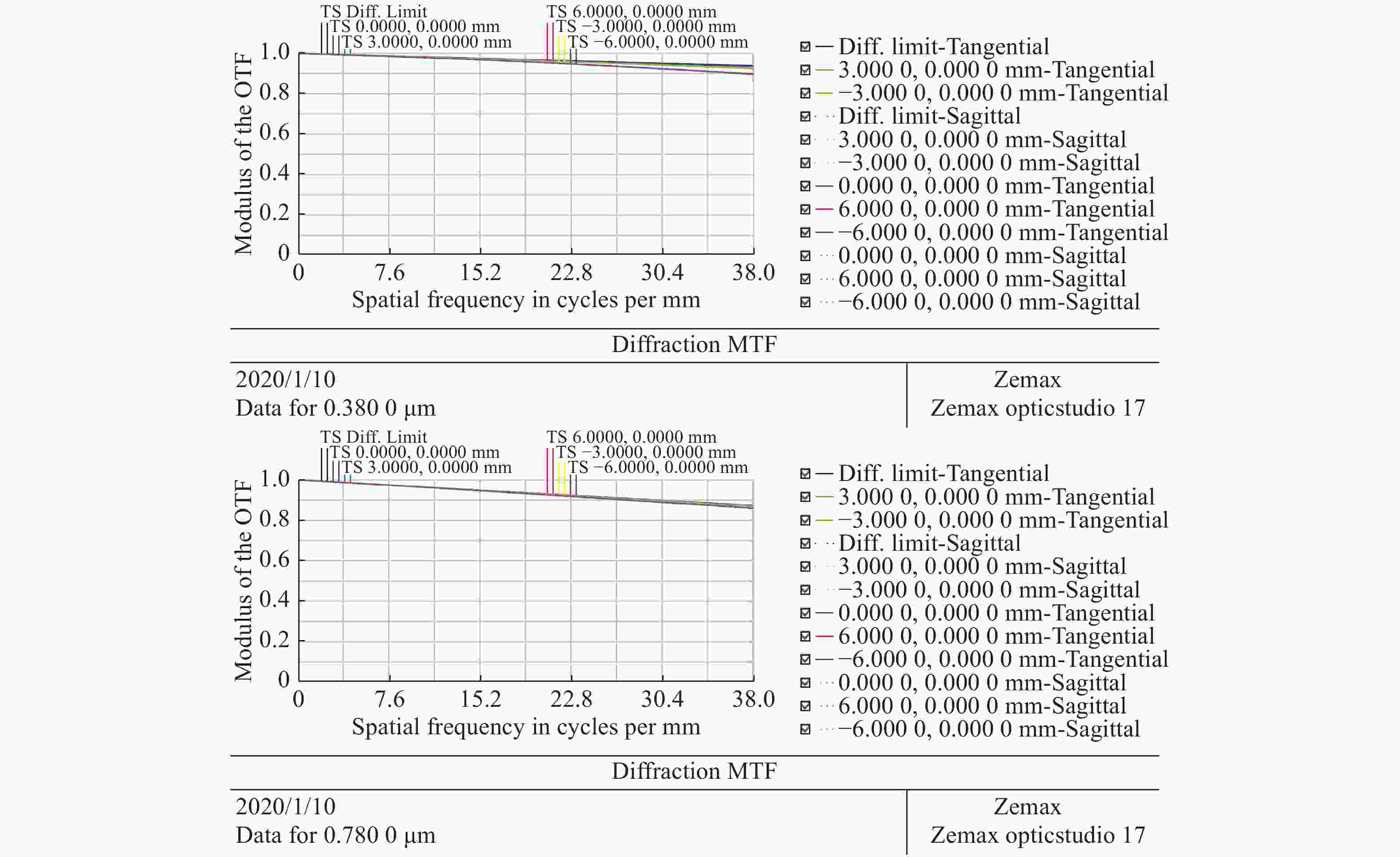
-
摘要: 本文根据像差理论，开发了一种计算次镜外反射的Offner型自由曲面棱镜光谱仪初始结构的算法。通过光线追迹获得光线在次镜外反射Offner型光谱仪各光学表面传播的公式，该公式可以确定光学元件的结构参数。应用轴外细光束像散理论分析系统产生的像散，并设定合理阈值作为结构算法的判断依据。在Matlab中迭代优化出符合设计要求的初始结构，使用Zemax软件对获得的初始结构进行优化。为验证算法效果，本文设计了光谱范围为380~780 nm，数值孔径为0.15，光谱分辨率为6 nm的自由曲面棱镜光谱仪的初始结构。在Zemax中完成优化后系统可达到设计指标且谱线弯曲和色畸变均优于0.1 pixels。设计结果表明采用本文算法可以快速计算出符合要求的初始结构，大大简化了后续优化的复杂程度。Abstract: In this paper, an algorithm for calculating the initial structure of the Offner freeform curved prism imaging spectrometer with secondary mirror external reflection is designed. The ray tracing method is used to obtain the formula for the propagation of light on the optical surfaces of an Offner spectrometer with secondary mirror external reflection. The formula can determine the structural parameters of the optical component. The off-axis beam astigmatism theory commonly used in the analysis of off-axis systems is used to analyze image quality, and a reasonable threshold is set to judge the structure algorithm. The initial structure that meets the design requirements is obtained through iterative optimization in Matlab and the initial structure is optimized in Zemax. To verify the performance of the proposed algorithm, the initial structure of a free-form prism spectrometer with a spectral range of 380~780 nm, a numerical aperture of 0.15 and a spectral resolution of 6 nm is designed. After being optimized in Zemax, the system reached the design index and the spectral line bending and color distortion are both less than 0.1 pixels. The algorithm proposed in this paper can quickly calculate the initial structure such that the requirements are satisfied, and can simplify its complexity.
-
Key words:
- freeform curved prism /
- ray tracing /
- anastigmatism /
- initial structure /
- optical design
-
图 1 次镜外反射型自由曲面棱镜光谱仪结构图
Figure 1. Structural diagram of the freeform curved prism imaging spectrometer with secondary mirror external reflection
图 2 次镜前自由曲面棱镜光谱仪光路示意图
Figure 2. Schematic diagram of the freeform curved prism spectrometer light path before secondary mirror
图 3 次镜后自由曲面棱镜光谱仪光路示意图
Figure 3. Schematic diagram of light path of the freeform curved prism spectrometer after secondary mirror
图 6 初始自由曲面棱镜光谱仪结构示意图
Figure 6. Schematic diagram of initial freeform curved prism spectrometer
图 7 优化后的自由曲面棱镜光谱仪结构示意图
Figure 7. Schematic diagram of the optimized freeform curved prism spectrometer
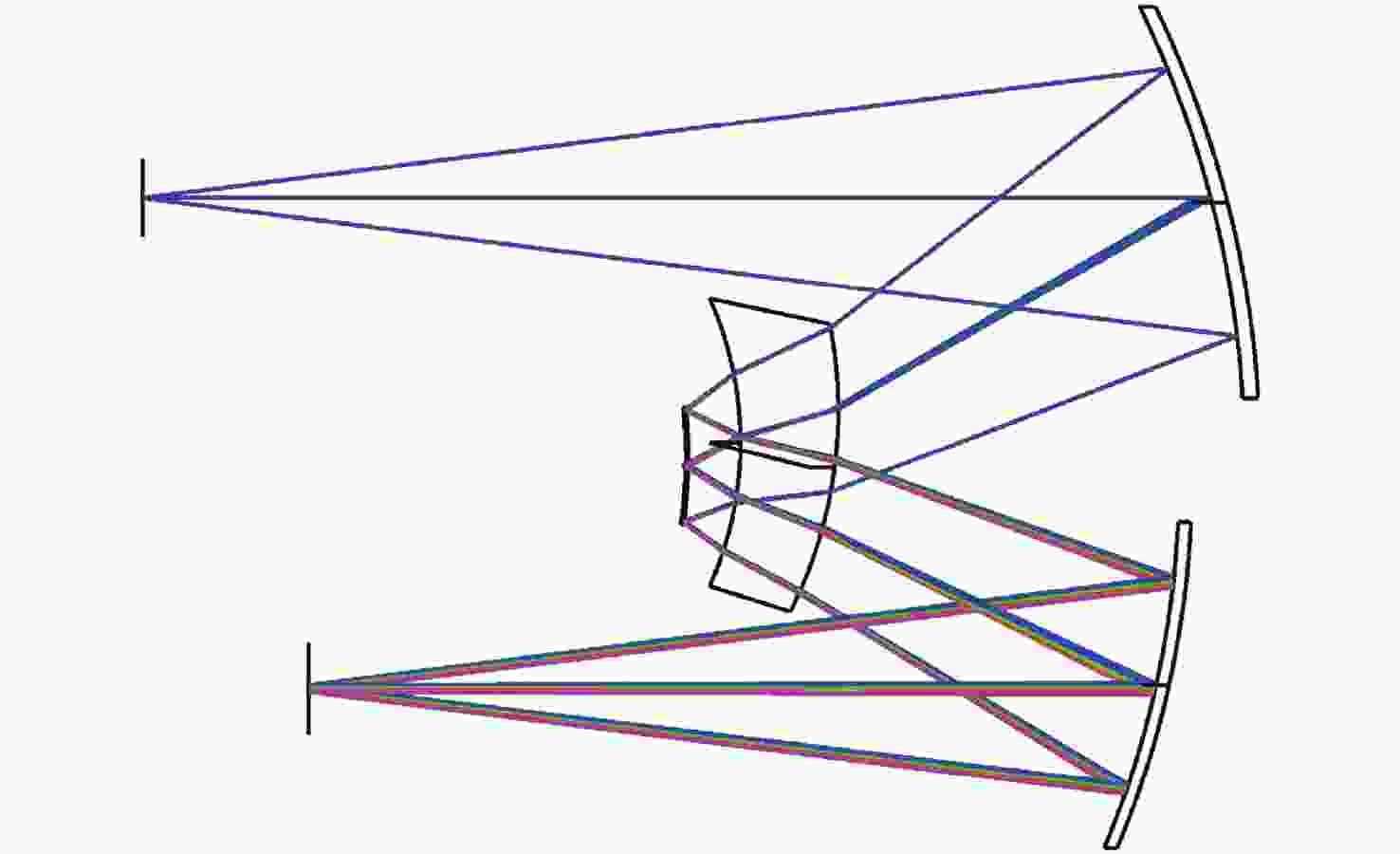
表 1 设计指标
Table 1. Specifications designed for the system
参数 设计值 光谱范围/nm 380~780 数值孔径 0.15 光谱分辨率/nm 6 像元尺寸/µm 13 × 13 色散元件材料 ZF6 色散面大小 1 mm 
下载: 导出CSV
表 2 初始结构数据
Table 2. Initial structural data (mm)
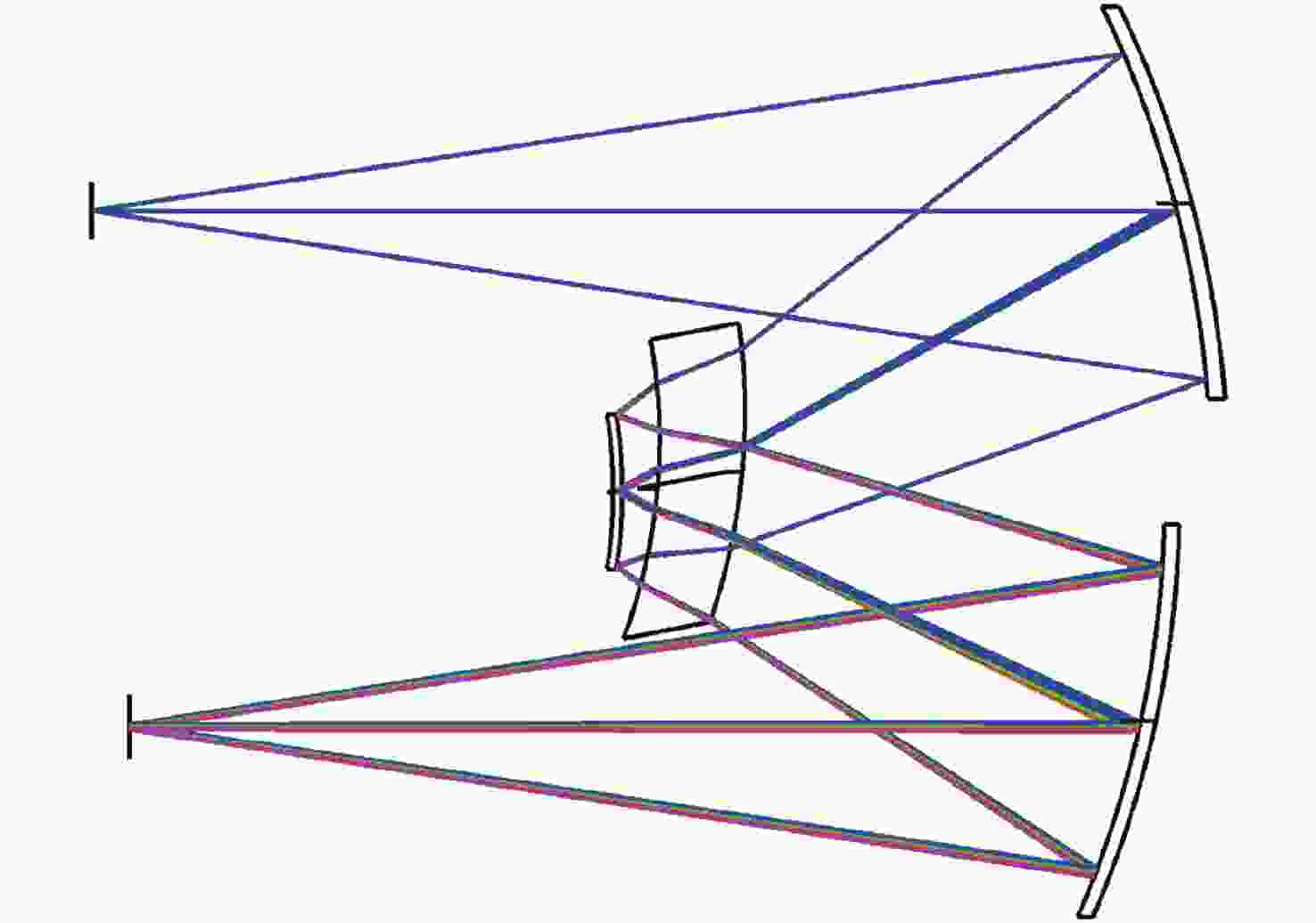
表面 半径 厚度 材料 偏心量 1 − 249.500 000 2 −248.510 000 −104.255 000 MIRROR −45.990 000 3 −138.305 000 −15.990 000 ZF6 −36.980 000 4 −122.315 000 −5.990 000 −43.980 000 5 −122.275 000 5.990 000 MIRROR −45.990 000 6 −122.315 000 15.990 000 ZF6 −43.980 000 7 −138.305 000 104.255 000 −36.980 000 8 −248.510 000 − MIRROR −45.990 000 9 − −
下载: 导出CSV
表 3 优化后结构数据
Table 3. Optimized structural data (mm)
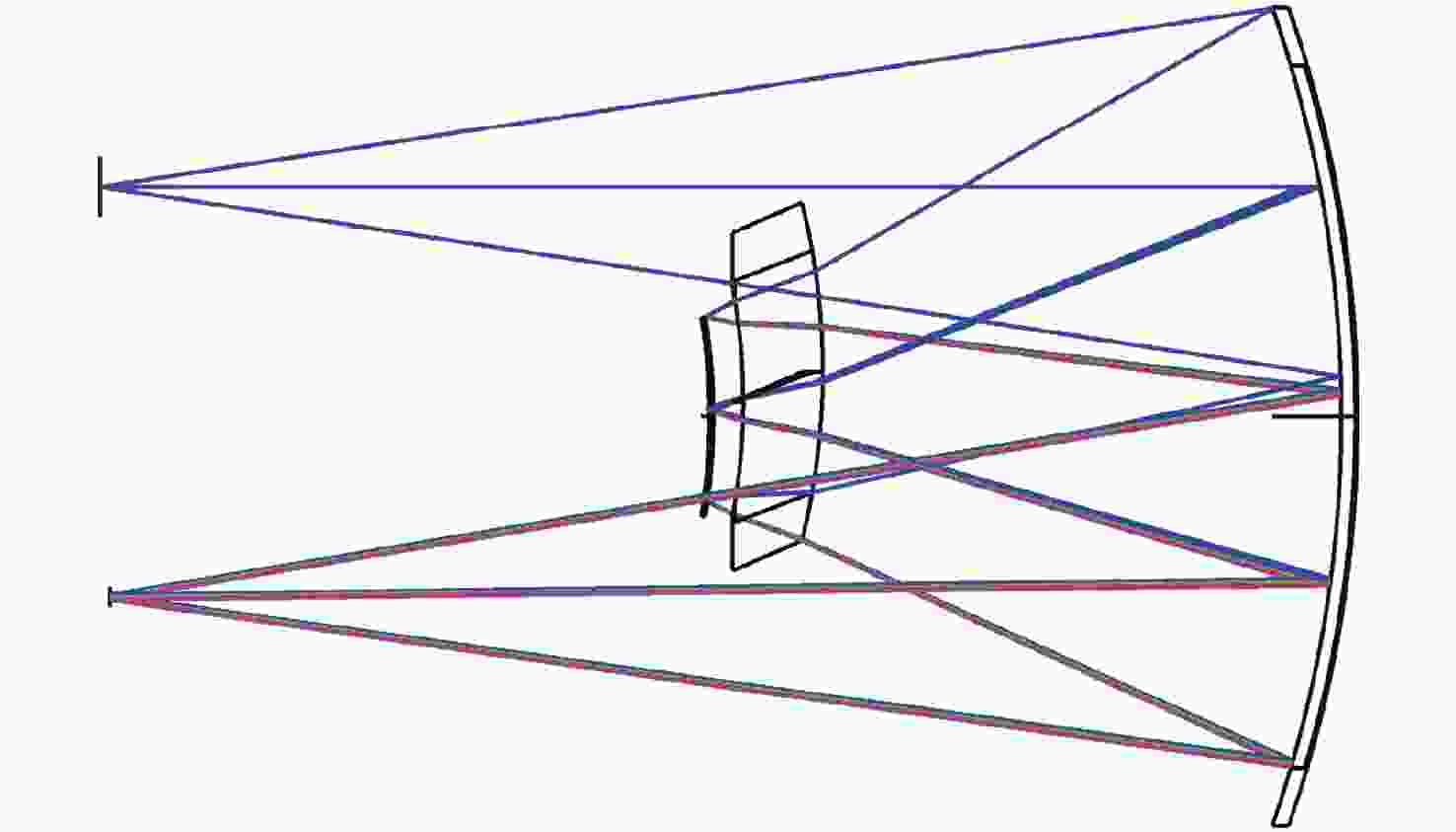
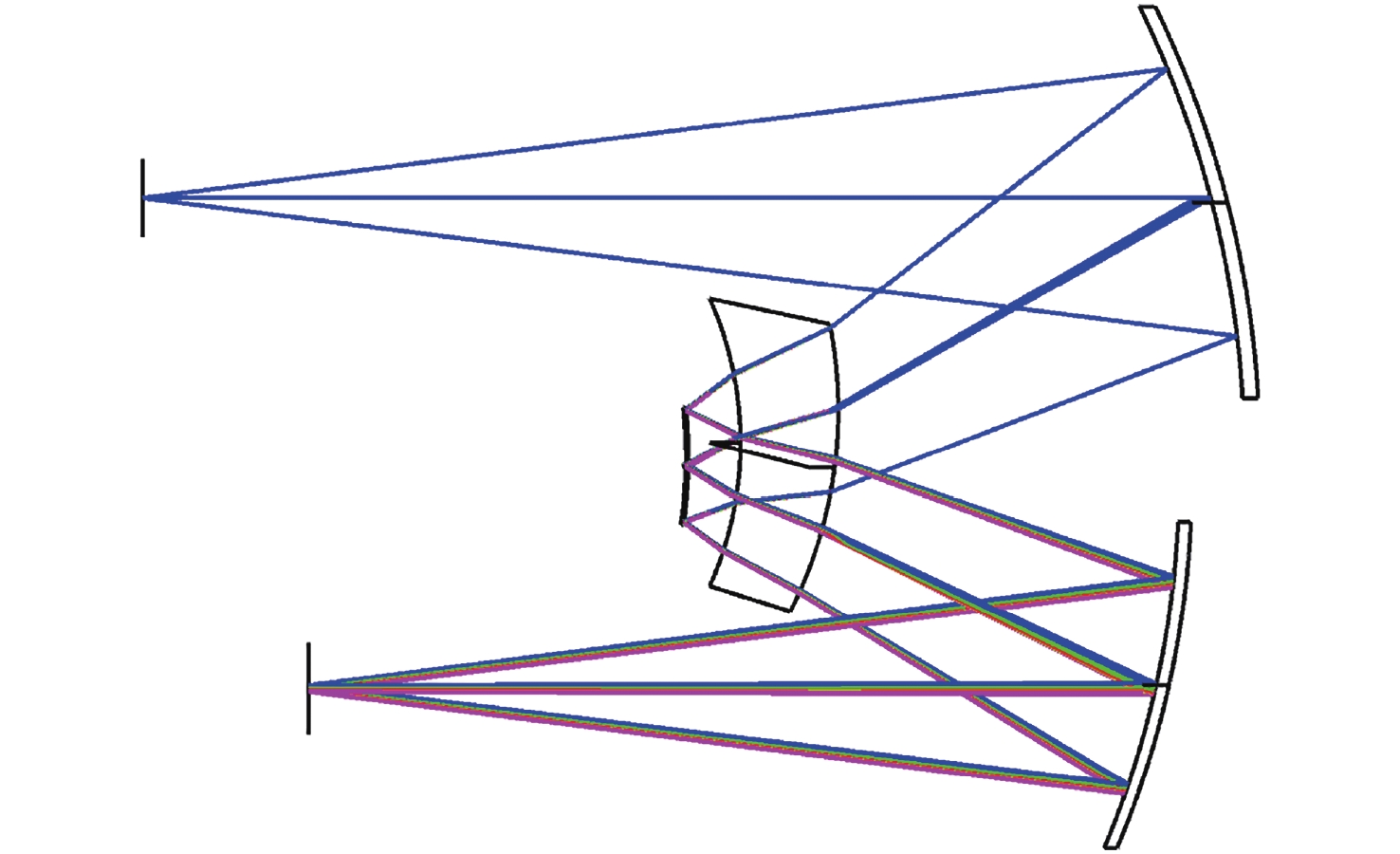
表面 半径 厚度 材料 偏心量 1 —— 240.045 897 2 −234.113 632 −99.964 613 MIRROR −58.302 387 3 −138.439 720 −18.303 653 ZF6 −42.950 734 4 −120.219 597 −7.986 594 −49.982 314 5 −105.485 631 7.986 594 MIRROR −60.171 600 6 −120.219 597 18.303 653 ZF6 −49.982 314 7 −138.439 720 89.943 651 −42.950 734 8 −223.969 005 —— MIRROR −61.713 353 9 —— ——
下载: 导出CSV
-
[1] 郑玉权. 小型Offner光谱成像系统的设计[J]. 光学精密工程,2005,13(6):650-657. doi: 10.3321/j.issn:1004-924X.2005.06.005ZHENG Y Q. Design of compact Offner spectral imaging system[J]. Optics and Precision Engineering, 2005, 13(6): 650-657. (in Chinese) doi: 10.3321/j.issn:1004-924X.2005.06.005 [2] SANG B, SCHUBERT J, KAISER S, et al. The EnMAP hyperspectral imaging spectrometer: instrument concept, calibration, and technologies[J]. Proceedings of SPIE, 2008, 7086: 708605. doi: 10.1117/12.794870 [3] FÉRY C. A prism with curved faces, for spectrograph or spectroscope[J]. The Astrophysical Journal, 1911, 34(1): 79. [4] MORRISSEY P F. Third-order aberrations of a prism with spherically curved surfaces[J]. Applied Optics, 1994, 33(13): 2539-2543. doi: 10.1364/AO.33.002539 [5] 刘力. Fery棱镜特性及应用研究[D]. 苏州: 苏州大学, 2013.LIU L. Research of the properties and application of Fery prism[D]. Suzhou: Soochow University, 2013. (in Chinese) [6] 刘立银. 曲面棱镜Offner高光谱成像系统的设计研究[D]. 南京: 南京理工大学, 2016.LIU L Y. Design and research of curved prism Offner hyperspectral imaging system[D]. Nanjing: Nanjing University of Science and Technology, 2016. (in Chinese) [7] 张营.长波红外高光谱成像仪光学技术研究[D].北京: 中国科学院大学,2016ZHANG Y. Optical technology of long-wave infrared hyperspectral imaging[D]. Beijing: University of Chinese Academy of Sciences, 2016. (in Chinese) [8] 胡海翔.空间光学自由曲面应用的关键技术研究[D].北京: 中国科学院大学,2017HU H X. Research on the key technologies in the application of space optical freeform surfaces[D]. Beijing: University of Chinese Academy of Sciences, 2017. (in Chinese) [9] LOBB D R. Imaging spectrometers using concentric optics[J]. Proceedings of SPIE, 1997, 3118: 339-347. doi: 10.1117/12.283838 [10] 张云翠, 刘龙, 曹冠英, 等. Fery棱镜光谱仪设计[J]. 红外与激光工程,2009,38(2):287-289. doi: 10.3969/j.issn.1007-2276.2009.02.021ZHANG Y C, LIU L, CAO G Y, et al. Design of spectrograph with novel Fery prism[J]. Infrared and Laser Engineering, 2009, 38(2): 287-289. (in Chinese) doi: 10.3969/j.issn.1007-2276.2009.02.021 [11] 聂云峰, 相里斌, 周锦松, 等. 基于曲面棱镜的宽视场推帚式高光谱成像仪设计[J]. 光谱学与光谱分析,2012,32(6):1708-1711. doi: 10.3964/j.issn.1000-0593(2012)06-1708-04NIE Y F, XIANG L B, ZHOU J S, et al. A wide-field push-broom hyperspectral imager based on curved prism[J]. Spectroscopy and Spectral Analysis, 2012, 32(6): 1708-1711. (in Chinese) doi: 10.3964/j.issn.1000-0593(2012)06-1708-04 [12] 刘光宏, 吴刚, 凌青, 等. Offner成像光谱仪建模及像差分析[J]. 光学学报,2011,31(3):0322001. doi: 10.3788/AOS201131.0322001LIU G H, WU G, LING Q, et al. Modelling of Offner imaging spectrometers and aberrations analysis[J]. Acta Optica Sinica, 2011, 31(3): 0322001. (in Chinese) doi: 10.3788/AOS201131.0322001 [13] FENG L, ZHOU J S, WANG D. A miniature design of near infrared spectrometer with wide field of view[J]. Proceedings of SPIE, 2014, 9298: 92980M. [14] 赵渊明. 消像散自由曲面离轴显示系统设计方法研究[D]. 长春: 长春理工大学, 2018.ZHAO Y M. Studies on the design of off-axis display systems with an astigmatic free-form surface[D]. Changchun: Changchun University of Science and Technology, 2018. (in Chinese) [15] FENG L, ZHOU J S, JING J J, et al. A design of miniature imaging spectrometer with Fery prism[J]. Proceedings of SPIE, 2016, 10000: 100001P. [16] DONG W, NIE Y F, ZHOU J S, et al. Design of a concise Féry-prism hyperspectral imaging system based on multi-configuration[J]. Proceedings of SPIE, 2013, 8910: 89100B. -
下载:
计量
- 文章访问数: 2348
- HTML全文浏览量: 981
- PDF下载量: 190
- 被引次数: 0
