Light intensity and spatial coherence characteristics of laser coherent detection in a turbulent atmosphere
-
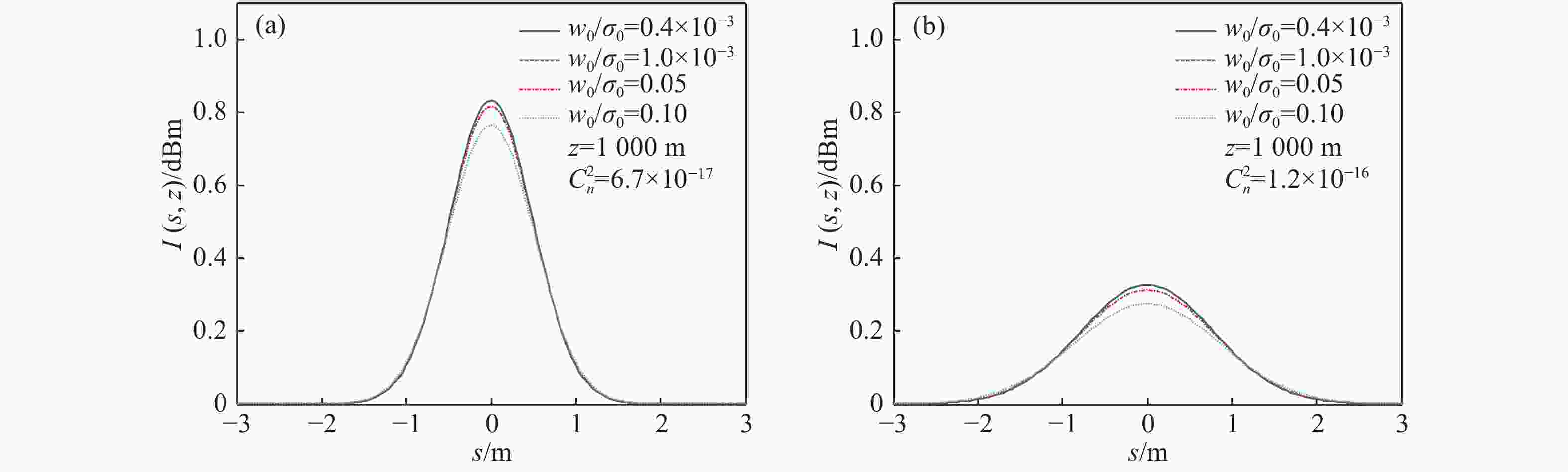
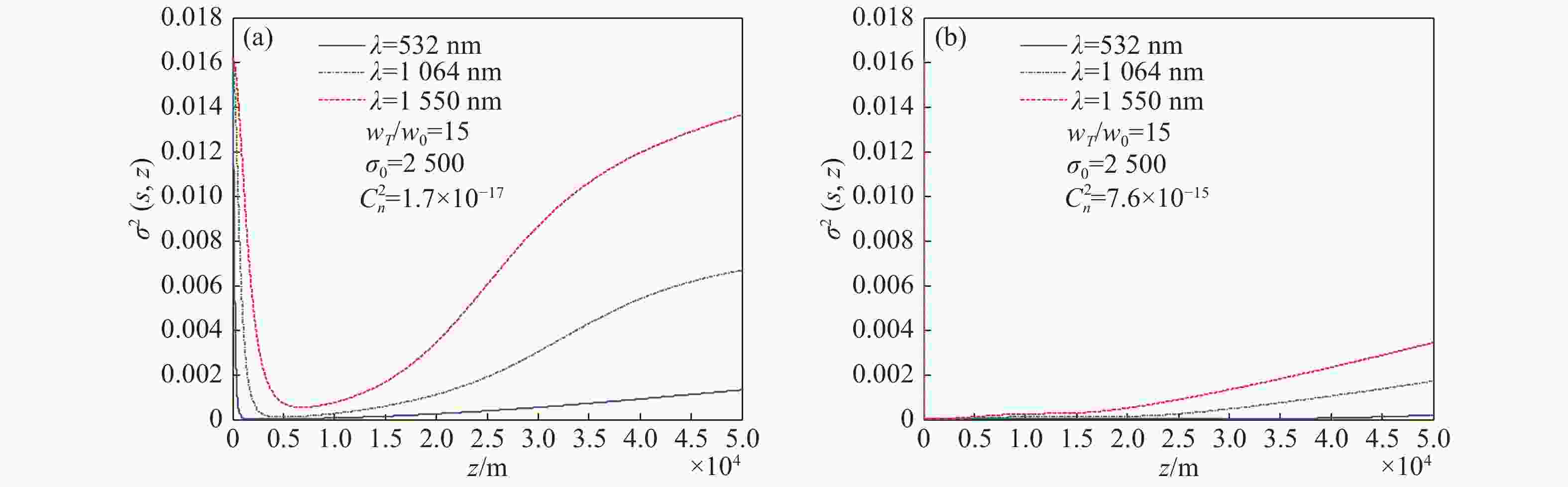
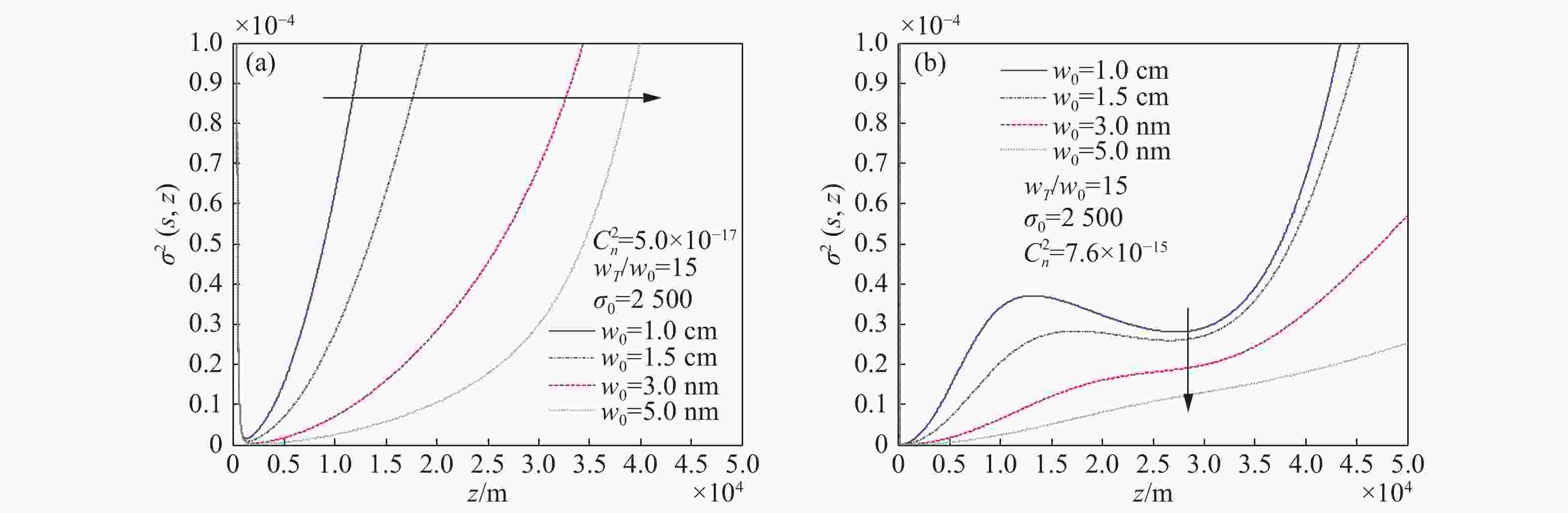
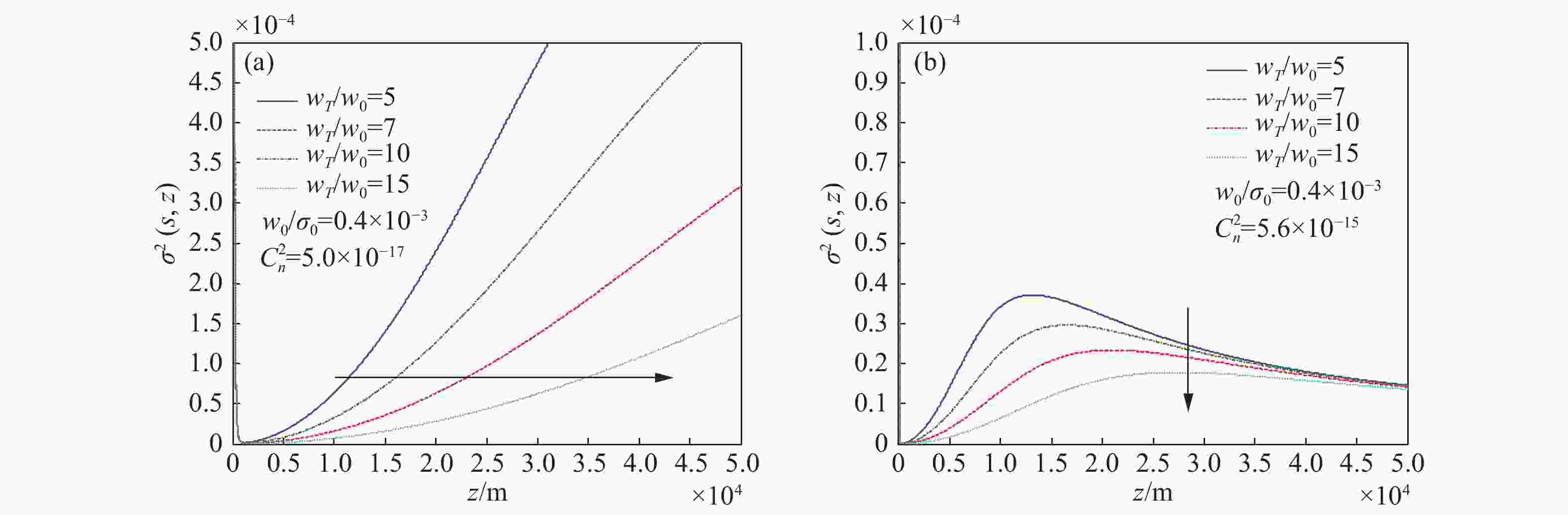
摘要: 本文利用广义惠更斯-菲涅尔原理结合Goodman目标散射理论，推导出了激光探测中目标反射光的交叉谱密度函数解析式，并进一步得到了目标反射光的光强分布和空间相干长度表达式。利用得到的表达式在湍流大气条件下，分析了不同光源参数和目标反射光参数对目标反射光光强分布和相干长度的影响。研究结果表明：光源相干长度对归一化反射光强影响较小；光源束腰半径和反射光斑半径值越大接收光的相干长度值越小；随着传输距离的增加，相干长度增加越来越缓慢；在弱湍流大气传输过程中，光源参数对接收光的影响占主导作用，光源束腰半径越大接收光的光强和相干长度值越小；在强湍流大气传输过程中，大气湍流对反射光的影响起主导作用。Abstract: In this paper, the cross-spectral density function of target reflected light in laser detection is obtained by using generalized Huygens-Fresnel principle and Goodman target scattering theory. On the basis of above, the expression of intensity distribution and spatial coherence length of target reflected light is derived. The influence of different light source and target reflected light parameters on the intensity distribution and coherent length of the target reflected light is simulated by using the expressions obtained in this paper under turbulent atmospheric conditions. The results show that the coherence length of the light source has little effect on the normalized light intensity distribution; the coherence length of the received light is smaller with a larger beam waist radius and reflected light radius, and the coherence length increases at a slower rate as the transmission distance increases. In the process of weak turbulent atmospheric transmission, the influence of light source parameters on the received light is much stronger. The larger the beam waist radius, the smaller the received light intensity and coherence length value. During strong turbulent atmospheric transmission, the influence of atmospheric turbulence on the received light is dominant.
-
Key words:
- laser detection /
- atmospheric turbulence /
- intensity distribution /
- coherence length
-
图 1 不同波长的归一化光强随传输距离的变化曲线
Figure 1. Curves of normalized intensity varying with transmission distance with different wavelengths
图 2 不同湍流强度和
${{{{w_0}} / {{\sigma _0}}}}$ 时，接收平面上的归一化光强分布Figure 2. Normalized intensity distributions at the receiving plane with different
$C_n^2$ and${{{{w_0}} / {{\sigma _0}}}}$ 
图 3 不同湍流强度和
${{{w_T}} / {{w_0}}}$ 时，中心接收光强随传输距离z的变化曲线Figure 3. Center average received light intensity varying with transmission distance with different
$C_n^2 $ and${{{w_T}} / {{w_0}}}$ 
图 4 不同湍流强度下3种波长接收光场的相干长度变化曲线
Figure 4. Coherent length curves of the received light field varying with the wavelength and
$C_n^2 $ 
图 5 不同光源束宽和湍流强度时，目标反射光的相干长度变化曲线
Figure 5. Coherent length curves of target reflected light varying with the beam width and turbulence intensity
图 6 不同湍流强度下，目标反射光与光源不同束腰比时，目标反射光的空间相干长度变化曲线
Figure 6. Spatial coherence length curves of the reflected light varying with beam waist ratio under different
$C_n^2 $ 表 1 数值模拟参数
Table 1. Parameters of numerical simulation
系统参数 符号 数值 激光波长 $\lambda $ 532 nm、1 064 nm、1 550 nm 束腰半径 ${w_0}$ 3 cm 湍流内尺度 ${l_0}$ 1~5 cm 束腰半径与相干长度比 ${{{w_0}}/ {{\sigma _0}}}$ 10−4~0.1 大气结构常数 $C_n^2$ $0 : {10^{ - 15} }{\rm{m}^{ { { - 2} / 3} } }$ 目标反射率 F 0~1 
下载: 导出CSV
-
[1] LU W, LIU L R, SUN J F, et al. Change in degree of coherence of partially coherent electromagnetic beams propagating through atmospheric turbulence[J]. Optics Communications, 2007, 271(1): 1-8. doi: 10.1016/j.optcom.2006.09.058 [2] 周鑫, 姜鹏, 孙剑峰, 等. 基于点目标大气闪烁的目标回波分布研究[J]. 红外与激光工程,2017,46(S1):74-81.ZHOU X, JIANG P, SUN J F, et al. Investigation on the distribution of target echo based on point target atmospheric scintillation[J]. Infrared and Laser Engineering, 2017, 46(S1): 74-81. (in Chinese) [3] COLLETT E, WOLF E. Beams generated by Gaussian quasi-homogeneous sources[J]. Optics Communications, 1980, 32(1): 27-31. doi: 10.1016/0030-4018(80)90307-7 [4] KOROTKOVA O, ANDREWS L C, PHILLIPS R L. Lidar model for a rough-surface target: method of partial coherence[J]. Proceedings of SPIE, 2004, 5237: 49-60. doi: 10.1117/12.515086 [5] GOODMAN J W. Statistical properties of laser speckle patterns[M]. DAINTY J C. Laser Speckle and Related Phenomena. Berlin, Heidelberg: Springer, 1975. [6] KOROTKOVA O, CAI Y, WATSON E. Stochastic electromagnetic beams for LIDAR systems operating through turbulent atmosphere[J]. Applied Physics B, 2009, 94(4): 681-690. doi: 10.1007/s00340-009-3404-4 [7] RICKLIN J C, DAVIDSON F M. Atmospheric turbulence effects on a partially coherent Gaussian beam: implications for free-space laser communication[J]. Journal of the Optical Society of America A, 2002, 19(9): 1794-1802. doi: 10.1364/JOSAA.19.001794 [8] RICKLIN J C, DAVIDSON F M. Atmospheric optical communication with a Gaussian Schell beam[J]. Journal of the Optical Society of America A, 2003, 20(5): 856-866. doi: 10.1364/JOSAA.20.000856 [9] WU J, BOARDMAN A D. Coherence length of a Gaussian-Schell beam and atmospheric turbulence[J]. Journal of Modern Optics, 1991, 38(7): 1355-1363. doi: 10.1080/09500349114551521 [10] FRIBERG A T, SUDOL R J. Propagation parameters of Gaussian Schell-model beams[J]. Optics Communications, 1982, 41(6): 383-387. doi: 10.1016/0030-4018(82)90161-4 [11] LI M N, TAN L Y, MA J, et al. Performance analysis of a free-space laser communication system with a Gaussian Schell model[J]. Journal of Modern Optics, 2015, 62(19): 1608-1615. doi: 10.1080/09500340.2015.1054907 [12] 柯熙政, 王婉婷. 部分相干光在大气湍流中的光束扩展及角扩展[J]. 红外与激光工程,2015,44(9):2726-2733. doi: 10.3969/j.issn.1007-2276.2015.09.032KE X ZH, WANG W T. Expansion and angular spread of partially coherent beam propagating in atmospheric turbulence[J]. Infrared and Laser Engineering, 2015, 44(9): 2726-2733. (in Chinese) doi: 10.3969/j.issn.1007-2276.2015.09.032 [13] WU ZH S, LI Y Q. Scattering of a partially coherent Gaussian-Schell beam from a diffuse target in slant atmospheric turbulence[J]. Journal of the Optical Society of America A, 2011, 28(7): 1531-1539. doi: 10.1364/JOSAA.28.001531 [14] 李成强, 张合勇, 王挺峰, 等. 高斯-谢尔模光束在大气湍流中传输的相干特性研究[J]. 物理学报,2013,62(22):224203. doi: 10.7498/aps.62.224203LI CH Q, ZHANG H Y, WANG T F, et al. Investigation on coherence characteristics of Gauss-Schell model beam propagating in atmospheric turbulence[J]. Acta Physica Sinica, 2013, 62(22): 224203. (in Chinese) doi: 10.7498/aps.62.224203 [15] LI M N, TAN L Y, MA J, et al. Statistical distribution of the optical intensity obtained using a Gaussian Schell model for space-to-ground link laser communications[J]. Journal of Modern Optics, 2016, 63(10): 921-931. doi: 10.1080/09500340.2015.1111452 [16] 向宁静, 王明军, 王太荣. 部分相干高斯-谢尔光束在大气湍流中的平均强度与展宽[J]. 激光杂志,2012,33(5):4-6. doi: 10.3969/j.issn.0253-2743.2012.05.003XIANG N J, WANG M J, WANG T R. Average intensity and spreading of a partially coherent Gaussian Schell-model beam propagation through atmospheric turbulence[J]. Laser Journal, 2012, 33(5): 4-6. (in Chinese) doi: 10.3969/j.issn.0253-2743.2012.05.003 [17] 埃米尔·沃尔夫. 光的相干与偏振理论导论[M]. 蒲继雄, 译. 北京: 北京大学出版社, 2014.WOLF E. Introduction to the Theory of Coherence and Polarization of light[M]. PU J X, trans. Beijing: Beijing University Press, 2014. (in Chinese) -
下载:
计量
- 文章访问数: 2358
- HTML全文浏览量: 1241
- PDF下载量: 88
- 被引次数: 0
