湍流大气对光束相干合成效果的影响

宋纪坤; 李远洋; 车东博; 郭劲; 王挺峰; 李志来

doi:10.37188/CO.2019-0197

湍流大气对光束相干合成效果的影响

宋纪坤^{1, 2,},
李远洋¹,
车东博^{1, 2},
郭劲¹,
王挺峰^1, ,,
李志来³

1.
中国科学院长春光学精密机械与物理研究所激光与物质相互作用国家重点实验室，吉林长春 130033
2.
中国科学院大学，北京 100049
3.
中国科学院长春光学精密机械与物理研究所空间光学研究二部，吉林长春 130033

详细信息

中图分类号: TN249
计量
- 文章访问数: 3246
- HTML全文浏览量: 1507
- PDF下载量: 120
- 被引次数: 0
出版历程
- 收稿日期: 2019-10-08
- 修回日期: 2019-11-09
- 刊出日期: 2020-08-01

Influence of turbulent atmosphere on the effect of coherent beam combining

doi: 10.37188/CO.2019-0197

SONG Ji-kun^{1, 2
,},
LI Yuan-yang¹,
CHE Dong-bo^{1, 2},
GUO Jin¹,
WANG Ting-feng^{1
, ,},
LI Zhi-lai³

1.
State Key Laboratory of Laser Interaction with Matter, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China;
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Space Optical Department Ⅱ, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

Funds: Supported by National Key R&D Program of China (No. 2016YFB0500100); National Natural Science Foundation of China (No. 61805234); Fund of the State Key Laboratory of Laser Interaction with Matter (No. SKLLIM1704); Key Research Program of Frontier Sciences, CAS(No. QYZDB-SSW-SLH014); Civil Aerospace Pre-research Project (No. D040101)

More Information

Author Bio:
SONG Ji-kun (1992—), male, born in Heze County, Shandong Province. He is a doctoral candidate. In 2015, he obtained his bachelor's degree from Shandong Jianzhu University. He is mainly engaged in the research of beam transmission and control. E-mail: song_jk@126.com

WANG Ting-feng (1977—), male, born in Wendeng City, Shandong Province. He is a doctor, researcher and doctoral supervisor. He obtained his bachelor's degree from former Jilin University of Technology in 1999, master's degree from Jilin University in 2002, and doctor's degree from Changchun Institute of Optics, Fine Mechanics and Physics, CAS in 2005. He is mainly engaged in the research of laser application and photoelectricity. E-mail: wangtingfeng@ciomp.ac.cn

Corresponding author: wangtingfeng@ciomp.ac.cn

摘要

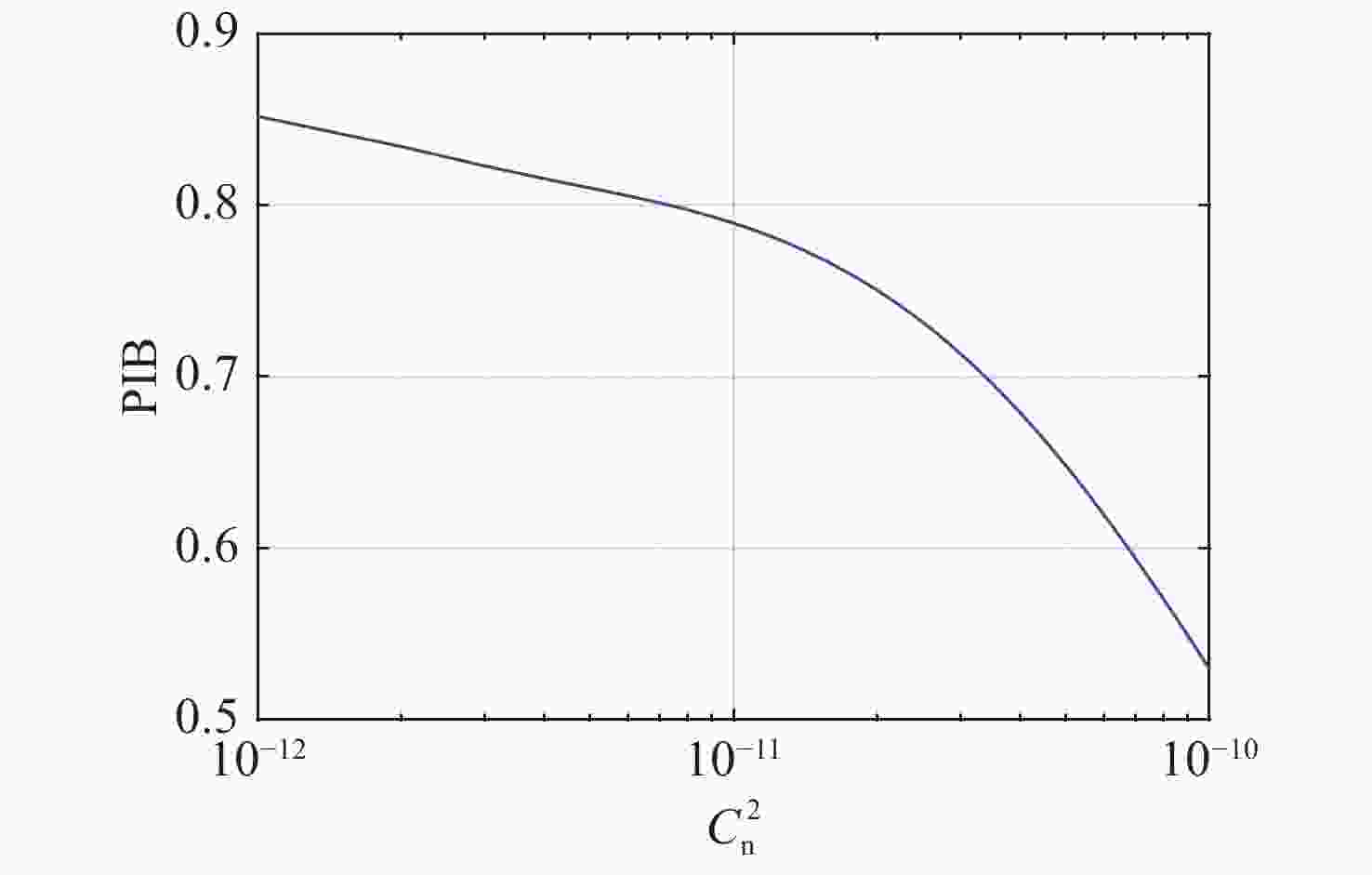
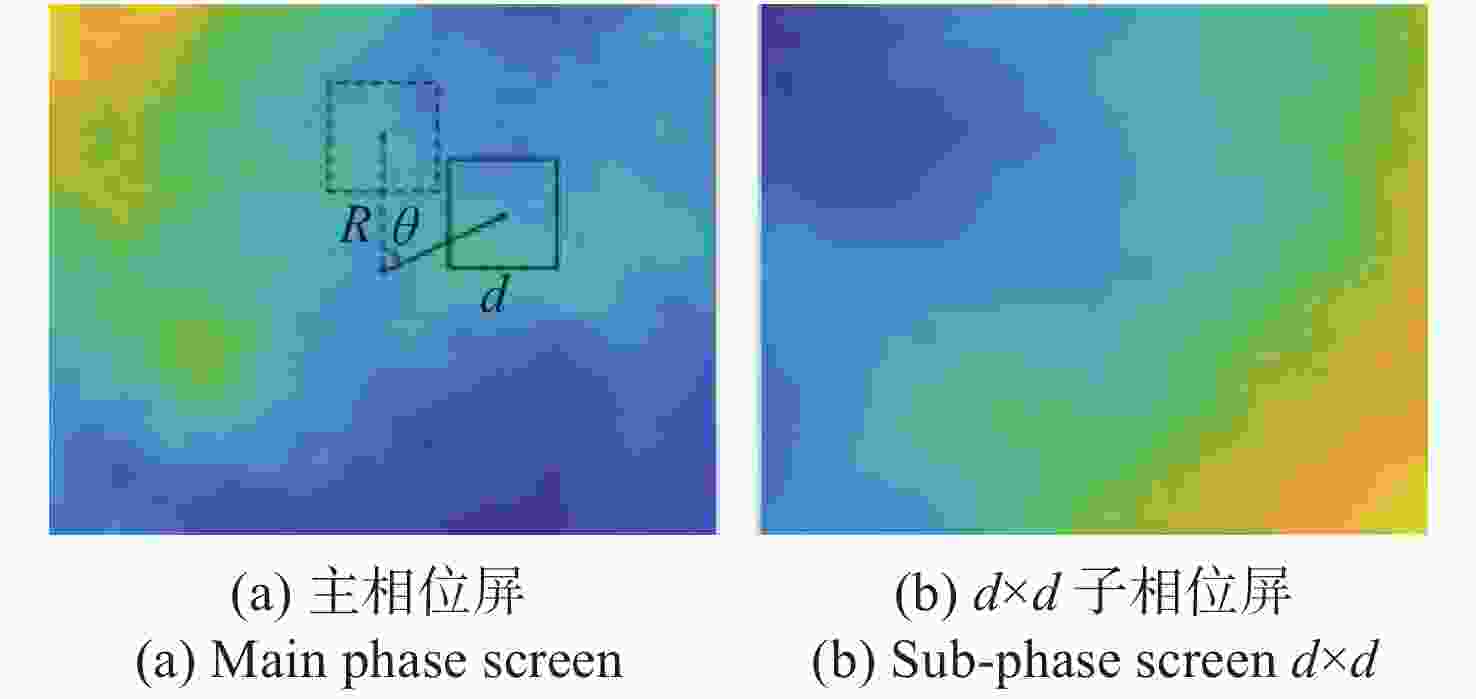
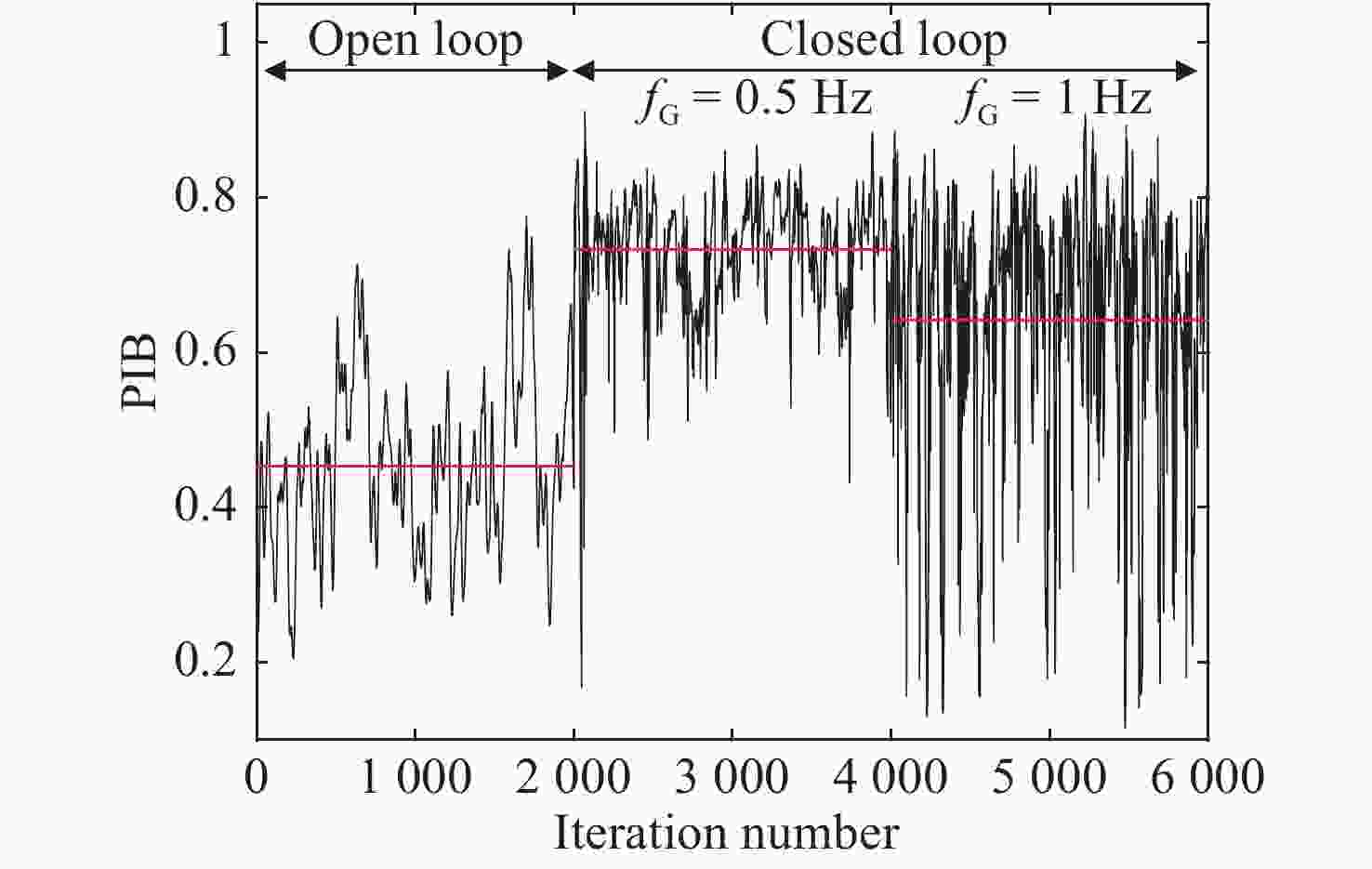
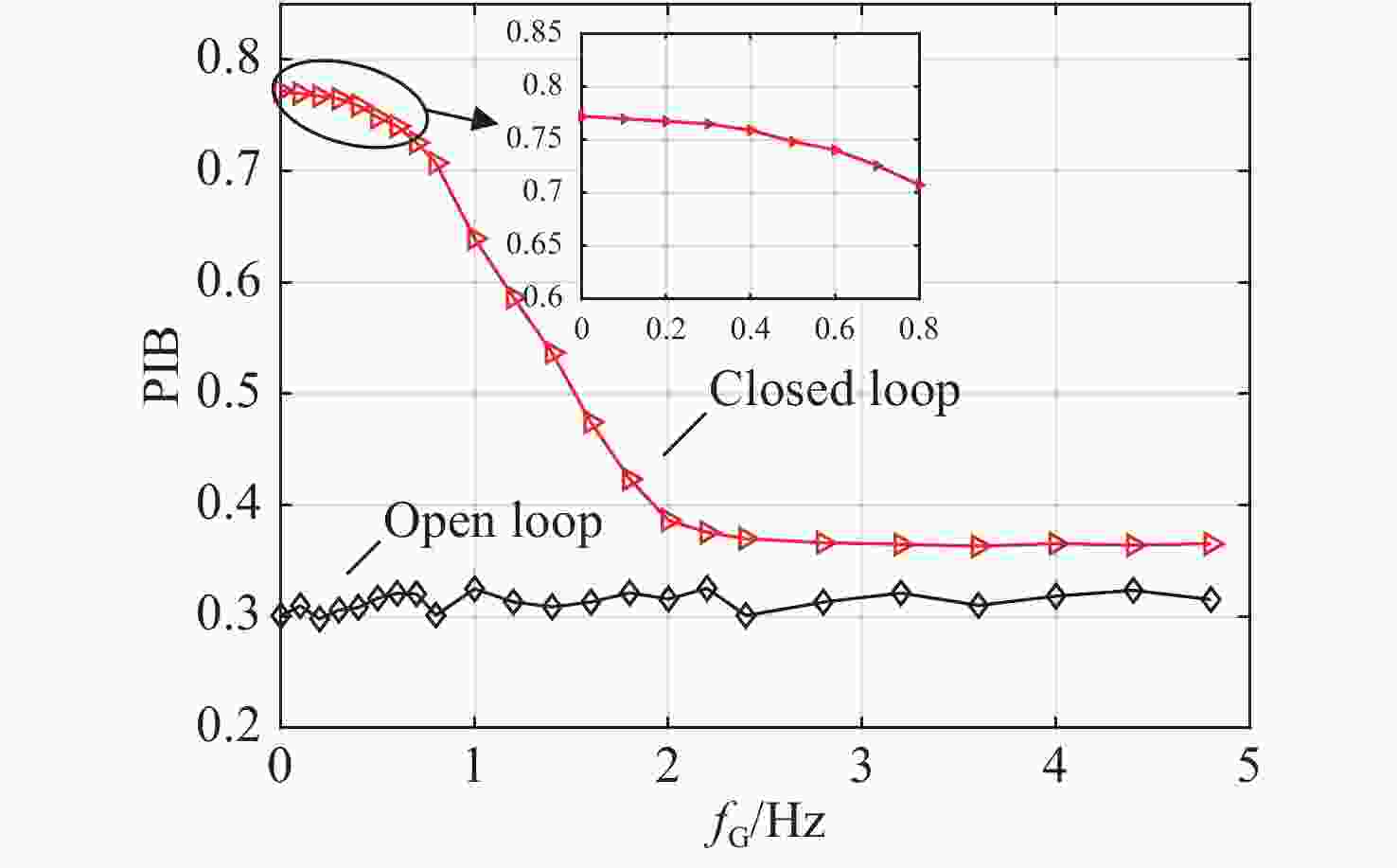
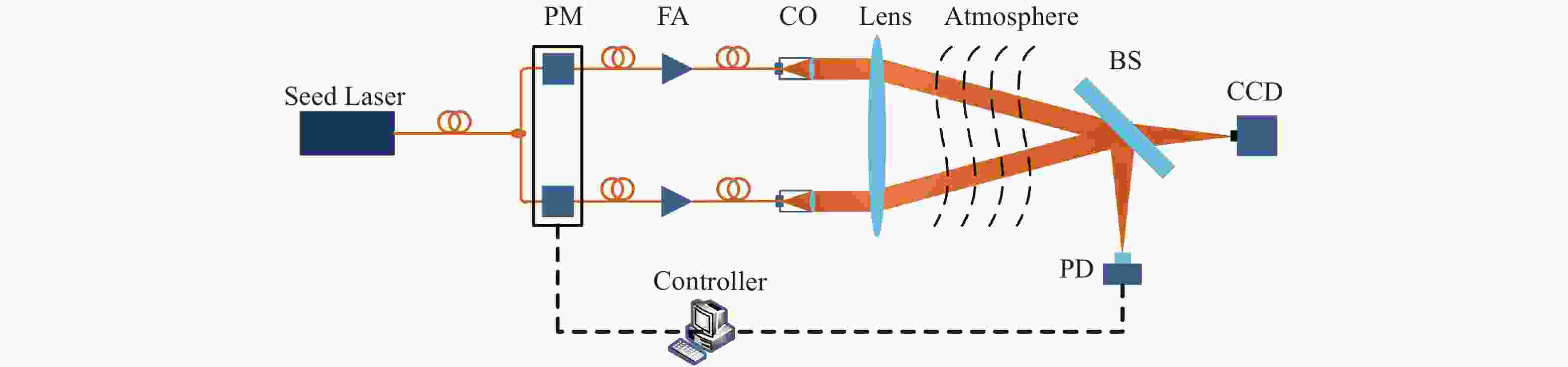
摘要: 光纤激光相干合成是获得高功率高光束质量输出较为有效的途径，而湍流大气是制约其应用与发展的关键因素之一。本文重点研究了大气格林伍德频率对基于随机并行梯度下降算法（SPGD）相干合成系统校正效果的影响。首先，在静态大气条件下，分析了不同湍流强度对相干合成系统校正效果的影响；然后，利用数值计算生成一组旋转的符合Kolmogorov统计规律的相位屏模拟湍流大气，对在不同大气格林伍德频率下相干合成系统的校正效果进行研究；最后，搭建两路光纤激光相干合成实验平台，进行实验验证。仿真和实验结果表明，在系统的控制算法迭代频率（350 Hz）一定时，随着大气格林伍德频率的增加，湍流大气对光束的相位和光强的扰动加剧，使得相干合成系统的合成效果变得越来越差。
- 相干合成 /
- SPGD算法 /
- 湍流大气 /
- 相位屏
Abstract: Coherent beam combining is a promising technology for achieving a high-power laser beam with good beam quality. However, turbulent atmosphere is one of the key factors that restrict its application and development. This paper focuses on the influence of atmospheric Greenwood frequency on the correction effect of the coherent combination system based on Stochastic Parallel Gradient Descent (SPGD) algorithm. At first, the influence of different turbulence intensities on the correction effect of coherent combination systems is analyzed by numerical simulation under static atmospheric conditions. Then, a set of rotating phase screens that meet Kolmogorov’s statistical law are generated by numerical calculation to simulate the turbulent atmosphere and study the correction effect of coherent combination system at different atmospheric Greenwood frequencies. Finally, an experimental platform is established to demonstrate the coherent combination effect of two laser beams. The simulated and experimental results show that when the system's control algorithm iteration frequency (350 Hz) is constant, the disturbance of turbulent atmosphere to the phase and light intensity of laser beams will increase with atmospheric Greenwood frequency, making the effect of coherent combination worse.
- coherent beam combining /
- SPGD algorithm /
- turbulent atmosphere /
- phase screen

HTML全文

图 1 两路光纤激光相干合成系统结构图。PM：相位调制器；FA：光纤放大器；CO：光纤准直器；BS：分光镜；PD：单点探测器。

Figure 1. The experimental scheme of coherent beam combining system of two fiber laser beams. PM: Phase Modulator; FA: Fiber Amplifiers; CO: Collimator; BS: Beam Splitting Mirror; PD: Photodetector

下载: 全尺寸图片幻灯片

图 2 系统评价指标PIB随湍流强度的变化曲线

Figure 2. System evaluation index PIB varies with iteration turbulence intensity

下载: 全尺寸图片幻灯片

图 3 旋转相位屏生成示意图

Figure 3. Schematic diagram of a rotating phase screen generation

下载: 全尺寸图片幻灯片

图 4 湍流大气下，系统PIB随迭代次数的变化曲线

Figure 4. System evaluation index PIB varies with iteration number under turbulent atmosphere

下载: 全尺寸图片幻灯片

图 5 评价函数随大气格林伍德频率的变化曲线

Figure 5. Evaluation function varying with atmospheric Greenwood frequency

下载: 全尺寸图片幻灯片

图 6 探测器输出电压随算法迭代次数的变化曲线

Figure 6. Detector′s output voltage varies with iteration number

下载: 全尺寸图片幻灯片

图 7 在不同的格林伍德频率下，探测器的输出电压与迭代次数的变化曲线

Figure 7. Detector′s output voltage varies with the number of iterations under different Greenwood frequencies

下载: 全尺寸图片幻灯片

图 8 系统开环和闭环时探测器输出电压随大气湍流格林伍德频率的变化曲线

Figure 8. Detector′s output voltage varies with Greenwood frequency when the system is open and closed

下载: 全尺寸图片幻灯片

表 1 System parameters used for simulation

Table 1. System parameters used for simulation

Parameter Value

Distance: L/m 2
Wavelength: λ/m 1 064 × 10⁻⁹
Beam radius: w₀/m 2.5 × 10⁻³
Number of samples: 256

下载: 导出CSV

参考文献(20)

[1]	WANG X L, ZHOU P, SU R T, et al. Current situation, tendency and challenge of coherent combining of high power fiber lasers[J]. Chinese Journal of Lasers, 2017, 44(2): 3-28. (in Chinese)
[2]	LIU Z J, ZHOU P, XU X J, et al. Coherent beam combining of high power fiber lasers: progress and prospect[J]. Science China Technological Sciences, 2013, 56(7): 1597-1606. doi: 10.1007/s11431-013-5260-z
[3]	ZENG H M, LI S, ZHANG ZH Y, et al. Risley-prism-based beam scanning system for mobile lidar[J]. Optics and Precision Engineering, 2019, 27(7): 1444-1450. (in Chinese) doi: 10.3788/OPE.20192707.1444
[4]	WANG H Q, SONG L H, CAO M H, et al. Compressed sensing detection of optical spatial modulation signal in turbulent channel[J]. Optics and Precision Engineering, 2018, 26(11): 2669-2674. (in Chinese) doi: 10.3788/OPE.20182611.2669
[5]	CHEN X, WANG J L, LIU CH H. Beam combining of high energy fibre lasers[J]. Infrared and Laser Engineering, 2018, 47(1): 0103011. (in Chinese) doi: 10.3788/IRLA201847.0103011
[6]	WANG X L, ZHOU P, MA Y X, et al. Active phasing a nine-element 1.14 kW all-fiber two-tone MOPA array using SPGD algorithm[J]. Optics Letters, 2011, 36(16): 3121-3123. doi: 10.1364/OL.36.003121
[7]	GOODNO G D, KOMINE H, MCNAUGHT S J, et al. Coherent combination of high-power, zigzag slab lasers[J]. Optics Letters, 2006, 31(9): 1247-1249. doi: 10.1364/OL.31.001247
[8]	MA Y X, ZHOU P, WANG X L, et al. Coherent beam combination with single frequency dithering technique[J]. Optics Letters, 2010, 35(9): 1308-1310. doi: 10.1364/OL.35.001308
[9]	ZHOU P, MA Y X, WANG X L, et al. Coherent beam combining of fiber amplifiers based on stimulated annealing algorithm[J]. High Power Laser and Particle Beams, 2010, 22(5): 973-977. (in Chinese) doi: 10.3788/HPLPB20102205.0973
[10]	ZHOU P, LIU Z J, WANG X L, et al. Coherent beam combining of two fiber amplifiers using stochastic parallel gradient descent algorithm[J]. Optics &Laser Technology, 2009, 41(7): 853-856.
[11]	ZHOU P, MA Y X, WANG X L, et al. Coherent beam combination of three two-tone fiber amplifiers using stochastic parallel gradient descent algorithm[J]. Optics Letters, 2009, 34(19): 2939-2941. doi: 10.1364/OL.34.002939
[12]	VORONTSOV M A, CARHART G W, RICKLIN J C. Adaptive phase-distortion correction based on parallel gradient-descent optimization[J]. Optics Letters, 1997, 22(12): 907-909. doi: 10.1364/OL.22.000907
[13]	VORONTSOV M. Adaptive Photonics Phase-Locked Elements (APPLE): system architecture and wavefront control concept[J]. Proceedings of SPIE, 2005, 5895: 589501. doi: 10.1117/12.617390
[14]	WEYRAUCH T, VORONTSOV M, CARHART G, et al. Experimental demonstration of coherent beam combining over a 7 km propagation path[J]. Optics Letters, 2011, 36(22): 4455-4457. doi: 10.1364/OL.36.004455
[15]	VORONTSOV M, FILIMONOV G, OVCHINNIKOV V, et al. Comparative efficiency analysis of fiber-array and conventional beam director systems in volume turbulence[J]. Applied Optics, 2016, 55(15): 4170-4185. doi: 10.1364/AO.55.004170
[16]	GENG CH, YANG Y, LI F, et al. Research progress of fiber laser coherent combining[J]. Opto-Electronic Engineering, 2018, 45(3): 170692. (in Chinese) doi: 10.12086/oee.2018.170692
[17]	SU R T, MA Y X, XI J CH, et al. 60-channel large array element fiber laser high efficiency coherent synthesis[J]. Infrared and Laser Engineering, 2019, 48(1): 331. (in Chinese)
[18]	ZHI D, MA Y X, MA P F, et al. Efficient coherent beam combining of fiber laser array through km-scale turbulent atmosphere[J]. Infrared and Laser Engineering, 2019, 48(10): 1005007. (in Chinese) doi: 10.3788/IRLA201948.1005007
[19]	LIU L, GUO J, ZHAO SH, et al. Application of stochastic parallel gradient descent algorithm in laser beam shaping[J]. Chinese Optics, 2014, 7(2): 260-266. (in Chinese)
[20]	LI D, NING Y, WU W M, et al. Numerical simulation and validation method of atmospheric turbulence of phase screen in rotation[J]. Infrared and Laser Engineering, 2017, 46(12): 1211003. (in Chinese) doi: 10.3788/IRLA201746.1211003