-
摘要: 球面检验镜口径不断增大导致其检验精度下降，针对该问题，本文优化设计了2.7米标准球面镜的重锤支撑参数，并对该标准球面镜的调整架以及支撑系统进行了结构设计。首先，利用有限元和遗传算法，对镜体进行了54点等力支撑环带优化，针对增加嵌套孔后镜体刚度变差的情况，对各环带底支撑力和侧支撑力分别进行了优化；然后，利用统计方法分析了支撑半径和支撑力误差对支撑变形的影响；最后，基于优化分析结果对标准检验镜的调整架和支撑系统进行了结构设计。分析结果表明，经过对标准球面镜54点支撑位置、各环带底支撑力和侧支撑力进行优化设计后，在球面镜支撑变形RMS（Root Mean Square）小于1/115λ（λ=632.8 nm），底支撑位置扰动为±2 mm，侧支撑位置扰动为±0.6 mm，以及支撑力扰动为±3 N的情况下，支撑变形小于1/70λ，满足标准球面镜的支撑要求。Abstract: Aiming at the problem that the decrease of inspection accuracy caused by an increase in the diameter of a spherical inspection mirror, the weight support parameters of the 2.7-meter standard spherical mirror are optimized and the structural design of its adjustment frame and support system is implemented. Firstly, the 54-point equal-force support ring is optimized for the mirror body using a finite element and genetic algorithm. In order to increase the rigidity of the mirror body when increasing the nesting hole, the bottom support force and the side support force of each ring are optimized separately and the influence of support radius and support force error on the support deformation is statistically analyzed. Finally, based on the analysis results, a structural frame of the standard inspection mirror and a support system are designed. The analysis results show that after optimization of the 54-point support position of the standard spherical mirror, the bottom support force and the side support force of each ring and under the condition that the spherical mirror support deformation is less than 1/115λ(λ=632.8 nm), the bottom support position is disturbed by ±2 mm, the side support position is disturbed by ±0.6 mm, and the support force disturbance is ±3 N, the support deformation is less than 1/70λ, which shows little deterioration. This meets the requirements of standard spherical mirror support.
-
图 1 标准球面检验镜系统结构示意图
Figure 1. Schematic diagram of standard spherical inspection mirror system
图 6 未开嵌套孔情况下球面镜的优化变形图
Figure 6. Deformation map of optimized spherical mirror without nesting holes
图 7 开嵌套孔球面镜支撑变形图
Figure 7. Deformation map of optimized spherical mirror with nesting holes
图 8 开嵌套孔镜体轴向支撑力优化后变形图
Figure 8. Deformation map of axial support force after optimization of mirror body with nesting holes
图 9 开嵌套孔镜体侧向支撑力优化后变形图
Figure 9. Deformation map of lateral support force after optimization of mirror body with nesting holes
图 11 轴向支撑力存在扰动时支撑变形统计图
Figure 11. Support deformation diagram when there is disturbance in axial support force
图 12 侧向支撑力存在扰动时的支撑变形统计图
Figure 12. Support deformation diagram when there is disturbance in lateral support force
图 10 45°俯仰镜体支撑变形图
Figure 10. Support deformation diagram of mirror body with pitch angle of 45°
图 13 支撑位置在XY平面内存在扰动时的支撑变形统计图
Figure 13. Support deformation map when there is disturbance of the support position in the XY plane
图 14 支撑位置存在Z向扰动时的支撑变形统计图
Figure 14. Support deformation map when there is disturbance of support position along Z-direction
图 15 支撑力、支撑位置在XY平面内存在扰动时的支撑变形统计图
Figure 15. Support deformation map when there are disturbance of forces and support positions in the XY plane
-
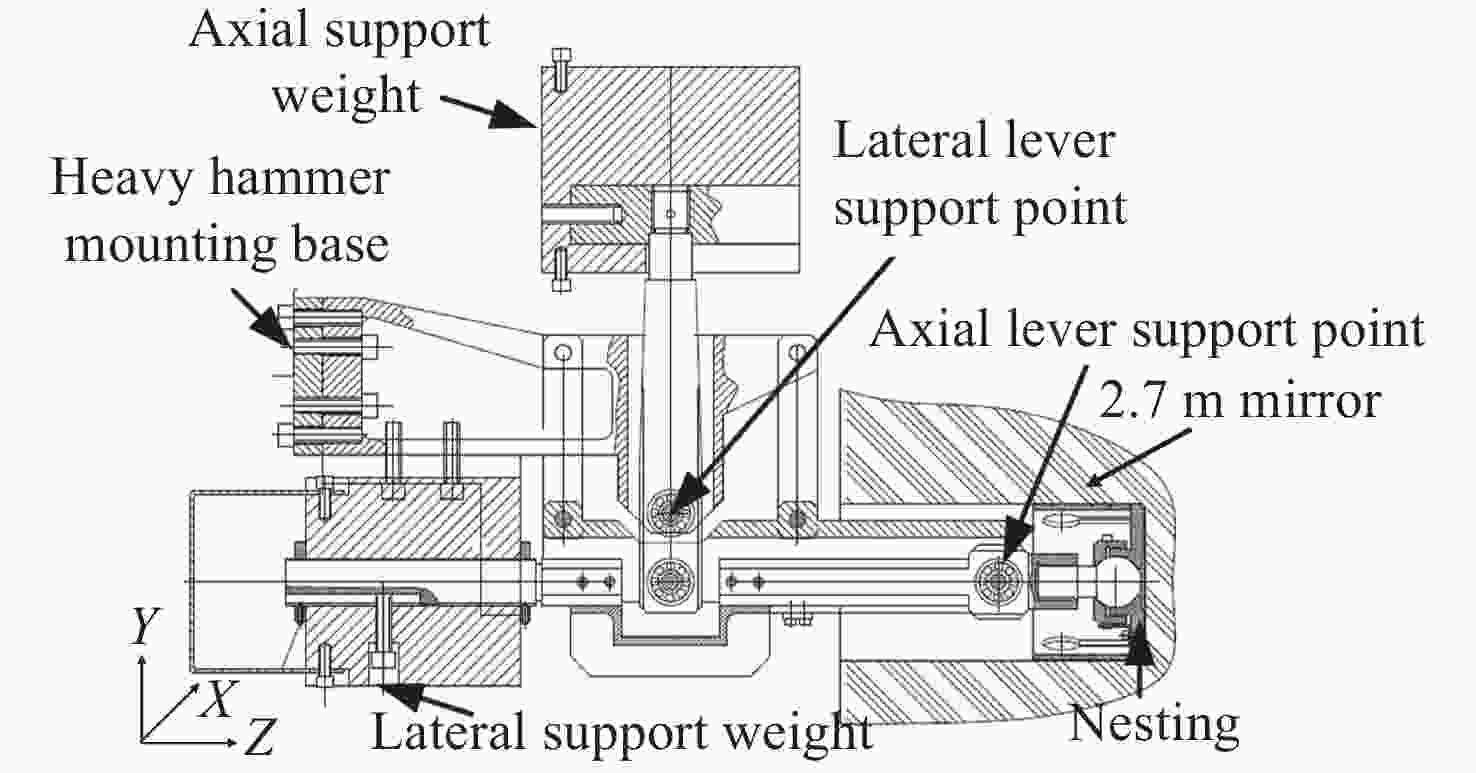
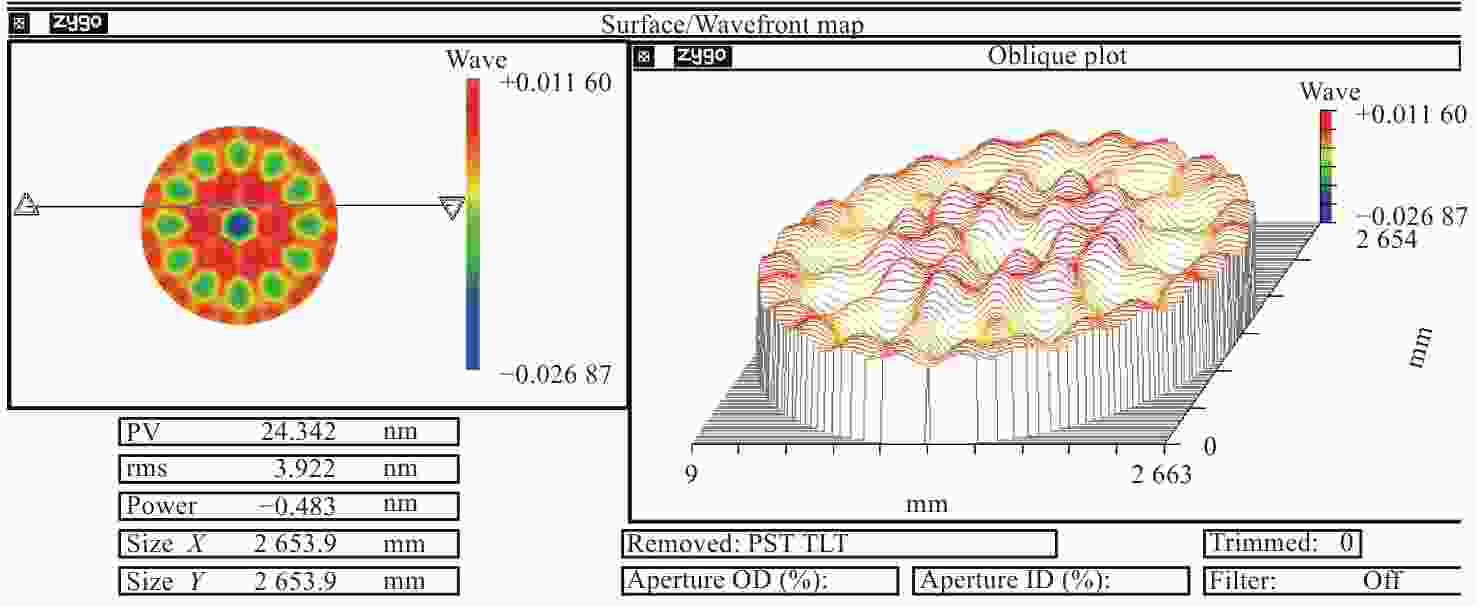
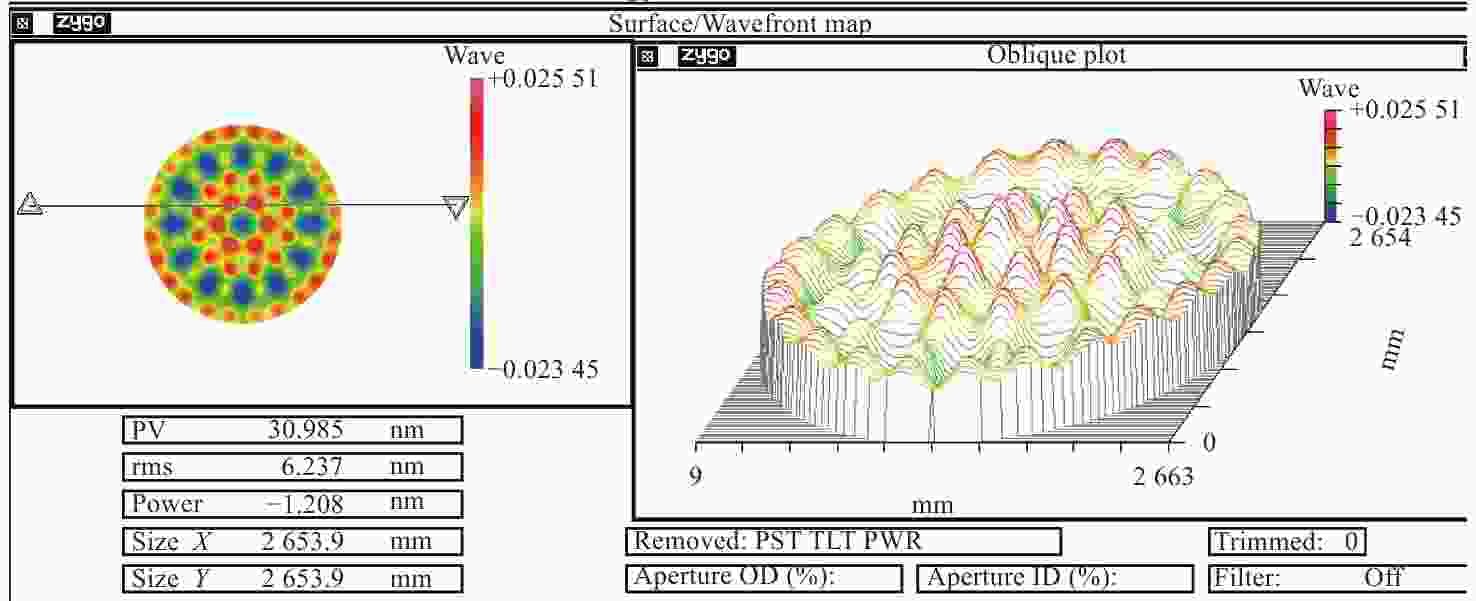
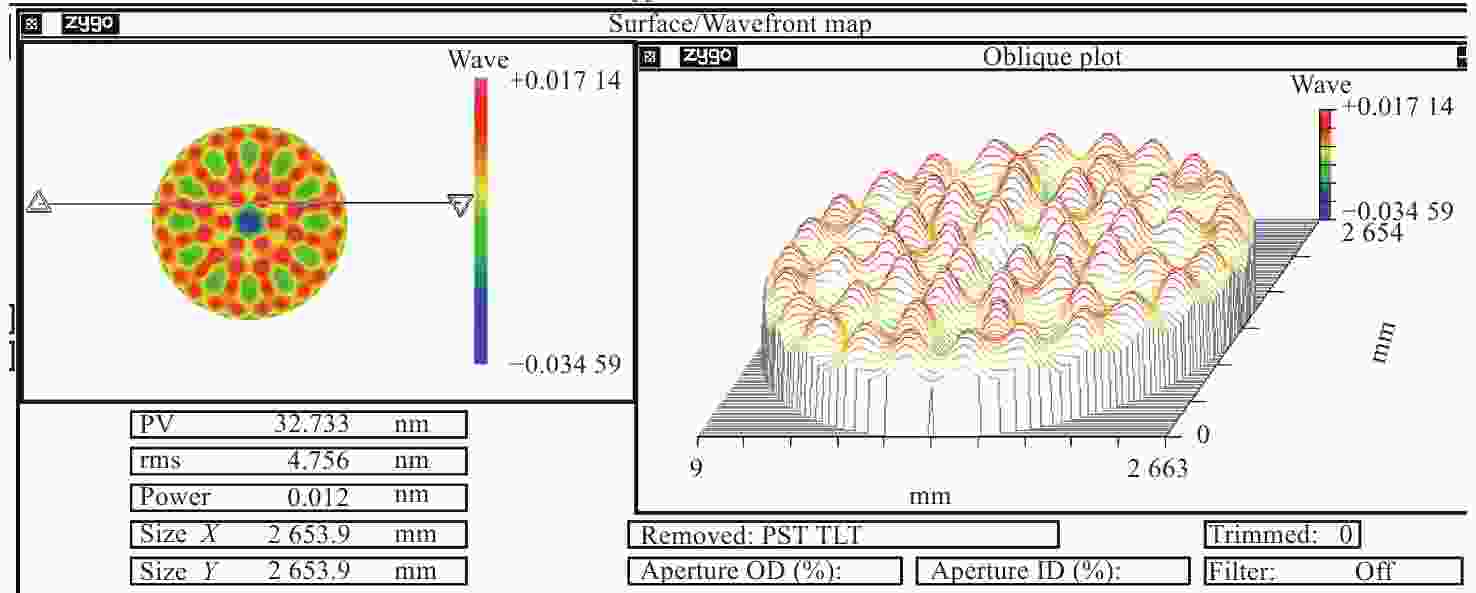
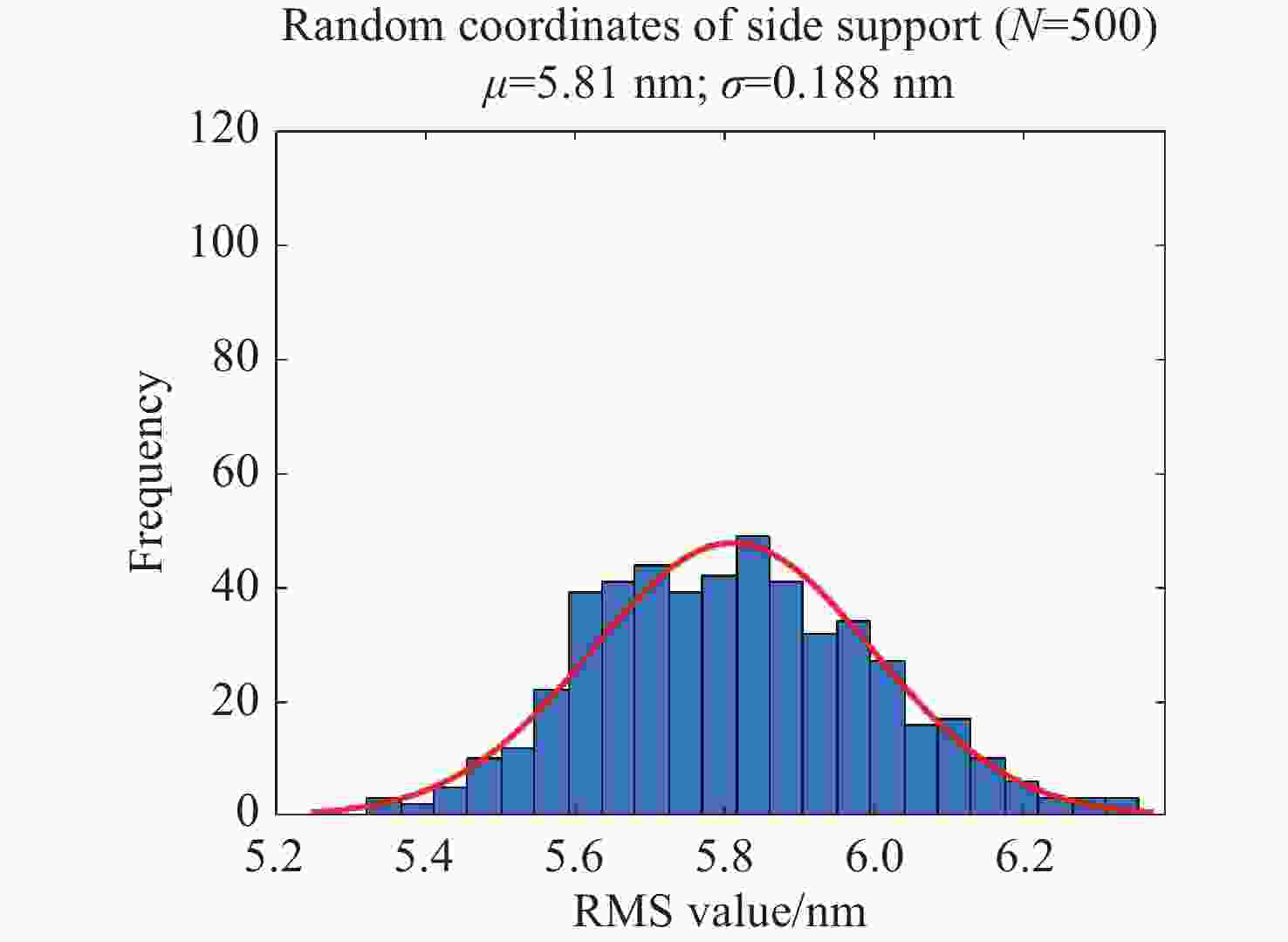
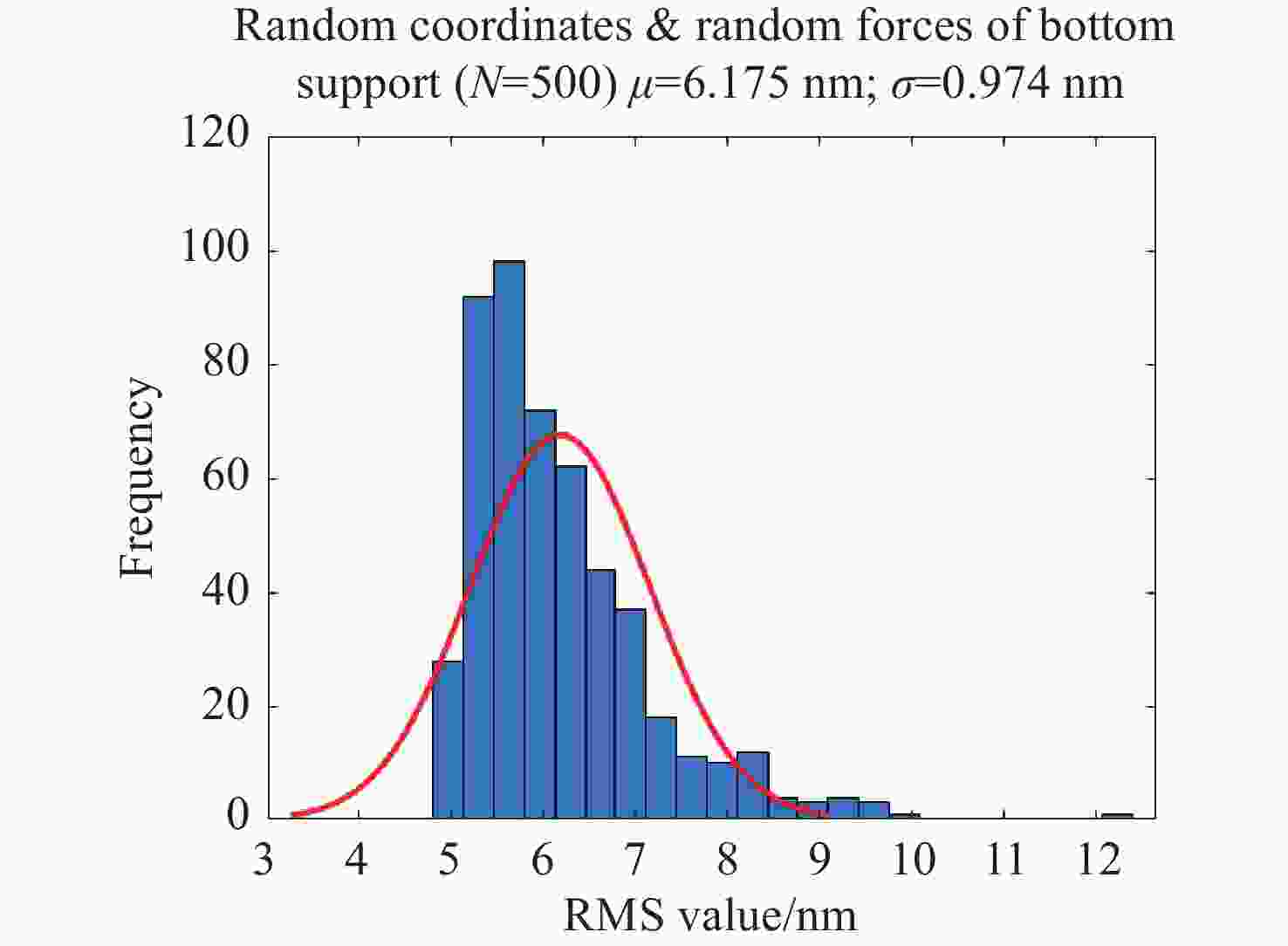
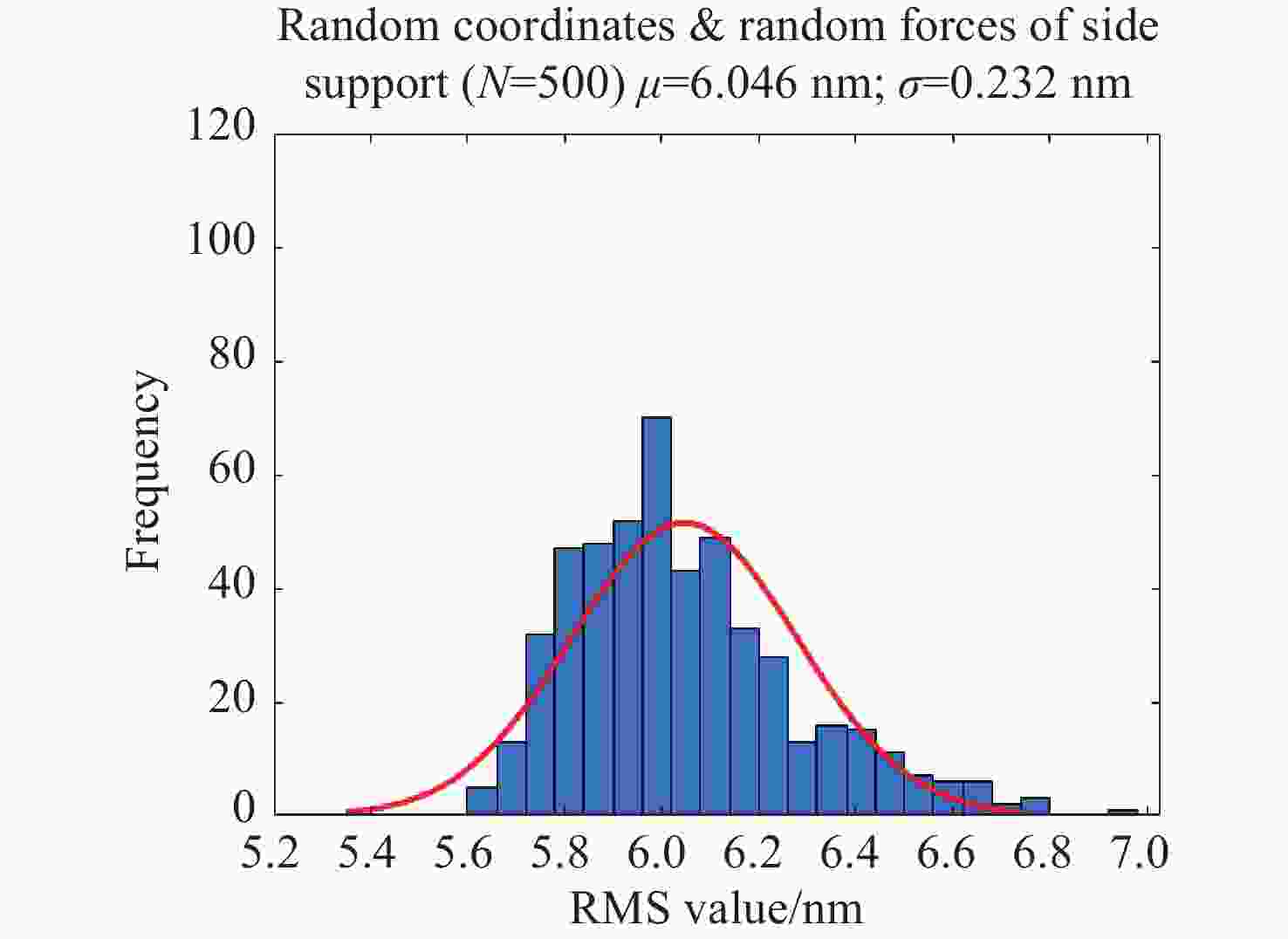
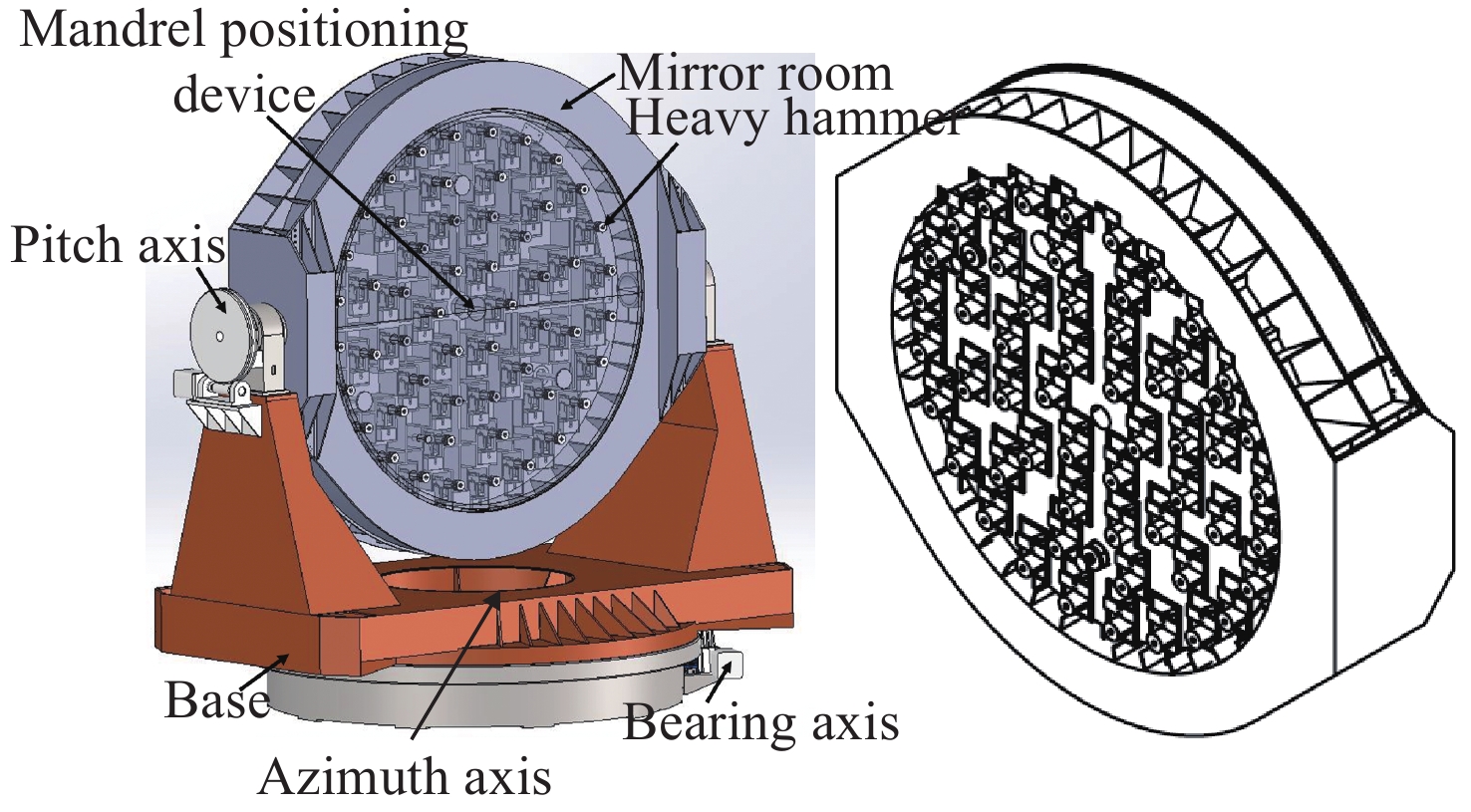
[1] 王忠善.天基大口径单体反射镜结构优化及其支撑技术研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2019.WANG ZH SH. Research on structure optimization of large aperture monolithic space-based mirror and its mounting technology[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2019. (in Chinese) [2] 郭疆, 朱磊, 赵继, 等. 大口径空间反射镜大容差支撑结构设计与优化[J]. 光学 精密工程,2019,27(5):1138-1147. doi: 10.3788/OPE.20192705.1138GUO J, ZHU L, ZHAO J, et al. Design and optimize of high tolerance support structure for large aperture space mirror[J]. Optics and Precision Engineering, 2019, 27(5): 1138-1147. (in Chinese) doi: 10.3788/OPE.20192705.1138 [3] 范磊. 2m级地基望远镜SiC主镜轻量化设计及支撑技术研究[D]. 长春: 中科院长春光学精密机械与物理研究所, 2013.FAN L. Research on the lightweight design and support of the 2m-SiC primary mirror for ground-based telescope[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2013. (in Chinese) [4] YODER JR P R. Opto-Mechanical Systems Design[M]. 3rd ed. Boca Raton: CRC Press, 2005. [5] 董得义, 庞新源, 张学军, 等. 空间大口径单体反射镜计量卸荷支撑研制中的关键技术[J]. 光学 精密工程,2019,27(10):2165-2179. doi: 10.3788/OPE.20192710.2165DONG D Y, PANG X Y, ZHANG X J, et al. Key technology in developing of metrology mount for large aperture monolithic space-based mirror[J]. Optics and Precision Engineering, 2019, 27(10): 2165-2179. (in Chinese) doi: 10.3788/OPE.20192710.2165 [6] 胡企千. 望远镜技术与天文测天[M]. 南京: 东南大学出版社, 2014.HU Q Q. Telescope Technology and Astrometry[M]. Nanjing: Southeast University Press, 2014. (in Chinese) [7] TSAI L W. Robot Analysis: The Mechanics of Serial and Parallel Manipulators[M]. New York: Wiley, 1999. [8] 王槐, 代霜. 大型望远镜轴系支撑结构的发展现状与分析[J]. 光机电信息,2011,28(3):17-27. doi: 10.3788/OMEI20112803.0017WANG H, DAI SH. Development actuality and analysis of large alt-azimuth telescope shafting supporting structure[J]. OME Information, 2011, 28(3): 17-27. (in Chinese) doi: 10.3788/OMEI20112803.0017 [9] 王克军.天基大口径反射镜轻量化设计及复合支撑技术研究[D]. 长春: 中科院长春光学精密机械与物理研究所, 2016.WANG K J. Research on the lightweight design and compound support of the large-aperture mirror for space-based telescope[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2016. (in Chinese) [10] 范磊, 张景旭, 邵亮, 等. 采用液压whiffle-tree的大口径主镜轴向支撑[J]. 红外与激光工程,2013,42(8):2126-2131. doi: 10.3969/j.issn.1007-2276.2013.08.035FAN L, ZHANG J X, SHAO L, et al. Axial support for large aperture primary mirror based on hydraulic Whiffle-tree[J]. Infrared and Laser Engineering, 2013, 42(8): 2126-2131. (in Chinese) doi: 10.3969/j.issn.1007-2276.2013.08.035 [11] 李钰鹏, 王智, 沙巍, 等. Bipod反射镜支撑结构的柔度计算及分析[J]. 光学 精密工程,2018,26(7):1691-1697. doi: 10.3788/OPE.20182607.1691LI Y P, WANG ZH, SHA W, et al. Flexibility calculation and analysis of Bipod reflector support structure[J]. Optics and Precision Engineering, 2018, 26(7): 1691-1697. (in Chinese) doi: 10.3788/OPE.20182607.1691 [12] 王富国, 乔兵, 张景旭. 2m SiC反射镜柔性被动支撑系统[J]. 光学 精密工程,2017,25(10):2591-2598. doi: 10.3788/OPE.20172510.2591WANG F G, QIAO B, ZHANG J X. Flexible passive support system for 2 m SiC reflective mirror[J]. Optics and Precision Engineering, 2017, 25(10): 2591-2598. (in Chinese) doi: 10.3788/OPE.20172510.2591 [13] 胡海飞, 赵宏伟, 刘振宇, 等. 4 m口径SiC反射镜原位检测用静压支撑系统[J]. 光学 精密工程,2017,25(10):2607-2613. doi: 10.3788/OPE.20172510.2607HU H F, ZHAO H W, LIU ZH Y, et al. Hydrostatic support system for in-situ optical testing of a 4 m aperture SiC mirror[J]. Optics and Precision Engineering, 2017, 25(10): 2607-2613. (in Chinese) doi: 10.3788/OPE.20172510.2607 [14] 田富湘, 何欣. 空间光学遥感器光学镜面有限元分析结果的后处理[J]. 红外,2014,35(9):19-22. doi: 10.3969/j.issn.1672-8785.2014.09.005TIAN F X, HE X. Post−processing of FEA results of optical mirrors for space remote sensor[J]. Infrared, 2014, 35(9): 19-22. (in Chinese) doi: 10.3969/j.issn.1672-8785.2014.09.005 [15] 张军强, 董得义, 吴清文, 等. 光学遥感器镜面面形误差及刚体位移处理方法[J]. 仪器仪表学报,2011,32(6):242-247.ZHANG J Q, DONG D Y, WU Q W, et al. Treatment of surface figure error and rigid body motion for mirror/lens in optical remote sensor[J]. Chinese Journal of Scientific Instrument, 2011, 32(6): 242-247. (in Chinese) [16] 胡海飞, 罗霄, 辛宏伟, 等. 超大口径光学制造均力支撑布局优化[J]. 光学学报,2014,34(4):0422003. doi: 10.3788/AOS201434.0422003HU H F, LUO X, XIN H W, et al. Layout optimization of equal-force supports for ultra-large optical fabrication[J]. Acta Optica Sinica, 2014, 34(4): 0422003. (in Chinese) doi: 10.3788/AOS201434.0422003 -
下载:
计量
- 文章访问数: 1886
- HTML全文浏览量: 607
- PDF下载量: 96
- 被引次数: 0
