K-B镜面形高精度检测技术研究进展

张帅; 侯溪

doi:10.37188/CO.2019-0231

K-B镜面形高精度检测技术研究进展

doi: 10.37188/CO.2019-0231

张帅^{1, 2,},
侯溪^1, ,

1.
中国科学院光电技术研究所，四川成都 610209
2.
中国科学院大学，北京 100049

基金项目: 国家自然科学基金面上资助项目(No. 61675209)

详细信息

作者简介:
张　帅(1994—)，男，河南平顶山人，硕士研究生，2018年于长春理工大学获得学士学位，主要从事高精度X射线光学元件面形检测装置研究。Email：zhangshuai18@mails.uacs.ac.cn

侯　溪(1980—)，男，四川阆中人，博士，研究员，博士生导师，2002年于电子科技大学获得学士学位，2007年于中国科学院研究生院获得博士学位，主要从事高精度光学检测技术研究及仪器研制。Email：hxxh6776@163.com

中图分类号: TN247
计量
- 文章访问数: 3777
- HTML全文浏览量: 1167
- PDF下载量: 310
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-04
- 修回日期: 2020-01-13
- 刊出日期: 2020-08-01

Research progress of high-precision surface metrology of a K-B mirror

ZHANG Shuai^{1, 2
,},
HOU Xi^{1
, ,}

1.
Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu 610209, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: Supported by General Program of National Natural Science Foundation of China (No. 61675209)

More Information

Corresponding author: hxxh6776@163.com

摘要

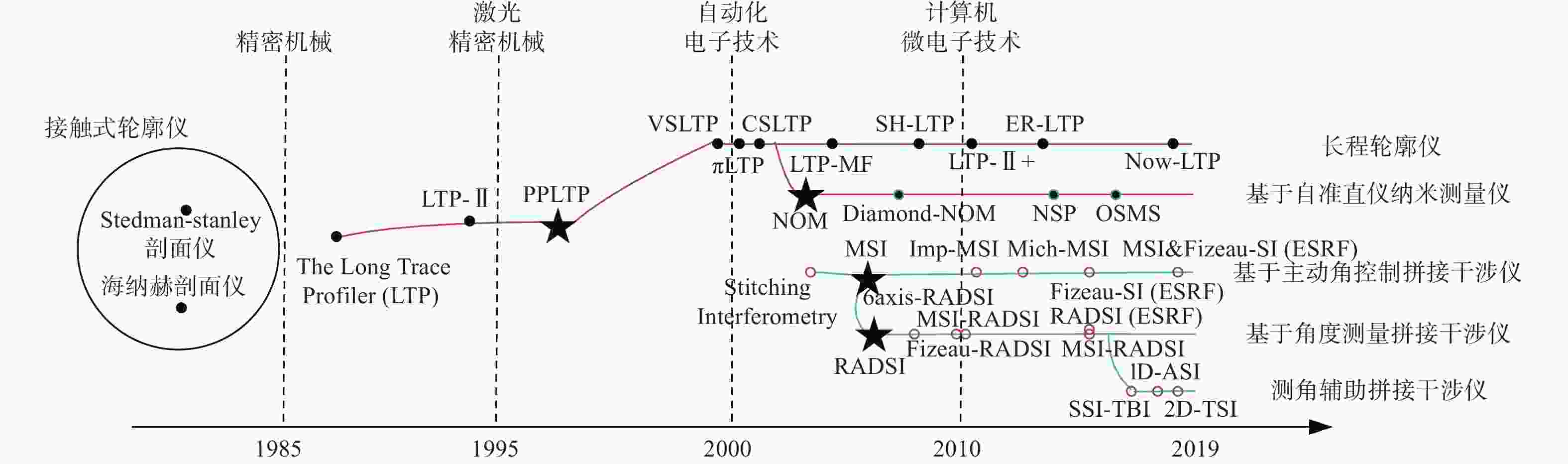
摘要: 以新一代同步辐射光源和全相干X射线自由电子激光为代表的先进光源已成为众多学科领域中一种不可或缺的研究工具。先进光源技术不断进步，驱动超精密光学制造快速发展，先进光源中关键聚焦光学元件K-B镜的面形精度是影响光源性能的重要指标，要求其在几十纳弧度以下。然而，高精度K-B镜面形检测技术依然存在较大技术挑战，一直是国内外研究热点。本文介绍了反射式轮廓测量技术即长程轮廓仪（LTP）、纳米测量仪（NOM）以及拼接干涉检测技术等典型K-B镜面形检测技术的基本原理，对比分析了其技术特点，综述了国内外K-B镜面形检测技术的研究现状和最新进展，对发展趋势进行了展望。
- X射线光学 /
- K-B镜 /
- 光学测量 /
- 面形检测 /
- 拼接干涉
Abstract: The advanced light source represented by the new generation of the diffraction limit synchrotron radiation source and the full-coherent X-ray free-electron laser has become an indispensable research tool in many fields. The continuous development of advanced light sources drives the rapid progress of ultra-precision optical manufacturing. The surface precision of a K-B mirror, a key focusing optical element in advanced light sources, is an important factor, which should be less than tens of nano radians. However, high precision K-B mirror surface metrology still has great technical challenges and is now a research hotspot in the scientific community. This paper introduces typical K-B mirror surface metrology, including reflection profile measuring technology such as the Long Trace Profiler (LTP), the Nanometer Optical component Measuring (NOM), and stitching interference metrology. Current K-B mirror surface shape technologies are summarized and the upcoming research progress is prospected.
- X-ray optics /
- K-B mirror /
- optical measurement /
- surface metrology /
- stitching interferometer

HTML全文

图 1 (a)经典一维K-B镜和(b)具有二维弯曲的K-B镜

Figure 1. (a) Typical K-B mirror and (b) K-B mirror with two-dimensional bending

下载: 全尺寸图片幻灯片

图 2 LTP光学系统原理图

Figure 2. Principle diagram of LTP optical system

下载: 全尺寸图片幻灯片

图 3 NOM原理图^[16]

Figure 3. Principle diagram of NOM system^[16]

下载: 全尺寸图片幻灯片

图 4 拼接原理图

Figure 4. The principle of stitching

下载: 全尺寸图片幻灯片

图 5 曲率变化剧烈的柱面镜的干涉条纹图

Figure 5. Interference fringe pattern of cylindrical mirror with sharp curvature change

下载: 全尺寸图片幻灯片

图 6 LTP/NOM发展历程^{[16, 21, 23, 25, 27, 28]}

Figure 6. The development of LTP/NOM^{[16, 21, 23, 25, 27, 28]}

下载: 全尺寸图片幻灯片

图 7 (a) ESRF中的拼接干涉仪及其(b)测量过程^[40]

Figure 7. (a) Fizeau stitching interferometer at ESRF and its (b) measurement process^[40]

下载: 全尺寸图片幻灯片

图 8 SPring-8中的MSI原理图^[43]

Figure 8. Diagram of microstitching interferometry at SPring-8^[43]

下载: 全尺寸图片幻灯片

图 9 ESRF中的MSI装置^[46]

Figure 9. Microstitching interferometry at ESRF^[46]

下载: 全尺寸图片幻灯片

图 10 SOLEIL中Michelson型显微拼接干涉仪^[47]

Figure 10. Michelson stitching interferometry at SOLEIL^[47]

下载: 全尺寸图片幻灯片

图 11 (a) RADSI装置图及其 (b) 测量过程^[48]

Figure 11. (a) Scheme of RADSI system and (b) its measurement process^[48]

下载: 全尺寸图片幻灯片

图 12 RADSI发展路线图^{[42, 48, 50, 52]}

Figure 12. The development of RADSI^{[42, 48, 50, 52]}

下载: 全尺寸图片幻灯片

图 13 2D-TSI装置原理图^[57]

Figure 13. The scheme of 2D-TSI device^[57]

下载: 全尺寸图片幻灯片

图 14 先进光源硬X射线聚焦尺寸演变

Figure 14. The trend of hard X-ray focusing size

下载: 全尺寸图片幻灯片

图 15 K-B镜面形精度趋势^[36]

Figure 15. The trend of K-B mirror shape accuracy ^[36]

下载: 全尺寸图片幻灯片

图 16 K-B镜面形检测技术发展过程图

Figure 16. Development of K-B mirror surface metrology

下载: 全尺寸图片幻灯片

表 1 LTP/NOM技术典型参数

Table 1. Specifications of LTP/NOM

类型	LTP	NOM
工作距离/mm	100~1100	300~1300
斜率/mrad	±5	±5
扫描速率/(mm·s⁻¹)	5~10	2~4
精度(RMS)/nrad	平面: ~50 曲面: ~250	平面: ~50 曲面: ~500
空间分辨率/mm	~1	2.5~5

下载: 导出CSV

表 2 国内外典型LTP/NOM技术参数

Table 2. Technical specifications of typical LTP/NOM technologies at home and abroad

类型	机构/装置	设备	时间	测量范围	性能	备注
LTP	日本JASRI/SPring-8	Laser-LTP	2014	3.6 mrad	0.2 μrad 重复精度60 nrad	激光校准测头误差分辨率30 nrad
	日本JASRI/SPring-8	LTP	2016	~1 m	5 nm	新型斜率传感器; 空间分辨率<1 mm
	美国LBNLALS	LTP-II⁺	2014	1 m ±2.5 mrad	平面：<80 rad rms 曲面(>15 m): 250 nrad rms	校正K-B位置误差
	中国台湾NSRRC	NLTP	2013	1.2 m	测量重复精度50 nrad	定位基准为衍射暗线；光束定位精度高
	中国SSRF上海光源	LTP	2016	1 m	平面：<50 nrad 曲面(>38 m): 0.27μrad	支持快速测量
	中国IHEP高能所	FSP	2019	1 m	平面:25 nrad rms 曲面(3 mrad): 32 nrad rms	空间分辨率优于1 mm
NOM	巴西LNLS	NOM	2017	1.5 m	平面：50 nrad rms	横向分辨率大
	德国BESSY-II	Diamond-NOM	2014	1.5 m ±5 mrad	平面：50 nrad rms 曲面：200 nrad rms (±24μrad) 500 nrad rms (±5 mrad)	曲率测量范围大
	美国BNL	DLTP	2014	1 m ±4.6 mrad	平面：60 nrad rms 曲面(>15 m): 200 nrad rms	曲面测量受限
	美国BNL	OSMS	2017	1.2 m	平面：<50 nrad rms 曲面(>60 m): 100 nrad rms	实现二维测量
	日本JASRI/SPring-8	AC-NOM	2014	9.7 mrad	±1.2μrad ±0.24μrad (48μrad) 重复精度100 nrad rms	校准扫描俯仰误差; 扫描速度慢分辨率24.2 nrad
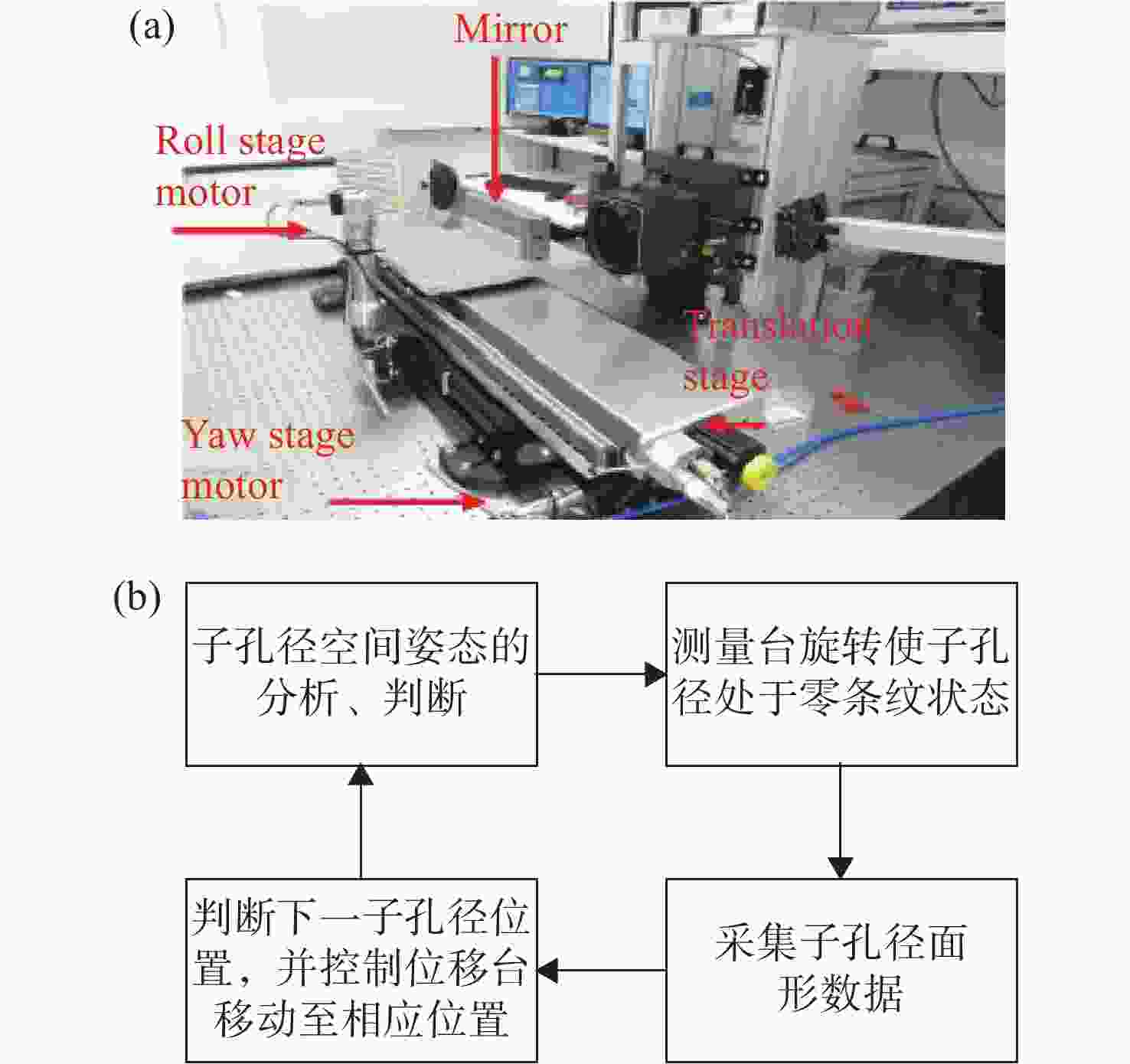
	中国SSRF上海光源	NOM	2015	1100 mm ±5 mrad	0.08μrad rms (±50μrad) 0.25μrad rms (±5 mrad)	空间采样频率在1~10 mm 重复精度50 nrad rms

下载: 导出CSV

表 3 3种类型拼接干涉仪对比^{[40, 51, 56]}

Table 3. Comparison of three types of stitching interferometer ^{[40, 51, 56]}

主动角控制拼接干涉仪控制算法+精密转台	测角拼接干涉仪测角系统(RADSI)	测角辅助拼接干涉仪测角辅助装置+拼接算法


大口径、小曲率长焦K-B镜 300~1000 mm; <20 mrad	小口径、大曲率短焦K-B镜 100~300 mm; >20 mrad	平面镜、小曲率椭圆柱镜(探索阶段)
平面优于0.30 nm rms 曲面优于0.30 μrad rms 步进单孔径测量(干涉仪尺寸)	平面优于0.2 nm rms 曲面优于2 nm rms 步进单孔径测量: 2 mm×2 mm	重复精度1.5 nm rms 步进单孔径量: 2 mm×2 mm
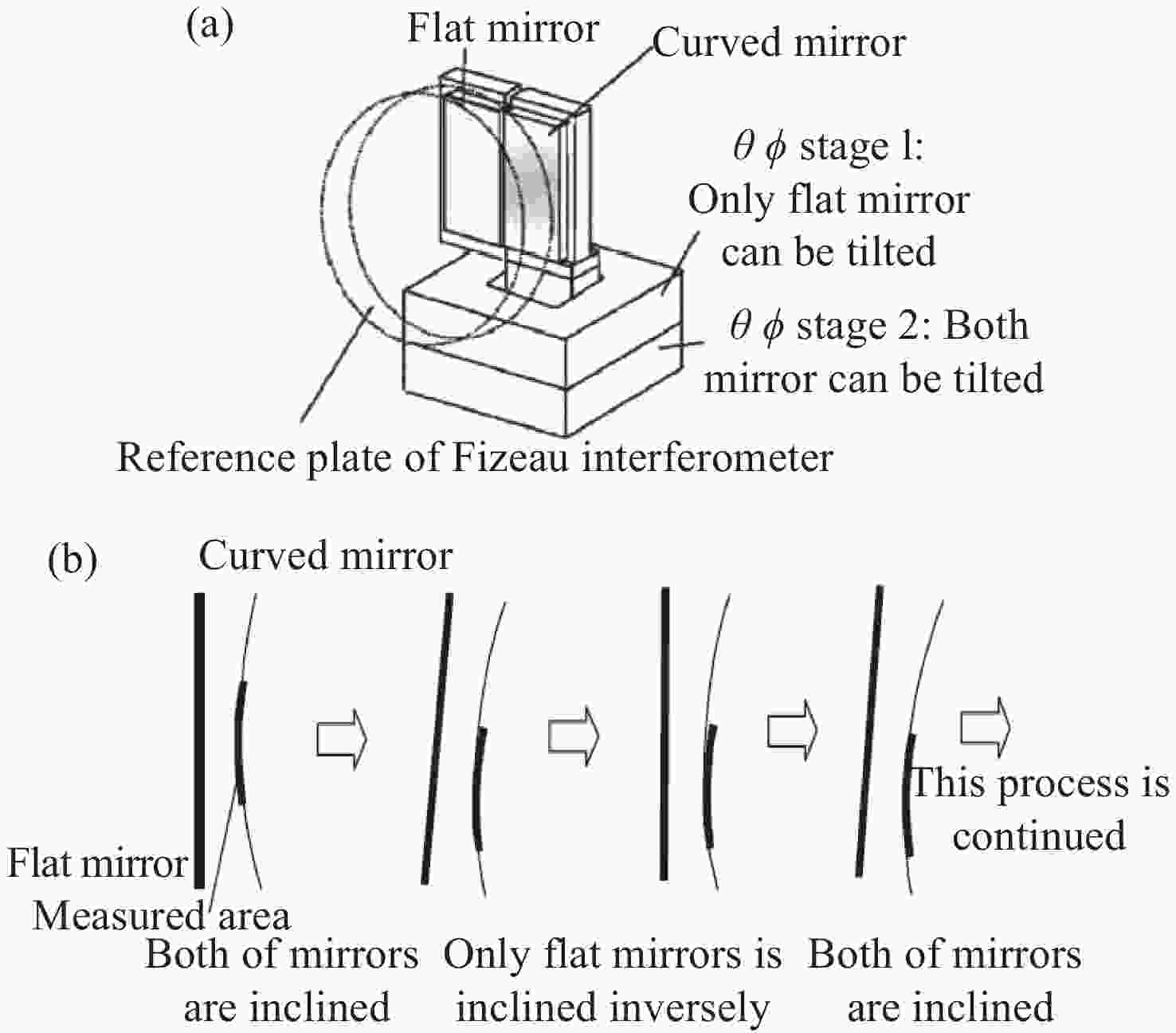
结构相对简单，测量口径范围大，测量效率高测量频段有限，测量精度受待测面曲率影响大	测量频段宽，测量精度高，曲率测量范围大，结构复杂，易受环境影响，测量口径范围受限	结构简单，动态范围大，测量精度高有待进一步完善具体结构

下载: 导出CSV

表 4 国内外典型拼接干涉仪技术参数

Table 4. Technical parameters of typical stitching interferometer at home and abroad

机构/装置	设备	时间	技术性能	备注
欧洲ERSF	Fizeau-SI	2019	平面镜：优于0.30 nm rms 椭面镜：优于0.30 μrad rms 球面镜：优于0.25 μrad rms	主镜法校正参考误差需弥补球面低频信息空间分辨率: 80 μm
欧洲ERSF	MSI	2019	平面: 0.2 nm rms 横向分辨率: (2.5倍) 16 μm; (1倍) 40 μm	适合于平面或强弯短镜；存在拼接伪影
美国BNL	MSI	2017	残余斜率偏差: 2 μrad rms	采用曲率拼接技术
美国BNL	ASI-AMS	2018	平面：重复精度0.5 nm rms 椭球面：重复精度2 nm rms	可以减小回程误差; 子孔径重叠面积小，测量速度快
日本大阪大学	MSI-RADSI	2016	面型高度误差：3 nm rms 重复精度:0.51 nm rms	可测极端曲率面形以及椭面镜；测量范围有限
法国SOLEIL	Mich-SI	2019	重复精度:0.2 nm rms	可测20 mm⁻¹频段面形信息
复旦大学	RADSI	2017	平面镜：重复精度0.5 nm rms 球面镜：曲率偏差为2.3%	验证了RADSI球面测量能力
国防科技大学	DST	2018	测量PV值8 nm；重复精度达到1.5 nm rms	一维测量;双扫描间隔; 减小回程误差及参考误差

下载: 导出CSV

参考文献(68)

[1]	KIRKPATRICK P, BAEZ A V. Formation of optical images by X-rays[J]. Journal of the Optical Society of America, 1948, 38(9): 766-774. doi: 10.1364/JOSA.38.000766
[2]	GIEWEKEMEYER K, WILKE R N, OSTERHOFF M, et al. Versatility of a hard X-ray kirkpatrick–baez focus characterized by ptychography[J]. Journal of Synchrotron Radiation, 2013, 20(3): 490-497. doi: 10.1107/S0909049513005372
[3]	NAULLEAU P P, GOLDBERG K A, BATSON P J, et al. Tolerancing of diffraction-limited Kirkpatrick-Baez synchrotron beamline optics for extreme-ultraviolet metrology[J]. Applied Optics, 2001, 40(22): 3703-3709. doi: 10.1364/AO.40.003703
[4]	MATSUYAMA S, YAMADA J, KOHMURA Y, et al. Full-field X-ray fluorescence microscope based on total-reflection advanced Kirkpatrick-Baez mirror optics[J]. Optics Express, 2019, 27(13): 18318-18328. doi: 10.1364/OE.27.018318
[5]	KODAMA R, IKEDA N, KATO Y, et al. Development of an advanced Kirkpatrick-Baez microscope[J]. Optics Letters, 1996, 21(17): 1321-1323. doi: 10.1364/OL.21.001321
[6]	HUDEC R, PINA L, VAN INNEMAN A, et al. Lightweight x-ray optics for future space missions[J]. Proceedings of SPIE, 2003, 4851: 656-665. doi: 10.1117/12.461590
[7]	YUMOTO H, MIMURA H, KOYAMA T, et al. Focusing of X-ray free-electron laser pulses with reflective optics[J]. Nature Photonics, 2012, 7(1): 43-47.
[8]	SIEWERT F, BUCHHEIM J, BOUTET S, et al. Ultra-precise characterization of LCLS hard X-ray focusing mirrors by high resolution slope measuring deflectometry[J]. Optics Express, 2012, 20(4): 4525-4536. doi: 10.1364/OE.20.004525
[9]	HEYNACHER E, REINHARDT D. Measuring equipment for testing the directrix of high-resolution wolter-type telescopes[J]. Proceedings of SPIE, 1979, 184: 167-169. doi: 10.1117/12.957446
[10]	COCCO D, IDIR M, MORTON D, et al. Advances in X-ray optics: from metrology characterization to wavefront sensing-based optimization of active optics[J]. Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment, 2018, 907: 105-115.
[11]	QIAN S, TAKACS P. Nano-accuracy Surface Figure Metrology of Precision Optics[M]. COCCO L. Modern Metrology Concerns. Rijeka: Intech Open, 2012.
[12]	OWADA S, TOGAWA K, INAGAKI T, et al. A soft X-ray free-electron laser beamline at SACLA: the light source, photon beamline and experimental station[J]. Journal of Synchrotron Radiation, 2018, 25(1): 282-288. doi: 10.1107/S1600577517015685
[13]	YANDAYAN T, GECKELER R D, SIEWERT F. Pushing the limits: latest developments in angle metrology for the inspection of ultra-precise synchrotron optics[J]. Proceedings of SPIE, 2014, 9206: 92060F.
[14]	TAKACS P Z, FENG S C K, CHURCH E L, et al. Long trace profile measurements on cylindrical aspheres[J]. Proceedings of SPIE, 1989, 966: 354-364. doi: 10.1117/12.948082
[15]	TAKACS P Z, QIAN SH N, COLBERT J. Design of a long trace surface profiler[J]. Proceedings of SPIE, 1987, 749: 59-64. doi: 10.1117/12.939842
[16]	SIEWERT F, LAMMERT H, NOLL T, et al. Advanced metrology: an essential support for the surface finishing of high performance x-ray optics[J]. Proceedings of SPIE, 2005, 5921: 592101. doi: 10.1117/12.622747
[17]	SIEWERT F, ZESCHKE T, ARNOLD T, et al. Linear chirped slope profile for spatial calibration in slope measuring deflectometry[J]. Review of Scientific Instruments, 2016, 87(5): 051907. doi: 10.1063/1.4950737
[18]	OTSUBO M, OKADA K, TSUJIUCHI J. Measurement of large plane surface shapes by connecting small-aperture interferograms[J]. Optical Engineering, 1994, 33(2): 608-613. doi: 10.1117/12.152248
[19]	IRICK S C, MCKINNEY W R, LUNT D L J, et al. Using a straightness reference in obtaining more accurate surface profiles from a long trace profiler[J]. Review of Scientific Instruments, 1992, 63(1): 1436-1438. doi: 10.1063/1.1143036
[20]	QIAN SH N, LI H ZH, TAKACS P Z. Penta-Prism Long Trace Profiler (PPLTP) for measurement of grazing incidence space optics[J]. Proceedings of SPIE, 1996, 2805: 108-114. doi: 10.1117/12.245083
[21]	QIAN SH N, SOSTERO G, TAKACS P Z. Precision calibration and systematic error reduction in the long trace profiler[J]. Optical Engineering, 2000, 39(1): 304-310. doi: 10.1117/1.602364
[22]	PEDREIRA P, NICOLAS J, ŠICS I, et al. Deflectometry encoding the measured angle in a time-dependent intensity signal[J]. Review of Scientific Instruments, 2019, 90(2): 021707. doi: 10.1063/1.5057768
[23]	QIAN SH N, TAKACS P Z. Design of multiple-function long trace profiler[J]. Optical Engineering, 2007, 46(4): 043602. doi: 10.1117/1.2724851
[24]	FLORIOT J, LEVECQ X, BUCOURT S, et al. A Shack–Hartmann measuring head for the two-dimensional characterization of X-ray mirrors[J]. Journal of Synchrotron Radiation, 2008, 15(2): 134-139. doi: 10.1107/S0909049507066083
[25]	IDIR M, KAZNATCHEEV K, DOVILLAIRE G, et al. A 2 D high accuracy slope measuring system based on a stitching shack hartmann optical head[J]. Optics Express, 2014, 22(3): 2770-2781. doi: 10.1364/OE.22.002770
[26]	ALCOCK S G, SAWHNEY K J S, SCOTT S, et al. The Diamond-NOM: a non-contact profiler capable of characterizing optical figure error with sub-nanometre repeatability[J]. Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment, 2010, 616(2-3): 224-228. doi: 10.1016/j.nima.2009.10.137
[27]	QIAN SH N, IDIR M. Innovative nano-accuracy surface profiler for sub-50 nrad rms mirror test[J]. Proceedings of SPIE, 2016, 9687: 96870D.
[28]	GECKELER R D. ESAD shearing deflectometry: potentials for synchrotron beamline metrology[J]. Proceedings of SPIE, 2006, 6317: 63171H. doi: 10.1117/12.716301
[29]	LACEY I, ADAM J, CENTERS G P, et al. Development of a high performance surface slope measuring system for two-dimensional mapping of x-ray optics[J]. Proceedings of SPIE, 2017, 10385: 103850G.
[30]	QIAN SH N, WANG Q P, HONG Y L, et al. Multiple Functions Long Trace Profiler (LTP-MF) for national synchrotron radiation laboratory of China[J]. Proceedings of SPIE, 2005, 5921: 592104. doi: 10.1117/12.618800
[31]	ZENG D H, XIAO T Q, DU G H, et al. New long trace profiler based on phase plate diffraction for optical metrology of SSRF[J]. Review of Scientific Instruments, 2006, 77(9): 093305. doi: 10.1063/1.2186253
[32]	李直, 赵洋, 李达成, 等. 衍射型长程大型非球面轮廓测量仪[J]. 光学学报,2002,22(10):1224-1228. doi: 10.3321/j.issn:0253-2239.2002.10.014 LI ZH, ZHANG Y, LI D CH, et al. A diffractive long trace profiler for large aspherical optics[J]. Acta Optica Sinica, 2002, 22(10): 1224-1228. (in Chinese) doi: 10.3321/j.issn:0253-2239.2002.10.014
[33]	SHUN L, YAN G, WEI ZH, et al. Design of co-path scanning long trace profiler for measurement of x-ray space optical elements[J]. Proceedings of SPIE, 2010, 7544: 754421. doi: 10.1117/12.885415
[34]	澎湃新闻. 高能同步辐射光源验证装置通过国家验收, 最亮光源年中开建[OL]. https://www.thepaper.cn/newsDetail_forward_2935727. 2019-1-31. The Paper. The verification device of high energy synchrotron radiation light source has passed acceptance, and the brightest light source will be built in the middle of the year [OL]. https://www.thepaper.cn/newsDetail_forward_2935727. 2019-1-31.
[35]	秦超.同步辐射椭圆柱面压弯镜机构的研究[D]. 北京: 中国科学院大学(中国科学院上海应用物理研究所), 2018. QIN CH. Research on synchrotron radiation elliptic cylinder mirror bender[D]. Beijing: University of Chinese Academy of Sciences (Shanghai Institute of Applied Physics, Chinese Academy of Sciences), 2018. (in Chinese)
[36]	SIEWERT F, BUCHHEIM J, ZESCHKE T, et al. On the characterization of ultra-precise X-ray optical components: advances and challenges in ex situ metrology[J]. Journal of Synchrotron Radiation, 2014, 21(5): 968-975. doi: 10.1107/S1600577514016221
[37]	ASSOUFID L, BRAY M, QIAN J, et al. 3D surface profile measurements of large x-ray synchrotron radiation mirrors using stitching interferometry[J]. Proceedings of SPIE, 2002: 4728.
[38]	VIVO A, LANTELME B, BAKER R, et al. Stitching methods at the European Synchrotron Radiation Facility (ESRF)[J]. Review of Scientific Instruments, 2016, 87(5): 051908. doi: 10.1063/1.4950745
[39]	VIVO A, BARRETT R. Fizeau stitching at the European Synchrotron Radiation Facility (ESRF)[J]. Proceedings of SPIE, 2017, 10385: 103850N.
[40]	VIVO A, BARRETT R, PERRIN F. Stitching techniques for measuring X-ray synchrotron mirror topography[J]. Review of Scientific Instruments, 2019, 90(2): 021710. doi: 10.1063/1.5063339
[41]	WIEGMANN A, STAVRIDIS M, WALZEL M, et al. Accuracy evaluation for sub-aperture interferometry measurements of a synchrotron mirror using virtual experiments[J]. Precision Engineering, 2011, 35(2): 183-190. doi: 10.1016/j.precisioneng.2010.08.007
[42]	YAMAUCHI K, YAMAMURA K, MIMURA H, et al. Microstitching interferometry for x-ray reflective optics[J]. Review of Scientific Instruments, 2003, 74(5): 2894-2898. doi: 10.1063/1.1569405
[43]	OHASHI H, TSUMURA T, OKADA H, et al. Microstitching interferometer and relative angle determinable stitching interferometer for half-meter-long x-ray mirror[J]. Proceedings of SPIE, 2007, 6704: 670405. doi: 10.1117/12.733476
[44]	GEVORKYAN G S, CENTERS G, POLONSKA K S, et al.. Surface slope metrology of highly curved x-ray optics with an interferometric microscope[C]. Proceedings of SPIE, 2017, 10385: 103850H.
[45]	ASSOUFID L, QIAN J, KEWISH C M, et al. A microstitching interferometer for evaluating the surface profile of precisely figured X-ray K-B mirrors[J]. Proceedings of SPIE, 2007, 6704: 670406. doi: 10.1117/12.736384
[46]	ROMMEVEAUX A, BARRETT R. Micro-stitching interferometry at the ESRF[J]. Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment, 2010, 616(2-3): 183-187.
[47]	POLACK F, THOMASSET M, BROCHET S, et al. Surface shape determination with a stitching Michelson interferometer and accuracy evaluation[J]. Review of Scientific Instruments, 2019, 90(2): 021708. doi: 10.1063/1.5061930
[48]	MIMURA H, YUMOTO H, MATSUYAMA S, et al.. Microstitching interferometry for nanofocusing mirror optics[C]. Proceedings of SPIE, 2004, 5533: 170-180.
[49]	KIMURA T, OHASHI H, MIMURA H, et al. A stitching figure profiler of large X-ray mirrors using RADSI for subaperture data acquisition[J]. Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment, 2010, 616(2-3): 229-232. doi: 10.1016/j.nima.2009.11.014
[50]	YUMOTO H, MIMURA H, KIMURA T, et al. Stitching interferometric metrology for steeply curved x-ray mirrors[J]. Surface and Interface Analysis, 2008, 40(6-7): 1023-1027. doi: 10.1002/sia.2807
[51]	YUMOTO H, MIMURA H, HANDA S, et al. Stitching-angle measurable microscopic-interferometer: surface-figure metrology tool for hard X-ray nanofocusing mirrors with large curvature[J]. Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment, 2010, 616(2-3): 203-206.
[52]	YUMOTO H, KOYAMA T, MATSUYAMA S, et al. Stitching interferometry for ellipsoidal x-ray mirrors[J]. Review of Scientific Instruments, 2016, 87(5): 051905. doi: 10.1063/1.4950714
[53]	EHRET G, LAUBACH S, SCHULZ M. Flatness metrology based on small-angle deflectometric procedures with electronic tiltmeters[J]. Proceedings of SPIE, 2017, 10326: 1032604.
[54]	MING L, SHANZHI T, FUGUI Y, et al.. Optical metrology at BSRF[C]. Advanced Optical Manufacturing and Testing Technologies, 2016.
[55]	XUE J P, HUANG L, GAO B, et al. One-dimensional stitching interferometry assisted by a triple-beam interferometer[J]. Optics Express, 2017, 25(8): 9393-9405. doi: 10.1364/OE.25.009393
[56]	HUANG L, XUE J P, GAO B, et al. One-dimensional angular-measurement-based stitching interferometry[J]. Optics Express, 2018, 26(8): 9882-9892. doi: 10.1364/OE.26.009882
[57]	HUANG L, IDIR M, ZUO CH, et al. Two-dimensional stitching interferometry based on tilt measurement[J]. Optics Express, 2018, 26(18): 23278-23286. doi: 10.1364/OE.26.023278
[58]	陈善勇. 非球面子孔径拼接干涉测量的几何方法研究[D]. 长沙: 国防科学技术大学, 2006. CHEN SH Y. Geometrical approach to subaperture stitching interferometry for aspheric surface[D]. Changsha: National University of Defense Technology, 2006. （in Chinese）
[59]	侯溪, 伍凡, 杨力, 等. 环形子孔径拼接检测大口径非球面镜的规划模型及分析[J]. 光学精密工程,2006,14(2):207-212. HOU X, WU F, YANG L, et al. Layout model and analysis of annular subaperture stitching technique for testing large aspheric mirror[J]. Optics and Precision Engineering, 2006, 14(2): 207-212. (in Chinese)
[60]	王孝坤, 王丽辉, 邓伟杰, 等. 用非零位补偿法检测大口径非球面反射镜[J]. 光学精密工程,2011,19(3):520-528. doi: 10.3788/OPE.20111903.0520 WANG X K, WANG L H, DENG W J, et al. Measurement of large aspheric mirrors by non-null testing[J]. Optics and Precision Engineering, 2011, 19(3): 520-528. (in Chinese) doi: 10.3788/OPE.20111903.0520
[61]	李长春, 程国民, 曹永刚. 自动调焦系统速度评估与仿真[J]. 液晶与显示,2019,34(5):515-520. doi: 10.3788/YJYXS20193405.0515 LI CH CH, CHENG G M, CAO Y G. Evaluation and simulation of auto-focus system speed[J]. Chinese Journal of Liquid Crystals and Displays, 2019, 34(5): 515-520. (in Chinese) doi: 10.3788/YJYXS20193405.0515
[62]	ZHAI D D, CHEN SH Y, PENG X Q, et al. Absolute profile test by multi-sensor scanning system with relative angle measurement[J]. Measurement Science and Technology, 2018, 29(11): 115205. doi: 10.1088/1361-6501/aade0d
[63]	SHI Y N, XU X D, HUANG Q SH, et al. Development of relative angle determinable stitching interferometry for high-accuracy x-ray focusing mirrors[J]. Proceedings of SPIE, 2017, 10385: 103850M.
[64]	FREISCHLAD K R. Absolute Interferometric testing based on reconstruction of rotational shear[J]. Applied Optics, 2001, 40(10): 1637-1648. doi: 10.1364/AO.40.001637
[65]	张敏, 隋永新, 杨怀江. 用于子孔径拼接干涉系统的机械误差补偿算法[J]. 光学精密工程,2015,23(4):934-940. doi: 10.3788/OPE.20152304.0934 ZHANG M, SUI Y X, YANG H J. Mechanical error compensation algorithm for subaperture stitching interferometr[J]. Optics and Precision Engineering, 2015, 23(4): 934-940. (in Chinese) doi: 10.3788/OPE.20152304.0934
[66]	MURPHY P, FORBES G, FLEIG J, et al. Stitching interferometry: a flexible solution for surface metrology[J]. Optics and Photonics News, 2003, 14(5): 38-43. doi: 10.1364/OPN.14.5.000038
[67]	NICOLAS J, NG M L, PEDREIRA P, et al. Completeness condition for unambiguous profile reconstruction by sub-aperture stitching[J]. Optics Express, 2018, 26(21): 27212-27220. doi: 10.1364/OE.26.027212
[68]	ASSOUFID L, BRAY M, SHU D M. Development of a linear stitching interferometric system for evaluation of very large X-ray synchrotron radiation substrates and mirrors[J]. AIP Conference Proceedings, 2004, 705(1): 851-854.