等截面反射镜椭圆压弯机构变像距压弯

周博文; 王楠; 祝万钱; 薛松; 田应仲

doi:10.37188/CO.2019-0250

等截面反射镜椭圆压弯机构变像距压弯

doi: 10.37188/CO.2019-0250

周博文^{1, 2,},
王楠^{2, 3},
祝万钱^{2, 3},
薛松^{2, 3, ,},
田应仲^1, ,

1.
上海大学机电工程与自动化学院，上海 201900
2.
中国科学院上海应用物理研究所，上海 201204
3.
中国科学院上海高等研究院，上海 201204

基金项目: 国家自然科学基金资助项目（No.11675253）

详细信息

作者简介:
周博文（1993—），男，内蒙古包头人，硕士研究生，2015年于河海大学获得学士学位，主要研究方向为压弯聚焦镜系统分析、测试。E-mail：597538834@qq.com

薛　松，（1962—），男，吉林长春人，研究员，博士生导师，1984年于东北大学获得学士学位，现任上海光源束线机械工程技术部主任，主要从事同步辐射光学工程、精密机械与光谱仪器的研究。E-mail：xuesong@zjlab.org.cn

田应仲（1973—），男，贵州安顺人，博士，副教授，博士生导师，2007年于上海大学获得博士学位，现从事移动机器人、软体机器人、图像处理领域的研究。E-mail：troytian@shu.edu.cn

中图分类号: TH744
计量
- 文章访问数: 2066
- HTML全文浏览量: 561
- PDF下载量: 75
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-29
- 修回日期: 2020-02-22
- 刊出日期: 2020-08-01

Variable image distance bending using an elliptical bending mechanism with a constant cross-section mirror

ZHOU Bo-wen^{1, 2
,},
WANG Nan^{2, 3},
ZHU Wan-qian^{2, 3},
XUE Song^{2, 3
, ,},
TIAN Ying-zhong^{1
, ,}

1.
School of Mechatronic Engineering and Automation, Shanghai University, Shanghai 201900, China
2.
Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201204, China
3.
Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai 201204, China

Funds: Supported by National Natural Science Foundation of China (No.11675253)

More Information

Corresponding author: xuesong@zjlab.org.cn; troytian@shu.edu.cn

摘要

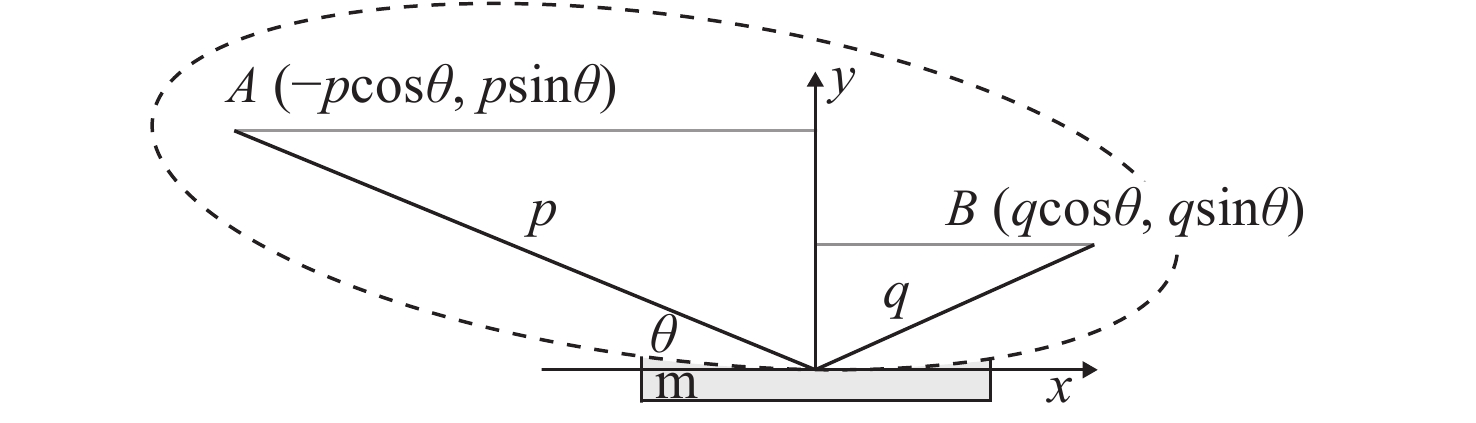
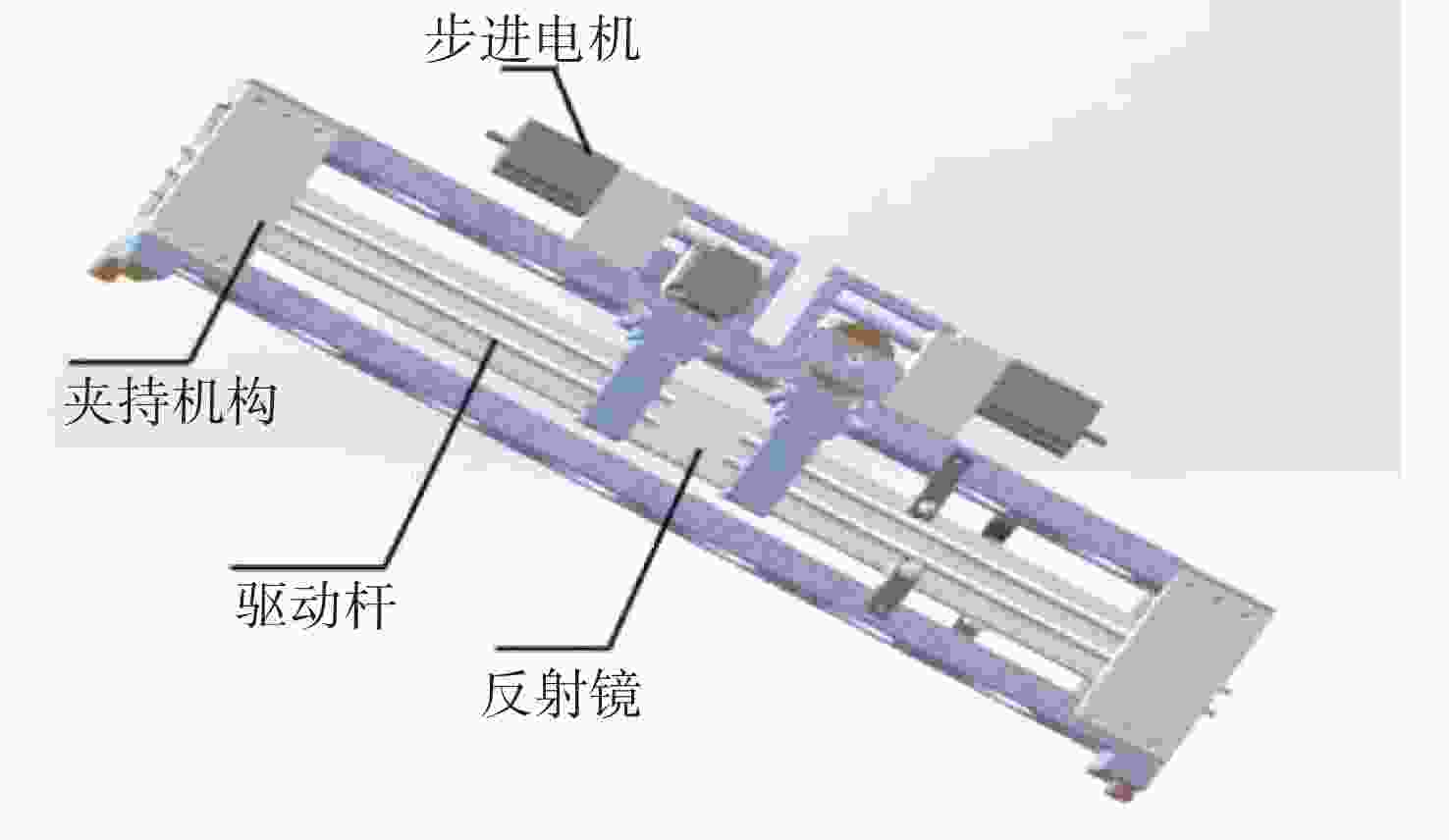
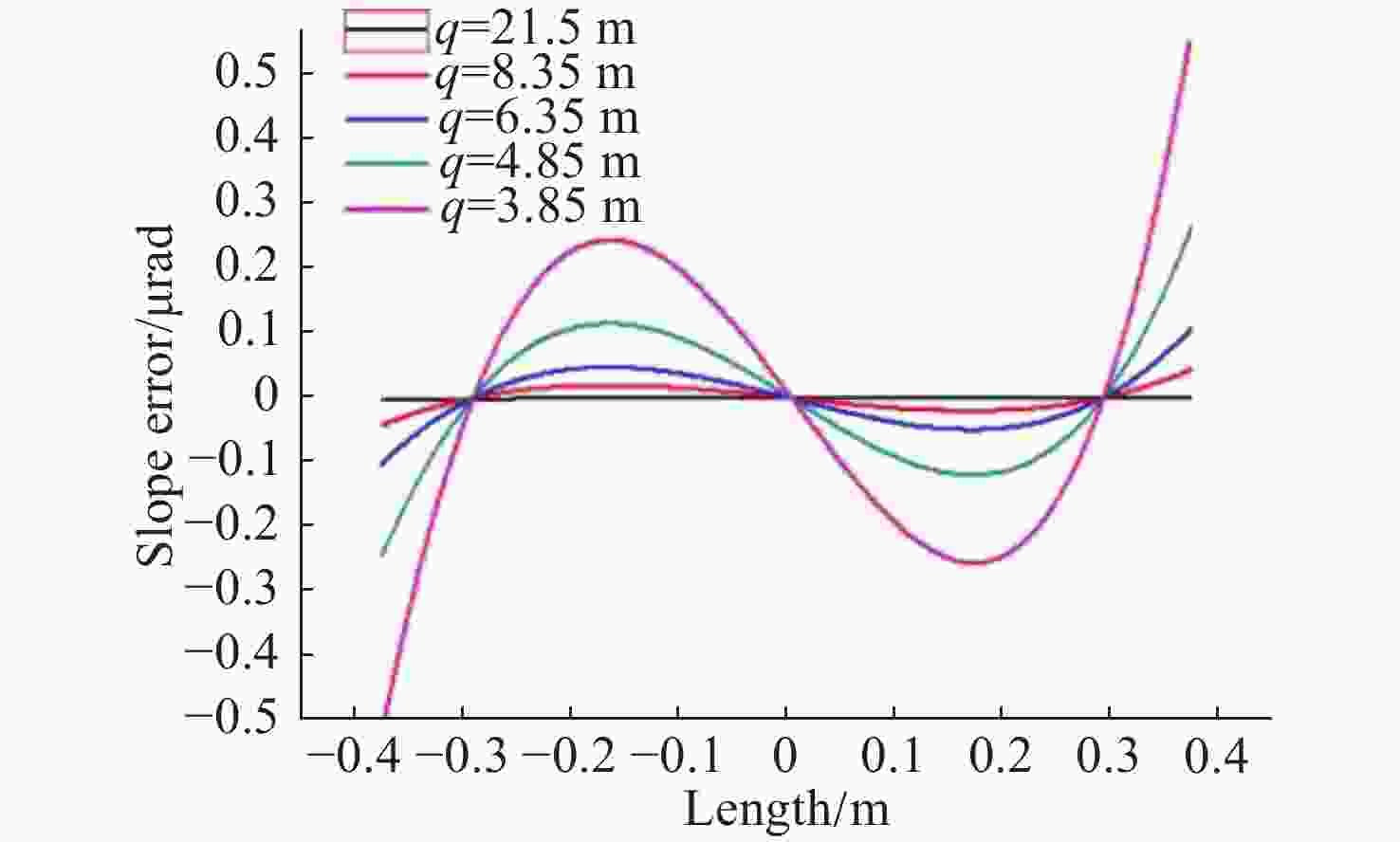
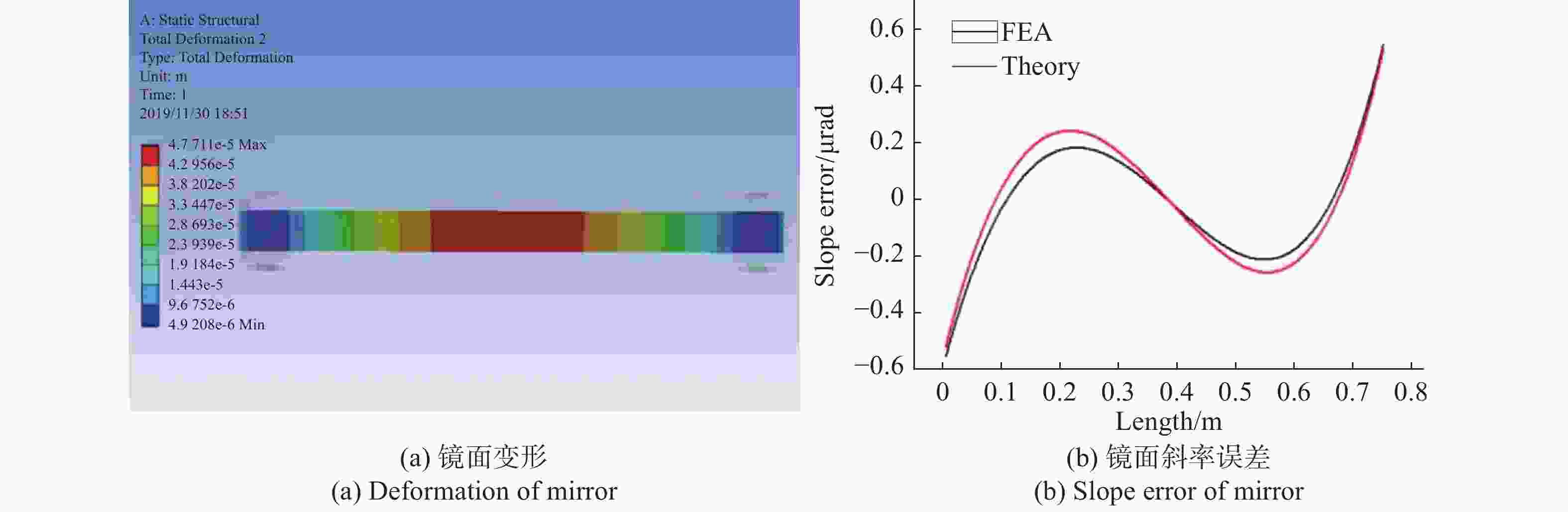
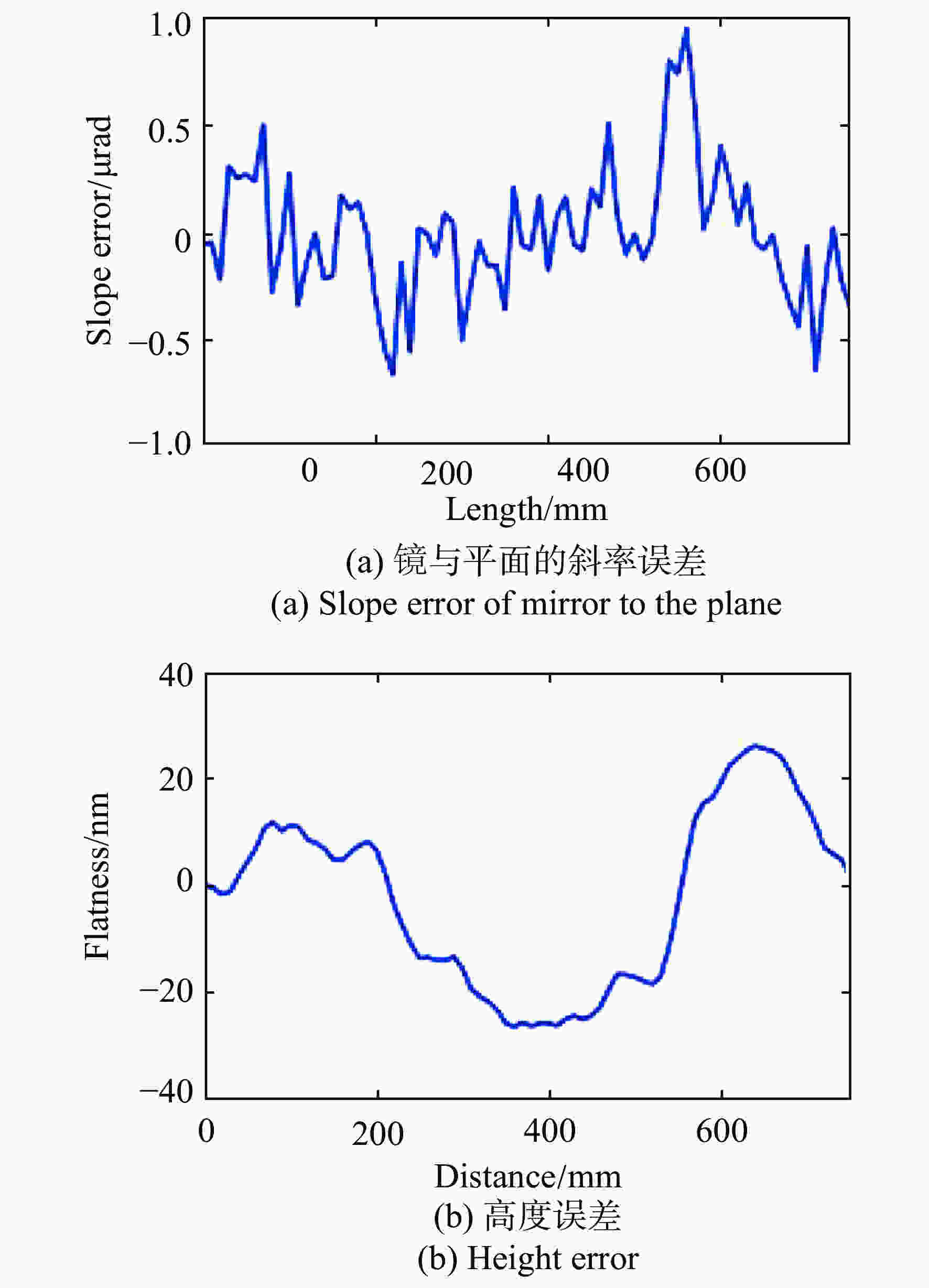
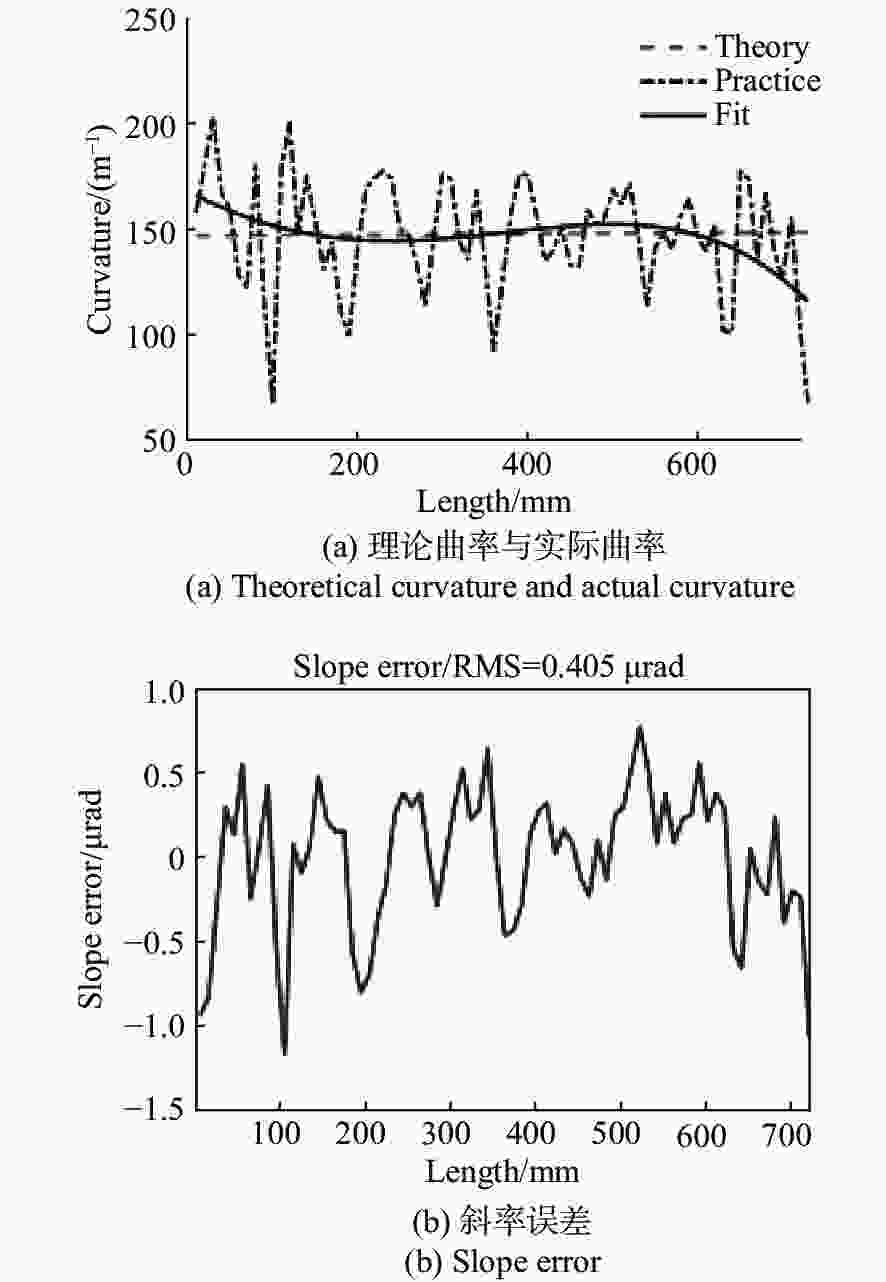
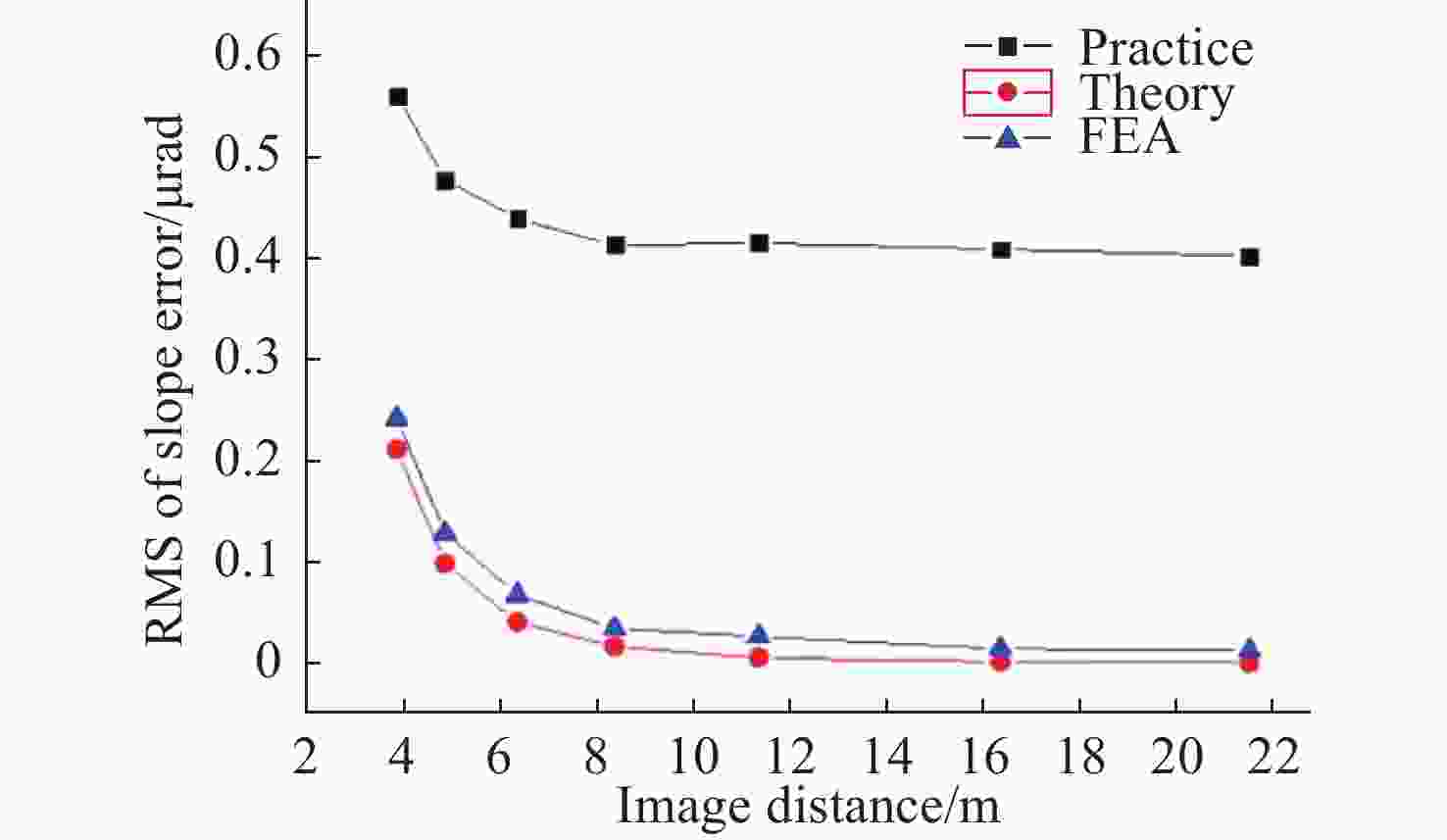
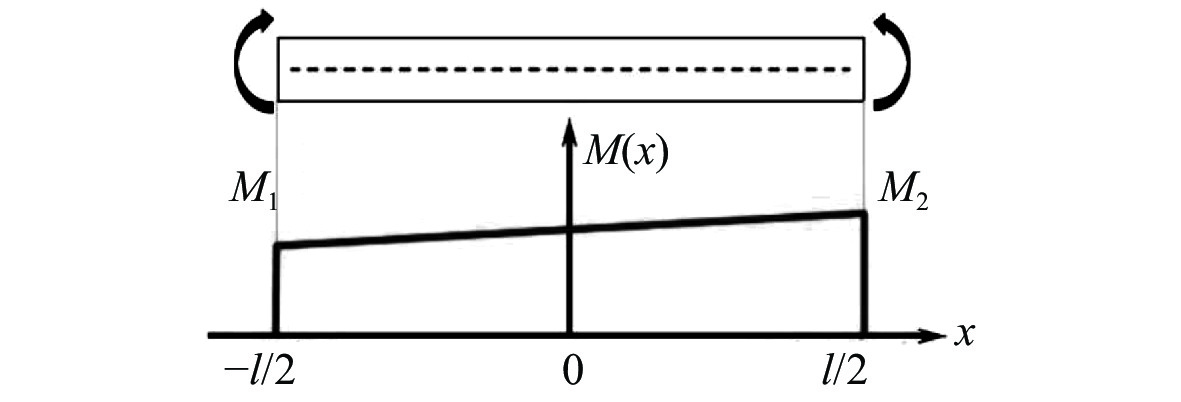
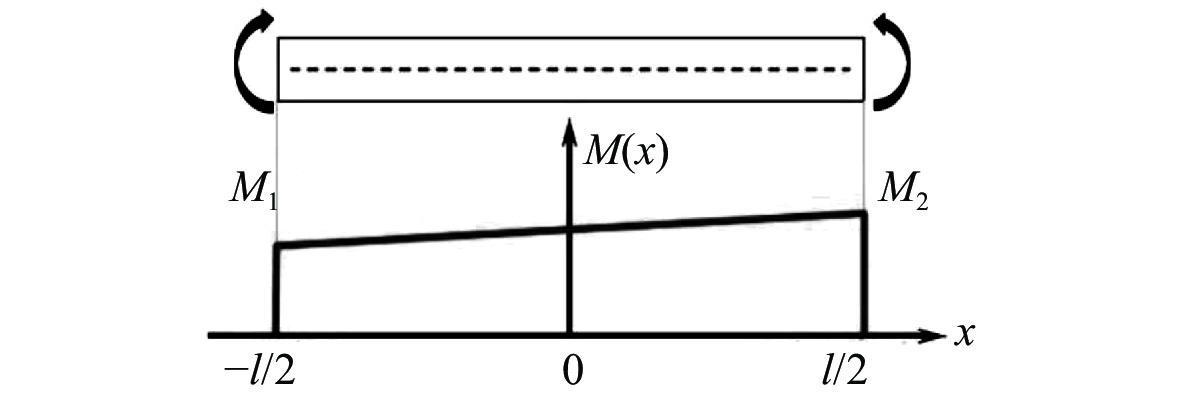
摘要: 针对新设计的等截面反射镜椭圆压弯机构在固定物距（即反射镜在光路中位置不变）的情况下，研究了实现大范围像距调整（即样品位置发生改变）时镜面面形误差等问题。通过理论分析并借助有限元分析软件计算等截面平面镜压弯至不同（反射点处像距不同）椭圆柱面时的理论斜率误差，最后对椭圆压弯机构样机进行了实际压弯测试。实验结果与计算分析均表明：保持物距、掠入射角不变，压弯镜面与理想椭圆柱面之间的斜率误差会随着像距的减小而增大，并且像距越小，镜面斜率误差的增加速度越大。实验测得在反射镜面初始斜率误差为0.397 μrad的情况下，全部像距范围（21.5~3.8 m）内压弯镜面的实际斜率误差在0.402~0.560 μrad之间，重复精度为0.051 μrad，均满足上海光源光束线的设计要求。本文研究证明了使用等截面反射镜压弯机构进行椭圆柱面压弯可以实现聚焦镜工作像距在大范围内的连续调节。
- 同步辐射 /
- 压弯机构 /
- 椭圆柱面镜 /
- 面形误差
Abstract: In this paper, the surface shape error of latest elliptical bending mechanism with a constant cross-section mirror is studied when the object distance is fixed (when the position of the mirror in the light path is invariable) and the image distance is adjusted drastically (when the position of the sample is changed). Based on theoretical analysis and the finite element analysis, theoretical slope error is calculated when it is caused by bending a mirror with a width equal to an elliptical cylinder with a different shape (different image distances at the reflection point). Then, a bending experiment of a prototype of the elliptical bending mechanism is conducted. Experimental results and analysis indicate that the slope error between the bending mirror and an ideal elliptic cylinder will increase with a decrease in image distance, and the slope error of the mirror will increase more quickly as the image distance is shortened. When the initial slope error of the reflecting mirror is 0.397 μrad, the slope error of the bent mirror in the whole range of image distance (21.5~3.8 m) is 0.402~0.560 μrad and the repeatable accuracy is 0.051 urad, which meets the design requirements of the beamline of the Shanghai Synchrotron Radiation Facility (SSRF). It is proven that in elliptically bending mirrors, continuous adjustment of the image distance from the focusing mirror can be achieved by using a bending mechanism with constant cross-section mirror.
- synchrotron radiation /
- bending mechanism /
- elliptical cylindrical mirror /
- slope error

HTML全文

图 1 压弯原理

Figure 1. Principle of bending

下载: 全尺寸图片幻灯片

图 2 椭圆聚焦的几何关系

Figure 2. Geometric relationship of elliptical focusing

下载: 全尺寸图片幻灯片

图 3 压弯机构的三维模型

Figure 3. 3D model of bending mechanism

下载: 全尺寸图片幻灯片

图 4 不同像距时理论斜率误差对比

Figure 4. Comparison of theoretical slope errors at different image distances

下载: 全尺寸图片幻灯片

图 5 理论斜率误差RMS值随像距的变化曲线

Figure 5. RMS value of theoretical slope error varying with image distance

下载: 全尺寸图片幻灯片

图 6 简化三维模型图

Figure 6. Simplified 3D model

下载: 全尺寸图片幻灯片

图 7 模型网格划分

Figure 7. Grids of 3D model

下载: 全尺寸图片幻灯片

图 8 镜面变形及斜率误差

Figure 8. Deformation and slope error of mirror

下载: 全尺寸图片幻灯片

图 9 压弯机构与NOM测量仪

Figure 9. Bending mechanism and NOM measuring instrument

下载: 全尺寸图片幻灯片

图 10 压弯前的镜面误差

Figure 10. Surface error of mirror before bending

下载: 全尺寸图片幻灯片

图 11 像距q=21.5 m时的测量结果

Figure 11. Measurement results when image distance is 21.5 m

下载: 全尺寸图片幻灯片

图 12 3种斜率误差RMS值随像距的变化情况

Figure 12. Three kinds of RMS values of slope error varying with image distance

下载: 全尺寸图片幻灯片

表 1 椭圆压弯反射镜的参数及设计指标

Table 1. Parameters and design indexes of elliptical bending mirror

材料	聚焦镜尺寸/mm	镜面有效尺寸/mm	自身斜率误差/μrad
单晶硅	1000×70×50	700×20	0.4

物距p/m	掠入射角θ/mrad	像距q/m	要求压完后斜率误差/μrad
26.5	3.5	21.5~3.8	<0.60

下载: 导出CSV

表 2 压弯部件材料属性

Table 2. Material properties of the bending mechanism^,s parts

材料	泊松比	杨氏模量/GPa	密度/kg·m⁻³
Si	0.3	169	2330
结构钢 Structural steel (OCr18Ni9)	0.33	206	7800
轴承钢 Beering steel (Gcr15)	0.3	208	7800

下载: 导出CSV

表 3 不同像距下镜面斜率误差RMS值的有限元计算结果

Table 3. FEA results of RMS values of slope error at different image distances

理论像距/m	斜率误差RMS	左右驱动杆位移/mm
21.5	0.013	3.96	4.27
16.5	0.015	4.53	5.18
11.5	0.027	5.57	7.32
8.5	0.035	6.10	7.93
6.5	0.078	7.42	8.96
4.8	0.128	9.05	12.83
3.8	0.242	10.10	17.20

下载: 导出CSV

表 4 实际压弯测试结果

Table 4. Actual bending experiment results

理论像距/m	斜率误差RMS/μrad	重复精度/μrad	驱动杆位移/mm
21.5	0.402	0.011	4.13，4.30
16.5	0.409	0.021	4.65，5.05
11.5	0.415	0.013	5.67，6.30
8.5	0.413	0.021	6.35，7.80
6.5	0.439	0.026	7.70，9.55
4.8	0.478	0.023	9.70，13.10
3.8	0.560	0.051	10.55，17.60

下载: 导出CSV

参考文献(18)

[1]	马礼敦. 同步辐射装置——上海光源及其应用[J]. 理化检验-物理分册,2009,45(11):717-723. MA L D. Shanghai synchrotron radiation facility and its application[J]. Physical Testing and Chemical Analysis (Part A:Physical Testing), 2009, 45(11): 717-723. (in Chinese)
[2]	卢启鹏, 高飒飒, 彭忠琦. 同步辐射水平偏转压弯镜面形误差分析与补偿[J]. 光学精密工程,2011,19(11):2644-2650. doi: 10.3788/OPE.20111911.2644 LU Q P, GAO S S, PENG ZH Q. Analysis and compensation of slope error for synchrotron radiation horizontal deflected mirror[J]. Optics and Precision Engineering, 2011, 19(11): 2644-2650. (in Chinese) doi: 10.3788/OPE.20111911.2644
[3]	秦超, 薛松, 王楠, 等. 压弯椭圆柱面镜的有限元分析[J]. 核技术,2018,41(1):010101. doi: 10.11889/j.0253-3219.2018.hjs.41.010101 QIN CH, XUE S, WANG N, et al. The finite element analysis of the bent elliptical cylindrical mirror[J]. Nuclear Techniques, 2018, 41(1): 010101. (in Chinese) doi: 10.11889/j.0253-3219.2018.hjs.41.010101
[4]	金利民, 罗红心, 王劼, 等. 双压电片镜在同步辐射光源光学系统中的应用[J]. 中国光学,2017,10(6):699-707. doi: 10.3788/co.20171006.0699 JIN L M, LUO H X, WANG J, et al. Application of bimorph mirror in the optical system of synchrotron radiation light source[J]. Chinese Optics, 2017, 10(6): 699-707. (in Chinese) doi: 10.3788/co.20171006.0699
[5]	程光宇, 黄智超, 王克逸, 等. 同步辐射聚焦镜压弯机构设计与面形误差分析[J]. 应用光学,2019,40(1):120-126. CHENG G Y, HUANG ZH CH, WANG K Y, et al. Design and surface shape error analysis of synchronous radiation focusing mirror bending mechanism[J]. Journal of Applied Optics, 2019, 40(1): 120-126. (in Chinese)
[6]	吕清涛, 薛松, 彭忠琦, 等. 拉杆式压弯聚焦镜组件线性与接触非线性方法的比较[J]. 光学精密工程,2010,18(8):1842-1848. LÜ Q T, XUE S, PENG ZH Q, et al. Comparison on linear and contact nonlinear analysis methods of pull-rod bent focusing mirror assembly[J]. Optics and Precision Engineering, 2010, 18(8): 1842-1848. (in Chinese)
[7]	黄智超, 程建高, 李飞, 等. 同步辐射压弯镜重力补偿方法[J]. 强激光与粒子束,2018,30(8):085102. doi: 10.11884/HPLPB201830.180066 HUANG ZH CH, CHENG J G, LI F, et al. Gravity compensation for bent mirror of synchrotron radiation[J]. High Power Laser and Particle Beams, 2018, 30(8): 085102. (in Chinese) doi: 10.11884/HPLPB201830.180066
[8]	毛成文, 余笑寒, 肖体乔. 变宽度压弯椭圆柱面聚焦镜的光学参数可调性[J]. 核技术,2009,32(5):333-336. doi: 10.3321/j.issn:0253-3219.2009.05.003 MAO CH W, YU X H, XIAO T Q. Tunability of optical parameters of width-variable bent elliptical microfocus mirror[J]. Nuclear Techniques, 2009, 32(5): 333-336. (in Chinese) doi: 10.3321/j.issn:0253-3219.2009.05.003
[9]	PADMORE H A, HOWELLS M R, IRICK S C, et al. New schemes for producing high-accuracy elliptical x-ray mirrors by elastic bending[J]. Proceedings of SPIE, 1996, 2856: 145-156. doi: 10.1117/12.259867
[10]	NISTEA I T, ALCOCK S G, KRISTIANSEN P, et al. Long, elliptically bent, active X-ray mirrors with slope errors <200 nrad[J]. Journal of Synchrotron Radiation, 2017, 24(3): 615-621. doi: 10.1107/S1600577517005422
[11]	徐乐, 张春雷, 代雷, 等. 高精度非回转对称非球面加工方法研究[J]. 中国光学,2016,9(3):364-370. doi: 10.3788/co.20160903.0364 XU L, ZHANG CH L, DAI L, et al. Research on manufacturing method of non-rotationally symmetrical aspheric surface with high accuracy[J]. Chinese Optics, 2016, 9(3): 364-370. (in Chinese) doi: 10.3788/co.20160903.0364
[12]	闫力松, 杨甬英, 马冬林, 等. 长条形镜面面形拟合技术研究[J]. 中国光学,2018,11(6):1011-1016. doi: 10.3788/co.20181106.1011 YAN L S, YANG Y Y, MA D L, et al. Surface fitting technology of rectangular mirror[J]. Chinese Optics, 2018, 11(6): 1011-1016. (in Chinese) doi: 10.3788/co.20181106.1011
[13]	秦超. 同步辐射椭圆柱面压弯镜机构的研究[D]. 上海: 中国科学院上海应用物理研究所, 2018. QIN CH. Research on synchrotron radiation elliptic cylinder mirror bender[D]. Shanghai: Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2018. (in Chinese)
[14]	HOWELLS M R, CAMBIE D, IRICK S C, et al. Theory and practice of elliptically bent x-ray mirrors[J]. Optical Engineering, 2000, 39(10): 2748-2762. doi: 10.1117/1.1289879
[15]	周泗忠, 杨晓许, 时惠霞. 压弯聚焦镜自重的平衡[J]. 核技术,2005,28(3):180-182. doi: 10.3321/j.issn:0253-3219.2005.03.004 ZHOU S ZH, YANG X X, SHI H X. Study of gravity compensation of bent focusing mirror[J]. Nuclear Techniques, 2005, 28(3): 180-182. (in Chinese) doi: 10.3321/j.issn:0253-3219.2005.03.004
[16]	卢启鹏, 彭忠琦. 压弯机构在同步辐射光束线中的应用[J]. 光机电信息,2011,28(6):8-13. doi: 10.3788/OMEI20112806.0008 LU Q P, PENG ZH Q. Application of bender in synchrotron radiation beamline[J]. OME Information, 2011, 28(6): 8-13. (in Chinese) doi: 10.3788/OMEI20112806.0008
[17]	MAO CH W, JIANG H, HE Y, et al. Compensation for gravitational sag of bent mirror[J]. Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment, 2017, 853: 20-26.
[18]	孙福权, 傅远, 祝万钱, 等. 压弯镜系统自重平衡多点调节方法的研究[J]. 核技术,2011,34(4):246-250. SUN F Q, FU Y, ZHU W Q, et al. A study on multi-point gravity compensation of mirror bending system[J]. Nuclear Techniques, 2011, 34(4): 246-250. (in Chinese)