可见光通信中正交频分复用调制技术

徐宪莹; 岳殿武

doi:10.37188/CO.2020-0051

可见光通信中正交频分复用调制技术

doi: 10.37188/CO.2020-0051

徐宪莹^{1, 2,},
岳殿武^1, ,

1.
大连海事大学信息科学技术学院，辽宁大连 116026
2.
大连科技学院电气工程学院，辽宁大连 116052

基金项目: 国家自然科学基金（No. 61371091）；大连海事大学研究生教育教学改革研究项目（No. YJG2019205）

详细信息

作者简介:
徐宪莹（1988—），女，山东莒县人，讲师，大连海事大学博士研究生，2011年、2014年于大连海事大学分别获得学士、硕士学位，主要从事可见光通信研究。E-mail：xuxianying@dlmu.edu.cn

岳殿武（1966—），男，吉林四平人，博士，教授，博士生导师，1986年，1989年于南开大学分别获得学士、硕士学位，1996年于北京邮电大学获得博士学位，主要从事无线通信方面的研究。E-mail：dwyue@dlmu.edu.cn

中图分类号: TN929.12
计量
- 文章访问数: 2248
- HTML全文浏览量: 463
- PDF下载量: 119
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-30
- 修回日期: 2020-05-26
- 网络出版日期: 2021-04-17
- 刊出日期: 2021-05-01

Orthogonal frequency division multiplexing modulation techniques in visible light communication

XU Xian-ying^{1, 2
,},
YUE Dian-wu^{1
, ,}

1.
College of Information Science and Technology, Dalian Maritime University, Dalian 116026, China
2.
College of Electrical Engineering, Dalian University of Science and Technology, Dalian 116052, China

Funds: Supported by National Natural Science Foundation of China (No. 61371091); Research Project on Postgraduate Education and Teaching Reform of Dalian Maritime University (No. YJG2019205)

More Information

Corresponding author: dwyue@dlmu.edu.cn

摘要

摘要: 可见光通信（VLC）由于可以弥补射频通信的不足而成为研究热点，正交频分复用（OFDM）技术因其高数据速率和抗频率选择性衰落被广泛应用在VLC中。本文从能量效率、频谱效率、误码率、计算复杂度等方面对可见光通信系统中OFDM调制技术进行研究和比较，主要包括基于离散傅立叶变换的单极性方案、改进或增强型方案和混合型方案，基于哈特莱变换的光OFDM，以及基于LED索引调制的光OFDM。文中介绍了多种光OFDM调制技术的工作原理综合对比了频谱效率等性能；研究了光OFDM系统接收机改进方案；总结了可见光OFDM系统存在的问题和未来研究方向。本文对可见光OFDM系统进行归纳和总结，为提出更加高效的单极化调制技术、进一步提高系统频谱效率及可靠性提供了参考。
- 可见光通信 /
- 正交频分复用 /
- 频谱效率 /
- 接收机 /
- 索引调制
Abstract: With its unique advantages, Visible Light Communication (VLC) can compensate for limitations in radio frequency communication, allowing it to become a recent avid topic of research. Orthogonal Frequency Division Multiplexing (OFDM) has been widely used in VLC due to its high rate of data transfer and frequency selective fading resistance. We compare the performance of several OFDM modulation techniques in VLC, including unipolar schemes, enhanced schemes and hybrid schemes based on discrete Fourier transformation, as well as optical OFDM systems based on Hartley transform and LED index modulation. We perform these comparisons in terms of energy efficiency, spectral efficiency, bit error rate, and algorithm complexity. The principles of some kinds of optical OFDM systems are firstly illustrated and their spectrum efficiencies are theoretically analyzed and compared. We also research and analysis the improved design of receivers in optical OFDM systems. The challenges and upcoming research of OFDM systems in VLC are summarized. The research in this paper can provide a research reference and propose more efficient unipolar modulation schemes to further improve the spectral efficiency and reliability of optical OFDM systems.
- visible light communication /
- orthogonal frequency division multiplexing /
- spectrum efficiency /
- improved receiver /
- index modulation

HTML全文

图 1 基于离散傅立叶变换的光OFDM系统框图

Figure 1. Block diagram of an optical OFDM system based on discrete Fourier transformation

下载: 全尺寸图片幻灯片

图 2 光OFDM系统BER=10⁻³时光功耗与频带利用率的关系

Figure 2. The relationship between optical power and spectral efficiency in the optical OFDM system under BER=10⁻³

下载: 全尺寸图片幻灯片

表 1 典型单极性光OFDM调制原理对比

Table 1. Comparison of modulation principles of typical optical OFDM

典型单极性光OFDM	频域子载波设置	时域信号极性	单极化处理
DCO-OFDM^[10]	$ {X}_{k}={X}_{N-k}^{\ast },0<k<\dfrac{N}{2}$	双极性实数	添加直流偏置
ACO-OFDM^[11]	${{X} }=\left(0,{X}_{1},0,{X}_{3},\cdots,{X}_{\frac{N}{2}-1},0,{X}_{\frac{N}{2}-1}^{\ast },\cdots,{X}_{3}^{\ast },0,{X}_{1}^{\ast }\right)$	双极性实数，具有特殊对称性：${x}_{n}=-{x}_{n+\frac{N}{2} }\left(0{\text{≤} } n < N/2\right)$	负值限幅
U-OFDM^[12]	$ {X}_{k}={X}_{N-k}^{\ast },0<k<\dfrac{N}{2}$	双极性实数	极性编码
Flip-OFDM^[13]	$ {X}_{k}={X}_{N-k}^{\ast },0<k<\dfrac{N}{2}$	双极性实数	“正”、“负”模块分别传输
PAM-DMT^[14]	$\begin{array}{l}{{X} }=(0,{\rm{j} }{X}_{\rm{PAM},1},{\rm{j} }{X}_{\rm{PAM,2} },\cdots,{\rm{j} }{X}_{ { {\rm{PAM} } },\frac{N}{2}-1},0,\\-{\rm{j} }{X}_{ {\rm{PAM} },\frac{N}{2}-1},\cdots,-{\rm{j} }{X}_{\rm{PAM},2},-{\rm{j} }{X}_{\rm{PAM},1})\end{array}$	双极性实数，具有特殊对称性：${x}_{N-n}=-{x}_{n},1{\text{≤} } n{\text{≤} } \dfrac{N}{2}-1$	负值限幅
MACO-OFDM^[15]	${{X} }=\left(0,{X}_{1},0,{X}_{3},\cdots,{X}_{\frac{N}{2}-1},0,{X}_{\frac{N}{2}-1 }^{\ast },\cdots,{X}_{3}^{\ast },0,{X}_{1}^{\ast }\right)$	双极性实数具有特殊对称性：${x}_{n}=-{x}_{n+\frac{N}{2} }\left(0{\text{≤} } n < \dfrac{N}{2}\right)$	极性编码

下载: 导出CSV

表 2 光OFDM性能比较

Table 2. Performance comparison of optical OFDM schemes

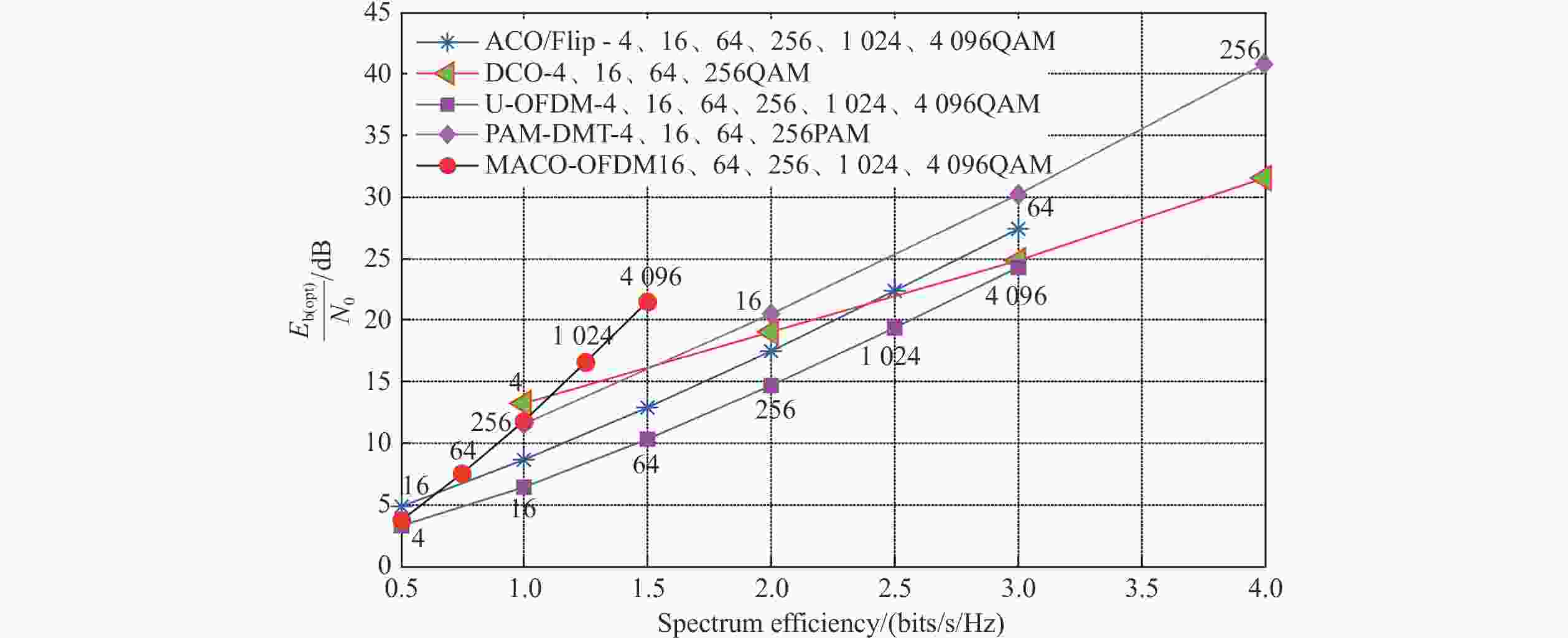
光OFDM	频谱效率（bits·s⁻¹·Hz⁻¹）	功率效率	接收机复杂度
DCO-OFDM^[10]	$\displaystyle \frac{N-2}{2N}{\rm{log} }_{2}\; M$	低	$ O\left(N{\rm{log}}_{2}\; N\right)$
ACO-OFDM^[11]	$\displaystyle \frac{1}{4}{\rm{log} }_{2}\; M$	高	$ O\left(N{\rm{log}}_{2}\; N\right)$
U-OFDM^[12]	$\displaystyle \frac{N-2}{4N}{\rm{log} }_{2}\; M$	高	$ O\left(N{\rm{log}}_{2}\; N\right)$
Flip-OFDM^[13]	$\displaystyle \frac{N-2}{4N}{\rm{log} }_{2}\; M$	高	$ O\left(N{\rm{log}}_{2}\; N\right)$
PAM-DMT^[14]	$\displaystyle\frac{N-2}{2N}{\rm{log} }_{2}\; M$	低	$ O\left(N{\rm{log}}_{2}\; N\right)$
MACO-OFDM^[15]	$\displaystyle\frac{1}{8}{\rm{log} }_{2}\; M$	高	$ O\left(N{\rm{log}}_{2}\; N\right)$
eU-OFDM^[16]	$\left(1-\displaystyle\frac{1}{ {2}^{D} }\right)\displaystyle\frac{N-2}{2N}{\rm{log} }_{2}\; M$	高	$ {O}\left[\left(2D-1\right)\left(N{\rm{log}}_{2}\; N\right)\right]$
GREENER-OFDM^[32]	$\displaystyle\frac{N-2}{4N}{\displaystyle \sum _{d=1}^{D}\displaystyle\frac{ {\rm{log} }_{2}\; {M}_{d} }{ {2}^{d-1} } }$	高	$ {O}\left[\left(2D-1\right)\left(N{\rm{log}}_{2}\; N\right)\right]$
ePAM-DMT^[33]	$ {\displaystyle \sum _{d=1}^{D}\frac{\left(N-2d\right){\rm{log}}_{2}{M}_{d}}{{2}^{d}N}}$	高	${O}\left({2\displaystyle \sum _{d=1}^{D}{N}_{d}{\rm{log} }_{2}{N}_{d} }-{N}_{D}{\rm{log} }_{2}{N}_{D}\right)$
eACO-OFDM^[34]	$ {\displaystyle \sum _{d=1}^{D}\frac{{\rm{log}}_{2}{M}_{d}}{{2}^{d+1}}}$	高	${ O }\left({\displaystyle \sum _{l=1}^{L}\displaystyle\frac{N}{ {2}^{l-2} } }{\rm{log} }_{2}\left(\displaystyle\frac{N}{ {2}^{l-1} }\right)-\displaystyle\frac{N}{ {2}^{L-1} }{\rm{log} }_{2}\left(\displaystyle\frac{N}{ {2}^{L-1} }\right)\right)$
LACO-OFDM^[17]	$\left(\displaystyle\frac{1}{2}-\displaystyle\frac{1}{ {2}^{L+1} }\right){\rm{log} }_{2}\; M$	高	${O}\left({\displaystyle \sum _{l=1}^{L}\displaystyle\frac{N}{ {2}^{l-2} } }{\rm{log} }_{2}\left(\displaystyle\frac{N}{ {2}^{l-1} }\right)-\displaystyle\frac{N}{ {2}^{L-1} }{\rm{log} }_{2}\left(\displaystyle\frac{N}{ {2}^{L-1} }\right)\right)$
THO-OFDM^[35]	$\displaystyle\frac{1}{4}{\rm{log} }_{2}\; {M}_{\rm{ACO} }^{1}+\frac{1}{8}{\rm{log} }_{2}\; {M}_{\rm{ACO} }^{2}+\left(\frac{1}{8}-\frac{1}{N}\right){\rm{log} }_{2}\; {M}_{\rm{PAM} }$	高	$\begin{array}{l}{\rm{TD} }:{O}\left[N\left({\rm{log} }_{2}N+{\rm{log} }_{2}\left(\displaystyle\frac{N}{2}\right)\right)\right]\\ {\rm{FD} }:{O}\left[N\left(3{\rm{log} }_{2}N+{\rm{log} }_{2}\left(\displaystyle\frac{N}{2}\right)\right)\right]\end{array}$
ADO-OFDM^[18]	$\displaystyle \frac{1}{4}{\rm{log} }_{2}\; {M}_{\rm{ACO} }+\left(\frac{1}{4}-\frac{1}{N}\right){\rm{log} }_{2}\; {M}_{\rm{DCO} }$	中	$ {O}\left(4N{\rm{log}}_{2}\; N\right)$
HACO-OFDM^[19]	$\displaystyle \frac{1}{4}{\rm{log} }_{2}\; {M}_{\rm{ACO} }+\left(\frac{1}{4}-\frac{1}{N}\right){\rm{log} }_{2}\; {M}_{\rm{PAM} }$	高	$ {O}\left(3N{\rm{log}}_{2}\; N\right)$
EHACO-OFDM^[20]	$\displaystyle\frac{1}{4}{\rm{log} }_{2}\; {M}_{\rm{ACO} }+\left(\frac{1}{4}-\frac{1}{N}\right)\left({\rm{log} }_{2}\; {M}_{\rm{DCO} }+{\rm{log} }_{2}\; {M}_{\rm{PAM} }\right)$	高	$ {O}\left(5N{\rm{log}}_{2}\; N\right)$
AAO-OFDM^[21]	$\displaystyle\frac{1}{4}\left({\rm{log} }_{2}\; {M}_{\rm{AVO} }+{\rm{log} }_{2}\; {M}_{\rm{ACO} }\right)-\frac{1}{N}{\rm{log} }_{2}\; {M}_{\rm{AVO} }-\frac{1}{2}$	高	$ {O}\left(4N{\rm{log}}_{2}\; N\right)$
PM-OFDM^[22]	$\displaystyle\frac{1}{4}{\rm{log} }_{2}\; M$	高	$ \begin{array}{l}{\rm{PM}}-1:{O}\left(N{\rm{log}}_{2}\; N\right)\\ {\rm{PM}}-2:{O}\left(9N{\rm{log}}_{2}\; N\right)\end{array}$
P-OFDM^[23]	$\displaystyle \frac{1}{2}{\rm{log} }_{2}\; M$	高	$ O\left(N{\rm{log}}_{2}\; N\right)$

下载: 导出CSV

表 3 基于FFT与FHT的光OFDM对比

Table 3. Comparison of optical OFDM with FFT and FHT

	FFT-OFDM	FHT-OFDM
定义式	$\begin{array}{l}{\rm{FFT} }: X(k)={\displaystyle \sum _{n=0}^{N-1}x(n){\rm{exp} }\;\left(-{\rm{j} }\frac{2{\text{π} } nk}{N}\right)},0{\text{≤} } k{\text{≤} } N-1\\ {\rm{IFFT} }: x(n)={\displaystyle \sum _{k=0}^{N-1}X(k){\rm{exp} }\;\left({\rm{j} }\frac{2{\text{π} }nk}{N}\right)},0{\text{≤} } n{\text{≤} } N-1\end{array}$	$\begin{array}{l}{\rm{FHT} }: X(k)={\displaystyle \sum _{n=0}^{N-1}x(n)}{\rm{cas} }\;(2{\text{π} } kn/N),0{\text{≤} } k{\text{≤} } N-1\\ {\rm{IFHT} }:x(n)={\displaystyle \sum _{k=0}^{N-1}X(k)}{\rm{cas} }(2{\text{π} } kn/N),0{\text{≤} } n{\text{≤} } N-1\\{\rm{cas} }(2{\text{π} }kn/N)={\rm{cos} }(2{\text{π} }kn/N)+{\rm{sin} }(2{\text{π} }kn/N)\end{array}$
调制方式	复星座（m-QAM）	实星座（BPSK，M-PAM）
星座尺寸	m	$ M=\sqrt{m}$
厄米特对称	需要	不需要
计算复杂度	有复数计算附加共轭运算	无复数计算无附加共轭运算
有用载波	N/2	N

下载: 导出CSV

参考文献(70)

[1]	杨秀清, 陈海燕. 光通信技术在物联网中的应用[J]. 中国光学,2014,7(6):889-896. YANG X Q, CHEN H Y. Application of optical communication technique in the internet of things[J]. Chinese Optics, 2014, 7(6): 889-896. (in Chinese)
[2]	周青超, 柏泽龙, 鲁路, 等. 白光LED远程荧光粉技术研究进展与展望[J]. 中国光学,2015,8(3):313-328. doi: 10.3788/co.20150803.0313 ZHOU Q CH, BAI Z L, LU L, et al. Remote phosphor technology for white LED applications: advances and prospects[J]. Chinese Optics, 2015, 8(3): 313-328. (in Chinese) doi: 10.3788/co.20150803.0313
[3]	侯启真, 薛荣荣, 王洁宁. LED阵列发光特性仿真和对比分析[J]. 液晶与显示,2017,32(12):961-967. doi: 10.3788/YJYXS20173212.0961 HOU Q ZH, XUE R R, WANG J N. Simulation and comparative analysis of LED arrays in light-emitting characteristics[J]. Chinese Journal of Liquid Crystals and Displays, 2017, 32(12): 961-967. (in Chinese) doi: 10.3788/YJYXS20173212.0961
[4]	李炳乾, 罗明浩, 俞理云, 等. COB封装全光谱LED光源及其光电特性[J]. 液晶与显示,2018,33(11):931-935. doi: 10.3788/YJYXS20183311.0931 LI B Q, LUO M H, YU L Y, et al. Full spectrum LED light in COB package and its characteristics[J]. Chinese Journal of Liquid Crystals and Displays, 2018, 33(11): 931-935. (in Chinese) doi: 10.3788/YJYXS20183311.0931
[5]	武文杰, 阿木古楞, 刘文全, 等. 氮(氧)化物荧光粉的合成与发光性能[J]. 液晶与显示,2017,32(9):663-676. doi: 10.3788/YJYXS20173209.0663 WU W J, AMUGULEN, LIU W Q, et al. Synthesis and luminescence of nitride and oxynitride luminescent materials[J]. Chinese Journal of Liquid Crystals and Displays, 2017, 32(9): 663-676. (in Chinese) doi: 10.3788/YJYXS20173209.0663
[6]	KARUNATILAKA D, ZAFAR F, KALAVALLY V, et al. LED based indoor visible light communications: state of the art[J]. IEEE Communications Surveys &Tutorials, 2015, 17(3): 1649-1678.
[7]	KUMAR S, SINGH P. A comprehensive survey of visible light communication: potential and challenges[J]. Wireless Personal Communications, 2019, 109(2): 1357-1375. doi: 10.1007/s11277-019-06616-3
[8]	曹婷, 陈华敏. 基于正交频分复用技术的低压电力线通信系统模型[J]. 液晶与显示,2019,34(9):928-934. doi: 10.3788/YJYXS20193409.0928 CAO T, CHEN H M. Low voltage power line communication system model based on orthogonal frequency division multiplexing technology[J]. Chinese Journal of Liquid Crystals and Displays, 2019, 34(9): 928-934. (in Chinese) doi: 10.3788/YJYXS20193409.0928
[9]	王旭东, 崔玉, 吴楠, 等. 室内可见光多维CAP空间调制[J]. 发光学报,2018,39(2):227-235. doi: 10.3788/fgxb20183902.0227 WANG X D, CUI Y, WU N, et al. Spatial modulation based on multi-dimensional carrierless amplitude and phase for indoor visible light communication system[J]. Chinese Journal of Luminescence, 2018, 39(2): 227-235. (in Chinese) doi: 10.3788/fgxb20183902.0227
[10]	GONZALEZ O, PEREZ-JIMENEZ R, RODRIGUEZ S, et al. OFDM over indoor wireless optical channel[J]. IEE Proceedings-Optoelectronics, 2005, 152(4): 199-204. doi: 10.1049/ip-opt:20045065
[11]	ARMSTRONG J, LOWERY A J. Power efficient optical OFDM[J]. Electronics Letters, 2006, 42(6): 370-372. doi: 10.1049/el:20063636
[12]	TSONEV D, SINANOVIC S, HAAS H. Novel Unipolar Orthogonal Frequency Division Multiplexing (U-OFDM) for optical wireless[C]. Proceedings of the 2012 IEEE 75th Vehicular Technology Conference, IEEE, 2012: 1-5.
[13]	FERNANDO N, HONG Y, VITERBO E. Flip-OFDM for optical wireless communications[C]. Proceedings of 2011 IEEE Information Theory Workshop, IEEE, 2011: 5-9.
[14]	LEE S C J, RANDEL S, BREYER F, et al. PAM-DMT for intensity-modulated and direct-detection optical communication systems[J]. IEEE Photonics Technology Letters, 2009, 21(23): 1749-1751. doi: 10.1109/LPT.2009.2032663
[15]	MOHAMED S D, ANDONOVIC I, SHALABY H, et al.. Modified asymmetrically-clipped optical orthogonal frequency-division multiplexing system performance[C]. Proceedings of 2013 IEEE Photonics Conference, IEEE, 2013: 289-290.
[16]	TSONEV D, HAAS H. Avoiding spectral efficiency loss in unipolar OFDM for optical wireless communication[C]. Proceedings of 2014 IEEE International Conference on Communications, IEEE, 2014: 3336-3341.
[17]	WANG Q, QIAN CH, GUO X H, et al. Layered ACO-OFDM for intensity-modulated direct-detection optical wireless transmission[J]. Optics Express, 2015, 23(9): 12382-12393. doi: 10.1364/OE.23.012382
[18]	DISSANAYAKE S D, ARMSTRONG J. Comparison of ACO-OFDM, DCO-OFDM and ADO-OFDM in IM/DD systems[J]. Journal of Lightwave Technology, 2013, 31(7): 1063-1172. doi: 10.1109/JLT.2013.2241731
[19]	RANJHA B, KAVEHRAD M. Hybrid asymmetrically clipped OFDM-based IM/DD optical wireless system[J]. IEEE/OSA Journal of Optical Communications and Networking, 2014, 6(4): 387-396. doi: 10.1364/JOCN.6.000387
[20]	GUAN R, HUANG N, WANG J Y, et al. Enhanced hybrid asymmetrically clipped orthogonal frequency division multiplexing for optical wireless communications[J]. Optical Engineering, 2016, 55(5): 056111. doi: 10.1117/1.OE.55.5.056111
[21]	BAI R W, WANG Q, WANG ZH CH. Asymmetrically clipped absolute value optical OFDM for intensity-modulated direct-detection systems[J]. Journal of Lightwave Technology, 2017, 35(17): 3680-3691. doi: 10.1109/JLT.2017.2716983
[22]	NUWANPRIYA A, GRANT A, HO S W, et al.. Position modulating OFDM for optical wireless communications[C]. Proceedings of 2012 IEEE Globecom Workshops, IEEE, 2012: 1219-1223.
[23]	ELGALA H, LITTLE T D C. Polar-based OFDM and SC-FDE links toward energy-efficient Gbps transmission under IM-DD optical system constraints [Invited][J]. Journal of Optical Communications and Networking, 2015, 7(2): A277-A284. doi: 10.1364/JOCN.7.00A277
[24]	MOREOLO M S. Power efficient and cost-effective solutions for optical OFDM systems using direct detection[C]. Proceedings of the 2010 12th International Conference on Transparent Optical Networks, IEEE, 2010: 1-4.
[25]	NADAL L, MOREOLO M S, FABREGA J M, et al.. Comparison of peak power reduction techniques in optical OFDM systems based on FFT and FHT[C]. Proceedings of the 2011 13th International Conference on Transparent Optical Networks, IEEE, 2011: 1-4.
[26]	AVERCHENKO A P, ZHENATOV B D. Comparison of computational costs of Hartley transform and Fourier transform[C]. Proceedings of the 2016 13th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering, IEEE, 2016: 436-438.
[27]	ZHOU J, QIAO Y J. Low-PAPR asymmetrically clipped optical OFDM for intensity-modulation/direct-detection systems[J]. IEEE Photonics Journal, 2015, 7(3): 7101608.
[28]	冯海燕, 王旭东, 吴楠, 等. 一种基于哈特莱变换的改进U-OFDM方法[J]. 光通信技术,2016,40(7):25-28. FENG H Y, WANG X D, WU N, et al. Modified U-OFDM scheme based on Hartley transform[J]. Optical Communication Technology, 2016, 40(7): 25-28. (in Chinese)
[29]	冯海燕, 王旭东, 吴楠, 等. 一种新的可见光通信光OFDM方法[J]. 光通信研究,2016,42(3):58-61. FENG H Y, WANG X D, WU N, et al. A novel optical-OFDM for visible light communication[J]. Study on Optical Communications, 2016, 42(3): 58-61. (in Chinese)
[30]	TANG J, ZHANG L. Efficient real-Fourier domain-based color shift keying OFDM implemented with Hartley transform for visible light communication system[C]. Proceedings of the 2017 IEEE 85th Vehicular Technology Conference, IEEE, 2017: 1-5.
[31]	AZIM A W, LE GUENNEC Y, MAURY G. Spectrally augmented Hartley transform precoded asymmetrically clipped optical OFDM for VLC[J]. IEEE Photonics Technology Letters, 2018, 30(23): 2029-2032. doi: 10.1109/LPT.2018.2874962
[32]	ISLIM M S, TSONEV D, HAAS H. A generalized solution to the spectral efficiency loss in unipolar optical OFDM-based systems[C]. Proceedings of 2015 IEEE International Conference on Communications, IEEE, 2015: 5126-5131.
[33]	ISLIM M S, TSONEV D, HAAS H. Spectrally enhanced PAM-DMT for IM/DD optical wireless communications[C]. Proceedings of the 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications, IEEE, 2015: 877-882.
[34]	ISLIM M S, TSONEV D, HAAS H. On the superposition modulation for OFDM-based optical wireless communication[C]. Proceedings of 2015 IEEE Global Conference on Signal and Information Processing, IEEE, 2015: 1022-1026.
[35]	ZHANG T, JI H, GHASSEMLOOY Z, et al. Spectrum-efficient triple-layer hybrid optical OFDM for IM/DD-based optical wireless communications[J]. IEEE Access, 2020, 8: 10352-10362. doi: 10.1109/ACCESS.2020.2964792
[36]	暴桐, 王旭东, 吴楠, 等. 一种基于星座协作映射的改进P-OFDM方法[J]. 半导体光电,2018,39(1):129-133. BAO T, WANG X D, WU N, et al. A modified P-OFDM scheme based on constellation collaborated mapping[J]. Semiconductor Optoelectronics, 2018, 39(1): 129-133. (in Chinese)
[37]	WANG ZH CH, MAO T Q, WANG Q. Optical OFDM for visible light communications[C]. Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference, IEEE, 2017: 1190-1194.
[38]	BRACEWELL R N. The Hartley Transform[M]. New York: Oxford University Press, 1986.
[39]	LI Y CH, TSONEV D, HAAS H. Non-DC-biased OFDM with optical spatial modulation[C]. Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications, IEEE, 2013: 486-490.
[40]	BAŞAR E, PANAYIRCI E, UYSAL M, et al.. Generalized LED index modulation optical OFDM for MIMO visible light communications systems[C]. Proceedings of 2016 IEEE International Conference on Communications, IEEE, 2016: 1-5.
[41]	ZHONG W D, CHEN CH, WU D H. Non-hermitian symmetry OFDM for indoor space division multiplexing visible light communications[C]. Proceedings of the 2016 18th International Conference on Transparent Optical Networks, IEEE, 2016: 1-4.
[42]	CAO Y L, ZHOU X T, SUN J, et al.. Optical spatial modulation with DHT-based OFDM in visible light communication systems[C]. Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing, IEEE, 2017: 1-5.
[43]	LE TRAN M, KIM S, KETSEOGLOU T, et al. LED selection and MAP detection for generalized LED index modulation[J]. IEEE Photonics Technology Letters, 2018, 30(19): 1695-1698. doi: 10.1109/LPT.2018.2865591
[44]	ASADZADEH K, DABBO A, HRANILOVIC S. Receiver design for asymmetrically clipped optical OFDM[C]. Proceedings of 2011 IEEE GLOBECOM Workshops, IEEE, 2011: 777-781.
[45]	DANG J, ZHANG Z, WU L. Frequency-domain diversity combining receiver for ACO-OFDM system[J]. IEEE Photonics Journal, 2015, 7(6): 7802510.
[46]	DANG J, ZHANG Z CH, WU L. A novel receiver for ACO-OFDM in visible light communication[J]. IEEE Communications Letters, 2013, 17(12): 2320-2323. doi: 10.1109/LCOMM.2013.111113.132223
[47]	DISSANAYAKE S D, ARMSTRONG J, HRANILOVIC S. Performance analysis of noise cancellation in a diversity Combined ACO-OFDM system[C]. Proceedings of the 2012 14th International Conference on Transparent Optical Networks, IEEE, 2012: 1-4.
[48]	张琦, 岳殿武. 室内MIMO ACO-OFDM可见光通信系统接收机设计[J]. 中国激光,2020,47(1):0106001. doi: 10.3788/CJL202047.0106001 ZHANG Q, YUE D W. Design of indoor receiver using multiple-input and multiple-output ACO-OFDM visible light communication system[J]. Chinese Journal of Lasers, 2020, 47(1): 0106001. (in Chinese) doi: 10.3788/CJL202047.0106001
[49]	XIANG N, ZHANG Z CH, DANG J, et al. A novel receiver design for PAM-DMT in optical wireless communication systems[J]. IEEE Photonics Technology Letters, 2015, 27(18): 1919-1922. doi: 10.1109/LPT.2015.2445793
[50]	HUANG N, WANG J B, WANG J ZH, et al. Receiver design for PAM-DMT in indoor optical wireless links[J]. IEEE Photonics Technology Letters, 2015, 27(2): 161-164. doi: 10.1109/LPT.2014.2363876
[51]	HUANG N, WANG J B, PAN C H, et al. Iterative receiver for flip-OFDM in optical wireless communication[J]. IEEE Photonics Technology Letters, 2015, 27(16): 1729-1732. doi: 10.1109/LPT.2015.2438338
[52]	DANG J, ZHANG Z CH, WU L. Improving the power efficiency of enhanced unipolar OFDM for optical wireless communication[J]. Electronics Letters, 2015, 51(21): 1681-1683. doi: 10.1049/el.2015.2024
[53]	WANG Q, WANG ZH CH, GUO X H, et al. Improved receiver design for layered ACO-OFDM in optical wireless communications[J]. IEEE Photonics Technology Letters, 2016, 28(3): 319-322. doi: 10.1109/LPT.2015.2495320
[54]	MOHAMMED M M A, HE C W, ARMSTRONG J. Diversity combining in layered asymmetrically clipped optical OFDM[J]. Journal of Lightwave Technology, 2017, 35(11): 2078-2085. doi: 10.1109/JLT.2017.2685591
[55]	WANG T Q, LI H, HUANG X J. Diversity combining for layered asymmetrically clipped optical OFDM using soft successive interference cancellation[J]. IEEE Communications Letters, 2017, 21(6): 1309-1312. doi: 10.1109/LCOMM.2017.2668421
[56]	BAI R W, JIANG R, MAO T Q, et al. Iterative receiver for ADO-OFDM with near-optimal optical power allocation[J]. Optics Communications, 2017, 387: 350-356. doi: 10.1016/j.optcom.2016.11.078
[57]	WANG T, HOU Y H, MA M D. A novel receiver design for HACO-OFDM by time-domain clipping noise elimination[J]. IEEE Communications Letters, 2018, 22(9): 1862-1865. doi: 10.1109/LCOMM.2018.2847650
[58]	ZHOU J, YAN Y, CAI ZH, et al. A cost-effective and efficient scheme for optical OFDM in short-range IM/DD systems[J]. IEEE Photonics Technology Letters, 2014, 26(13): 1372-1374. doi: 10.1109/LPT.2014.2325602
[59]	王志斌, 董伟, 任英, 等. 可见光通信中的白光LED非线性噪声分析[J]. 发光学报,2018,39(5):745-750. doi: 10.3788/fgxb20183905.0745 WANG ZH B, DONG W, REN Y, et al. Nonlinear noise analysis about white LED in visible light communication[J]. Chinese Journal of Luminescence, 2018, 39(5): 745-750. (in Chinese) doi: 10.3788/fgxb20183905.0745
[60]	唐芳, 徐智勇, 汪井源, 等. DCO-OFDM系统中导频辅助峰均比抑制技术[J]. 光电子·激光,2019,30(10):1116-1122. TANG F, XU ZH Y, WANG J Y, et al. Pilot-assisted PAPR reduction technique for DCO-OFDM systems[J]. Journal of Optoelectronics·Laser, 2019, 30(10): 1116-1122. (in Chinese)
[61]	MOSSAAD M S A, HRANILOVIC S, LAMPE L. Visible light communications using OFDM and multiple LEDs[J]. IEEE Transactions on Communications, 2015, 63(11): 4304-4313. doi: 10.1109/TCOMM.2015.2469285
[62]	SHI L N, ZHANG X, WANG W X, et al.. PAPR reduction based on deep autoencoder for VLC DCO-OFDM system[C]. Proceedings of 2019 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, IEEE, 2019: 1-4.
[63]	BAŞAR E, PANAYIRCI E. Optical OFDM with index modulation for visible light communications[C]. Proceedings of the 2015 4th International Workshop on Optical Wireless Communications, IEEE, 2015: 11-15.
[64]	YANG Y, ZENG ZH M, CHENG J L, et al. An enhanced DCO-OFDM scheme for dimming control in visible light communication systems[J]. IEEE Photonics Journal, 2016, 8(3): 7904813.
[65]	徐宪莹, 王旭东, 吴楠. 基于U-OFDM的室内可见光通信系统调光控制方法[J]. 半导体光电,2015,36(3):455-460. XU X Y, WANG X D, WU N. A scheme of U-OFDM based dimming control for indoor visible light communication systems[J]. Semiconductor Optoelectronics, 2015, 36(3): 455-460. (in Chinese)
[66]	王旭东, 徐宪莹, 吴楠, 等. 室内可见光OFDM通信系统调光控制技术[J]. 光子学报,2015,44(11):1106002. doi: 10.3788/gzxb20154411.1106002 WANG X D, XU X Y, WU N, et al. Dimming control technique for OFDM based indoor visible light communication system[J]. Acta Photonica Sinica, 2015, 44(11): 1106002. (in Chinese) doi: 10.3788/gzxb20154411.1106002
[67]	WANG C C, YANG Y, CHENG J L, et al. A dimmable OFDM scheme with dynamic subcarrier activation for VLC[J]. IEEE Photonics Journal, 2020, 12(1): 7900112.
[68]	NAJAFI M, SCHOBER R. Intelligent reflecting surfaces for free space optical communications[C]. Proceedings of 2019 IEEE Global Communications Conference, IEEE, 2019: 1-7.
[69]	WANG H B, ZHANG Z CH, ZHU B CH, et al.. Performance of wireless optical communication with reconfigurable intelligent surfaces and random obstacles[EB/OL]. (2020-01-16)[2020-01-17]. https://arxiv.org/abs/2001.05715.
[70]	BASAR E. Reconfigurable intelligent surface-based index modulation: a new beyond MIMO paradigm for 6G[J]. IEEE Transactions on Communications, 2020, 68(5): 3187-3196. doi: 10.1109/TCOMM.2020.2971486