强爆炸光辐射作用下材料的能量耦合特性

高银军; 高丽红; 张相华; 马壮; 刘峰; 彭国良; 田宙

doi:10.37188/CO.2020-0053

强爆炸光辐射作用下材料的能量耦合特性

doi: 10.37188/CO.2020-0053

高银军^{1, 3,},
高丽红^{1, 2},
张相华³,
马壮^{1, 2, ,},
刘峰^{3, 4},
彭国良^{3, 4},
田宙³

1.
北京理工大学材料学院，北京 100081
2.
北京理工大学冲击环境材料技术重点实验室，北京 100081
3.
西北核技术研究院，陕西西安 710024
4.
西北核技术研究院激光与物质相互作用国家重点实验室，陕西西安 710024

基金项目: 国家自然科学基金资助项目（No. 51772027，No. 91330205）

详细信息

作者简介:
高银军(1983—)，男，陕西宝鸡人，硕士研究生，2009年于中国科学技术大学获得硕士学位，主要从事强光与物质相互作用方面的研究。E-mail：gyj@mail.ustc.edu.cn

马　壮(1974—)，男，河北昌黎人，博士，教授，博士生导师，1996年、2001年于北京理工大学分别获得学士、博士学位，主要从事高温高能防护涂层材料和金属/陶瓷复合材料方面的研究。E-mail：hstrong929@bit.edu.cn

中图分类号: O432.1; O381
计量
- 文章访问数: 1705
- HTML全文浏览量: 398
- PDF下载量: 78
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-31
- 修回日期: 2020-05-26
- 网络出版日期: 2020-09-07
- 刊出日期: 2020-12-01

Energy coupling characteristic of materials under thermal radiation produced by strong explosion

GAO Yin-jun^{1, 3
,},
GAO Li-hong^{1, 2},
ZHANG Xiang-hua³,
MA Zhuang^{1, 2
, ,},
LIU Feng^{3, 4},
PENG Guo-liang^{3, 4},
TIAN Zhou³

1.
School of Materials Science and Engineering, Beijing Institute of Technology, Beijing 100081, China
2.
National Key of Laboratory of Science and Technology on Materials under Shock and Impact, Beijing 100081, China
3.
Northwest Institute of Nuclear Technology, Xi’an 710024, China
4.
State Key Laboratory of Laser Interaction with Matter, Northwest Institute of Nuclear Technology, Xi’an 710024, China

Funds: Supported by National Natural Science Foundation of China (No. 51772027, No. 91330205)

More Information

Corresponding author: hstrong929@bit.edu.cn

摘要

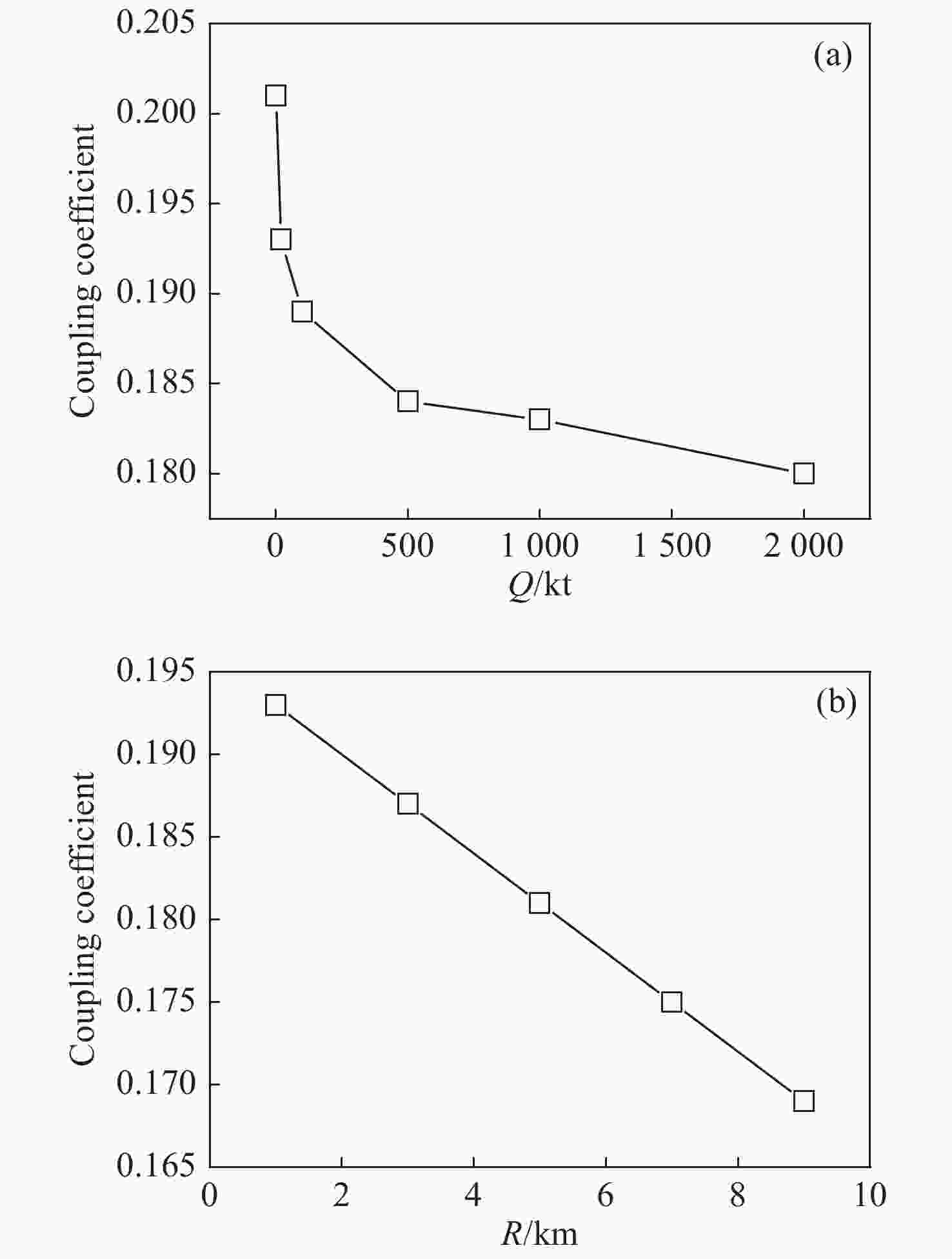
摘要: 为了获取强爆炸光辐射作用下材料的能量耦合特性，发展了强爆炸辐射源参数以及光辐射传输的物理模型和计算方法，计算给出了不同条件下目标位置处的光辐射谱特征。利用材料光谱反射率测量方法，结合光辐射耦合系数计算方法获取了几类材料的能量耦合系数。结果显示：金属、陶瓷材料的光辐射耦合系数相对较小，而碳纤维环氧复合材料的耦合系数可达0.92；采用实际光辐射能谱计算的耦合系数比近似6000 K黑体谱的结果要高，最大约14%。以铝材料为例，光辐射耦合系数随当量及爆心距离增加均表现出逐渐减小的趋势，但总体变化幅度不大。
- 强爆炸 /
- 光辐射 /
- 谱分布 /
- 能量耦合特性
Abstract: To obtain the energy coupling characteristic of materials under strong explosive thermal radiation, a physical model for calculating radiation source parameters and atmospheric transmission is constructed, and the characteristics of the radiation spectrum at the target location under different conditions are obtained. The energy coupling coefficients of several kinds of materials are produced by spectral reflectance measurement and by calculating the average absorption coefficient of thermal radiation. The coupling coefficients of metal and ceramic materials are relatively small while it can be as high as 0.92 for carbon fiber epoxy composites. The coupling coefficient calculated from the actual thermal radiation spectrum is higher than that calculated from 6000 K blackbody radiation spectrum, and the maximum difference is about 14%. Taking aluminum material as an example, the coupling coefficient of thermal radiation decreases gradually with the increase of explosion yield and distance, but the overall variation is small.
- strong explosion /
- thermal radiation /
- spectral distribution /
- energy coupling coefficient

HTML全文

图 1 当量10 kt下不同时刻火球半径及有效温度的计算结果

Figure 1. Calculated results of the fireball’s radius and effective temperature at different moments with 10 kt explosion yield

下载: 全尺寸图片幻灯片

图 2 光辐射可见、红外和紫外波段能量比例的实测结果与计算结果的对比

Figure 2. Comparison of measured and calculated energy ratios in visible, infrared and ultraviolet bands of thermal radiation

下载: 全尺寸图片幻灯片

图 3 不同当量下距爆心投影点1 km的归一化光辐射能谱

Figure 3. Normalized spectral distribution under different explosion yields at a range of 1 km from the center of burst projection point

下载: 全尺寸图片幻灯片

图 4 20 kt下不同距离处光辐射归一化能谱

Figure 4. Normalized spectral distribution of thermal radiation at different distances when the explosion yield is 20 kt

下载: 全尺寸图片幻灯片

图 5 材料光谱反射率测量原理及示意图

Figure 5. Principle and schematic diagram of the spectral reflectivity measurement system for different materials

下载: 全尺寸图片幻灯片

图 6 几类材料在0.2~2.0 µm范围内的光谱反射率

Figure 6. Spectral reflectances of typical materials in the range of 0.2 ~ 2.0 µm

下载: 全尺寸图片幻灯片

图 7 铝材料光谱吸收率及光辐射能谱分布

Figure 7. Spectral absorptivity of aluminum material and its thermal spectrum distribution

下载: 全尺寸图片幻灯片

图 8 铝材料背表面温升实测结果与采用耦合系数分别为0.19和0.17的计算结果对比

Figure 8. Comparison of the measured temperature rise on the back surface of aluminum material with the calculated results under coupling coefficients of 0.19 and 0.17

下载: 全尺寸图片幻灯片

图 9 铝材料光辐射耦合系数与当量(a)及爆心距离(b)的关系

Figure 9. Relationship between the coupling coefficients of aluminum material and the explosion yield (a) and burst center distance (b)

下载: 全尺寸图片幻灯片

表 1 不同群内光子能量范围（21群）

Table 1. Photon energy in different groups (21)

g	1	2	3	4	5	6	7	8	9	10	11	12	13
p_e (eV)	0.01−0.5	0.5−1.0	1.0−1.8	1.8−2.1	2.1−2.5	2.5−3.1	3.1−4.0	4.0−7.0	7.0−10	10−20	20−40	40−70	70−100
g	14	15	16	17	18		19		20			21
p_e (eV)	100−200	200−400	400−1000	1000−2 000	2 000−5000		5000−10000		10000−20000			20000−80000

下载: 导出CSV

表 2 不同当量下光辐射中心波长及其对应的等效黑体温度

Table 2. Central wavelength of thermal radiation under different explosion yields and their equivalent blackbody temperatures

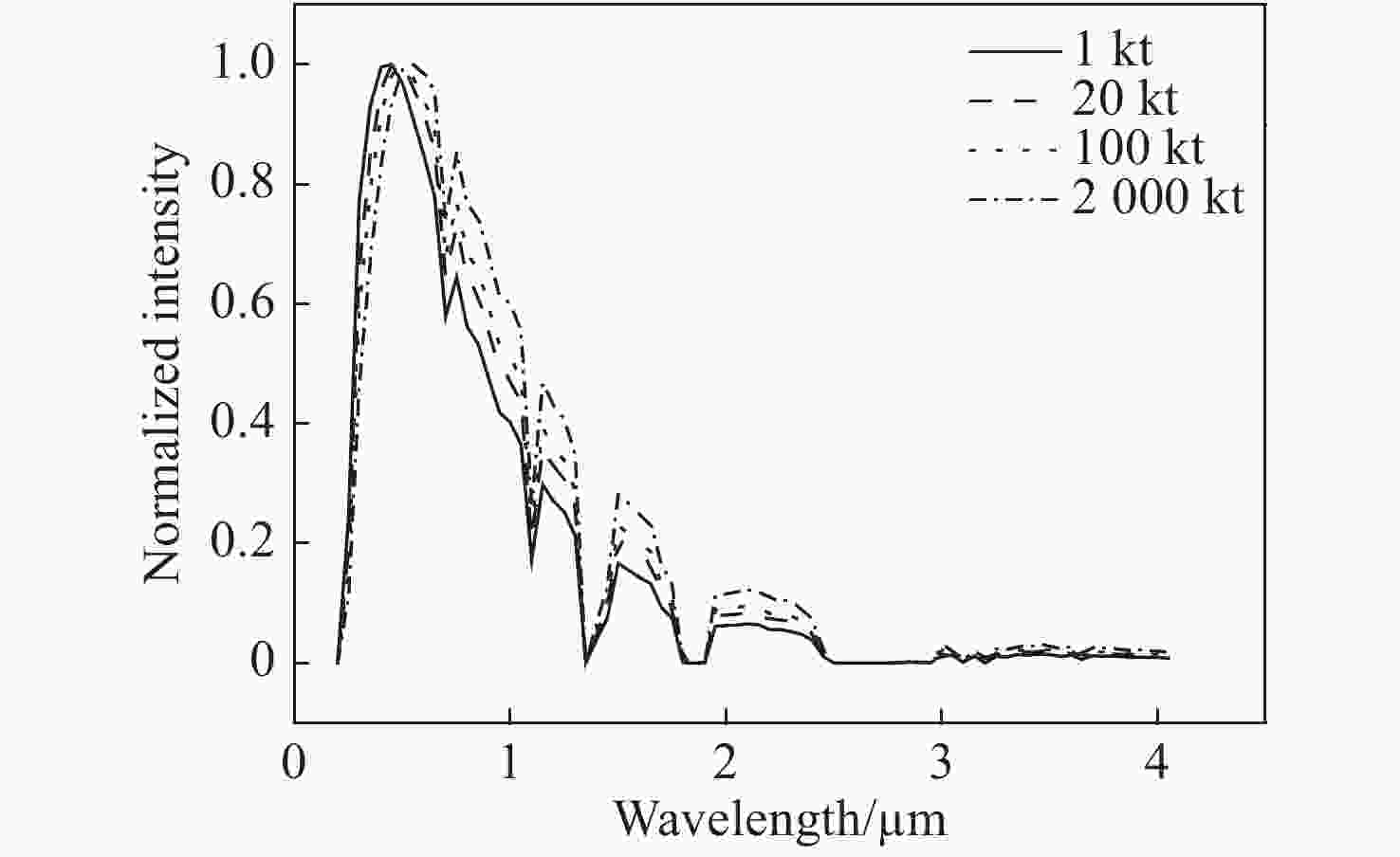
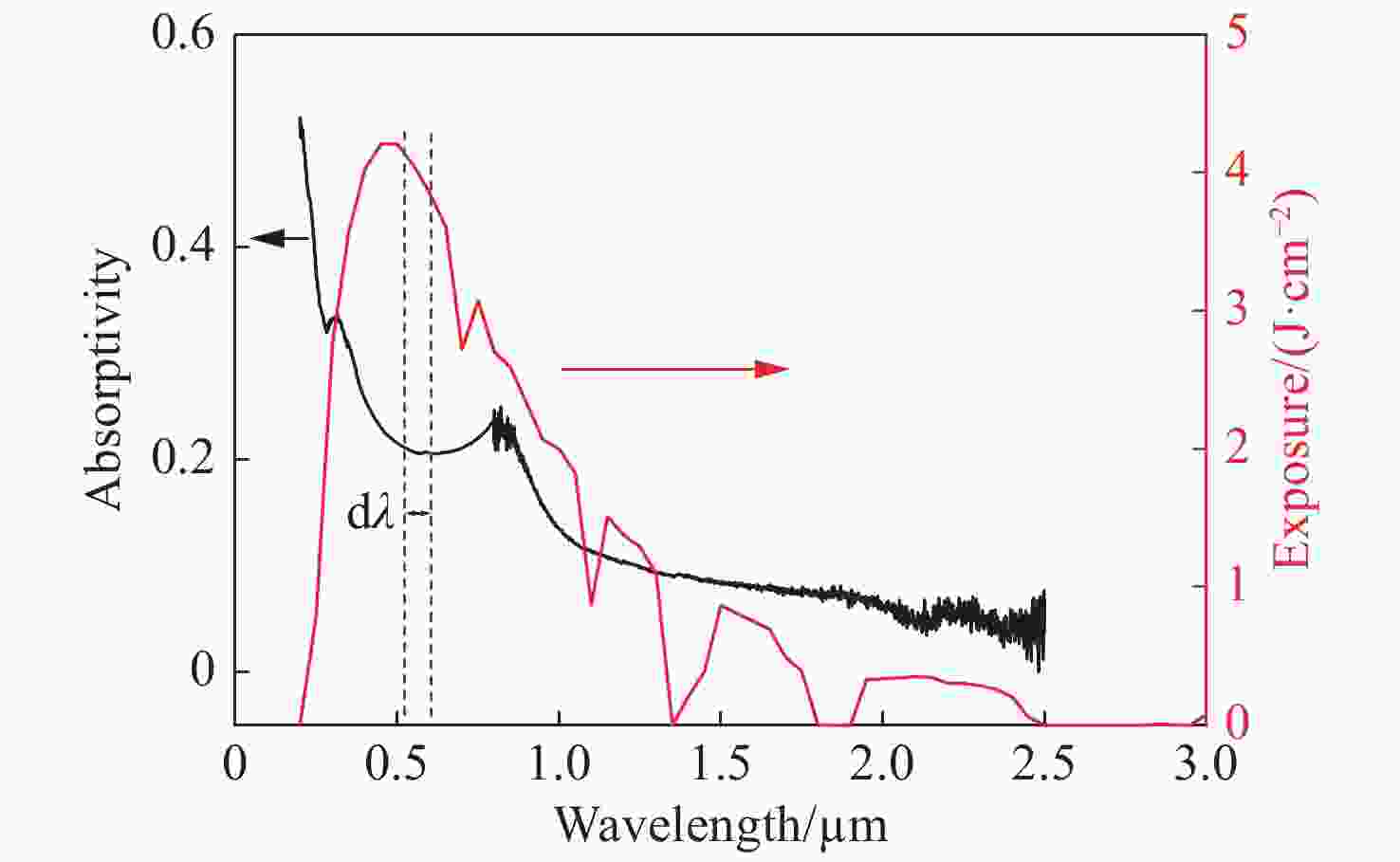
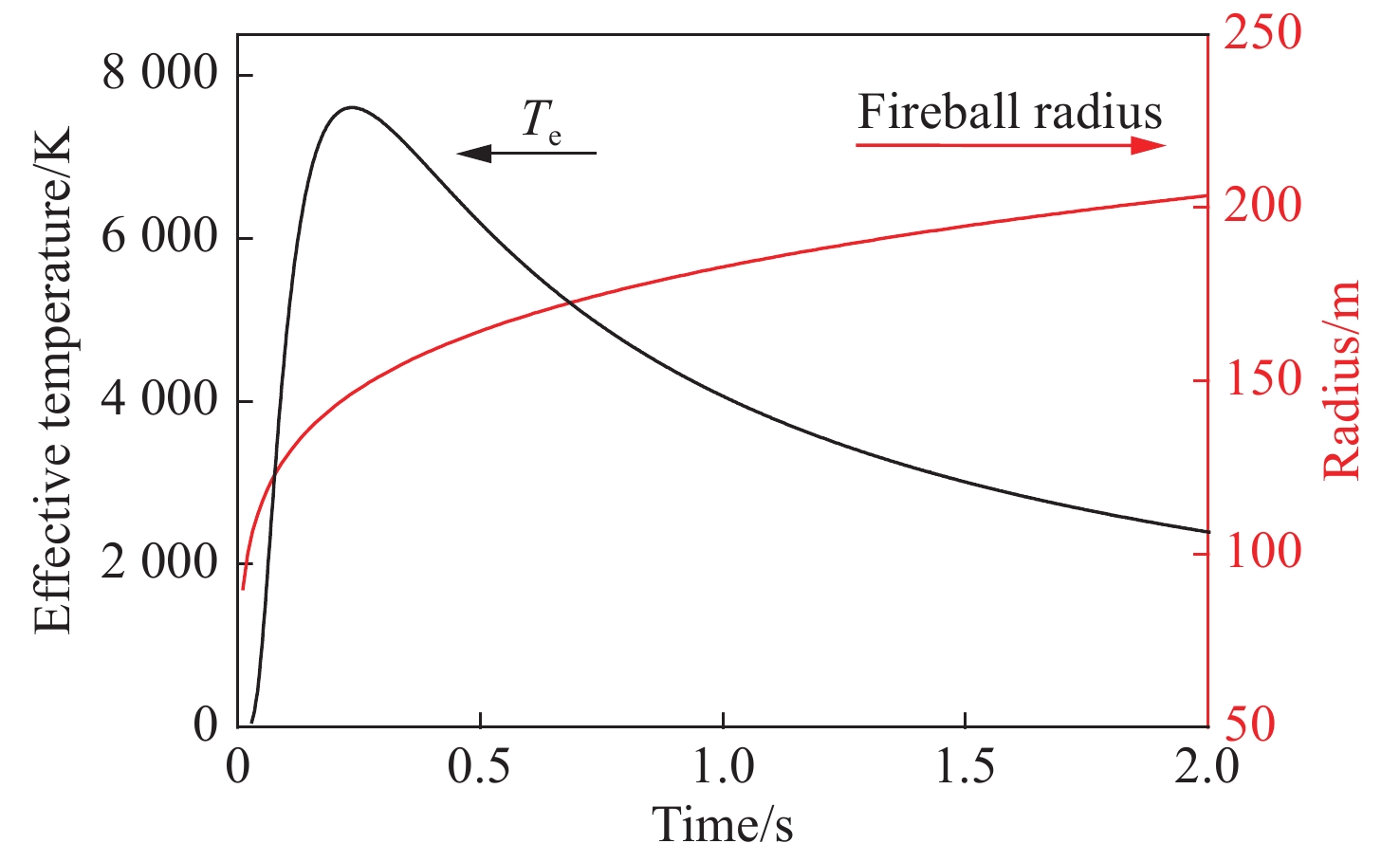
当量/kt	20	100	2000
中心波长/µm	0.46	0.48	0.52
等效温度/K	6.3×10³	6.0×10³	5.6×10³

下载: 导出CSV

表 3 采用实际光辐射和6000 K黑体辐射谱计算的耦合系数

Table 3. Coupling coefficients calculated from the actual thermal radiation spectrum and 6000 K black-body radiation spectrum

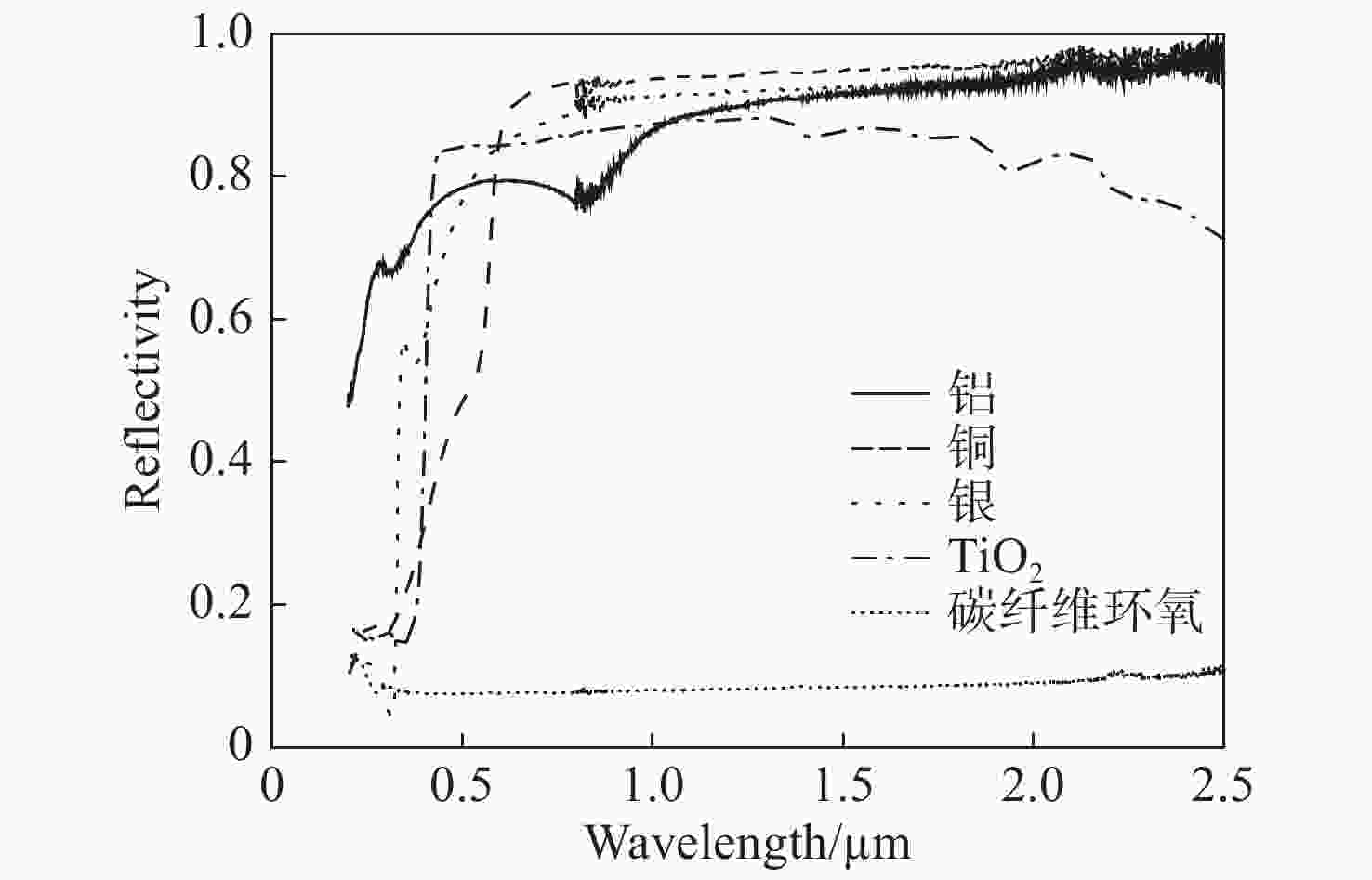
材料类型		光辐射耦合系数
材料类型		实际光谱	6000 K黑体辐射	相差（%）
金属	Al	0.19	0.17	−10%
	Cu	0.28	0.25	−10%
	Ag	0.21	0.18	−14%
陶瓷	TiO₂	0.25	0.23	−8%
复合材料	C/E	0.92	0.89	−3.3%

下载: 导出CSV

表 4 实际光辐射以及6000 K黑体在不同光谱区间的能量份额

Table 4. Energy proportion in different spectral intervals for actual thermal radiation and 6000 K blackbody

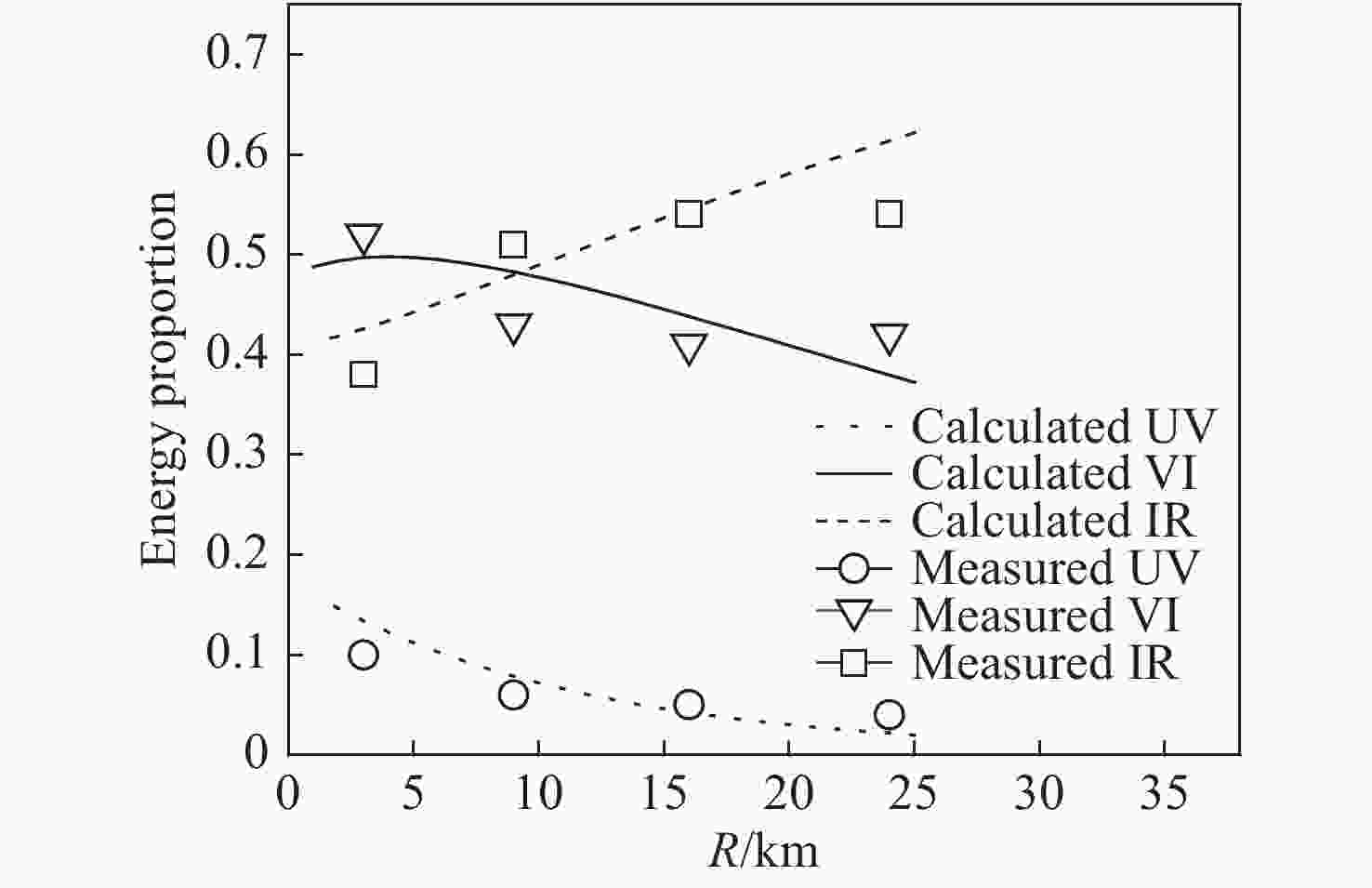
	所占能量比例（%）
	<0.4 µm	0.4~0.76 µm	>0.76 µm
光辐射	11	40	49
6000 K黑体辐射	14	43	43

下载: 导出CSV

参考文献(26)

[1]	乔登江. 核爆炸物理概论[M]. 北京: 国防工业出版社, 2003. QIAO D J. Conspectus on Physics of Nuclear Weapon[M]. Beijing: National Defense Industry Press, 2003. (in Chinese)
[2]	BRODE H L, HILLENDAHL R W, LANDSHOFF R K. Thermal radiation phenomena. Volume V. Radiation hydrodynamics of high temperature air[R]. Sunnyvale: Lockheed Missiles and Space Co., 1967.
[3]	GLASSTONE S, DOLAN P J. The Effects of Nuclear Weapons[M]. 3rd ed. Washington, D.C.: United State Department of Defense and the United States Department of Energy, 1977.
[4]	肇文丽, 张恩山, 李润新. 星载核爆炸光辐射能量分析[C]. 第十届全国核电子学与核探测技术学术年会论文集, 中国核学会, 中国电子学会, 2000. ZHAO W L, ZHANG E SH, LI R X. The optical radiation energy analysis of nuclear explosion in the satellite[C]. Proceedings of the Tenth National Conference on Nuclear Electronics & Nuclear Exploration Technology, China Nuclear Society, China Electronics Society, 2000. (in Chinese)
[5]	MARRS R E, MOSS W C, WHITLOCK B. Thermal radiation from nuclear detonations in urban environments[R]. Livermore: Lawrence Livermore National Lab., 2007.
[6]	庞磊, 张奇. 无约束气云爆炸热辐射伤害效应研究[J]. 北京理工大学学报,2010,30(10):1147-1150. PANG L, ZHANG Q. Study into injury effect of thermal radiation from unconfined vapor cloud explosion[J]. Transactions of Beijing Institute of Technology, 2010, 30(10): 1147-1150. (in Chinese)
[7]	孙承伟. 激光辐照效应[M]. 北京: 国防工业出版社, 2002. SUN CH W. Laser Irradiation Effect[M]. Beijing: National Defense Industry Press, 2002. (in Chinese)
[8]	刘峰, 王立君, 王玉恒, 等. 金属材料表面激光耦合系数的反演[J]. 光学精密工程,2011,19(2):421-428. doi: 10.3788/OPE.20111902.0421 LIU F, WANG L J, WANG Y H, et al. Inversion for laser coupling coefficient on metal material surfaces[J]. Optics and Precision Engineering, 2011, 19(2): 421-428. (in Chinese) doi: 10.3788/OPE.20111902.0421
[9]	吴丽雄, 叶锡生, 王立君, 等. 激光作用下环氧/硅树脂复合涂层的1.3 μm反射特性研究[J]. 光学学报,2011,31(8):0814002. doi: 10.3788/AOS201131.0814002 WU L X, YE X SH, WANG L J, et al. Reflectance of epoxy/organsilicone composite coating at 1.3 μm under laser irradiation[J]. Acta Optica Sinica, 2011, 31(8): 0814002. (in Chinese) doi: 10.3788/AOS201131.0814002
[10]	齐立涛. 真空条件下不同波长固体激光烧蚀单晶硅的实验研究[J]. 中国光学,2014,7(3):442-448. QI L T. Different wavelength solid-state laser ablation of silicon wafer in vacuum[J]. Chinese Optics, 2014, 7(3): 442-448. (in Chinese)
[11]	王贵兵, 刘仓理. 芳纶纤维复合材料对激光的吸收特性研究[J]. 强激光与粒子束,2003,15(11):1065-1067. WANG G B, LIU C L. Absorption characteristics of the composite reinforced by polyaryl amide fibers irradiated by high power laser[J]. High Power Laser and Particle Beams, 2003, 15(11): 1065-1067. (in Chinese)
[12]	张翔宇. 激光辐照下金属样品的能量耦合特性研究[D]. 长沙: 国防科技大学, 2016. ZHANG X Y. Research on the energy coupling characteristic of metal samples under laser irradiation[D]. Changsha: National University of Defense Technology, 2016. (in Chinese)
[13]	绪梅, 朱继, 王良厚, 等. 核爆炸光辐射对物体热效应的数值模拟[C]. 第十七届全国核电子学与核探测技术学术年会论文集, 中国电子学会, 2014. XU M, ZHU J, WANG L H, et al.. Thermal effect simulation of nuclear explosion light radiation on objects[C]. Proceedings of the Seventeenth National Conference on Nuclear Electronics and Nuclear Exploration Technology, Gansu Lanzhou, 2014. (in Chinese)
[14]	关志远, 绪梅, 徐鸿明. 橡胶材料的核爆炸热毁伤效应分析[J]. 工兵装备研究,2019,38(3):45-47. GUAN ZH Y, XU M, XU H M. Analysis on thermal damage effect of rubber materials by nuclear explosion[J]. Engineer Equipment Research, 2019, 38(3): 45-47. (in Chinese)
[15]	SYMBALISTY E M D, ZINN J, WHITAKER R W. RADFLO physics and algorithms[R]. Washington: Los Alamos National Lab., 1995.
[16]	陈健华, 王心正, 谢龙生, 等. 均匀大气中的强爆炸一维辐射流体力学数值解[J]. 爆炸与冲击,1981,1(2):37-49. CHEN J H, WANG X ZH, XIE L SH, et al. An one-dimensional radiation hydrodynamic numerical solution for a strong explosion in uniform atmosphere[J]. Explosion and Shock Waves, 1981, 1(2): 37-49. (in Chinese)
[17]	田宙, 乔登江, 郭永辉. 不同高度强爆炸早期火球数值研究[J]. 兵工学报,2009,30(8):1078-1083. TIAN ZH, QIAO D J, GUO Y H. Numerical investigation of early fireball of strong explosion for different altitudes[J]. Acta Armamentarii, 2009, 30(8): 1078-1083. (in Chinese)
[18]	高银军, 闫凯, 田宙, 等. 强爆炸早期火球光辐射能谱的数值计算[J]. 爆炸与冲击,2015,35(3):289-295. GAO Y J, YAN K, TIAN ZH, et al. Numerical calculation of early fireball radiation spectrum in strong explosion[J]. Explosion and Shock Waves, 2015, 35(3): 289-295. (in Chinese)
[19]	SHESTAKOV A I, OFFNER S S R. A multigroup diffusion solver using pseudo transient continuation for a radiation-hydrodynamic code with patch-based AMR[J]. Journal of Computational Physics, 2008, 227(3): 2154-2186. doi: 10.1016/j.jcp.2007.09.019
[20]	吴健辉. 核爆炸光辐射特性及探测技术的理论与实验研究[D]. 武汉: 华中科技大学, 2009. WU J H. Study on Theory and experiment of the characteristics and detection technology of nuclear explosion radiation[D]. Wuhan: Huazhong University of Science & Technology, 2009. (in Chinese)
[21]	高银军, 关奇, 陈志华, 等. 强爆炸热辐射在大气中的传输计算与分析[J]. 现代应用物理,2014,5(3):191-195. GAO Y J, GUAN Q, CHEN ZH H, et al. Calculation and analysis of atmospheric transmission of thermal radiation from strong explosion[J]. Modern Applied Physics, 2014, 5(3): 191-195. (in Chinese)
[22]	LYU Y Y, GAO SH, XU Q J. Scattering characteristics of C@H₂O composite particle based on Mie light scattering theory[J]. Chinese Journal of Luminescence, 2019, 40(3): 298-303.
[23]	吴健辉, 杨坤涛, 张南洋生. 核爆炸光辐射探测中的大气传输性能研究[J]. 应用光学,2008,29(5):815-820. WU J H, YANG K T, ZHANG N Y SH. Atmosphere transmission in detection of nuclear explosion light radiation[J]. Journal of Applied Optics, 2008, 29(5): 815-820. (in Chinese)
[24]	王飞翔, 郭杰, 许方宇, 等. 不同海拔地区红外大气透过率的计算和测量[J]. 中国光学,2019,12(4):843-852. doi: 10.3788/co.20191204.0843 WANG F X, GUO J, XU F Y, et al. Calculation and measurement of infrared atmospheric transmittance at different altitudes[J]. Chinese Optics, 2019, 12(4): 843-852. (in Chinese) doi: 10.3788/co.20191204.0843
[25]	刘志伟, 路远, 侯典心, 等. 激光辐照VO₂薄膜温度场分布及透射特性研究[J]. 发光学报,2018,39(11):1604-1612. doi: 10.3788/fgxb20183911.1604 LIU ZH W, LU Y, HOU D X, et al. Temperature field distribution and transmittance characteristics of VO₂ films irradiated by laser[J]. Chinese Journal of Luminescence, 2018, 39(11): 1604-1612. (in Chinese) doi: 10.3788/fgxb20183911.1604
[26]	孙毅, 高云国, 邵帅. 高功率激光热效应对合束系统的影响[J]. 光学精密工程,2015,23(11):3097-3106. doi: 10.3788/OPE.20152311.3097 SUN Y, GAO Y G, SHAO SH. Influence of high power laser thermal effect on beam combination system[J]. Optics and Precision Engineering, 2015, 23(11): 3097-3106. (in Chinese) doi: 10.3788/OPE.20152311.3097