土壤多组分PAHs激光诱导二维荧光光谱定量方法研究

黄尧; 赵南京; 孟德硕; 左兆陆; 程钊; 陈宇男; 陈晓伟; 谷艳红

doi:10.37188/CO.2020-0059

土壤多组分PAHs激光诱导二维荧光光谱定量方法研究

黄尧^{1, 2, 3,},
赵南京^{1, 3, ,},
孟德硕^{1, 3},
左兆陆^{1, 2, 3},
程钊^{1, 2, 3},
陈宇男^{1, 2, 3},
陈晓伟^{1, 2, 3},
谷艳红⁴

1.
中国科学院安徽光学精密机械研究所环境光学与技术重点实验室，合肥 230031
2.
中国科学技术大学，合肥 230026
3.
安徽省环境光学监测技术重点实验室，合肥 230031
4.
合肥学院先进制造工程学院，合肥 230601

详细信息

中图分类号: O657.319
计量
- 文章访问数: 1322
- HTML全文浏览量: 392
- PDF下载量: 75
- 被引次数: 0
出版历程
- 收稿日期: 2020-04-08
- 修回日期: 2020-05-25
- 网络出版日期: 2020-11-09
- 刊出日期: 2020-12-01

Study on quantitative methods of laser-induced two-dimensional fluorescence spectroscopy of multicomponent PAHs in soils

doi: 10.37188/CO.2020-0059

HUANG Yao^{1, 2, 3
,},
ZHAO Nan-jing^{1, 3
, ,},
MENG De-shuo^{1, 3},
ZUO Zhao-lu^{1, 2, 3},
CHENG Zhao^{1, 2, 3},
CHEN Yu-nan^{1, 2, 3},
CHEN Xiao-wei^{1, 2, 3},
GU Yan-hong⁴

1.
Key Laboratory of Environmental Optics & Technology, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China
2.
University of Science and Technology of China, Hefei 230026, China
3.
Key Laboratory of Optical Monitoring Technology for Environment of Anhui Province, Hefei 230031, China
4.
Hefei University, Institute of Advanced Manufacturing Engineering, Hefei 230601, China

More Information

Author Bio:
HUANG Yao (1991—), Male, born in Xinyang City of Henan province, Ph.D Candidate, University of Science and Technology of China. He got his master's degree from Nanchang University in 2017. His research interests are on spectral detection and analysis of pollutants in soils. E-mail: yhuang@aiofm.ac.cn

ZHAO Nanjing (1976—), Male, born in Dangshan County of Anhui province, PhD, professor. He got his PhD from Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences in 2005. His research interests are on new methods and techniques for environmental optics. E-mail: njzhao@aiofm.ac.cn

Corresponding author: njzhao@aiofm.ac.cn

摘要

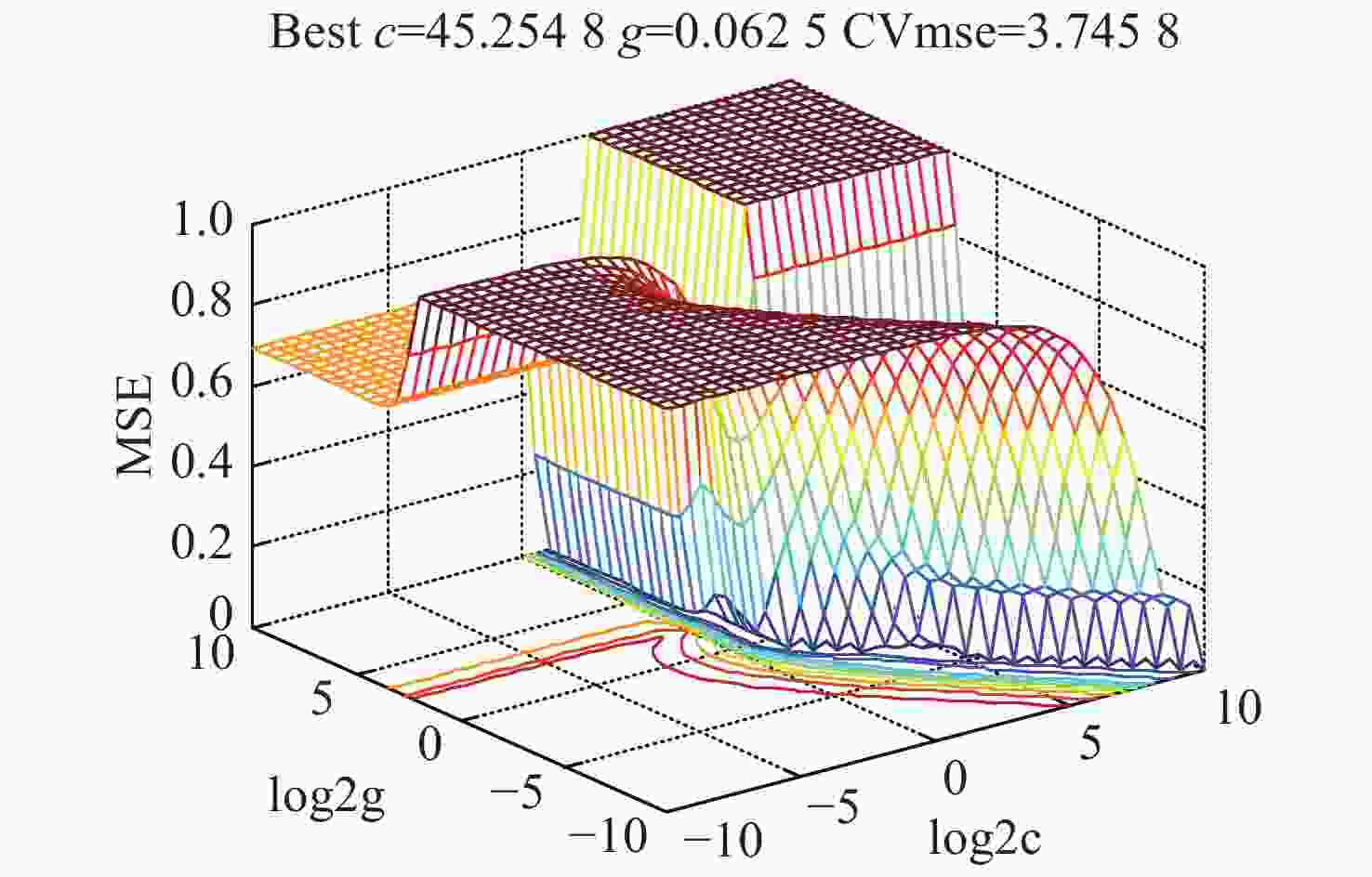
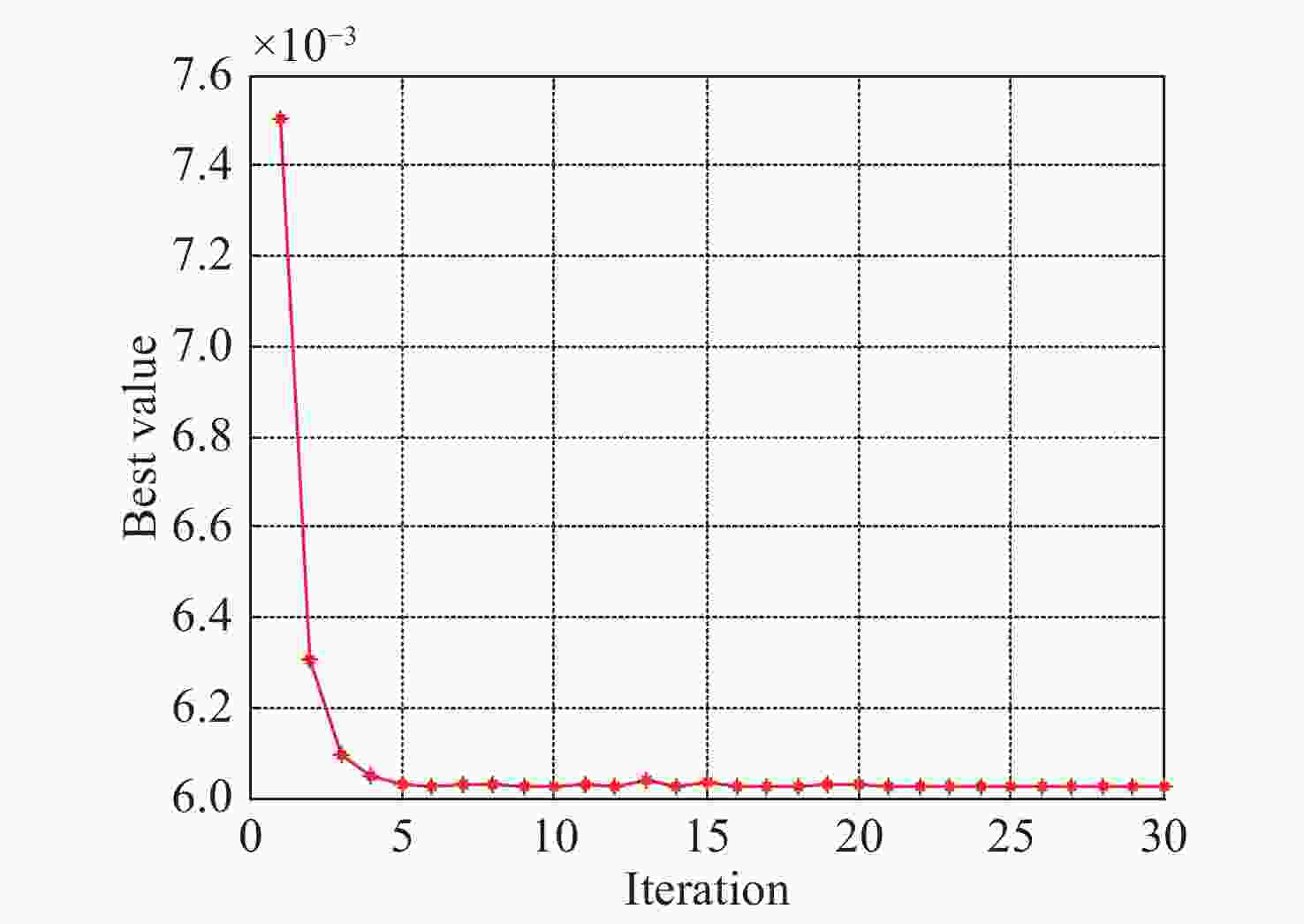
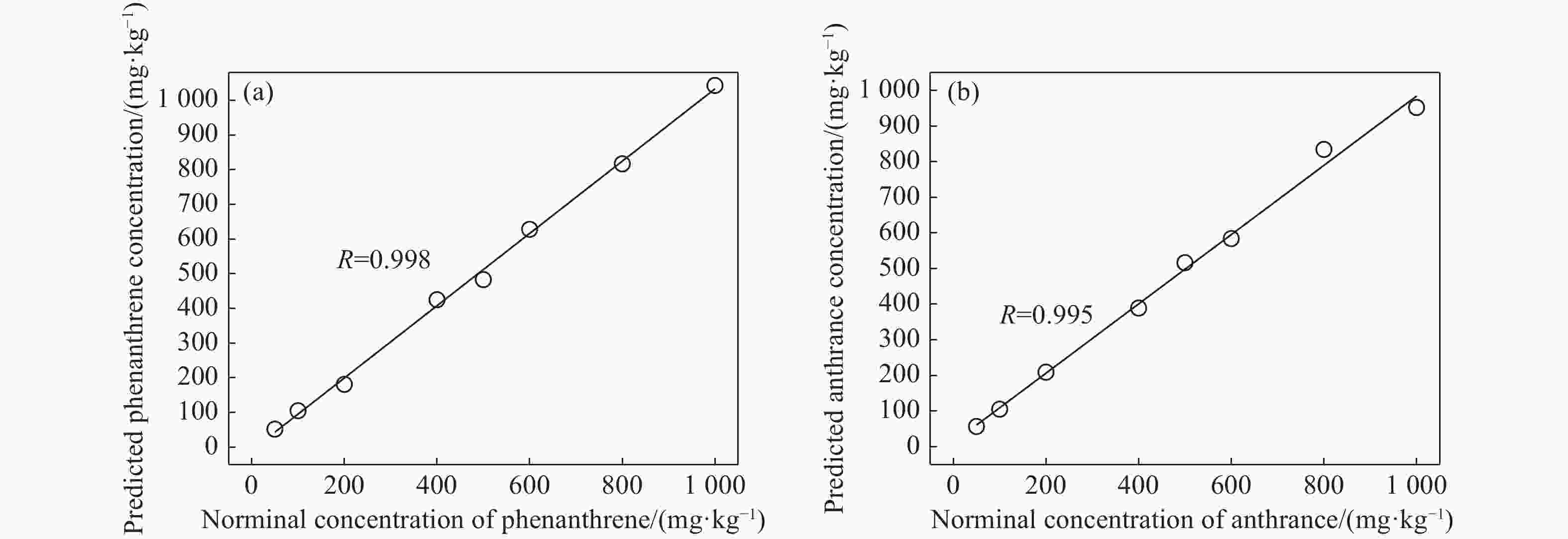
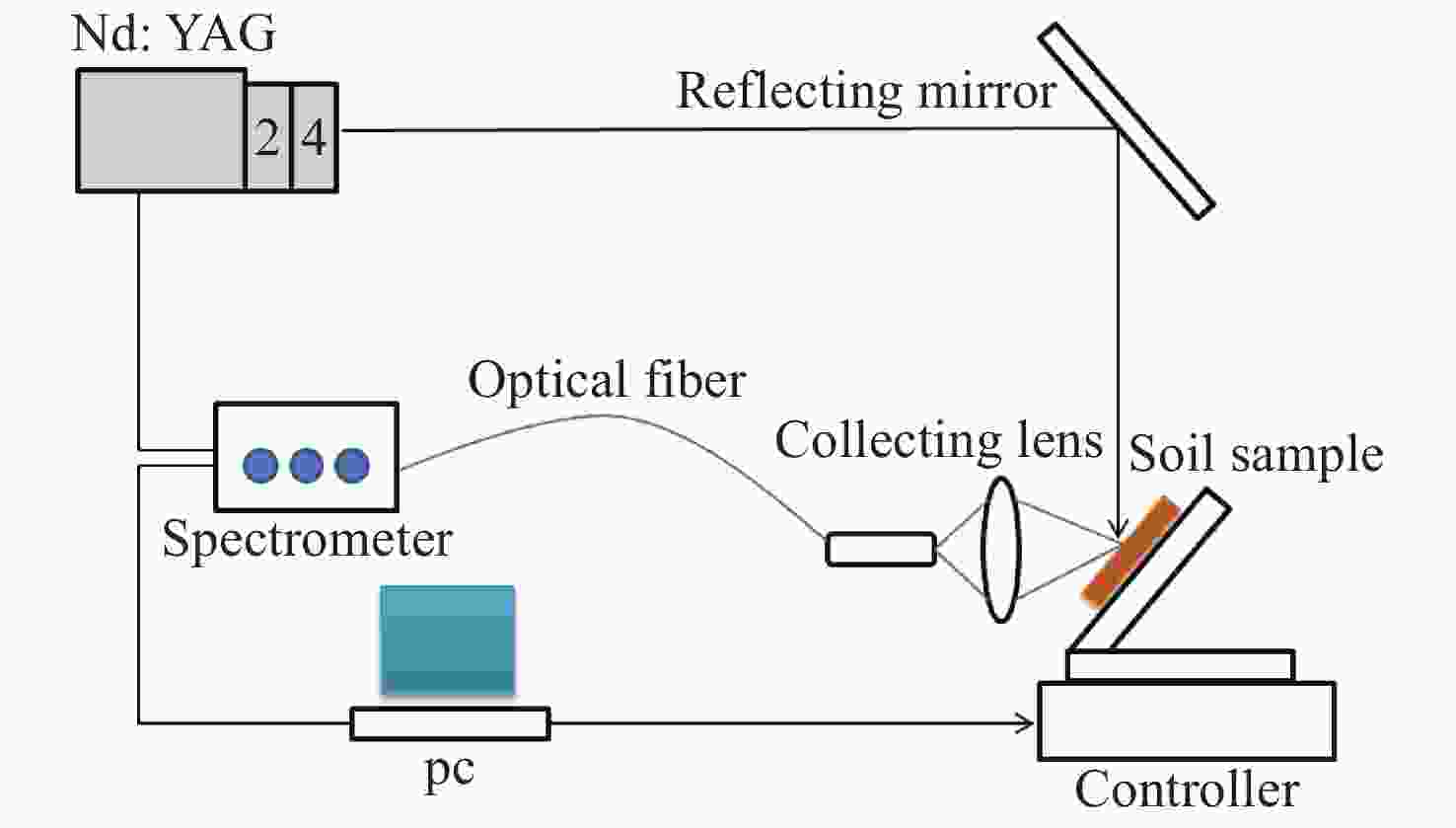
摘要: 激光诱导荧光技术具有实时、快速的优势，并且无需对样品做预处理，是土壤多环芳烃定量分析检测的一种重要分析手段。然而土壤中多环芳烃种类繁多，激光诱导荧光光谱重叠严重，在无法进行化学分离的情况下实现土壤中多环芳烃的精确定量是难点之一。本文采用266 nm可移动激光诱导荧光系统获取了农田土壤多环芳烃的荧光光谱，研究了基于单变量线性回归、加权非负最小二乘多元线性回归和支持向量回归的多组分多环芳烃定量分析方法。结果表明：采用单变量线性回归，蒽和菲的相关系数均小于0.90，平均相对误差均大于20%；与单变量线性回归相比，加权非负最小二乘多元线性回归提高了两组分多环芳烃污染土壤中蒽和菲的预测精度，但在多组分多环芳烃污染土壤中的平均相对误差仍在20%以上。最后，采用GWO-DE优化的支持向量机回归模型分析了多组分多环芳烃污染土壤中的蒽和菲，蒽的平均相对误差由多元线性回归的23.1%下降至5.02%，菲的平均相对误差从20.8%下降到4.83%。该研究为提高土壤多组分多环芳烃激光诱导荧光定量分析的准确性提供了方法支撑。
- 多环芳烃 /
- 激光诱导荧光光谱 /
- 定量分析
Abstract: Laser-Induced Fluorescence(LIF) has become a powerful technology for quantitative analysis of Polycyclic Aromatic Hydrocarbons(PAHs) in soils due to its fast detection speed and low operational cost, without sample preparation. However, there are many types of PAHs in soils, and their similar structures lead to overlapped issues in their laser-induced fluorescence spectra. It is challenging to quantify a single PAH in complicated soil without the chemical separation. In this paper, fluorescence spectra of PAHs in agricultural soil are obtained by a 266 nm mobile LIF system, and quantification methods are investigated for PAHs, based on univariate linear regression, weighted non-negative least squares Multivariate Linear Regression(MRL) and Support Vector Regression(SVR). The results show that the correlation coefficients of anthracene and phenanthrene are both less than 0.90, and the average relative errors are both more than 20% by using univariate linear regression. Compared with univariate linear regression, MLR improves the prediction accuracy of anthracene and phenanthrene in the soil contaminated with bi-component PAHs. However, the average relative errors are still over 20% in the soil contaminated with multicomponent PAHs. Finally, a SVR model optimized by grey wolf optimization combined with differential evolution(GWO-DE) is applied for concentration measurement of anthracene and phenanthrene in agricultural soil contaminated with multicomponent PAHs. The average relative error of anthracene decreases from 23.1% (MLR) to 5.02%, while in the case of phenanthrene decreases from 20.8% (MLR) to 4.83%. This study provides an efficient method to improve the accuracy of LIF in quantifying multicomponent PAHs in soils.
- polycyclic aromatic hydrocarbons /
- laser-induced fluorescence spectra /
- quantitative analysis

HTML全文

Figure 1. Schematic diagram of the LIF experimental setup

下载: 全尺寸图片幻灯片

Figure 2. Photograph of the mobile LIF system

下载: 全尺寸图片幻灯片

Figure 3. LIF spectra of multicomponent PAHs in soils

下载: 全尺寸图片幻灯片

Figure 4. The calibration curve of PAHs by MLR

下载: 全尺寸图片幻灯片

Figure 5. The optimized 3D view for AN by grid search

下载: 全尺寸图片幻灯片

Figure 6. Optimization process of GWO-DE model for AN

下载: 全尺寸图片幻灯片

Figure 7. The calibration curve of PAHs by SVR model

下载: 全尺寸图片幻灯片

Table 1. Characteristic fluorescence peaks for univariate regression

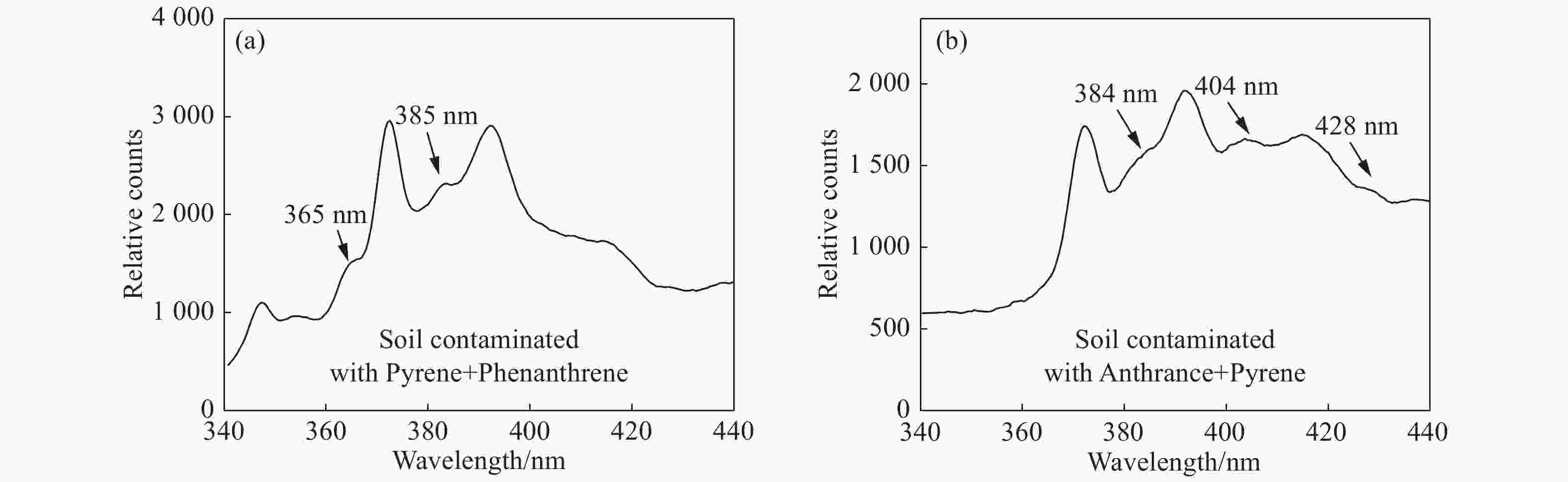
PAHs	analyte	characteristic fluorescence peak/nm
AN+PY	AN	404
AN+PY	PY	484
PHE+PY	PHE	347
PHE+PY	PY	484
AN+PY+PHE	AN	404
	PY	484
	PHE	347

下载: 导出CSV

Table 2. Results of univariate quantitative analysis

PAHs	analyte	correlation coefficient	average relative error (%)
AN+PY	AN	0.867	23.5
AN+PY	PY	0.956	14.9
PHE+PY	PHE	0.882	24.7
PHE+PY	PY	0.961	13.0
AN+PY+PHE	AN	0.896	25.1
	PY	0.939	16.1
	PHE	0.873	26.4

下载: 导出CSV

Table 3. Characteristic fluorescence peaks or data points for multivariate regression

PAHs	analyte	characteristic fluorescence peaks(nm)
AN+PY	AN	384, 393, 396, 400,404, 406, 408, 416
AN+PY	PY	476, 480, 484, 488, 492
PHE+PY	PHE	345, 347, 349, 361, 365, 372, 381, 385
PHE+PY	PY	476, 480, 484, 488, 492
AN+PY+PHE	AN	384, 385, 393, 396, 400, 404, 406, 408
	PY	476, 480, 484, 488, 492
	PHE	347, 363, 365, 367, 380, 384, 385, 390

下载: 导出CSV

Table 4. Results of MLR quantitative analysis

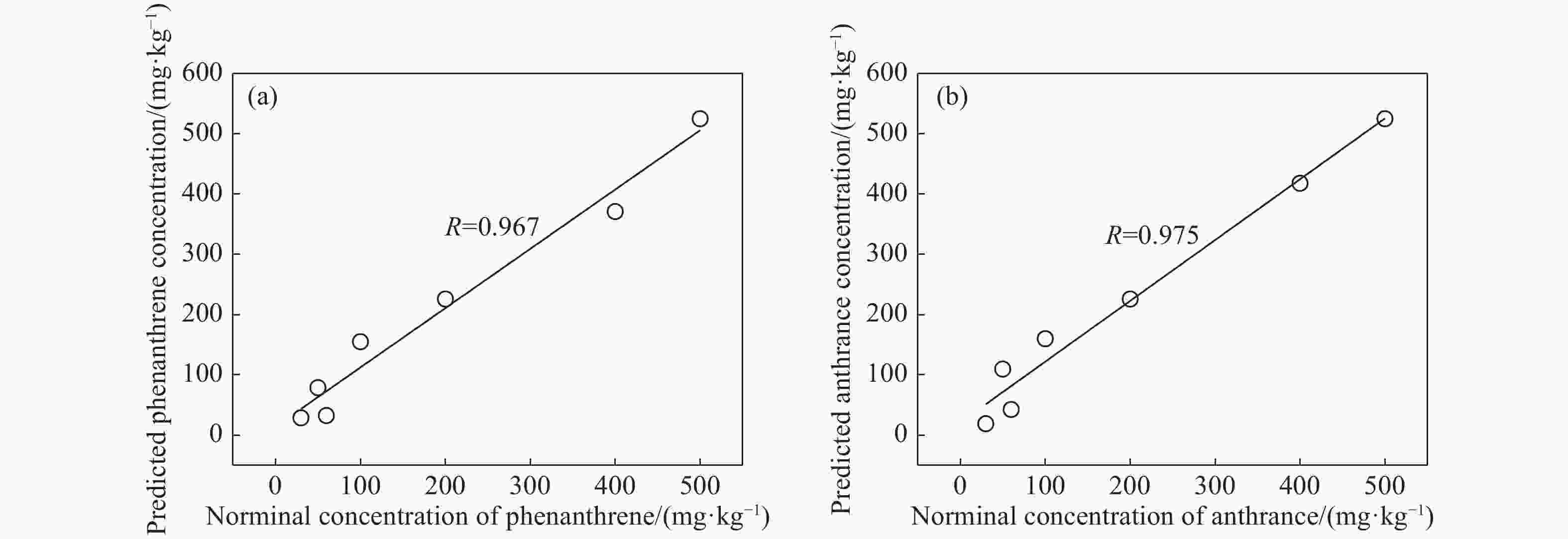
PAHs	analyte	correlation coefficient	average relative error (%)
AN+PY	AN	0.975	11.7
AN+PY	PY	0.977	12.4
PHE+PY	PHE	0.967	11.8
PHE+PY	PY	0.963	12.4
AN+PY+PHE	AN	0.910	23.1
	PY	0.952	15.9
	PHE	0.938	20.8

下载: 导出CSV

参考文献(25)

[1]	ABDEL-SHAFY H I, MANSOUR M S M. A review on polycyclic aromatic hydrocarbons: source, environmental impact, effect on human health and remediation[J]. Egyptian Journal of Petroleum, 2016, 25(1): 107-123. doi: 10.1016/j.ejpe.2015.03.011
[2]	KIM K H, JAHAN S A, KABIR E, et al. A review of airborne polycyclic aromatic hydrocarbons (PAHs) and their human health effects[J]. Environment International, 2013, 60: 71-80. doi: 10.1016/j.envint.2013.07.019
[3]	ABBAS I, BADRAN G, VERDIN A, et al. Polycyclic aromatic hydrocarbon derivatives in airborne particulate matter: sources, analysis and toxicity[J]. Environmental Chemistry Letters, 2018, 16(2): 439-475. doi: 10.1007/s10311-017-0697-0
[4]	ODABASI M, OZGUNERGE FALAY E, TUNA G, et al. Biomonitoring the spatial and historical variations of persistent organic pollutants (POPs) in an industrial region[J]. Environmental Science &Technology, 2015, 49(4): 2105-2114.
[5]	BI X, LUO W, GAO J J, et al. Polycyclic aromatic hydrocarbons in soils from the Central-Himalaya region: distribution, sources, and risks to humans and wildlife[J]. Science of the Total Environment, 2016, 556: 12-22. doi: 10.1016/j.scitotenv.2016.03.006
[6]	SUMAN S, SINHA A, TARAFDAR A. Polycyclic aromatic hydrocarbons (PAHs) concentration levels, pattern, source identification and soil toxicity assessment in urban traffic soil of Dhanbad, India[J]. Science of the Total Environment, 2016, 545-546: 353-360. doi: 10.1016/j.scitotenv.2015.12.061
[7]	HUMEL S, SCHMIDT S N, SUMETZBERGER-HASINGER M, et al. Enhanced accessibility of polycyclic aromatic hydrocarbons (PAHs) and heterocyclic PAHs in industrially contaminated soil after passive dosing of a competitive sorbate[J]. Environmental Science &Technology, 2017, 51(14): 8017-8026.
[8]	KUŚMIERZ M, OLESZCZUK P, KRASKA P, et al. Persistence of polycyclic aromatic hydrocarbons (PAHs) in biochar-amended soil[J]. Chemosphere, 2016, 146: 272-279. doi: 10.1016/j.chemosphere.2015.12.010
[9]	JONES K C, STRATFORD J A, TIDRIDGE P, et al. Polynuclear aromatic hydrocarbons in an agricultural soil: long-term changes in profile distribution[J]. Environmental Pollution, 1989, 56(4): 337-351. doi: 10.1016/0269-7491(89)90079-1
[10]	SHANG Q B, QUAN Y H, XU L SH, et al. Spatial distribution and genesis of polycyclic aromatic hydrocarbons (PAHs) in the surface soil in China[J]. Journal of Ecology and Rural Environment, 2019, 35(7): 917-924.
[11]	LI Y, CUI X, LI ZH CH, et al. Purification and enrichment of polycyclic aromatic hydrocarbons pollutions in oil-field water by column clean-up coupled with dispersive liquid-liquid microextraction[J]. Chinese Journal of Analytical Chemistry, 2018, 46(5): 787-795.
[12]	WANG CH H, WU SH H, ZHOU SH L, et al. Characteristics and source identification of polycyclic aromatic hydrocarbons (PAHs) in urban soils: a review[J]. Pedosphere, 2017, 27(1): 17-26. doi: 10.1016/S1002-0160(17)60293-5
[13]	LI X L, LI Q X, AN SH Q, et al. Determination of fluorine in soil sample by X-ray fluorescence spectrometry[J]. Chinese Journal of Analytical Chemistry, 2019, 47(11): 1864-1869.
[14]	KANG Q W, ZHANG G, CHAI R T, et al. Synthesis of carbon nanodots for detection of aluminum ion with fluorescence enhancement[J]. Chinese Journal of Analytical Chemistry, 2019, 47(12): 1901-1908.
[15]	LEE C K, KO E J, KIM K W, et al. Partial least square regression method for the detection of polycyclic aromatic hydrocarbons in the soil environment using laser-induced fluorescence spectroscopy[J]. Water,Air,and Soil Pollution, 2004, 158(1): 261-275. doi: 10.1023/B:WATE.0000044858.39836.e2
[16]	OKPARANMA R N, MOUAZEN A M. Determination of total petroleum hydrocarbon (TPH) and polycyclic aromatic hydrocarbon (PAH) in soils: a review of spectroscopic and nonspectroscopic techniques[J]. Applied Spectroscopy Reviews, 2013, 48(6): 458-486. doi: 10.1080/05704928.2012.736048
[17]	YANG R J, SHANG L P, BAO ZH B, et al. Feasibility of using laser-induced fluorescence to detect directly polycyclic aromatic hydrocarbons in soil[J]. Spectroscopy and Spectral Analysis, 2011, 31(8): 2148-2150.
[18]	HE J, SHANG L P, DENG H, et al. Detection system of 250 nm laser induce fluorescence of polycyclic aromatic hydrocarbons in soil[J]. Opto-Electronic Engineering, 2014, 41(9): 51-55.
[19]	SARKAR S K. Some multivariate linear regression testing problems with additional observations[J]. Journal of Multivariate Analysis, 1981, 11(4): 556-567. doi: 10.1016/0047-259X(81)90096-8
[20]	BASAK D, PAL S, PATRANABIS D C. Support vector regression[J]. Neural Information Processing-Letters and Reviews, 2007, 11(10): 203-224.
[21]	LU H X, XU M CH, ZHANG W D, et al. Identification of citrus Huanglongbing based on contractive auto-encoder combined extreme learning machine[J]. Chinese Journal of Analytical Chemistry, 2019, 47(5): 652-660.
[22]	FENG Y, PENG CH Y, ZHANG SH W, et al. Preparation of graphene oxide grafted silica monolith and application in determination of polycyclic aromatic hydrocarbons[J]. Chinese Journal of Analytical Chemistry, 2019, 47(6): 814-822.
[23]	ZHAI M Y, ZHAO Y, GAO H, et al. Quantitative study on articular cartilage by fourier transform infrared spectroscopic imaging and support vector machine[J]. Chinese Journal of Analytical Chemistry, 2018, 46(6): 896-901.
[24]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007
[25]	ZHU A J, XU CH P, LI ZH, et al. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J]. Journal of Systems Engineering and Electronics, 2015, 26(2): 317-328. doi: 10.1109/JSEE.2015.00037