Photon-assisted Fano resonance tunneling periodic double-well potential characteristics
doi: 10.37188/CO.2020-0068
-
摘要: 周期双阱势的光学性质是激光物理和量子光学的前沿研究领域之一。该文研究了具有时间周期双阱势的石墨烯系统中光子辅助狄拉克电子的Fano型共振隧穿。利用双量子阱结构，电子通过两量子阱之间的薄势垒的共振隧穿将导致束缚态能级的分裂，Fano型共振谱将分裂为两个不对称共振峰。通过改变相位、频率和振幅来调制Fano峰的形状，可以用来调制Dirac在石墨烯中的电子输运性质。数值分析表明，两个振荡场的相对相位可以调节非对称Fano型共振峰的形状。当相对相位从0增加到
${\text{π}}$ 时，共振峰谷从峰的一侧移到另一侧；在临界相位${{3{\text{π}} }/{11}}$ 处，不对称共振峰变得对称。此外，还可以通过改变振荡场的频率和振幅以及静态势阱的结构来调制Fano峰的分布。这些有趣的物理性质可以用来调节石墨烯中Dirac的电子输运性质。Abstract: Optical properties of periodic double-well potential are one of the frontier research fields in laser physics and quantum optics. In this work, we have employed time-periodic double-well potential for the investigation of Fano-type resonant tunneling of photon-assisted Dirac electrons in a graphene system. Using a double quantum well structure, it is found that the resonant tunneling of electrons in a thin barrier between the two quantum wells splits the bound state energy levels, and the Fano-type resonance spectrum splits into two asymmetric resonance peaks. The shape of Fano peak is regulated by changing the phase, frequency, and amplitude, that can directly modulate the electronic transport properties of Dirac in graphene. Our numerical analysis shows that the relative phase of two oscillating fields can adjust the shape of the asymmetric Fano type resonance peak. When the relative phase increases from 0 to${\text{π}}$ , the resonance peak valley moves from one side of the peak to the other. In addition, the asymmetric resonance peak becomes symmetric at critical phase${{3{\text{π}} }/{11}}$ . Furthermore, the distribution of Fano peaks can be modulated by varying the frequency and amplitude of oscillating field and the structure of the static potential well. Finally, we suggest that these interesting physical properties can be used for the modulation of Dirac electron transport properties in graphene.-
Key words:
- physical optics /
- resonant tunneling /
- photon-assisted tunneling /
- dirac electrons /
- quantum optics
-
Figure 1. Sketch model of Dirac electron transport through a double-well potential and two applied oscillating fields.
${V_0}$ is the depth of the static well;$d$ is the width of wells,$a$ is the thickness of barrier. V1 cos (ωt + α) and V1 cos (ωt + β) are the applied oscillating fields
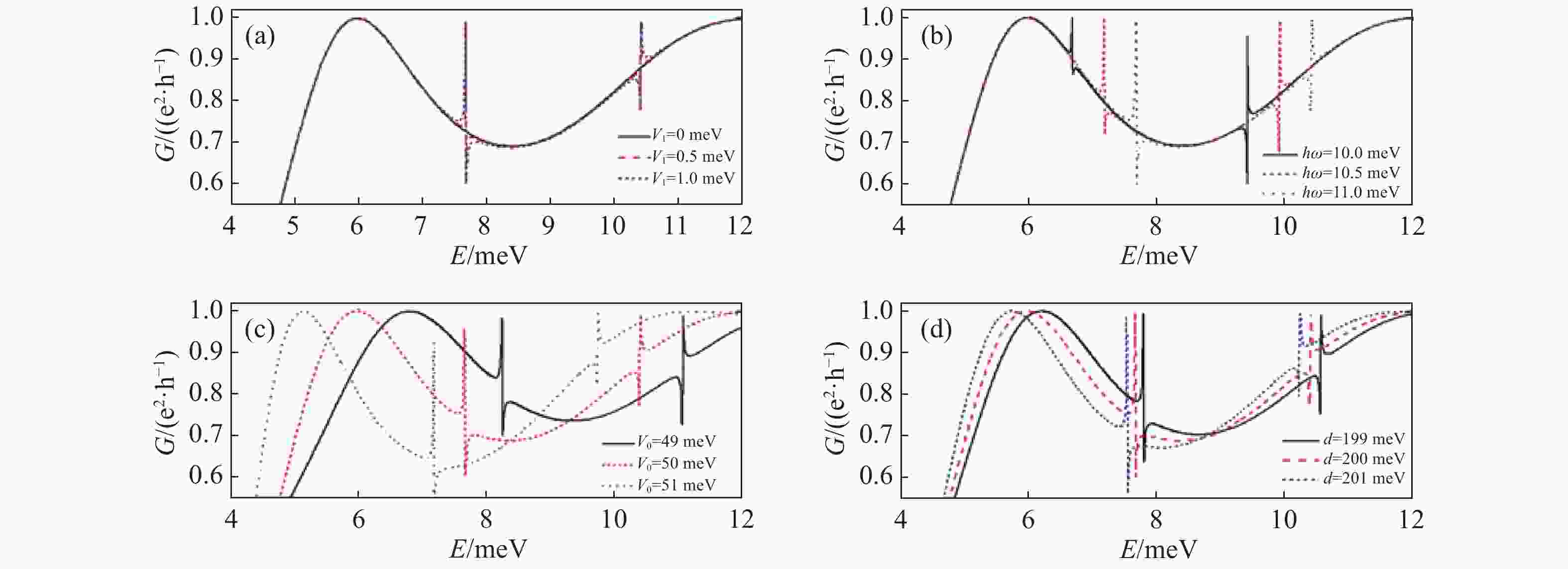
Figure 2. Fano-type resonance in conductance
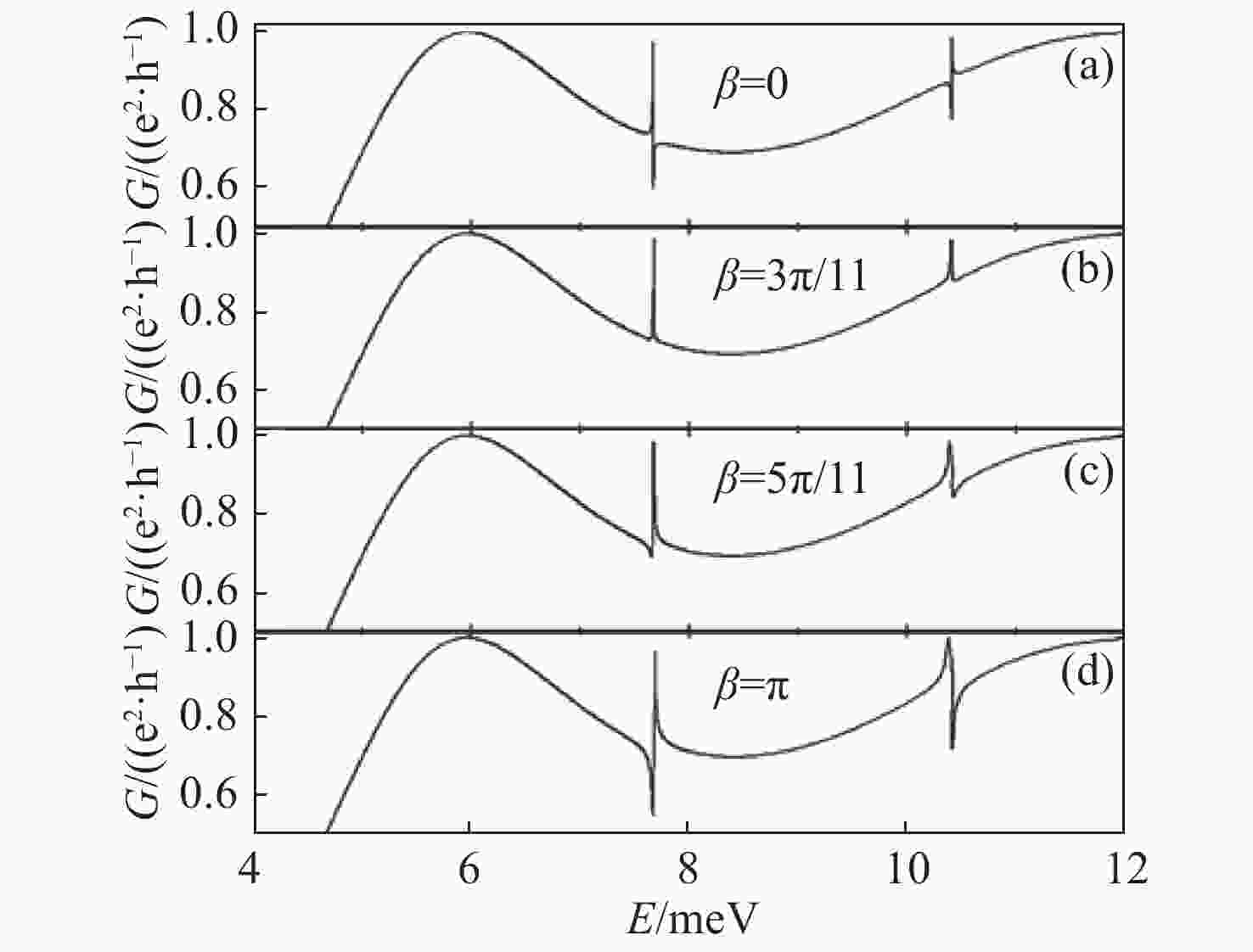
$G$ for$\alpha = \beta = 0$ ,$a = 40\;{\rm{ nm}}$ ，${k_y} = 0.006\;{\rm{ n}}{{\rm{m}}^{ - 1}}$ . (a) ћ$\omega = 11\;{\rm{ meV}}$ ,${V_0} = - 50\;{\rm{ meV}}$ ，$d = 200\;{\rm{ nm}}$ ; (b)${V_1} = 1.0\;{\rm{ meV}}$ ,${V_0} = - 50\;{\rm{ meV}}$ ，$d = 200\;{\rm{ nm}}$ ; (c) ћ$ \omega = 11\;{\rm{ meV}}$ ，${V_1} = 1.0\;{\rm{ meV}}$ ,$d = 200\;{\rm{ nm}}$ ; (d)${V_1} = 1.0\;{\rm{ meV}}$ ，ћ$ \omega = 11\;{\rm{ meV}}$ ，${V_0} = - 50\;{\rm{ meV}}$ .
Figure 3. Conductance G as a function of E for different separation distance between two quantum wells at
$\alpha = \beta = 0$ ,${k_y} = 0.006\;{\rm{ n}}{{\rm{m}}^{ - 1}}$ , ћ$ \omega = 11\;{\rm{ meV}}$ ,${V_1} = 1.0\;{\rm{ meV}}$ ,${V_0} = - 50\;{\rm{ meV}}$ and$d = 200\;{\rm{ nm}}$ .
Figure 4. Variation of Fano-type resonance line-shape in conductance
$G$ with$\beta $ at$\alpha = 0$ ,$a = 40\;{\rm{ nm}}$ ,${k_y} = $ $ 0.006\;{\rm{ n}}{{\rm{m}}^{ - 1}}$ , ћ$ \omega = 11\;{\rm{ meV}}$ ,${V_1} = 1.0\;{\rm{ meV}}$ ,${V_0} = - 50\;{\rm{ meV}}$ and$d = 200\;{\rm{ nm}}$ . (a)$\,\beta$ =0; (b)$\,\beta=\dfrac{3\pi}{11}$ ; (c)$\,\beta= \dfrac{5\pi}{11}$ ; (d)$\,\beta=\pi $ . -
[1] NOVOSELOV K S, GEIM A K, MOROZOV S V, et al. Two-dimensional gas of massless Dirac fermions in graphene[J]. Nature, 2005, 438(7065): 197-200. doi: 10.1038/nature04233 [2] NOVOSELOV K S, MOROZOV S V, MOHINDDIN T M G, et al. Electronic properties of graphene[J]. Physica Status Solidi (B) , 2007, 244(11): 4106-4111. doi: 10.1002/pssb.200776208 [3] ZHANG H J, LEE G, GONG CH, et al. Grain boundary effect on electrical transport properties of graphene[J]. The Journal of Physical Chemistry C, 2014, 118(5): 2338-2343. doi: 10.1021/jp411464w [4] SEMENOFF G W. Condensed-matter simulation of a three-dimensional anomaly[J]. Physical Review Letters, 1984, 53(26): 2449-2452. doi: 10.1103/PhysRevLett.53.2449 [5] LI T, DUCA L, REITTER M, et al. Bloch state tomography using wilson lines[J]. Science, 2016, 352(6289): 1094-1097. doi: 10.1126/science.aad5812 [6] RUSIN T M, ZAWADZKI W. Trembling motion (Zitterbewegung) of electrons in semiconductors[J]. AIP Conference Proceedings, 2007, 893(1): 135. [7] ZAWADZKI W, RUSIN T M. Nature of electron zitterbewegung in crystalline solids[J]. Physics Letters A, 2010, 374(34): 3533-3537. doi: 10.1016/j.physleta.2010.06.028 [8] ALLAIN P E, FUCHS J N. Klein tunneling in graphene: optics with massless electrons[J]. The European Physical Journal B, 2011, 83(3): 301-317. doi: 10.1140/epjb/e2011-20351-3 [9] LEO S D, ROTELLI P P. Barrier paradox in the klein zone[J]. Physical Review A, 2006, 73(4): 042107. doi: 10.1103/PhysRevA.73.042107 [10] LEO S D, ROTELLI P P. Dirac equation studies in the tunneling energy zone[J]. The European Physical Journal C, 2007, 51(1): 241-247. doi: 10.1140/epjc/s10052-007-0297-4 [11] DAS SARMA S, ADAM S, HWANG E H, et al. Electronic transport in two-dimensional graphene[J]. Reviews of Modern Physics, 2011, 83(2): 407-470. doi: 10.1103/RevModPhys.83.407 [12] ZHANG Y T. Coherent perfect absorption and transmission of a generalized three-mode cavity optico-mechanical system[J]. Acta Physica Sinica, 2017, 66(10): 107101. (in Chinese) doi: 10.7498/aps.66.107101 [13] ZHU Y G, FANG Y T. Design of absorber at visible frequencies based on compound structure of one-dimensional photonic crystal and graphene[J]. Chinese Journal of Luminescence, 2019, 40(11): 1394-1400. (in Chinese) doi: 10.3788/fgxb20194011.1394 [14] KUSMARTSEV F V, WU W M, PIERPOINT M P, et al. . Application of graphene within optoelectronic devices and transistors[M]. MISRA P. Applied Spectroscopy and the Science of Nanomaterials. Singapore: Springer, 2015: 191-221. [15] ZHANG Y T. Coherent optical effect of a nano cavity optico-mechanical system[J]. Acta Photonica Sinica, 2018, 47(10): 1027002. (in Chinese) doi: 10.3788/gzxb20184710.1027002 [16] ZHANG ZH Y. One-piece flow target type based on fiber bragg grating sensing technology[J]. Chinese Journal of Luminescence, 2020, 41(2): 217-223. (in Chinese) [17] RODRIGUES J N B. Intervalley scattering of graphene massless Dirac fermions at 3-periodic grain boundaries[J]. Physical Review B, 2016, 94(13): 134201. doi: 10.1103/PhysRevB.94.134201 [18] ZHANG SH H, YANG W, PEETERS F M. Veselago focusing of anisotropic massless Dirac fermions[J]. Physical Review B, 2018, 97(20): 205437. doi: 10.1103/PhysRevB.97.205437 [19] LE H A, HO S T, NGUYEN D C, et al. Optical properties of graphene superlattices[J]. Journal of Physics:Condensed Matter, 2014, 26(40): 405304. doi: 10.1088/0953-8984/26/40/405304 [20] MIRYALA S, OLEIRO M, PÖHLS L M B, et al. Modeling of physical defects in PN junction based graphene devices[J]. Journal of Electronic Testing, 2014, 30(3): 357-370. doi: 10.1007/s10836-014-5458-4 [21] ZHANG Y T, XIAN M Y. Research on thermal effects of mid-infrared 2 μm Tm: YLF laser[J]. Laser &Infrared, 2017, 47(7): 813-816. (in Chinese) doi: 10.3969/j.issn.1001-5078.2017.07.005 [22] YANG ZH G, ZHOU J, HUANG H. Solar vector measurement algorithm based on multiple polarization sensors[J]. Acta Photonica Sinica, 2018, 47(2): 0212001. (in Chinese) doi: 10.3788/gzxb20184702.0212001 [23] ZHANG Y Q, DOU X J, DAI Y M, et al. All-optical manipulation of micrometer-sized metallic particles[J]. Photonics Research, 2018, 6(2): 66-71. doi: 10.1364/PRJ.6.000066 [24] WANG X, ZHAO Y H, DING Y H, et al. Tunable optical delay line based on integrated grating-assisted contradirectional couplers[J]. Photonics Research, 2018, 6(9): 880-886. doi: 10.1364/PRJ.6.000880 [25] KANG Y H, RUAN H, CLAUS R O, et al. Observation of quantized and partial quantized conductance in polymer-suspended graphene nanoplatelets[J]. Nanoscale Research Letters, 2016, 11(1): 179. doi: 10.1186/s11671-016-1387-8 [26] KRINNER S, STADLER D, HUSMANN D, et al. Observation of quantized conductance in neutral matter[J]. Nature, 2015, 517(7532): 64-67. doi: 10.1038/nature14049 [27] MIROSHNICHENKO A E, FLACH S, KIVSHAR Y S. Fano resonances in nanoscale structures[J]. Review of Modern Physics, 2010, 82(3): 2257-2298. doi: 10.1103/RevModPhys.82.2257 [28] DAYEM A H, MARTIN R J. Quantum interaction of microwave radiation with tunneling between superconductors[J]. Physical Review Letters, 1962, 8(6): 246-248. doi: 10.1103/PhysRevLett.8.246 [29] PESTOV E E, LEVITCHEV M Y, KLUSHIN A M. On the cryocooler-based cooling of josephson microchips fabricated from cuprate superconductors for use in voltage standards[J]. Journal of Surface Investigation. X-ray,Synchrotron and Neutron Techniques, 2016, 10(2): 302-306. doi: 10.1134/S1027451016020154 [30] MENDES U C, MORA C. Cavity squeezing by a quantum conductor[J]. New Journal of Physics, 2015, 17(11): 113014. doi: 10.1088/1367-2630/17/11/113014 [31] ARPAIA R, EJRNAES M, PARLATO L, et al. High-temperature superconducting nanowires for photon detection[J]. Physica C:Superconductivity and Its Applications, 2015, 509: 16-21. doi: 10.1016/j.physc.2014.09.017 [32] WU J J, YOU L X, CHEN S J, et al. Improving the timing jitter of a superconducting nanowire single-photon detection system[J]. Applied Optics, 2017, 56(8): 2195-2200. doi: 10.1364/AO.56.002195 [33] NAJAFI F, MARSILI F, VERMA V B, et al.. Superconducting nanowire architectures for single photon detection[M]. HADFIELD R H, JOHANSSON G. Superconducting Devices in Quantum Optics. Cham: Springer, 2016. [34] XU R Y, LI Y CH, ZHENG F, et al. Demonstration of a superconducting nanowire single photon detector with an ultrahigh polarization extinction ratio over 400[J]. Optics Express, 2018, 26(4): 3947-3955. doi: 10.1364/OE.26.003947 [35] LI H, CHEN S J, YOU L X, et al. Superconducting nanowire single photon detector at 532 nm and demonstration in satellite laser ranging[J]. Optics Express, 2016, 24(4): 3535-3542. doi: 10.1364/OE.24.003535 [36] YAO W, CUI P, HU X Q. Electrochemiluminescent aptasensor based on signal enhancement for determination of adenosine triphosphate[J]. Chinese Journal of Luminescence, 2020, 41(6): 744-752. (in Chinese) [37] YOGI P, POONIA D, MISHRA S, et al. Spectral anomaly in Raman scattering from p-type silicon nanowires[J]. The Journal of Physical Chemistry C, , 2017, 121(9): 5372-5378. doi: 10.1021/acs.jpcc.6b12811 [38] ZHANG Y T. Erbium-doped fiber laser based on the noise-like square wave pulse[J]. Acta Photonica Sinica, 2017, 46(6): 0614002. (in Chinese) doi: 10.3788/gzxb20174606.0614002 [39] ZHAO Z ZH, CAO Y D, GARCÍA R E. Kinetically stabilized metastable polarization states in ferroelectric ceramics[J]. Journal of the European Ceramic Society, 2017, 37(2): 573-581. doi: 10.1016/j.jeurceramsoc.2016.08.022 [40] WANG H B, TAO J, LV J G, et al. Absorption enhancement of silicon via localized surface plasmons resonance in blue band[J]. Chinese Optics, 2020, 13(6): 1362-1384. (in Chinese) doi: 10.37188/CO.2020-0056 -
下载:
图(4)
计量
- 文章访问数: 956
- HTML全文浏览量: 384
- PDF下载量: 82
- 被引次数: 0
