Differentiation of polarization scattering characteristics of surface nanoparticle defects
-
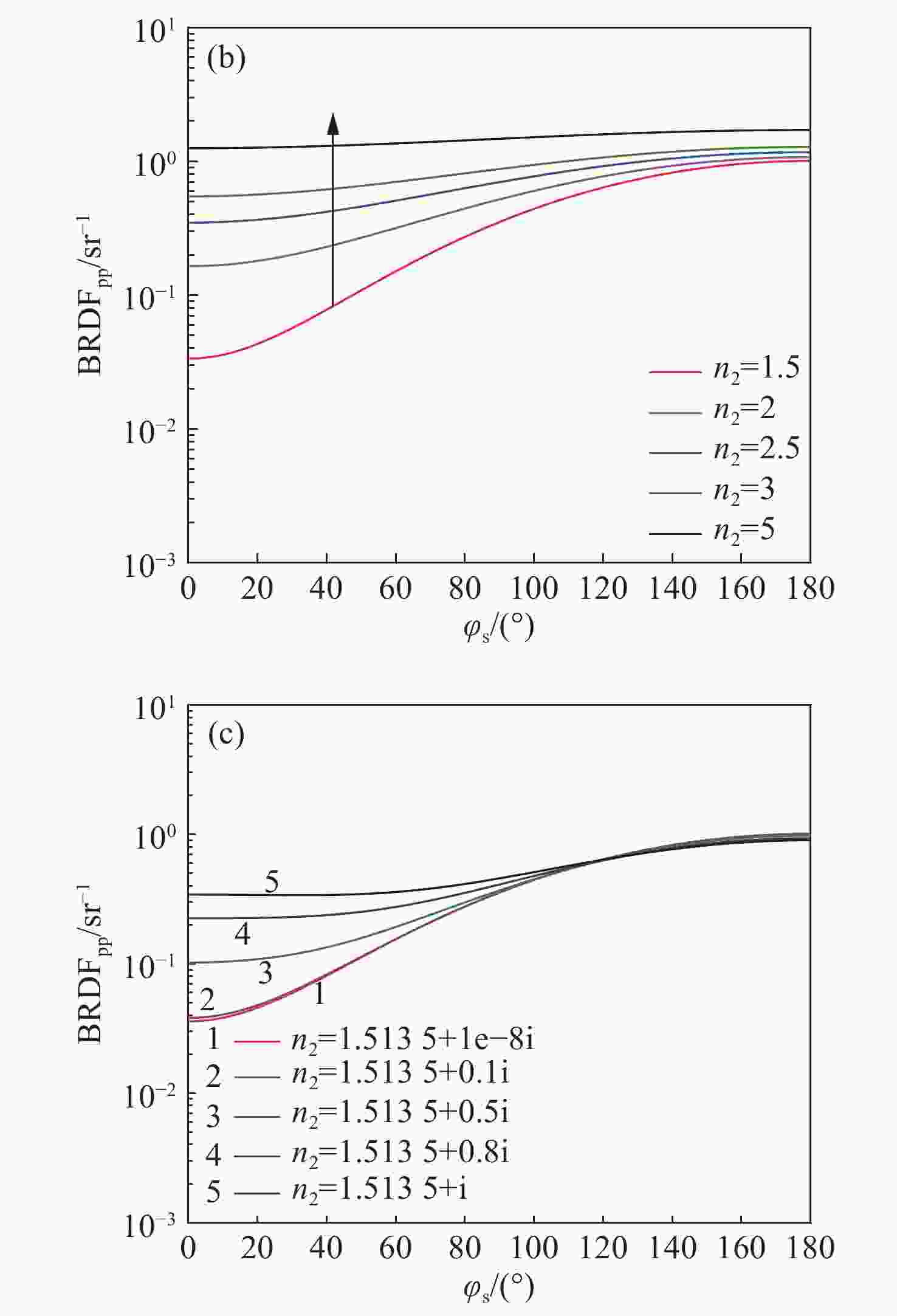
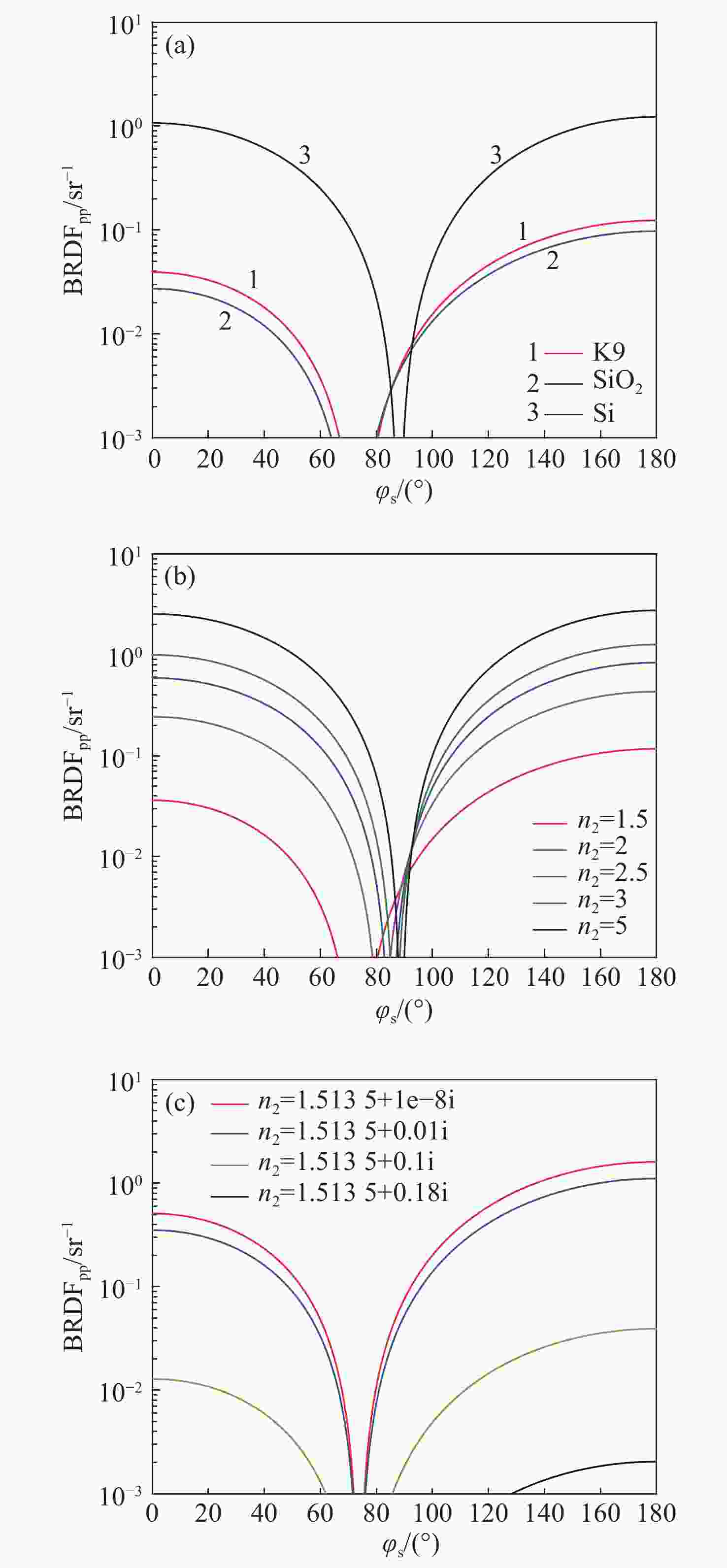
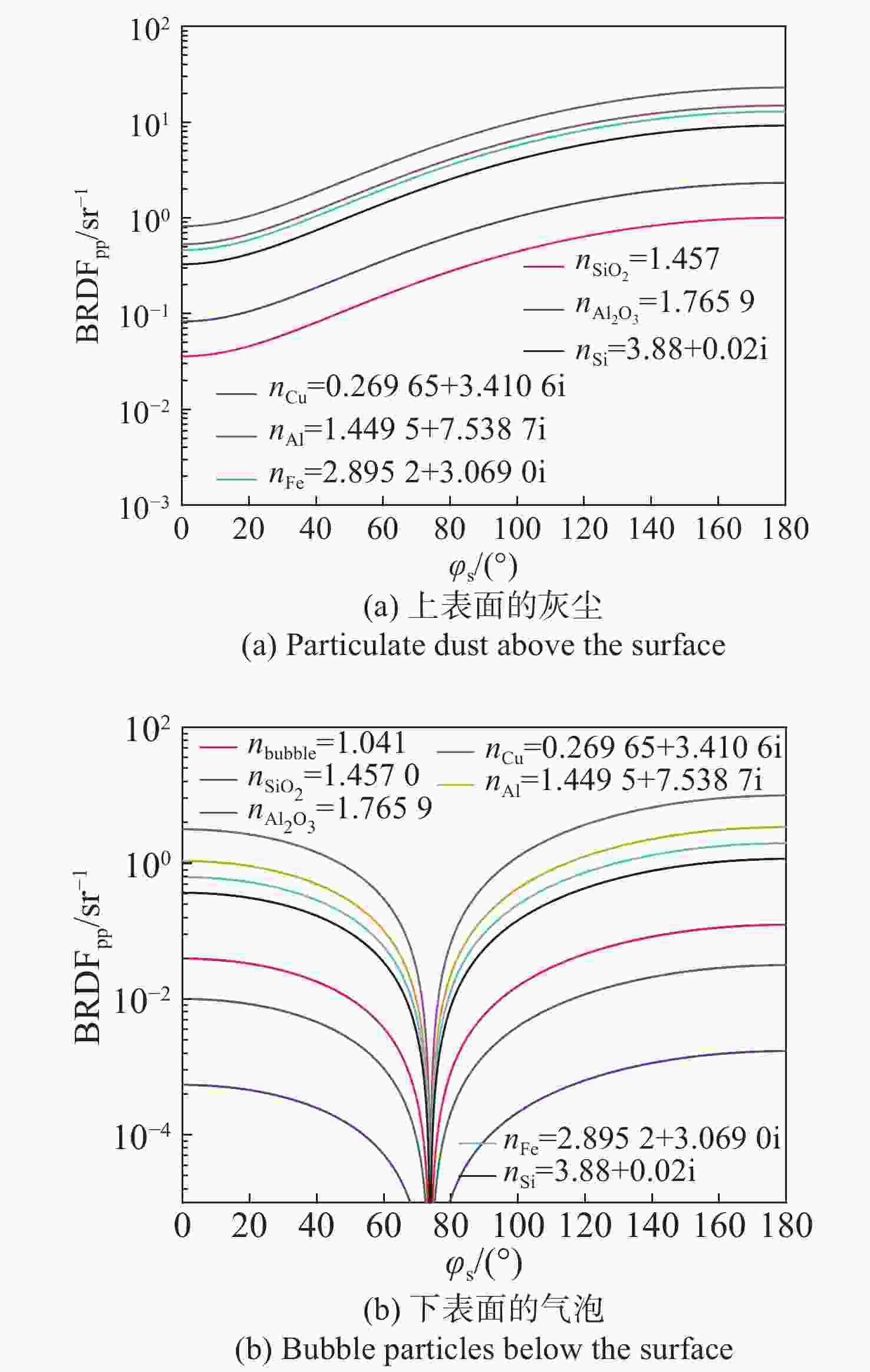
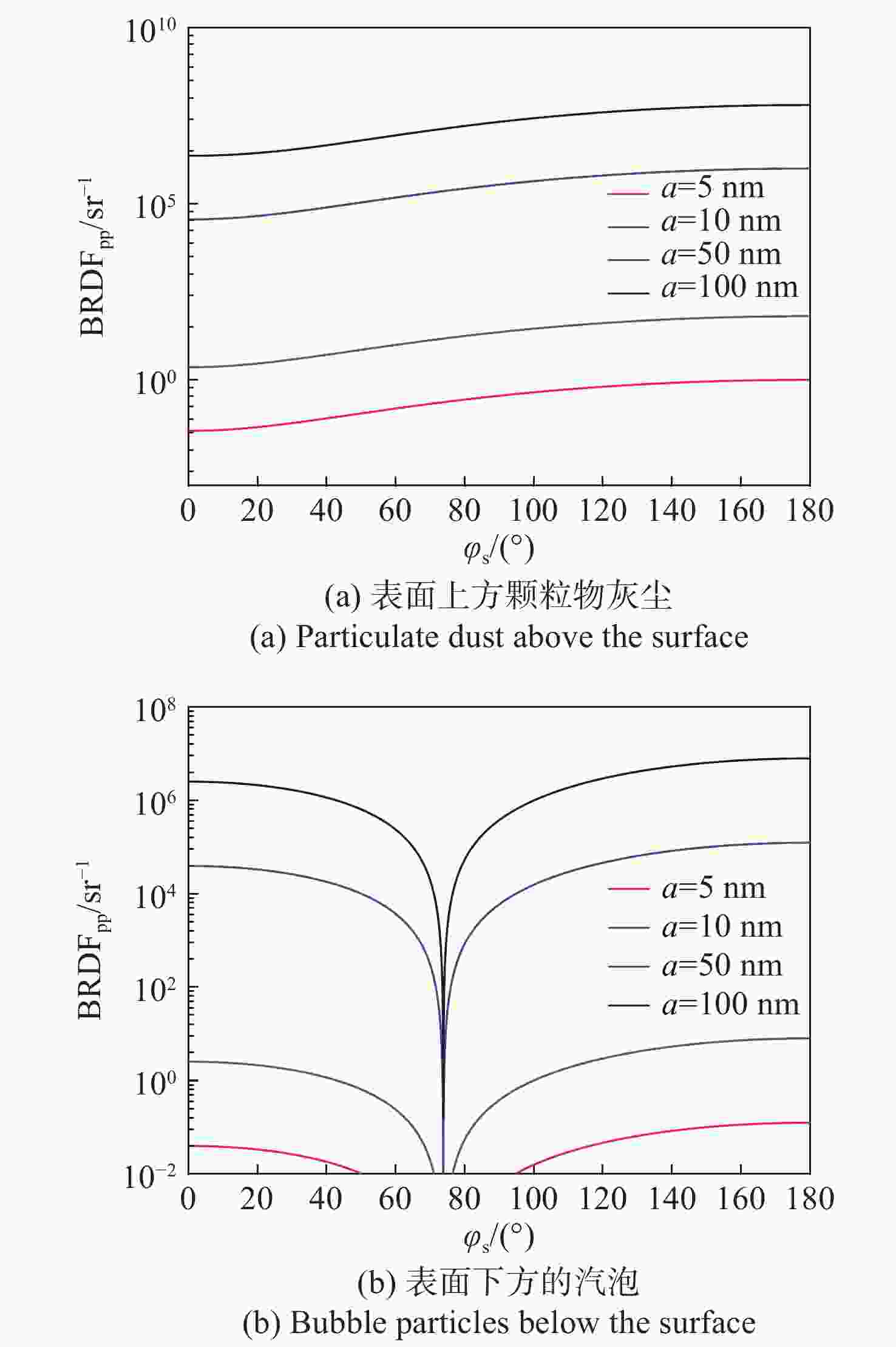
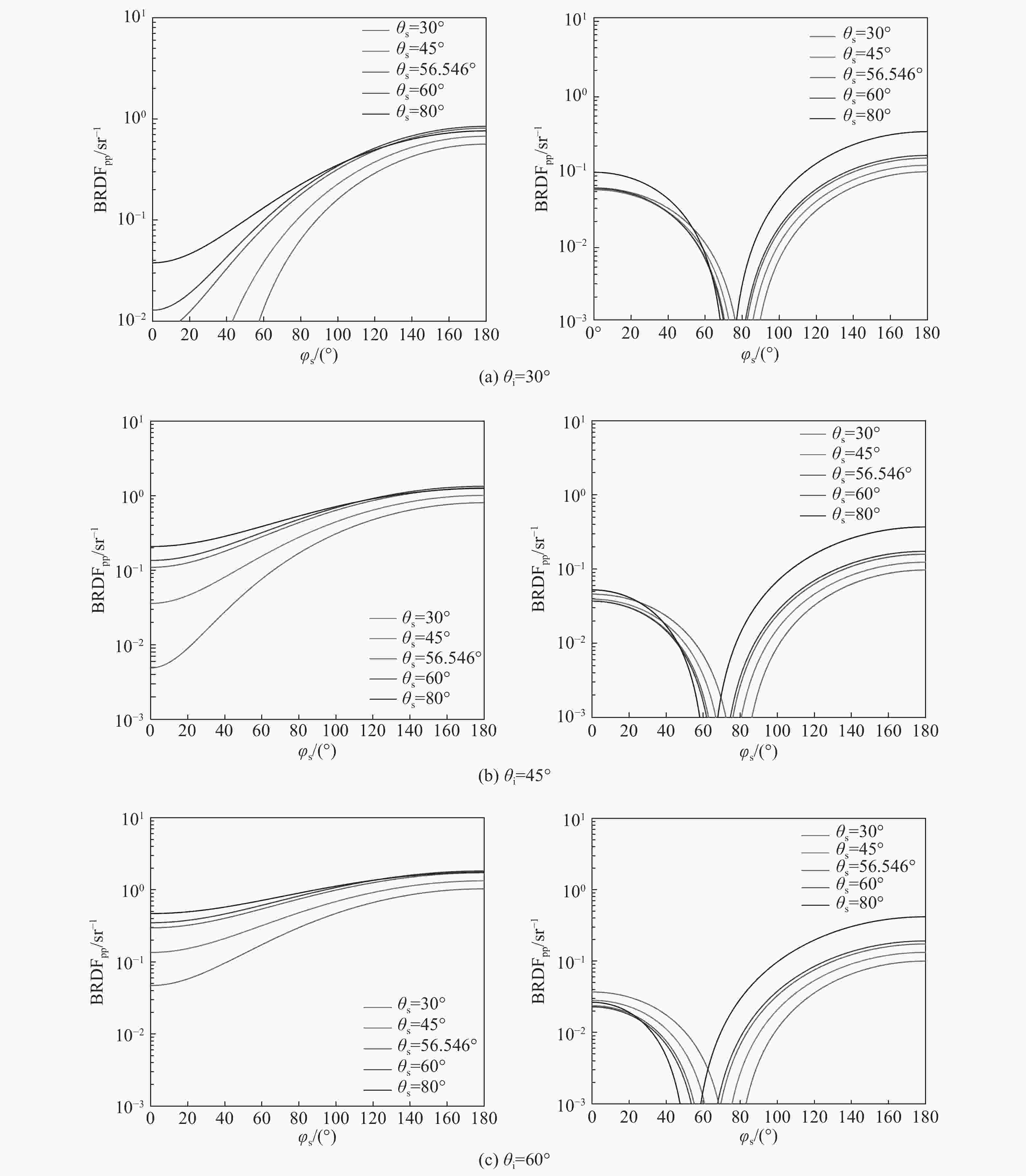
摘要: 为了区分纳米量级的表面上方颗粒物灰尘与表面下方气泡粒子这两种表面缺陷，且获得该方法的适用环境与最佳观测条件，根据瑞利散射理论结合偏振双向反射分布函数，建立了两种表面缺陷的偏振散射模型并进行了验证。在此基础上，通过仿真分析得到不同缺陷环境、不同观测条件对两种表面缺陷粒子偏振散射特性的影响。结果表明：利用p偏振光入射表面，而后探测p偏振光的双向反射分布函数值随散射方位角的变化趋势可区分两种表面缺陷；无论表面下方气泡粒子位置如何改变，均不影响该趋势的变化情况；不同光学元件表面材料、缺陷粒子种类、缺陷粒子大小对两种表面缺陷的偏振散射模型有一定影响，但整体趋势不变。实验中，针对本文所述两种表面缺陷进行区分时，可选取入射角度和探测散射角度均为 45°，采用较小波长入射光进行实验。Abstract: In order to distinguish between the two types of surface defects such as dust on the surface and bubble particles below the surface, and to obtain the applicable environmental range and optimal observation conditions of the method, we established and verified two polarization scattering models for surface defects based on Rayleigh scattering theory and a polarization bidirectional reflection distribution function. On this basis, the effects of the different defect environments and different observation conditions on the polarization scattering characteristics of the two surface defect particles were obtained through simulation analysis. The results show that by detecting the changing trend of the bidirectional reflection distribution function value of the p-polarized light incident on the surface with the scattering azimuth angle, we can distinguish between the two surface defects; no matter how the position of the bubble particles under the surface change, it will not affect the change of the trend. Different optical element surface materials, defect particle types, and defect particle size have certain effects on the polarization scattering models of the two surface defects, but the overall relationship remains unchanged. In order to distinguish between the two types of surface defects described in this article, the incident angle and the detection scattering angle are both 45° and an incident light with a smaller wavelength is used in an experiment.
-
图 2 光与表面上方颗粒物灰尘的一阶相互作用
Figure 2. The first-order interaction between light and particulate dust above the surface
图 3 表面下方气泡粒子复合散射示意图
Figure 3. Schematic diagram of the composite scattering of bubble particles under the surface
图 5 表面上方颗粒物灰尘和表面下方气泡BRDFpp值随散射方位角的变化
Figure 5. BRDFpp of particle smudge above the surface and bubble below the surface changing with scattering azimuth
图 6 不同表面下方气泡粒子位置对BRDFpp的影响情况
Figure 6. Influence of bubble particle position under different surfaces for the BRDFpp
图 7 不同表面材料（a），不同表面材料折射率实部（b）及虚部（c）对表面上方缺陷粒子BRDFpp项的影响
Figure 7. Influence of different surface materials (a), different real parts (b) and imaginary parts (c) of refractive index on the BRDFpp of defective particles above the surface
图 8 不同表面材料（a），不同表面材料折射率实部（b）和虚部（c）对表面下方缺陷粒子BRDFpp项的影响情况
Figure 8. Influence of different surface materials (a), different real parts (b) and different imaginary parts (c) of refractive index on the BRDFpp of defective particles under the surface
图 9 不同表面缺陷粒子类型对BRDFpp项的影响情况
Figure 9. Influence of different types of surface defective particles on the BRDFpp
图 10 表面缺陷粒子大小对BRDFpp项的影响情况
Figure 10. Influence of surface defects particle size on the BRDFpp
图 11 不同波长条件下表面上方颗粒物灰尘（a）及表面下方气泡粒子（b）BRDFpp随散射方位角的变化情况
Figure 11. Variations of BRDFpp of particle dust above the surface (a) and bubble particle below the surface (b) with the scattering azimuth at different wavelengthes
图 12 不同入射角探测时表面上方颗粒物灰尘粒子（左侧）及表面下方气泡粒子（右侧）BRDFpp随散射方位角的变化情况
Figure 12. Variations of BRDFpp of dust particles above the surface (left) and bubble particles below the surface (right) with the scattering azimuth at different incidence angles
表 1 两种表面缺陷的不同特性
Table 1. Different characteristics of two types of surface defects
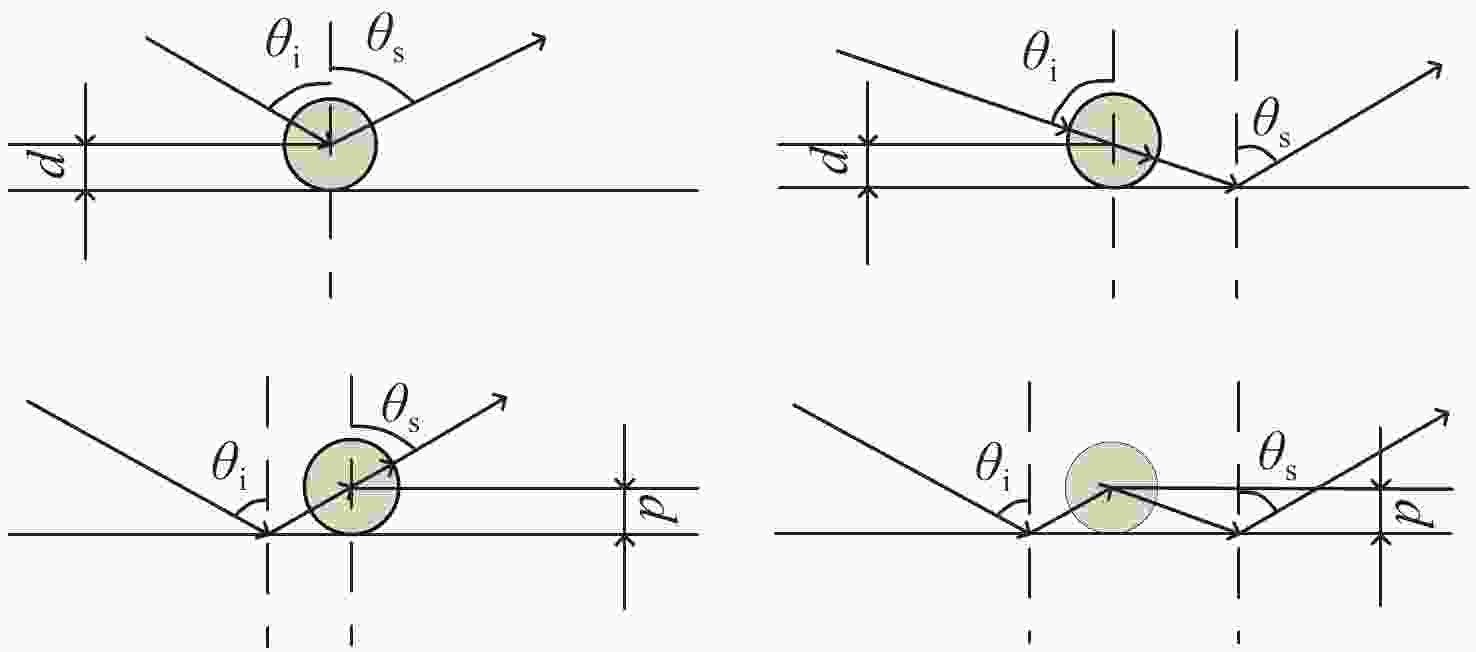
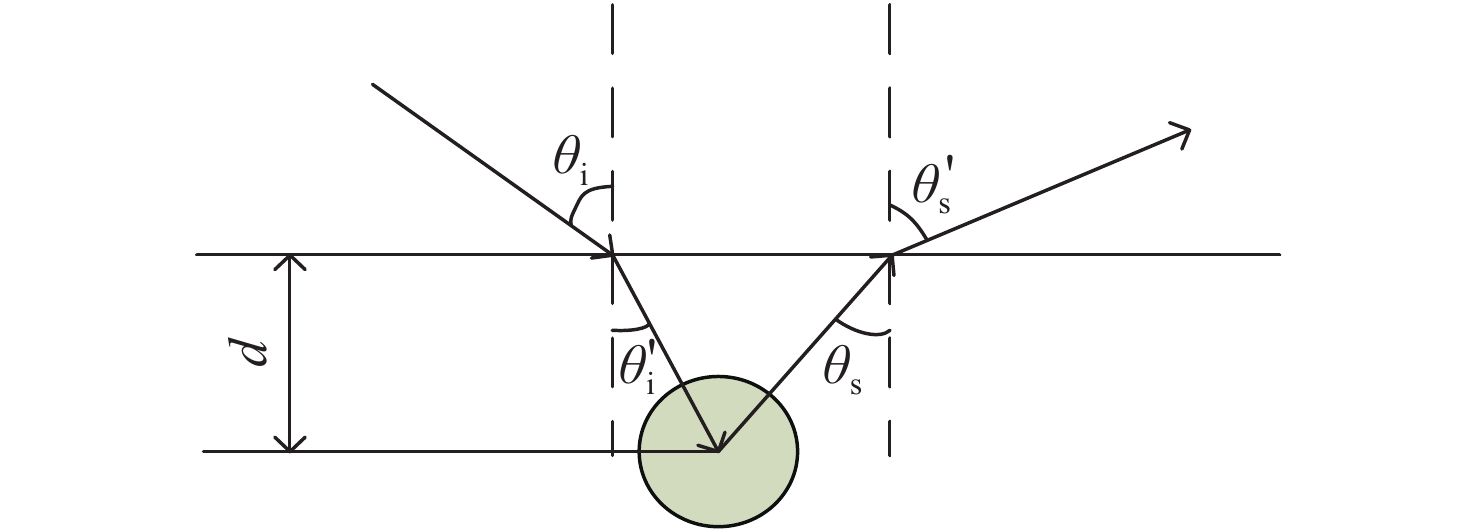
颗粒物脏污 气泡 图示 
位置 界面以上 界面以下 缺陷材料 主要为灰尘 主要为空气 光束一阶
相互作用三种散射情况：一次、
二次及三次散射一种情况：
一次散射
下载: 导出CSV
表 2 颗粒物灰尘折射率(近似SiO2)
Table 2. Refractive index of particulate dust (approximate SiO2)
波长(μm) 实部 虚部 0.403 1.4698 0 0.473 1.4639 0 0.520 1.4613 0 0.633 1.4570 0
下载: 导出CSV
表 3 K9玻璃折射率
Table 3. Refractive index of K9 glass
波长(μm) 实部 虚部 0.403 1.5305 9.524 3e-9 0.473 1.5234 1.005 6e-8 0.520 1.5202 8.442 3e-9 0.633 1.5151 1.212 6e-8
下载: 导出CSV
-
张静, 叶玉堂, 谢煜, 等. 金属圆柱工件缺陷的光电检测[J]. 光学 精密工程,2014,22(7):1871-1876. doi: 10.3788/OPE.20142207.1871ZHANG J, YE Y T, XIE Y, et al. Optoelectronic inspection of defects for metal cylindrical workpieces[J]. Optics and Precision Engineering, 2014, 22(7): 1871-1876. (in Chinese) doi: 10.3788/OPE.20142207.1871 王强, 胡秋平, 邱金星, 等. 航空复合材料内部缺陷差动式激光红外热成像检测[J]. 红外与激光工程,2019,48(5):0504003. doi: 10.3788/IRLA201948.0504003WANG Q, HU Q P, QIU J X, et al. Detection of internal defects in aviation composites with differential laser infrared thermal imaging[J]. Infrared and Laser Engineering, 2019, 48(5): 0504003. (in Chinese) doi: 10.3788/IRLA201948.0504003 刘红婕, 王凤蕊, 耿峰, 等. 荧光成像技术无损探测光学元件亚表面缺陷[J]. 光学 精密工程,2020,28(1):50-59. doi: 10.3788/OPE.20202801.0050LIU H J, WANG F R, GENG F, et al. Nondestructive detection of optics subsurface defects by fluorescence image technique[J]. Optics and Precision Engineering, 2020, 28(1): 50-59. (in Chinese) doi: 10.3788/OPE.20202801.0050 艾立夫. 基于散射光暗场显微的基片表面颗粒检测方法研究[D]. 成都: 中国科学院大学(中国科学院光电技术研究所), 2019: 35-45.AI L F. The detection method of substrate surface particles based on dark field microscopy of scattered light[D]. Chengdu: University of Chinese Academy of Sciences (Institute of Optics and Electronics, Chinese Academy of Sciences), 2019: 35-45. (in Chinese) 王震, 杨正伟, 陶胜杰, 等. 基于移相技术的含缺陷复合材料锁相热波检测[J]. 红外与激光工程,2019,48(S2):S204002.WANG ZH, YANG ZH W, TAO SH J, et al. Lock-in thermal wave detection of defective composite material based on phase-shifting technology[J]. Infrared and Laser Engineering, 2019, 48(S2): S204002. (in Chinese) GERMER T A. Polarized light scattering by microroughness and small defects in dielectric layers[J]. Journal of the Optical Society of America A, 2001, 18(6): 1279-1288. doi: 10.1364/JOSAA.18.001279 GERMER T A. Angular dependence and polarization of out-of-plane optical scattering from particulate contamination, subsurface defects, and surface microroughness[J]. Applied Optics, 1997, 36(33): 8798-8805. doi: 10.1364/AO.36.008798 巩蕾, 吴振森, 潘永强. 利用光散射特性研究光学表面中瑞利缺陷粒子的方位诊断[J]. 光子学报,2014,43(8):0831003. doi: 10.3788/gzxb20144308.0831003GONG L, WU ZH S, PAN Y Q. The diagnosis of Rayleigh defect particle position by light scattering character on the optical surface[J]. Acta Photonica Sinica, 2014, 43(8): 0831003. (in Chinese) doi: 10.3788/gzxb20144308.0831003 解格飒, 王红军, 王大森, 等. 超光滑表面缺陷的分类检测研究[J]. 红外与激光工程,2019,48(11):1113003. doi: 10.3788/IRLA201948.1113003XIE G S, WANG H J, WANG D S, et al. Study on classification and detection of supersmooth surface defects[J]. Infrared and Laser Engineering, 2019, 48(11): 1113003. (in Chinese) doi: 10.3788/IRLA201948.1113003 COX C, MUNK W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter[J]. Journal of the Optical Society of America, 1954, 44(11): 838-850. doi: 10.1364/JOSA.44.000838 YANG M, XU W B, SUN ZH Y, et al. Degree of polarization modeling based on modified microfacet pBRDF model for material surface[J]. Optics Communications, 2019, 453: 124390. doi: 10.1016/j.optcom.2019.124390 -
下载:
计量
- 文章访问数: 1990
- HTML全文浏览量: 444
- PDF下载量: 96
- 被引次数: 0
