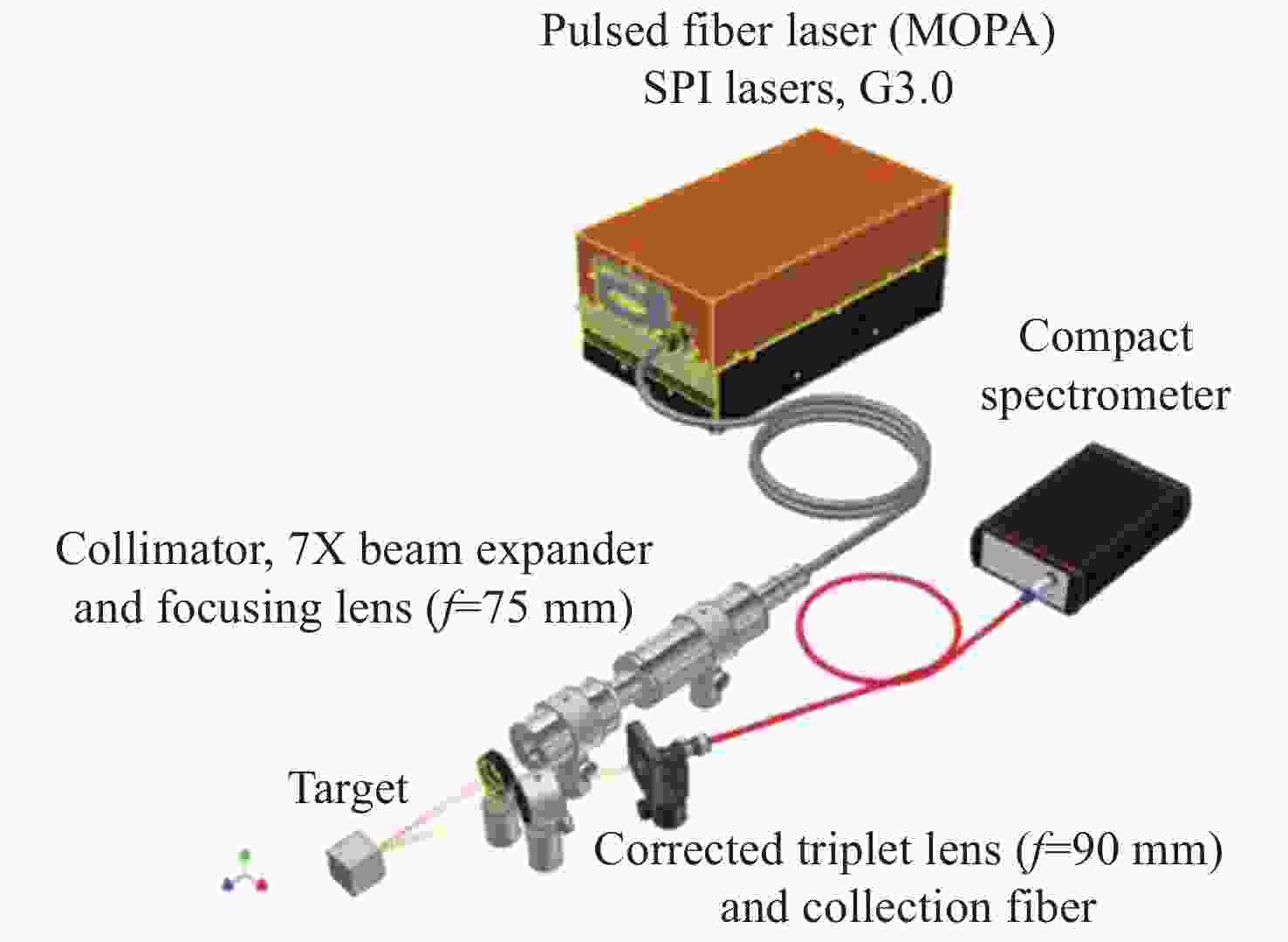
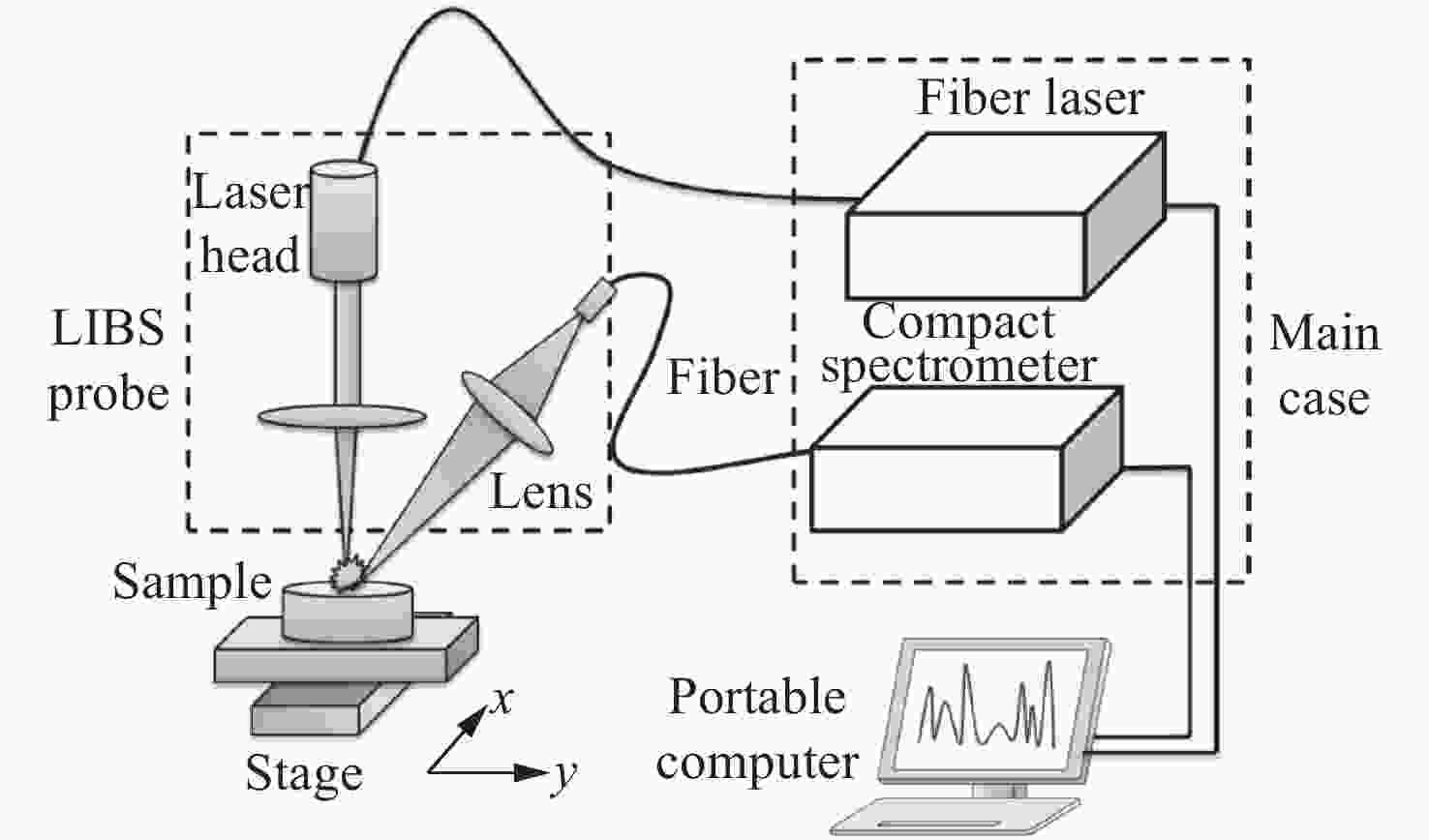
-
摘要: 作为一种新型快速的物质成分分析技术，激光诱导击穿光谱（Laser-Induced Breakdown Spectroscopy, LIBS）已经在越来越多的工业领域中被证明具有巨大的应用潜力。然而，由于野外作业或工业现场检测环境嘈杂恶劣，对仪器设备的尺寸和抗恶劣环境的能力提出了更高的要求。近年来，新型激光器的发展进一步促进了LIBS仪器化的进程，使得其逐渐从实验室迈向工业应用，同时也使得LIBS系统逐渐趋于仪器化、专业化、便携化。本文综述了便携式LIBS的发展历程，对各种激光光源（小型Nd:YAG固体激光器、二极管泵浦固体激光器、微片激光器、光纤激光器以及光纤传能的方案）应用于便携式LIBS系统的最新研究进展进行了综述和分类讨论，探讨了当前便携式LIBS存在的基本问题，并对其未来发展趋势进行了展望。Abstract:As a new rapid element analysis technique, Laser-Induced Breakdown Spectroscopy (LIBS) has proven iteself to have great potential for applications in increasingly numerous industrial fields. However, due to harsh outdoor and industrial environments, newer and higher requirements are being demanded of the LIBS system, such as the size of its instruments and the ability to resist a harsh environment. The rapid development of new laser technology promotes instrumentation for LIBS, allowing it to gradually step outside the laboratory and into the industry, and allows the LIBS system to gradually move towards instrumentation, miniaturization and portability.In this paper, the development of a portable LIBS that was developed in recent years was reviewed. The application and latest research progress of different kinds of laser source (small lamp pumped solid-state laser, diode pump solid-state laser and micro laser, fiber laser) applied to the portable LIBS system were summarized and discussed, providing insight into both the fiber optic LIBS (FO-LIBS) and the handheld LIBS. In addition, the basic problems of current portable LIBS and the prospects of its future were proposed and discussed.
-
Key words:
- laser-induced breakdown spectroscopy /
- portable /
- laser /
- element detection
-
1. Introduction
The slow light technology has attracted more and more attention due to its quite broad potential application prospect in optical field regulation and optical storage devices[1-3]. Controlling the structure dispersion to realize slow light is one of the commonly used technologies at present. The main method of this technology is to control the light group velocity by designing a slow optical waveguide with a specific structure. Slow light generated in such photonic crystal waveguides has been observed in several studies[4-5]. However, in the previous slow optical waveguide structure, when the group velocity becomes slow, its supported bandwidth is very narrow, and it is also accompanied by a huge group velocity dispersion effect. Scheuer J. et al. used a complex coupled resonant optical waveguide to achieve internal dispersion compensation and solved the problem of distortion[6]. In recent years, Surface Plasmon Polaritons (SPPs) waveguides have been used to realize slow light, which can achieve higher slow light capacity with a fixed structure, but the adjustment of slow light performance is limited[7]. In addition, the large group velocity dispersion effect of the chirped structure can cause seriously distortion of the optical signal, and the device has a limited operating frequency range[8]. Furthermore, the structural design of traditional slow-light devices is complicated and their tunability is poor once the structure is fixed, which limits their practical applications.
Photonic crystals have good topological band effects, and their topological concepts have great potential in the application of photonics, which has attracted extensive attention. Topological photonic structures have subverted some conventional views on wave propagation and manipulation. Applying topological photonic crystals to wave propagation makes it possible to realize new photonic devices with specific funtions, such as sharp bending waves without reflection, robust delay lines, spin polarization switches and non-reciprocal devices[9]. Recently, Chen Xiaodong et al. proposed and proved that the valley states in topological photonic crystals can be used as topological protection to realize light transmission. The design is to place two topological photonic crystals with different topological structures in mirror images to form an interface that can achieve topological protection[10]. Later, Yoshimi et al. proposed a method to realize topological slow optical waveguides in valley photonic crystals[11]. The waveguide structure is based on a semiconductor substrate to realize slow light transmission with a group index greater than 100 in the topological band gap range, but the manufacturing process is complex, and the structure has no tunability and does not involve the change of field strength caused by slow light. With the deepening of research, it is found that the topological band gap structure of valley state can be realized in photonic time crystal materials whose refractive index changes periodically with time[12]. The method is that by breaking the crystal time translation symmetry, photonic time crystals can achieve topologically non-trivial phases[13-15], thereby affecting the propagation of light in the crystal.
It is well known that graphene has unique electrical and optical properties, especially it supports surface plasmonic excitation waves, and has relatively low ohmic loss and high tunability[16]. Jin et al. designed monolayer graphene with periodic patterns to achieve topological unidirectional boundary transport by introducing a static magnetic field[17]. Later, Wang Yang et al. realized topological valley plasmonic transport in bilayer graphene metasurfaces for sensing applications[18]. Recently, Guo Xiang et al. designed a graphene SPP equivalent two-dimensional photonic crystal slow light waveguide through photonic crystal line defects, and achieved slow light modulation through the gradual change of chemical potential of graphene in space[19]. Likewise, it is very important to realize the modulation of the slow light transport in the valley state topology of graphene plasmonic crystals in time. In this paper, we propose a novel approach to achieve topological slow light transport in waveguides constructed from graphene plasmonic time crystals. Two-dimensional graphene plasmonic time crystals consist of a set of graphene nanodisks periodically arranged in a honeycomb pattern. By controlling the periodic change of the chemical potential of graphene with time, the time-translational symmetry of graphene plasmonic time crystals is broken. Numerical simulations show that the plasmonic time crystal band gap can open and close periodically with time. Further, we find that the Zigzag edges can support near-zero electromagnetic transport group velocities within the topological bandgap. Numerical simulation results of electromagnetic transmission in slow light waveguide show that the topological waveguide can generate slow light. The advantages of this method are simple structure, good field enhancement effect and dynamic tuning ability, which provides a new way for dynamically realizing optical field regulation.
2. Numerical simulation methods and models
In this paper, a valley state topological slow optical transmission waveguide is implemented based on graphene plasmonic time crystals. As shown in Fig. 1(a) (Color online), the waveguide adopts the Zigzag structure topological interface as the transmission channel, and the top is composed of graphene nanodisks. Graphene is in contact with air, SiO2 is selected as the background material, and Si as the substrate material. It can be seen from the cross-sectional view of the waveguide in the figure that the bias voltage is applied to the graphene nanodisk and the silicon substrate. The silicon pillars are arranged in a triangular lattice, and V1(t), V2(t) and V3(t) are the bias voltages applied to the graphene nanodisks, respectively. This method is based on the photonic crystal realization mechanism of the graphene plasmonic exciton[20]. When the distance between graphene and the substrate is constant, the chemical potential of graphene can be changed by changing the applied voltage.
Figure 1. (a) The three-dimensional schematic of slow light waveguide, with a single layer of graphene nanodisks at the top. The graphene is exposed to air on the top, the background material is SiO2, and the substrate material is Si. Different graphene nanodisks are applied with different bias voltages: V1(t), V2(t) and V3(t). The diagram on the right shows how voltage is applied. (b) The graphene nanodisk’s external bias voltage changes periodically with timeIt is assumed that the relative permittivity of the surrounding environment of graphene is
$ {\varepsilon _{{\rm{r}}1}} $ and$ {\varepsilon _{{\rm{r}}2}} $ , respectively. The relative permittivity of the substrate SiO2 is$ {\varepsilon _{{\rm{r}}1}} $ =3.9, and the relative permittivity of the air on the upper surface of the graphene is$ {\varepsilon _{\rm{{r}}2}} $ =1. In our numerical simulation, the TM mode is considered and the electric field form of TM mode is assumed to be[21]:$$ \left\{ {\begin{array}{*{20}{c}} {{E_x} = A{{\rm{e}}^{{\rm{i}}\beta x - {Q_1}\textit{z}}},}\;{{E_y} = 0,}{{E_\textit{z}} = B{{\rm{e}}^{{\rm{i}}qx - {Q_1}x}},}\;{(\textit{z} > 0)} \\ {{E_x} = A{{\rm{e}}^{{\rm{i}}\beta x + {Q_2}\textit{z}}},}\;{{E_y} = 0,}{{E_\textit{z}} = B{{\rm{e}}^{{\rm{i}}qx + {Q_2}x}},}\;{(\textit{z} < 0)} \end{array}} \right.\quad. $$ (1) Substituting equation (1) into Maxwell's equations, adding the surface conductivity of graphene
$ \left( {{\sigma _{\rm{g}}}} \right) $ to participate in the formula transformation, and matching the corresponding boundary conditions, the dispersion relation of the TM mode is obtained as[22]:$$ \frac{{{\varepsilon _{{\rm{r}}1}}}}{{\sqrt {{\beta ^2} - \dfrac{{{\varepsilon _{{\rm{r}}1}}{\omega ^2}}}{{{c^2}}}} }} + \frac{{{\varepsilon _{{\rm{r}}2}}}}{{\sqrt {{\beta ^2} - \dfrac{{{\varepsilon _{{\rm{r}}2}}{\omega ^2}}}{{{c^2}}}} }} = - \frac{{{\sigma _{\rm{g}}}i}}{{\omega {\varepsilon _0}}}\quad, $$ (2) where
$ {\varepsilon _0} $ is the vacuum permittivity in free space,$ \omega $ is the angular frequency of the plasmon, and$ c $ is the propagation speed of light in vacuum. In the whole calculation process, we only consider the case of the propagation constant$\beta \ll \dfrac{\omega}{c}$ , so equation (2) can be simplified to the following form[23]:$$ \beta = {\varepsilon _0}\left(\frac{{{\varepsilon _{{\rm{r}}1}} + {\varepsilon _{{\rm{r}}2}}}}{2}\right)\frac{{2\omega i}}{{{\sigma _{\rm{g}}}}}\quad, $$ (3) where
$ \beta $ is the propagation constant based on graphene SPP, the surface conductivity of graphene$ {\sigma _{\rm{g}}} $ can be adjusted with temperature T, chemical potential$ {\mu _{\rm{c}}} $ , scattering rate$ \tau $ and angular frequency$ \omega $ , which consists of two parts: intra-band electron scattering${\sigma _{{{\rm{intra}}} }}$ and inter-band electron transition${\sigma _{{{\rm{inter}} }}}$ , according to Kubo Formula[23]:$$ {\sigma _{\rm{g}}} = {\sigma _{{{\rm{intra}}} }} + {\sigma _{{{\rm{inter}}} }}\quad, $$ (4) $$ {\sigma _{{{\rm{intra}}} }} = - {\rm{j}}\frac{{{{\rm{e}}^2}{{\rm{k_B}}}T}}{{{\text{π}} {{{\hbar}} ^2}(\omega - {\rm{j}}{\tau ^{ - 1}})}}\left[ {\frac{{{\mu _{\rm{c}}}}}{{{{\rm{k_B}}}T}} + 2\ln ({{\rm{e}}^{{{ - {\mu _{\rm{c}}}} / {{{\rm{k_B}}}T}}}} + 1)} \right] \quad,$$ (5) $$ {\sigma _{{{\rm{inter}}} }} = \frac{{ - {\rm{j{e}}^2}}}{{4{\text{π}} {{\hbar}} }}\ln \left( {\frac{{2\left| {{\mu _{\rm{c}}}} \right| - \left( {\omega - {\rm{j}}{\tau ^{ - 1}}} \right){{\hbar}} }}{{2\left| {{\mu _{\rm{c}}}} \right| + \left( {\omega - {\rm{j}}{\tau ^{ - 1}}} \right){{\hbar}} }}} \right)\quad, $$ (6) where
$ {{\rm{k_B}}} $ is the Boltzmann constant,$ {\rm{e}} $ is the charge of the electron, and${{\hbar}} $ is the reduced Planck constant. Specifically, the chemical potential of graphene$ {\mu _{\rm{c}}} $ can be effectively tuned by an externally applied voltage[20-21, 24-25].$$ {\mu _c}\left( t \right) = {{\hbar}} {v_{\rm{F}}}\sqrt {\frac{{{\text{π}} {C_{{\rm{ox}}}}{V_{\rm{g}}}\left( t \right)}}{{\rm{e}}}} \quad,$$ (7) where
${v_{\rm{F}}}$ is the Fermi velocity,$ {C_{{\rm{ox}}}} $ is the gate capacitance[26], and$ {V_{\rm{g}}}\left( t \right) $ is the applied voltage that changes periodically with time. In this paper, the curve of the applied bias voltage of graphene nanodisk changing periodically with time is shown in Fig. 1(b) (Color online). By changing the bias voltages V1(t), V2(t) and V3(t) applied to the graphene nanodisks, the graphene chemical potentials$ {\mu _{{\rm{c}}1}}(t) $ ,$ {\mu _{{\rm{c}}2}}(t) $ and$ {\mu _{{\rm{c}}3}}(t) $ are changed.3. Numerical simulation results and discussion
3.1 Graphene plasmonic time crystal model and properties
First, we explored the energy band topology of 2D graphene plasmonic crystals composed of graphene nanodisk arrays arranged in a triangular lattice. The time crystal structure of graphene plasmon is shown in Figure 2 (a). The dotted line area is the crystal cell, and the solid line part is the Brillouin region of the crystal, where
$\varGamma-{{M}}-{K}-\varGamma$ is the reduced wedge of Brillouin region, a is the crystal lattice constant, a=40 mm, and the radius of graphene nanodisk is expressed as r and r=0.21a.$ {\mu _{{\rm{c}}1}} $ ,$ {\mu _{{\rm{c}}2}} $ and$ {\mu _{{\rm{c}}3}} $ are the chemical potentials of different graphene nanodiscs, respectively. From equation (7), it can be seen that the chemical potentials of these graphene nanodiscs can also change periodically with time, which can be written as$ {\mu _{{\rm{c}}1}}(t) $ ,$ {\mu _{{\rm{c}}2}}(t) $ and$ {\mu _{{\rm{c}}3}}(t) $ [27-29]. The chemical potential of graphene nanodisks can be flexibly controlled in time by applying periodic changed bias voltage of V1(t), V2(t) and V3(t). Here, we calculate the energy bands of graphene plasmonic time crystals at several moments in one cycle, as shown in Fig. 2(b) (Color online), where the black line depicts that, when t=0 s (i.e.$\Delta {\mu _{\rm{c}}} $ =$ {\mu _{{\rm{c}}1}} - {\mu _{{\rm{c}}2}} $ =0 eV), the chemical potentials of the graphene nanodisk are${\mu _{{\rm{c}}1}} $ =$ {\mu _{{\rm{c}}2}}$ =0.3 eV and${\mu _{{\rm{c}}3}}$ =0.6 eV, respectively, the two energy bands degenerate at the K point and intersect at the Dirac point, and there is obviously no band gap. During the periodic change of chemical potential with time, the time-translation symmetry of the graphene plasmonic time crystal is broken, the Dirac cone dispersion will be split, and the band gap will be opened[30]. The green, blue and red curves in Fig. 2(b) depict the band structures of the following three time nodes:${t_1} $ =1 e−12s (i.e.$\Delta {\mu _{\rm{c}}} $ =0.1 eV),${t_2} $ =1.5 e−12s (i.e.$\Delta {\mu _{\rm{c}}} $ =0.12 eV) and${t_3} $ =2 e−12s (i.e.$\Delta {\mu _{\rm{c}}} $ =0.14 eV), respectively. It is clear that the crystal band gap undergoes a process from closing to opening over time. It is worth noting here that this graphene plasmonic time crystal energy band change over time can be performed without changing the geometry.
Figure 2. (a) Schematic diagram of graphene plasmon time crystal structure. (b) Energy band diagrams of graphene plasmon time crystals at four different moments in a cycle of external bias voltage changeIn order to verify the properties of graphene plasmonic time crystals, a numerical simulation study is designed in this work. As shown in Fig. 3(d), in a region composed of graphene plasmonic time crystals, an excitation source is placed at point P, and the relationship between the chemical potentials of graphene nanodisks satisfies the variation law shown in Fig. 3 (a). Here, electromagnetic waves with a frequency of 46.50 THz are excited from the excitation source. We further explored the change trend of crystal energy band gap with the change of graphene chemical potential. By analyzing the opening and closing of the band gap, the propagation phenomenon occurs when the frequency of the excitation wave is in the conduction band; however, when the frequency is in the band gap, the wave will not propagate in this time interval[31-33]. The simulation results are shown in Figure 3 (Color online), in which screenshots are taken of the electric fields at four time nodes during the transmission process. With the periodic change of
$ \Delta {\mu _{\rm{c}}} $ in time, the transmission and inhibition alternate phenomenon occurs in the timing of${t_{\rm{b}}} $ =3.20 e−12s,${t_{\rm{c}}} $ =4.16 e−12s,${t_{\rm{d}}} $ = 5.82 e−12s and${t_{\rm{f}}} $ =8.24 e−12s, respectively. This result can well illustrate that the graphene plasmonic time crystal can realize the periodic opening and closing of the energy band gap with time by periodically adjusting the chemical potential.
Figure 3. (a) When μc3=0.6 eV, the relationship between ∆μc and t. (d) A region composed of 5×10 graphene plasmon time crystals. P is the position of the excitation source. (b), (c), (e) and (f) Screenshots of four moments in the propagation process at the time nodes of${t_{\rm{b}}} $ =3.20 e−12s,${t_{\rm{c}}} $ =4.16 e−12s,${t_{\rm{d}}} $ =5.82 e−12s and${t_{\rm{f}}} $ =8.24 e−12s, respectively3.2 Zigzag topological boundary structure theory and model
When the time-translational symmetry of the graphene plasmonic time crystal is broken, the Dirac cone dispersion is not preserved. From the point of view of group theory, when the inversion symmetry is broken, the group symmetry of the point (K or K′) will be reduced from C3v to C3. In the energy band, the Dirac cone is destroyed, and the two energy bands originally degenerated to the point K will be opened[34-35]. By analyzing the change of the orbital angular momentum at the valley of the energy band after the energy band is opened, we obtain the phase distribution at point K at time of
${t_1} $ =1 e−12s (i.e.$\Delta {\mu _{\rm{c}}} $ =0.1 eV),${t_2} $ =1.5 e−12s (i.e.$\Delta {\mu _{\rm{c}}} $ =0.12 eV) and${t_3} $ =2 e−12s (i.e.$\Delta {\mu _{\rm{c}}} $ =0.14 eV). As shown in Figure 4 (Color online), it can be seen that, at different times, the two energy bands appear the phase distribution of Left-handed Circular Polarization (LCP) and Right-handed Circular Polarization (RCP) at the degenerate point K, respectively, that is, in the process of$ \Delta {\mu _{\rm{c}}} $ changing with time, the energy valley at any moment has the circularly polarized orbital angular momentum in the opposite direction after the time crystal energy band is opened. Therefore, we construct electromagnetic transport at the topological edge through electromagnetic modes that can be loaded with different orbital angular momentums, which provides a theoretical basis for the use of topological boundary to construct slow light waveguides.
Figure 4. The phase distributions of Left-handed Circularly Polarized (LCP) and Right-handed Circularly Polarized (RCP) of the time crystal appear at point K, which are expressed as the component of the electric field in the direction Z and the in-plane Poynting vector (Px, Py). (a) and (d) the phase distribution diagram of point K at the time of$ \Delta {\mu _{\rm{c}}} $ =0.1 eV; (b) and (e) the phase distribution diagram of point K at the time of$ \Delta {\mu _{\rm{c}}} $ =0.12 eV; (c) and (f) the phase distribution diagram of point K at the time$ \Delta {\mu _{\rm{c}}} $ =0.14 eVIn this study, Zigzag topological boundaries are used to construct slow light waveguides. This topology is constructed from graphene plasmonic time crystals, which generate “temporal topological boundary states”, they are temporal analogs of topological edge states[13]. Breaking the time-translational symmetry of graphene plasmonic time crystals will lead to the opening of Dirac points at band degeneracy, thus forming a full band gap in which topologically protected boundary modes exist. The red dotted line in Figure 5(a) (Color online) is the Zigzag topology interface. By sampling the area within the black dotted line, a finite period (N=19) supercell model is established in the commercial simulation software COMSOL Multiphysics. Part of the simulation results are shown at the bottom of Fig. 5(a) (Color online), and it can be seen that the electric field distribution is concentrated at the boundary. We also calculated the dispersion relation of this boundary mode at different times (Fig. 5(b)), and the gray area represents the projected body energy band diagram. Fig. 5(b) also depicts the projected energy bands of three boundary states at the time
${t_1} $ =1 e−12s,${t_2} $ =1.5 e−12s and${t_3} $ =2 e−12s[36]. Obviously, when$ \Delta {\mu _{\rm{c}}} $ changes with time, there is always a corresponding boundary state at each moment, which means that the time simulation based on the Zigzag topology boundary state of the graphene plasmon time crystal is realized.
Figure 5. (a) Schematic diagram of the Zigzag interface based on graphene plasmon time crystals, in which the bottom is the calculation model of the finite period super cell unit and the simulation electric field distribution results. (b) The dispersion curves of the Zigzag interface mode at different times3.3 Slow light phenomenon and field enhancement effects
By further analyzing the dispersion relation of the above boundary modes, we can deduce a phenomenon that the group velocity is zero (slow light) at the extreme point of the dispersion curve. In order to better study the group velocity of guided modes existing in this boundary state, the partial dispersion curves at three different times are plotted in Fig. 6(a) (Color online). It is obvious that the dispersion is accompanied by severe bending, which leads to the existence of slow light mode in the gap. Based on the dispersion curves of these boundary modes, the change curve of the group velocity with angular frequency w can be calculated with the relationship
${v_{\rm{g}}} = {{{\rm{d}}\omega } /{{\rm{d}}k}}$ [37-38]. As shown in Figure 6(b) (Color online), the red curve is the group velocity at${t_1} $ =1 e−12s and$\Delta {\mu _{\rm{c}}} $ =0.1 eV, the group velocity tends to zero, and the frequency to 50.2370 THz. At${t_2} $ =1.5 e−12s and$\Delta {\mu _{\rm{c}}} $ =0.12 eV, the electromagnetic wave group velocity is close to zero at the frequency of 50.1149 THz, which is depicted in Fig. 6(b) by the blue curve. At${t_3} $ =2 e−12s and$\Delta {\mu _{\rm{c}}} $ =0.14 eV, the group velocity is close to zero at a frequency of 49.9292 THz, which is marked by the green curve. Numerical calculation results show that the group velocity of electromagnetic waves with different frequencies reach zero at different moments, that is, the topological boundary can realize slow light that its certain frequency electromagnetic wave group velocity near zero at different moments.
Figure 6. (a) The boundary mode dispersion curve supported by the topological boundary under different$ \Delta {\mu _{\rm{c}}} $ . (b) The relationship between group velocity and frequency under different$ \Delta {\mu _{\rm{c}}} $ Finally, with the slow light waveguide model given in Fig. 1(a), a two-dimensional modeling is carried out in the simulation software COMSOL, the Zigzag boundary structure is used as the transmission channel, and the excitation source is located at P (as shown in Fig. 1(a)). The chemical potential of graphene nanodisks can be flexibly controlled in time by applying a bias voltage that varies periodically with V1(t), V2(t), and V3(t). The graphene SPP wave with a certain frequency is emitted from point P, and the whole process of its transmission in the waveguide over time can be obtained. Figure 7 (Color online) shows the electric field intensity distribution results of plane waves with frequencies of 50.2370 THz, 50.1147 THz and 49.9292 THz propagating in the waveguide respectively. In this simulation, the plane wave with a frequency of 50.2370 THz is continuously excited from point P at
$ {t_0}$ =0 s , and reaches a state where the group velocity is close to zero after traveling along the waveguide for time$ 1\;{{\rm{e}}^{ - 12}}{\rm{s}} $ , and the SPP wave transmission stagnates at the position of X=307.998 nm. Figure 7(a) shows the electric field screenshot of a plane wave with a frequency of 50.2370 THz at time$ {t_1} $ =1 e−12s during the transmission process. After the plane wave group velocity is close to zero, the excitation in the slow light mode is continued, and it is found that the electric field intensity at the position of X=307.998 nm (the green dot in Fig. 7(a)) reaches the maximum value at t=1.4 e−12s, and the electric field intensity at this time is much greater than that at the excitation source. Plotting the electric field intensity in the waveguide at t=1.4 e−12s in Fig. 7 (b), it can be found that the field intensity B at the light energy capture point is greater than the field intensity A at the excitation source. By plotting the change process of the electric field intensity at the green dot position in the time period from$ {t_0} $ =0 s to t=1.4 e−12s is depicted in Fig. 7(c), we can see that the waveguide achieves a continuous superposition of the electric field strength at the light energy trapping point (green dot) and is higher than the enhancement effect of the excitation source due to the field enhancement effect in slow light transmission[4]. Figure 7(d) shows the electric field distribution of the SPP wave with a frequency of 50.1147 THz from point P, which is continuously excited from time$ {t_0} $ =0 s, and propagates along the waveguide for time$1.5\;{{\rm{e}}^{ - 12}}{\rm{s}}$ . When SPPs wave is transmitted to${t_2} $ =1.5 e−12s, the group velocity at X=667.879 nm decreases to zero. In addition, we also continuously observed the electric field at the light energy capture point X=667.879 nm (blue dot in Fig. 7 (d)), and obtained the cross-section of the electric field distribution at the boundary at t=2.98 e−12s, as shown in Fig. 7 (e). This result shows that at time t=2.98 e−12s, the electric field intensity at the light energy capture point reaches the maximum D and is greater than the electric field intensity C at point P. Figure 7(f) depicts the superposition process of the electric field strength at the blue dot from time$ {t_0} $ =0 s to t=2.98 e−12s. Similarly, as shown in Fig. 7(g), the SPP wave with a frequency of 49.9292 THz is continuously excited from point P at time$ {t_0} $ =0 s, and reaches a near-zero group velocity after traveling along the waveguide for$ 2\;{{\rm{e}}^{ - 12}}{\rm{s}} $ . The light energy trapping is located at X=1029.122 nm (red dot in Fig. 7(g)). Continuous excitation is carried out in the slow light mode, and it is observed that the electric field at the light energy capture place reaches the maximum intensity F at time t=3.22 e−12s, which is much greater than the electric field intensity E at the excitation source, as shown in Figure 7(j). During the time period from$ {t_0} $ =0 s to t=3.22 e−12s, the change process of the electric field intensity at the position of the red dot is depicted in Fig. 7(j), which also experienced a process of superposition of the electric field intensity. The above simulation process takes SPP waves with three different frequencies, and modulates the light group velocity close to zero by changing the applied bias voltage on the graphene nanodisk respectively. It can be seen that under the influence of the field enhancement effect, the waveguide realizes the continuous superposition of electric field intensity at the light energy capture point, which is higher than that at the excitation source. These results show that the slow light waveguide can make the SPP waves with different frequencies stop at different times and positions, and the field enhancement effect occurs at the corresponding optical energy capture points. In this work, graphene plasmonic time crystals are used to construct transmission waveguides, realizing the modulation of slow light group velocity simply by tuning the chemical potential of graphene. Compared with traditional waveguides such as photonic crystal line defect waveguides[19], its structure is simpler. Even if the structure is fixed, the waveguide performance can be flexibly modulated by changing the applied voltage, which greatly improves the electrical tunability of slow light waveguides. In addition, the SPP wave propagates at the topological boundary as an evanescent wave whose electric field amplitude is continuously attenuated, and the longer the transmission distance, the stronger the attenuation. By applying continuous excitation at the excitation source and recording the field strength superposition process at the optical energy capture point of the waveguide, we intuitively show the electric field change caused by the field strength superposition effect in time, which is not found in the previous slow light research work[11]. Since the modes in the waveguide are not discrete, degeneracy of the forward and backward modes will occur, resulting in energy loss. Therefore, when the optical group velocity is zero in the time sequence, the phenomenon of completely stopping the optical group velocity, the so-called "stationary rainbow", does not actually occur.
Figure 7. (a, d, g) Screenshots of the electric field intensity distribution at t1, t2 and t3. (b, e, h) Cross-sectional electric field diagrams at the Zigzag boundary at different time t. (c, f, j) The changing process of the electric field at the capture point of light energy4. Conclusion
In this paper, the time crystal band gap is periodically opened and closed by dynamically controlling the periodic change of the external voltage of the graphene nanodisk with time. Slow light transmission with the group velocity near zero is realized by the slow light waveguide made of graphene plasmon time crystal. The simulation results show that when the light propagates in the waveguide, a group velocity close to zero can be obtained, which is accompanied by the appearance of the field enhancement effect at the corresponding optical energy trapping point of the waveguide. In the case of adjusting the external bias voltage, the operating frequency of the slow optical waveguide can be effectively adjusted. Our research will be applied in the future to devices in the fields of on-chip light buffering and enhanced light-matter interactions.
-
图 3 Laserna等人研发的两种便携式LIBS设备：（a）箱式（Nd: YAG, 1064 nm, 50 mJ/pulse, 6.5 ns）[26], （b）背包式 （Nd: YAG, 1064 nm, 50 mJ/pulse, 10 ns）[27]
Figure 3. Two types of portable LIBS equipment developed by Laserna et al. : (a) a box type (Nd: YAG, 1064 nm, 50 mJ/pulse, 6.5 ns)[26], (b) a backpack type (Nd: YAG, 1064 nm, 50 mJ/pulse, 10 ns)[27]
表 1 基于DPSS激光器、光纤激光器和光纤传能的便携式LIBS的比较
Table 1. The comparison of several kinds of LIBS systems based on a DPSS laser, a fiber laser and FO-LIBS
激光器 优点 缺点 分析性能 适用领域 DPSS激光器 工作寿命长、功耗低、
自然冷却、小巧便携能量较低、谱线波动性较大 生铁中Mn、V、Ti和Cr元素的LOD分别为171 μg/g、128 μg/g、99 μg/g和
59 μg/g，R2分别为0.994、0.996、
0.994和0.991[2]手持式野外测量、电池
供电、原位测量光纤激光器 抗恶劣环境、体积小、
价格便宜连续背景干扰、烧蚀坑深，
破坏性较大铝基中Mg的LOD为1.1 μg/g，R2=0.994；黄铜中Ni的LOD为21.3 ug/g，R2=0.997[52]；生铁中的Mn、V，Si的LOD分别为195 μg/g、48 μg/g和110 μg/g, R2分别为0.997、0.991和0.992[54] 工厂、矿山等恶劣工作
环境，在线测量光纤传能 避免复杂光路系统和外界
干扰、降低自吸收效应能量低，LOD较差 生铁中Mn和Ti元素LOD分别为1219 μg/g, 257 μg/g, R2分别为0.997, 0.998[61] 在线、原位测量，
移动式测量
下载: 导出CSV
表 2 几种手持式LIBS的参数比较
Table 2. Parameters of several handheld LIBS
型号 研发单位 激光光源 体积、重量 参数及性能 LEA Handheld LIBS[62] 芬兰Lasersec Systems公司 DPSS激光器 22.6 cm×9 cm×29 cm,
1.75 kg平均功率0.5 W，光谱范围220~400 nm，续航2 h，LOD可达到μg/g级，可用于爆炸物、金属、食品与药品分类。 MPulse[63] 英国牛津公司 准连续固体调Q激光器 9 cm×23 cm×21 cm,
1.8 kg频率4 kHz，峰值功率小于0.5 W，电池支持250次测试，可用于合金鉴别与金属分拣。 高能手持式LIBS[65] 四川大学 被动调Q的Nd: YAG
激光器33 cm×11 cm×32 cm,
2.95 kg单脉冲能量达100 mJ，光谱范围220~397 nm，可元素定量测定，岩屑岩性识别等。 KT-100S[64] 美国Rigaku公司 波长1064 nm的3B级
激光器24.3 cm×8.4 cm×25.7 cm,
1.5 kg光谱范围200~480 nm，分辨率小于0.2 nm，电池供电10 h，可用于样品分类。 ChemLite[66] 美国TSI公司 波长1574 nm的人眼安全激光器 30.5 cm×25.4 cm×10.2 cm,
2.4 kg1574 nm人眼安全波长，光谱范围200~700 nm，一次充电支持1300次检测，探测范围低至0.01%。 μ-LIBS[67] 必达泰克公司 DPSS激光器 27.9 cm×8.9 cm×27.9 cm,
1.8 kg最大输出功率200 mW，脉宽小于1 ns,脉冲频率2 kHz，波长范围185~680 nm，分辨率0.4 nm。 z-200c+手持式LIBS
分析仪[68]SciAps公司 波长1064 nm的Nd: YAG激光器 21 cm×30 cm×12 cm,
1.82 kg脉宽1~2 ns，单脉冲能量5.5 mJ，重复频率50 Hz，光谱范围190~620 nm，用于原位分析钢中C含量。
下载: 导出CSV
-
[1] CIUCCI A, CORSI M, PALLESCHI V, et al. New procedure for quantitative elemental analysis by laser-induced plasma spectroscopy[J]. Applied Spectroscopy, 1999, 53(8): 960-964. doi: 10.1366/0003702991947612 [2] 曾庆栋. 移动式/便携式激光探针成分分析仪的研究与开发[D]. 武汉: 华中科技大学, 2016.ZENG Q D. Research and development on portable laser-induced breakdown spectroscopy[D]. Wuhan: Huazhong University of Science and Technology, 2016. (in Chinese) [3] 曾坤, 马源源, 郭庆中, 等. 电感耦合等离子发射光谱法快速测定对苯二甲酰氯中氯化亚砜残留量[J]. 分析化学,2019,47(3):410-414.ZENG K, MA Y Y, GUO Q ZH, et al. Determination of thionyl chloride residue in terephthaloyl chloride by inductively coupled plasma-optical emission spectrometry[J]. Chinese Journal of Analytical Chemistry, 2019, 47(3): 410-414. (in Chinese) [4] 付东旭, 郑令娜, 刘金辉, 等. 激光剥蚀-电感耦合等离子体质谱定量分析单细胞中的银纳米颗粒[J]. 分析化学,2019,47(9):1390-1394.FU D X, ZHENG L N, LIU J H, et al. Quantitative analysis of silver nanoparticles in single cell by laser ablation inductively coupled plasma-mass spectrometry[J]. Chinese Journal of Analytical Chemistry, 2019, 47(9): 1390-1394. (in Chinese) [5] 李小莉, 李庆霞, 安树清, 等. X射线荧光光谱法测定土壤样品中的氟[J]. 分析化学,2019,47(11):1864-1869.LI X L, LI Q X, AN SH Q, et al. Determination of fluorine in soil sample by X-ray fluorescence spectrometry[J]. Chinese Journal of Analytical Chemistry, 2019, 47(11): 1864-1869. (in Chinese) [6] 陈国成, 黎应芬. 火花直读光谱法测定铝及铝合金中的钒含量[J]. 中国无机分析化学,2017,7(3):59-61. doi: 10.3969/j.issn.2095-1035.2017.03.015CHEN G CH, LI Y F. Determination of vanadium content in aluminum and aluminum alloys by spark emission spectrometry[J]. Chinese Journal of Inorganic Analytical Chemistry, 2017, 7(3): 59-61. (in Chinese) doi: 10.3969/j.issn.2095-1035.2017.03.015 [7] NG C W, HO W F, CHEUNG N H. Spectrochemical analysis of liquids using laser-induced plasma emissions: effects of laser wavelength on plasma properties[J]. Applied Spectroscopy, 1997, 51(7): 976-983. doi: 10.1366/0003702971941638 [8] WIENS R C, ARVIDSON R E, CREMERS D A, et al. Combined remote mineralogical and elemental identification from rovers: field and laboratory tests using reflectance and laser-induced breakdown spectroscopy[J]. Journal of Geophysical Research, 2002, 107(E11): 8004. [9] SALLÉ B, CREMERS D A, MAURICE S, et al. Laser-induced breakdown spectroscopy for space exploration applications: influence of the ambient pressure on the calibration curves prepared from soil and clay samples[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2005, 60(4): 479-490. doi: 10.1016/j.sab.2005.02.009 [10] 郭连波. 激光诱导击穿光谱中的等离子体发射光谱增强方法研究[D]. 武汉: 华中科技大学, 2012.GUO L B. Investigation of enhancement method for optical emission spectroscopy of plasmas from laser-induced breakdown spectrum[D]. Wuhan: Huazhong University of Science and Technology, 2012. (in Chinese). [11] 袁冬青, 周明, 刘长隆, 等. 激光感生击穿光谱技术(LIBS)的原理及影响因素[J]. 光谱学与光谱分析,2008,28(9):2019-2023. doi: 10.3964/j.issn.1000-0593(0008)09-2019-05YUAN D Q, ZHOU M, LIU CH L, et al. The theory and the influential factors of laser induced breakdown spectroscopy[J]. Spectroscopy and Spectral Analysis, 2008, 28(9): 2019-2023. (in Chinese) doi: 10.3964/j.issn.1000-0593(0008)09-2019-05 [12] NOLL R. Laser-Induced Breakdown Spectroscopy: Fundamentals and Applications[M]. Berlin: Springer, 2012. [13] RAKOVSKÝ J, ČERMÁK P, MUSSET O, et al. A review of the development of portable laser induced breakdown spectroscopy and its applications[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2014, 101(3): 269-287. [14] SINGH J P, ALMIRALL J R, SABSABI M, et al. Laser-induced breakdown spectroscopy (LIBS)[J]. Analytical and Bioanalytical Chemistry, 2011, 400(10): 3191-3192. doi: 10.1007/s00216-011-5073-5 [15] 段忆翔, 林庆宇. 激光诱导击穿光谱分析技术及其应用[M]. 北京: 科学出版社, 2016: 11.DUAN Y X, LIN Q Y. Laser-Induced Breakdown Spectroscopy and Its Application[M]. Beijing: Science Press, 2016: 11. (in Chinese) [16] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 20125-2006 低合金钢 多素的测定 电感耦合等离子体发射光谱法[S]. 北京: 中国标准出版社, 2006.General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, National Standardization Administration of China. GB/T 20125-2006 Low-alloy steel—Determination of multi-element contents—Inductively coupled plasma atomic emission spectrometric method[S]. Beijing: China standard Press, 2006. (in Chinese). [17] HAHN D W, OMENETTO N. Laser-Induced Breakdown Spectroscopy (LIBS), Part Ⅱ: review of instrumental and methodological approaches to material analysis and applications to different fields[J]. Applied Spectroscopy, 2012, 66(4): 347-419. doi: 10.1366/11-06574 [18] ZENG Q D, CHEN G H, CHEN X G, et al. Rapid online analysis of trace elements in steel using a mobile fiber-optic laser-induced breakdown spectroscopy system[J]. Plasma Science and Technology, 2020, 22(7): 074013. doi: 10.1088/2058-6272/ab8a0b [19] YAMAMOTO K Y, CREMERS D A, FERRIS M J, et al. Detection of metals in the environment using a portable laser-induced breakdown spectroscopy instrument[J]. Applied Spectroscopy, 1996, 50(2): 222-233. doi: 10.1366/0003702963906519 [20] CASTLE B C, KNIGHT A K, VISSER K, et al. Battery powered laser-induced plasma spectrometer for elemental determinations[J]. Journal of Analytical Atomic Spectrometry, 1998, 13(7): 589-595. doi: 10.1039/a708844b [21] HARMON R S, DE LUCIA F C, MUNSON C A, et al. Laser-induced breakdown spectroscopy (LIBS): an emerging field-portable sensor technology for real-time chemical analysis for military, security and environmental applications[J]. Proceedings of SPIE, 2005, 5(1): 59940K. [22] DELUCIA F C, SAMUELS A C, HARMON R S, et al. Laser-induced breakdown spectroscopy (LIBS): a promising versatile chemical sensor technology for hazardous material detection[J]. IEEE Sensors Journal, 2005, 5(4): 681-689. doi: 10.1109/JSEN.2005.848151 [23] WALTERS R A, ROSE J B, MIZIOLEK A W, et al.. MP-LIBS, a laser induced breakdown spectroscopy tool for homeland security[C]. Laser Applications to Chemical, Security and Environmental Analysis, Optical Society of America, 2006. [24] CUÑAT J, FORTES F J, CABALÍN L M, et al. Man-portable laser-induced breakdown spectroscopy system for in situ characterization of karstic formations[J]. Applied Spectroscopy, 2008, 62(11): 1250-1255. doi: 10.1366/000370208786401662 [25] FORTES F J, CUÑAT J, CABALÍN L M, et al. In situ analytical assessment and chemical imaging of historical buildings using a man-portable laser system[J]. Applied Spectroscopy, 2007, 61(5): 558-564. doi: 10.1366/000370207780807722 [26] CUÑAT J, PALANCO S, CARRASCO F, et al. Portable instrument and analytical method using laser-induced breakdown spectrometry for in situ characterization of speleothems in Karstic caves[J]. Journal of Analytical Atomic Spectrometry, 2005, 20(4): 295-300. doi: 10.1039/B417161F [27] CUÑAT J, FORTES F J, LASERNA J J. Real time and in situ determination of lead in road sediments using a man-portable laser-induced breakdown spectroscopy analyzer[J]. Analytica Chimica Acta, 2009, 633(1): 38-42. doi: 10.1016/j.aca.2008.11.045 [28] GOUJON J, GIAKOUMAKI A, PIÑON V, et al. A compact and portable laser-induced breakdown spectroscopy instrument for single and double pulse applications[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2008, 63(10): 1091-1096. doi: 10.1016/j.sab.2008.08.019 [29] BAREFIELD I J E, CLEGG S M, LOPEZ L N, et al.. Application of laser induced breakdown spectroscopy (LIBS) instrumentation for international safeguards[C]. Proceedings of the INMM 51st Annual Meeting, LANL, 2010: 11. [30] RAKOVSKÝ J, MUSSET O, BUONCRISTIANI J F, et al. Testing a portable laser-induced breakdown spectroscopy system on geological samples[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2012, 74-75: 57-65. doi: 10.1016/j.sab.2012.07.018 [31] PIERCE W, CHRISTIAN S M, MYERS M J, et al.. Field-testing for environmental pollutants using briefcase sized portable LIBS system[C]. Proceedings of the 3rd International Conference on Laser Induced Plasma Spectroscopy and Applications, 2004. [32] FERREIRA E C, MILORI D M B P, FERREIRA E J, et al. Artificial neural network for Cu quantitative determination in soil using a portable laser induced breakdown spectroscopy system[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2008, 63(10): 1216-1220. doi: 10.1016/j.sab.2008.08.016 [33] Applied Photonics, Inc. LIBSCAN 25+[EB/OL]. (2020-08-13) [2020-08-13]. http://www.appliedphotonics.co.uk/. [34] 北京众创辉煌科技有限公司. EasyLIBS-3C便携式激光光谱元素分析仪[EB/OL]. (2019-04-23) [2020-08-13]. http://bjzchh.idc154.bjhyn.cn/cpzx/trlyq/turangyuansufenxiyi/935.html. [35] HARMON R S, DELUCIA JR F C, LAPOINTE A, et al. LIBS for landmine detection and discrimination[J]. Analytical and Bioanalytical Chemistry, 2006, 385(6): 1140-1148. doi: 10.1007/s00216-006-0513-3 [36] 邓奔, 王杰, 姜培培, 等. 高峰值功率微片激光器及其在LIBS中的应用[J]. 中国激光,2014,41(11):36-41. doi: 10.3788/CJL201441.1102005DENG B, WANG J, JIANG P P, et al. High peak power microchip laser and its LIBS application[J]. Chinese Journal of Lasers, 2014, 41(11): 36-41. (in Chinese) doi: 10.3788/CJL201441.1102005 [37] FREEDMAN A, IANNARILLI JR F J, WORMHOUDT J C. Aluminum alloy analysis using microchip-laser induced breakdown spectroscopy[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2005, 60(7-8): 1076-1082. doi: 10.1016/j.sab.2005.03.020 [38] LOPEZ-MORENO C, SMITH B W, GORNUSHKIN I B, et al. Quantitative analysis of low-alloy steel by microchip laser induced breakdown spectroscopy[J]. Journal of Analytical Atomic Spectrometry, 2005, 20(6): 552-556. doi: 10.1039/b419173k [39] AMPONSAH-MANAGER K, OMENETTO N, SMITH B W, et al. Microchip laser ablation of metals: investigation of the ablation process in view of its application to laser-induced breakdown spectroscopy[J]. Journal of Analytical Atomic Spectrometry, 2005, 20(6): 544-551. doi: 10.1039/b419109a [40] HWANG G M H. Feasibility study of micro-laser induced breakdown spectroscopy applied to lead identification in metal alloys and environmental matrices[D]. Cambridge: Massachusetts Institute of Technology, 1998: 1-7. [41] WORMHOUDT J, IANNARILLI JR F J, JONES S, et al. Determination of carbon in steel by laser-induced breakdown spectroscopy using a microchip laser and miniature spectrometer[J]. Applied Spectroscopy, 2005, 59(9): 1098-1102. doi: 10.1366/0003702055012528 [42] SECOPTA, Inc. FiberLIBS inline[EB/OL]. [2020-08-13] https://www.secopta.com/products/fiberlibs-inline-metal-applications. [43] MAREK H, IGOR G, SVEN M, et al. Assessment of suitability of diode pumped solid state lasers for laser induced breakdown and Raman spectroscopy[J]. Journal of Analytical Atomic Spectrometry, 2011(26): 414-424. [44] NOHARET B, STERNER C, IREBO T, et al. A compact LIBS system for industrial applications[J]. Proceedings of SPIE, 2015, 9369: 936904. [45] MYERS M J, MYERS J D, SARRACINO J T, et al. LIBS system with compact fiber spectrometer, head mounted spectra display and hand held eye-safe erbium glass laser gun[J]. Proceedings of SPIE, 2010, 7578: 75782G. doi: 10.1117/12.841901 [46] CREMERS D A, BEDDINGFIELD A, SMITHWICK R, et al. Monitoring uranium, hydrogen, and lithium and their isotopes using a compact laser-induced breakdown spectroscopy (LIBS) probe and high-resolution spectrometer[J]. Applied Spectroscopy, 2012, 66(3): 250-261. doi: 10.1366/11-06314 [47] TORTSCHANOFF A, BAUMGART M, KROUPA G. Application of a compact diode pumped solid-state laser source for quantitative laser-induced breakdown spectroscopy analysis of steel[J]. Optical Engineering, 2017, 56(12): 124104. [48] 闫久江, 李祥友. 新型便携式激光诱导击穿光谱仪器及其应用研究[J]. 冶金分析,2020,40(12):66-71. doi: 10.13228/j.boyuan.issn1000-7571.011200YAN J J, LI X Y. Research on a new portable laser-induced breakdown spectroscopy system and its application[J]. Metallurgical Analysis, 2020, 40(12): 66-71. (in Chinese) doi: 10.13228/j.boyuan.issn1000-7571.011200 [49] BOHLING C, HOHMANN K, SCHEEL D, et al. All-fiber-coupled laser-induced breakdown spectroscopy sensor for hazardous materials analysis[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2007, 62(12): 1519-1527. doi: 10.1016/j.sab.2007.10.038 [50] DE LUCIA F C, GOTTFRIED J L, MIZIOLEK A W. Evaluation of femtosecond laser-induced breakdown spectroscopy for explosive residue detection[J]. Optics Express, 2009, 17(2): 419-425. doi: 10.1364/OE.17.000419 [51] BAUDELET M, WILLIS C C C, SHAH L, et al. Laser-induced breakdown spectroscopy of copper with a 2 μm thulium fiber laser[J]. Optics Express, 2010, 18(8): 7905-7910. doi: 10.1364/OE.18.007905 [52] GRAVEL J F Y, DOUCET F R, BOUCHARD P, et al. Evaluation of a compact high power pulsed fiber laser source for laser-induced breakdown spectroscopy[J]. Journal of Analytical Atomic Spectrometry, 2011, 26(7): 1354-1361. doi: 10.1039/c0ja00228c [53] SCHARUN M, FRICKE-BEGEMANN C, NOLL R. Laser-induced breakdown spectroscopy with multi-kHz fibre laser for mobile metal analysis tasks — A comparison of different analysis methods and with a mobile spark-discharge optical emission spectroscopy apparatus[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2013, 87: 198-207. doi: 10.1016/j.sab.2013.05.007 [54] 曾庆栋, 朱志恒, 邓凡, 等. 便携式激光诱导击穿光谱结合小波变换去背景算法定量分析钢铁中Mn元素[J]. 光子学报,2018,47(8):102-111. doi: 10.3788/gzxb20184708.0847014ZENG Q D, ZHU ZH H, DENG F, et al. Quantitative analyses of element Mn in iron using portable laser-induced breakdown spectroscopy with algorithm of background removal based on wavelet transform[J]. Acta Photonica Sinica, 2018, 47(8): 102-111. (in Chinese) doi: 10.3788/gzxb20184708.0847014 [55] ZENG Q D, GUO L B, LI X Y, et al. Quantitative analyses of Mn, V, and Si elements in steels using a portable laser-induced breakdown spectroscopy system based on a fiber laser[J]. Journal of Analytical Atomic Spectrometry, 2016, 31(3): 767-772. doi: 10.1039/C5JA00453E [56] DAVIES C M, TELLE H H, MONTGOMERY D J, et al. Quantitative analysis using remote laser-induced breakdown spectroscopy (LIBS)[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 1995, 50(9): 1059-1075. doi: 10.1016/0584-8547(95)01314-5 [57] GRUBER J, HEITZ J, STRASSER H, et al. Rapid in-situ analysis of liquid steel by laser-induced breakdown spectroscopy[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2001, 56(6): 685-693. doi: 10.1016/S0584-8547(01)00182-3 [58] WHITEHOUSE A I, YOUNG J, BOTHEROYD I M, et al. Remote material analysis of nuclear power station steam generator tubes by laser-induced breakdown spectroscopy[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2001, 56(6): 821-830. doi: 10.1016/S0584-8547(01)00232-4 [59] PASQUINI C, CORTEZ J, SILVA L M C, et al. Laser induced breakdown spectroscopy[J]. Journal of the Brazilian Chemical Society, 2007, 18(3): 463-512. doi: 10.1590/S0103-50532007000300002 [60] RAI A K, ZHANG H SH, YUEH F Y, et al. Parametric study of a fiber-optic laser-induced breakdown spectroscopy probe for analysis of aluminum alloys[J]. Spectrochimica Acta Part B:Atomic Spectroscopy, 2001, 56(12): 2371-2383. doi: 10.1016/S0584-8547(01)00299-3 [61] ZENG Q D, GUO L B, LI X Y, et al. Laser-induced breakdown spectroscopy using laser pulses delivered by optical fibers for analyzing Mn and Ti elements in pig iron[J]. Journal of Analytical Atomic Spectrometry, 2015, 30(2): 403-409. doi: 10.1039/C4JA00462K [62] LASERSEC SYSTEMS CORPORATION. LEA Handheld LIBS[EB/OL]. (2020-08-13) [2020-08-13]. http://www.lasersec-systems.com. [63] BERG ENGINEERING AND SALES COMPANY, INC. Oxford mPulse Handheld LIBS Analyzer (MPULSE) [EB/OL]. (2020-08-13) [2020-08-13]. https://www.bergeng.com/product/MPULSE.html. [64] Rigaku, Inc. KT-100S – LIBS Analyzer[EB/OL]. (2019) [2020-08-13]. https://www.rigaku.com/en/products/libs/kt100s. [65] 林庆宇, 查方发, 王杰, 等. 高能手持式激光诱导击穿光谱分析仪器的研制及相关应用[J]. 现代科学仪器,2015(6):50-54.LIN Q Y, ZHA F F, WANG J. et al. Development and application of handheld instrument based on laser induced breakdown spectroscopy[J]. Modern Scientific Instruments, 2015(6): 50-54. (in Chinese) [66] TSI, INC. CHEMLITE PLUS METAL ANALYZER 4240 [EB/OL]. (2018) [2020-08-13]. https://tsi.com/products/metal-analyzers/chemlite-plus-laser-metals-analyzer-4240/. [67] AFGAN M S, HOU Z Y, WANG ZH. Quantitative analysis of common elements in steel using a handheld μ-LIBS instrument[J]. Journal of Analytical Atomic Spectrometry, 2017, 32(10): 1905-1915. doi: 10.1039/C7JA00219J [68] POCHON A, DESAULTY A M, BAILLY L. Handheld Laser-Induced Breakdown Spectroscopy (LIBS) as a fast and easy method to trace gold[J]. Journal of Analytical Atomic Spectrometry, 2020, 35(2): 254-264. doi: 10.1039/C9JA00437H 期刊类型引用(0)
其他类型引用(1)
-
DownLoad:
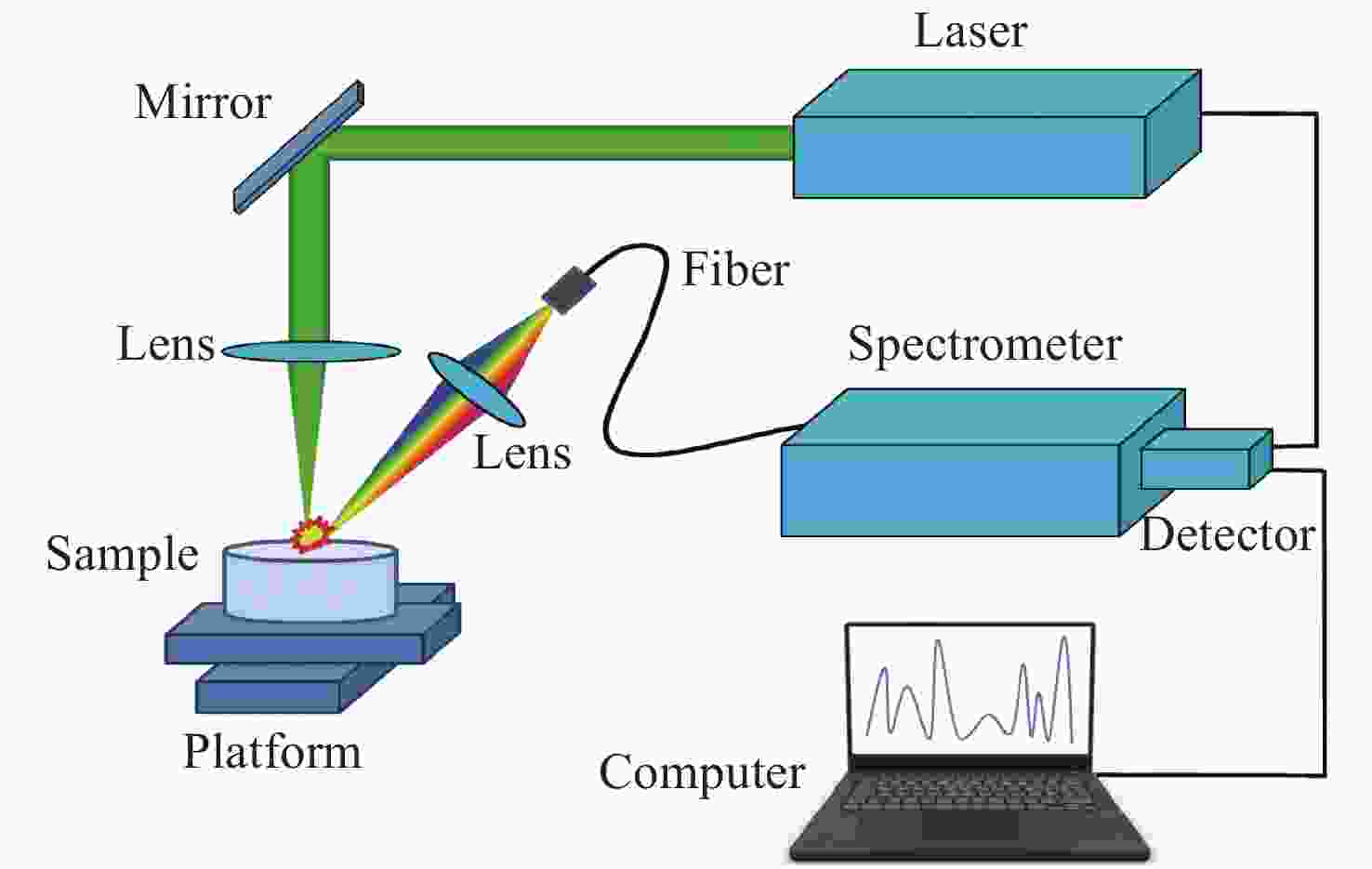
下载:
计量
- 文章访问数: 4254
- HTML全文浏览量: 1690
- PDF下载量: 411
- 被引次数: 1
