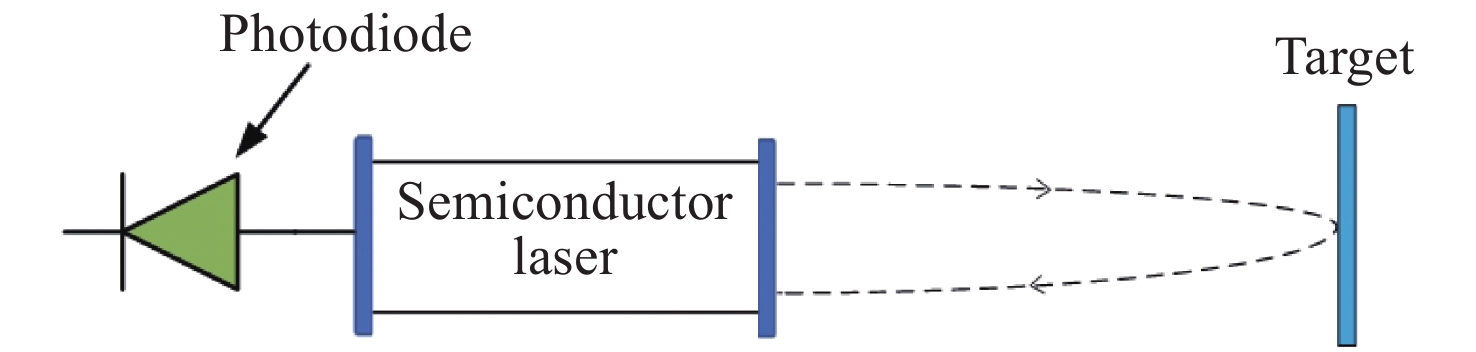
Research progress of the laser vibration measurement techniques for acoustic-to-seismic coupling landmine detection
doi: 10.37188/CO.2020-0134
-
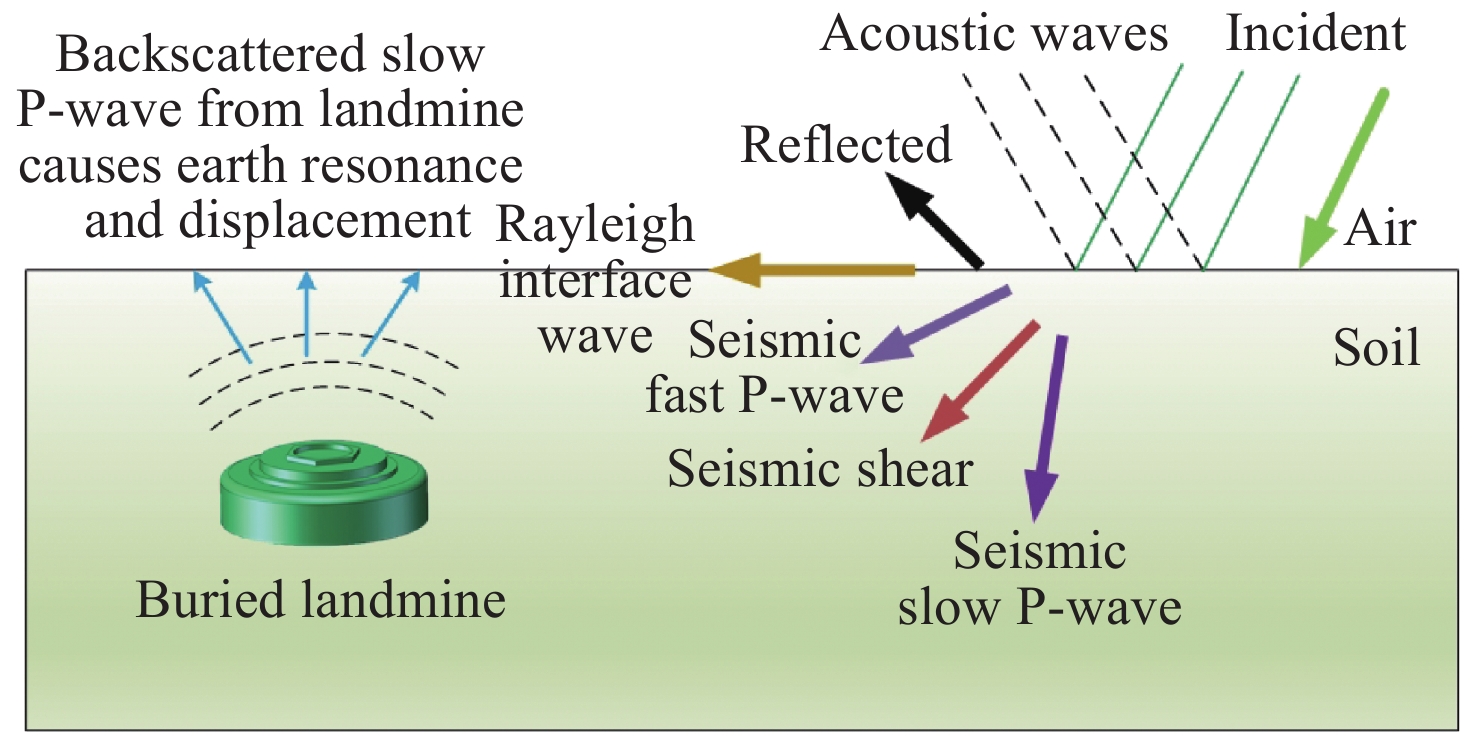
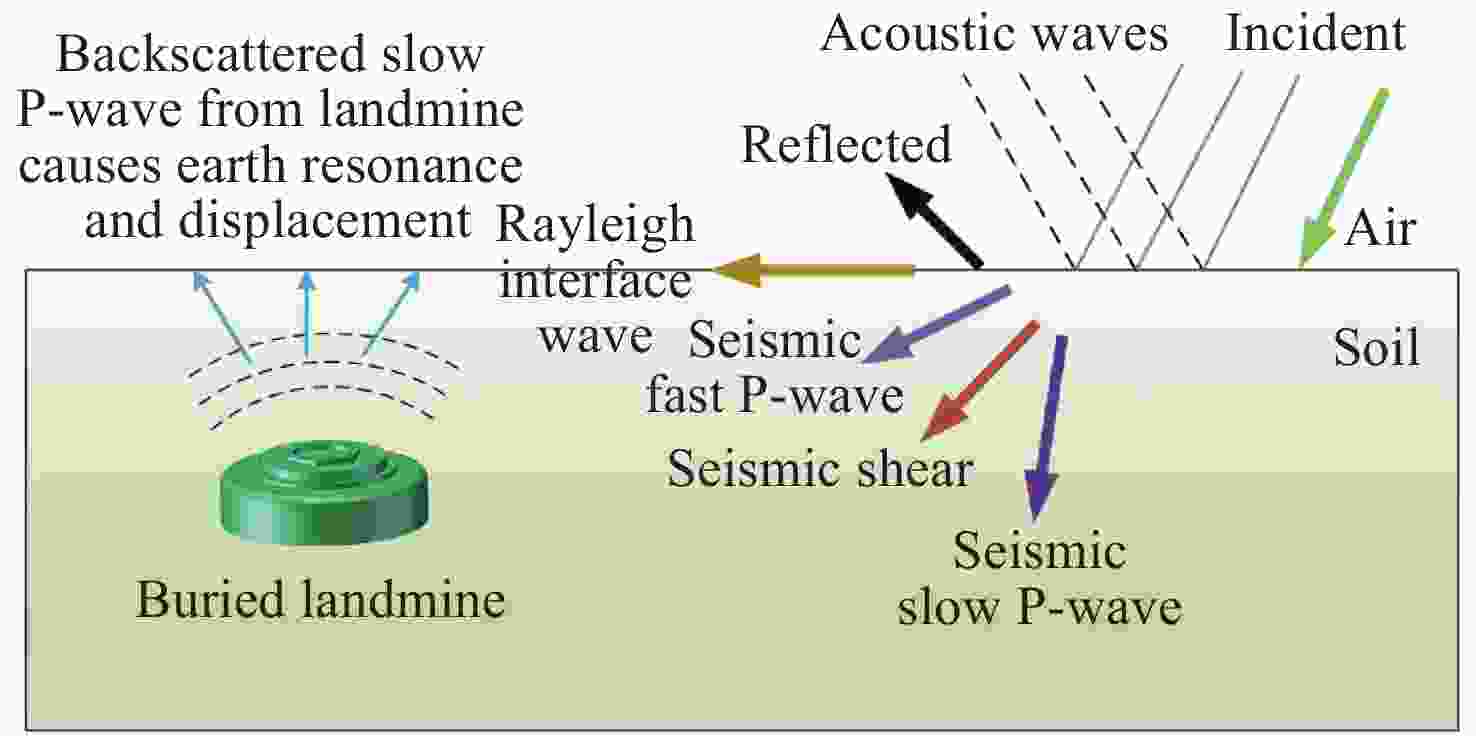
摘要: 基于地雷独特机械特性和声-地震耦合原理的声-地震耦合探雷技术,在埋设地雷的安全有效探测方面具有广阔的应用前景,但针对实用工程探雷系统的研究还需要做大量工作。其中,声波耦合的地表振动信号非常微弱复杂,如何对其进行精确快速测量是一个关键难题。本文在声-地震耦合探雷技术原理的基础上,对地表振动的非接触激光测量技术(包括激光多普勒干涉技术、电子散斑干涉技术和激光自混合干涉技术)进行综述分析,并分析了电子剪切散斑干涉技术用于声-地震耦合探雷的可行性。Abstract: Acoustic-to-seismic coupling landmine detection technology based on the unique mechanical characteristics of landmines and the acoustic-to-seismic coupling principle has broad application prospects in safe and effective detection of landmines. However, a significant amount of work must be done to study the practical landmine detection system. Among them, the acoustic coupled surface vibration signals are very weak and complicated, which has always been a challenging problem to detect such signals accurately and quickly. In this paper, the non-contact laser measurement techniques of surface vibrations based on the principle of the acoustic-to-seismic coupling landmine detection technology were reviewed, including laser Doppler interferometry, electronic speckle pattern interferometry and laser self-mixing interferometry, etc., and the application feasibility of electronic speckle-shearing pattern interferometry in acoustic-to-seismic coupling landmine detection was analyzed.
-
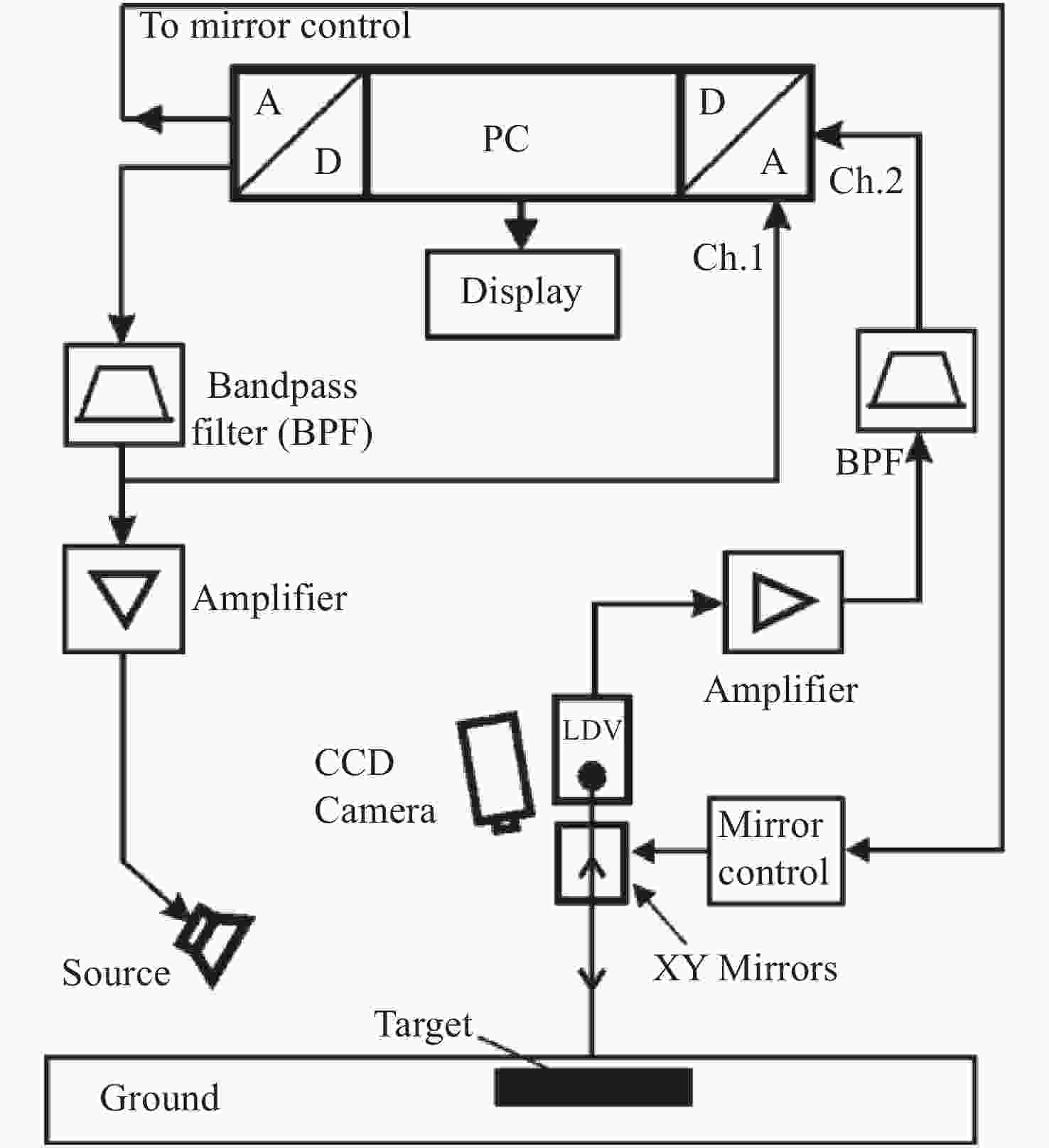
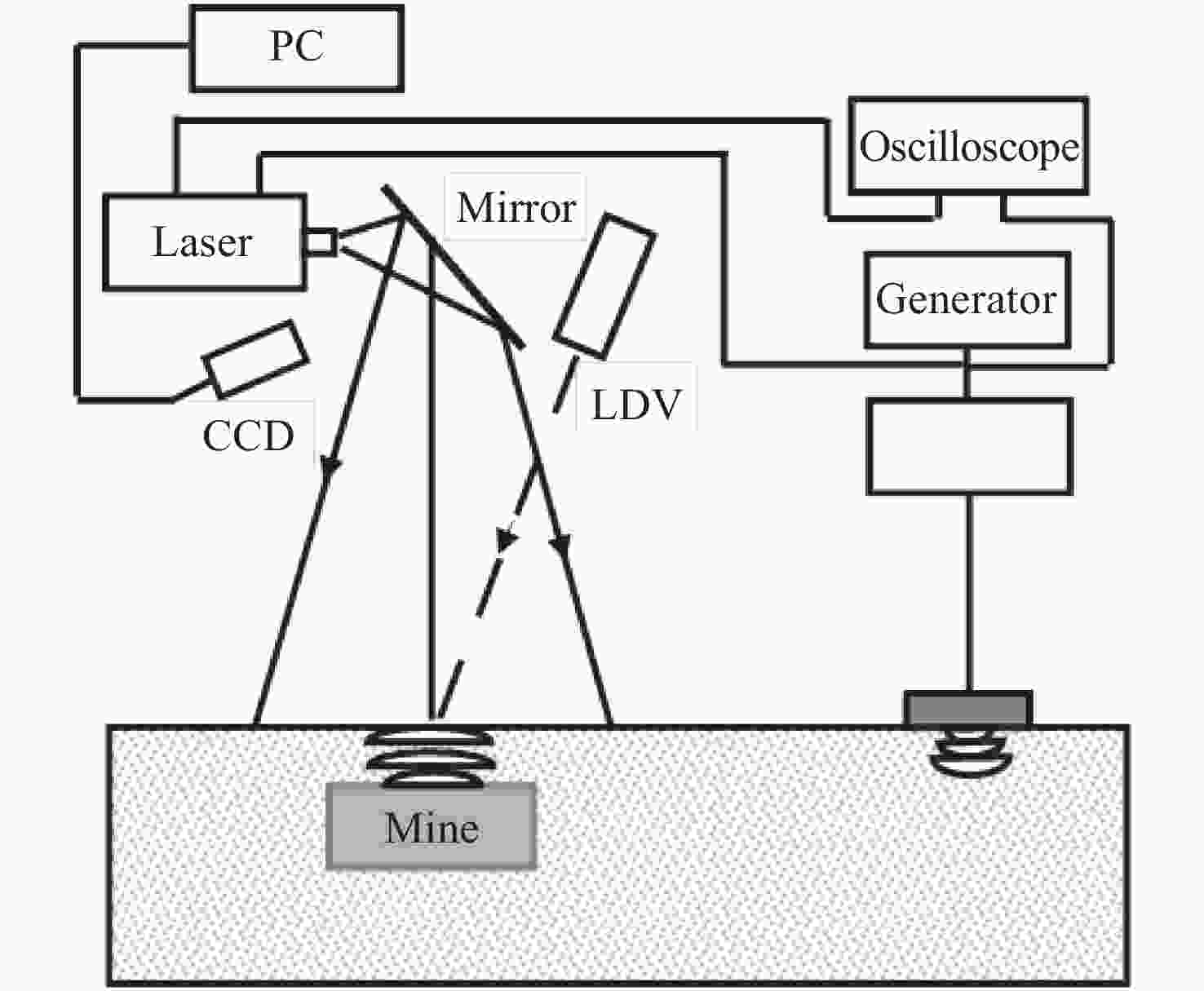
Figure 4. Typical set-up of the acoustic landmine detection system based on LDV[30]
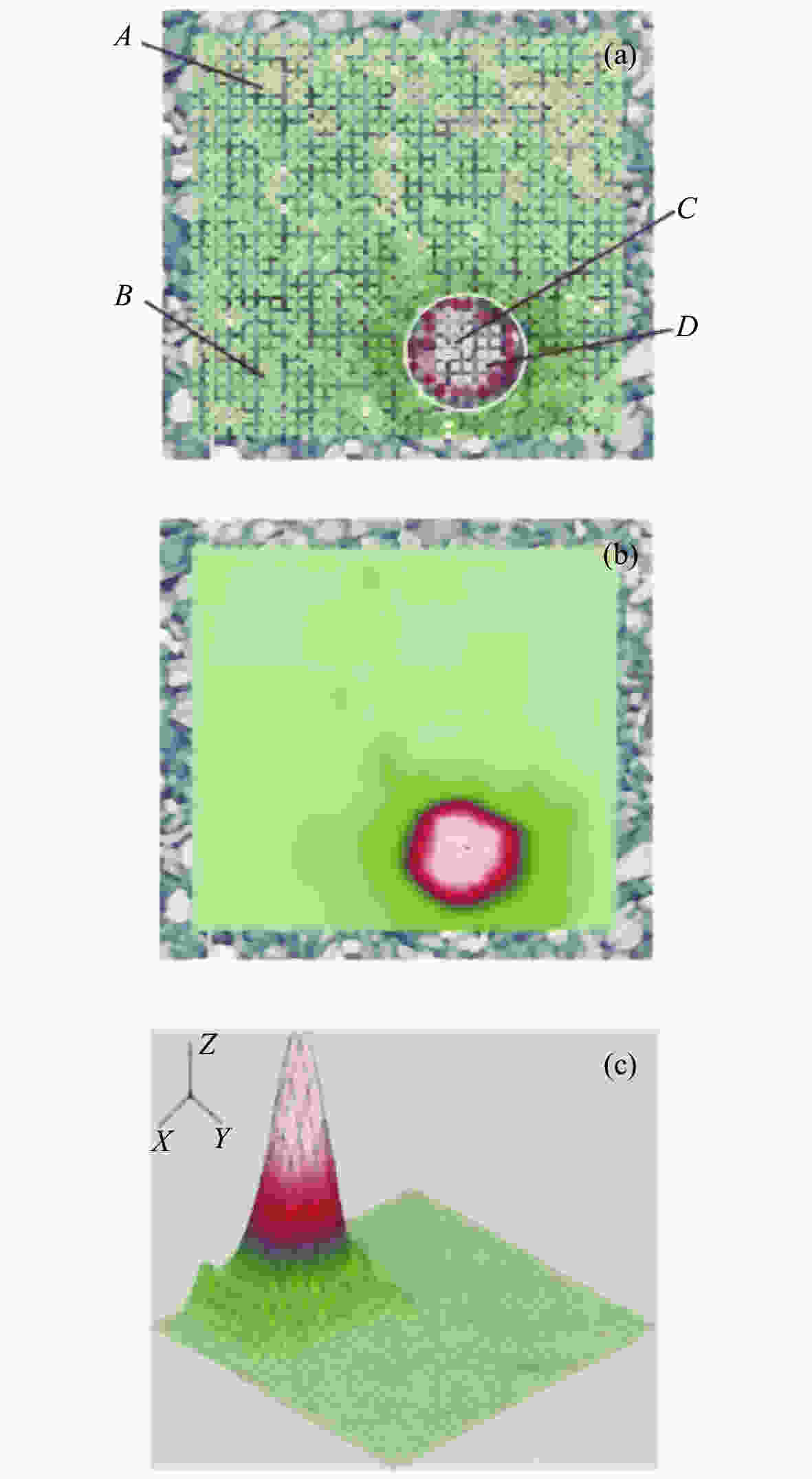
Figure 5. Experimental measurement results based on a single-beam LDV[30]. (a) A scanned patch of 1 m × 1 m. (b) 2-D color map. (c) 3-D color map.
Figure 7. Trace of a moving beam when scanning an area[32]
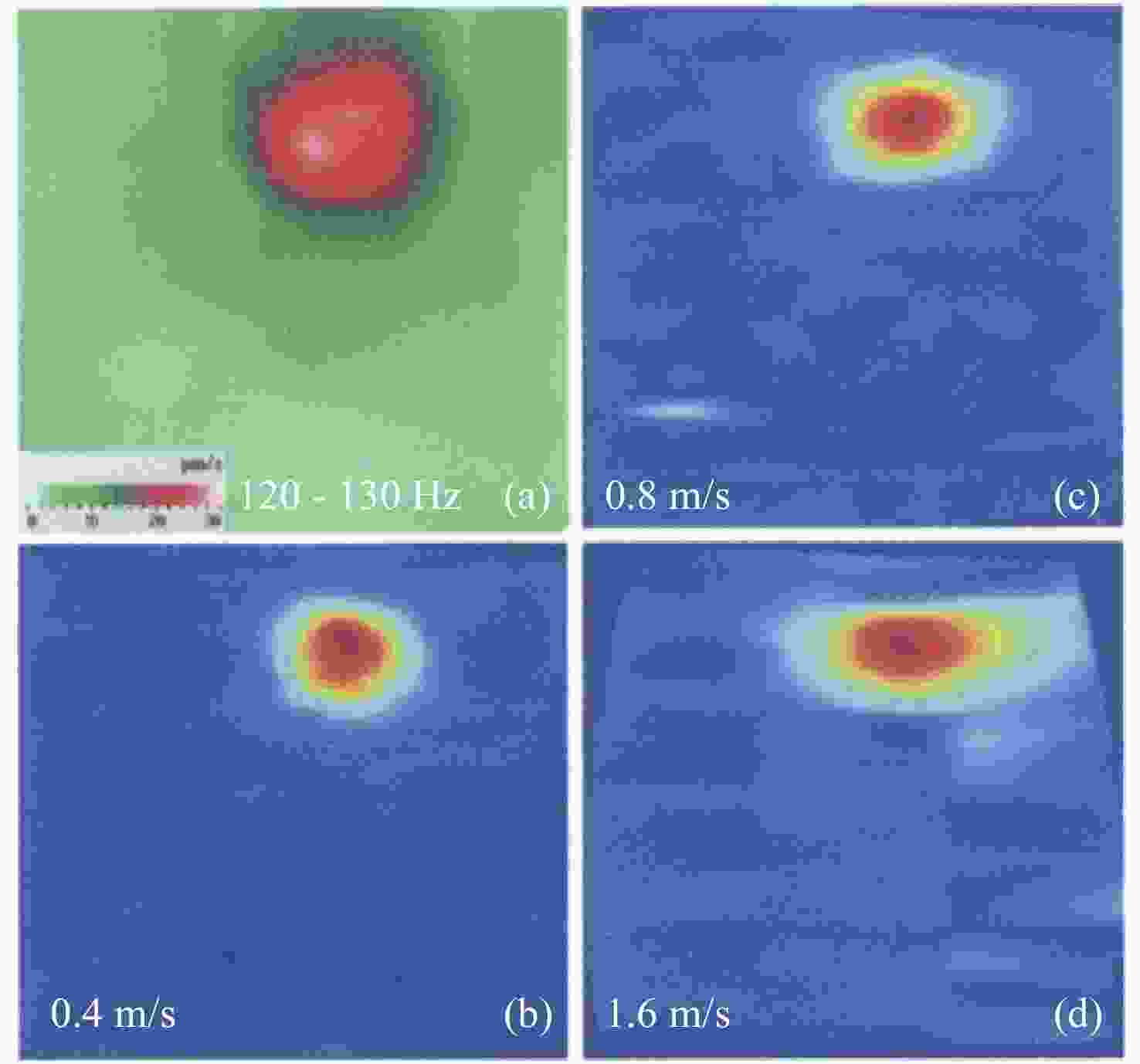
Figure 8. Scanning results of the single-beam LDV (a) and the moving beam LDVs[32] at 0.4 m/s (b), 0.8 m/s (c), and 1.6 m/s (d) moving speed
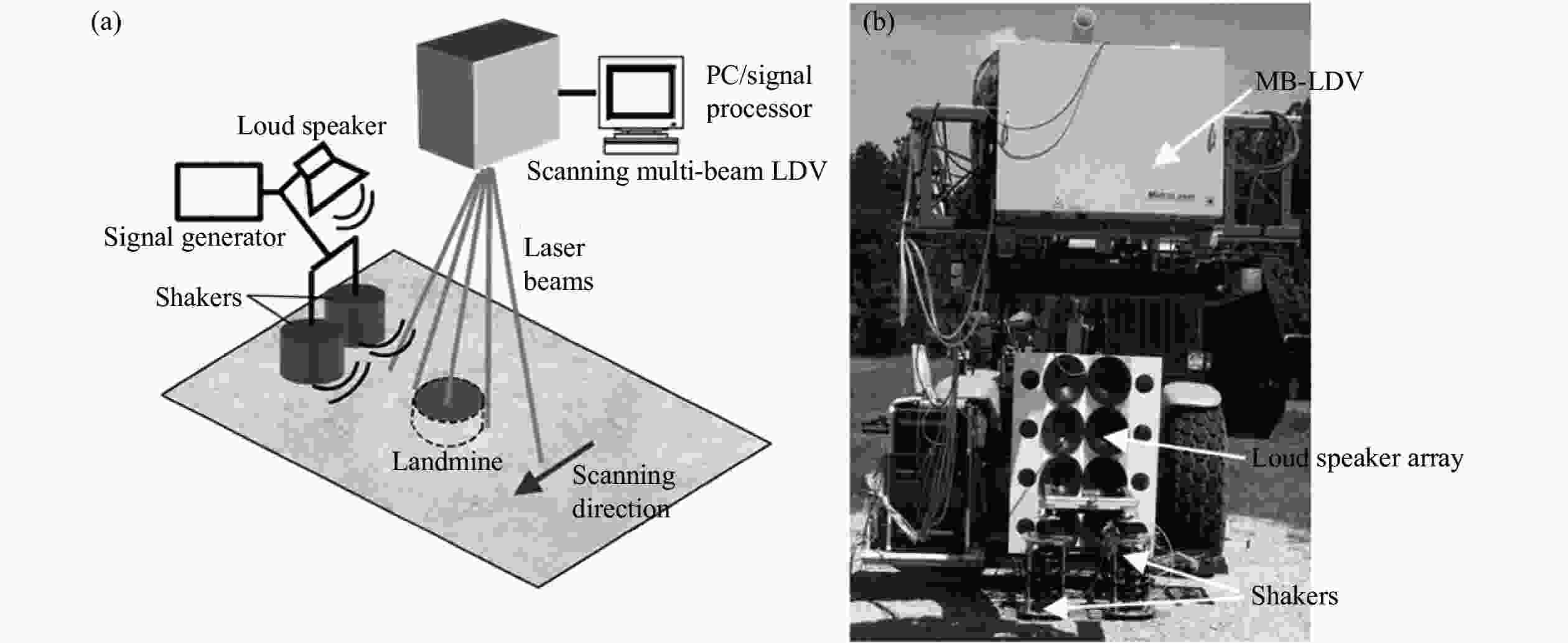
Figure 9. Multi-beam LDV[35]. (a) Schema of the experimental setup. (b) Multi-beam LDV mounted on a forklift.
Figure 10. Anti-tank landmine VS2.2 buried 15 cm deep at different scanning speeds[35]. (a) 10 cm/s. (b) 20 cm/s. (c) 50 cm/s. (d) 100 cm/s.
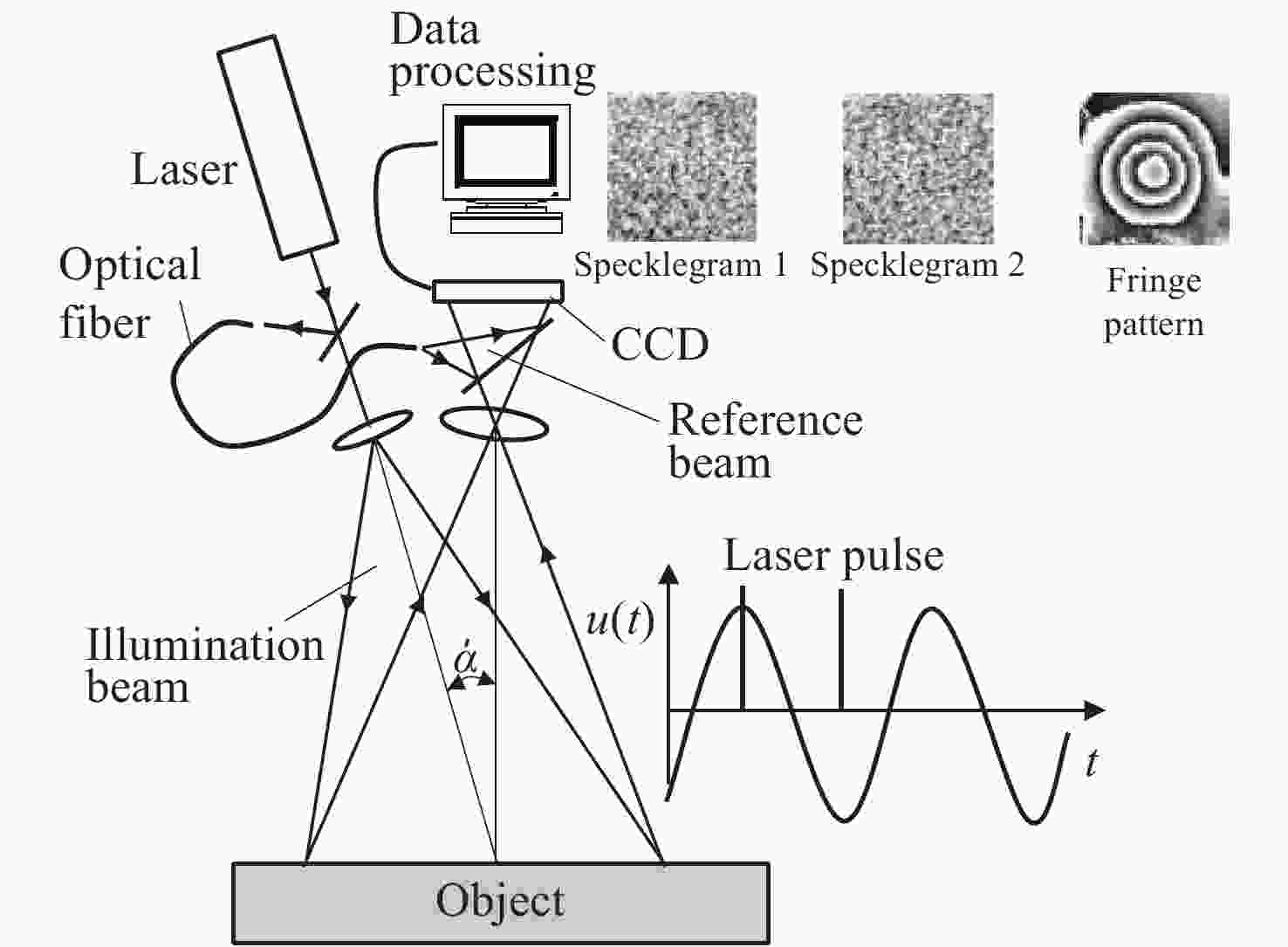
Figure 11. Schema of ESPI for measurement of out-of-plane vibrations[44]
Figure 12. Diagram of the experimental setup based on ESPI[44]
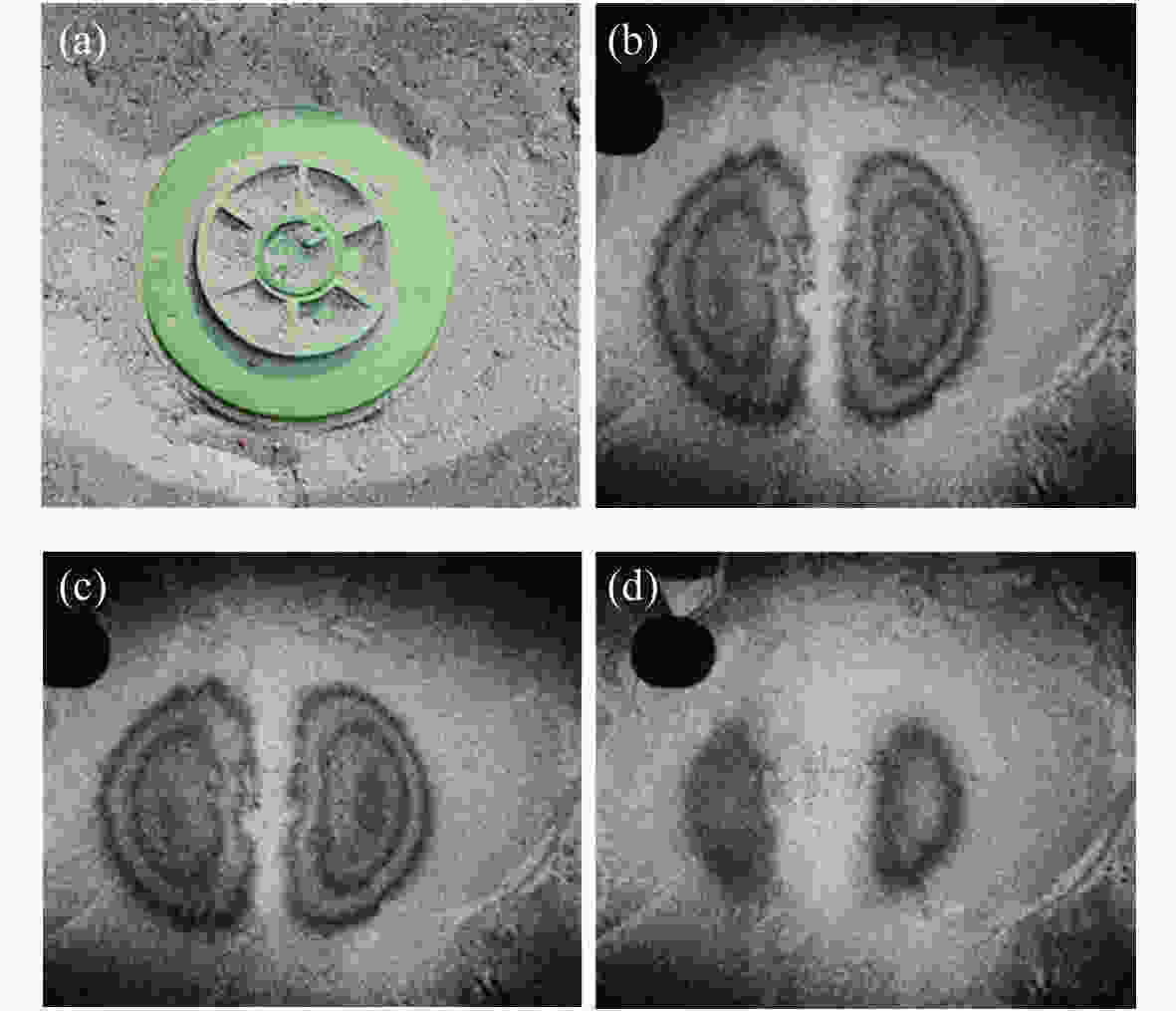
Figure 13. Spatial maps of buried landmines[44]. (a) Fringe pattern. (b) Grayscale image.
Figure 15. Position of buried objects[50]
Figure 16. Color maps of the test-bed[50]. (a) Two-dimensional (2D) color map. (b) Three-dimensional (3D) color map, derived from (a).
Table 1. Characteristics of the above laser vibrometers
Laser Vibrometers LDV ESPI Laser self-mixing vibrometer Displacement sensitivity 1 nm 0.1 μm 0.01 nm Types of detectable landmines metal and non-metal landmines metal and non-metal landmines metal and non-metal landmines Response speed need to collect multiple points of vibration signals for further processing real-time display of interference fringes need to collect multiple points of vibration signals for further processing Measurement area at one time single or multiple points 50 cm×50 cm single point Influence of environment susceptible to vegetation susceptible to the vibration of the surrounding environment susceptible to vegetation Structure complicated and large in size complicated and large in size simple optical path and small in size Table 2. Advantages and disadvantages of the above laser vibrometers
Laser Vibrometers Advantages Disadvantages LDV high sensitivity; high measurement accuracy; easy to
control large-area laser beam scanninglong scanning time; susceptible to vegetation;
the structure is very complicatedESPI Achieves fast scanning detection of a large area;
real-time display of interference fringeshigh vibration isolation requirements; the structure is complicated and the size is large Laser self-mixing vibrometer simple optical path; great stability; high sensitivity
and high measurement accuracylong scanning time; susceptible to vegetation -
[1] ZUCCHETTI M, KHODOR M, MAKKI I, et al.. Landmines. Crisis, legacy, international and local action[C]. Proceedings of the 2017 First International Conference on Landmine: Detection, Clearance and Legislations, LDCL, 2017. [2] WU ZH Q, ZHANG Y L, WANG CH, et al. 3D characteristic diagram of acoustically induced surface vibration with different landmines buried[J]. Transactions of Tianjin University, 2016, 22(4): 367-373. doi: 10.1007/s12209-016-2759-y [3] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168-178. doi: 10.1121/1.1908239 [4] BIOT M A. Theory of propagation of elastic waves in a fluid‐saturated porous solid. II. Higher frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 179-191. doi: 10.1121/1.1908241 [5] BIOT M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33(4): 1482-1498. doi: 10.1063/1.1728759 [6] LI H Y, WANG Y J, CHANG H W, et al. Acoustic impedance and its application in seismo-acoustic landmines detection models[J]. Journal of Coastal Research, 2020, 99(SI): 92-98. [7] SABATIER J M, KORMAN M S, XIANG N. Linear and nonlinear acoustic velocity profiles over buried land mines[J]. Proceedings of SPIE, 2002, 4742: 695-700. doi: 10.1117/12.479141 [8] DONSKOY D. Nonlinear seismo-acoustic landmine detection[J]. The Journal of the Acoustical Society of America, 2008, 123(5): 3042-3043. [9] YU S H, GANDHE A, WITTEN T R, et al. Physically based method for automatic mine detection using acoustic data: a transmission zero approach[J]. Proceedings of SPIE, 2002, 4742: 701-708. doi: 10.1117/12.479143 [10] ZAGRAI A, DONSKOY D, EKIMOV A. Structural vibrations of buried land mines[J]. The Journal of the Acoustical Society of America, 2005, 118(6): 3619-3628. doi: 10.1121/1.2108754 [11] WANG CH, LIU ZH G, LI X F, et al. Technology for acoustic landmine detection based on relative acoustic-to-seismic coupling ratio[J]. Journal of Tianjin University, 2008, 41(6): 745-750. (in Chinese) [12] WANG CH, YU Y J, LI X F, et al. Analysis of earth-mine resonance model[J]. Acta Physica Sinica, 2010, 59(9): 6319-6325. (in Chinese) doi: 10.7498/aps.59.6319 [13] WANG CH, YU Y J, LI X F. An acoustic-to-seismic coupling based landmines detection system in lab-scale experimental environment[J]. Journal of Tianjin University, 2011, 44(1): 79-84. (in Chinese) [14] WANG CH, ZHOU Y Q, SHEN G W, et al. Numerical analysis of the resonance mechanism of the lumped parameter system model for acoustic mine detection[J]. Chinese Physics B, 2013, 22(12): 124601. doi: 10.1088/1674-1056/22/12/124601 [15] DING W, WU W W, WANG CH, et al. Propagation characteristics of seismic waves in shallow soil with the unsaturated three-phase poroelastic model[J]. Acta Physica Sinica, 2014, 63(22): 224301. (in Chinese) doi: 10.7498/aps.63.224301 [16] SONG Z Y, ZHANG Y L, WANG CH, et al. Experimental measurement of acoustically induced surface vibration with different soil conditions[J]. Advances in Manufacturing, 2016, 4(3): 278-285. doi: 10.1007/s40436-016-0153-6 [17] WU ZH Q, MA H, WANG CH, et al. Numerical analysis of a sensorized prodder for landmine detection by using its vibrational characteristics[J]. Applied Sciences, 2019, 9(4): 744. doi: 10.3390/app9040744 [18] ZHANG Q K, ZHONG SH C, LIN J W, et al. High-performance optical coherence velocimeter: theory and applications[J]. Optics Express, 2019, 27(2): 965-979. doi: 10.1364/OE.27.000965 [19] LIBBEY B, PEREA J. Doppler-vibrometer landmine-detection system operated from a moving vehicle[J]. Proceedings of SPIE, 2019, 11012: 110120W. [20] MARTIN J S, LARSON G D, SCOTT JR W R. An investigation of surface-contacting sensors for the seismic detection of buried landmines[J]. The Journal of the Acoustical Society of America, 2006, 120(5): 2676-2685. doi: 10.1121/1.2345911 [21] BULLETTI A, BORGIOLI G, CALZOLAI M, et al. Acoustoseismic method for buried-object detection by means of surface-acceleration measurements and audio facilities[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(8): 3134-3138. doi: 10.1109/TGRS.2010.2044888 [22] LARSON G D, MARTIN J S, SCOTT JR W R, et al. Detection of buried landmines using seismic waves and microphones[J]. Proceedings of SPIE, 2005, 5794: 655-664. doi: 10.1117/12.603861 [23] LARSON G D, MARTIN J S, SCOTT JR W R. Investigation of microphones as near-ground sensors for seismic detection of buried landmines[J]. The Journal of the Acoustical Society of America, 2007, 122(1): 253-258. doi: 10.1121/1.2743155 [24] SCOTT W R, MARTIN J S, LARISON G D. Experimental model for a seismic landmine detection system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(6): 1155-1164. doi: 10.1109/36.927432 [25] LEE S H, SCOTT JR W R. A focused radar antenna for use in seismic mine detection systems[J]. Radio Science, 2004, 39(4): RS4S01. [26] PETCULESCU A G, SABATIER J M. Doppler ultrasound techniques for landmine detection[J]. Proceedings of SPIE, 2004, 5414: 30-34. [27] RAJESH K R, MURALI R, MOHANACHANDRAN R. Advanced acousto-ultrasonic landmine detector for humanitarian mine sweeping[C]. Proceedings of 2011 IEEE Global Humanitarian Technology Conference, IEEE, 2011. [28] BÉRES M, PARIPÁS B. Measurements of vibration by laser doppler method in the course of drilling[C]. Proceedings of the 2nd ed Vehicle and Automotive Engineering, Springer, 2018. [29] LV T, HAN X Y, WU SH S, et al. The effect of speckles noise on the laser Doppler vibrometry for remote speech detection[J]. Optics Communications, 2019, 440: 117-125. doi: 10.1016/j.optcom.2019.02.014 [30] XIANG N, SABATIER J M. An experimental study on antipersonnel landmine detection using acoustic-to-seismic coupling[J]. The Journal of the Acoustical Society of America, 2003, 113(3): 1333-1341. doi: 10.1121/1.1543554 [31] SABATIER J M, XIANG N. An investigation of acoustic-to-seismic coupling to detect buried antitank landmines[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(6): 1146-1154. doi: 10.1109/36.927429 [32] XIANG N, SABATIER J M. Acoustic-to-seismic landmine detection using a continuously scanning laser Doppler vibrometer[J]. Proceedings of SPIE, 2003, 5089: 591-595. doi: 10.1117/12.487535 [33] LAL A K, ZHANG H SH, ARANCHUK V, et al. Multiple-beam LDV system for buried landmine detection[J]. Proceedings of SPIE, 2003, 5089: 579-590. doi: 10.1117/12.487154 [34] ARANCHUK V, LAL A K, ZHANG H SH, et al. Acoustic sensor for landmine detection using a continuously scanning multibeam LDV[J]. Proceedings of SPIE, 2004, 5415: 61-69. doi: 10.1117/12.541562 [35] ARANCHUK V, SABATIER J M, LAL A K, et al. Multi-beam laser Doppler vibrometry for acoustic landmine detection using airborne and mechanically coupled vibration[J]. Proceedings of SPIE, 2005, 5794: 624-631. doi: 10.1117/12.603512 [36] LAL A, ARANCHUK S, DOUSHKINA V, et al. Advanced LDV instruments for buried landmine detection[J]. Proceedings of SPIE, 2006, 6217: 621715. doi: 10.1117/12.668927 [37] ARANCHUK V, SABATIER J M, BURGETT R D, et al. Fast acoustic landmine detection using multiple beam laser Doppler vibrometry[J]. The Journal of the Acoustical Society of America, 2008, 123(5): 3043. [38] BURGETT R, SABATIER J M, ARANCHUK V. Carrier tracking and tunable passband filters for TDM-LDV mine detection[J]. Proceedings of SPIE, 2010, 7664: 76641X. doi: 10.1117/12.853105 [39] BURGETT R, ARANCHUK V, ARANCHUK I. Experimental investigation of buried landmine detection using time division multiplexing of multibeam laser Doppler vibrometer channels[J]. Proceedings of SPIE, 2012, 8357: 83570H. [40] PADGHAN P P, PANDE V D, INGLE P U, et al. Measurement of nanoscale surface roughness using electronic speckle pattern interferometer[J]. AIP Conference Proceedings, 2019, 2100(1): 020062. [41] SCHWARZ A, SHEMER A, OZANA N, et al.. Laser vibrometer interferometry for speckle patterns tracking systems[C]. Proceedings of 2017 Conference on Lasers and Electro-Optics, IEEE, 2017. [42] RITTER K, UNGLAUB J, THIELE K. Untersuchung der mikroschädigung in baustahl mit ESPI[J]. Bautechnik, 2020, 97(3): 180-187. doi: 10.1002/bate.201800006 [43] PAGLIARULO V, FERRARO P. New applications of electronic speckle pattern interferometry in novel materials and structures[J]. Proceedings of SPIE, 2019, 11059: 1105910. [44] SABATIER J M, ARANCHUK V, ALBERTS II W C. Rapid high-spatial-resolution imaging of buried landmines using ESPI[J]. Proceedings of SPIE, 2004, 5415: 14-20. doi: 10.1117/12.540517 [45] WANG X F, SONG X M, TAN R X, et al. Micro-vibration measurement based on current modulation and secondary feedback self-mixing interference technology[J]. Optical Review, 2019, 26(2): 241-246. doi: 10.1007/s10043-018-00489-w [46] ZHANG Z H, SUN L Q, LI CH W, et al. Laser self-mixing interferometry for micro-vibration measurement based on inverse Hilbert transform[J]. Optical Review, 2020, 27(1): 90-97. doi: 10.1007/s10043-019-00568-6 [47] HE G, GORDENKER R, WOO J K, et al.. Laser self-mixing interferometry for precision displacement measurement in resonant gyroscopes[C]. Proceedings of 2019 IEEE International Symposium on Inertial Sensors and Systems, IEEE, 2019. [48] ZHANG Z H, JIANG CH L, SHEN L Q, el al. Vibration measurement based on the local maximum detection algorithm for laser self-mixing interferometry[J]. IEEE Access, 2020, 8: 63462-63469. doi: 10.1109/ACCESS.2020.2984282 [49] WANG CH, DUAN N Y, WU ZH Q, et al. Method for detecting multi-modal vibration characteristics of landmines[J]. Instrumentation, 2018, 5(4): 39-45. [50] WU ZH Q, DUAN N Y, WANG CH, et al. Experimental study on acoustic-to-seismic landmine detection based on laser self-mixing interferometer[J]. Proceedings of SPIE, 2018, 108271: 108271W. [51] JING CH, LIU ZH L, GUO CH L, el al.. Vibration measurement with electrical speckle shearing pattern interferometry[C]. Proceedings of 2016 International Conference on Identification, Information and Knowledge in the Internet of Things, IEEE, 2016. [52] MA Y H, JIANG H Y, DAI M L, et al. Cantilevered plate vibration analysis based on electronic speckle pattern interferometry and digital shearing speckle pattern interferometry[J]. Acta Optica Sinica, 2019, 39(4): 0403001. (in Chinese) doi: 10.3788/AOS201939.0403001 [53] WANG Y H, LYU Y B, GAO X Y, et al. Research progress in shearography and its applications[J]. Chinese Optics, 2017, 10(3): 300-309. (in Chinese) doi: 10.3788/co.20171003.0300 [54] ASEMANI H, SOLTANI N. Application of electronic speckle pattern shearing interferometry with high-speed camera in vibration analysis of piezoelectric transducer[J]. International Journal of Applied Mechanics, 2019, 11(6): 1950056. doi: 10.1142/S175882511950056X -





 下载:
下载: