Polarization lidar gain ratio calibration method: a comparison
doi: 10.37188/CO.2020-0136
-
摘要: 增益比定标误差是影响偏振激光雷达退偏比精度的主要因素之一，观测前必须进行准确的增益比定标。本文分析了现存多种增益比定标方法的基本原理，并通过实验对比了+45°法、±45°法、∆45°法、旋转拟合法与退偏器法等增益比定标方法的定标准确性与优缺点。实验结果表明：∆45°法、±45°法与旋转拟合法在对准偏失角较小的情况下定标相对准确，但±45°法与旋转拟合法操作较为繁琐。+45°法在无对准偏失角的情况下定标误差仍较大。退偏器法操作最简便，但会受到非理想退偏器的制约。通过理论分析与实验对比，本文给出了增益比定标方法的最佳选择，即在一般情况下采用∆45°法定标，在有高精度退偏器的情况下采用退偏器法定标。Abstract: Gain ratio calibration error is one of the most significant factors affecting the accuracy of a polarization lidar depolarization ratio. This paper analyzes the basic principles of various existing gain ratio calibration methods and compares the advantages and disadvantages of the +45° method, ±45° method, ∆45° method, rotation fitting method and pseudo-depolarizer method in practice though experiments. Results show that: the ∆45° method, ±45° method and rotation fitting method are relatively accurate when the misalignment angle is small, but the operation of the ±45° method and rotation fitting method are more complicated. The +45° method still has a large calibration error without a misalignment angle. The pseudo-depolarizer method is the easiest to operate, but it is restricted by a non-ideal pseudo-depolarizer. Through comparison of theory and experiment, this paper provides a suggestion for the best choice of gain ratio calibration method. It is recommended that the ±45° method be used for calibration with a half-wave plate, and the pseudo-depolarizer method be used for calibration with a high-precision depolarizer.
-
Key words:
- polarization lidar /
- gain ratio /
- calibration /
- depolarization ratio
-
图 1 偏振激光雷达系统基本原理与结构图
Figure 1. Basic principle and structure diagram of polarization lidar system
图 2 +45°法原理图。(a)半波片旋转之前；(b)半波片旋转+45°之后
Figure 2. Schematic diagram of +45° method. (a) Before HWP rotation. (b) After HWP rotation by +45°
图 3 ±45°法原理图。(a)半波片旋转之前；(b)半波片旋转+22.5°之后；(c)半波片旋转−22.5°之后
Figure 3. Schematic diagram of ±45° method. (a) Before HWP rotation. (b) After HWP rotation by +22.5°. (c) After HWP rotation by −22.5°
图 4 ∆45°法原理图。(a)半波片旋转之前；(b)半波片旋转45°之后
Figure 4. Schematic diagram of ∆45° method. (a) Before HWP rotation. (b) After HWP rotation by 45°
图 7 5种定标方法相对误差随对准偏失角的变化曲线
Figure 7. Relative errors changing with the misalignment angle for the five calibration methods
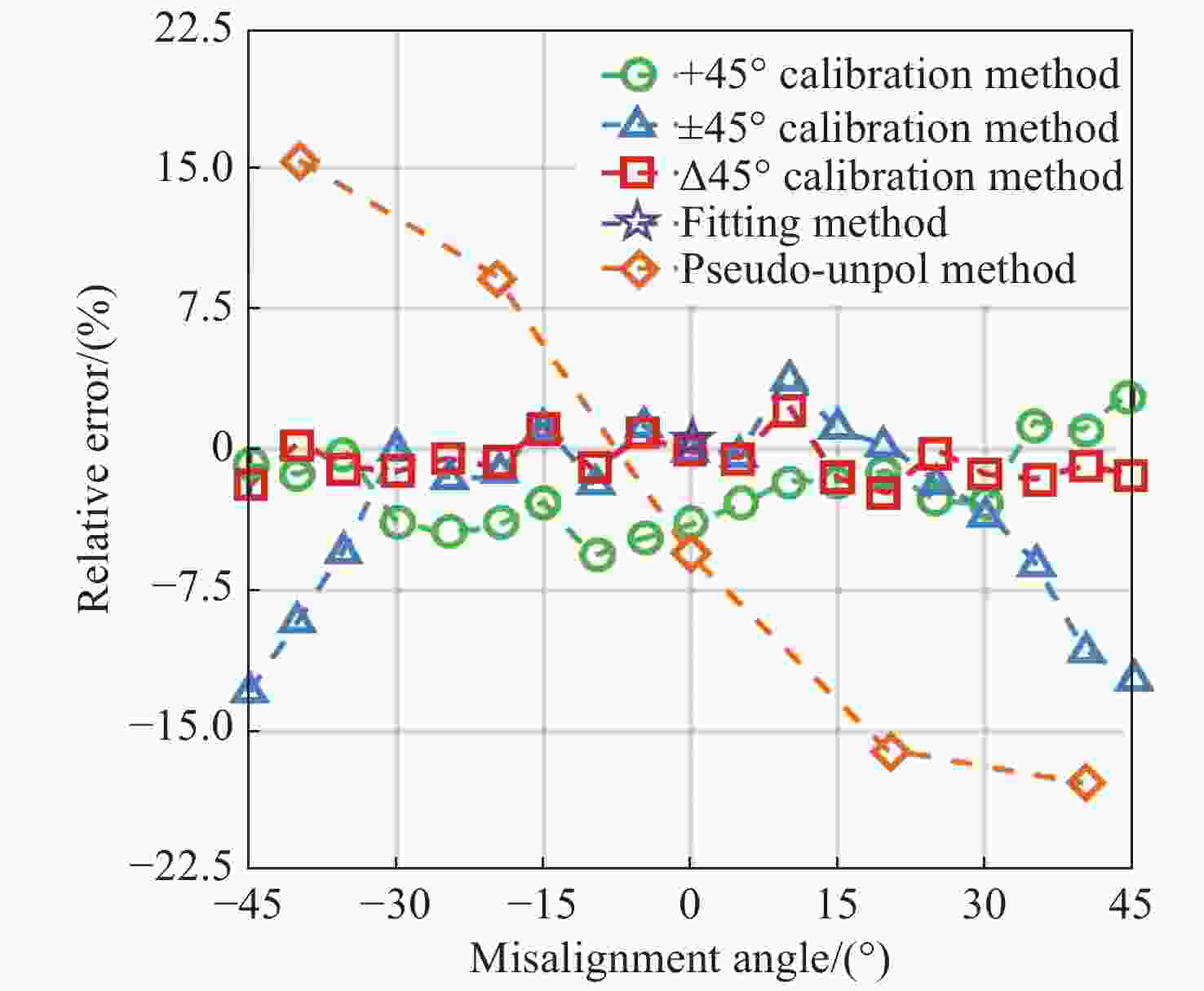
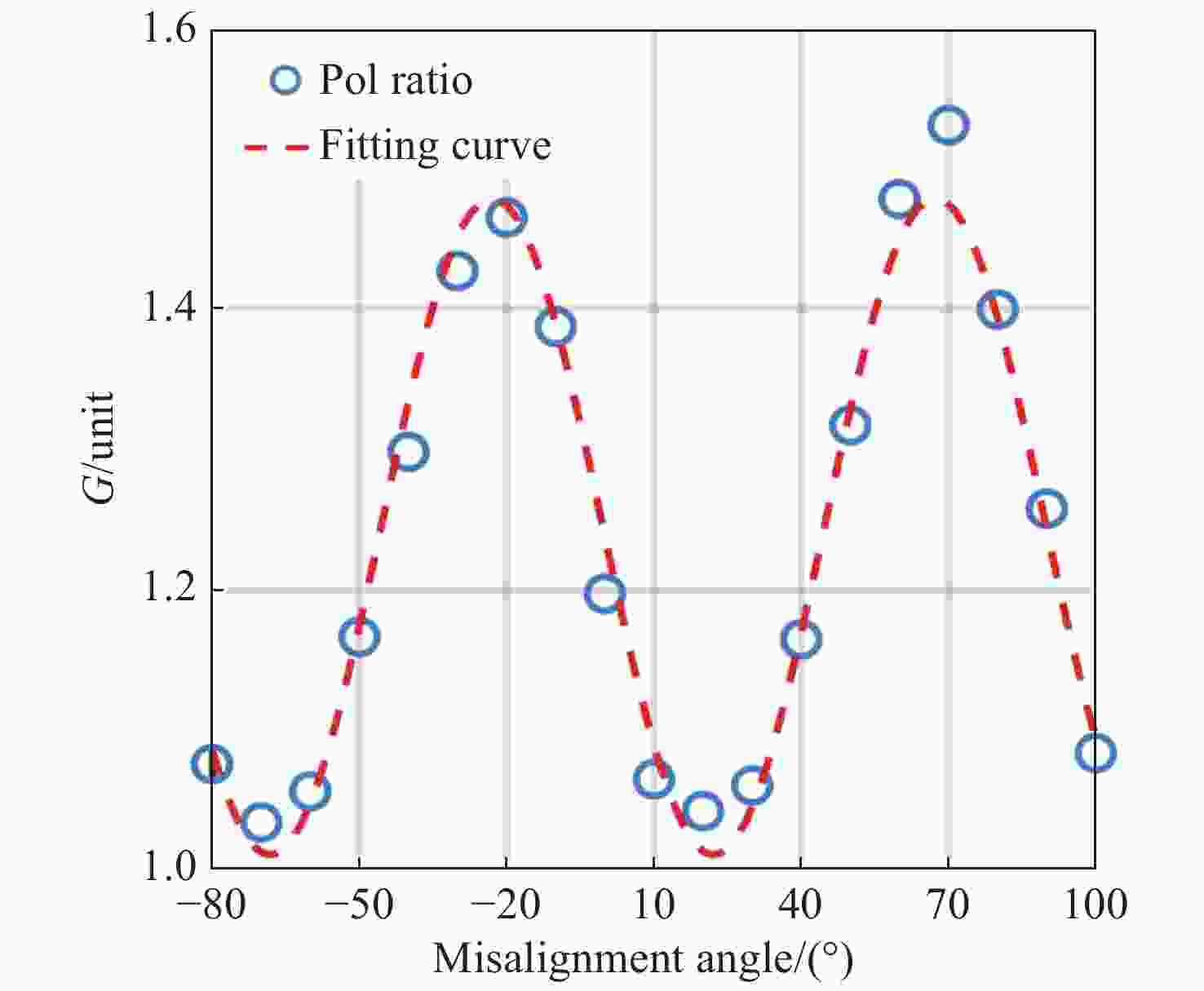
图 8 实际测量退偏比随对准偏失角的变化曲线图。其中蓝色圆圈代表在不同
$\theta $ 情况下测量的${\delta ^{\rm{*}}}\left( \theta \right)$ ，红色虚线代表拟合曲线，绿色虚线代表${\theta _{{\rm{init}}}}$ Figure 8. Curve of the actually measured depolarization ratio changing with the misalignment angle, where the blue circle represents the
${\delta ^{\rm{*}}}\left( \theta \right)$ values measured at different$\theta $ angles, and the red and green dotted lines represent the fitting curve and${\theta _{{\rm{init}}}}$ , respectively
图 9 退偏器法增益比定标结果。蓝色圆圈代表半波片在不同角度下测量的增益比，红色虚线代表余弦函数多项式拟合曲线
Figure 9. Gain ratio calibration result of pseudo-depolarizer method. The blue circles represent the gain ratios measured at different misalignment angles, and the red dotted line represents the cosine polynomial fitting curve
图 5 旋转拟合法原理图。(a)半波片旋转之前；(b)半波片旋转
${\theta _{{\rm{h}},j}}$ 角之后Figure 5. Schematic diagram of rotation fitting method. (a) Before HWP rotation. (b) After HWP rotation by
${\theta _{{\rm{h}},j}}$ 表 1 Main parameters for polarization lidar system
Table 1. Main parameters for polarization lidar system
Main parameters Value Laser center wavelength 532 nm Laser energy 5 mJ Repetition frequency 10 Hz Pulse width 8 ns Diameter of telescope primary mirror 210 mm Field of view of telescope 1 mrad Focal length of telescope 2000 mm Filter bandwidth 3 nm 
下载: 导出CSV
表 2 Calibration results of five methods at
${\theta _{\rm{h}}}{\rm{ = }}{0^\circ }$ Table 2. Calibration results of five methods at
${\theta _{\rm{h}}}{\rm{ = }}{0^\circ }$ Calibration method +45° ±45° △45° Rotation fitting Pseudo-depolarizer Calibration result 1.2185±0.1379 1.2679±0.1518 1.2676±0.1524 1.2716±0.0250 1.1977±0.1483
下载: 导出CSV
-
[1] SCHOTLAND R M, SASSEN K, STONE R. Observations by lidar of linear depolarization ratios for hydrometeors[J]. Journal of Applied Meteorology, 1971, 10(5): 1011-1017. doi: 10.1175/1520-0450(1971)010<1011:OBLOLD>2.0.CO;2 [2] SASSEN K. Polarization in lidar: a review[J]. Proceedings of SPIE, 2003, 5158: 151-160. doi: 10.1117/12.507006 [3] LIU D, YANG Y Y, ZHANG Y P, et al. Pattern recognition model for aerosol classification with atmospheric backscatter lidars: principles and simulations[J]. Journal of Applied Remote Sensing, 2015, 9(1): 096006. doi: 10.1117/1.JRS.9.096006 [4] CHENG ZH T, LIU D, LUO J, et al. Tolerance evaluation for anti-reflection coatings in field-widened michelson spectroscopic filter[J]. Chinese Journal of Lasers, 2015, 42(8): 0813002. (in Chinese) doi: 10.3788/CJL201542.0813002 [5] QIU J W, XIA H Y, SHANGGUAN M J, et al. Micro-pulse polarization lidar at 1.5 μm using a single superconducting nanowire single-photon detector[J]. Optics Letters, 2017, 42(21): 4454-4457. doi: 10.1364/OL.42.004454 [6] GOBBI G P, BARNABA F, GIORGI R, et al. Altitude-resolved properties of a Saharan dust event over the Mediterranean[J]. Atmospheric Environment, 2000, 34(29-30): 5119-5127. doi: 10.1016/S1352-2310(00)00194-1 [7] DIONISI D, BARNABA F, COSTABILE F, et al. Retrieval of aerosol parameters from continuous h24 lidar-ceilometer measurements[J]. EPJ Web of Conferences, 2016, 119(4): 23004. [8] BINIETOGLOU I, AMODEO A, D’AMICO G, et al. Examination of possible synergy between lidar and ceilometer for the monitoring of atmospheric aerosols[J]. Proceedings of SPIE, 2011, 8182: 818209. doi: 10.1117/12.897530 [9] CAIRO F, DI DONFRANCESCO G, ADRIANI A, et al. Comparison of various linear depolarization parameters measured by lidar[J]. Applied Optics, 1999, 38(21): 4425-4432. doi: 10.1364/AO.38.004425 [10] LUO J, LIU D, XU P T, et al. High-precision polarizing beam splitting system based on polarizing beam splitter[J]. Chinese Journal of Lasers, 2016, 43(12): 1210001. (in Chinese) doi: 10.3788/CJL201643.1210001 [11] BEHRENDT A, NAKAMURA T. Calculation of the calibration constant of polarization lidar and its dependency on atmospheric temperature[J]. Optics Express, 2002, 10(16): 805-817. doi: 10.1364/OE.10.000805 [12] YOUNG A T. Rayleigh scattering[J]. Physics Today, 1982, 35(1): 42-48. doi: 10.1063/1.2890003 [13] SHE C Y. Spectral structure of laser light scattering revisited: bandwidths of nonresonant scattering lidars[J]. Applied Optics, 2001, 40(27): 4875-4884. doi: 10.1364/AO.40.004875 [14] LUO J, LIU D, HUANG Z H, et al. Polarization properties of receiving telescopes in atmospheric remote sensing polarization lidars[J]. Applied Optics, 2017, 56(24): 6837-6845. doi: 10.1364/AO.56.006837 [15] FREUDENTHALER V, ESSELBORN M, WIEGNER M, et al. Depolarization ratio profiling at several wavelengths in pure Saharan dust during SAMUM 2006[J]. Tellus B:Chemical and Physical Meteorology, 2009, 61(1): 165-179. doi: 10.1111/j.1600-0889.2008.00396.x [16] SASSEN K, BENSON S. A midlatitude cirrus cloud climatology from the facility for atmospheric remote sensing. Part II: microphysical properties derived from lidar depolarization[J]. Journal of the Atmospheric Sciences, 2001, 58(15): 2103-2112. [17] LUO J, LIU D, BI L, et al. Rotating a half-wave plate by 45°: an ideal calibration method for the gain ratio in polarization lidars[J]. Optics Communications, 2018, 407: 361-366. doi: 10.1016/j.optcom.2017.09.065 [18] ALVAREZ J M, VAUGHAN M A, HOSTETLER C A, et al. Calibration technique for polarization-sensitive lidars[J]. Journal of Atmospheric and Oceanic Technology, 2006, 23(5): 683-699. doi: 10.1175/JTECH1872.1 [19] MATTIS I, TESCHE M, GREIN M, et al. Systematic error of lidar profiles caused by a polarization-dependent receiver transmission: quantification and error correction scheme[J]. Applied Optics, 2009, 48(14): 2742-2751. doi: 10.1364/AO.48.002742 [20] HUNT W H, WINKER D M, VAUGHAN M A, et al. CALIPSO lidar description and performance assessment[J]. Journal of Atmospheric and Oceanic Technology, 2008, 26(7): 1214-1228. [21] QU Y. Technical status and development tendency of atmosphere optical remote and monitoring[J]. Chinese Optics, 2013, 6(6): 834-840. (in Chinese) [22] YANG Z J, CHEN F, LI CH, et al. Transient effect of dead time of photon-counting in micro-pulse lidar[J]. Optics and Precision Engineering, 2015, 23(2): 408-414. (in Chinese) doi: 10.3788/OPE.20152302.0408 [23] DUAN L L, LIU D, ZHANG Y P, et al. Lidar data gluing technology based on hybrid intelligent algorithm[J]. Acta Optica Sinica, 2017, 37(6): 0601002. (in Chinese) doi: 10.3788/AOS201737.0601002 [24] LUO J, LIU D, WANG B Y, et al. Effects of a nonideal half-wave plate on the gain ratio calibration measurements in polarization lidars[J]. Applied Optics, 2017, 56(29): 8100-8108. doi: 10.1364/AO.56.008100 [25] D'AMICO G, AMODEO A, MATTIS I, et al. EARLINET single calculus chain - technical - Part 1: pre-processing of raw lidar data[J]. Atmospheric Measurement Techniques, 2016, 9(2): 491-507. doi: 10.5194/amt-9-491-2016 [26] LIU Q, LIU CH, ZHU X L, et al. Analysis of the optimal operating wavelength of spaceborne oceanic lidar[J]. Chinese Optics, 2020, 13(1): 148-155. (in Chinese) doi: 10.3788/co.20201301.0148 [27] LU X Y, LI X B, QIN W B, et al. Retrieval of horizontal distribution of aerosol mass concentration by micro pulse lidar[J]. Optics and Precision Engineering, 2017, 25(7): 1697-1704. (in Chinese) [28] CHENG ZH T, LIU D, LUO J, et al. Influences analysis of the spectral filter transmission on the performance of high-spectral-resolution lidar[J]. Acta Optica Sinica, 2014, 34(8): 0801003. (in Chinese) doi: 10.3788/AOS201434.0801003 -
下载:
计量
- 文章访问数: 2753
- HTML全文浏览量: 582
- PDF下载量: 242
- 被引次数: 0
