针对光栅图像的快速盲去噪方法

张申华; 杨延西; 秦峤孟

doi:10.37188/CO.2020-0166

针对光栅图像的快速盲去噪方法

doi: 10.37188/CO.2020-0166

张申华^{1, 2,},
杨延西^{1, 3,},
秦峤孟¹

1.
西安理工大学自动化学院，陕西西安 710048
2.
安康学院电子与信息工程学院，陕西安康 725000
3.
陕西省复杂系统控制与智能信息处理重点实验室，陕西西安 710048

基金项目: 国家重点研发计划专项（No. 2018YFB1703000）；陕西省重点研发计划项目（No. 2020ZDLGR07-06）；陕西省现代装备绿色制造协同创新中心项目（No. 304-210891702）

详细信息

作者简介:
张申华（1982—），河南信阳人，2010年于西北大学获得硕士学位，现为西安理工大学博士研究生，主要研究方向为光学测量。E-mail：zhang_shenhua@126.com

杨延西（1975—），山东郓城人，博士，教授，2003年于西安理工大学获得博士学位，现为西安理工大学教授、博士生导师，主要研究方向为复杂系统控制、机器视觉和智能机器人。E-mail：yangyanxi@xaut.edu.cn

中图分类号: O439
计量
- 文章访问数: 1587
- HTML全文浏览量: 458
- PDF下载量: 74
- 被引次数: 0
出版历程
- 收稿日期: 2020-09-11
- 修回日期: 2020-10-21
- 网络出版日期: 2021-04-09
- 刊出日期: 2021-05-14

A fast blind denoising method for grating image

ZHANG Shen-hua^{1, 2
,},
YANG Yan-xi^{1, 3
,},
QIN Qiao-meng¹

1.
College of Automation, Xi’an University of Technology, Xi’an 710048, China
2.
College of Electronic and Information Engineering, Ankang University, Ankang 725000, China
3.
Shaanxi Key Laboratory of Complex system Control and Intelligent Information Processing, Xi’an 710048, China

Funds: Supported by National Key R&D Program of China (No. 2018YFB1703000); Key R&D Program of Shaanxi Province (No. 2020ZDLGR07-06); Collaborative Innovation Center of Shaanxi Province for Green Manufacturing of Modern Equipment (No. 304-210891702)

摘要

摘要: 基于正弦光栅条纹投影的三维测量技术是当前研究的热点问题。然而，受噪声的影响，采集到的光栅条纹图像质量降低，导致提取的相位发生扰动，而相位的提取结果直接决定着测量结果的准确性。实际测量中噪声未知，针对这一问题，本文提出了一种盲去噪方法。首先，根据残差模型，完成光栅条纹图像的真值图像与噪声图像的分离，然后，引入主成分分析技术估计出噪声图像的方差值。最后，根据噪声方差的估计值，利用基于相图的高斯滤波方法，将针对多帧光栅图像的噪声滤波转换到提取的相位图上完成。由实验结果可知，和对比方法相比，本文方法的均方根相位误差最高下降了88.5%，所提方法处理后的相位更加接近测量体的真值相位。本文方法可在最短的执行时间内实现对噪声导致的相位扰动进行抑制。所提方法能够快速处理光栅图像噪声引起的相位误差，在光栅投影测量中具有较强的实用性。
- 光栅图像 /
- 盲去噪 /
- 主成分分析 /
- 相位图滤波
Abstract: The three-dimensional measurement technology based on the projection of sine grating fringe image is a hot-topic. However, due to the influence of noise, the quality of the captured grating image is worse, resulting in the disturbance of the extracted phase, which directly determines the accuracy of the measurement. Since the noise is unknown in actual measurement, a blind denoising method is proposed in this paper. Firstly, according to the residual model, the grating fringe image is separated into the true value and the noise, then the Principal Component Analysis (PCA) technology is introduced to estimate the variance of the noise. Finally, according to the estimated value of the variance, the filtering on multi-frame fringe images is replaced by employing Gaussian filtering on the phase map. In contrast to other methods, the results of the proposed method showed that the Root Mean Square Error (RMSE) decreased by 88.5% (up to most), which indicated that the phase values of the proposed method were closer to the ground-truth of the measured object. By employing the proposed method, the phase disturbance caused by noise were significantly suppressed in the shortest execution time. The proposed method can quickly deal with the phase error caused by the noise of the grating image and has strong practicability in the grating image projection measurement.
- grating image /
- blind denoising /
- PCA /
- phase map filtering

HTML全文

图 1 PCA方法对仿真噪声的估计

Figure 1. The estimation of simulation noise by PCA method

下载: 全尺寸图片幻灯片

图 2 主成分分量占比

Figure 2. Proportion of principal component

下载: 全尺寸图片幻灯片

图 3 测量系统结构图

Figure 3. Framework of measuring system

下载: 全尺寸图片幻灯片

图 4 采集的光栅图像

Figure 4. Captured grating image

下载: 全尺寸图片幻灯片

图 5 几种不同方法的滤波效果

Figure 5. Filtering effect obtained by different methods

下载: 全尺寸图片幻灯片

图 6 各种方法的相位差

Figure 6. Phase errors obtained by different methods

下载: 全尺寸图片幻灯片

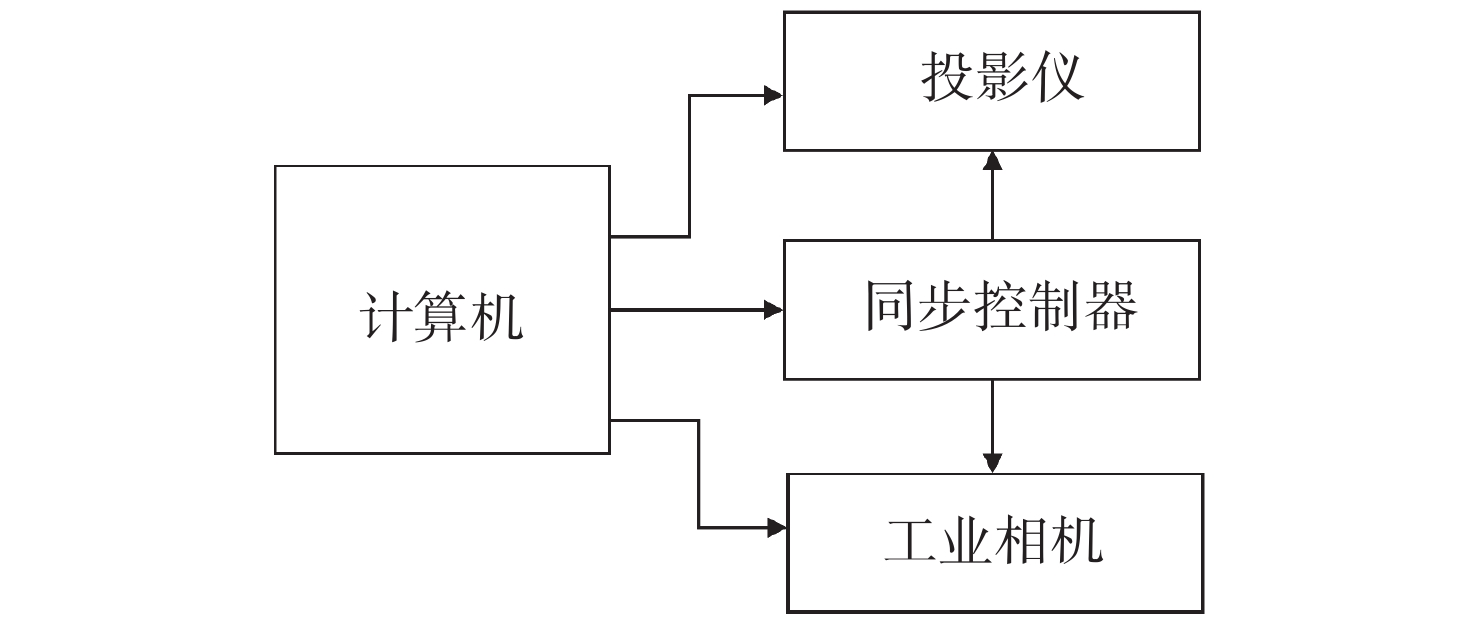
表 1 仪器设备型号和参数

Table 1. The instrument types and parameters

仪器设备	型号	主要性能及参数
投影仪	DLP4500	分辨率912 pixel×1140 pixel
工业相机	MV-UB130M	分辨率1024 pixel×1280 pixel 曝光时间：200 ms 帧率：30 frame/s 信噪比：45 dB
电脑	Intel Core (TM) i5-8250U CPU	主频：1.6 GHz

下载: 导出CSV

表 2 各种方法的噪声方差估计值

Table 2. The estimated noise variances of different methods

方法	文献[5]方法	文献[7]方法	文献[8]方法	本文方法
估计值	−	3.3737	1.6025	2.7823

下载: 导出CSV

表 3 几种算法的量化指标对比

Table 3. Comparison of quantitative indicators for different methods

	中值滤波方法	Ref.[10] 方法	Ref.[12] 方法	Ref.[13] 方法	本文方法
MPE	0.3856	9.2343	1.8268	1.7301	0.7003
RMSE	0.0961	0.5122	0.1029	0.1038	0.0591

下载: 导出CSV

表 4 几种算法的执行时间对比

Table 4. Comparison of computing time for different methods (s)

对比方法	中值滤波方法	Ref.[10] 方法	Ref.[12] 方法	Ref.[13] 方法	本文方法
执行时间	16.12	758.36	7.18	11.67	6.74

下载: 导出CSV

参考文献(27)

[1]	王建华, 杨延西. 基于彩色编码光栅投影的双N步相移轮廓术[J]. 中国光学,2019,12(3):616-627. doi: 10.3788/co.20191203.0616 WANG J H, YANG Y X. Double N-step phase-shifting profilometry using color-encoded grating projection[J]. Chinese Optics, 2019, 12(3): 616-627. (in Chinese) doi: 10.3788/co.20191203.0616
[2]	张申华, 杨延西. 一种针对投影仪gamma效应的相位误差补偿方法[J]. 仪器仪表学报,2019,40(11):1-8. ZHANG SH H, YANG Y X. A phase error compensation method for the gamma effect of projector[J]. Chinese Journal of Scientific Instrument, 2019, 40(11): 1-8. (in Chinese)
[3]	邓吉, 李健, 封皓, 等. 不连续相位跳变点的三维深度分割[J]. 光学精密工程,2019,27(11):2459-2466. doi: 10.3788/OPE.20192711.2459 DENG J, LI J, FENG H, et al. Three-dimensional depth segmentation technique utilizing discontinuities of wrapped phase sequence[J]. Optics and Precision Engineering, 2019, 27(11): 2459-2466. (in Chinese) doi: 10.3788/OPE.20192711.2459
[4]	丁超, 唐力伟, 曹立军, 等. 深孔内表面结构光图像几何畸变校正[J]. 光学精密工程,2018,26(10):2555-2564. doi: 10.3788/OPE.20182610.2555 DING CH, TANG L W, CAO L J, et al. Geometric distortion correction for structured-light image of deep-hole inner-surface[J]. Optics and Precision Engineering, 2018, 26(10): 2555-2564. (in Chinese) doi: 10.3788/OPE.20182610.2555
[5]	韩玉兰, 赵永平, 王启松, 等. 稀疏表示下的噪声图像超分辨率重构[J]. 光学精密工程,2017,25(6):1619-1626. doi: 10.3788/OPE.20172506.1619 HAN Y L, ZHAO Y P, WANG Q S, et al. Reconstruction of super resolution for noise image under the sparse representation[J]. Optics and Precision Engineering, 2017, 25(6): 1619-1626. (in Chinese) doi: 10.3788/OPE.20172506.1619
[6]	谢斌, 黄安, 黄辉. 本征图像分解的稀疏表示彩色图像去噪算法[J]. 液晶与显示,2019,34(11):1104-1114. doi: 10.3788/YJYXS20193411.1104 XIE B, HUANG A, HUANG H. Color image denoising algorithm based on intrinsic image decomposition and sparse representation[J]. Chinese Journal of Liquid Crystals and Displays, 2019, 34(11): 1104-1114. (in Chinese) doi: 10.3788/YJYXS20193411.1104
[7]	马逸东, 周顺勇. 基于连通性检测的图像椒盐噪声滤波算法[J]. 液晶与显示,2020,35(2):167-172. doi: 10.3788/YJYXS20203502.0167 MA Y D, ZHOU SH Y. Salt and pepper noise filtering algorithm based on connectivity detection[J]. Chinese Journal of Liquid Crystals and Displays, 2020, 35(2): 167-172. (in Chinese) doi: 10.3788/YJYXS20203502.0167
[8]	WANG J H, YANG Y X. An efficient phase error self-compensation algorithm for nonsinusoidal gating fringes in phase-shifting profilometry[J]. Review of Scientific Instrument, 2018, 89(6): 063115. doi: 10.1063/1.5025593
[9]	WANG H X, QIAN K M, GAO W J, et al. Fringe pattern denoising using coherence-enhancing diffusion[J]. Optics Letters, 2009, 34(8): 1141-1143. doi: 10.1364/OL.34.001141
[10]	TANG CH, HAN L, REN H W, et al. Second-order oriented partial-differential equations for denoising in electronic-speckle-pattern interferometry fringes[J]. Optics Letters, 2008, 33(19): 2179-2181. doi: 10.1364/OL.33.002179
[11]	ZHOU Q L, TANG CH, LI B Y, et al. Adaptive oriented PDEs filtering methods based on new controlling speed function for discontinuous optical fringe patterns[J]. Optics and Lasers in Engineering, 2018, 100: 111-117. doi: 10.1016/j.optlaseng.2017.07.018
[12]	DONOHO D L, JOHNSTONE I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455. doi: 10.1093/biomet/81.3.425
[13]	PYATYKH S, HESSER J, ZHENG L. Image noise level estimation by principal component analysis[J]. IEEE Transactions on Image Processing, 2013, 22(2): 687-699. doi: 10.1109/TIP.2012.2221728
[14]	LIU X H, TANAKA M, OKUTOMI M. Single-image noise level estimation for blind denoising[J]. IEEE Transactions on Image Processing, 2013, 22(12): 5226-5237. doi: 10.1109/TIP.2013.2283400
[15]	汪浩然, 夏克文, 任苗苗, 等. 结合PCA及字典学习的高光谱图像自适应去噪方法[J]. 计算机应用,2016,36(12):3411-3417, 3422. doi: 10.11772/j.issn.1001-9081.2016.12.3411 WANG H R, XIA K W, REN M M, et al. Adaptive denoising method of hyperspectral remote sensing image based on PCA and dictionary learning[J]. Journal of Computer Applications, 2016, 36(12): 3411-3417, 3422. (in Chinese) doi: 10.11772/j.issn.1001-9081.2016.12.3411
[16]	肖进胜, 朱力, 赵博强, 等. 基于主成分分析的分块视频噪声估计[J]. 自动化学报,2018,44(9):1618-1625. XIAO J SH, ZHU L, ZHAO B Q, et al. Block-based video noise estimation algorithm via principal component analysis[J]. Acta Automatica Sinica, 2018, 44(9): 1618-1625. (in Chinese)
[17]	乔双, 吴晓阳, 赵辰一, 等. 基于PCA和BM3D的噪声估计方法及其在中子图像去噪中的应用[J]. 原子能科学技术,2018,52(4):729-736. doi: 10.7538/yzk.2017.youxian.0457 QIAO SH, WU X Y, ZHAO CH Y, et al. Noise level estimation method based on PCA and BM3D for neutron image denoising[J]. Atomic Energy Science and Technology, 2018, 52(4): 729-736. (in Chinese) doi: 10.7538/yzk.2017.youxian.0457
[18]	杨华. 基于稀疏主成分分析的图像噪声估计方法[J]. 液晶与显示,2019,34(9):913-920. doi: 10.3788/YJYXS20193409.0913 YANG H. Image noise estimation method based on sparse principal component analysis[J]. Chinese Journal of Liquid Crystals and Displays, 2019, 34(9): 913-920. (in Chinese) doi: 10.3788/YJYXS20193409.0913
[19]	叶杨, 徐志伟, 陈仁文, 等. 基于KPCA和SVM的直升机旋翼桨叶损伤源定位[J]. 电子测量与仪器学报,2020,34(4):118-123. YE Y, XU ZH W, CHEN R W, et al. Damage source location of helicopter rotor blade based on KPCA and SVM[J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(4): 118-123. (in Chinese)
[20]	吴疆, 尤飞, 蒋平. 基于回归分析和主成分分析的噪声方差估计方法[J]. 电子与信息学报,2018,40(5):1195-1201. doi: 10.11999/JEIT170624 WU J, YOU F, JIANG P. Noise variance estimation method based on regression analysis and principal component analysis[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1195-1201. (in Chinese) doi: 10.11999/JEIT170624
[21]	ZUO CH, HUANG L, ZHANG M L, et al. Temporal phase unwrapping algorithms for fringe projection profilometry: a comparative review[J]. Optics and Lasers in Engineering, 2016, 85: 84-103. doi: 10.1016/j.optlaseng.2016.04.022
[22]	JIANG P, WANG Q, WU J. Efficient noise-level estimation based on principal image texture[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2020, 30(7): 1987-1999.
[23]	TOWERS C E, TOWERS D P, JONES J D C. Absolute fringe order calculation using optimised multi-frequency selection in full-field profilometry[J]. Optics and Lasers in Engineering, 2005, 43(7): 788-800. doi: 10.1016/j.optlaseng.2004.08.005
[24]	ZUO CH, FENG SH J, HUANG L, et al. Phase shifting algorithms for fringe projection profilometry: a review[J]. Optics and Lasers in Engineering, 2018, 109: 23-59. doi: 10.1016/j.optlaseng.2018.04.019
[25]	MAO C L, LU R S, LIU Z J. A multi-frequency inverse-phase error compensation method for projector nonlinear in 3D shape measurement[J]. Optics Communications, 2018, 419: 75-85. doi: 10.1016/j.optcom.2018.03.006
[26]	ZHANG CH W, ZHAO H, ZHANG L, et al. Full-field phase error detection and compensation method for digital phase-shifting fringe projection profilometry[J]. Measurement Science and Technology, 2015, 26(3): 035201. doi: 10.1088/0957-0233/26/3/035201
[27]	GAI SH Y, DA F P, LIU CH. Multiple-gamma-value based phase error compensation method for phase measuring profilometry[J]. Applied Optics, 2018, 57(35): 10290-10299. doi: 10.1364/AO.57.010290