Coupling between Meta-atoms: a new degree of freedom in metasurfaces manipulating electromagnetic waves
-
摘要: 近年来,纳米光学体系中共振体间耦合引起了人们的广泛关注。相对于单一光子共振结构体系,由多个光子共振体组成的复杂耦合体系有着更大的调控自由度和更令人着迷的现象。然而,相比人们在实验方面取得的进步,对于耦合问题的理论描述仍远未令人满意。本文从少体问题到周期性超构表面,从光子封闭体系到开放体系,系统介绍了多种处理共振体间耦合的理论工具,以及如何利用这些工具设计具有特定电磁波调控功能的新型超构表面。本文将着重展示本研究团队近些年在这一领域的研究进展,为相关领域研究人员提供指引与参考。Abstract: Nanophotonic systems have attracted tremendous attention due to their exotic abilities to freely control electromagnetic (EM) waves. In particular, much attention has been given to metasurfaces consisting of multiple plasmonic/dielectric meta-atoms coupled in different ways. Compared to simple systems containing only one type of resonator, coupled photonic systems exhibit more fascinating capabilities to manipulate EM waves. However, despite the great advances already achieved in experimental conditions, theoretical understandings of these complex systems are far from satisfactory. In this article, we summarize the theorized tools for developing nanophotonic systems including both coupled resonators and periodic metasurfaces. We aim to understand the EM properties in closed and open systems, and introduce methods of employing them to design new functional metasurfaces for various applications. We will mainly focus on works done in our own group and we hope that this short review can provide useful guidance and act as a reference for researchers in related fields.
-
Key words:
- metasurfaces /
- metamaterials /
- Meta-atoms /
- coupling /
- tight-binding theory /
- angular dispersion /
- open system
-
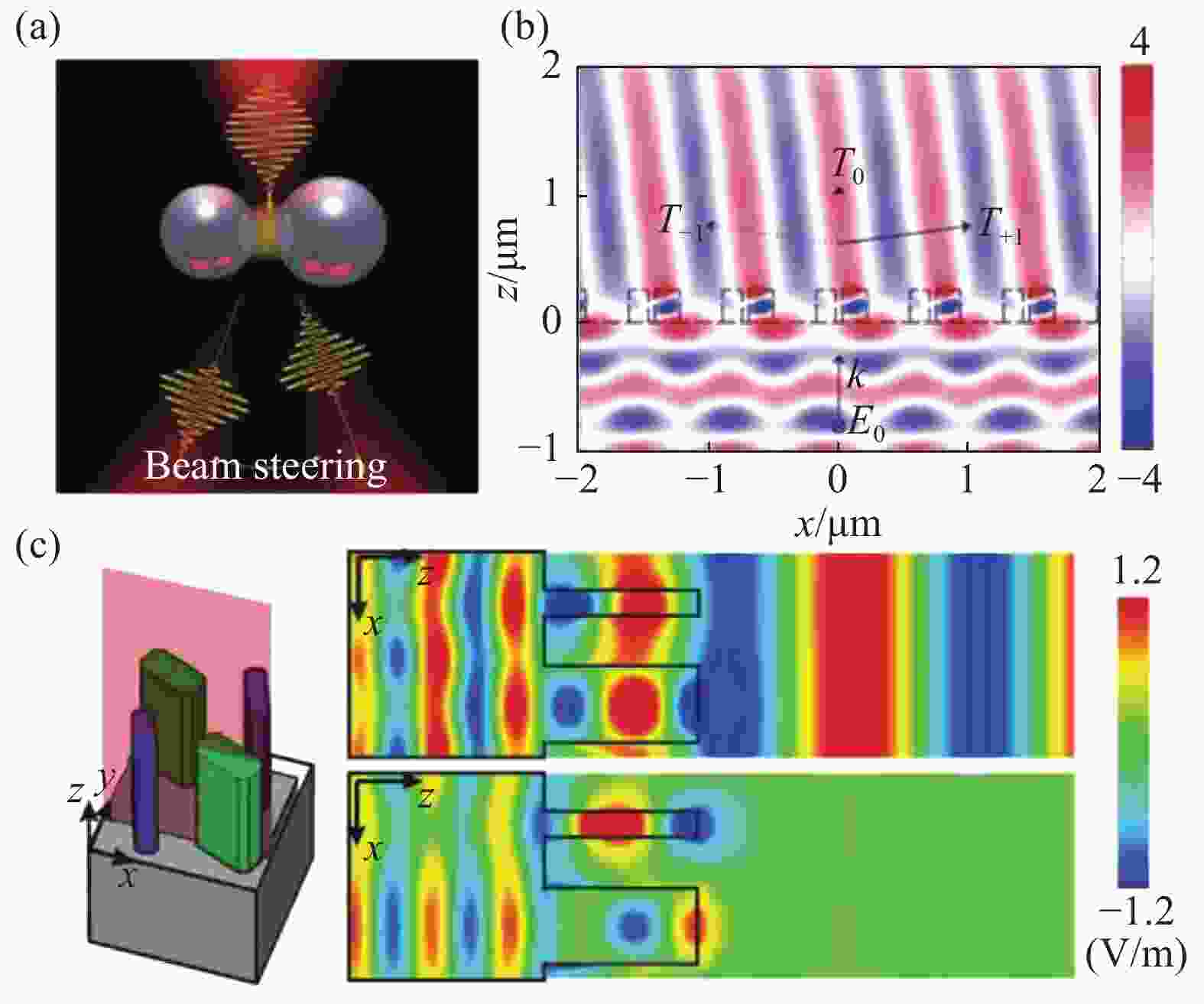
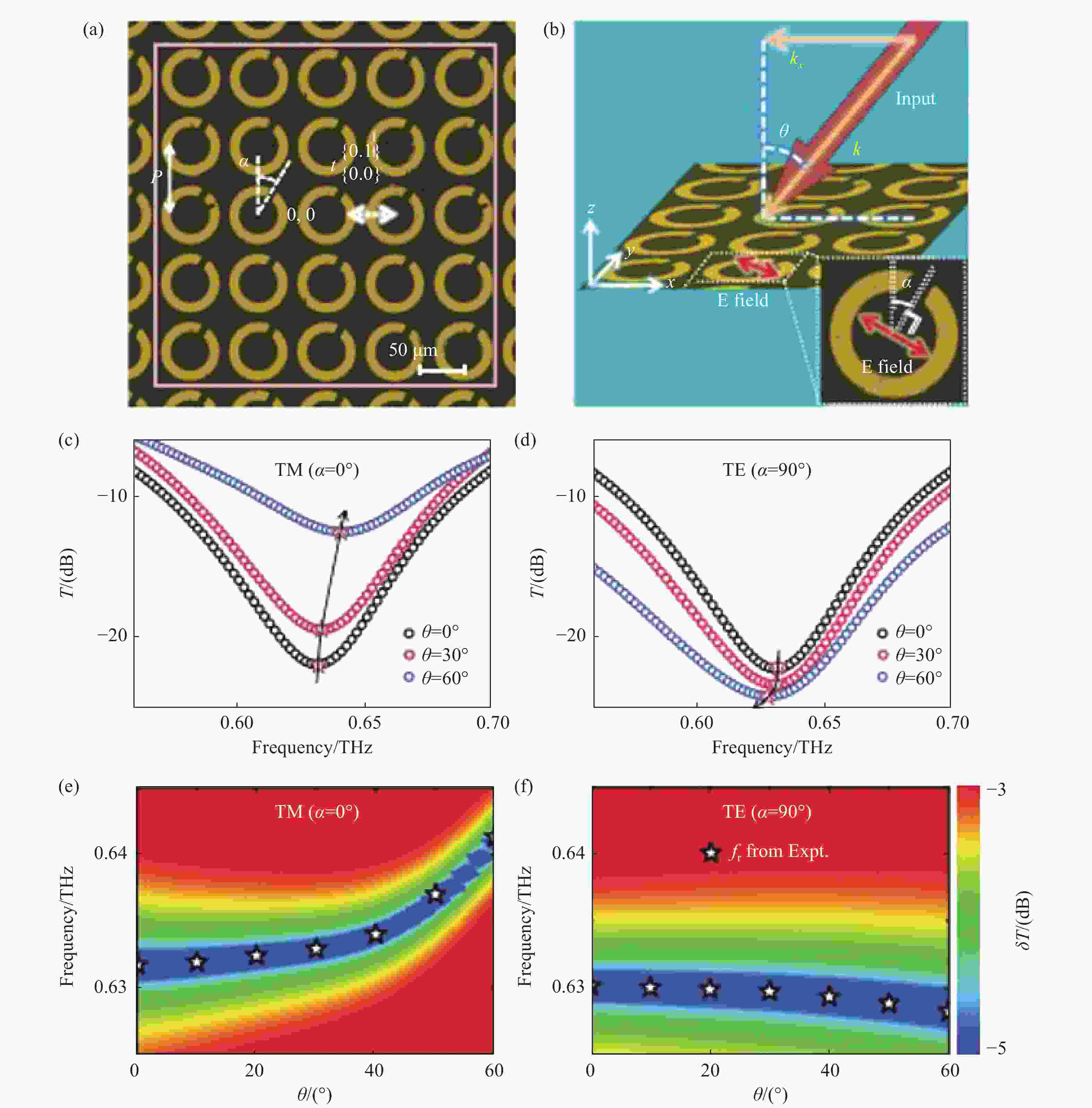
图 8 基于调制耦合与辐射实现的 (a)无角度色散全吸收器件;(b)角度选择性的全吸收器件;(c)角度依赖的多功能偏振调控器件;(d)非均匀超表面的角度依赖双功能波前调控器件[59]
Figure 8. (a) Incident-angle-insensitive meta-absorber;(b) incident-angle-selective meta-absorber ; (c) angle-multiplexed meta-polarizer ;(d) angle-multiplexed wavefront controller based on modulation coupling and radiation[59]
-
[1] SHELBY R A, SMITH D R, SCHULTZ S. Experimental verification of a negative index of refraction[J]. Science, 2001, 292(5514): 77-79. [2] PENDRY J B. Negative refraction makes a perfect lens[J]. Physical Review Letters, 2000, 85(18): 3966-3969. doi: 10.1103/PhysRevLett.85.3966 [3] FANG N, LEE H, SUN CH, et al. Sub–diffraction-limited optical imaging with a silver superlens[J]. Science, 2005, 308(5721): 534-537. doi: 10.1126/science.1108759 [4] CAI W SH, CHETTIAR U K, KILDISHEV A V, et al. Optical cloaking with metamaterials[J]. Nature Photonics, 2007, 1(4): 224-227. doi: 10.1038/nphoton.2007.28 [5] YU N F, GENEVET P, KATS M A, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction[J]. Science, 2011, 334(6054): 333-337. doi: 10.1126/science.1210713 [6] CHEN W T, YANG K Y, WANG C M, et al. High-efficiency broadband meta-hologram with polarization-controlled dual images[J]. Nano Letters, 2014, 14(1): 225-230. doi: 10.1021/nl403811d [7] YIN X B, YE Z L, RHO J, et al. Photonic spin Hall effect at metasurfaces[J]. Science, 2013, 339(6126): 1405-1407. doi: 10.1126/science.1231758 [8] ZHANG X Q, TIAN ZH, YUE W SH, et al. Broadband terahertz wave deflection based on C-shape complex metamaterials with phase discontinuities[J]. Advanced Materials, 2013, 25(33): 4567-4572. doi: 10.1002/adma.201204850 [9] KHORASANINEJAD M, CAPASSO F. Metalenses: versatile multifunctional photonic components[J]. Science, 2017, 358(6367): eaam8100. doi: 10.1126/science.aam8100 [10] SUN W J, HE Q, SUN SH L, et al. High-efficiency surface plasmon meta-couplers: concept and microwave-regime realizations[J]. Light:Science &Applications, 2016, 5(1): e16003. [11] MAIER S A, KIK P G, ATWATER H A, et al. Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides[J]. Nature Materials, 2003, 2(4): 229-232. doi: 10.1038/nmat852 [12] MAIER S A, KIK P G, SWEATLOCK L A, et al. Energy transport in metal nanoparticle plasmon waveguides[J]. MRS Online Proceedings Library, 2003, 777(1): 71. [13] LIU N, LANGGUTH L, WEISS T, et al. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit[J]. Nature Materials, 2009, 8(9): 758-762. doi: 10.1038/nmat2495 [14] BAO K, MIRIN N A, NORDLANDER P. Fano resonances in planar silver nanosphere clusters[J]. Applied Physics A, 2010, 100(2): 333-339. doi: 10.1007/s00339-010-5861-3 [15] PRODAN E, RADLOFF C, HALAS N J, et al. A hybridization model for the plasmon response of complex nanostructures[J]. Science, 2003, 302(5644): 419-422. doi: 10.1126/science.1089171 [16] LIU H, LIU Y M, LI T, et al. Coupled magnetic plasmons in metamaterials[J]. Physica Status Solidi (B) , 2009, 246(7): 1397-1406. doi: 10.1002/pssb.200844414 [17] FUNSTON A M, NOVO C, DAVIS T J, et al. Plasmon coupling of gold nanorods at short distances and in different geometries[J]. Nano Letters, 2009, 9(4): 1651-1658. doi: 10.1021/nl900034v [18] NORDLANDER P, OUBRE C, PRODAN E, et al. Plasmon hybridization in nanoparticle dimers[J]. Nano Letters, 2004, 4(5): 899-903. doi: 10.1021/nl049681c [19] SUH W, WANG ZH, FAN SH H. Temporal coupled-mode theory and the presence of non-orthogonal modes in lossless multimode cavities[J]. IEEE Journal of Quantum Electronics, 2004, 40(10): 1511-1518. doi: 10.1109/JQE.2004.834773 [20] FAN SH H, SUH W, JOANNOPOULOS J D. Temporal coupled-mode theory for the Fano resonance in optical resonators[J]. Journal of the Optical Society of America A, 2003, 20(3): 569-572. doi: 10.1364/JOSAA.20.000569 [21] GIANNINI V, FRANCESCATO Y, AMRANIA H, et al. Fano resonances in nanoscale plasmonic systems: a parameter-free modeling approach[J]. Nano Letters, 2011, 11(7): 2835-2840. doi: 10.1021/nl201207n [22] FANO U. Effects of configuration interaction on intensities and phase shifts[J]. Physical Review, 1961, 124(6): 1866-1878. doi: 10.1103/PhysRev.124.1866 [23] DING F, PORS A, BOZHEVOLNYI S I. Gradient metasurfaces: a review of fundamentals and applications[J]. Reports on Progress in Physics, 2018, 81(2): 026401. doi: 10.1088/1361-6633/aa8732 [24] JACKSON J D. Classical Electrodynamics[M]. 3rd ed. New York: Wiley, 1999. [25] PAPASIMAKIS N, FEDOTOV V A, MARINOV K, et al. Gyrotropy of a metamolecule: wire on a torus[J]. Physical Review Letters, 2009, 103(9): 093901. doi: 10.1103/PhysRevLett.103.093901 [26] DECKER M, STAUDE I, FALKNER M, et al. High-efficiency dielectric Huygens’ surfaces[J]. Advanced Optical Materials, 2015, 3(6): 813-820. doi: 10.1002/adom.201400584 [27] BOHREN C F, HUFFMAN D R. Absorption and Scattering of Light by Small Particles[M]. New York: John Wiley & Sons, 1983. [28] HOLLOWAY C L, KUESTER E F, BAKER-JARVIS J, et al. A double negative (DNG) composite medium composed of magnetodielectric spherical particles embedded in a matrix[J]. IEEE Transactions on Antennas and Propagation, 2003, 51(10): 2596-2603. doi: 10.1109/TAP.2003.817563 [29] ZHAO Q, ZHOU J, ZHANG F L, et al. Mie resonance-based dielectric metamaterials[J]. Materials Today, 2009, 12(12): 60-69. doi: 10.1016/S1369-7021(09)70318-9 [30] DEVLIN R C, KHORASANINEJAD M, CHEN W T, et al. Broadband high-efficiency dielectric metasurfaces for the visible spectrum[J]. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113(38): 10473-10478. doi: 10.1073/pnas.1611740113 [31] LIU N, LIU H, ZHU SH N, et al. Stereometamaterials[J]. Nature Photonics, 2009, 3(3): 157-162. doi: 10.1038/nphoton.2009.4 [32] BARANOV D G, MAKAROV S V, KRASNOK A E, et al. Tuning of near-and far-field properties of all‐dielectric dimer nanoantennas via ultrafast electron-hole plasma photoexcitation[J]. Laser &Photonics Reviews, 2016, 10(6): 1009-1015. [33] PANIAGUA-DOMÍNGUEZ R, YU Y F, KHAIDAROV E, et al. A metalens with a near-unity numerical aperture[J]. Nano Letters, 2018, 18(3): 2124-2132. doi: 10.1021/acs.nanolett.8b00368 [34] ZHANG F, PU M B, LI X, et al. All‐dielectric metasurfaces for simultaneous giant circular asymmetric transmission and wavefront shaping based on asymmetric photonic spin–orbit interactions[J]. Advanced Functional Materials, 2017, 27(47): 1704295. doi: 10.1002/adfm.201704295 [35] LUO X G. Subwavelength artificial structures: opening a new era for engineering optics[J]. Advanced Materials, 2019, 31(4): 1804680. doi: 10.1002/adma.201804680 [36] DRAINE B T, FLATAU P J. Discrete-dipole approximation for scattering calculations[J]. Journal of the Optical Society of America A, 1994, 11(4): 1491-1499. doi: 10.1364/JOSAA.11.001491 [37] KELLY K L, CORONADO E, ZHAO L L, et al. The optical properties of metal nanoparticles: the influence of size, shape, and dielectric environment[J]. The Journal of Physical Chemistry B, 2003, 107(3): 668-677. doi: 10.1021/jp026731y [38] MONTICONE F, ALÙ A. Metamaterial, plasmonic and nanophotonic devices[J]. Reports on Progress in Physics, 2017, 80(3): 036401. doi: 10.1088/1361-6633/aa518f [39] ENGHETA N, SALANDRINO A, ALV A. Circuit elements at optical frequencies: nanoinductors, nanocapacitors, and nanoresistors[J]. Physical Review Letters, 2005, 95(9): 095504. [40] SHI J W, MONTICONE F, ELIAS S, et al. Modular assembly of optical nanocircuits[J]. Nature Communications, 2014, 5: 3896. doi: 10.1038/ncomms4896 [41] RYBIN M V, FILONOV D S, BELOV P A, et al. Switching from visibility to invisibility via Fano resonances: theory and experiment[J]. Scientific Reports, 2015, 5(1): 1-6. [42] LIMONOV M F, RYBIN M V, PODDUBNY A N, et al. Fano resonances in photonics[J]. Nature Photonics, 2017, 11(9): 543-554. doi: 10.1038/nphoton.2017.142 [43] JOANNOPOULOS J D, JOHNSON S G, WINN J N, et al.. Photonic Crystals: Molding the Flow of Light[M]. 2nd ed. Princeton: Princeton University Press, 2008, . [44] GUPTA V P. Principles and Applications of Quantum Chemistry[M]. Amsterdam: Academic Press, 2016. [45] LIDORIKIS E, SIGALAS M M, ECONOMOU E N, et al. Tight-binding parametrization for photonic band gap materials[J]. Physical Review Letters, 1998, 81(7): 1405. [46] HARA Y, MUKAIYAMA T, TAKEDA K, et al. Heavy photon states in photonic chains of resonantly coupled cavities with supermonodispersive microspheres[J]. Physical Review Letters, 2005, 94(20): 203905. doi: 10.1103/PhysRevLett.94.203905 [47] NOTOMI M, KURAMOCHI E, TANABE T. Large-scale arrays of ultrahigh-Q coupled nanocavities[J]. Nature Photonics, 2008, 2(12): 741-747. doi: 10.1038/nphoton.2008.226 [48] BUSCH K, MINGALEEV S F, GARCIA-MARTIN A, et al. The Wannier function approach to photonic crystal circuits[J]. Journal of Physics:Condensed Matter, 2003, 15(30): R1233-R1256. doi: 10.1088/0953-8984/15/30/201 [49] LEUENBERGER D, FERRINI R, HOUDRÉ R. Ab initio tight-binding approach to photonic-crystal based coupled cavity waveguides[J]. Journal of Applied Physics, 2004, 95(3): 806-809. doi: 10.1063/1.1635668 [50] RAMAN A, FAN SH H. Photonic band structure of dispersive metamaterials formulated as a Hermitian eigenvalue problem[J]. Physical Review Letters, 2010, 104(8): 087401. doi: 10.1103/PhysRevLett.104.087401 [51] XI B, XU H, XIAO SH Y, et al. Theory of coupling in dispersive photonic systems[J]. Physical Review B, 2011, 83(16): 165115. doi: 10.1103/PhysRevB.83.165115 [52] XI B, QIU M, XIAO SH Y, et al. Effective model for plasmonic coupling: a rigorous derivation[J]. Physical Review B, 2014, 89(3): 035110. doi: 10.1103/PhysRevB.89.035110 [53] DAVIS T J, HENTSCHEL M, LIU N, et al. Analytical model of the three-dimensional plasmonic ruler[J]. ACS Nano, 2012, 6(2): 1291-8. [54] BABA T. Slow light in photonic crystals[J]. Nature Photonics, 2008, 2(8): 465-473. doi: 10.1038/nphoton.2008.146 [55] PAPASIMAKIS N, ZHELUDEV N I. Metamaterial-induced transparency: sharp fano resonances and slow light[J]. Optics and Photonics News, 2009, 20(10): 22-27. doi: 10.1364/OPN.20.10.000022 [56] QIU M, JIA M, MA SH J, et al. Angular dispersions in terahertz metasurfaces: physics and applications[J]. Physical Review Applied, 2018, 9(5): 054050. doi: 10.1103/PhysRevApplied.9.054050 [57] HAO J M, WANG J, LIU X L, et al. High performance optical absorber based on a plasmonic metamaterial[J]. Applied Physics Letters, 2010, 96(25): 251104. doi: 10.1063/1.3442904 [58] LALANNE P, LEMERCIER-LALANNE D. On the effective medium theory of subwavelength periodic structures[J]. Journal of Modern Optics, 1996, 43(10): 2063-2085. doi: 10.1080/09500349608232871 [59] ZHANG X Y, LI Q, LIU F F, et al. Controlling angular dispersions in optical metasurfaces[J]. Light:Science &Applications, 2020, 9: 76. [60] KRISTENSEN P T, HERRMANN K, INTRAVAIA F, et al. Modeling electromagnetic resonators using quasinormal modes[J]. Advances in Optics and Photonics, 2020, 12(3): 612-708. doi: 10.1364/AOP.377940 [61] CHING E S C, LEUNG P T, YOUNG K. Optical Processes in Microcavities-the Role of Quasi-Normal Modes[M]. CHANG R K, CAMPILLO A J. Optical Processes in Microcavities. Singapore: World Scientific, 1996. [62] KRISTENSEN P T, DE LASSON J R, HEUCK M, et al. On the theory of coupled modes in optical cavity-waveguide structures[J]. Journal of Lightwave Technology, 2017, 35(19): 4247-4259. doi: 10.1109/JLT.2017.2714263 [63] TRØST KRISTENSEN P, HEUCK M, MØRK J. Optimal switching using coherent control[J]. Applied Physics Letters, 2013, 102(4): 041107. doi: 10.1063/1.4789372 [64] KRISTENSEN P T, DE LASSON J R, GREGERSEN N. Calculation, normalization, and perturbation of quasinormal modes in coupled cavity-waveguide systems[J]. Optics Letters, 2014, 39(22): 6359-6362. doi: 10.1364/OL.39.006359 [65] LIN J, QIU M, ZHANG X Y, et al. Tailoring the lineshapes of coupled plasmonic systems based on a theory derived from first principles[J]. Light:Science &Applications, 2020, 9: 158. -






 下载:
下载: