-
摘要: 光学频率梳(光频梳)具有脉冲宽度窄、频率精度高、频率梳齿稳定以及相干性好等优良的时频域特性，近年来成为超快激光技术及计量科学等领域的研究热点，并发展成为一种重要的科研工具。近期，一类基于光频梳相干合成的新型光源，可实现对光的偏振或轨道角动量进行射频波段的周期性且高速稳定的调制。本文从光频梳的基本概念出发，分别就偏振调制和轨道角动量调制两个方面，详细介绍了基于光频梳相干合成新型光源的基本原理、实验技术以及表征手段等的最新研究进展。最后简要讨论光频梳相干合成技术在固体光谱学、光学操控、光与物质相互作用等领域的应用前景。Abstract: Optical Frequency Comb (OFC) possesses unique time(frequency) domain characteristics such as narrow pulse width, high frequency precision, stable frequency comb teeth and well-defined optical coherence, etc. Therefore, it has become a hot research topic in various fields including ultra-fast laser technology and metrology science in recent years. Meanwhile, OFC has also been developed into an important scientific research instrument. Recently, a novel light source based on the coherent synthesis of OFCs has been developed, which can realize the periodical, high-speed (up to radio frequency) and stable modulation of the polarization or the orbital angular momentum of light. In this review, we try to introduce recent developments on the fundamental principles, experimental techniques and characterization methods of the novel light source based on the coherent synthesis of OFCs, starting from the basic concepts of OFC and mainly covering two aspects: polarization modulation and orbital angular momentum modulation respectively. We also try to provide some perspectives on the applications of OFC based on the coherent synthesis techniques in the fields of solid-state spectroscopy, optical manipulation and the interaction between light and matter, etc.
-
图 1 (a)光频梳的时域表示; (b)光频梳的频域表示。
$ T $ 为脉冲周期;${f}_{{\rm{rep}}}$ 为重复频率;${\phi }_{{\rm{CEP}},{\rm{P}}-{\rm{P}}}$ 为相邻两脉冲间的载波包络相位差;${f}_{{\rm{ceo}}}$ 为载波包络偏移频率;$ {f}_{n} $ 为第n个梳齿的频率Figure 1. (a)The time domain representation and (b) the frequency domain representation of an OFC; T: the pulse repetition period;
${f}_{{\rm{rep}}}$ : the repetition rate;${\phi }_{{\rm{CEP}},{\rm{P}}-{\rm{P}}}$ : the pulse-to-pulse variation of the carrier-envelope phase;${f}_{{\rm{ceo}}}$ : the carrier-envelope offset frequency;$ {f}_{n} $ : the frequency of the nth comb tooth
图 3 (a)产生偏振调制光源的第一种方式[19]; (b)产生偏振调制光源的第二种方式[20]。EDFA：掺铒光纤放大器; AOM: 声光调制器; Q: 1/4波片; H(HWP): 半波片; VND: 可变中性密度衰减片; SMF: 单模光纤; PBS: 偏振分束器; BS: 分束器; P: 偏振片
Figure 3. (a) Schematic diagram of the first optical setup to obtain polarization modulated light source[19]; (b) schematic diagram of the second optical setup to obtain polarization modulated light source[20]. EDFA: Er-doped fiber amplifier; AOM: acousto-optical modulator; Q: quarter waveplate; H(HWP): half waveplate; VND: variable neutral density filter; SMF: single-mode fiber; PBS: polarization beam splitter; BS: beam splitter; P: polarizer
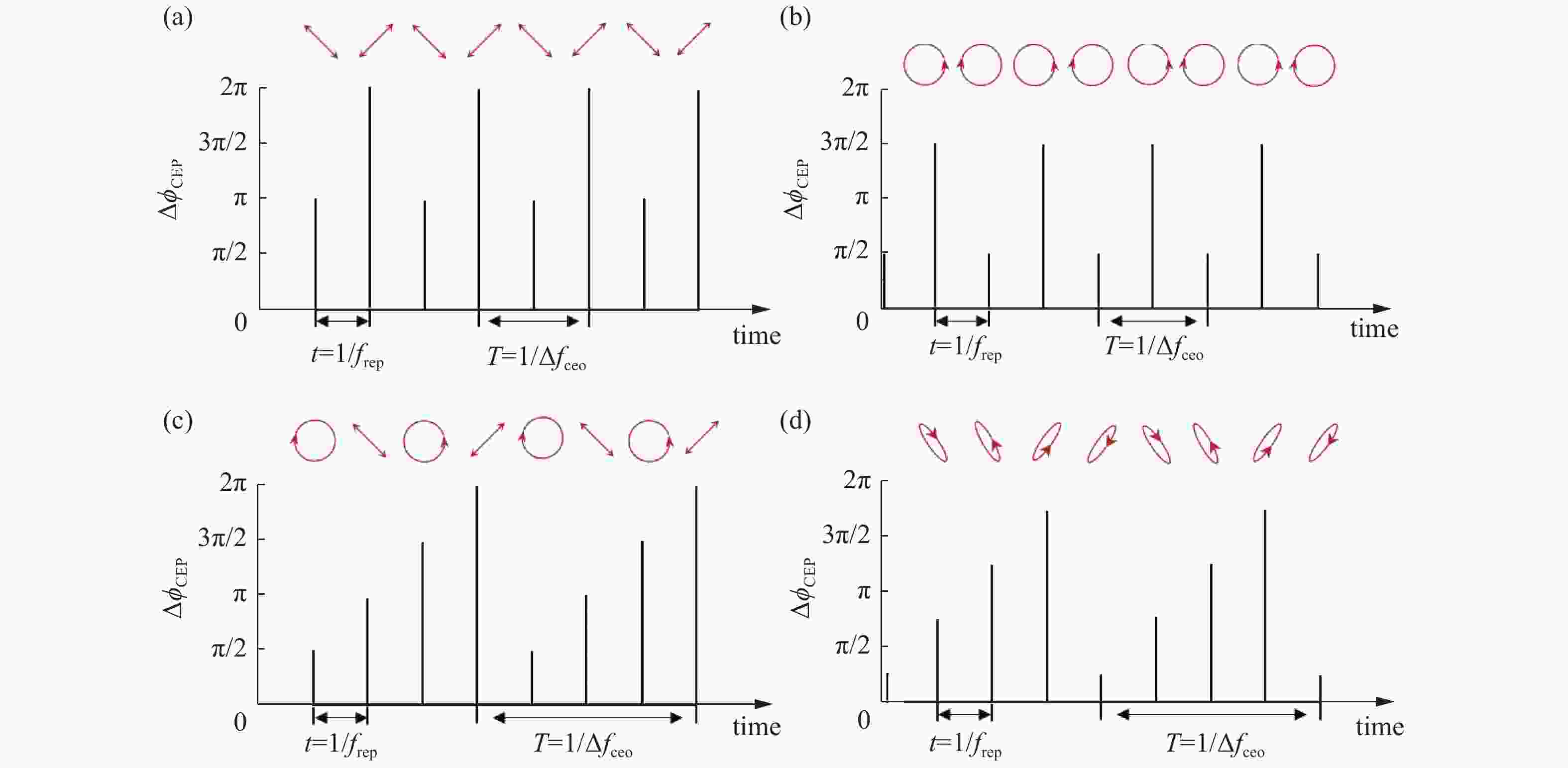
图 4 偏振调制光源输出脉冲的偏振态及
$\Delta {\phi }_{{\rm{CEP}}}$ 周期变化图。两光频梳从$ t=0 $ 同时开始传播 (a)当${{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/2$ ，初始${\Delta }{\phi }_{{\rm{CEP}}}=0$ 时; (b)当${{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/2$ ，初始${\Delta }{\phi }_{{\rm{CEP}}}={\text{π}} /2$ 时; (c)当${{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/4$ ，初始${\Delta }{\phi }_{{\rm{CEP}}}=0$ 时; (d)当${{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/4$ ，初始${\Delta }{\phi }_{{\rm{CEP}}}={\text{π}} /4$ 时。注：图中竖线高低代表用于相干合成的两光频梳脉冲对间的$\Delta {\phi }_{{\rm{CEP}}}$ (对($2{\text{π}} )$ 取模之后)，同时为了清楚，对$ t=0 $ 时刻的竖线进行了微小偏移Figure 4. Diagram of polarization states of the output pulses of the polarization modulated light source and periodic evolution of
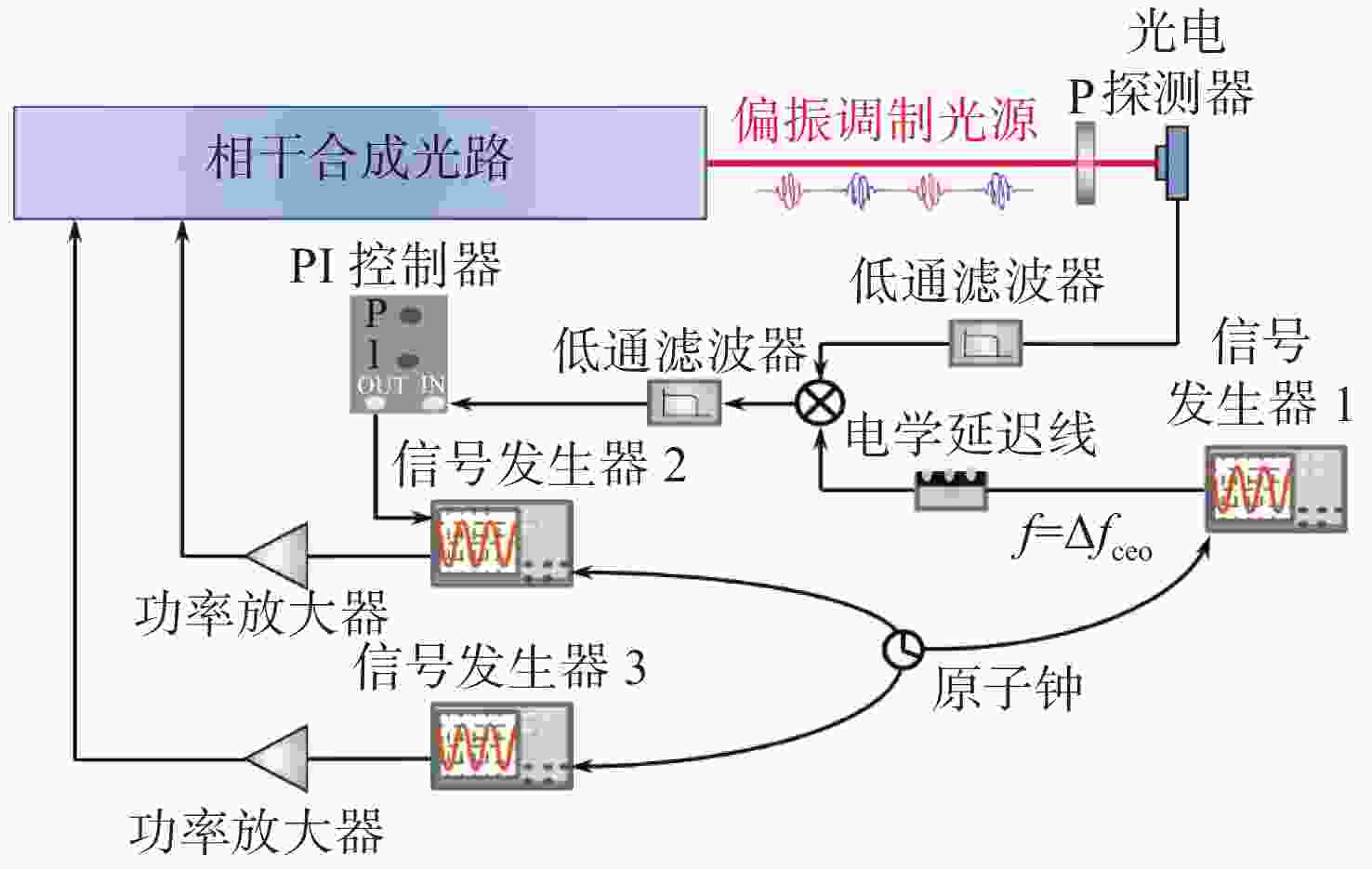
${\Delta }{\phi }_{{\rm{CEP}}}$ . The two optical frequency combs propagate simultaneously starting from$ t=0 $ , (a) when$ {{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/2 $ and initial$ {\Delta }{\phi }_{{\rm{CEP}}}=0 $ ; (b) when$ {{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/2 $ and initial$ \Delta {\phi }_{{\rm{CEP}}}={\text{π}} /2 $ ; (c) when$ {{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/4 $ and initial$ {\Delta }{\phi }_{{\rm{CEP}}}=0 $ ; (d) when$ {{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/4 $ and initial$ \Delta {\phi }_{{\rm{CEP}}}={\text{π}} /4 $ . Note: The height of the vertical lines represents$ {\Delta }{\phi }_{{\rm{CEP}}} $ (after$\mathrm{m}\mathrm{o}\mathrm{d}\left(2{\text{π}}\right)$ ) between pulse pairs from two optical frequency combs which are used for coherent synthesis. The vertical lines at$ t=0 $ have been slightly offset for clarity
图 5 用于稳定偏振调制光源输出脉冲的偏振态的电反馈回路结构示意图。注：图中相干合成光路的细节如图3(b)所示，两个功率放大器输出信号分别作用于两个声光调制器上
Figure 5. Schematic diagram of the electrical feedback loop which is used to stabilize the polarization states of the output pulses for the polarization-modulated light source. Note: The details of the optical path for coherent synthesis are shown in Figure 3(b). The two power amplifiers are used to drive the two acousto-optic modulators, respectively
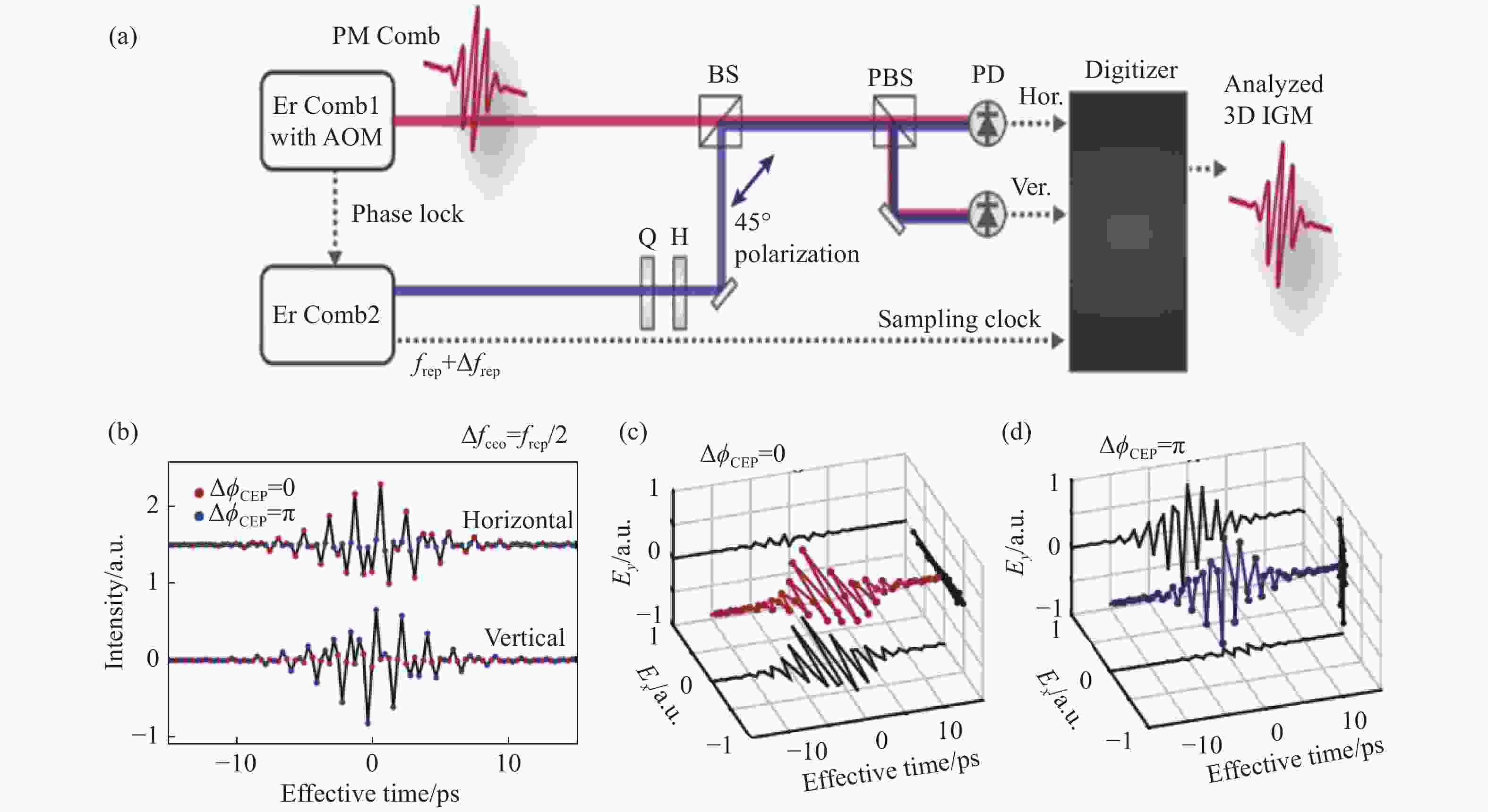
图 6 (a)利用传统的双光梳光谱技术表征偏振调制光源的输出脉冲的偏振态; (b)当
${{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/2$ ，初始${\Delta }{\phi }_{{\rm{CEP}}}=0$ 时，光电探测器探测得到的IGMs; (c)、(d)分别提取图(b)中所有红色和蓝色数据点连接而成的IGM，分别得到水平和垂直线偏振态[19]Figure 6. (a) The polarization states of the output pulses for the polarized modulated light source were characterized by the traditional dual-comb spectroscopy; (b) when
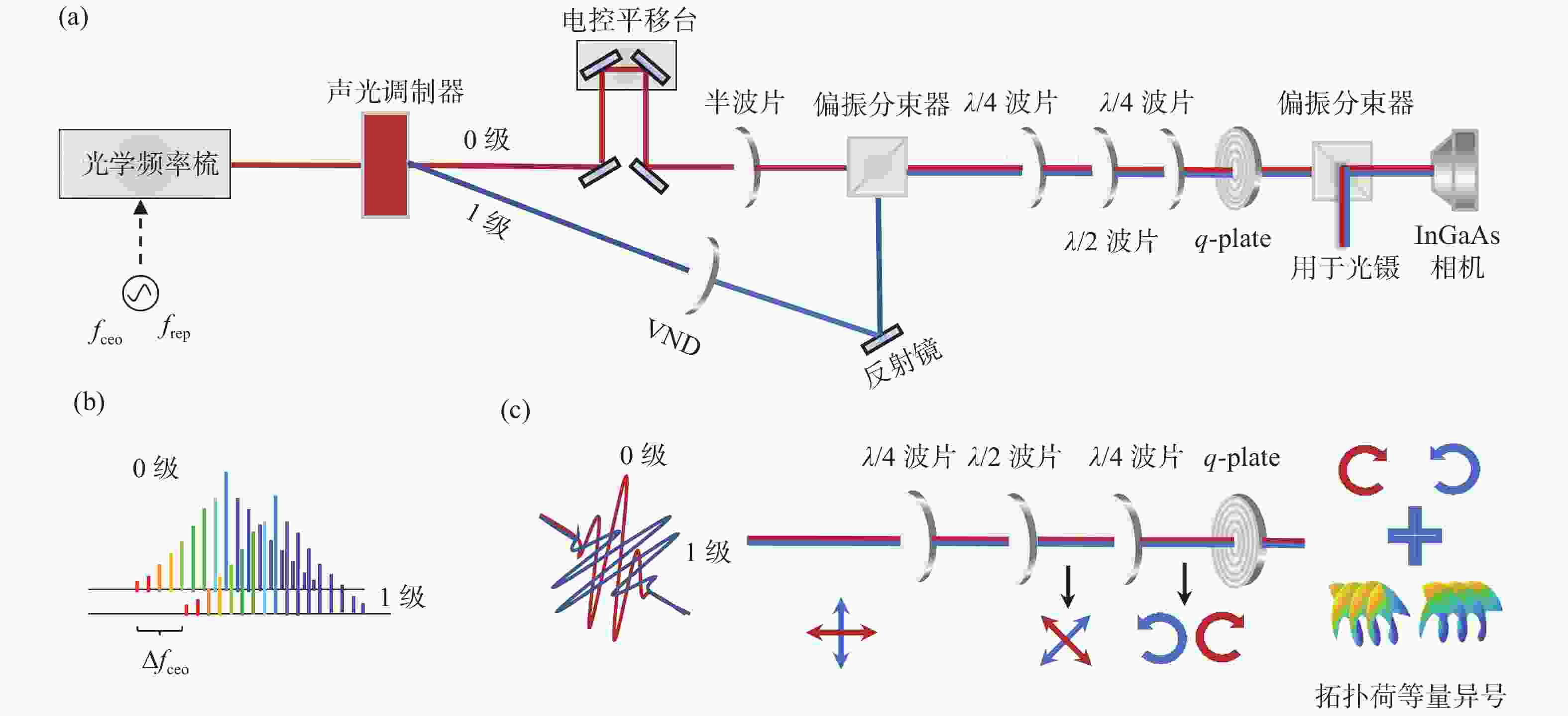
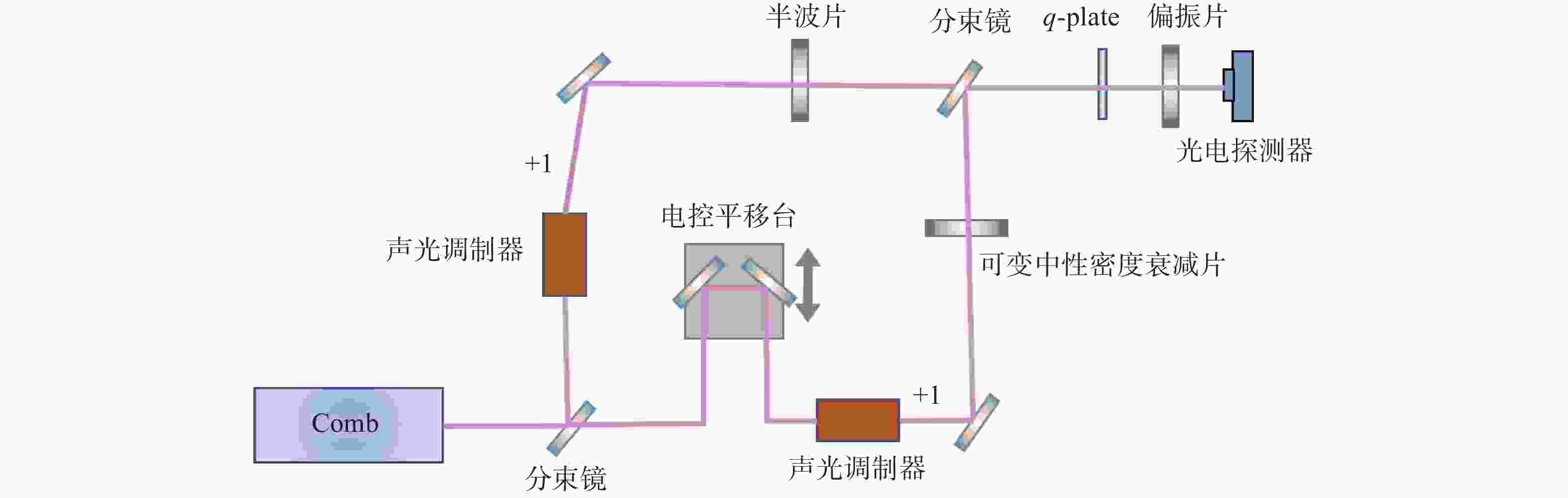
${{\Delta }f}_{{\rm{ceo}}}={f}_{{\rm{rep}}}/2$ , initial${\Delta }{\phi }_{{\rm{CEP}}}=0$ , IGMs were obtained by a fast photodetector. (c)、(d) the IGM formed by extracting all the red and blue points in Fig.6(b), obtaining the horizontal and vertical linear polarization states respectively[19]
图 8 (a)相干合成生成环形晶格的实验装置; (b)利用AOM产生具有
$\Delta {f}_{{\rm{ceo}}}$ 可调的双光频梳; (c)利用q-plate将具有$\Delta {f}_{{\rm{ceo}}}$ 可调的双光频梳转换为$\Delta {f}_{{\rm{ceo}}}$ 可调且拓扑荷为等量异号的双涡旋光频梳Figure 8. (a) Experimental setup for coherently synthesized optical ring lattice; (b) generation of a dual-comb with an adjustable
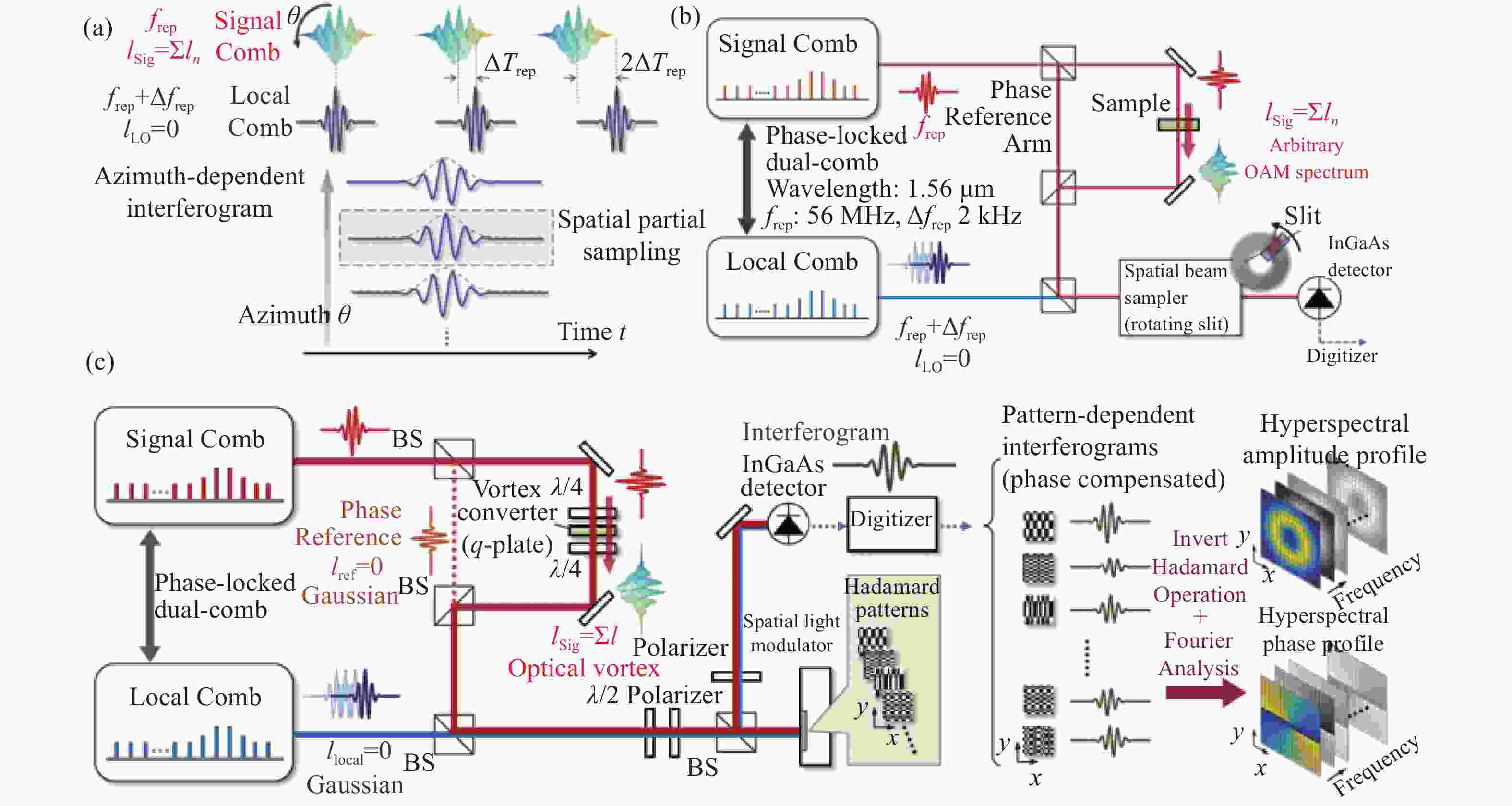
$\Delta {f}_{{\rm{ceo}}}$ using AOM; (c) the dual-comb with an adjustable$\Delta {f}_{{\rm{ceo}}}$ was converted by a q-plate into a dual-vortex comb with an adjustable$\Delta {f}_{{\rm{ceo}}}$ and different topological charges
图 9 （a）拓扑荷数等量异号的涡旋光束的干涉图样；（b）当
$ \Delta l=4 $ 时，环形晶格周期性旋转的图样Figure 9. (a) Interference patterns of vortex light with opposite topological charges; (b) images of the optical ring lattice rotates periodically when
$\Delta l=4 $ 
图 10 相干合成的轨道角动量调制光源光路图
Figure 10. Schematic diagram of coherently synthesized orbital angular momentum modulated light source
图 11 固定拓扑荷数涡旋光频梳轨道角动量的表征。(a)基于空间部分采样对涡旋光频梳轨道角动量表征的原理; (b)表征轨道角动量的空间部分采样方法[30]; (c)表征轨道角动量的单像素成像方法[31]
Figure 11. Characterization of orbital angular momentum of optical vortex comb with fixed topological charges. (a) Principle of spatial partial sampling to characterize orbital angular momentum of optical vortex comb; (b) spatial partial sampling method for the characterization of orbital angular momentum[30]; (c) single-pixel imaging method for the characterization of orbital angular momentum[31]
-
[1] DIDDAMS S A, JONES D J, MA L S, et al. Optical frequency measurement across a 104-THz gap with a femtosecond laser frequency comb[J]. Optics Letters, 2000, 25(3): 186-188. doi: 10.1364/OL.25.000186 [2] UDEM T, HOLZWARTH R, HÄNSCH T W. Optical frequency metrology[J]. Nature, 2002, 416(6877): 233-237. doi: 10.1038/416233a [3] HOLLBERG L, DIDDAMS S, BARTELS A, et al. The measurement of optical frequencies[J]. Metrologia, 2005, 42(3): S105-S124. doi: 10.1088/0026-1394/42/3/S12 [4] LUDLOW A D, BOYD M M, YE J, et al. Optical atomic clocks[J]. Reviews of Modern Physics, 2015, 87(2): 637-701. doi: 10.1103/RevModPhys.87.637 [5] GIORGETTA F R, SWANN W C, SINCLAIR L C, et al. Optical two-way time and frequency transfer over free space[J]. Nature Photonics, 2013, 7(6): 434-438. doi: 10.1038/nphoton.2013.69 [6] MILLO J, BOUDOT R, LOURS M, et al. Ultra-low-noise microwave extraction from fiber-based optical frequency comb[J]. Optics Letters, 2009, 34(23): 3707-3709. doi: 10.1364/OL.34.003707 [7] FORTIER T M, KIRCHNER M S, QUINLAN F, et al. Generation of ultrastable microwaves via optical frequency division[J]. Nature Photonics, 2011, 5(7): 425-429. doi: 10.1038/nphoton.2011.121 [8] CODDINGTON I, SWANN W C, NENADOVIC L, et al. Rapid and precise absolute distance measurements at long range[J]. Nature Photonics, 2009, 3(6): 351-356. doi: 10.1038/nphoton.2009.94 [9] JANG Y S, KIM S W. Distance measurements using mode-locked lasers: a review[J]. Nanomanufacturing and Metrology, 2018, 1(3): 131-147. doi: 10.1007/s41871-018-0017-8 [10] CODDINGTON I, NEWBURY N, SWANN W. Dual-comb spectroscopy[J]. Optica, 2016, 3(4): 414-426. doi: 10.1364/OPTICA.3.000414 [11] LOMSADZE B, SMITH B C, CUNDIFF S T. Tri-comb spectroscopy[J]. Nature Photonics, 2018, 12(11): 676-680. doi: 10.1038/s41566-018-0267-4 [12] IDEGUCHI T, HOLZNER S, BERNHARDT B, et al. Coherent Raman spectro-imaging with laser frequency combs[J]. Nature, 2013, 502(7471): 355-358. doi: 10.1038/nature12607 [13] SUMIHARA K A, OKUBO S, OKANO M, et al. Polarization-sensitive dual-comb spectroscopy[J]. Journal of the Optical Society of America B, 2017, 34(1): 154-159. doi: 10.1364/JOSAB.34.000154 [14] DURÁN V, de CHATELLUS H G, SCHNEBÉLIN C, et al. Optical frequency combs generated by acousto-optic frequency-shifting loops[J]. IEEE Photonics Technology Letters, 2019, 31(23): 1878-1881. doi: 10.1109/LPT.2019.2947655 [15] PARRIAUX A, HAMMANI K, MILLOT G. Electro-optic frequency combs[J]. Advances in Optics and Photonics, 2020, 12(1): 223-287. doi: 10.1364/AOP.382052 [16] SUMIHARA K A, OKUBO S, OGUCHI K, et al. Polarization-sensitive dual-comb spectroscopy with an electro-optic modulator for determination of anisotropic optical responses of materials[J]. Optics Express, 2019, 27(24): 35141-35165. doi: 10.1364/OE.27.035141 [17] TORRES-COMPANY V, WEINER A M. Optical frequency comb technology for ultra-broadband radio-frequency photonics[J]. Laser &Photonics Reviews, 2014, 8(3): 368-393. [18] ASAHARA A, KONDO K I, WANG Y, et al.. Coherent control of relative carrier envelope phase in dual-comb spectroscopy[C]. Proceedings of Science and Innovations 2017, Optical Society of America, 2017: SF1C.6. [19] ASAHARA A, MINOSHIMA K. Coherent multi-comb pulse control demonstrated in polarization-modulated dual-comb spectroscopy technique[J]. Applied Physics Express, 2019, 12(7): 072014. doi: 10.7567/1882-0786/ab2991 [20] ZHANG R X, GONG Y M, DAY M W, et al. Radio frequency polarization modulation based on an optical frequency comb[J]. Review of Scientific Instruments, 2020, 91(8): 083111. doi: 10.1063/5.0016256 [21] ASAHARA A, SHOJI S, KONDO K I, et al.. Coherent spatiotemporal phase control by combining optical frequency combs and optical vortices[C]. Proceedings of Science and Innovations 2018, Optical Society of America, 2018: STu4P.3. [22] ASAHARA A, SHOJI S, MINOSHIMA K. Optical combs and optical vortices combined for spatiotemporal manipulation of light and matter[J]. arXiv: 2005.04705, 2020. [23] FRANKE-ARNOLD S, LEACH J, PADGETT M J, et al. Optical ferris wheel for ultracold atoms[J]. Optics Express, 2007, 15(14): 8619-8625. doi: 10.1364/OE.15.008619 [24] ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185-8189. doi: 10.1103/PhysRevA.45.8185 [25] WANG X W, NIE ZH Q, LIANG Y, et al. Recent advances on optical vortex generation[J]. Nanophotonics, 2018, 7(9): 1533-1556. doi: 10.1515/nanoph-2018-0072 [26] MARRUCCI L, MANZO C, PAPARO D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media[J]. Physical Review Letters, 2006, 96(16): 163905. doi: 10.1103/PhysRevLett.96.163905 [27] MARRUCCI L, KARIMI E, SLUSSARENKO S, et al. Spin-to-orbital conversion of the angular momentum of light and its classical and quantum applications[J]. Journal of Optics, 2011, 13(6): 064001. doi: 10.1088/2040-8978/13/6/064001 [28] SHEN Y J, WANG X J, XIE ZH W, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities[J]. Light:Science &Applications, 2019, 8: 90. [29] JI ZH R, LIU W J, KRYLYUK S, et al. Photocurrent detection of the orbital angular momentum of light[J]. Science, 2020, 368(6492): 763-767. doi: 10.1126/science.aba9192 [30] ASAHARA A, ADACHI T, WANG Y, et al.. Orbital angular momentum-resolved dual-comb spectroscopy towards topological material studies[C]. Proceedings of Science and Innovations 2019, Optical Society of America, 2019: SM2H.8. [31] ASAHARA A, ADACHI T, AKIYAMA S, et al.. Spatiotemporal characterization of optical vortex light-wave using hyperspectral dual-comb imaging[C]. Proceedings of Science and Innovations 2020, Optical Society of America, 2020: STu4N.6. [32] ASAHARA A, ADACHI T, AKIYAMA S, et al.. Detection of optical vortices with various topological charges using single-pixel dual-comb imaging[C]. Proceedings of Laser Science 2020, Optical Society of America, 2020: LM7F.4. -
下载:
计量
- 文章访问数: 2291
- HTML全文浏览量: 909
- PDF下载量: 438
- 被引次数: 0
