-
摘要: 受凝聚态拓扑绝缘体研究的启发,整数量子霍尔效应、量子自旋霍尔效应、拓扑半金属、高阶拓扑绝缘体等拓扑物理相继在光学系统中实现。光子系统因能带干净,样品设计简单且制作精度高等优势,逐渐成为研究物理拓扑模型和新型拓扑效应的重要平台。拓扑光子学提供了全新的调控光场和操控光子的方法,其拓扑保护的边界态可实现光子对材料杂质缺陷免疫的传播,这种传统光子系统不具备的理想的传输态有望驱动新型光学集成器件的变革。本文将从二维光学体系出发,简要介绍几种典型的光拓扑绝缘体的最新进展,例如光整数量子霍尔效应、光量子自旋霍尔效应、光Floquet拓扑绝缘体、拓扑安德森绝缘体和高阶拓扑绝缘体。文中重点介绍了上述几种光拓扑绝缘体的拓扑模型及其新型的拓扑现象,并在最后展望了新型光学拓扑效应及其在光学器件中的应用前景。Abstract: Inspired by the exciting discovery of topological insulators in condensed-state physics, some topological physics phenomena, such as integer quantum Hall effect, quantum spin Hall effect, topological semimetals and higher order topological insulators, have successively realized in photonic system. Thanks to the clean energy band, simple design and accurate production of samples, the optical system has gradually become an important platform for studying physical topological models and novel topological phenomena. Topological photonics provides new methods to manipulate light fields and photons. The topological protected edge states can realize the propagation of photons which immune to material defects and impurity. Such ideal transport states are unprecedented in traditional optics, which may lead to radical changes in novel integrated optical devices. In this review, based on the two-dimensional optical system, we briefly introduce the exciting developments of topological photonics, such as photonic integer quantum Hall effect, photonic quantum spin Hall effect, photonic Floquet topological insulators, topological Anderson insulators and photonic higher order topological insulators. We focus on the topological insulators mentioned above and its topological model and novel topological phenomena. Finally, we conclude with the novel topological effects in optics and their applications in novel optical device.
-
图 1 (a)由旋磁铁氧体棒和金属壁组成的二维光整数量子霍尔效应的实验装置图[7]。(b)在垂直方向磁场作用下,模拟手性边缘态绕障碍物周围的传播示意图[7]。(c)以磁场和频率为函数的理论拓扑带隙图,其中每个带隙的拓扑不变量用带隙陈数标记[91]。(d)实验测量的拓扑带隙图[91]。(e)和(f)分别表示不同陈数的边缘态实验和理论的示意图[91],其中灰色部分为体带,红色线表示边缘态。
Figure 1. (a) Experimental setup of 2D optical integer quantum Hall effect consisting of gyromagnetic ferrite rods and metal walls[7]. (b) Simulated propagation of chiral edge states around obstacles in the presence of a vertical magnetic field[7]. (c) Theoretical topological gap map as a function of the magnetic field and the frequency, in which the topological invariants of each band gaps are labeled by its gap Chern number[91]. (d) Experimental topological gap map[91]. (e) and (f) represent the schematic of experimental and theoretical edge states with different gap Chern numbers[91], respectively, in which gray part is bulk bands and the red lines represent the edge states.
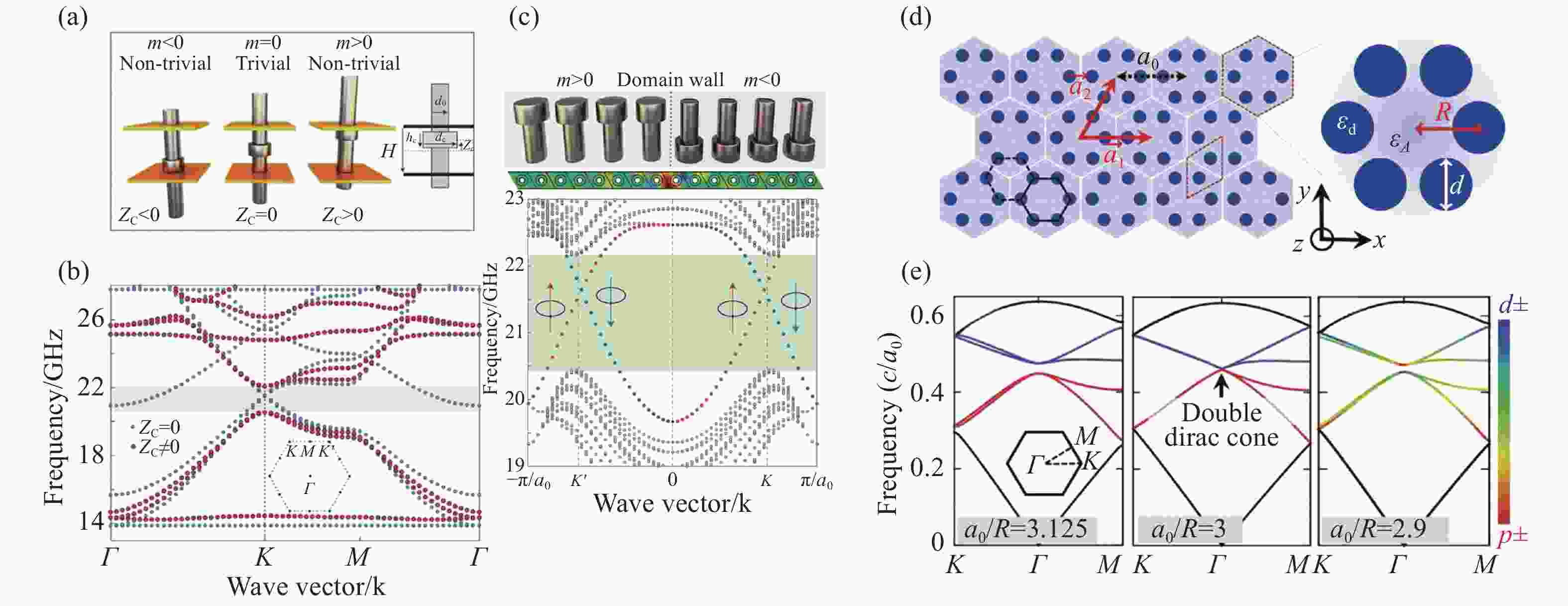
图 2 (a)可重构拓扑超晶的设计示意图[107]。移动金属环与金属板的相对位置可在简并处引入负的(左)、零(中)或正的(右)有效质量。(b)可重构拓扑超晶的体带示意图[107],其中蓝色点线和红色点线分别对应对称(无双各向异性)和非对称(有双各向异性)结构。(c)有效质量相反的两种超晶结构的界面及相应的边带图[107]。(d)基于六角晶格的二维电介质光子晶体示意图[28]。(e)改变人工原子之间的距离,将
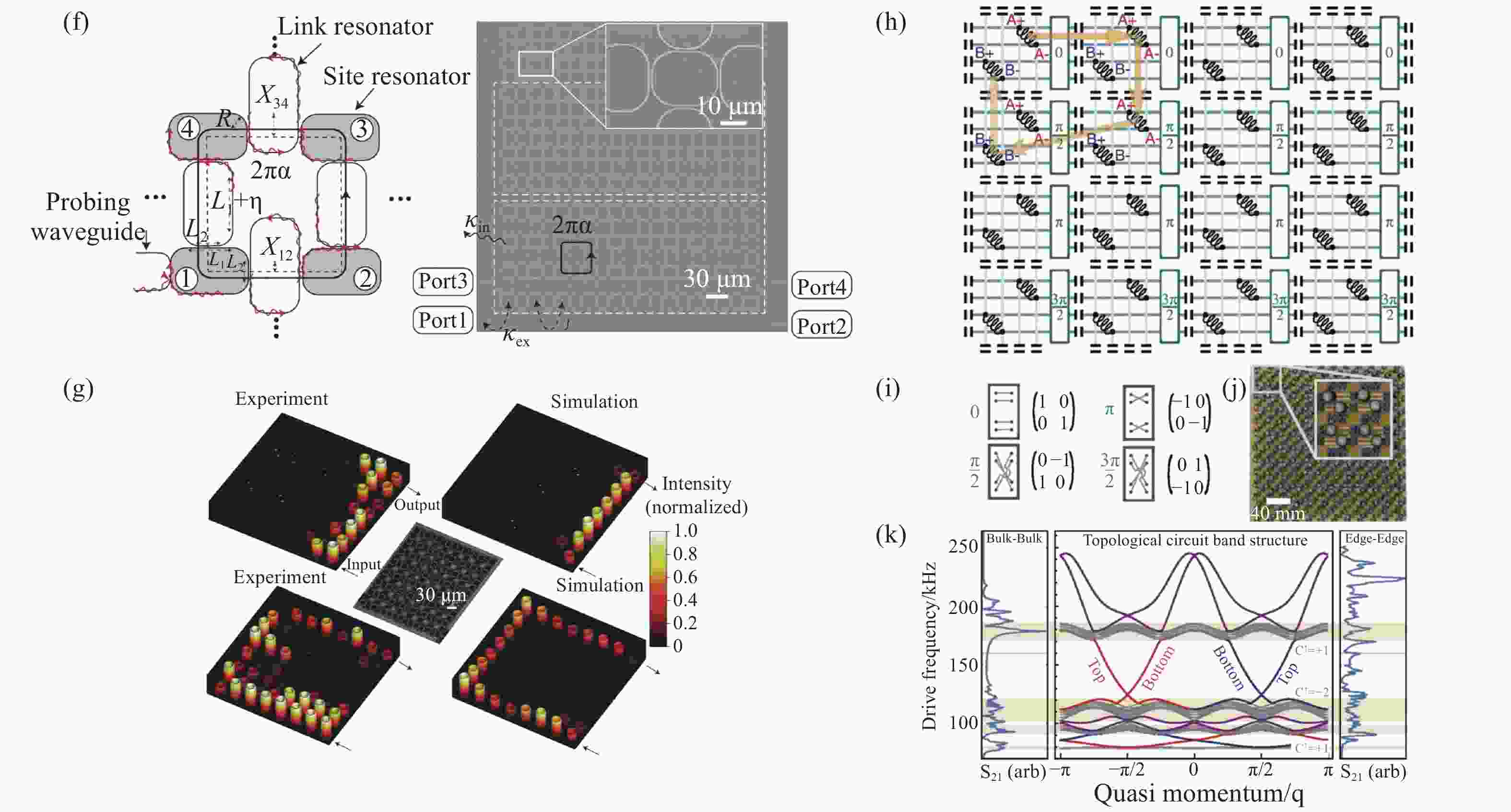
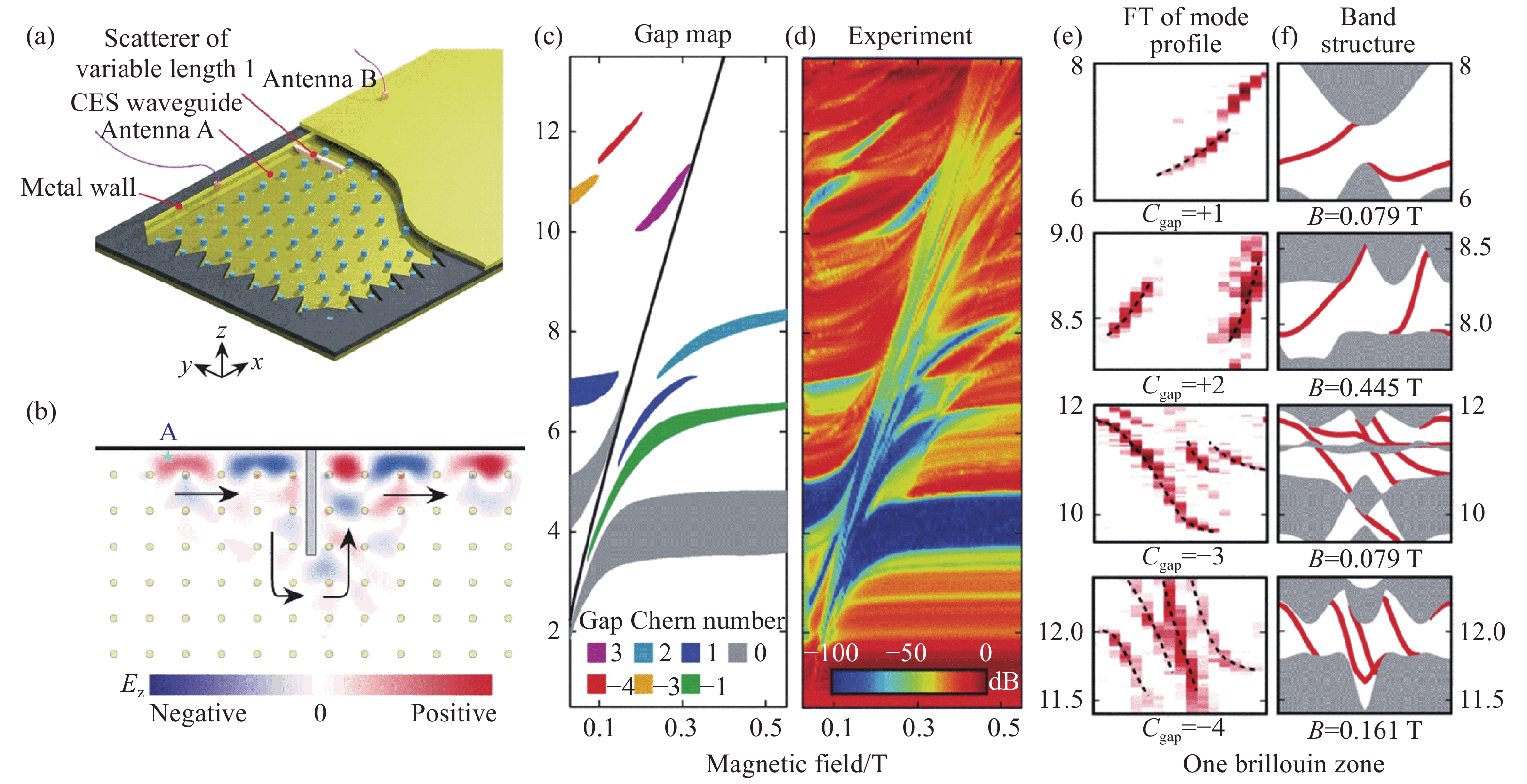
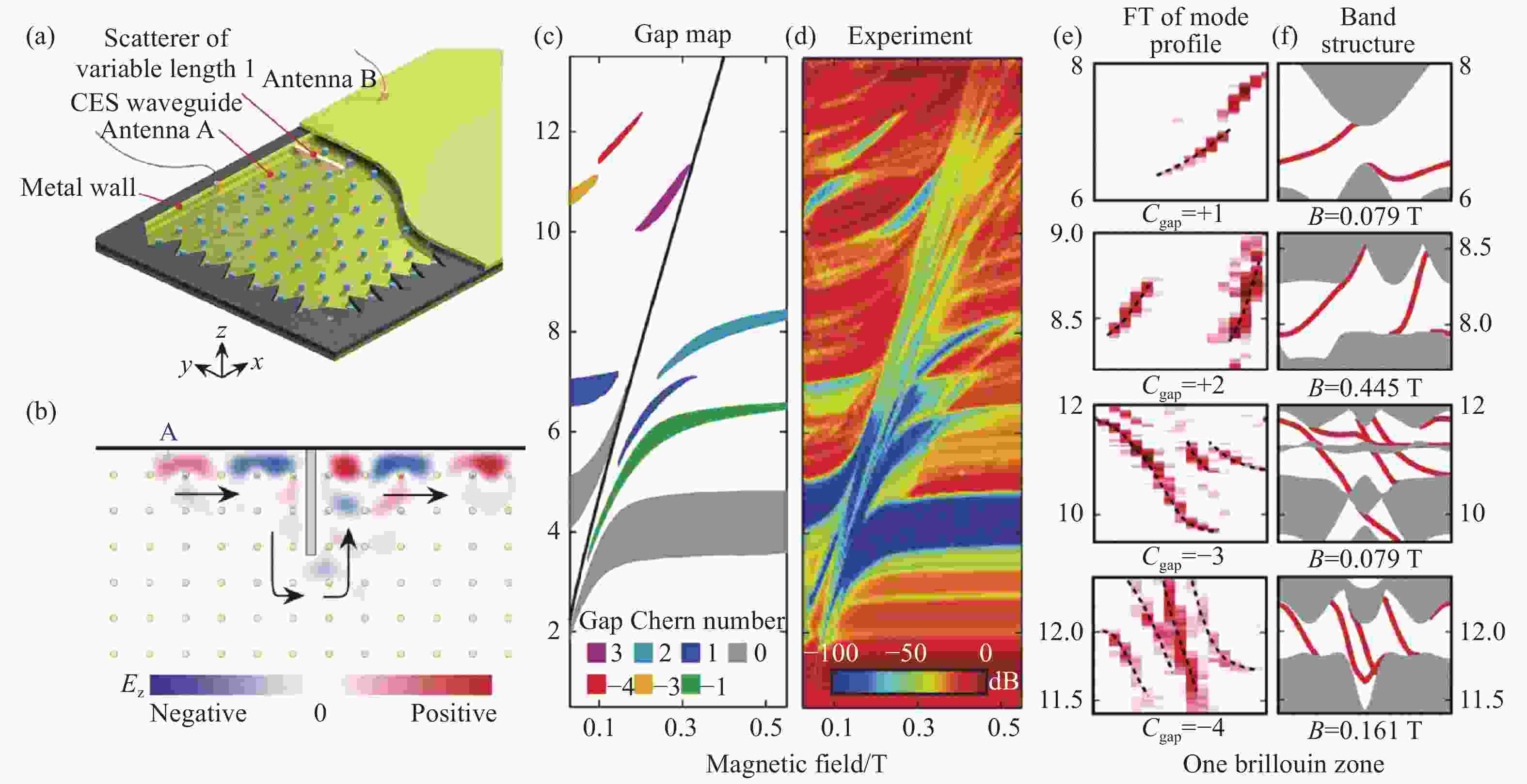
${a_0}/R$ 的比值设定为3.125 (左)、3(中)、2.9(右)的二维光子晶体能带结构,其中彩色能带展现了能带杂化[28]。(f)由位置谐振器和连接谐振器组成的光学耦合环谐振器单元(左)及其组成的二维硅光子平台的实验装置图(右)[27]。(g)不同激励频率下实验(左)和模拟(右)的边缘态示意图[27]。(h)射频电路拓扑绝缘体示意图,周期结构由位置电感器和耦合电容组成[31]。(i)格点间耦合元件结构[31]。(j)射频电路拓扑绝缘体实验样品图[31]。(k)射频电路的理论能带结构(中),实验测量的体态密度(左)和边缘态密度(右)[31]。Figure 2. (a) Schematic of reconfigurable topological metacrystal[107].Moving the relative position of the metal ring to the metal plate introduces negative (left), zero (middle), or positive (right) effective masses at the degeneracy. (b) Bulk band structures of reconfigurable topological metacrystal[107], in which blue dotted line and red dotted line correspond to symmetric (no bianisotropy) and asymmetric (with bianisotropy) structures, respectively. (c) The interface of two meta-crystal structures with opposite effective masses and the corresponding edge band diagrams[107]. (d) Schematic of 2D dielectric photonic crystal of honeycomb lattice[28]. (e) The band structure of 2D photonic crystals with
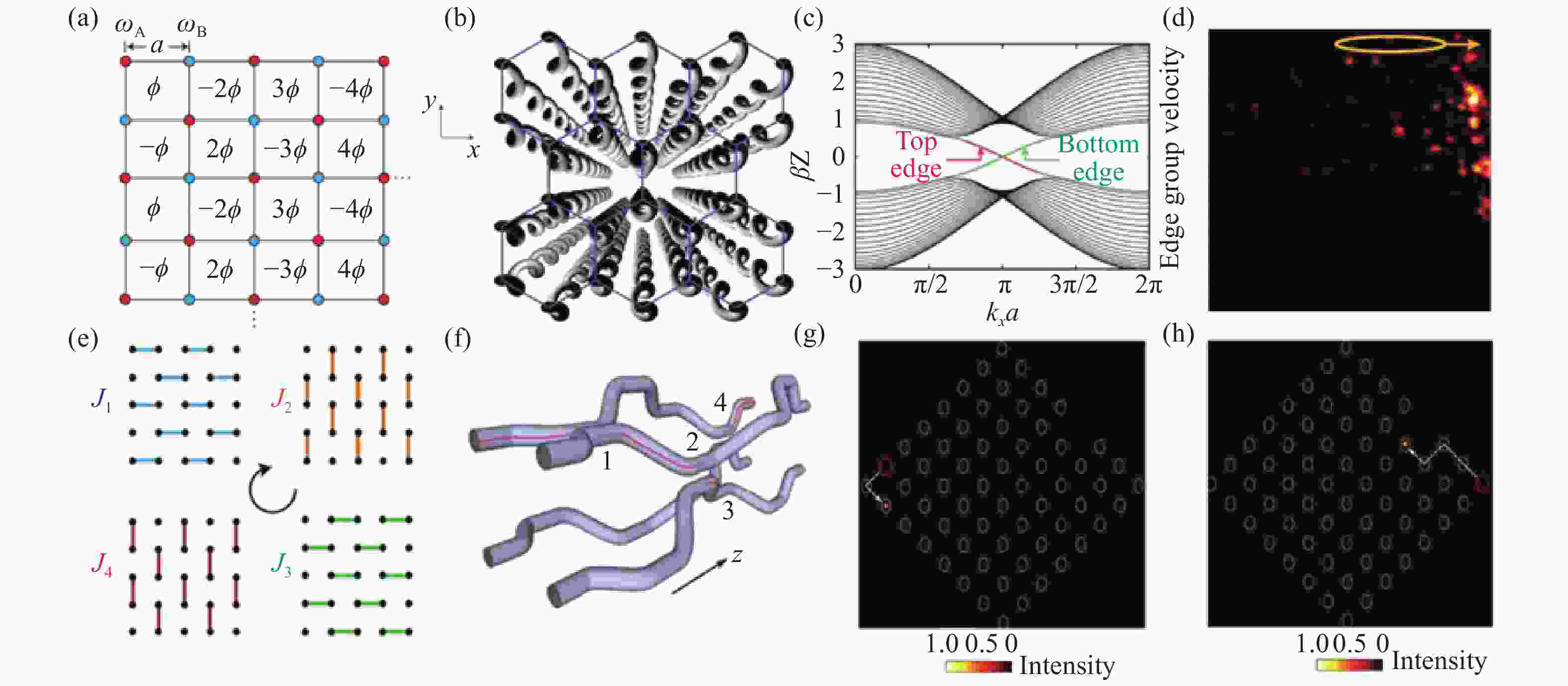
${a_0}/R$ ratios of 3.125 (left), 3(middle), and 2.9(right) was set by changing the distance between the artificial atoms where the rainbow for band hybridization[28]. (f) The unit of 2D coupled optical-ring resonators with site resonators and link resonators (left) and the experimental setup diagram of 2D silicon photonic platform (right)[27]. (g) Schematic of edge states of experiment (left) and simulation (right) at different excited frequency[27]. (h) Schematic of radio-frequency(RF) circuit topological insulators in which the periodic structure consists of position inductor and coupling capacitor[31]. (i) Structure of the coupling elements between lattice sites[31]. (j) Sample diagram of radio-frequency(RF) circuit topological insulators[31]. (k) Theoretical band structure of RF circuit (middle). Experimental density of states of bulk state(left) and edge state (right)[31].图 3 (a)光学谐振腔阵列动态调控产生的有效磁场[118]。(b)通过激光直写技术制作的螺旋波导阵列[34]。(c)螺旋波导R=8 μm的投影能带图[34]。(d)实验测量的出射面光强分布图,黄色的椭圆代表输入光束位置[34]。(e)一个传播周期内4种不同的耦合方式(J1-J4)[37]。(f)精心设计的波导结构示意图,传播方向z轴和时间轴等价[37]。(g-h)场强分布的实验测量图,不被拐角(g)和缺陷(h)散射的手性边界态[37]。
Figure 3. (a) Effective magnetic field generated by dynamic control of photonic cavity array[118]. (b) Helical waveguide array made by laser direct writing technology[34]. (c) Projected band diagram of spiral waveguide R=8 μm[34]. (d) The experimentally measured light intensity distribution of the output facet, the yellow ellipse shows the position of the input beam[34]. (e) Four different coupling modes(J1-J4) in one propagation cycle[37]. (f) Schematic diagram of finely engineered waveguide structure, the propagation direction z axis and time axis are equivalent[37]. (g-h) Experimental measurement diagram of field intensity distribution, chiral edge states that are not scattered by corners (g) and defects (h)[37].
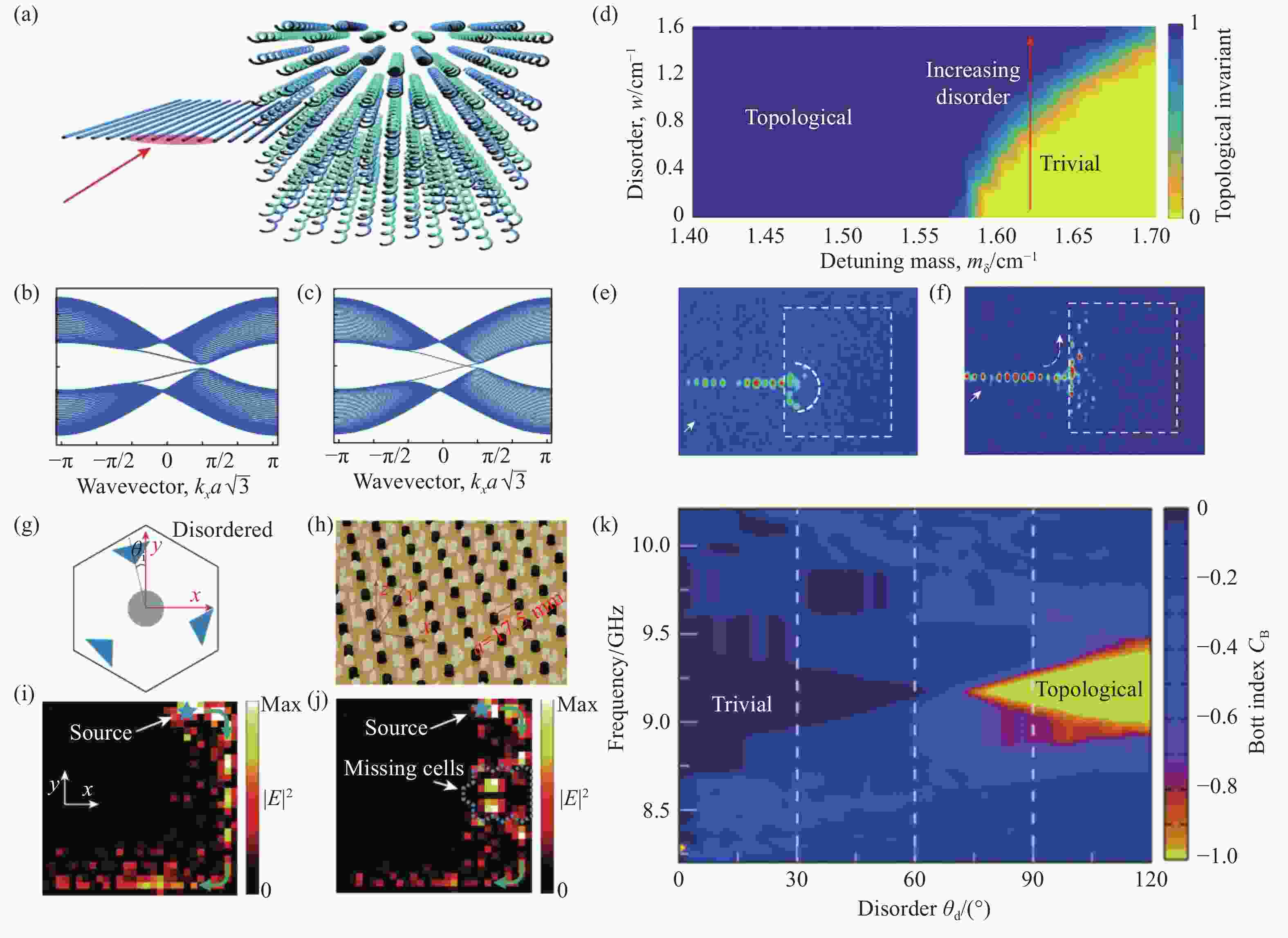
图 4 (a)一维波导和螺旋的二维蜂窝波导阵列组成的联合结构[127]。(b)打破中心反演对称性的平庸带隙[127]。(c)添加足够多无序的非平庸带隙[127]。(d)拓扑不变量在无序强度w和调谐质量
$ {m}_{\delta } $ 共同作用下的相图[127]。(e)处于拓扑非平庸相的实验测量图[127]。(f)加入足够多无序,处于安德森拓扑相的实验测量图[127]。(g)旋转电介质散射体引入无序的示意图[128]。(h)光子晶体的局部图[128],晶格常数a=17.5 mm。(i-j)场强分布的实验测量图[128],单向传播(i)和经过缺陷无散射(j)的手性边界态。(k) Bott因子$ {C}_{B} $ 随无序强度变化的模拟图[128],无序增加,平庸的带隙闭合又重新打开,成为非平庸的带隙。Figure 4. (a) Hybrid structure composed of a one-dimensional straw and a two-dimensional honeycomb lattice of helical waveguides[127]. (b) Breaking the parity symmetry of the structure causes a trivial bandgap[127]. (c) Sufficiently strong disorder induces a non-trivial bandgap[127]. (d) Phase diagram showing the trivial and topological phases as a function of the detuning mass
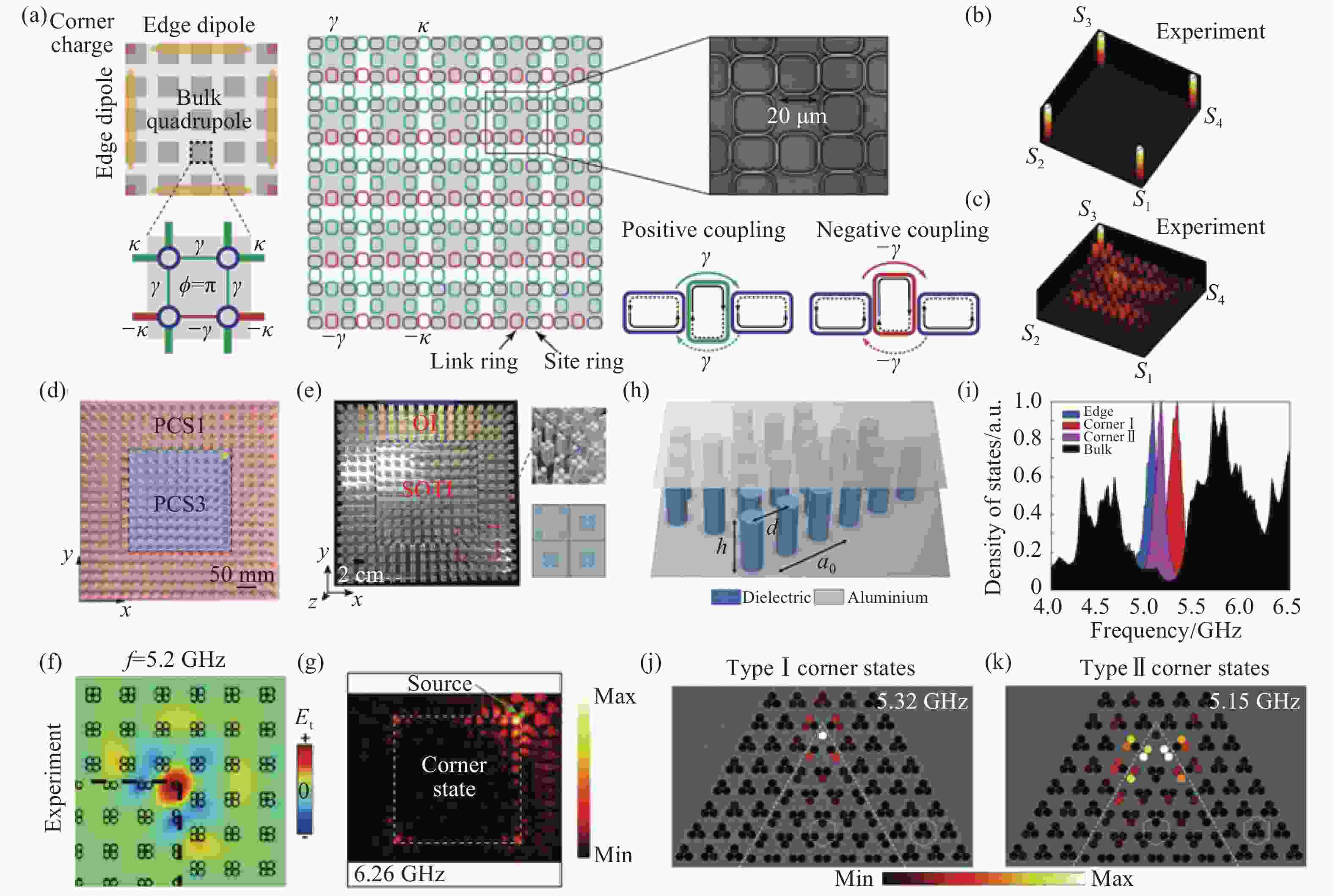
$ {m}_{\delta } $ and disorder strength w[127]. (e) Experimental measurement diagram in topological trival phase[127]. (f) Add sufficient disorder, experimental measurements in the Anderson topological phase[127]. (g) Schematic diagram of disorder introduced by rotating dielectric scatterers[128]. (h) The partial picture of the photonic crystal, the lattice constant a=17.5 mm[128]. (i-j) Experimental measurement diagrams of field intensity distribution[128], chiral edge states that are unidirectional propagation (i) and without scattering (j) through defects. (k) A simulation diagram of the Bott index$ {C}_{B} $ . With increasing disorder strength, the trival band gap closes and reopens as a nontrival band gap[128].图 5 (a)环形谐振腔构成的光子四极拓扑系统[150]。(b)非零四极矩时测量的空间强度分布,显示局域的角态[150]。(c)零四极矩时观测的空间强度分布,显示耦合到体态的角态[150]。(d-e)电介质材料构成的二阶拓扑系统[157-158]。(f-g)微波范围内实验测量的电场分布图,显示局域的角态[157-158]。(h) kagome格子的光子晶体结构示意图[48]。(i)实验测量的态密度谱[48]。(j-k)实验测量的场分布图[48],分别显示类型I的角态(j)和类型II的角态(k)。
Figure 5. (a) Schematic of the photonic quadrupole topological system composed of ring resonators[150]. (b) At nonzero quantized quadrupole moment the measured spatial intensity profiles shows the localized corner modes[150]. (c) At zero quantized quadrupole moment the measured spatial intensity profiles shows the corner modes coupling to the bulk modes[150]. (d-e) A second-order photonic system composed of dielectric materials[157-158]. (f-g) The electric field profiles measured experimentally in the microwave range showing the localized corner modes[157-158]. (h) Schematic diagram of the photonic crystal structure with kagome lattice[48]. (i) Experimentally measured densities of states[48]. (f-g) The experimentally measured field profiles respectively show the type I corner state (j) and the type II coner state (k)[48].
-
[1] CHEN L, RONG Y W. Digital topological method for computing genus and the Betti numbers[J]. Topology and its Applications, 2010, 157(12): 1931-1936. doi: 10.1016/j.topol.2010.04.006 [2] KLITZING K V, DORDA G, PEPPER M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance[J]. Physical Review Letters, 1980, 45(6): 494-497. doi: 10.1103/PhysRevLett.45.494 [3] DEN NIJS M. Quantized Hall conductance in a two dimensional periodic potential[J]. Physica A:Statistical Mechanics and its Applications, 1984, 124(1-3): 199-210. doi: 10.1016/0378-4371(84)90239-5 [4] HALDANE F D M, RAGHU S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry[J]. Physical Review Letters, 2008, 100(1): 013904. doi: 10.1103/PhysRevLett.100.013904 [5] RAGHU S, HALDANE F D M. Analogs of quantum-Hall-effect edge states in photonic crystals[J]. Physical Review A, 2008, 78(3): 033834. doi: 10.1103/PhysRevA.78.033834 [6] WANG ZH, CHONG Y D, JOANNOPOULOS J D, et al. Reflection-free one-way edge modes in a gyromagnetic photonic crystal[J]. Physical Review Letters, 2008, 100(1): 013905. doi: 10.1103/PhysRevLett.100.013905 [7] WANG ZH, CHONG Y D, JOANNOPOULOS J D, et al. Observation of unidirectional backscattering-immune topological electromagnetic states[J]. Nature, 2009, 461(7265): 772-775. doi: 10.1038/nature08293 [8] LIU SH Y, LU W L, LIN ZH F, et al. Magnetically controllable unidirectional electromagnetic waveguiding devices designed with metamaterials[J]. Applied Physics Letters, 2010, 97(20): 201113. doi: 10.1063/1.3520141 [9] HE CH, CHEN X L, LU M H, et al. Left-handed and right-handed one-way edge modes in a gyromagnetic photonic crystal[J]. Journal of Applied Physics, 2010, 107(12): 123117. doi: 10.1063/1.3374470 [10] QIU W J, WANG ZH, SOLJAČIĆ M. Broadband circulators based on directional coupling of one-way waveguides[J]. Optics Express, 2011, 19(22): 22248-22257. doi: 10.1364/OE.19.022248 [11] WANG ZH Y, SHEN L F, YU Z H, et al. Highly efficient photonic-crystal splitters based on one-way waveguiding[J]. Journal of the Optical Society of America B, 2013, 30(1): 173-176. doi: 10.1364/JOSAB.30.000173 [12] BAHARI B, TELLEZ-LIMON R, KANTÉ B. Topological terahertz circuits using semiconductors[J]. Applied Physics Letters, 2016, 109(14): 143501. doi: 10.1063/1.4963789 [13] WU Y, LI CH, HU X Y, et al. Applications of topological photonics in integrated photonic devices[J]. Advanced Optical Materials, 2017, 5(18): 1700357. doi: 10.1002/adom.201700357 [14] NI X, HE CH, SUN X CH, et al. Topologically protected one-way edge mode in networks of acoustic resonators with circulating air flow[J]. New Journal of Physics, 2015, 17(5): 053016. doi: 10.1088/1367-2630/17/5/053016 [15] DING Y J, PENG Y G, ZHU Y F, et al. Experimental demonstration of acoustic chern insulators[J]. Physical Review Letters, 2019, 122(1): 014302. doi: 10.1103/PhysRevLett.122.014302 [16] JO G B, GUZMAN J, THOMAS C K, et al. Ultracold atoms in a tunable optical kagome lattice[J]. Physical Review Letters, 2012, 108(4): 045305. doi: 10.1103/PhysRevLett.108.045305 [17] SOLTAN-PANAHI P, STRUCK J, HAUKE P, et al. Multi-component quantum gases in spin-dependent hexagonal lattices[J]. Nature Physics, 2011, 7(5): 434-440. doi: 10.1038/nphys1916 [18] NAKAJIMA S, TOMITA T, TAIE S, et al. Topological thouless pumping of ultracold fermions[J]. Nature Physics, 2016, 12(4): 296-300. doi: 10.1038/nphys3622 [19] HUBER S D. Topological mechanics[J]. Nature Physics, 2016, 12(7): 621-623. doi: 10.1038/nphys3801 [20] WANG P, LU L, BERTOLDI K. Topological phononic crystals with one-way elastic edge waves[J]. Physical Review Letters, 2015, 115(10): 104302. doi: 10.1103/PhysRevLett.115.104302 [21] SÜSSTRUNK R, HUBER S D. Observation of phononic helical edge states in a mechanical topological insulator[J]. Science, 2015, 349(6243): 47-50. doi: 10.1126/science.aab0239 [22] KANE C L, MELE E J. Z2 topological order and the quantum spin hall effect[J]. Physical Review Letters, 2005, 95(14): 146802. doi: 10.1103/PhysRevLett.95.146802 [23] KANE C L, MELE E J. Quantum Spin hall effect in graphene[J]. Physical Review Letters, 2005, 95(22): 226801. doi: 10.1103/PhysRevLett.95.226801 [24] BERNEVIG B A, HUGHES T L, ZHANG SH CH. Quantum spin hall effect and topological phase transition in HgTe quantum wells[J]. Science, 2006, 314(5806): 1757-1761. doi: 10.1126/science.1133734 [25] KÖNIG M, WIEDMANN S, BRÜNE C, et al. Quantum Spin Hall Insulator State in HgTe Quantum Wells[J]. Science, 2007, 318(5851): 766-770. doi: 10.1126/science.1148047 [26] HAFEZI M, DEMLER E A, LUKIN M D, et al. Robust optical delay lines with topological protection[J]. Nature Physics, 2011, 7(11): 907-912. doi: 10.1038/nphys2063 [27] HAFEZI M, MITTAL S, FAN J, et al. Imaging topological edge states in silicon photonics[J]. Nature Photonics, 2013, 7(12): 1001-1005. doi: 10.1038/nphoton.2013.274 [28] WU L H, HU X. Scheme for achieving a topological photonic crystal by using dielectric material[J]. Physical Review Letters, 2015, 114(22): 223901. doi: 10.1103/PhysRevLett.114.223901 [29] YANG Y T, XU Y F, XU T, et al. Visualization of a unidirectional electromagnetic waveguide using topological photonic crystals made of dielectric materials[J]. Physical Review Letters, 2018, 120(21): 217401. doi: 10.1103/PhysRevLett.120.217401 [30] ZHU X, WANG H X, XU CH Q, et al. Topological transitions in continuously deformed photonic crystals[J]. Physical Review B, 2018, 97(8): 085148. doi: 10.1103/PhysRevB.97.085148 [31] JIA N Y, OWENS C, SOMMER A, et al. Time- and site-resolved dynamics in a topological circuit[J]. Physical Review X, 2015, 5(2): 021031. doi: 10.1103/PhysRevX.5.021031 [32] KITAGAWA T, BERG E, RUDNER M, et al. Topological characterization of periodically driven quantum systems[J]. Physical Review B, 2010, 82(23): 235114. doi: 10.1103/PhysRevB.82.235114 [33] LINDNER N H, REFAEL G, GALITSKI V. Floquet topological insulator in semiconductor quantum wells[J]. Nature Physics, 2011, 7(6): 490-495. doi: 10.1038/nphys1926 [34] RECHTSMAN M C, ZEUNER J M, PLOTNIK Y, et al. Photonic Floquet topological insulators[J]. Nature, 2013, 496(7444): 196-200. doi: 10.1038/nature12066 [35] RUDNER M S, LINDNER N H, BERG E, et al. Anomalous edge states and the bulk-edge correspondence for periodically driven two-dimensional systems[J]. Physical Review X, 2013, 3(3): 031005. doi: 10.1103/PhysRevX.3.031005 [36] NATHAN F, RUDNER M S. Topological singularities and the general classification of Floquet-Bloch systems[J]. New Journal of Physics, 2015, 17(12): 125014. doi: 10.1088/1367-2630/17/12/125014 [37] MUKHERJEE S, SPRACKLEN A, VALIENTE M, et al. Experimental observation of anomalous topological edge modes in a slowly driven photonic lattice[J]. Nature Communications, 2017, 8(1): 3918. [38] MACZEWSKY L J, ZEUNER J M, NOLTE S, et al. Observation of photonic anomalous Floquet topological insulators[J]. Nature Communications, 2017, 8(1): 13756. doi: 10.1038/ncomms13756 [39] LUMER Y, PLOTNIK Y, RECHTSMAN M C, et al. Self-localized states in photonic topological insulators[J]. Physical Review Letters, 2013, 111(24): 243905. doi: 10.1103/PhysRevLett.111.243905 [40] LEYKAM D, RECHTSMAN M C, CHONG Y D. Anomalous topological phases and unpaired dirac cones in photonic floquet topological insulators[J]. Physical Review Letters, 2016, 117(1): 013902. doi: 10.1103/PhysRevLett.117.013902 [41] KRAUS Y E, LAHINI Y, RINGEL Z, et al. Topological states and adiabatic pumping in quasicrystals[J]. Physical Review Letters, 2012, 109(10): 106402. doi: 10.1103/PhysRevLett.109.106402 [42] ZILBERBERG O, HUANG SH, GUGLIELMON J, et al. Photonic topological boundary pumping as a probe of 4D quantum Hall physics[J]. Nature, 2018, 553(7686): 59-62. doi: 10.1038/nature25011 [43] VERBIN M, ZILBERBERG O, LAHINI Y, et al. Topological pumping over a photonic Fibonacci quasicrystal[J]. Physical Review B, 2015, 91(6): 064201. doi: 10.1103/PhysRevB.91.064201 [44] KE Y G, QIN X ZH, MEI F, et al. Topological phase transitions and thouless pumping of light in photonic waveguide arrays[J]. Laser &Photonics Reviews, 2016, 10(6): 995-1001. [45] BENALCAZAR W A, BERNEVIG B A, HUGHES T L. Quantized electric multipole insulators[J]. Science, 2017, 357(6346): 61-66. doi: 10.1126/science.aah6442 [46] BENALCAZAR W A, BERNEVIG B A, HUGHES T L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators[J]. Physical Review B, 2017, 96(24): 245115. doi: 10.1103/PhysRevB.96.245115 [47] PETERSON C W, BENALCAZAR W A, HUGHES T L, et al. A quantized microwave quadrupole insulator with topologically protected corner states[J]. Nature, 2018, 555(7696): 346-350. doi: 10.1038/nature25777 [48] LI M Y, ZHIRIHIN D, GORLACH M, et al. Higher-order topological states in photonic kagome crystals with long-range interactions[J]. Nature Photonics, 2020, 14(2): 89-94. doi: 10.1038/s41566-019-0561-9 [49] EZAWA M. Higher-order topological insulators and semimetals on the breathing kagome and pyrochlore lattices[J]. Physical Review Letters, 2018, 120(2): 026801. doi: 10.1103/PhysRevLett.120.026801 [50] BENALCAZAR W A, LI T H, HUGHES T L. Quantization of fractional corner charge in Cn-symmetric higher-order topological crystalline insulators[J]. Physical Review B, 2019, 99(24): 245151. doi: 10.1103/PhysRevB.99.245151 [51] ZHANG X J, XIAO M, CHENG Y, et al. Topological sound[J]. Communications Physics, 2018, 1(1): 97. doi: 10.1038/s42005-018-0094-4 [52] YANG ZH J, GAO F, SHI X H, et al. Topological acoustics[J]. Physical Review Letters, 2015, 114(11): 114301. doi: 10.1103/PhysRevLett.114.114301 [53] HE CH, NI X, GE H, et al. Acoustic topological insulator and robust one-way sound transport[J]. Nature Physics, 2016, 12(12): 1124-1129. doi: 10.1038/nphys3867 [54] XIAO M, CHEN W J, HE W Y, et al. Synthetic gauge flux and Weyl points in acoustic systems[J]. Nature Physics, 2015, 11(11): 920-924. doi: 10.1038/nphys3458 [55] XIE B Y, LIU H, CHENG H, et al. Experimental realization of type-II weyl points and fermi arcs in phononic crystal[J]. Physical Review Letters, 2019, 122(10): 104302. doi: 10.1103/PhysRevLett.122.104302 [56] XIE B Y, LIU H, CHENG H, et al. Acoustic topological transport and refraction in a Kekulé Lattice[J]. Physical Review Applied, 2019, 11(4): 044086. doi: 10.1103/PhysRevApplied.11.044086 [57] ROCKLIN D Z, ZHOU SH N, SUN K, et al. Transformable topological mechanical metamaterials[J]. Nature Communications, 2017, 8(1): 14201. doi: 10.1038/ncomms14201 [58] LU L, GAO H ZH, WANG ZH. Topological one-way fiber of second Chern number[J]. Nature Communications, 2018, 9(1): 5384. doi: 10.1038/s41467-018-07817-3 [59] YANG Y H, GAO ZH, XUE H R, et al. Realization of a three-dimensional photonic topological insulator[J]. Nature, 2019, 565(7741): 622-626. doi: 10.1038/s41586-018-0829-0 [60] SLOBOZHANYUK A, MOUSAVI S H, NI X, et al. Three-dimensional all-dielectric photonic topological insulator[J]. Nature Photonics, 2017, 11(2): 130-136. doi: 10.1038/nphoton.2016.253 [61] LU L, FANG CH, FU L, et al. Symmetry-protected topological photonic crystal in three dimensions[J]. Nature Physics, 2016, 12(4): 337-340. doi: 10.1038/nphys3611 [62] YOUNG S M, ZAHEER S, TEO J C Y, et al. Dirac Semimetal in Three Dimensions[J]. Physical Review Letters, 2012, 108(14): 140405. doi: 10.1103/PhysRevLett.108.140405 [63] LU L, FU L, JOANNOPOULOS J D, et al. Weyl points and line nodes in gyroid photonic crystals[J]. Nature Photonics, 2013, 7(4): 294-299. doi: 10.1038/nphoton.2013.42 [64] GUO Q H, YOU O B, YANG B, et al. Observation of three-dimensional photonic dirac points and spin-polarized surface arcs[J]. Physical Review Letters, 2019, 122(20): 203903. doi: 10.1103/PhysRevLett.122.203903 [65] CHENG H, GAO W L, BI Y G, et al. Vortical reflection and spiraling fermi arcs with weyl metamaterials[J]. Physical Review Letters, 2020, 125(9): 093904. doi: 10.1103/PhysRevLett.125.093904 [66] OZAWA T, PRICE H M, GOLDMAN N, et al. Synthetic dimensions in integrated photonics: From optical isolation to four-dimensional quantum Hall physics[J]. Physical Review A, 2016, 93(4): 043827. doi: 10.1103/PhysRevA.93.043827 [67] LIN Q, SUN X Q, XIAO M, et al. A three-dimensional photonic topological insulator using a two-dimensional ring resonator lattice with a synthetic frequency dimension[J]. Science Advances, 2018, 4(10): eaat2774. doi: 10.1126/sciadv.aat2774 [68] YUAN L Q, LIN Q, XIAO M, et al. Synthetic dimension in photonics[J]. Optica, 2018, 5(11): 1396-1405. doi: 10.1364/OPTICA.5.001396 [69] LUSTIG E, WEIMANN S, PLOTNIK Y, et al. Photonic topological insulator in synthetic dimensions[J]. Nature, 2019, 567(7748): 356-360. doi: 10.1038/s41586-019-0943-7 [70] CHEN Y, ZHANG Y L, SHEN ZH, et al. Synthetic gauge fields in a single optomechanical resonator[J]. Physical Review Letters, 2021, 126(12): 123603. doi: 10.1103/PhysRevLett.126.123603 [71] LI G ZH, ZHENG Y L, DUTT A, et al. Dynamic band structure measurement in the synthetic space[J]. Science Advances, 2021, 7(2): eabe4335. doi: 10.1126/sciadv.abe4335 [72] WANG Q, XIAO M, LIU H, et al. Optical interface states protected by synthetic weyl points[J]. Physical Review X, 2017, 7(3): 031032. doi: 10.1103/PhysRevX.7.031032 [73] LIN Q, XIAO M, YUAN L Q, et al. Photonic Weyl point in a two-dimensional resonator lattice with a synthetic frequency dimension[J]. Nature Communications, 2016, 7(1): 13731. doi: 10.1038/ncomms13731 [74] SUN B Y, LUO X W, GONG M, et al. Weyl semimetal phases and implementation in degenerate optical cavities[J]. Physical Review A, 2017, 96(1): 013857. doi: 10.1103/PhysRevA.96.013857 [75] ZHANG Y, ZHU Y Y. Generation of Weyl points in coupled optical microdisk-resonator arrays via external modulation[J]. Physical Review A, 2017, 96(1): 013811. doi: 10.1103/PhysRevA.96.013811 [76] LIU ZH ZH, ZHANG Q, QIN F F, et al. Surface states ensured by a synthetic Weyl point in one-dimensional plasmonic dielectric crystals with broken inversion symmetry[J]. Physical Review B, 2019, 99(8): 085441. doi: 10.1103/PhysRevB.99.085441 [77] LEYKAM D, CHONG Y D. Edge solitons in nonlinear-photonic topological insulators[J]. Physical Review Letters, 2016, 117(14): 143901. doi: 10.1103/PhysRevLett.117.143901 [78] PODDUBNY A N, SMIRNOVA D A. Ring Dirac solitons in nonlinear topological systems[J]. Physical Review A, 2018, 98(1): 013827. doi: 10.1103/PhysRevA.98.013827 [79] HADAD Y, KHANIKAEV A B, ALÙ A. Self-induced topological transitions and edge states supported by nonlinear staggered potentials[J]. Physical Review B, 2016, 93(15): 155112. doi: 10.1103/PhysRevB.93.155112 [80] GREENTREE A D, TAHAN C, COLE J H, et al. Quantum phase transitions of light[J]. Nature Physics, 2006, 2(12): 856-861. doi: 10.1038/nphys466 [81] HARTMANN M J, BRANDÃO F G S L, PLENIO M B. Strongly interacting polaritons in coupled arrays of cavities[J]. Nature Physics, 2006, 2(12): 849-855. doi: 10.1038/nphys462 [82] ANGELAKIS D G, SANTOS M F, BOSE S. Photon-blockade-induced Mott transitions and XY spin models in coupled cavity arrays[J]. Physical Review A, 2007, 76(3): 031805(R). doi: 10.1103/PhysRevA.76.031805 [83] ZHAO H, QIAO X D, WU T W, et al. Non-Hermitian topological light steering[J]. Science, 2019, 365(6458): 1163-1166. doi: 10.1126/science.aay1064 [84] ZHEN B, HSU C W, IGARASHI Y, et al. Spawning rings of exceptional points out of Dirac cones[J]. Nature, 2015, 525(7569): 354-358. doi: 10.1038/nature14889 [85] LEE T E. Anomalous edge state in a non-hermitian lattice[J]. Physical Review Letters, 2016, 116(13): 133903. doi: 10.1103/PhysRevLett.116.133903 [86] SEPKHANOV R A, NILSSON J, BEENAKKER C W J. Proposed method for detection of the pseudospin- Berry phase in a photonic crystal with a Dirac spectrum[J]. Physical Review B, 2008, 78(4): 045122. doi: 10.1103/PhysRevB.78.045122 [87] XIAO D, CHANG M C, NIU Q. Berry phase effects on electronic properties[J]. Reviews of Modern Physics, 2010, 82(3): 1959-2007. doi: 10.1103/RevModPhys.82.1959 [88] THOULESS D J, KOHMOTO M, NIGHTINGALE M P, et al. Quantized hall conductance in a two-dimensional periodic potential[J]. Physical Review Letters, 1982, 49(6): 405-408. doi: 10.1103/PhysRevLett.49.405 [89] SKIRLO S A, LU L, SOLJAČIĆ M. Multimode one-way waveguides of large chern numbers[J]. Physical Review Letters, 2014, 113(11): 113904. doi: 10.1103/PhysRevLett.113.113904 [90] SKIRLO S A, LU L, IGARASHI Y, et al. Experimental observation of large chern numbers in photonic crystals[J]. Physical Review Letters, 2015, 115(25): 253901. doi: 10.1103/PhysRevLett.115.253901 [91] YANG Y, POO Y, WU R X, et al. Experimental demonstration of one-way slow wave in waveguide involving gyromagnetic photonic crystals[J]. Applied Physics Letters, 2013, 102(23): 231113. doi: 10.1063/1.4809956 [92] FU J X, LIU R J, LI Z Y. Robust one-way modes in gyromagnetic photonic crystal waveguides with different interfaces[J]. Applied Physics Letters, 2010, 97(4): 041112. doi: 10.1063/1.3470873 [93] WANG D L, QIU CH W, RAKICH P T, et al.. Guide-wave photonic pulling force using one-way photonic chiral edge states[C]. CLEO: QELS_Fundamental Science 2015, OSA, 2015: FM2D. 7. [94] RYCERZ A, TWORZYDŁO J, BEENAKKER C W J. Valley filter and valley valve in graphene[J]. Nature Physics, 2007, 3(3): 172-175. doi: 10.1038/nphys547 [95] JU L, SHI ZH W, NAIR N, et al. Topological valley transport at bilayer graphene domain walls[J]. Nature, 2015, 520(7549): 650-655. doi: 10.1038/nature14364 [96] DONG J W, CHEN X D, ZHU H Y, et al. Valley photonic crystals for control of spin and topology[J]. Nature Materials, 2017, 16(3): 298-302. doi: 10.1038/nmat4807 [97] WU X X, MENG Y, TIAN J X, et al. Direct observation of valley-polarized topological edge states in designer surface plasmon crystals[J]. Nature Communications, 2017, 8(1): 1304. doi: 10.1038/s41467-017-01515-2 [98] NOH J, HUANG SH, CHEN K P, et al. Observation of photonic topological valley hall edge states[J]. Physical Review Letters, 2018, 120(6): 063902. doi: 10.1103/PhysRevLett.120.063902 [99] CHEN Q L, ZHANG L, HE M J, et al. Valley-hall photonic topological insulators with dual-band kink states[J]. Advanced Optical Materials, 2019, 7(15): 1900036. doi: 10.1002/adom.201900036 [100] HE X T, LIANG E T, YUAN J J, et al. A silicon-on-insulator slab for topological valley transport[J]. Nature Communications, 2019, 10(1): 872. doi: 10.1038/s41467-019-08881-z [101] LU J Y, QIU CH Y, YE L P, et al. Observation of topological valley transport of sound in sonic crystals[J]. Nature Physics, 2017, 13(4): 369-374. doi: 10.1038/nphys3999 [102] LU J Y, QIU CH Y, DENG W Y, et al. Valley topological phases in bilayer sonic crystals[J]. Physical Review Letters, 2018, 120(11): 116802. doi: 10.1103/PhysRevLett.120.116802 [103] ZHANG X J, LIU L, LU M H, et al. Valley-selective topological corner states in sonic crystals[J]. Physical Review Letters, 2021, 126(15): 156401. doi: 10.1103/PhysRevLett.126.156401 [104] CHEN W J, JIANG SH J, CHEN X D, et al. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide[J]. Nature Communications, 2014, 5(1): 5782. doi: 10.1038/ncomms6782 [105] LAI K, MA T, BO X, et al. Experimental realization of a reflections-free compact delay line based on a photonic topological insulator[J]. Scientific Reports, 2016, 6(1): 28453. doi: 10.1038/srep28453 [106] XIAO B, LAI K, YU Y, et al. Exciting reflectionless unidirectional edge modes in a reciprocal photonic topological insulator medium[J]. Physical Review B, 2016, 94(19): 195427. doi: 10.1103/PhysRevB.94.195427 [107] CHENG X J, JOUVAUD C, NI X, et al. Robust reconfigurable electromagnetic pathways within a photonic topological insulator[J]. Nature Materials, 2016, 15(5): 542-548. doi: 10.1038/nmat4573 [108] MA T, KHANIKAEV A B, MOUSAVI S H, et al. Guiding electromagnetic waves around sharp corners: topologically protected photonic transport in metawaveguides[J]. Physical Review Letters, 2015, 114(12): 127401. doi: 10.1103/PhysRevLett.114.127401 [109] YVES S, FLEURY R, LEMOULT F, et al. Topological acoustic polaritons: Robust sound manipulation at the subwavelength scale[J]. New Journal of Physics, 2017, 19(7): 075003. doi: 10.1088/1367-2630/aa66f8 [110] GORLACH M A, NI X, SMIRNOVA D A, et al. Far-field probing of leaky topological states in all-dielectric metasurfaces[J]. Nature Communications, 2018, 9(1): 909. doi: 10.1038/s41467-018-03330-9 [111] BARIK S, KARASAHIN A, FLOWER C, et al. A topological quantum optics interface[J]. Science, 2018, 359(6376): 666-668. doi: 10.1126/science.aaq0327 [112] IMHOF S, BERGER C, BAYER F, et al. Topolectrical-circuit realization of topological corner modes[J]. Nature Physics, 2018, 14(9): 925-929. doi: 10.1038/s41567-018-0246-1 [113] LEE C H, IMHOF S, BERGER C, et al. Topolectrical circuits[J]. Communications Physics, 2018, 1(1): 39. doi: 10.1038/s42005-018-0035-2 [114] LU Y H, JIA N Y, SU L, et al. Probing the Berry curvature and Fermi arcs of a Weyl circuit[J]. Physical Review B, 2019, 99(2): 020302(R). doi: 10.1103/PhysRevB.99.020302 [115] WALLRAFF A, SCHUSTER D I, BLAIS A, et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics[J]. Nature, 2004, 431(7005): 162-167. doi: 10.1038/nature02851 [116] SALA V G, SOLNYSHKOV D D, CARUSOTTO I, et al. Spin-orbit coupling for photons and polaritons in microstructures[J]. Physical Review X, 2015, 5(1): 011034. doi: 10.1103/PhysRevX.5.011034 [117] CAYSSOL J, DÓRA B, SIMON F, et al. Floquet topological insulators[J]. Physica Status Solidi, 2013, 7(1-2): 101-108. doi: 10.1002/pssr.201206451 [118] FANG K J, YU Z F, FAN SH H. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation[J]. Nature Photonics, 2012, 6(11): 782-787. doi: 10.1038/nphoton.2012.236 [119] OZAWA T, PRICE H M, AMO A, et al. Topological photonics[J]. Reviews of Modern Physics, 2019, 91(1): 015006. doi: 10.1103/RevModPhys.91.015006 [120] PASEK M, CHONG Y D. Network models of photonic Floquet topological insulators[J]. Physical Review B, 2014, 89(7): 075113. doi: 10.1103/PhysRevB.89.075113 [121] GAO F, GAO ZH, SHI X H, et al. Probing topological protection using a designer surface plasmon structure[J]. Nature Communications, 2016, 7(48): 11619. [122] YANG ZH J, LUSTIG E, LUMER Y, et al. Photonic Floquet topological insulators in a fractal lattice[J]. Light:Science &Applications, 2020, 9(1): 128. [123] LI J, CHU R L, JAIN J K, et al. Topological anderson insulator[J]. Physical Review Letters, 2009, 102(13): 136806. doi: 10.1103/PhysRevLett.102.136806 [124] GROTH C W, WIMMER M, AKHMEROV A R, et al. Theory of the topological anderson insulator[J]. Physical Review Letters, 2009, 103(19): 196805. doi: 10.1103/PhysRevLett.103.196805 [125] TITUM P, LINDNER N H, RECHTSMAN M C, et al. Disorder-induced Floquet topological insulators[J]. Physical Review Letters, 2015, 114(5): 056801. doi: 10.1103/PhysRevLett.114.056801 [126] TITUM P, LINDNER N H, REFAEL G. Disorder-induced transitions in resonantly driven Floquet topological insulators[J]. Physical Review B, 2017, 96(5): 054207. doi: 10.1103/PhysRevB.96.054207 [127] STÜTZER S, PLOTNIK Y, LUMER Y, et al. Photonic topological Anderson insulators[J]. Nature, 2018, 560(7719): 461-465. doi: 10.1038/s41586-018-0418-2 [128] LIU G G, YANG Y H, REN X, et al. Topological anderson insulator in disordered photonic crystals[J]. Physical Review Letters, 2020, 125(13): 133603. doi: 10.1103/PhysRevLett.125.133603 [129] HUANG H Q, LIU F. Theory of spin Bott index for quantum spin Hall states in nonperiodic systems[J]. Physical Review B, 2018, 98(12): 125130. doi: 10.1103/PhysRevB.98.125130 [130] HUANG H Q, LIU F. Quantum Spin hall effect and spin bott index in a quasicrystal lattice[J]. Physical Review Letters, 2018, 121(12): 126401. doi: 10.1103/PhysRevLett.121.126401 [131] SHINDOU R, MURAKAMI S. Effects of disorder in three-dimensional Z2 quantum spin Hall systems[J]. Physical Review B, 2009, 79(4): 045321. doi: 10.1103/PhysRevB.79.045321 [132] HUANG X Q, LU J Y, YAN Z B, et al.. Acoustic corner states in topological insulators with built-in Zeeman-like fields[J]. arXiv: 2008.06272, 2020. [133] LORING T A, HASTINGS M B. Disordered topological insulators via C*-algebras[J]. EPL (Europhysics Letters) , 2011, 92(6): 67004. [134] HASTINGS M B, LORING T A. Topological insulators and C*-algebras: theory and numerical practice[J]. Annals of Physics, 2011, 326(7): 1699-1759. doi: 10.1016/j.aop.2010.12.013 [135] LORING T A. A guide to the bott index and localizer index[J]. arXiv: 1907.11791, 2019. [136] TONIOLO D. On the equivalence of the Bott index and the Chern number on a torus, and the quantization of the Hall conductivity with a real space Kubo formula[J]. arXiv: 1708.05912, 2017. [137] MEIER E J, AN F A, DAUPHIN A, et al. Observation of the topological Anderson insulator in disordered atomic wires[J]. Science, 2018, 362(6417): 929-933. doi: 10.1126/science.aat3406 [138] GUO H M, ROSENBERG G, REFAEL G, et al. Topological Anderson insulator in three dimensions[J]. Physical Review Letters, 2010, 105(21): 216601. doi: 10.1103/PhysRevLett.105.216601 [139] SMIRNOVA D, LEYKAM D, CHONG Y D, et al. Nonlinear topological photonics[J]. Applied Physics Reviews, 2020, 7(2): 021306. doi: 10.1063/1.5142397 [140] DU Z Z, WANG C M, LI SH, et al. Disorder-induced nonlinear Hall effect with time-reversal symmetry[J]. Nature Communications, 2019, 10(1): 3047. doi: 10.1038/s41467-019-10941-3 [141] ZENG Y Q, CHATTOPADHYAY U, ZHU B F, et al. Electrically pumped topological laser with valley edge modes[J]. Nature, 2020, 578(7794): 246-250. doi: 10.1038/s41586-020-1981-x [142] BANDRES M A, WITTEK S, HARARI G, et al. Topological insulator laser: Experiments[J]. Science, 2018, 359(6381): eaar4005. doi: 10.1126/science.aar4005 [143] TANG L ZH, ZHANG L F, ZHANG G Q, et al. Topological Anderson insulators in two-dimensional non-Hermitian disordered systems[J]. Physical Review A, 2020, 101(6): 063612. doi: 10.1103/PhysRevA.101.063612 [144] LUO X W, ZHANG CH W. Non-hermitian disorder-induced topological insulators[J]. arXiv: 1912.10652, 2019. [145] SILVEIRINHA M G. Proof of the bulk-edge correspondence through a link between topological photonics and fluctuation-electrodynamics[J]. Physical Review X, 2019, 9(1): 011037. doi: 10.1103/PhysRevX.9.011037 [146] LU L, JOANNOPOULOS J D, SOLJAČIĆ M. Topological photonics[J]. Nature Photonics, 2014, 8(11): 821-829. doi: 10.1038/nphoton.2014.248 [147] PARAMESWARAN S A, WAN Y. Topological insulators turn a corner[J]. Physics, 2017, 10: 132. doi: 10.1103/Physics.10.132 [148] SCHINDLER F, COOK A M, VERGNIORY M G, et al. Higher-order topological insulators[J]. Science Advances, 2018, 4(6): eaat0346. doi: 10.1126/sciadv.aat0346 [149] SERRA-GARCIA M, PERI V, SÜSSTRUNK R, et al. Observation of a phononic quadrupole topological insulator[J]. Nature, 2018, 555(7696): 342-345. doi: 10.1038/nature25156 [150] MITTAL S, ORRE V V, ZHU G Y, et al. Photonic quadrupole topological phases[J]. Nature Photonics, 2019, 13(10): 692-696. doi: 10.1038/s41566-019-0452-0 [151] HE L, ADDISON Z, MELE E J, et al. Quadrupole topological photonic crystals[J]. Nature Communications, 2020, 11(1): 3119. doi: 10.1038/s41467-020-16916-z [152] ZHOU X X, LIN Z K, LU W X, et al. Twisted quadrupole topological photonic crystals[J]. Laser &Photonics Reviews, 2020, 14(8): 2000010. [153] SU W P, SCHRIEFFER J R, HEEGER A J. Solitons in polyacetylene[J]. Physical Review Letters, 1979, 42(25): 1698-1701. doi: 10.1103/PhysRevLett.42.1698 [154] XUE H R, YANG Y H, GAO F, et al. Acoustic higher-order topological insulator on a kagome lattice[J]. Nature Materials, 2019, 18(2): 108-112. doi: 10.1038/s41563-018-0251-x [155] LIU F, WAKABAYASHI K. Novel topological phase with a zero berry curvature[J]. Physical Review Letters, 2017, 118(7): 076803. doi: 10.1103/PhysRevLett.118.076803 [156] XIE B Y, WANG H F, WANG H X, et al. Second-order photonic topological insulator with corner states[J]. Physical Review B, 2018, 98(20): 205147. doi: 10.1103/PhysRevB.98.205147 [157] CHEN X D, DENG W M, SHI F L, et al. Direct observation of corner states in second-order topological photonic crystal slabs[J]. Physical Review Letters, 2019, 122(23): 233902. doi: 10.1103/PhysRevLett.122.233902 [158] XIE B Y, SU G X, WANG H F, et al. Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals[J]. Physical Review Letters, 2019, 122(23): 233903. doi: 10.1103/PhysRevLett.122.233903 [159] KIM M, RHO J. Topological edge and corner states in a two-dimensional photonic Su-Schrieffer-Heeger lattice[J]. Nanophotonics, 2020, 9(10): 3227-3234. doi: 10.1515/nanoph-2019-0451 [160] OTA Y, LIU F, KATSUMI R, et al. Photonic crystal nanocavity based on a topological corner state[J]. Optica, 2019, 6(6): 786-789. doi: 10.1364/OPTICA.6.000786 [161] NOH J, BENALCAZAR W A, HUANG SH, et al. Topological protection of photonic mid-gap defect modes[J]. Nature Photonics, 2018, 12(7): 408-415. doi: 10.1038/s41566-018-0179-3 [162] EL HASSAN A, KUNST F K, MORITZ A, et al. Corner states of light in photonic waveguides[J]. Nature Photonics, 2019, 13(10): 697-700. doi: 10.1038/s41566-019-0519-y [163] XIE X, ZHANG W X, HE X W, et al. Cavity quantum electrodynamics with second-order topological corner state[J]. Laser &Photonics Reviews, 2020, 14(8): 1900425. [164] ZHANG W X, XIE X, HAO H M, et al. Low-threshold topological nanolasers based on the second-order corner state[J]. Light:Science &Applications, 2020, 9(1): 109. [165] ZHANG L, YANG Y H, LIN Z K, et al. Higher-order topological states in surface-wave photonic crystals[J]. Advsnced Science, 2020, 7(6): 1902724. [166] LUO X W, ZHANG C W. Higher-order topological corner states induced by gain and loss[J]. Physical Review Letters, 2019, 123(7): 73601. doi: 10.1103/PhysRevLett.123.073601 [167] LIU T, ZHANG Y R, AI Q, et al. Second-order topological phases in non-hermitian systems[J]. Physical Review Letters, 2019, 122(7): 76801. doi: 10.1103/PhysRevLett.122.076801 -





 下载:
下载: