拓扑电路——新奇拓扑物理现象的研究平台

刘硕; 张霜; 崔铁军

doi:10.37188/CO.2021-0095

拓扑电路——新奇拓扑物理现象的研究平台

刘硕^1,,
张霜^3, ,,
崔铁军^2, ,

1.
英国伯明翰大学天文与物理学院，伯明翰英国，B152TT
2.
东南大学毫米波国家重点实验室，江苏南京，210096
3.
香港大学物理系，中国香港，999077

详细信息

中图分类号: 140.5099
计量
- 文章访问数: 4137
- HTML全文浏览量: 2625
- PDF下载量: 704
- 被引次数: 0
出版历程
- 收稿日期: 2021-04-29
- 修回日期: 2021-06-08
- 网络出版日期: 2021-06-22
- 刊出日期: 2021-07-01

Topological circuit: a playground for exotic topological physics

doi: 10.37188/CO.2021-0095

LIU Shuo^1
,,
ZHANG Shuang^{3
, ,},
CUI Tie-jun^{2
, ,}

1.
School of Physics and Astronomy, University of Birmingham, Birmingham B15 2TT, United Kingdom
2.
State Key Laboratory of Millimeter Waves, Southeast University, Nanjing 210096, China
3.
Department of Physics, The University of Hong Kong, Pokfulam road 999077, Hong Kong, China

Funds: Supported by European Union′s Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie (No. 833797); Royal Society, the Wolfson Foundation, Horizon 2020 Action Project (No. 734578, D-SPA; 648783, Topological); National key Research and Development Program of China (No. 2017YFA0700201, No. 2017YFA0700202, No. 2017YFA0700203); National Natural Science Foundation of China (No. 61631007, No. 61571117, No. 61875133, No. 11874269); Part by the 111 Project (No. 111-2-05)

More Information

Author Bio:
刘　硕（1988—），男，河北赞皇人，博士，伯明翰大学天文与物理学院玛丽居里学者，2017年于东南大学获得博士学位，主要从事信息超材料、电路拓扑绝缘体的理论与实验方面的研究工作。E-mail：liushuo.china@seu.edu.cn

张　霜（1975—），男，辽宁大连人，香港大学物理系和电子工程系讲座教授，2005年于美国新墨西哥大学电子工程系获得博士学位，2016年当选美国光学学会会士。在超构材料领域作出了很多重要成果。首次在光学波段实现了负折射率材料、首次通过贝里相位实现了谐波产生的非线性系数的连续控制、首次提出了有效介质（超构材料）的光学拓扑现象、首次实现了理想外尔点并实验上观测到光学系统的朗道手性零级模式、提出了等离激元结构的电磁诱导透明、首次实现了可见光波段宏观尺度的隐身斗篷等。2010年获国际物理联合会的青年科学家光学奖，2016年获英国皇家学会的Wolfson 科研奖。2018−2020连续三年入选科睿唯安全球“高被引科学家”名录。共发表论文200余篇，论文总被引用次数26000余次（谷歌学术）。E-mail：shuzhang@hku.hk

崔铁军（1965—），男，河北承德人，计算电磁学和电磁超材料专家，中国科学院院士，东南大学首席教授，IEEE Fellow。长期从事电磁超材料和计算电磁学研究，创造性地提出从信息科学角度研究超材料的思想，提出数字编码和可编程超材料及其控制电磁波的新方法，创建了信息超材料新体系；提出了电磁波与复杂目标及环境相互作用的一系列高效算法，开发了具有自主知识产权的系列专用电磁仿真软件；在中国航天、航空、电子和船舶等工业部门进行了大量应用，取得了显著的经济效益与社会效益。发表学术论文500余篇，被引用37000余次（H因子95）。研究成果入选2010年中国科学十大进展、2016年中国光学重要成果；获2011年教育部自然科学一等奖、2014年国家自然科学二等奖、2016年军队科学技术进步一等奖、2018年国家自然科学二等奖。E-mail：tjcui@seu.edu.cn

Corresponding author: zhangs75@gmail.com; Tjcui@seu.edu.cn

摘要

摘要: 在过去的十年里，材料的拓扑相变以及它们的奇异物理现象在固态电子学领域掀起了研究热潮。近些年来，人们开始在其他系统中重现和模拟电子体系中的各种拓扑现象，包括冷原子气体、离子阱、光子学、声子学、机械波和电路体系。在这些体系平台中，由电感电容所组成的拓扑电路因具有高度灵活的设计自由度、高性价比、易加工和易集成的独特优势而备受关注。除此之外，在拓扑电路中可以方便地设计具有任意长程耦合、非线性、非互易、增益等效应的拓扑模型，从而实现很多在电子体系和光学体系中难以实现的非线性、非阿贝尔和非厄米的拓扑相变材料。本文作为拓扑电路领域的第一篇综述，系统性地回顾了过去六年拓扑电路领域的主要进展，重点关注其理论建模、电路设计与实验测量，并对拓扑电路与电子和光学体系中的拓扑绝缘体着重进行讨论和区别。本综述涵盖了多种不同类型的拓扑电路，包括含有非平庸边界态、高阶拓扑角模式以及外尔粒子的厄米拓扑电路，拥有拓扑节线和节点态的高维拓扑电路，具有趋肤效应和由增益/衰减导致的非厄米拓扑电路，自感应拓扑边界态的非线性拓扑电路，以及具有非阿贝尔规范场效应的拓扑电路。
- 拓扑绝缘体 /
- 拓扑半金属 /
- 电路 /
- 边界态 /
- 体-边对应关系
Abstract: Exploring topological phases of matter and their exotic physics appeared as a rapidly growing field of study in solid-state electron systems in the past decade. In recent years, there has been a trend on the emulation of topological insulators/semimetals in many other systems, including ultracold quantum gases, trapped ions, photonic, acoustic, mechanical, and electrical circuit systems. Among these platforms, topological circuits made of simple capacitive and inductive circuit elements emerged as a very competitive platform because of its highly controllable degrees of freedom, lowercost, easy implementation, and great flexibility for integration. Owing to the unique advantages of electrical circuits such as arbitrary engineering of long-range hopping, convenient realization of nonlinear, nonreciprocal, and gain effects, highly flexible measurement, many of the nonlinear, non-abelian, and non-Hermitian physics can be potentially realized and investigated using the electrical circuit platform. In this review, we provide the first short overview of the main achievements of topological circuits developed in the past six years, primarily focusing on their theoretical modeling, circuit construction, experimental characterization, and their distinction from their counterparts in quantum electronics and photonics. The scope of this review covers a wide variety of topological circuits, including Hermitian topological circuits hosting nontrivial edge state, higher-order corner state, Weyl particles; higher dimensional topological circuits exhibiting nodal link and nodal knot states; non-Hermitian topological circuits showing skin effects, gain and loss induced nontrivial edge state; self-induced topological edge state in nonlinear topological circuit; topological circuit having non-Abelian gauge potential.
- topological insulator /
- topological semimetal /
- electrical circuit /
- edge stage /
- bulk-edge correspondence

HTML全文

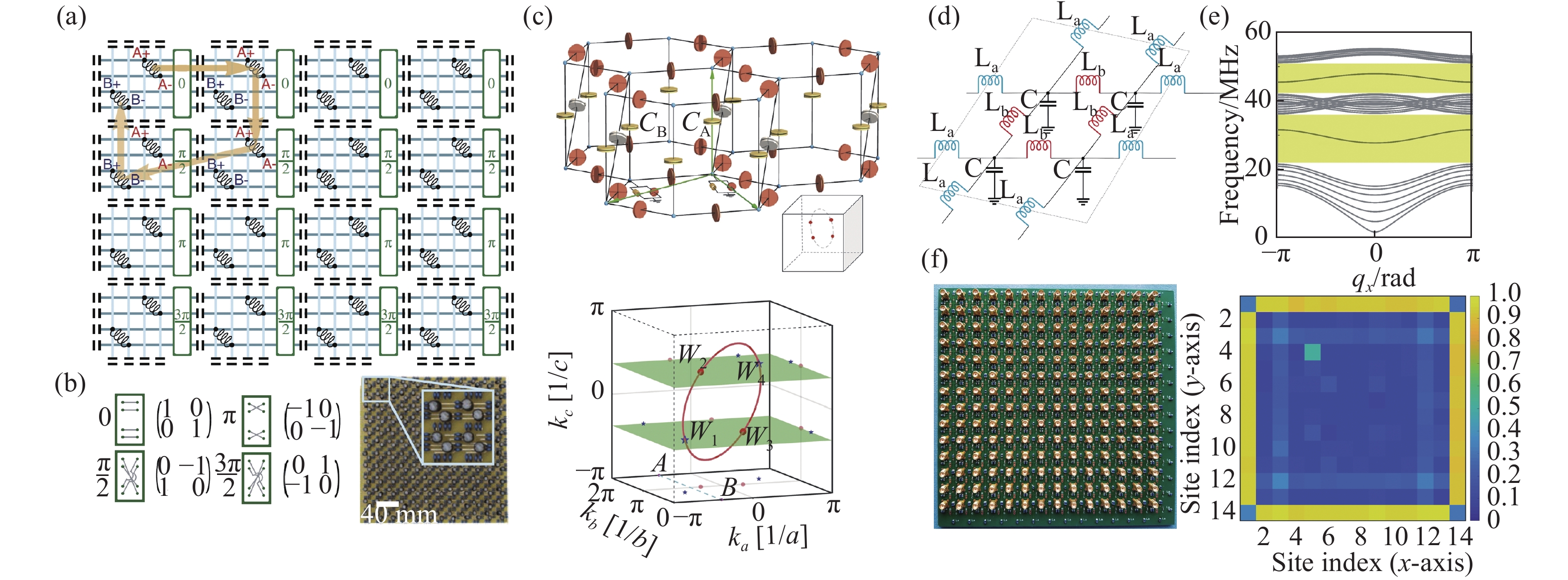
图 1 （a-b）具有π/2感应强度的Hofstadter电路模型中的自旋依赖的拓扑边界态^[9]。（c）三维拓扑电路中受电路参数调控的拓扑节线态和外尔态^[16]。（d-f）二维形式的Su–Schrieffer–Heeger拓扑电路^[17]。

Figure 1. (a-b) Spin-dependent topological edge state in an electrical circuit mimicking π/2 flux Hofstadter model^[9]. (c) 3D topological circuit with topological nodal line state and Weyl state controlled by the circuit parameters^[16]. (d-f) Two-dimensional version of the Su–Schrieffer–Heeger model circuit^[17].

下载: 全尺寸图片幻灯片

图 2 （a-c）由电容和电感构成的三维拓扑电路中的外尔点的实验观测^[23]。（d-e）三维拓扑电路中的理想II型外尔点的实验观测^[23]。

Figure 2. (a-c) Experimental observation of WPs in a 3D circuit lattice built with inductors and capacitors^[15]. (d-e) Experimental observationof ideal type-II WPs realized in a 3D topological circuits^[23].

下载: 全尺寸图片幻灯片

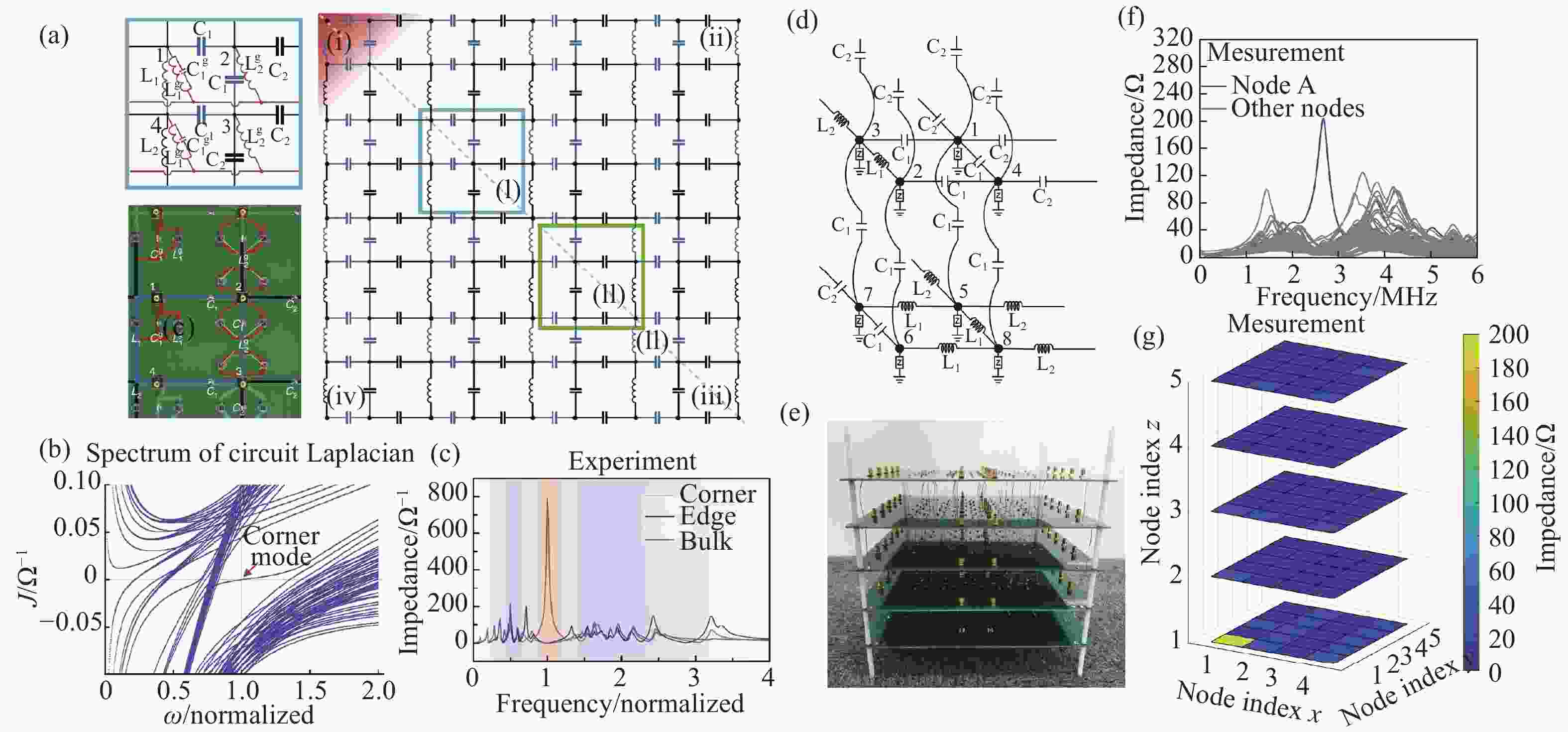
图 3 （a-c）二维高阶拓扑电路中由四极子动量导致的拓扑角模式的实验观测^[33]。（d-e）三维高阶拓扑电路中由八极子动量所保护的零维拓扑角模式^[34]。

Figure 3. (a-c) Experimental observation of a quadrupole moment induced corner state in a 2D electrical circuit^[33]. (d-e) 3D topological circuit exhibiting 0D corner state topologically protected by octupole moment of the bulk circuit^[34].

下载: 全尺寸图片幻灯片

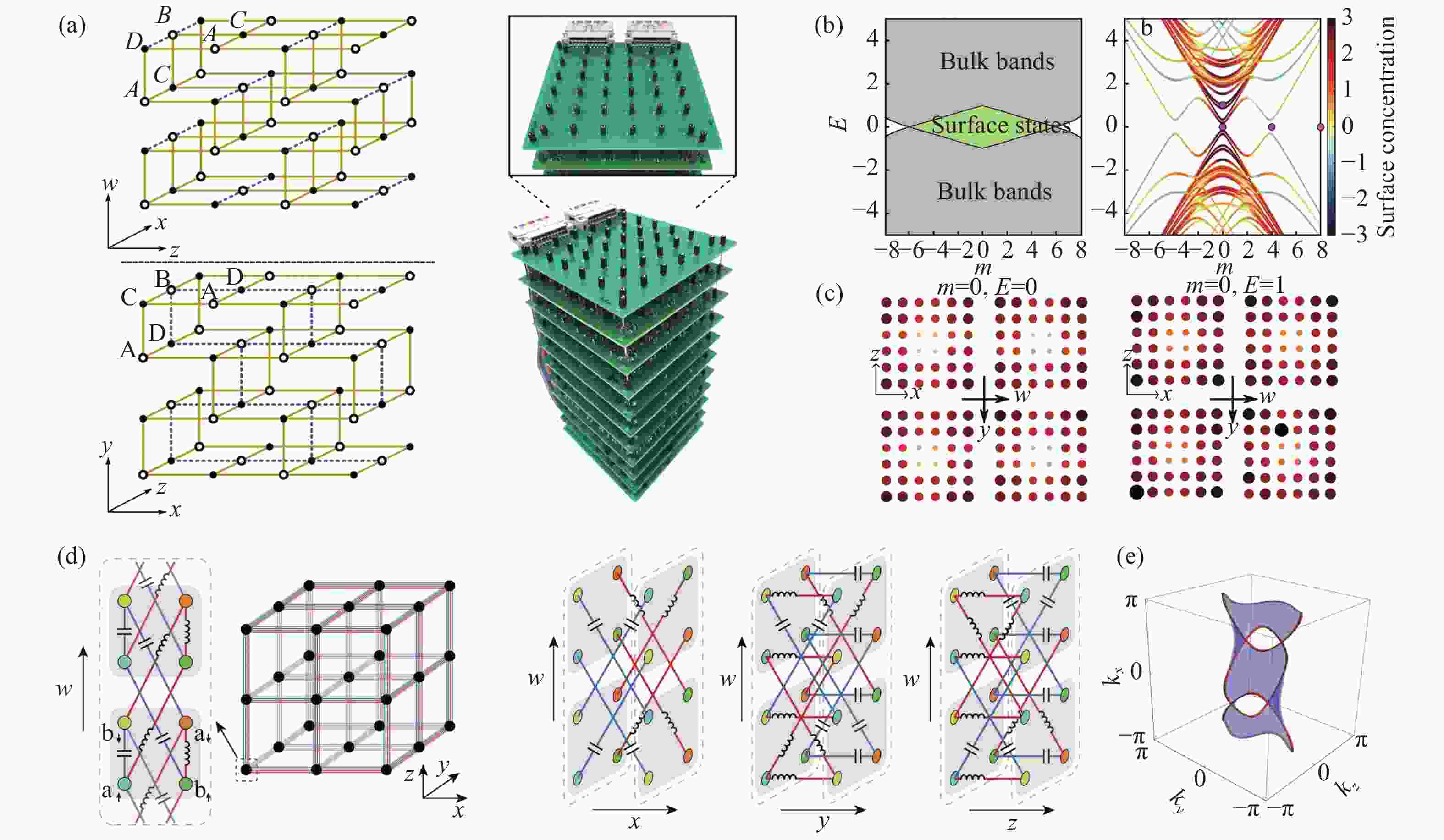
图 4 （a-c）具有二阶陈数的四维拓扑电路中的量子霍尔效应的实验验证^[40]。（d,e）四维拓扑电路中的Seifert表面，即三维动量空间中二维表面引出的节线或者节点^[41]。

Figure 4. (a-c) Experimental implementation of the first 4D quantum Hall model in electrical circuit characterized by a nonzero second Chern number^[40]. (d,e) 4D circuit topological circuit exhibiting a Seifert surface, which is 2D surface with its boundary tracing out a link or knot in 3D momentum space^[41].

下载: 全尺寸图片幻灯片

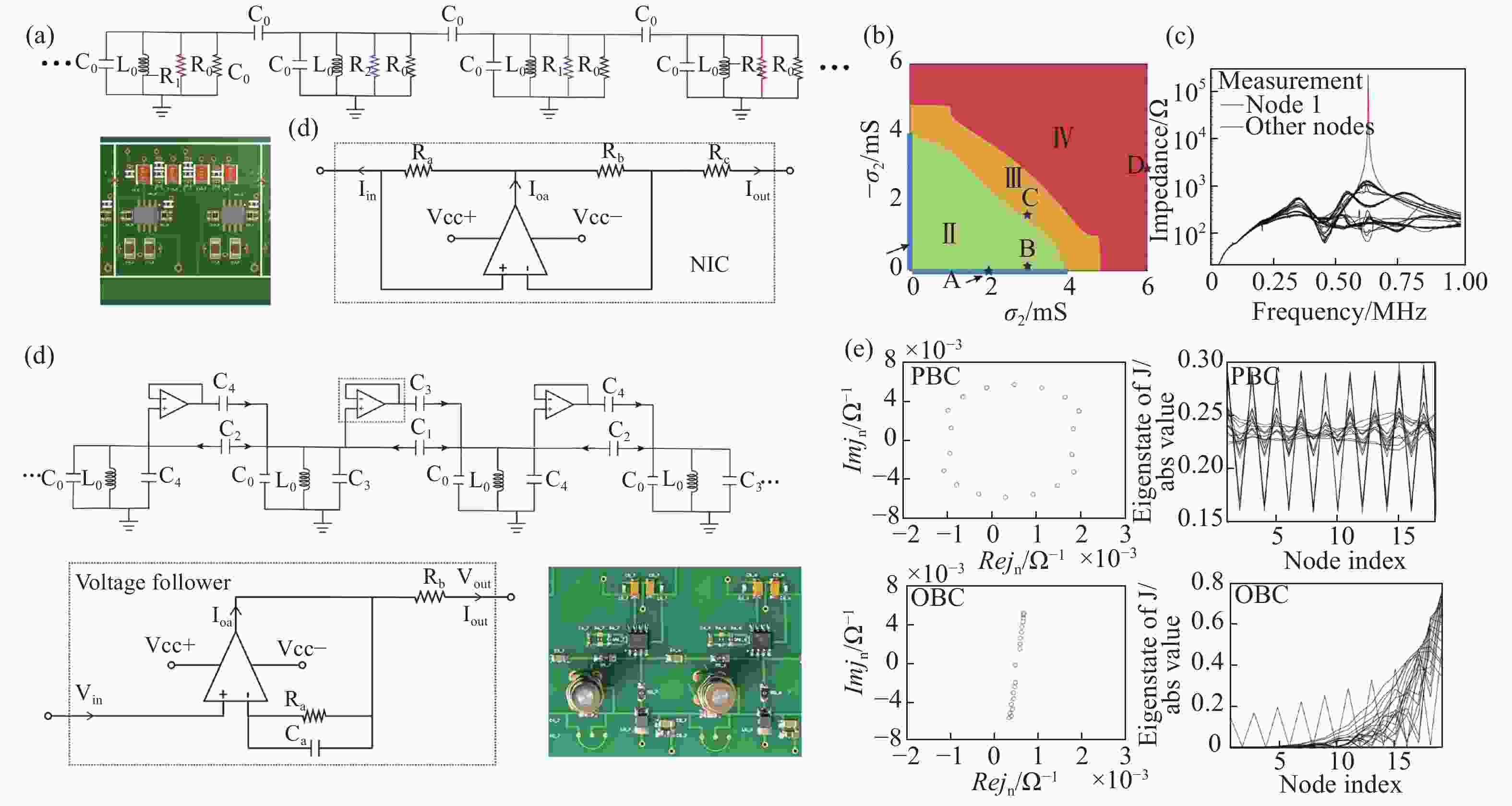
图 5 （a-c）由增益和衰减导致的拓扑相变的实验验证^[48]。（d,e）具有非互易效应的非厄米拓扑电路中的趋肤效应的实验验证^[13]。

Figure 5. (a-c) Experimental realization of a non-Hermitian electrical circuit whose nontrivial topology is induced by the introduction of gain and loss^[48]. (d,e) Experimental observation of non-Hermitian skin effect in a variation of SSH topological circuit with nonreciprocity^[13].

下载: 全尺寸图片幻灯片

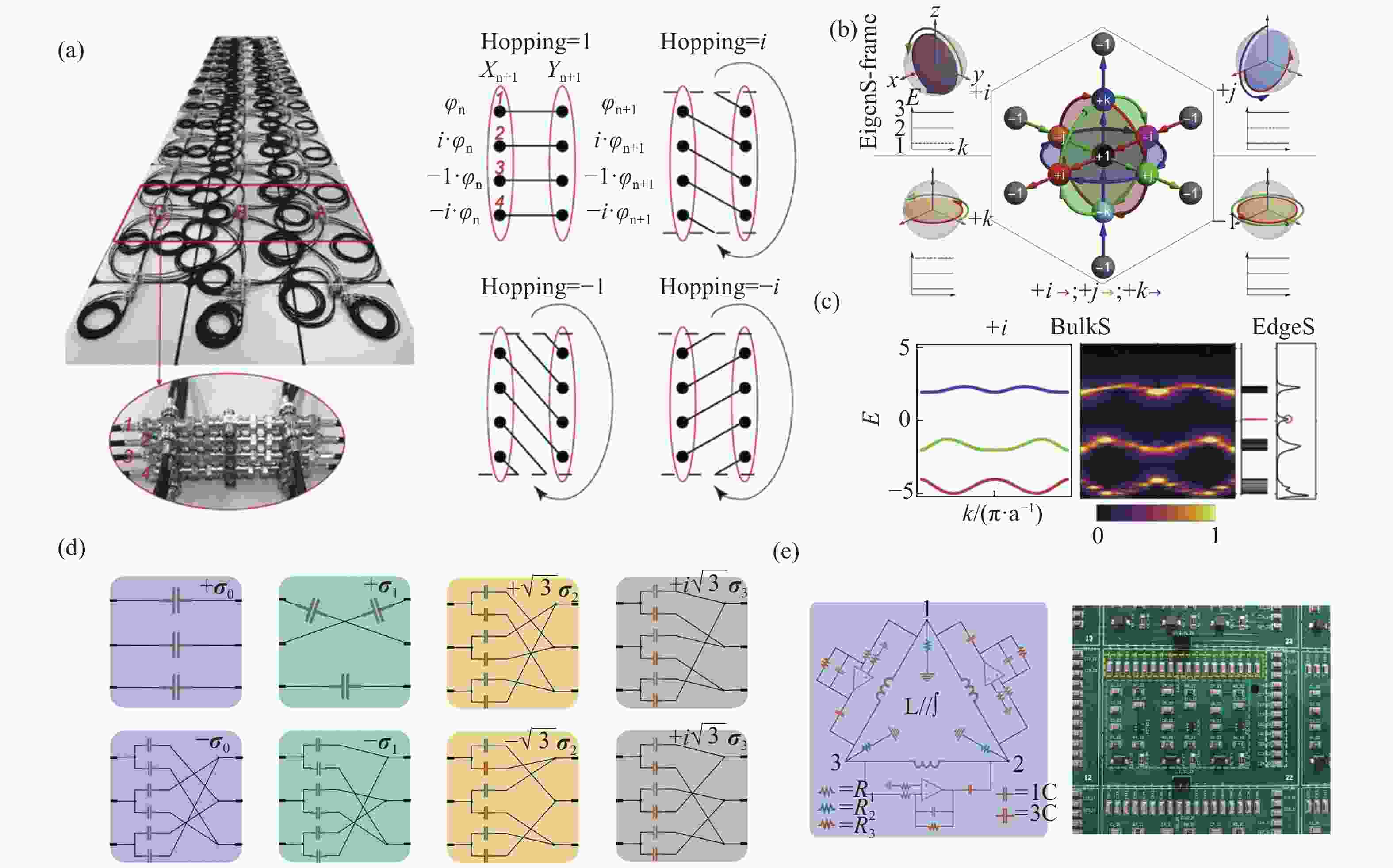
图 6 （a-c）具有编织耦合的传输线网络中的非阿贝尔拓扑电荷的实验观测^[63]。（d,e）具有非阿贝尔规范场效应的拓扑电路中的Rashba-Dresselhaus自旋-轨道耦合现象的实验验证^[65]。

Figure 6. (a-c) Experimental observation of non-Abelian topological charges in a transmission line network with braiding connectivity^[63]. (d,e) Experimental demonstration of the Rashba-Dresselhaus spin-orbit interaction (SOI) in a passive electrical circuit with non-Abelian gauge fields^[65].

下载: 全尺寸图片幻灯片

图 7 （a,b）非线性拓扑电路中的自感应拓扑保护^[68]。（c,d）非线性电路中的拓扑增强的谐波产生^[70]。

Figure 7. (a,b) Self-induced topological protection in a nonlinear SSH model circuit^[68]. (c,d) Topologically enhanced harmonic generation in a nonlinear circuit^[70].

下载: 全尺寸图片幻灯片

参考文献(78)

[1]	HASAN M Z, KANE C L. Colloquium: topological insulators[J]. Reviews of Modern Physics, 2010, 82(4): 3045-3067. doi: 10.1103/RevModPhys.82.3045
[2]	QI X L, ZHANG SH CH. Topological insulators and superconductors[J]. Reviews of Modern Physics, 2011, 83(4): 1057-1110. doi: 10.1103/RevModPhys.83.1057
[3]	BERNEVIG B A, HUGHES T L. Topological Insulators and Topological Superconductors[M]. Princeton: Princeton University Press, 2013.
[4]	HUGHES T L. Photonic topological insulators[B]. Taylor L. Hughes, 2013.
[5]	LU L, JOANNOPOULOS J D, SOLJAČIĆ M. Topological photonics[J]. Nature Photonics, 2014, 8(11): 821-829. doi: 10.1038/nphoton.2014.248
[6]	MA G C, XIAO M, CHAN C T. Topological phases in acoustic and mechanical systems[J]. Nature Reviews Physics, 2019, 1(4): 281-294. doi: 10.1038/s42254-019-0030-x
[7]	DONG J K, JURICIC V, ROY B. Topolectric circuits: theory and construction[J]. arXiv preprint arXiv: 2008.11202, 2020.
[8]	LU L. Topology on a breadboard[J]. Nature Physics, 2018, 14(9): 875-877. doi: 10.1038/s41567-018-0235-4
[9]	JIA N Y, OWENS C, SOMMER A, et al. Time- and site-resolved dynamics in a topological circuit[J]. Physical Review X, 2015, 5(2): 021031. doi: 10.1103/PhysRevX.5.021031
[10]	LEE C H, IMHOF S, BERGER C, et al. Topolectrical circuits[J]. Communications Physics, 2018, 1: 39. doi: 10.1038/s42005-018-0035-2
[11]	HOFMANN T, HELBIG T, LEE C H, et al. Chiral voltage propagation and calibration in a topolectrical chern circuit[J]. Physical Review Letters, 2019, 122(24): 247702. doi: 10.1103/PhysRevLett.122.247702
[12]	ZHAO E H. Topological circuits of inductors and capacitors[J]. Annals of Physics, 2018, 399: 289-313. doi: 10.1016/j.aop.2018.10.006
[13]	LIU SH, SHAO R W, MA SH J, et al. Non-Hermitian skin effect in a non-Hermitian electrical circuit[J]. Research, 2021, 2021: 5608038.
[14]	PETERSON C W, BENALCAZAR W A, HUGHES T L, et al. A quantized microwave quadrupole insulator with topologically protected corner states[J]. Nature, 2018, 555(7696): 346-350. doi: 10.1038/nature25777
[15]	LU Y H, JIA N Y, SU L, et al. Probing the berry curvature and Fermi arcs of a Weyl circuit[J]. Physical Review B, 2019, 99(2): 020302. doi: 10.1103/PhysRevB.99.020302
[16]	LUO K F, YU R, WENG H M. Topological nodal states in circuit lattice[J]. Research, 2018, 2018: 6793752.
[17]	LIU SH, GAO W L, ZHANG Q, et al. Topologically protected edge state in two-dimensional Su–Schrieffer–Heeger Circuit[J]. Research, 2019, 2019: 8609875.
[18]	XU S Y, BELOPOLSKI I, ALIDOUST N, et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs[J]. Science, 2015, 349(6248): 613-617. doi: 10.1126/science.aaa9297
[19]	HUANG L N, MCCORMICK T M, OCHI M, et al. Spectroscopic evidence for a type II Weyl semimetallic state in MoTe₂[J]. Nature Materials, 2016, 15(11): 1155-1160. doi: 10.1038/nmat4685
[20]	LU L, WANG ZH Y, YE D X, et al. Experimental observation of Weyl points[J]. Science, 2015, 349(6248): 622-624. doi: 10.1126/science.aaa9273
[21]	YANG B, GUO Q H, TREMAIN B, et al. Ideal Weyl points and helicoid surface states in artificial photonic crystal structures[J]. Science, 2018, 359(6379): 1013-1016. doi: 10.1126/science.aaq1221
[22]	OWENS C, LACHAPELLE A, SAXBERG B, et al. Quarter-flux Hofstadter lattice in a qubit-compatible microwave cavity array[J]. Physical Review A, 2018, 97(1): 013818. doi: 10.1103/PhysRevA.97.013818
[23]	LI R J, LV B, TAO H B, et al. Ideal type-II Weyl points in topological circuits[J]. National Science Review, 2020: nwaa192. doi: 10.1093/nsr/nwaa192
[24]	SOLUYANOV A A, GRESCH D, WANG ZH J, et al. Type-II Weyl semimetals[J]. Nature, 2015, 527(7579): 495-498. doi: 10.1038/nature15768
[25]	JIANG J, LIU Z K, SUN Y, et al. Signature of type-II Weyl semimetal phase in MoTe2[J]. Nature Communications, 2017, 8: 13973. doi: 10.1038/ncomms13973
[26]	NOH J, HUANG SH, LEYKAM D, et al. Experimental observation of optical Weyl points and Fermi arc-like surface states[J]. Nature Physics, 2017, 13(6): 611-617. doi: 10.1038/nphys4072
[27]	YANG B, GUO Q H, TREMAIN B. Direct observation of topological surface-state arcs in photonic metamaterials[J]. Nature Communications, 2017, 8: 97. doi: 10.1038/s41467-017-00134-1
[28]	RAFI-UL-ISLAM SM, SIU BZ, SUN CH, et al. Realization of Weyl semimetal phases in topoelectrical circuits[J]. New Journal of Physics, 2020, 22: 023025. doi: 10.1088/1367-2630/ab6eaf
[29]	RAFI-UI-ISLAM SM, SIU Z B, JALI L M. Topoelectrical circuit realization of a Weyl semimetal heterojunction[J]. Communication Physics, 2020, 3: 72.
[30]	BENALCAZAR W A, BERNEVIG B A, HUGHES T L. Quantized electric multipole insulators[J]. Science, 2017, 357(6346): 61-66. doi: 10.1126/science.aah6442
[31]	LANGBEHN J, PENG Y, TRIFUNOVIC L, et al. Reflection-symmetric second-order topological insulators and superconductors[J]. Physical Review Letters, 2017, 119(24): 246401. doi: 10.1103/PhysRevLett.119.246401
[32]	KHALAF E. Higher-order topological insulators and superconductors protected by inversion symmetry[J]. Physical Review B, 2018, 97(20): 205136. doi: 10.1103/PhysRevB.97.205136
[33]	IMHOF S, BERGER C, BAYER F, et al. Topoelectrical-circuit realization of topological corner modes[J]. Nature Physics, 2018, 14(9): 925-929. doi: 10.1038/s41567-018-0246-1
[34]	LIU SH, MA SH J, ZHANG L, et al. Octupole corner state in a three-dimensional topological circuit[J]. Light:Science &Applications, 2020, 9: 145.
[35]	BAO J CH, ZOU D Y, ZHANG W X, et al. Topoelectrical circuit octupole insulator with topologically protected corner states[J]. Physical Review B, 2019, 100(200): 201406.
[36]	EZAWA M. Braiding of Majorana-like corner states in electric circuits and its non-Hermitian generalization[J]. Physical Review B, 2019, 100(4): 045407. doi: 10.1103/PhysRevB.100.045407
[37]	CHIU C K, TEO J C Y, SCHNYDER A P, et al. Classification of topological quantum matter with symmetries[J]. Review Modern Physics, 2016, 88(3): 035005. doi: 10.1103/RevModPhys.88.035005
[38]	PRICE H M, ZILBERBERG O, OZAWA T, et al. Four-dimensional quantum hall effect with ultracold atoms[J]. Physical Review Letters, 2015, 115(19): 195303. doi: 10.1103/PhysRevLett.115.195303
[39]	OZAWA T, PRICE H M, GOLDMAN N, et al. Synthetic dimensions in integrated photonics: from optical isolation to four-dimensional quantum Hall physics[J]. Physical Review A, 2016, 93(4): 043827. doi: 10.1103/PhysRevA.93.043827
[40]	WANG Y, PRICE H M, ZHANG B L, et al. Circuit implementation of a four-dimensional topological insulator[J]. Nature Communications, 2020, 11: 2356. doi: 10.1038/s41467-020-15940-3
[41]	LI L H, LEE C H, GONG J B. Boundary states of 4D topological matter: emergence and full 3D-imaging of nodal Seifert surfaces[J]. Communications Physics, 2019, 2: 135. doi: 10.1038/s42005-019-0235-4
[42]	TAKATA K, NOTOMI M. Photonic topological insulating phase induced solely by gain and loss[J]. Physical Review Letters, 2018, 121(21): 213902. doi: 10.1103/PhysRevLett.121.213902
[43]	YAO SH Y, WANG ZH. Edge states and topological invariants of non-hermitian systems[J]. Physical Review Letters, 2018, 121(8): 086803. doi: 10.1103/PhysRevLett.121.086803
[44]	SHEN H T, ZHEN B, FU L. Topological band theory for non-Hermitian Hamiltonians[J]. Physical Review Letters, 2018, 120(14): 146402. doi: 10.1103/PhysRevLett.120.146402
[45]	KAWABATA K, HIGASHIKAWA S, GONG Z P, et al. Topological unification of time-reversal and particle-hole symmetries in non-Hermitian physics[J]. Nature Communications, 2019, 10: 297. doi: 10.1038/s41467-018-08254-y
[46]	YAO SH Y, SONG F, WANG ZH. Non-hermitian chern bands[J]. Physical Review Letters, 2018, 121(12): 136802.
[47]	YOKOMIZO K, MURAKAMI S. Non-bloch band theory of non-Hermitian systems[J]. Physical Review Letters, 2019, 123(6): 066404. doi: 10.1103/PhysRevLett.123.066404
[48]	LIU SH, MA SH J, YANG CH, et al. Gain-and loss-induced topological insulating phase in a non-Hermitian electrical circuit[J]. Physical Review Applied, 2020, 13(1): 014047. doi: 10.1103/PhysRevApplied.13.014047
[49]	HELBIG T, HOFMANN T, IMHOF M, et al. Generalized bulk–boundary correspondence in non-Hermitian topolectrical circuits[J]. Nature Physics, 2020, 16(7): 747-750. doi: 10.1038/s41567-020-0922-9
[50]	EZAWA M. Non-Hermitian boundary and interface states in nonreciprocal higher-order topological metals and electrical circuits[J]. Physical Review B, 2019, 99(12): 121411. doi: 10.1103/PhysRevB.99.121411
[51]	EZAWA M. Electric circuits for non-Hermitian Chern insulators[J]. Physical Review B, 2019, 100(8): 081401. doi: 10.1103/PhysRevB.100.081401
[52]	LUO K F, FENG J J, ZHAO Y X, et al.. Nodal manifolds bounded by exceptional points on non-hermitian honeycomb lattices and electrical-circuit realizations[J]. arXiv preprint arXiv: 1810.09231, 2018.
[53]	WU Q SH, SOLUYANOV A A, BZDUŠEK T. Non-Abelian band topology in noninteracting metals[J]. Science, 2019, 365(6459): 1273-1277. doi: 10.1126/science.aau8740
[54]	TIWARI A, BZDUŠEK T. Non-Abelian topology of nodal-line rings in PT-symmetric systems[J]. Physical Review B, 2020, 101(19): 195130. doi: 10.1103/PhysRevB.101.195130
[55]	YANG E CH, YANG B, YOU O B, et al. Observation of non-Abelian nodal links in photonics[J]. Physical Review Letters, 2020, 125(3): 033901. doi: 10.1103/PhysRevLett.125.033901
[56]	JACOB A, ÖHBERG P, JUZELIŪNAS G, et al. Cold atom dynamics in non-Abelian gauge fields[J]. Applied Physics B, 2007, 89(4): 439-445. doi: 10.1007/s00340-007-2865-6
[57]	STERN A, LINDNER N H. Topological quantum computation—from basic concepts to first experiments[J]. Science, 2013, 339(6124): 1179-1184. doi: 10.1126/science.1231473
[58]	WU ZH, ZHANG L, SUN W, et al. Realization of two-dimensional spin-orbit coupling for Bose-Einstein condensates[J]. Science, 2016, 354(6308): 83-88. doi: 10.1126/science.aaf6689
[59]	CHEN Y T, ZHANG R Y, XIONG ZH F, et al. Non-Abelian gauge field optics[J]. Nature Communications, 2019, 10: 3125. doi: 10.1038/s41467-019-10974-8
[60]	YANG Y, PENG CH, ZHU D, et al. Synthesis and observation of non-Abelian gauge fields in real space[J]. Science, 2019, 365(6457): 1021-1025. doi: 10.1126/science.aay3183
[61]	RECHCIŃSKA K, KRÓL M, MAZUR R, et al. Engineering spin-orbit synthetic Hamiltonians in liquid-crystal optical cavities[J]. Science, 2019, 366(6466): 727-730. doi: 10.1126/science.aay4182
[62]	GIANFRATE A, BLEU O, DOMINICI L, et al. Measurement of the quantum geometric tensor and of the anomalous Hall drift[J]. Nature, 2020, 578(7795): 381-385. doi: 10.1038/s41586-020-1989-2
[63]	GUO Q H, JIANG T SH, ZHANG R Y, et al.. Experimental observation of non-Abelian topological charges and bulk-edge correspondence[J]. arXiv preprint arXiv: 2008.06100, 2020.
[64]	SONG Z Y, WU T Y, WU W Q, et al.. Experimental realization of non-Abelian gauge potentials and topological Chern state in circuit system[J]. arXiv preprint arXiv: 2009.04870, 2020.
[65]	DRESSELHAUS G. Spin-orbit coupling effects in zinc blende structures[J]. Physical Review, 1955, 100(2): 580-586. doi: 10.1103/PhysRev.100.580
[66]	EZAWA M. Non-Abelian braiding of Majorana-like edge states and topological quantum computations in electric circuits[J]. Physical Review B, 2020, 102(7): 075424. doi: 10.1103/PhysRevB.102.075424
[67]	NAYAK C, SIMON S H, STERN A, et al. Non-Abelian anyons and topological quantum computation[J]. Reviews of Modern Physics, 2008, 80(3): 1083-1159. doi: 10.1103/RevModPhys.80.1083
[68]	HADAD Y, SORIC J C, KHANIKAEV A B, et al. Self-induced topological protection in nonlinear circuit arrays[J]. Nature Electronics, 2018, 1(3): 178-182. doi: 10.1038/s41928-018-0042-z
[69]	HADAD Y, VITELLI V, ALU A, et al. Solitons and propagating domain walls in topological resonator arrays[J]. ACS Photonics, 2017, 4(8): 1974-1979. doi: 10.1021/acsphotonics.7b00303
[70]	WANG Y, LANG L J, LEE C H, et al. Topologically enhanced harmonic generation in a nonlinear transmission line metamaterial[J]. Nature Communications, 2019, 10: 1102. doi: 10.1038/s41467-019-08966-9
[71]	HIROTA R, SUZUKI K. Theoretical and experimental studies of lattice solitons in nonlinear lumped networks[J]. Proceedings of the IEEE, 1973, 61(10): 1483-1491. doi: 10.1109/PROC.1973.9297
[72]	NAGASHIMA H, AMAGISHI Y. Experiment on solitons in the dissipative Toda lattice using nonlinear transmission line[J]. Journal of the Physical Society of Japan, 1979, 47(6): 2021-2027. doi: 10.1143/JPSJ.47.2021
[73]	MUROYA K, WATANABE S. Experiment on soliton in inhomogeneous electric circuit. I. Dissipative case[J]. Journal of the Physical Society of Japan, 1981, 50(9): 3159-3165. doi: 10.1143/JPSJ.50.3159
[74]	MUROYA K, SAITOH N, WATANABE S. Experiment on lattice soliton by nonlinear LC Circuit—observation of a dark soliton[J]. Journal of the Physical Society of Japan, 1982, 51(3): 1024-1029. doi: 10.1143/JPSJ.51.1024
[75]	KUUSELA T, HIETARINTA J, KOKKO K, et al. Soliton experiments in a nonlinear electrical transmission line[J]. European Journal of Physics, 1987, 8(1): 27-33. doi: 10.1088/0143-0807/8/1/007
[76]	LEE C H, SUTRISNO A, HOFMANN T, et al. Imaging nodal knots in momentum space through topolectrical circuits[J]. Nature Communications, 2020, 11: 4385. doi: 10.1038/s41467-020-17716-1
[77]	ZHANG W X, ZOU D Y, BAO J CH, et al. Topolectrical-circuit realization of a four-dimensional hexadecapole insulator[J]. Physical Review B, 2020, 102(10): 100102. doi: 10.1103/PhysRevB.102.100102
[78]	HOFMANN T, HELBIG T, SCHINDLER F, et al. Reciprocal skin effect and its realization in a topolectrical circuit[J]. Physical Review Research, 2020, 2(2): 023265. doi: 10.1103/PhysRevResearch.2.023265