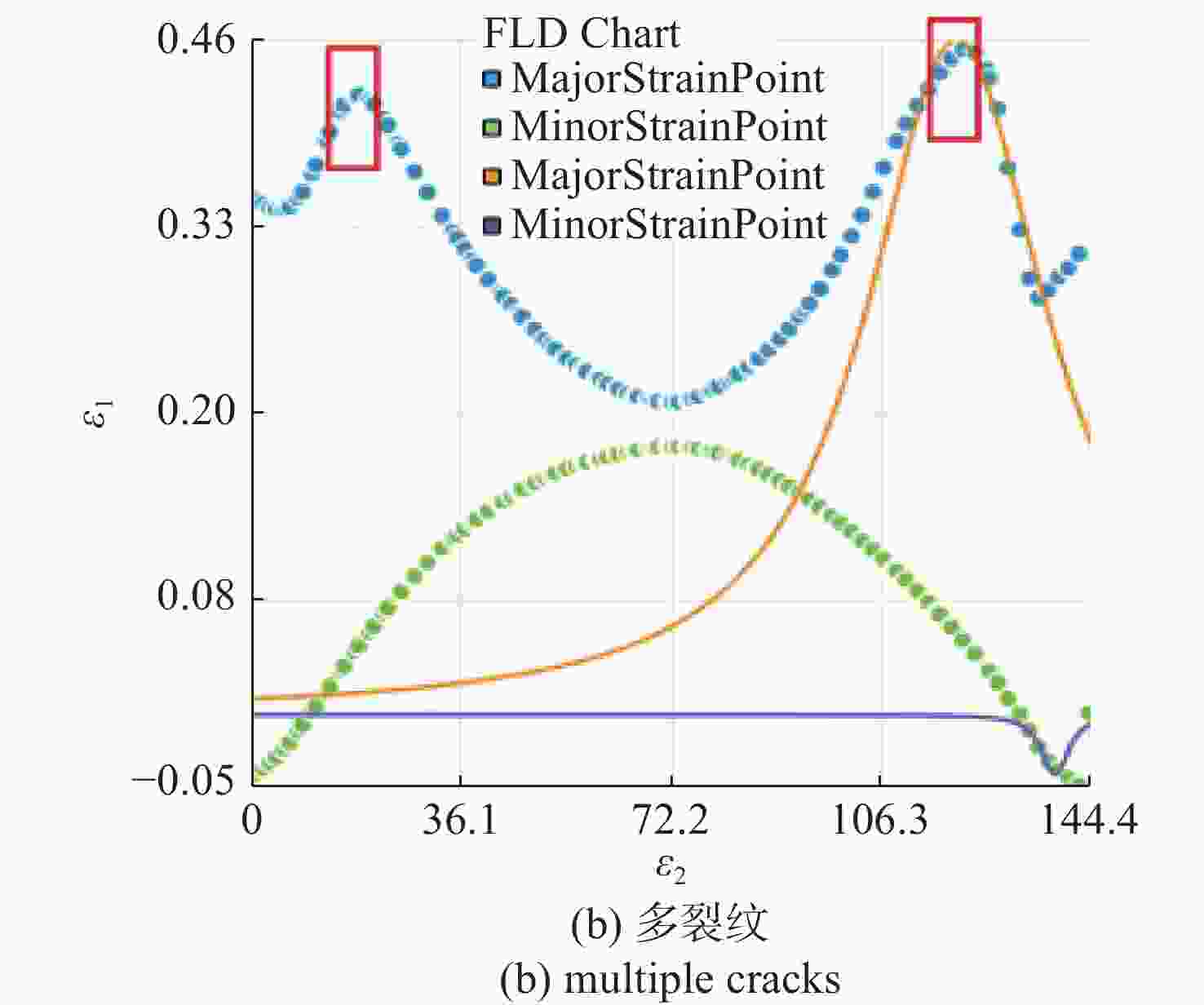
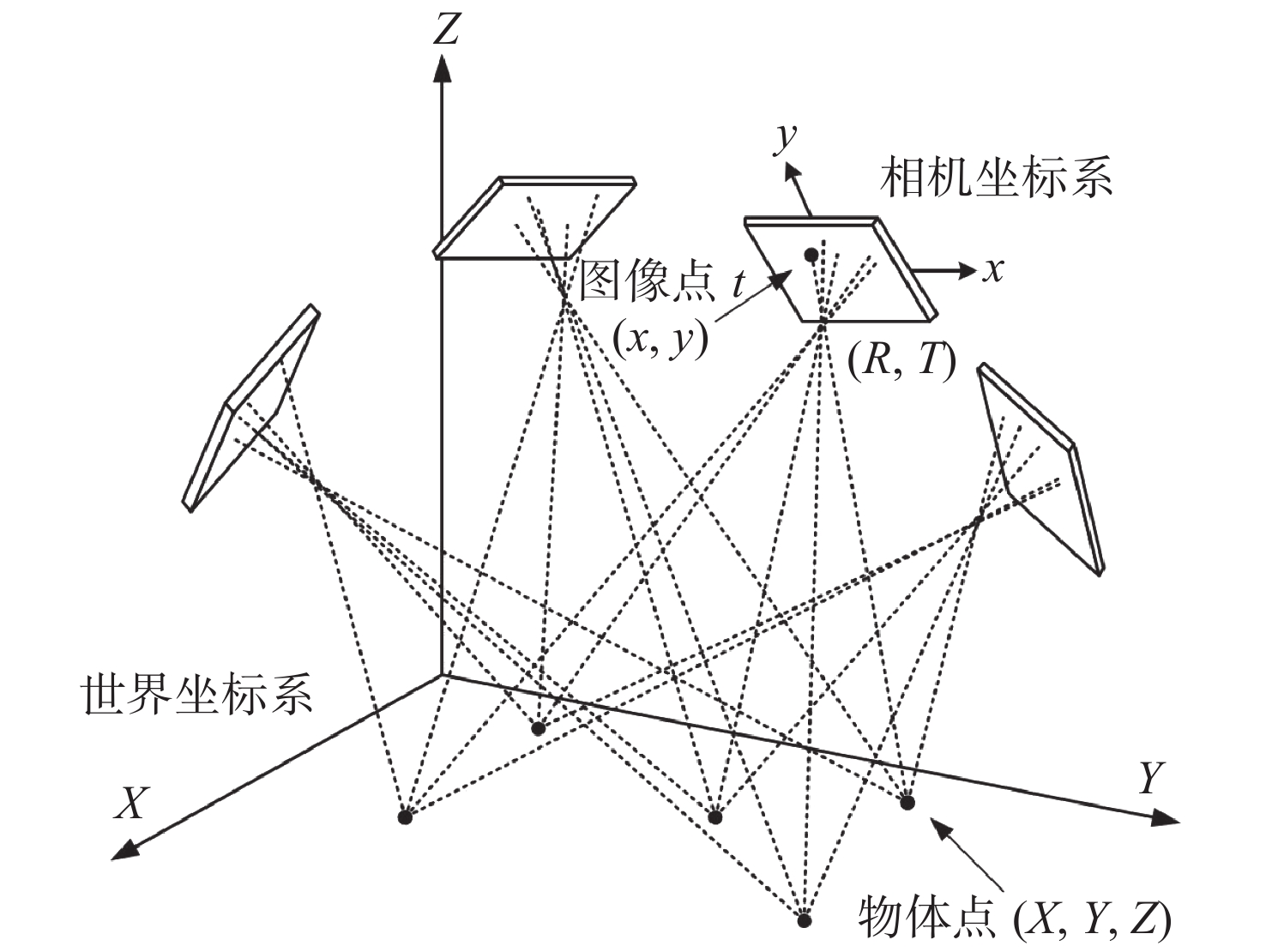
-
摘要: 针对柔性复合薄膜成形试验中极限应变难以测量的问题,提出一种基于双目立体视觉结合数字图像相关法的测量方法。首先对于薄膜材料成形过程中产生大变形或裂纹时图像难以匹配的问题,根据系列图像相邻状态变形的连续性,提出了一种图像匹配基准自适应更新的弱相关分步匹配方法;然后根据薄膜材料表面应变分布不同于钢制件的特性,提出了一种构建应变场截线来拟合薄膜材料的极限应变曲线的方法。专门组建视觉测定的软、硬件系统,通过Q235钢试件进行极限应变曲线测量并与坐标网格方法进行对比,材料极限应变精度能够提高0.02%,证明了本文方法的可行性和精确性。用7组PET/Nylon/Al foil/PP材料制备成的柔性复合薄膜试件进行实测,此方法及系统成功地完成了柔性复合薄膜材料的成形极限曲线测定。对比实验和实际测试证明,本文方法能够快速、准确地测量柔性复合薄膜材料在整个成形过程中的表面应变分布,与传统的坐标网格方法相比具有明显的优势,为测定薄膜材料的成形极限应变曲线提供了一种高可靠性、高精度的手段。Abstract: To address the difficulty in measuring the strain limit of pliable composite film forming tests, a measurement method based on binocular stereo vision combined with digital image correlation is proposed. Firstly, to address the image matching problem in large deformations or cracks in thin films, a weak-correlation step-by-step matching method based on adaptive updating of image matching benchmarks is proposed according to the continuity of adjacent state deformation of series images. Then, according to the differences in the surface strain distribution of the film material with that of the steel parts, a strain field is proposed to fit the limit strain curve of the film material. The software and hardware system of visual measurement is built, and the limit strain curve of a Q235 steel specimen is measured and compared to results from the coordinate grid method. The limit strain accuracy can be improved by 0.02%, which proves the feasibility and accuracy of this method. The pliable composite film specimens prepared by PET, Nylon, Al foil, PP were each measured. The method and system successfully completed the measurement of the forming limit curve of the pliable composite film. The comparative experiments show that the proposed method can quickly and accurately measure the surface strain distribution of pliable composite film during forming. Compared with the coordinate grid method, it has obvious advantages and provides a highly reliable and highly precise method for solving the forming limit strain curve of film materials.
-
表 1 极限应变对
$ ({\varepsilon }_{1},{\varepsilon }_{2}) $ Table 1. Limit strain pair
$ ({\varepsilon }_{1},{\varepsilon }_{2}) $ 型号 第1组 第2组 第3组 第4组 第5组 第6组 第7组 网格方法 (0.46,−0.17) (0.45,−0.14) (0.42,−0.04) (0.39,0.01) (0.43,0.10) (0.46,0.17) (0.51,0.30) 本文方法 (0.44,−0.15) (0.43,−0.13) (0.40,−0.03) (0.37,0.03) (0.42,0.11) (0.46,0.19) (0.50,0.29) 表 2 相机标定内参数
Table 2. Camera calibration internal parameters
内参数 左相机 右相机 f/pixel 26.586 26.633 x0/pixel 1.042 6.006 y0/pixel 5.867 14.286 K1 −1.37×10−9 −1.623×10−9 K2 −3.291×10−17 1.003×10−16 K3 8.614×10−23 5.813×10−23 B1 −2.302×10−8 −1.703×10−7 B2 −2.052×10−8 −7.343×10−8 E1 −0.0002241 −0.0003031 E2 0.000443 0.0003076 -
[1] 陈培忠, 王克俭. 塑料包装材料共挤复合技术发展[J]. 塑料包装,2021,31(1):29-33. doi: 10.3969/j.issn.1006-9828.2021.01.007CHEN P ZH, WANG K J. Development of coextrusion technology for plastic packaging materials[J]. Plastics Packaging, 2021, 31(1): 29-33. (in Chinese) doi: 10.3969/j.issn.1006-9828.2021.01.007 [2] 李强, 殷新意, 于妍妍, 等. 取向碳纳米管/环氧树脂复合薄膜制备及结构/性能表征[J]. 复合材料学报,2021,38(9):2767-2775.LI Q, YIN X Y, YU Y Y, et al. Preparation and characterization of aligned carbon nanotubes/epoxy composite films[J]. Acta Materiae Compositae Sinica, 2021, 38(9): 2767-2775. (in Chinese) [3] 张璐. 板料塑性成形极限预测的研究[D]. 秦皇岛: 燕山大学, 2018.ZHANG L. Research on prediction of plastic forming limit of sheet metal[D]. Qinhuangdao: Yanshan University, 2018. (in Chinese) [4] 谭富星, 李明哲, 蔡中义, 等. 钛合金网板多点成形起皱缺陷的数值模拟[J]. 西安交通大学学报,2007,41(9):1026-1030. doi: 10.3321/j.issn:0253-987x.2007.09.005TAN F X, LI M ZH, CAI ZH Y, et al. Numerical simulation of wrinkling in multi-point forming process of titanium alloy retiary sheet[J]. Journal of Xi'an Jiaotong University, 2007, 41(9): 1026-1030. (in Chinese) doi: 10.3321/j.issn:0253-987x.2007.09.005 [5] RAND J L, GRANT D A. Optical measurement of biaxial strain in thin film polymers[J]. ASTM Special Technical Publication, 1997, 131(8): 123-137. [6] PEPELNJAK T, BARISIC B. Computer-assisted engineering determination of the formability limit for thin sheet metals by a modified Marciniak method[J]. The Journal of Strain Analysis for Engineering Design, 2009, 44(6): 459-472. doi: 10.1243/03093247JSA503 [7] 梁晋, 史宝全, 唐正宗, 等. 三维网格应变测量方法: 中国, 102322813A[P]. 2012-01-18.LIANG J, SHI B Q, TANG ZH Z, et al.. 3D grid strain measurement method: CN, 102322813A[P]. 2011-01-18. (in Chinese) [8] 梁伟, 黄启斌, 杨晓翔. 基于热转印技术的应变测量网格印制法[J]. 锻压技术,2012,37(6):101-103. doi: 10.3969/j.issn.1000-3940.2012.06.026LIANG W, HUANG Q B, YANG X X. Grid-scribed technology for sheet forming strain measuring based on thermal transfer[J]. Forging &Stamping Technology, 2012, 37(6): 101-103. (in Chinese) doi: 10.3969/j.issn.1000-3940.2012.06.026 [9] 朱凯博, 吕晓东, 王敬涛, 等. Android平台下的应变网格测量方法[J]. 工程与试验,2015,55(3):11-13, 54. doi: 10.3969/j.issn.1674-3407.2015.03.004ZHU K B, LV X D, WANG J T, et al. Grid strain measurement based on Android mobile phone[J]. Engineering &Test, 2015, 55(3): 11-13, 54. (in Chinese) doi: 10.3969/j.issn.1674-3407.2015.03.004 [10] 胡悦, 王永红, 鲍思源, 等. 高温下数字图像相关散斑最优成像探究[J]. 中国光学,2018,11(5):728-735. doi: 10.3788/co.20181105.0728HU Y, WANG Y H, BAO S Y, et al. Optimal imaging of digital image correlation speckle under high temperature[J]. Chinese Optics, 2018, 11(5): 728-735. (in Chinese) doi: 10.3788/co.20181105.0728 [11] 朱飞鹏, 龚琰, 白鹏翔, 等. 基于数字图像相关的光学引伸计应变测量精度研究[J]. 光学 精密工程,2018,26(5):1061-1069. doi: 10.3788/OPE.20182605.1061ZHU F P, GONG Y, BAI P X, et al. Study on strain measurement accuracy of optical extensometers based on digital image correlation[J]. Optics and Precision Engineering, 2018, 26(5): 1061-1069. (in Chinese) doi: 10.3788/OPE.20182605.1061 [12] 陈志新, 梁晋, 郭成. 数字散斑相关法在变形测量中的应用[J]. 光学 精密工程,2011,19(7):1480-1485. doi: 10.3788/OPE.20111907.1480CHEN ZH X, LIANG J, GUO CH. Application of digital speckle correlation method to deformation measurement[J]. Optics and Precision Engineering, 2011, 19(7): 1480-1485. (in Chinese) doi: 10.3788/OPE.20111907.1480 [13] 唐正宗, 梁晋, 肖振中, 等. 用于三维变形测量的数字图像相关系统[J]. 光学 精密工程,2010,18(10):2244-2253.TANG ZH Z, LIANG J, XIAO ZH ZH, et al. Digital image correlation system for three-dimensional deformation measurement[J]. Optics and Precision Engineering, 2010, 18(10): 2244-2253. (in Chinese) [14] 梁晋, 肖振中, 唐正宗, 等. 大型飞机风洞变形测量的相机标定研究[J]. 西安交通大学学报,2009,43(3):55-59. doi: 10.3321/j.issn:0253-987X.2009.03.012LIANG J, XIAO ZH ZH, TANG ZH Z, et al. Large space camera calibration for three-dimensional videogrammetric vibration measurement of large aeroplane model in wind tunnels[J]. Journal of Xi'an Jiaotong University, 2009, 43(3): 55-59. (in Chinese) doi: 10.3321/j.issn:0253-987X.2009.03.012 [15] 杨建柏, 赵建, 孙强. 基于交比不变性的投影仪标定[J]. 中国光学,2021,14(2):320-328. doi: 10.37188/CO.2020-0111YANG J B, ZHAO J, SUN Q. Projector calibration based on cross ratio invariance[J]. Chinese Optics, 2021, 14(2): 320-328. (in Chinese) doi: 10.37188/CO.2020-0111 [16] TANG ZH Z, LIANG J, XIAO ZH ZH, et al. Three-dimensional digital image correlation system for deformation measurement in experimental mechanics[J]. Optical Engineering, 2010, 49(10): 103601. doi: 10.1117/1.3491204 [17] TANG ZH Z, LIANG J, XIAO ZH ZH, et al. Large deformation measurement scheme for 3D digital image correlation method[J]. Optics and Lasers in Engineering, 2012, 50(2): 122-130. doi: 10.1016/j.optlaseng.2011.09.018 [18] 王立忠, 汪耀, 梁晋, 等. 高速三维数字图像法测量手机跌落全场应变[J]. 光学 精密工程,2018,26(9):2174-2180. doi: 10.3788/OPE.20182609.2174WANG L ZH, WANG Y, LIANG J, et al. Measurement of full-field strain incell phone dropping test by high-speed 3D digital image correlation method[J]. Optics and Precision Engineering, 2018, 26(9): 2174-2180. (in Chinese) doi: 10.3788/OPE.20182609.2174 -






 下载:
下载: