1.   引　言

超构透镜是由一系列亚波长尺寸的单元结构组成的新型衍射透镜，与传统的折射透镜相比，其厚度只有光波长量级，具有轻薄的优势^[1-2]；而与传统的衍射透镜相比，由于它由亚波长尺寸单元结构组成，能有效抑制高阶衍射，因此具有更高效的调控效率^[3-4]。不过，超构透镜继承了传统衍射透镜的色散特性，具有较大的色差，而色差的存在会严重影响透镜在非单色光照明下的成像性能。虽然近年来人们已经发展出一些设计方案用以实现在连续波长范围内消色差的超构透镜（简称为宽谱消色差超构透镜）^[5-10]，但是这些方案设计的透镜存在尺寸较小、数值孔径较低或工作带宽过窄的问题。实际上这是由于这些参数之间存在一定的制约关系所致^{[7, 11]}。因此，如何设计大尺寸、高数值孔径并且工作带宽较宽的超构透镜仍然是一个挑战。幸运的是，在很多白光成像的实际应用场景中，光电探测器往往并不直接接收整个连续光谱的光场，而是采用滤波器阵列将光场过滤为红绿蓝三色（RGB），然后利用三种单色探测器单元进行接收^[12]。此时仅针对几个离散波长进行透镜的消色差设计就能够满足成像系统的要求，同时也可以克服连续波段消色差在器件尺寸和工作效率上的局限。近年来人们提出了一些离散消色差超构透镜的设计方案^[13-16]。结果显示，离散消色差超构透镜确实可以突破宽带消色差透镜制约关系的限制，同时实现较大尺寸、较高数值孔径及更高的工作效率。

不过，对于离散消色差超构透镜，仍有两个问题值得讨论。一是在尺寸和数值孔径均相同的情况下，离散消色差超构透镜相对于宽带消色差超构透镜在设计原理上有什么差异，能否在指定工作频率下获得更高的效率？二是离散消色差超构透镜孤立工作频率之间的间隔对所设计的透镜的效率是否存在影响？理解这两个问题对于具体实际应用中透镜参数的选择具有重要的指导作用。本文将通过理论分析和模拟计算的方式，讨论相同参数下离散消色差超构透镜和宽谱消色差超构透镜在效率上的差异，并考察离散消色差超构透镜的聚焦效率与对应频率间隔大小之间的关系。

2.   离散与宽带消色差超构透镜差异分析

2.1   理论分析

一般而言，为了使入射光场会聚到焦点处，超构透镜提供的波前相位调制需要满足双曲相位^[17]：

式中ω为角频率，c为真空中光速，R为透镜半径，f为焦距，ρ为径向坐标。对于消色差超构透镜，需要波前相位在多个频率或整个频率范围内都满足式(1)。实际提供调制相位的是一系列不同尺寸不同形状的亚波长结构单元。单个结构提供的相位可以表示为^[18]：

式中H为结构高度，n_eff为有效折射率，γ为结构形状参数。式(2)等号右边的第一部分为导波模式带来的传播相位，第二部分为传播相位以外的突变相位，主要包括共振相位和几何相位。一般来说突变相位的调控范围不大，其值通常在0到2π之间。

现在考察离散消色差与宽带消色差超构透镜的设计差异。为了方便分析，引入相位色散空间的概念：假设所考察的消色差频谱范围为[ω₁, ω₂]，设最低频率ω₁对应的相位为Φ，最高频率ω₂与最低频率ω₁对应相位的差值为ΔΦ，则可以定义一个以Φ和ΔΦ作为横纵轴组成的空间，这里将其称为相位色散空间。图1(a)为关于两个频率的相位分布示意图，图1(b)为其对应的相位色散空间。离散消色差超构透镜和宽带消色差超构透镜设计上的差异主要体现在对于相位差ΔΦ的处理上。对于离散消色差超构透镜（以两个频率为例），由于相位只需要在两个频率处满足式(1)，因此可以通过取模2π的方式将所需相位差ΔΦ_n约化到[0, 2π]。以图1(c)左图为例（以Multiwavelength表示离散消色差超构透镜结果），红色虚线为[ω₁,ω₂]区间内原本的色散关系，ω₂对应的相位由红点表示，若将ω₂处的相位减少2π，则ω₂转移到蓝点位置，此时色散关系变为蓝色虚线。两种色散对于离散频率ω₁和ω₂等价，因此，单元结构提供蓝色虚线对应的相位色散便可以满足两个频率处所需相位。对于宽带消色差超构透镜，如图1(c)右图所示（以Broadband表示离散消色差超构透镜结果），所需的相位色散由红色直线表示，此时结构在任一频率处提供的相位都要在这一直线上。若ω₂处所需相位减少2π，使相位色散变为蓝色直线，虽然此时在ω₁与ω₂处的相位均满足理论需求，但是处于这两个频率之间的其它频率（设为ω₃）对应的相位却不满足理论需求，因为其变化的相位小于2π，而不为2π的整数倍，如图中绿色箭头所示。因此，在宽带消色差超构透镜的设计中，无法通过取模2π的方式将所需的相位差ΔΦ约化到[0, 2π]。图1(d)为将图1(b)中相位和相位差均约化后得到的分布，对于离散消色差超构透镜，横纵坐标均可以取模2π，所需要结构提供的最大相位差maxΔΦ为2π，而对于宽带消色差超构透镜，只能对横坐标取模2π，所需要结构提供的最大相位差maxΔΦ约为28π。由于共振相位一般只能提供2π以内的相位，对于大于2π的相位差需要由传播相位提供。根据式(2)，传播相位大小主要由结构高度决定，在结构高度为波长量级的情况下，传播相位只能提供一到两倍2π的相位差，可以满足离散消色差超构透镜所要求的相位差，但无法满足宽带消色差透镜所要求的远大于2π的相位差，因此基于该尺寸的结构所设计的宽带消色差透镜调制波前与理论值会有较大的误差。基于以上分析，可以预测在透镜尺寸与数值孔径较大、而厚度维持在波长量级的情况下，设计得到的离散消色差超构透镜在设计波长处的平均效率会显著高于宽带消色差超构透镜在整个消色差带宽内的平均效率。

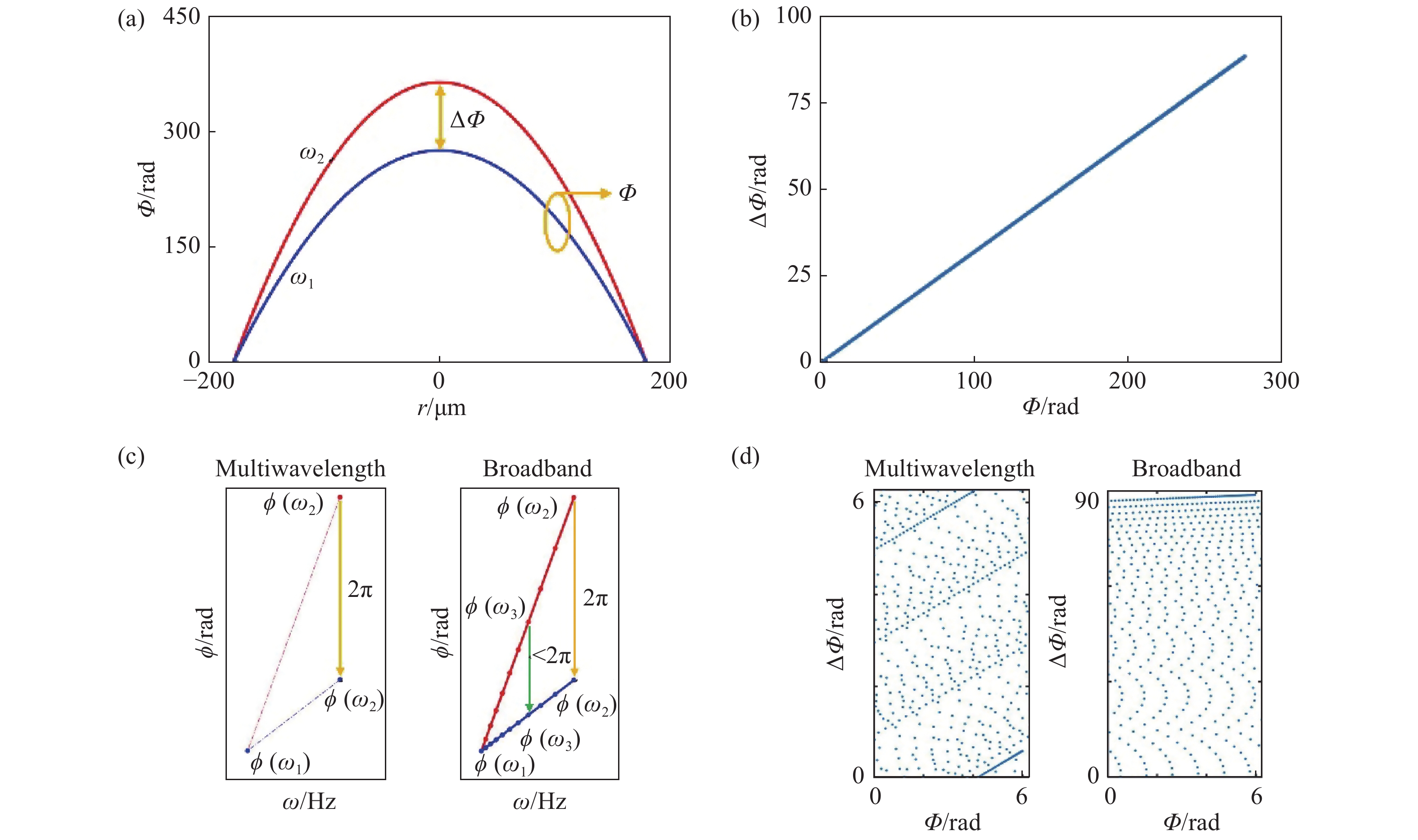
图  1  理论分析示意图。（a）两个频率ω₁与ω₂的相位分布示意图；（b）相位色散空间示意图；（c）离散消色差与宽带消色差超构透镜相位处理上的差异；（d）约化后的相位色散空间。

Figure  1.  Diagram for analyzation. (a) The phase distribution at frequency ω₁and ω₂; (b) phase-dispersion space; (c) difference in multiwavelength metalens and broadband metalens when it comes to phase processing; (d) phase-dispersion space after mod 2π.

下载: 全尺寸图片 幻灯片

2.2   计算验证

为了验证以上结论，需要设计相同参数下的离散波长消色差超构透镜和宽带消色差超构透镜。实际设计的透镜直径为360 μm，数值孔径为0.3。组成透镜的单元结构周期为350 nm，高度为1 μm，材料为SiNx，设计波段为450~650 nm。所采用的结构一共包括4个种类，均为偏振不敏感类型：四方柱，圆柱，圆环柱，十字柱，如图2(a)所示。通过有限时域差分法，可以得到这些结构在不同尺寸下的相位色散分布(Φ,ΔΦ)，如图2(b)所示，其中结构所提供的最大相位差约为2π。而在该尺寸和数值孔径下实现宽带消色差需要的相位差约为28π，因此单元结构无法提供所需的相位差值。此时，可以采用优化的设计方法来实现消色差功能^[5]。采用这种设计方法首先需要确定目标函数和优化算法。本文采取的目标函数为焦点强度，基本思路为寻找最合适的结构分布，使焦点强度达到最大$\mathop {\max }\limits_\Gamma {\rm{ }}{I_0}(\Gamma )$，其中，Γ表示组成透镜的结构分布，I₀为焦点处的光场强度。用于求解该优化问题的方法为Hook-Jeeves（HJ）算法^[19]，是一种直接搜索算法。

图  2  单元结构示意图及色散分布。（a）单元结构示意图。高度H=1 μm，周期p=350 nm；（b）结构提供的相位色散分布图。

Figure  2.  Schematic of meta-unit and it’s phase-dispersion distribution. (a) Schematic of meta-unit. Height H=1 μm, periodic p=350 nm; (b) phase-dispersion provided by the meta-unit

下载: 全尺寸图片 幻灯片

基于上述提到的方法，首先设计了一个离散双波长消色差超构透镜（设计波长分别为450 nm、650 nm）和一个准宽带消色差超构透镜（设计波长在450~650 nm中取21个波长，间隔为10 nm）。利用标量衍射理论，计算了沿传播方向的衍射场，如图3(a)、3(b)所示。可以看到，所设计波长对应的光场均聚焦在指定的焦距处。定义聚焦效率为焦面上焦斑三倍半高宽内的能量与透镜出瞳处的能量比值^{[7, 11]}，不同波长下的聚焦效率，如图3(c)所示。可以看到，对于离散消色差超构透镜，所设计频率处的平均聚焦效率大概在75%左右，而对于宽带消色差超构透镜，平均聚焦效率大概为18%。上述结果证明了之前分析得出的结论。其次，设计了针对不同频率数的离散消色差超构透镜。在保持波段为450~650 nm不变的前提下，设计了针对1个频率聚焦、2个频率消色差、3个频率消色差…21个频率消色差的超构透镜，并按照之前的方案计算其设计频率处的平均聚焦效率。图3(d)为平均聚焦效率关于设计波长数目的分布，可以看到，随着优化波长数目的逐渐增加，平均聚焦效率从80%逐步下降到18%。同时，在波长数大于11后，效率变化极小，基本处于20%左右，此时可以认为所设计的透镜类似于一个宽带消色差超构透镜。综上所述，在设计尺寸和数值孔径较大的情况下，离散消色差超构透镜的平均聚焦效率会显著高于宽带消色差超构透镜。随着设计频率数目的增加，平均聚焦效率下降，最终会与宽带消色差超构透镜效率一致。不过，对于离散波长消色差超构透镜而言，其参量之间是否也存在一定的制约关系？实际上，与宽带消色差超构透镜相比，离散波长消色差超构透镜的参量仅有一项有所改变，即消色差频谱宽度Δω变为了离散波长对应的间隔δω，接下来将讨论双波长离散波长消色差超构透镜的聚焦效率与δω之间的关系。

图  3  设计样品对应的光场分布及聚焦效率。（a）离散消色差超构透镜在设计波长处轴向光场分布。比例尺为500 nm；（b）宽带消色差超构透镜在6个波长处轴向光场分布。比例尺为1 μm；（c）离散消色差超构透镜和宽带消色差超构透镜在设计波长处的聚焦效率；（d）离散消色差超构透镜在平均聚焦效率随设计波长数目的变化

Figure  3.  The light fields and focus efficiencies of the designed samples. (a) Light field of multiwavelength metalens at the wavelengths 450 nm and 650 nm along the propagation axis. Scale bar, 500 nm; (b) light field of broadband achromatic metalens at six wavelengths along the propagation axis. Scale bar, 1 μm; (c) the focus efficiency of multiwavelength metalens and broadband achromatic metalens at the designed wavelengths; (d) the distribution of focus efficiency with respect to the number of designed wavelength

下载: 全尺寸图片 幻灯片

3.   离散波段消色差效率与消色差频率间隔的关系

3.1   理论分析

对于双波长消色差超构透镜，效率关于频率间隔的分布可以分为两个区间进行讨论。第一个区间为频率间隔较小的区间。基于波动光学理论，聚焦光场沿轴向有一定的焦深（Depth Of Focus, DOF）^[1]：

其中，λ为光场的波长，NA为透镜的数值孔径。若两频率间隔极小，满足其焦距差值小于其中一个频率光场对应的焦深，即：

此时可以认为，即便是针对单一频率ω₁设计的超构透镜，对另外一个频率ω₂也基本不存在色差，此时超构透镜对两种频率光场的平均聚焦效率均会接近理想状态。随着频率间隔的增大，焦距差值逐渐增大，最终使得式(4)不再成立，相应的聚焦效率也会下降。因此在这个区间内，效率随频率间隔呈下降趋势。第二个区间为频率间隔较大的区间，此时的分析将基于之前提出的相位色散空间。本文把通过电磁仿真得到的单元结构实际提供的相位和相位差记为(Φ_r, ΔΦ_r)，实现消色差功能理论所需的相位和相位差记为(Φ_n, ΔΦ_n)。如前所述，对于离散消色差超构透镜，相位色散空间总可以将表示成一个[0, 2π]× [0, 2π]的空间。利用这个空间，可以直观地表示出单元结构所能提供的相位色散分布(Φ_r, ΔΦ_r)以及实现消色差超构透镜所需要的相位色散分布(Φ_n, ΔΦ_n)。图4(a)给出了几组不同频率下，单元结构所能提供的相位色散分布(Φ_r, ΔΦ_r)。可以看到，在频率间隔较小的情况下，相位色散分布占整个相位色散空间的比例较小，而在频率间隔较大的情况下，对应分布占比较大。这是因为对于高度为波长量级的结构(如1 μm高度的SiNx结构)，在非共振峰附近，其提供的相位关于频率接近线性分布(主要由传播相位提供，对应式(2)的第一项)^[6]。因此，在频率间隔较小的情况下，单元结构所能提供的相位差值ΔΦ_r较小，随着频率间隔的增大，结构所能提供的相位差值ΔΦ_r也随之增大。图4(b)给出了对应频率实现消色差超构透镜所需要的相位色散分布(Φ_n, ΔΦ_n)，该分布由式(1)计算得到(其中R=180 μm，NA=0.3)。从图中可以看出，即便在频率间隔较小的情况下，所需的相位色散分布在整个空间中的占比也较大，而随着频率间隔增大，所需分布覆盖了整个[0, 2π]× [0, 2π]空间。这是因为根据式(1)，随着透镜尺寸增大，两频率下的相位差值也会增大，使得对于一个尺寸相对较大的超构透镜，即便两频率间隔较小，所需提供的相位差值也会较大。通过对比(Φ_r, ΔΦ_r) 和(Φ_n, ΔΦ_n)，可以发现在频率间隔较小时，两者重合程度较低，也即最终设计得到的相位分布相对于理想情况偏离较大，而随着频率间隔增大，两者重合程度增大，偏离会逐渐减小。因此可以预测，在这个区间内，效率随频率间隔呈上升趋势。

图  4  结构提供的色散分布和实际所需色散分布。（a）不同频率下结构所能提供的相位色散分布;（b）不同频率下实现离散消色差超构透镜所需的相位色散分布。每一列的两幅图对应频率相同。

Figure  4.  The phase-dispersion provided by meta-unit and required for achromatic performance. (a) The phase-dispersion provided by meta-unit at different frequencies; (b) the phase-dispersion required for achromatic performance at different frequencies. Diagrams in the same column has the same frequencies

下载: 全尺寸图片 幻灯片

考察(Φ_r, ΔΦ_r) 相对于(Φ_n, ΔΦ_n)的偏离程度可以更加直观地将上述关于两个区间的结论表现出来。定义相位色散误差Θ为：

式中min表示寻找最优的相位色散(Φ_r, ΔΦ_r)，使得r处被积函数最小。显然，Θ越大表示相位色散(Φ_r, ΔΦ_r) 相对于(Φ_n, ΔΦ_n)偏离越大。取中心频率ω_c=342 THz (对应λ=550 nm)，在不同间隔δω下可以得到不同的频率(ω₁, ω₂)=(ω_c−δω, ω_c+δω)。将该频率代入式(5)，可以计算出Θ关于频率间隔δω的分布，如图5(a)所示。在接近坐标原点的地方Θ较小，随着δω的增大Θ先呈现出迅速上升的趋势，对应于之前讨论的第一个区间；当Θ增加到一定程度，随着δω的增加，其值又会呈现缓慢下降的趋势，对应于之前讨论的第二个区间。

3.2   计算验证

基于HJ优化算法，本文设计出对应频率的离散消色差超构透镜，同时计算了这些透镜在设计频率处的平均聚焦效率，如图5(b)所示。计算结果验证了之前分析得出的结论，即对于双波长消色差超构透镜，其聚焦效率随两频率间隔的分布呈现出先下降再上升的趋势。另一方面，对比图5(a)和图5(b)可以发现，效率与误差Θ关于δω的分布几乎呈现出一一对应的关系：当误差Θ增大时，效率会随之降低，而误差Θ减小时，效率会随之上升。这种对应关系说明用相位色散的误差Θ来分析最终设计结果的效率是较为合理的。

上述方法可以直接推广到三波长消色差超构透镜的分析上。对于三波长消色差超构透镜，假设频率从小到大依次为ω₁、ω₂、ω₃，此时需要考察的频率间隔变为两个：δω₁=ω₂−ω₁，δω₂=ω₃−ω₂。相位差ΔΦ也变为两个：ω₂与ω₁的相位差ΔΦ₁，ω₃与ω₂的相位差ΔΦ₂。类比于双波长的情形，用下标n表示所需要的相位色散分布，下标r表示结构能提供的相位色散分布，此时可以定义相位误差色散为：

保持尺寸和数值孔径不变，将可见光波段内不同的频率(ω₁, ω₂, ω₃)代入式(6)，可以计算出Θ关于频率间隔δω₁和δω₂的分布，如图5(c)所示。在接近坐标原点的地方Θ较小，随着任意一个δω增大Θ首先呈现出迅速上升的趋势，然后再缓慢下降。可以预测，对于三波长消色差超构透镜，随着两个频率间隔增大，其聚焦效率也呈现出先下降再上升的趋势。

图  5  相位色散误差及聚焦效率随频率间隔的分布。（a）双波长离散消色差超构透镜对应的相位色散误差；（b）双波长离散消色差超构透镜平均聚焦效率；（c）三波长离散消色差超构透镜对应的相位色散误差Θ随频率间隔δω₁和δω₂的分布。

Figure  5.  The distributions of the phase-dispersion error and focus efficiency with respect to frequency interval. (a) The phase-dispersion error of dual-wavelength achromatic metalens. (b) The average focus efficiency of dual-wavelength achromatic metalens. (c) The phase-dispersion error of three-wavelength achromatic metalens.

下载: 全尺寸图片 幻灯片

4.   结　论

通过理论分析和计算验证，本文给出了离散消色差超构透镜和宽带消色差超构透镜在聚焦效率上的差异，同时也讨论了离散消色差超构透镜设计频率的间隔对于聚焦效率的影响。从结果来看，在设计尺寸和数值孔径较大的情况下，双波长离散消色差超构透镜的聚焦效率会显著高于宽带消色差超构透镜，以文中给出的参数为例（直径为360 μm，数值孔径为0.3，厚度为1 μm），双波长离散消色差超构透镜聚焦效率约为宽带消色差超构透镜的4倍。如果增加消色差的波长数目，则平均聚焦效率会降低。同时，离散消色差超构透镜的聚焦效率随频率间隔增大会呈现出先降后升的趋势，不过效率整体变化不超过30%。因此，对于工作在几个孤立波段的系统，如RGB成像系统，设计对应的离散消色差超构透镜将会优于设计宽带消色差超构透镜。