-
摘要: 莫尔晶格是指两个相同或者相似的周期结构重叠形成的复合结构。受二维材料中范德华尔斯(van der Waals)异质结形成的莫尔超晶格研究的影响,光学、声学、力学、热学领域中莫尔晶格的研究也相继重拾热情或不断涌现。本文主要回顾了光学莫尔晶格的研究进展,包括构成莫尔晶格的两个周期结构在空间上处于同层的单层莫尔晶格结构和处于不同层的双层莫尔晶格结构,讨论了由不同材料、不同形式构成的各类光学莫尔结构的线性和非线性光学特性。Abstract: Moiré lattices are composite structures composed of two identical or similar periodic structures. Inspired by the research in the van der Waals heterostructures, the research interest on moiré physics in optical, acoustic, mechanical, and thermal systems is either renewing or emerging. Here we review the recent research developments on optical/photonic moiré lattices, including monolayered and bilayered moiré structures, discussing their linear and nonlinear optical properties of different realization of moiré lattices.
-
Key words:
- photonic moiré lattices /
- localization /
- delocalization /
- solitons /
- surface plasmonic polaritons (SPPs)
-
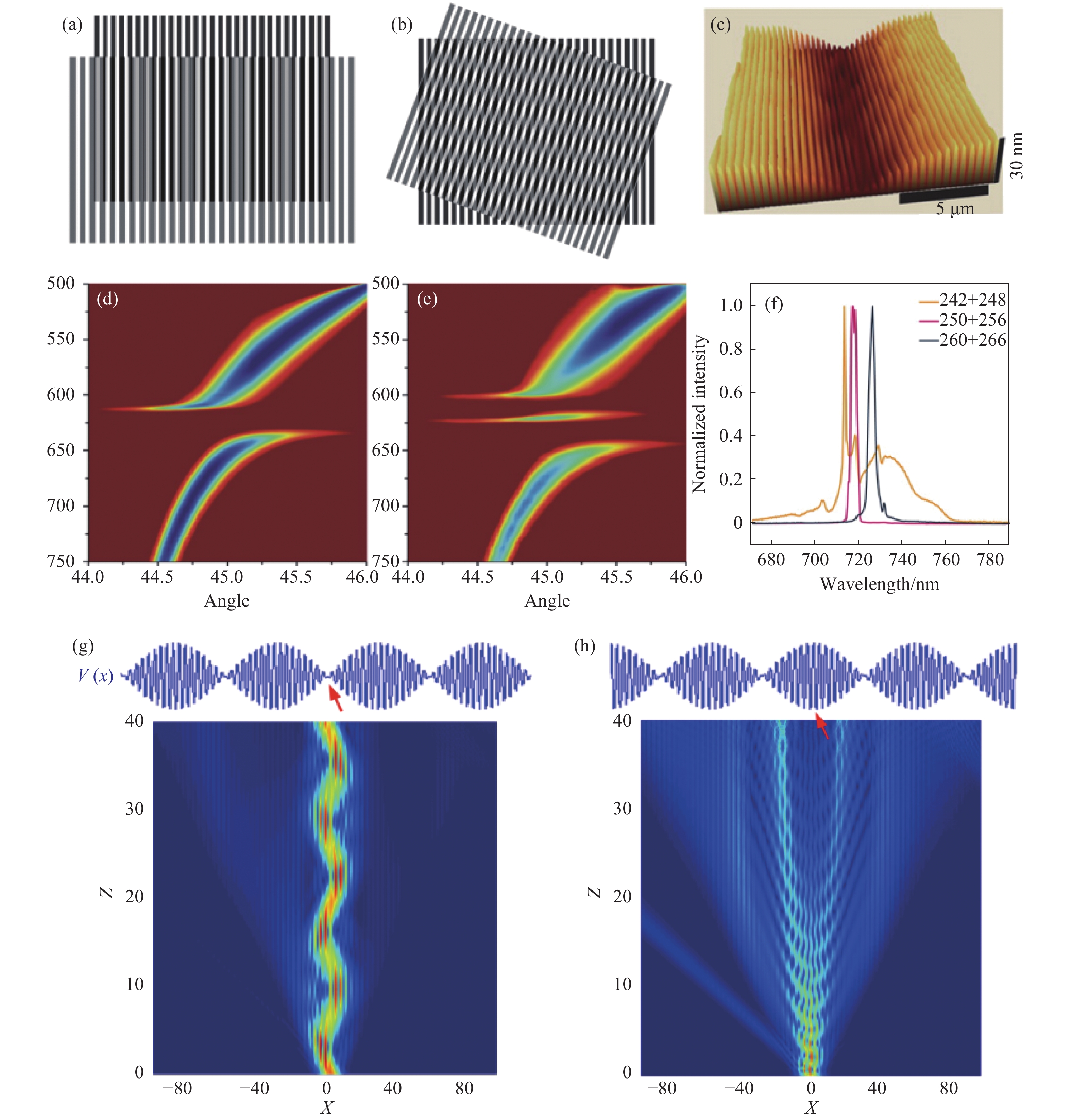
图 1 (a)由周期略有差异的两个一维光栅构成的莫尔光栅; (b)由两个周期相同的一维光栅,旋转一定角度后构成的二维莫尔光栅;(c)一个莫尔周期内的一维金属莫尔结构形貌图[32];(d,e)实验测得的金属光栅的SPP色散曲线和金属莫尔光栅的SPP色散曲线[30];(f)两个金属子光栅的周期(即d1,d2)发生改变时,相应的金属莫尔微腔辐射的激光发生频移[32];在一维莫尔晶格的节点(g)和最大包络处 (h)激发莫尔晶格,光在晶格中的传输图像[34]。
Figure 1. (a) Moiré gratings constituted from two 1D gratings with slightly detuned periods. (b) 2D moiré pattern constituted from two 1D gratings with a relative rotation angle. (c) Landscape of 1D metallic moiré structure shown within one moiré period [32]. (d,e) Experimentally measured dispersion curves of SPP on metallic 1D gratings and on moiré gratings [30]. (f) With the change of the period (i.e. d1, d2) of the two constituent metallic gratings, the lasing frequency of the corresponding metallic moiré cavity changes [32]. Light propagating dynamics when a 1D moiré lattice is optically excited at its node (g) or at its peak (h) of the structural envelop [34].
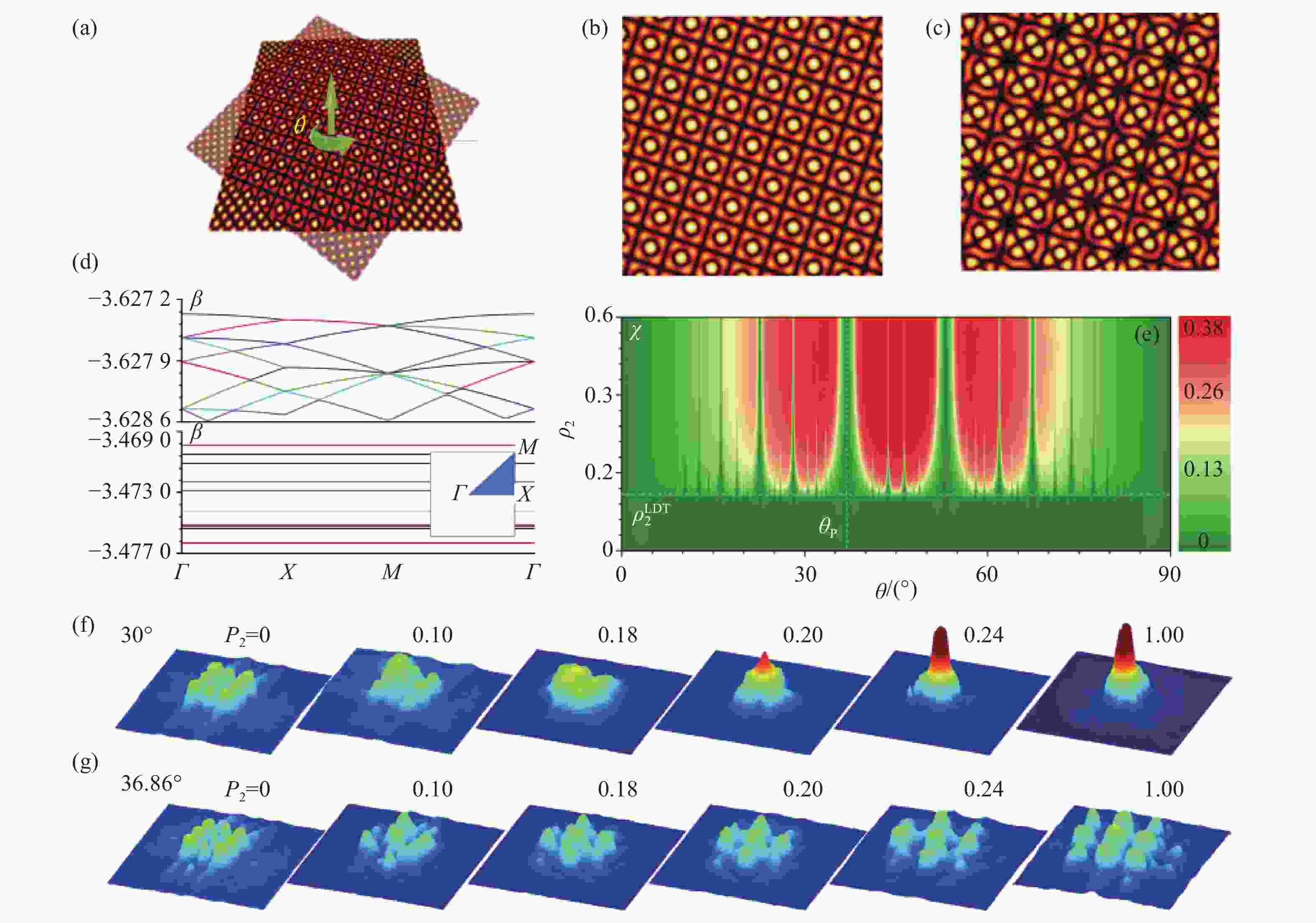
图 2 (a)由两个方形子晶格重叠,且转过相对角度θ后,构成的二维光子莫尔晶格;(b)周期莫尔晶格;(c)非周期莫尔晶格;(d)非周期莫尔晶格对应的准能带图,上图p2<p2cr, 下图p2>p2cr;(e) 本征模在二维平面(θ,p2)的形式因子分布图,图中绿色代表模式处于非局域状态,红色代表模式处于局域状态;(f,g)用高斯光激发莫尔晶格,在不同p2(固定p1≡1)对应的晶格中传输2 cm后的光强输出图。上行图代表光束在非周期莫尔晶格中传输的情形,可以看到当p2超过0.18(p2cr=0.15)时,光束开始局域;下行图代表光束在周期莫尔晶格中传输的情形,可以看到光束始终处于离散衍射的状态[20]。
Figure 2. (a) 2D photonic moiré lattices obtained by superpositioning two square lattices with a relative rotational angles θ; (b) A moiré lattice in a commensurate phase; (c) A moiré lattice in an incommensurate phase; (d) Quasi-bandstructure for an incommensurate moiré lattice: upper row for p2<p2cr, lower row for p2>p2cr;(e) Form factor of the eigen modes shown in the plane (θ, p2), where the blue-colored domains imply mode delocalization, while the red-colored domains imply mode localization; (f, g) After propagating 2 cm in the moiré lattice of an initially narrow Gaussian beam, the lightintensity distribution at the output facet of the lattice with different p2(with fixed p1≡1). Upper row shows the results in incommensurate moiré lattices, and one can see that the light beam starts localizing when p2 exceeds 0.18 (p2cr=0.15); Bottom row shows the results in commensurate moiré lattices, and one sees the delocalization of the light persists for all values of p2[20].
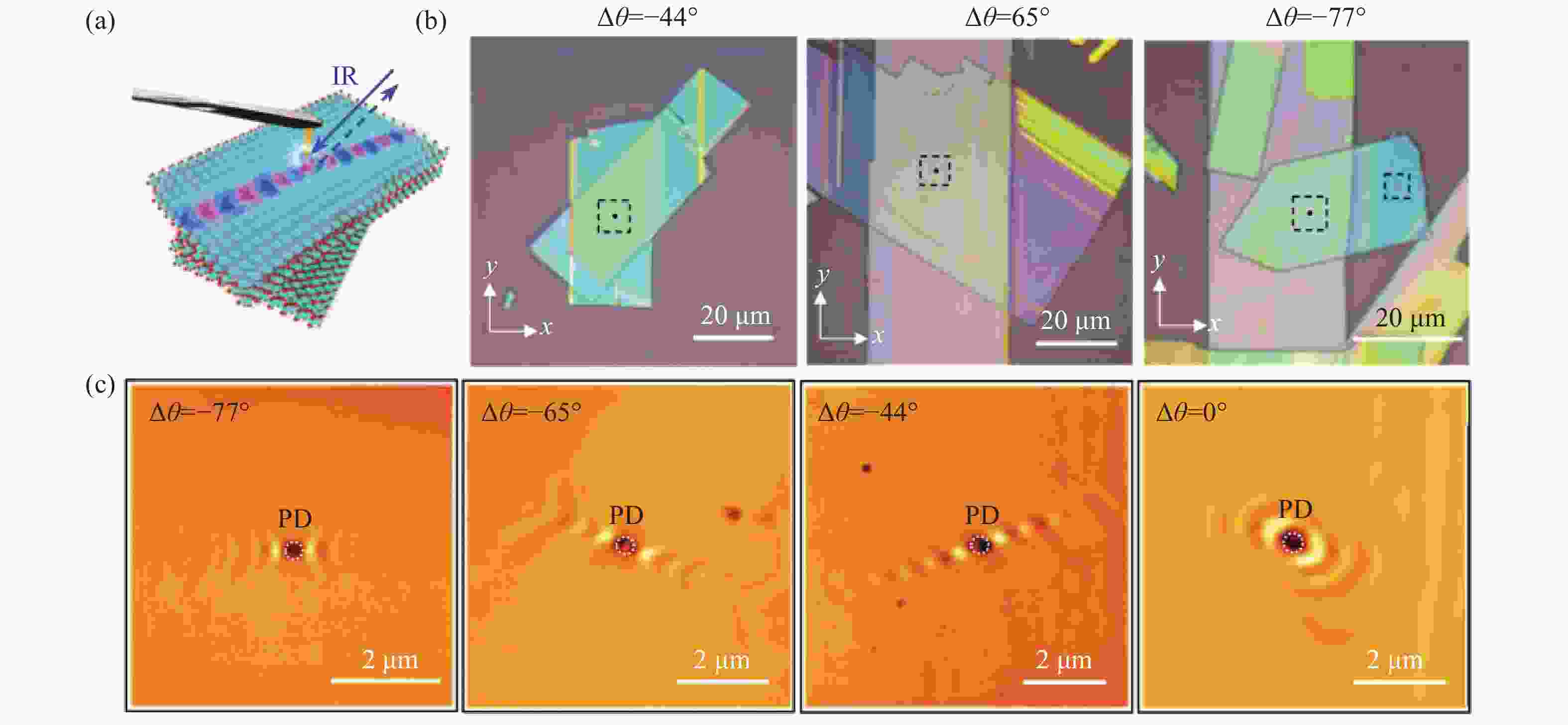
图 3 (a) 两层α-MoO3堆叠构成的莫尔超晶格结构;(b)α-MoO3莫尔超晶格结构在不同莫尔角下的光学照片;(c)声极化激元在不同莫尔角度下的波形分布图,显示出双曲-平带-椭圆三类拓扑上不同的色散带的转变[55]。
Figure 3. (a) Moiré superlattice constituted by twist-stacked α-MoO3 bilayer; (b)Optical images of α-MoO3 moiré superlattice as a function of rotation angle;(c) In-plane propagation of phonon polaritons at different twist angle of an α-MoO3 bilayer, indicating a transition among three topologically different dispersion:hyperbolic, flat and elliptic [55].
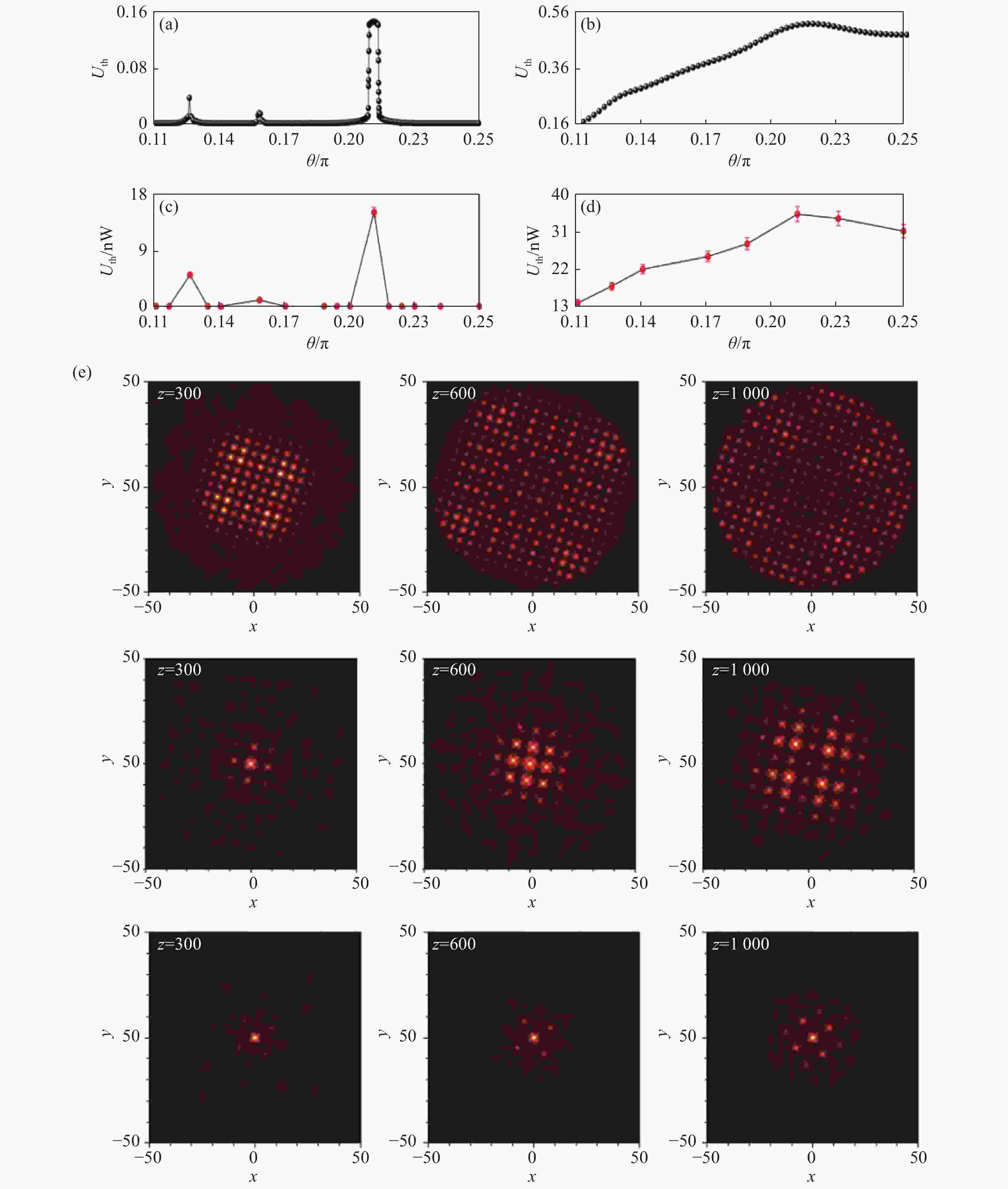
图 4 (a-d)激发莫尔光孤子的阈值功率随莫尔角的变化,(a,c)对应p2>p2cr的情形,(b,d)对应p2<p2cr的情形。(a,b)是模拟结果,(c,d)是实验结果[21]。(e)给出了在莫尔角为三个不同勾股角时,莫尔晶格中光的衍射程度的比较。从上往下分别对应勾股角(3,4,5),(5,12,13),(8,5,17)。可以看到,随着勾股角的级次增加,光在莫尔晶格中的衍射效应不断降低,从而解释了图(a,c)中孤子阈值功率随着勾股角级次的增加不断降低的现象。
Figure 4. (a-d) Dependencies of the threshold power on rotational angle for optical soliton formation in moiré lattices, (a, c) p2>p2cr, (b, d) p2<p2cr. Theoretically calculated results are shown in (a, c) and experimentally measured results are shown in(b, d) [21]. (e) Comparison of diffraction strength of light propagating in moiré lattices for three different Pythagorean angles, corresponding, from upper to bottom, to (3,4,5), (5,12,13), (8,5,17). Note the continuous decreasing of the light diffraction strength with the increasing of the order of Pythagorean triples, which explains the continuous decrease of the soliton threshold power with the Pythagorean angles seen in figure (a, c).
-
[1] 叶芳伟. 生活中的莫尔晶格[EB/OL][2021.07.21] https://www.physics.sjtu.edu.cn/fangweiye/moire.YE F W. Moiré lattices in life[EB/OL][2021.07.21] https://www.physics.sjtu.edu.cn/fangweiye/moire. [2] OHTA T, BOSTWICK A, SEYLLER T, et al. Controlling the electronic structure of bilayer graphene[J]. Science, 2006, 313(5789): 951-954. doi: 10.1126/science.1130681 [3] GEIM A K, GRIGORIEVA I V. Van der Waals heterostructures[J]. Nature, 2013, 499(7459): 419-425. doi: 10.1038/nature12385 [4] OOSTINGA J B, HEERSCHE H B, LIU X L, et al. Gate-induced insulating state in bilayer graphene devices[J]. Nature Materials, 2008, 7(2): 151-157. doi: 10.1038/nmat2082 [5] LIU L X, ZHOU H L, CHENG R, et al. High-yield chemical vapor deposition growth of high-quality large-area AB-stacked bilayer graphene[J]. ACS Nano, 2012, 6(9): 8241-8249. doi: 10.1021/nn302918x [6] LAI Y H, HO J H, CHANG C P, et al. Magnetoelectronic properties of bilayer Bernal graphene[J]. Physical Review B, 2008, 77(8): 085426. doi: 10.1103/PhysRevB.77.085426 [7] LI J, ZHANG R X, YIN ZH X, et al. A valley valve and electron beam splitter[J]. Science, 2018, 362(6419): 1149-1152. doi: 10.1126/science.aao5989 [8] BITTENCOURT V A S V, BERNARDINI A E. Lattice-layer entanglement in Bernal-stacked bilayer graphene[J]. Physical Review B, 2017, 95(19): 195145. doi: 10.1103/PhysRevB.95.195145 [9] LI H Y, YING H, CHEN X P, et al. Thermal conductivity of twisted bilayer graphene[J]. Nanoscale, 2014, 6(22): 13402-13408. doi: 10.1039/C4NR04455J [10] CAO Y, FATEMI V, DEMIR A, et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices[J]. Nature, 2018, 556(7699): 80-84. doi: 10.1038/nature26154 [11] CAO Y, FATEMI V, FANG SH A, et al. Unconventional superconductivity in magic-angle graphene superlattices[J]. Nature, 2018, 556(7699): 43-50. doi: 10.1038/nature26160 [12] PARK M J, KIM Y, CHO G Y, et al. Higher-order topological insulator in twisted bilayer graphene[J]. Physical Review Letters, 2019, 123(21): 216803. doi: 10.1103/PhysRevLett.123.216803 [13] SEYLER K L, RIVERA P, YU H Y, et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers[J]. Nature, 2019, 567(7746): 66-70. doi: 10.1038/s41586-019-0957-1 [14] YUAN L, ZHENG B Y, KUNSTMANN J, et al. Twist-angle-dependent interlayer exciton diffusion in WS2-WSe2 heterobilayers[J]. Nature Materials, 2020, 19(6): 617-623. doi: 10.1038/s41563-020-0670-3 [15] CHEN G R, JIANG L L, WU SH, et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice[J]. Nature Physics, 2019, 15(3): 237-241. doi: 10.1038/s41567-018-0387-2 [16] JIANG B Y, NI G X, ADDISON Z, et al. Plasmon reflections by topological electronic boundaries in bilayer graphene[J]. Nano Letters, 2017, 17(11): 7080-7085. doi: 10.1021/acs.nanolett.7b03816 [17] LIU Y, WEISS N O, DUAN X D, et al. Van der Waals heterostructures and devices[J]. Nature, 2016, 1(9): 16042. [18] CARR S, MASSATT D, FANG SH A, et al. Twistronics: manipulating the electronic properties of two-dimensional layered structures through their twist angle[J]. Physical Review B, 2017, 95(7): 075420. doi: 10.1103/PhysRevB.95.075420 [19] HUANG CH M, YE F W, CHEN X F, et al. Localization-delocalization wavepacket transition in Pythagorean aperiodic potentials[J]. Scientific reports, 2016, 6: 32546. doi: 10.1038/srep32546 [20] WANG P, ZHENG Y L, CHEN X F, et al. Localization and delocalization of light in photonic moiré lattices[J]. Nature, 2020, 577(7788): 42-46. doi: 10.1038/s41586-019-1851-6 [21] FU Q D, WANG P, HUANG CH M, et al. Optical soliton formation controlled by angle twisting in photonic moiré lattices[J]. Nature Photonics, 2020, 14(11): 663-668. doi: 10.1038/s41566-020-0679-9 [22] DENG Y CH, OUDICH M, GERARD N J R K, et al. Magic-angle bilayer phononic graphene[J]. Physical Review B, 2020, 102(18): 180304(R). doi: 10.1103/PhysRevB.102.180304 [23] GARDEZI S M, PIRIE H, DORRELL W, et al.. Acoustic twisted bilayer graphene[J]. arXiv: 2010.10037, 2020. [24] LÓPEZ M R, PEÑARANDA F, CHRISTENSEN J, et al. Flat bands in magic-angle vibrating plates[J]. Physical Review Letters, 2020, 125(21): 214301. doi: 10.1103/PhysRevLett.125.214301 [25] O’RIORDAN L J, WHITE A C, BUSCH T. Moiré superlattice structures in kicked Bose-Einstein condensates[J]. Physical Review A, 2016, 93(2): 023609. doi: 10.1103/PhysRevA.93.023609 [26] GONZÁLEZ-TUDELA A, CIRAC J I. Cold atoms in twisted-bilayer optical potentials[J]. Physical Review A, 2019, 100(5): 053604. doi: 10.1103/PhysRevA.100.053604 [27] DURELLI A J, PARKS V J. Moiré Analysis of Strain[M]. Englewood Cliffs: Prentice-Hall, 1970. [28] TAKASAKI H. Moiré topography[J]. Applied Optics, 1970, 9(6): 1467-1472. doi: 10.1364/AO.9.001467 [29] CADARSO V J, CHOSSON S, SIDLER K, et al. High-resolution 1D moirés as counterfeit security features[J]. Light:Science &Applications, 2013, 2(7): e86. [30] KOCABAS A, SENLIK S S, AYDINLI A. Slowing down surface plasmons on a moiré surface[J]. Physical Review Letters, 2009, 102(6): 063901. doi: 10.1103/PhysRevLett.102.063901 [31] BALCI S, KARABIYIK M, KOCABAS A, et al. Coupled plasmonic cavities on moire surfaces[J]. Plasmonics, 2010, 5(4): 429-436. doi: 10.1007/s11468-010-9161-8 [32] KARADEMIR E, BALCI S, KOCABAS C, et al. Lasing in a slow Plasmon moiré cavity[J]. ACS Photonics, 2015, 2(7): 805-809. doi: 10.1021/acsphotonics.5b00168 [33] KHURGIN J B. Light slowing down in Moiré fiber gratings and its implications for nonlinear optics[J]. Physical Review A, 2000, 62(1): 013821. doi: 10.1103/PhysRevA.62.013821 [34] XUE R D, WANG W, WANG L Q, et al. Localization and oscillation of optical beams in Moiré lattices[J]. Optics Express, 2017, 25(5): 5788-5796. doi: 10.1364/OE.25.005788 [35] WANG Y, LAN Y J, SONG Q, et al. Colorful efficient Moiré-perovskite solar cells[J]. Advanced Materials, 2021, 33(15): 2008091. doi: 10.1002/adma.202008091 [36] GUO CH, GUO Y, LOU B CH, et al. Wide wavelength-tunable narrow-band thermal radiation from moiré patterns[J]. Applied Physics Letters, 2021, 118(13): 131111. doi: 10.1063/5.0047308 [37] HUANG SH F, ZHANG H F, WU Z L, et al. Large-area ordered P-type Si nanowire arrays as photocathode for highly efficient photoelectrochemical hydrogen generation[J]. ACS Applied Materials &Interfaces, 2014, 6(15): 12111-12118. [38] WU Z L, CHEN K, MENZ R, et al. Tunable multiband metasurfaces by moiré nanosphere lithography[J]. Nanoscale, 2015, 7(48): 20391-20396. doi: 10.1039/C5NR05645D [39] WU Z L, LI W, YOGEESH M N, et al. Tunable graphene metasurfaces with gradient features by self-assembly-based Moiré nanosphere lithography[J]. Advanced Optical Materials, 2016, 4(12): 2035-2043. doi: 10.1002/adom.201600242 [40] HAN J H, KIM I, RYU J W, et al. Rotationally reconfigurable metamaterials based on moiré phenomenon[J]. Optics Express, 2015, 23(13): 17443-17449. doi: 10.1364/OE.23.017443 [41] GAO Y M, WEN Z R, ZHENG L R, et al. Complex periodic non-diffracting beams generated by superposition of two identical periodic wave fields[J]. Optics Communications, 2017, 389: 123-127. doi: 10.1016/j.optcom.2016.12.022 [42] JIN W T, SONG M, XUE Y L, et al. Construction of photorefractive photonic quasicrystal microstructures by twisted square lattices[J]. Applied Optics, 2020, 59(22): 6638-6641. doi: 10.1364/AO.397622 [43] FLEISCHER J W, SEGEV M, EFREMIDIS N K, et al. Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices[J]. Nature, 2003, 422(6928): 147-150. doi: 10.1038/nature01452 [44] 陈俞安. 五类莫尔晶格的光学特性[D]. 上海: 上海交通大学, 2020.CHEN Y A. Optical properties of five kinds Moiré lattice[D]. Shanghai: Shanghai Jiaotong University, 2020. (in Chinese). [45] 李静. 基于复杂晶格的莫尔晶格的光学性质[D]. 上海: 上海交通大学, 2020.LI J. Optical properties of Moiré lattice based on complex lattice[D]. Shanghai: Shanghai Jiaotong University, 2020. (in Chinese). [46] MUKHERJEE S, SPRACKLEN A, CHOUDHURY D, et al. Observation of a localized flat-band state in a photonic lieb lattice[J]. Physical Review Letters, 2015, 114(24): 245504. doi: 10.1103/PhysRevLett.114.245504 [47] VICENCIO R A, CANTILLANO C, MORALES-INOSTROZA L, et al. Observation of localized states in lieb photonic lattices[J]. Physical Review Letters, 2015, 114(24): 245503. doi: 10.1103/PhysRevLett.114.245503 [48] XIA SH Q, RAMACHANDRAN A, XIA SH Q, et al. Unconventional flatband line states in photonic lieb lattices[J]. Physical Review Letters, 2018, 121(26): 263902. doi: 10.1103/PhysRevLett.121.263902 [49] LEYKAM D, ANDREANOV A, FLACH S. Artificial flat band systems: from lattice models to experiments[J]. Advances in Physics:X, 2018, 3(1): 1473052. doi: 10.1080/23746149.2018.1473052 [50] GÓMEZ-URREA H A, OSPINA-MEDINA M C, CORREA-ABAD J D, et al. Tunable band structure in 2D Bravais-Moiré photonic crystal lattices[J]. Optics Communications, 2020, 459: 125081. doi: 10.1016/j.optcom.2019.125081 [51] BISTRITZER R, MACDONALD A H. Moiré bands in twisted double-layer graphene[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(30): 12233-12237. doi: 10.1073/pnas.1108174108 [52] ZHANG ZH M, WANG Y M, WATANABE K, et al. Flat bands in twisted bilayer transition metal dichalcogenides[J]. Nature Physics, 2020, 16(11): 1093-1096. doi: 10.1038/s41567-020-0958-x [53] UTAMA M I B, KOCH R J, LEE K, et al. Visualization of the flat electronic band in twisted bilayer graphene near the magic angle twist[J]. Nature Physics, 2021, 17(2): 184-188. doi: 10.1038/s41567-020-0974-x [54] HU G W, KRASNOK A, MAZOR Y, et al. Moiré hyperbolic metasurfaces[J]. Nano Letters, 2020, 20(5): 3217-3224. doi: 10.1021/acs.nanolett.9b05319 [55] HU G W, OU Q D, SI G Y, et al. Topological polaritons and photonic magic angles in twisted α-MoO3 bilayers[J]. Nature, 2020, 582(7811): 209-213. doi: 10.1038/s41586-020-2359-9 [56] LOU B CH, ZHAO N, MINKOV M, et al. Theory for twisted bilayer photonic crystal slabs[J]. Physical Review Letters, 2021, 126(13): 136101. doi: 10.1103/PhysRevLett.126.136101 [57] WANG W H, GAO W L, CHEN X D, et al. Moiré fringe induced gauge field in photonics[J]. Physical Review Letters, 2020, 125(20): 203901. doi: 10.1103/PhysRevLett.125.203901 [58] OUDICH M, SU G X, DENG Y CH, et al.. Bilayer photonic graphene[J]. arXiv: 2103.03686, 2021. [59] LIU ZH, DU ZH Y, HU B, et al. Wide-angle Moiré metalens with continuous zooming[J]. Journal of the Optical Society of America B, 2019, 36(10): 2810-2816. doi: 10.1364/JOSAB.36.002810 [60] CHEN ZH G, SEGEV M, CHRISTODOULIDES D N. Optical spatial solitons: historical overview and recent advances[J]. Reports on Progress in Physics, 2012, 75(8): 086401. doi: 10.1088/0034-4885/75/8/086401 [61] YE F, MIHALACHE D, HU B, et al. Subwavelength plasmonic lattice solitons in arrays of metallic nanowires[J]. Physical Review Letters, 2010, 104(10): 106802. doi: 10.1103/PhysRevLett.104.106802 [62] BAĞCI M. Soliton dynamics in quadratic nonlinear media with two-dimensional Pythagorean aperiodic lattices[J]. Journal of the Optical Society of America B, 2021, 38(4): 1276-1282. doi: 10.1364/JOSAB.416299 [63] LEI F Q, WANG CH F. Study on the properties of solitons in moiré lattice[J]. Optik, 2020, 219: 165169. doi: 10.1016/j.ijleo.2020.165169 [64] FEI Z, RODIN A S, ANDREEV G O, et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging[J]. Nature, 2012, 487(7405): 82-85. doi: 10.1038/nature11253 [65] CHEN J N, BADIOLI M, ALONSO-GONZALEZ P, et al. Optical nano-imaging of gate-tunable graphene plasmons[J]. Nature, 2012, 487(7405): 77-81. doi: 10.1038/nature11254 [66] SUNKU S S, NI G X, JIANG B Y, et al. Photonic crystals for nano-light in moiré graphene superlattices[J]. Science, 2018, 362(6419): 1153-1156. doi: 10.1126/science.aau5144 [67] LIN X, LIU Z F, STAUBER T, et al. Chiral plasmons with twisted atomic bilayers[J]. Physical Review Letters, 2020, 125(7): 077401. doi: 10.1103/PhysRevLett.125.077401 [68] BREY L, STAUBER T, SLIPCHENKO T, et al. Plasmonic Dirac cone in twisted bilayer graphene[J]. Physical Review Letters, 2020, 125(25): 256804. doi: 10.1103/PhysRevLett.125.256804 [69] ZHANG X Y, ZHONG Y H, LOW T, et al. Emerging chiral optics from chiral interfaces[J]. Physical Review B, 2021, 103(19): 195405. doi: 10.1103/PhysRevB.103.195405 [70] JIANG L L, SHI ZH W, ZENG B, et al. Soliton-dependent plasmon reflection at bilayer graphene domain walls[J]. Nature Materials, 2016, 15(8): 840-844. doi: 10.1038/nmat4653 [71] WU F CH, LOVORN T, MACDONALD A H. Topological exciton bands in Moiré heterojunctions[J]. Physical Review Letters, 2017, 118(14): 147401. doi: 10.1103/PhysRevLett.118.147401 [72] YU H Y, LIU G B, TANG J J, et al. Moiré excitons: from programmable quantum emitter arrays to spin-orbit-coupled artificial lattices[J]. Science Advances, 2017, 3(11): e1701696. doi: 10.1126/sciadv.1701696 [73] KIM C J, BROWN L, GRAHAM M W, et al. Stacking order dependent second harmonic generation and topological defects in h-BN bilayers[J]. Nano Letters, 2013, 13(11): 5660-5665. doi: 10.1021/nl403328s [74] HSU W T, ZHAO Z A, LI L J, et al. Second harmonic generation from artificially stacked transition metal dichalcogenide twisted bilayers[J]. ACS Nano, 2014, 8(3): 2951-2958. doi: 10.1021/nn500228r [75] YAO K Y, YANEV E, CHUANG H J, et al. Continuous wave sum frequency generation and imaging of monolayer and heterobilayer two-dimensional semiconductors[J]. ACS Nano, 2020, 14(1): 708-714. doi: 10.1021/acsnano.9b07555 [76] LIU F, WU W J, BAI Y S, et al. Disassembling 2D van der Waals crystals into macroscopic monolayers and reassembling into artificial lattices[J]. Science, 2020, 367(6480): 903-906. doi: 10.1126/science.aba1416 [77] YAO K Y, FINNEY N R, ZHANG J, et al.. Nonlinear twistoptics at symmetry-broken interfaces[J]. arXiv: 2006.13802, 2020. [78] ZHANG L, WU F CH, HOU SH C, et al. Van der Waals heterostructure polaritons with moiré-induced nonlinearity[J]. Nature, 2021, 591(7848): 61-65. doi: 10.1038/s41586-021-03228-5 -






 下载:
下载: