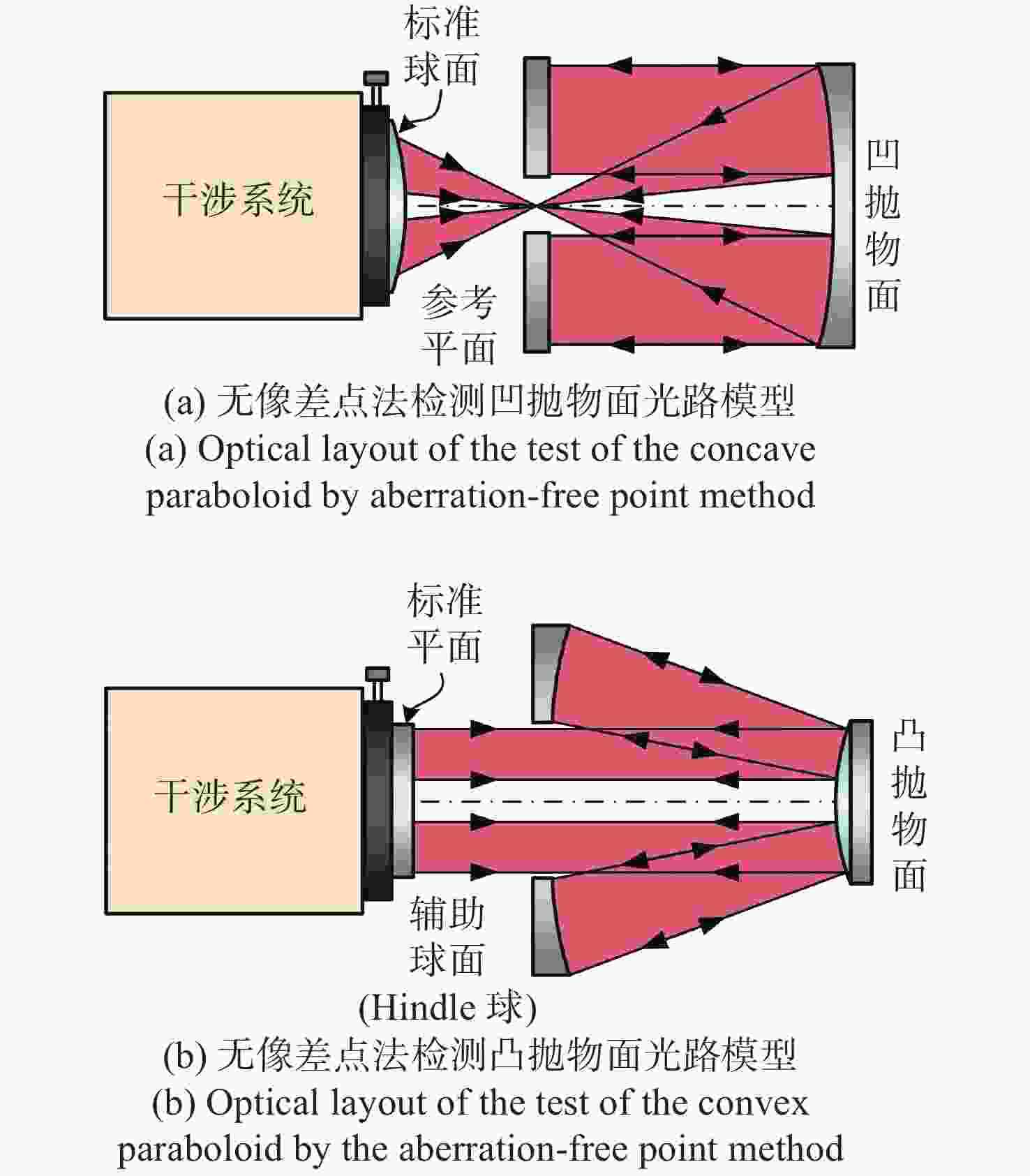
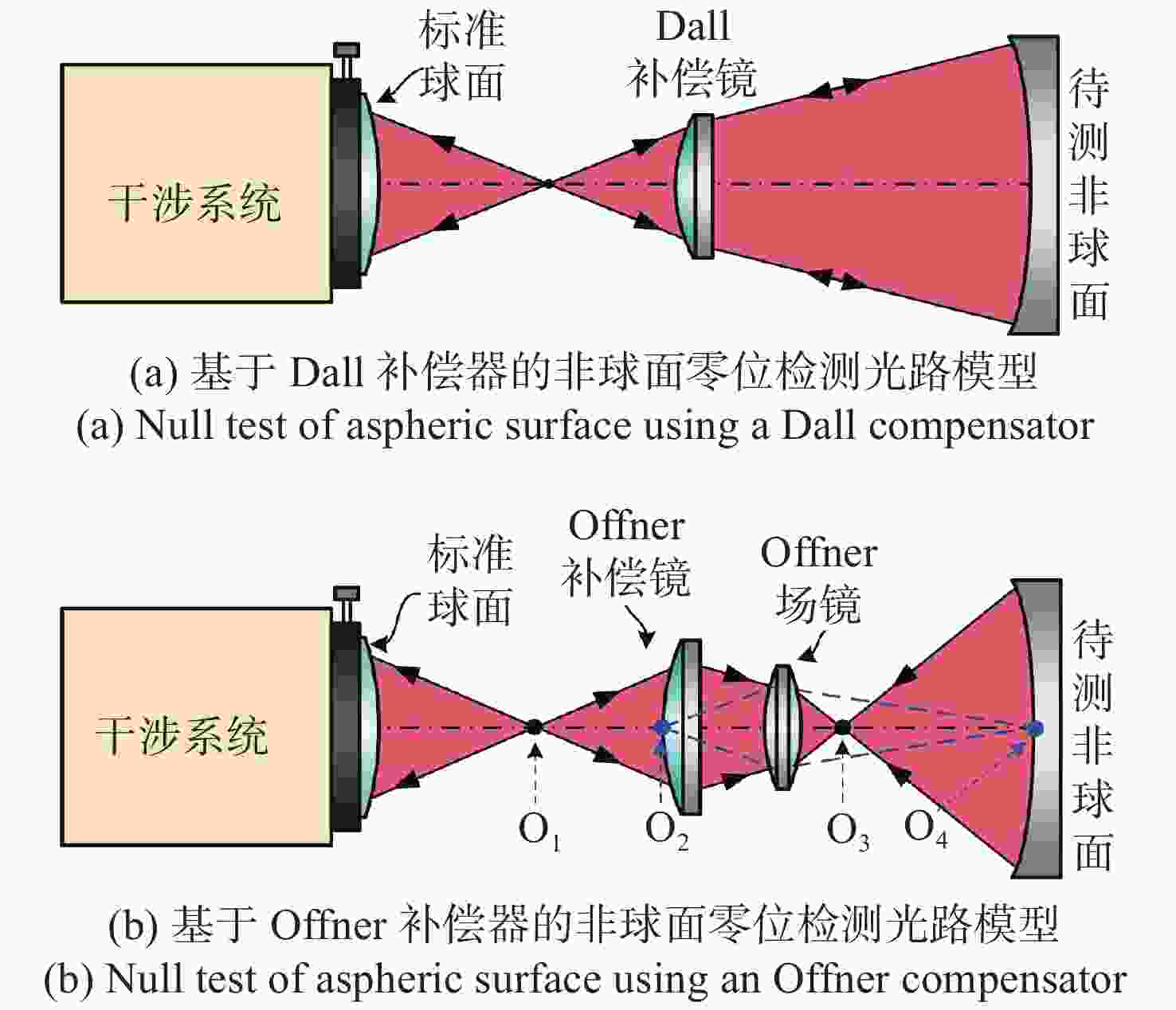
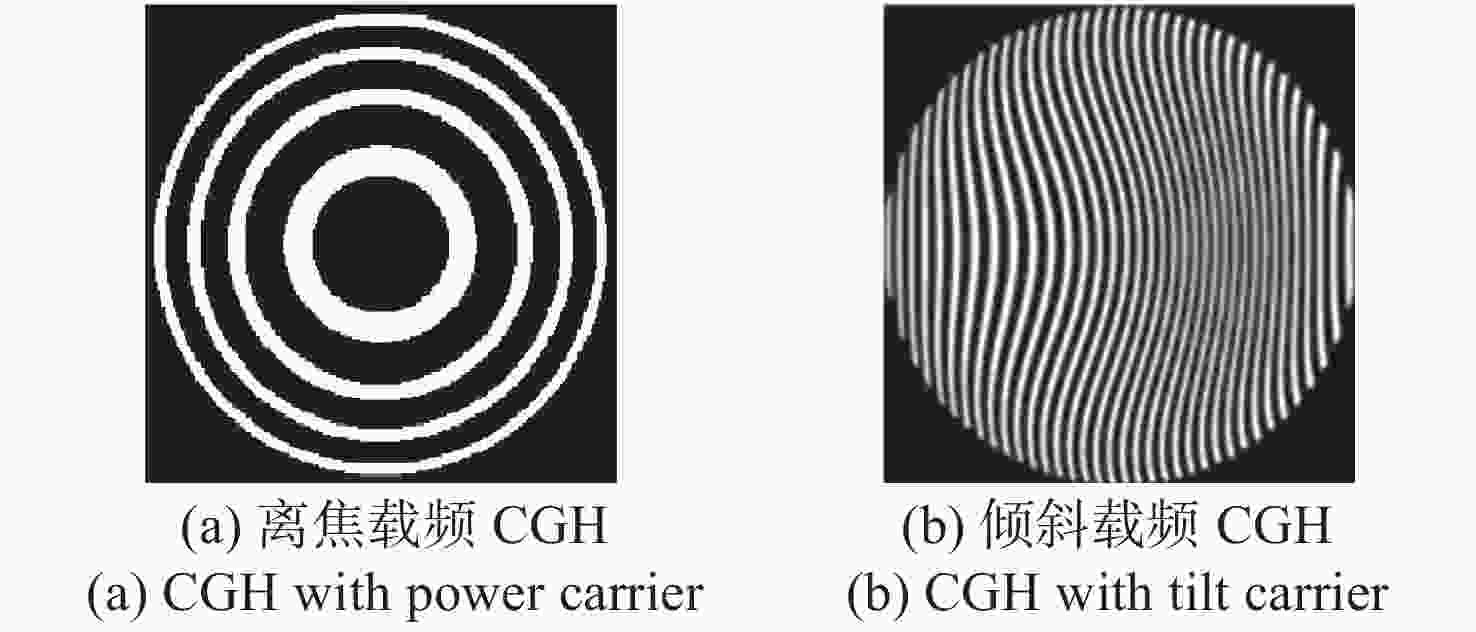
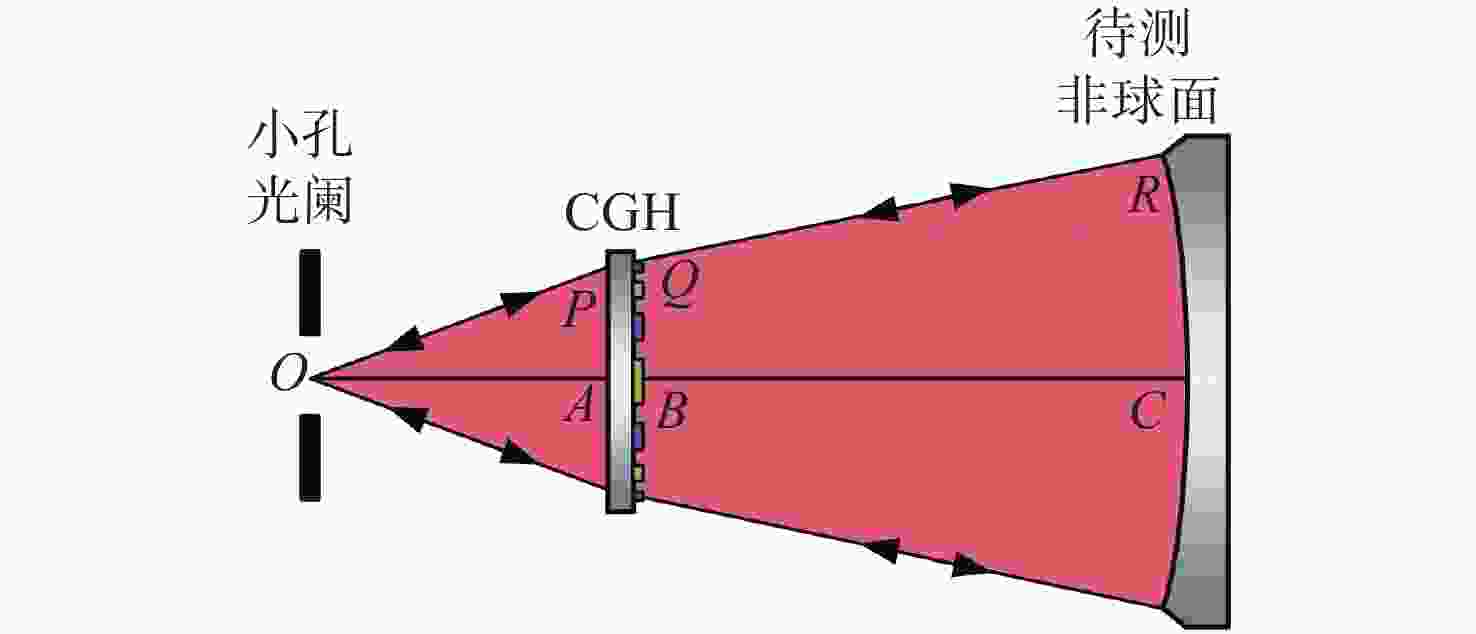
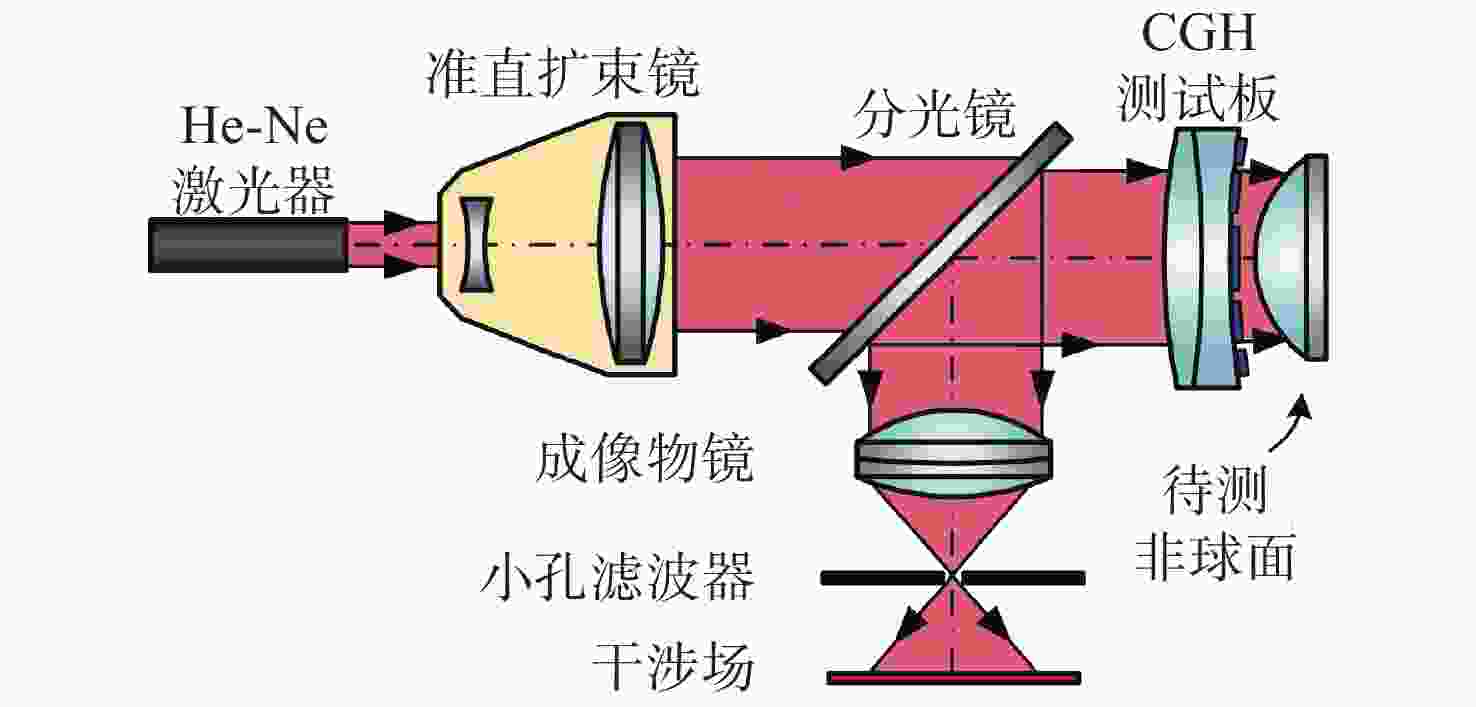
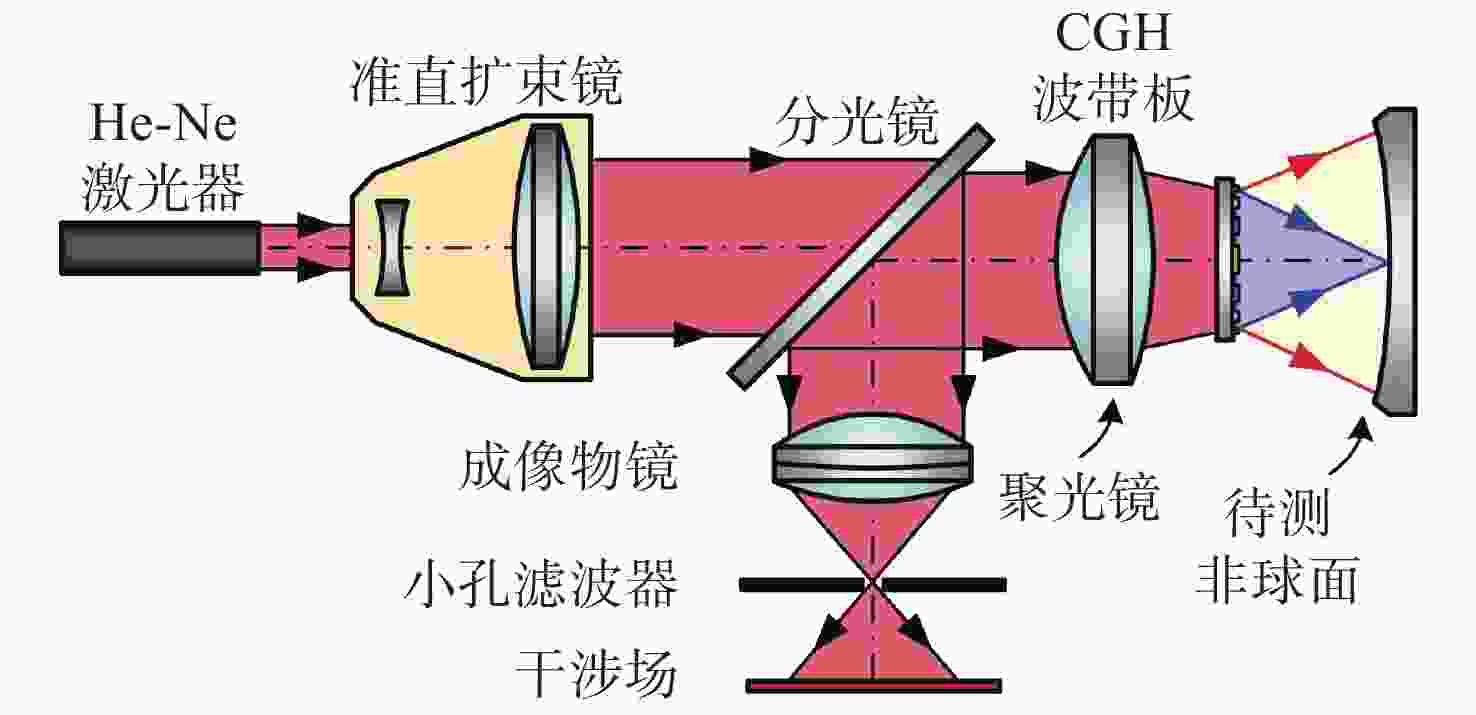
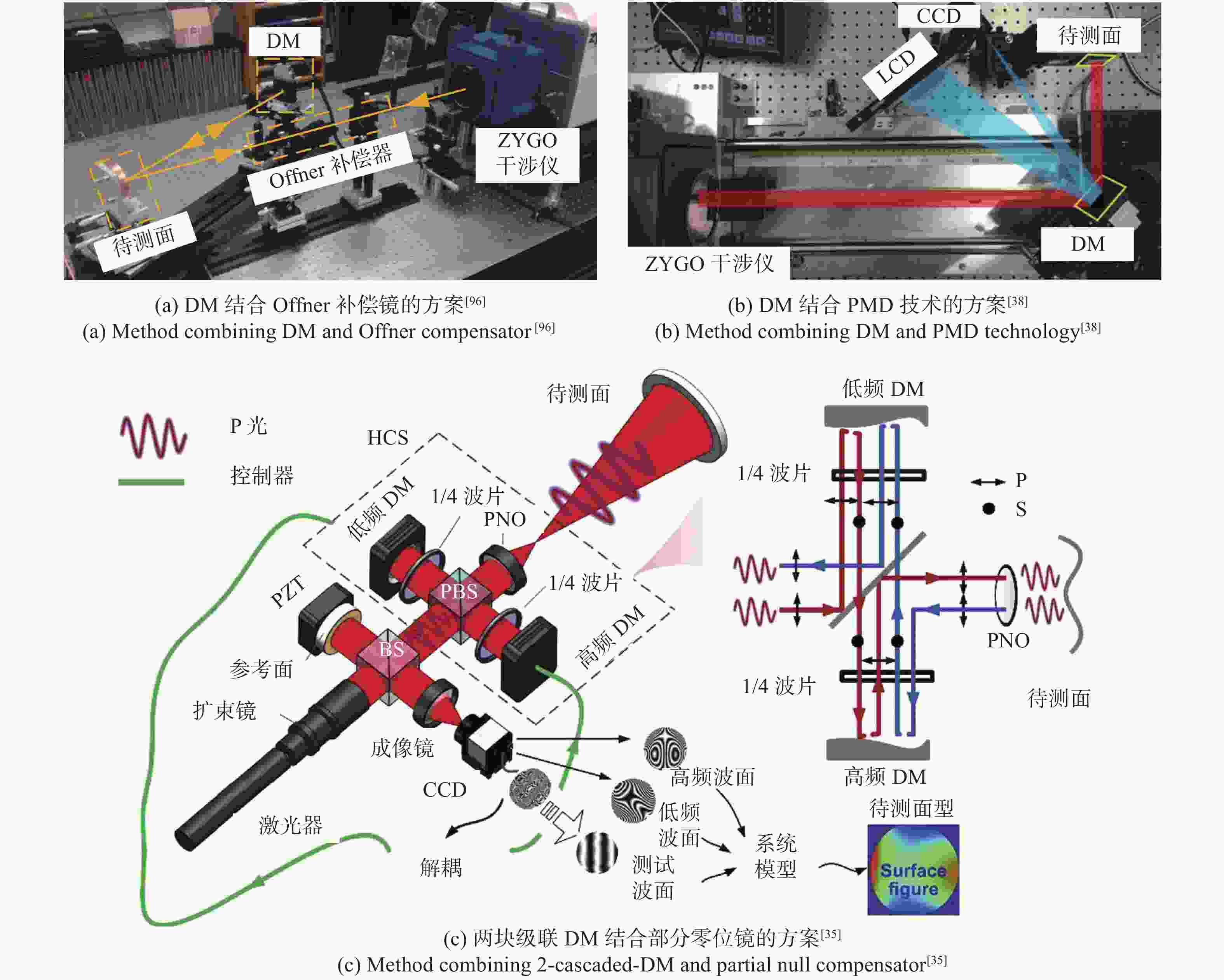
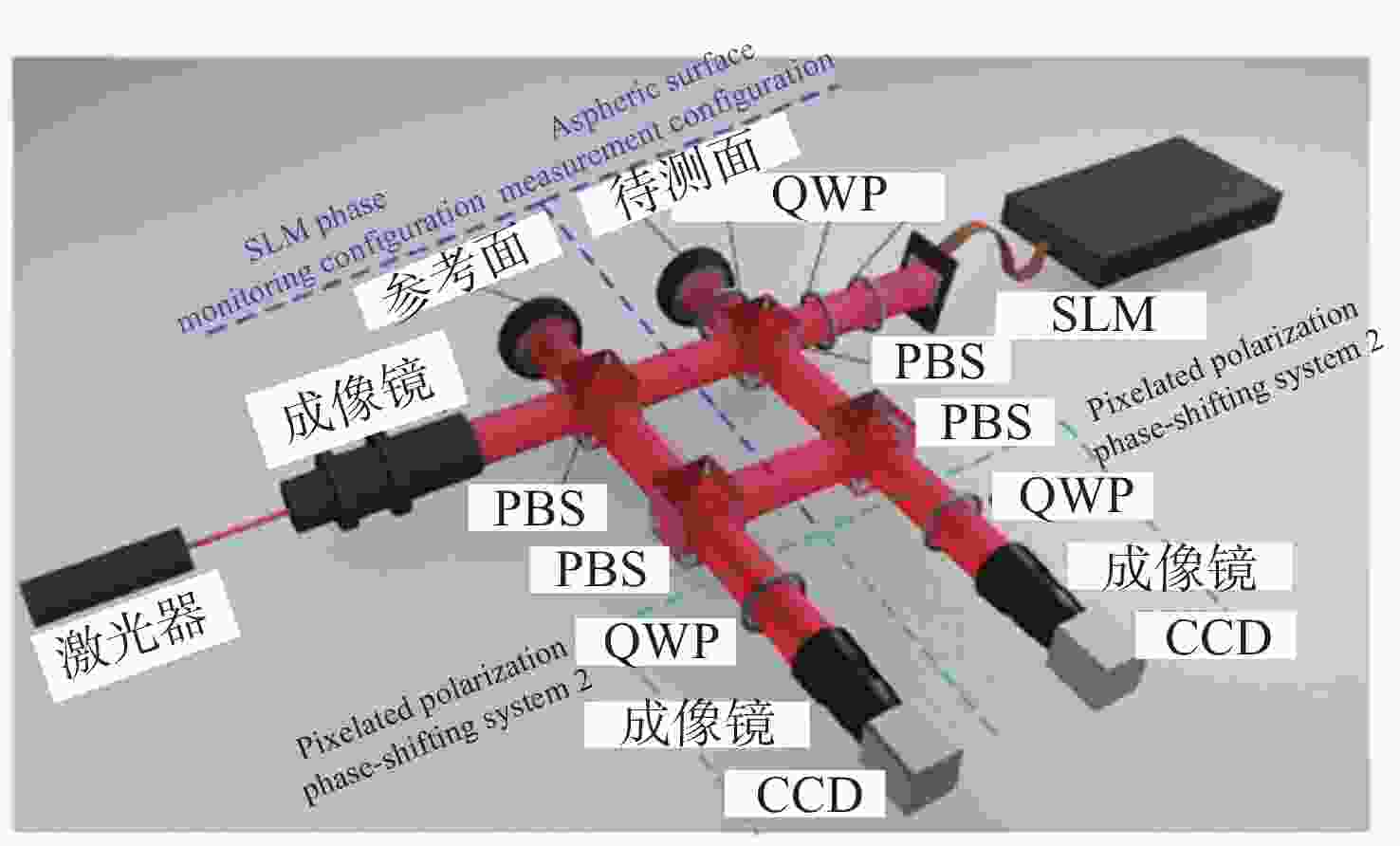
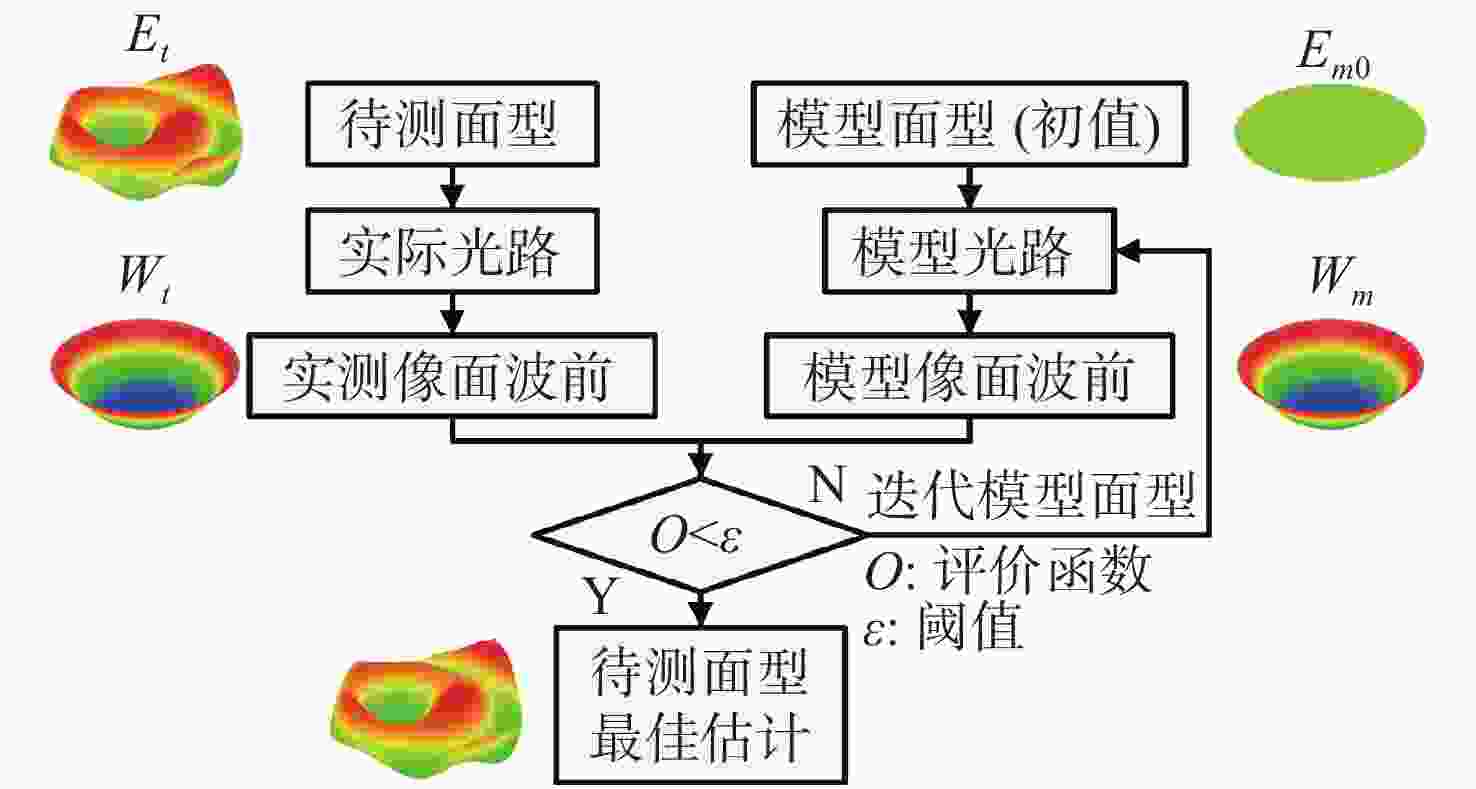
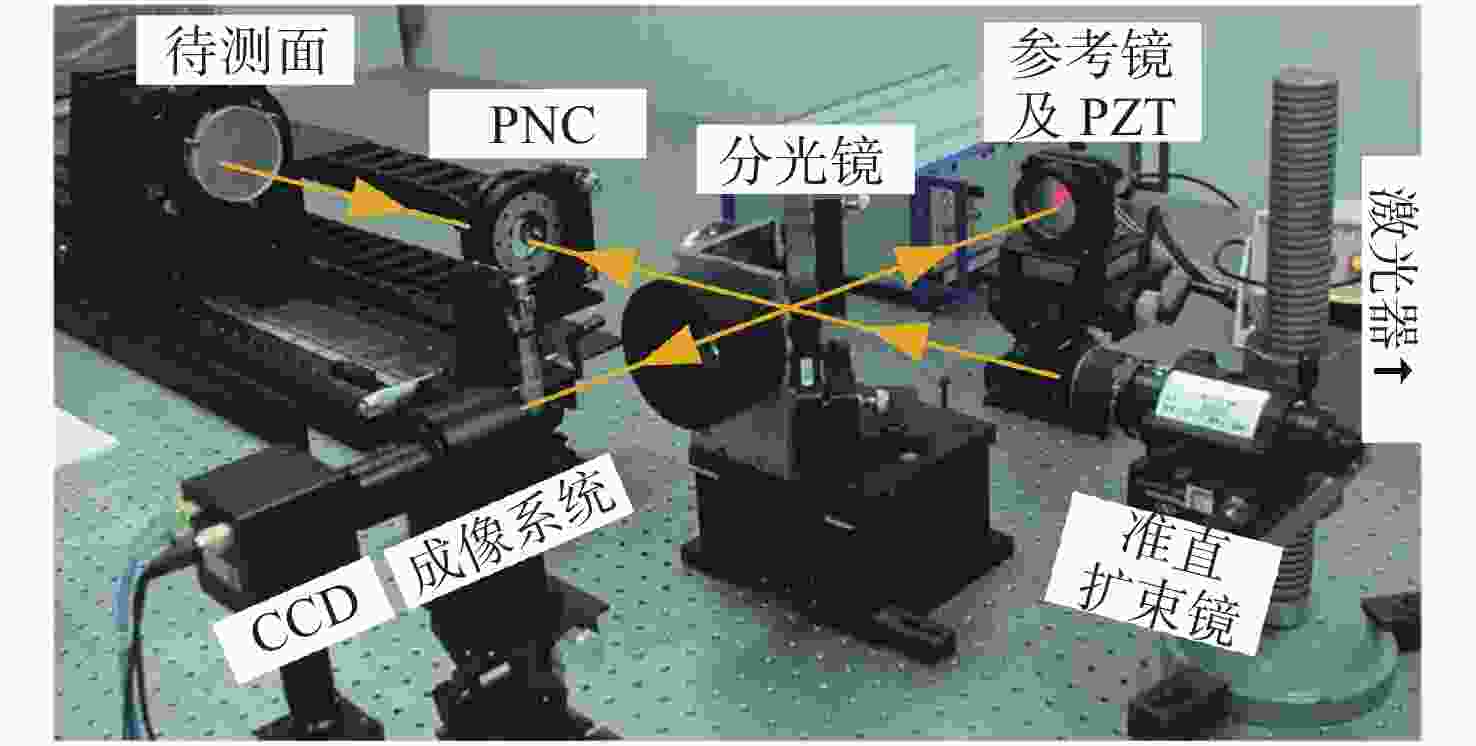
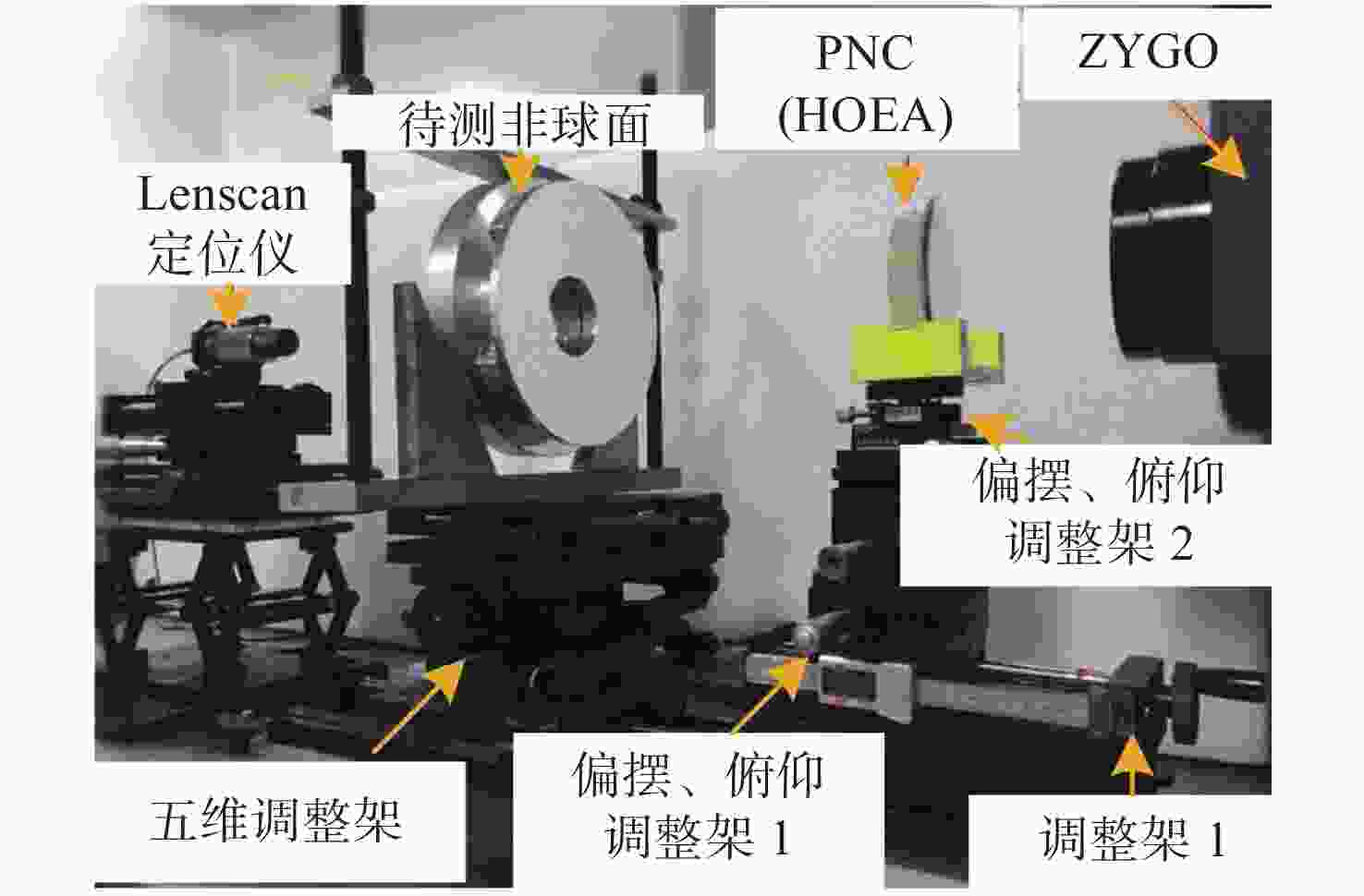
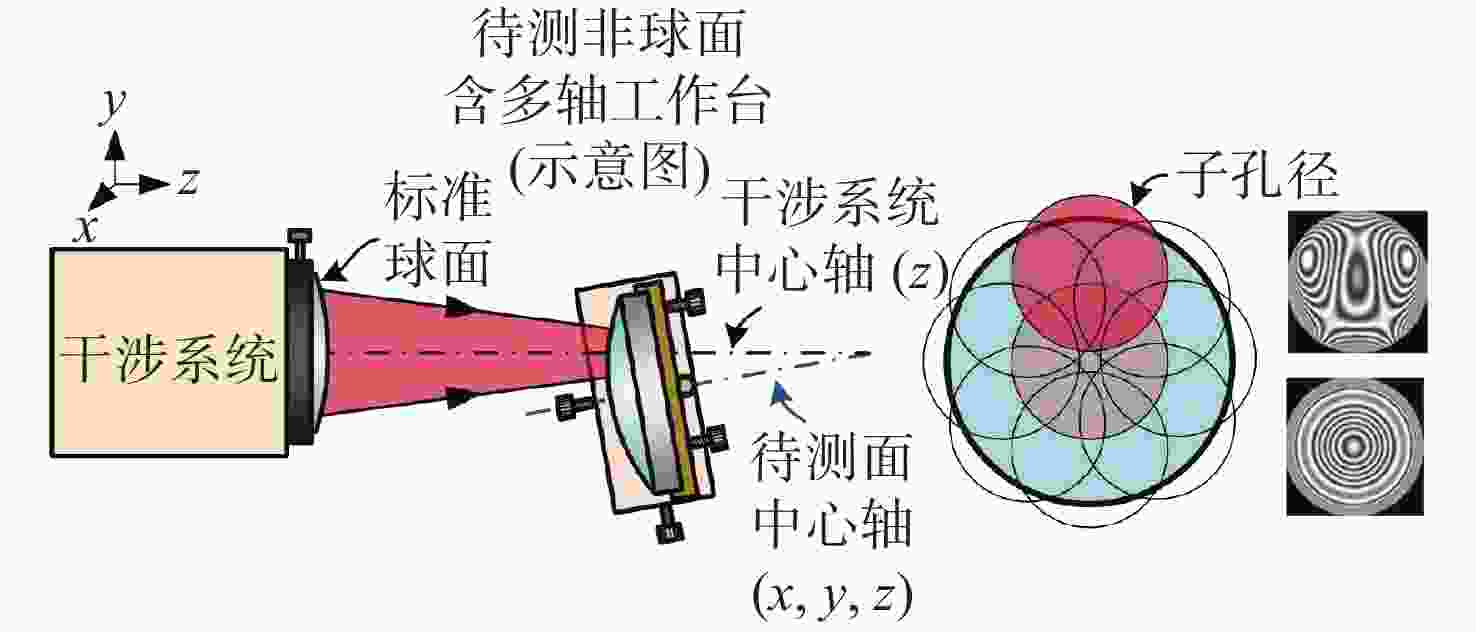
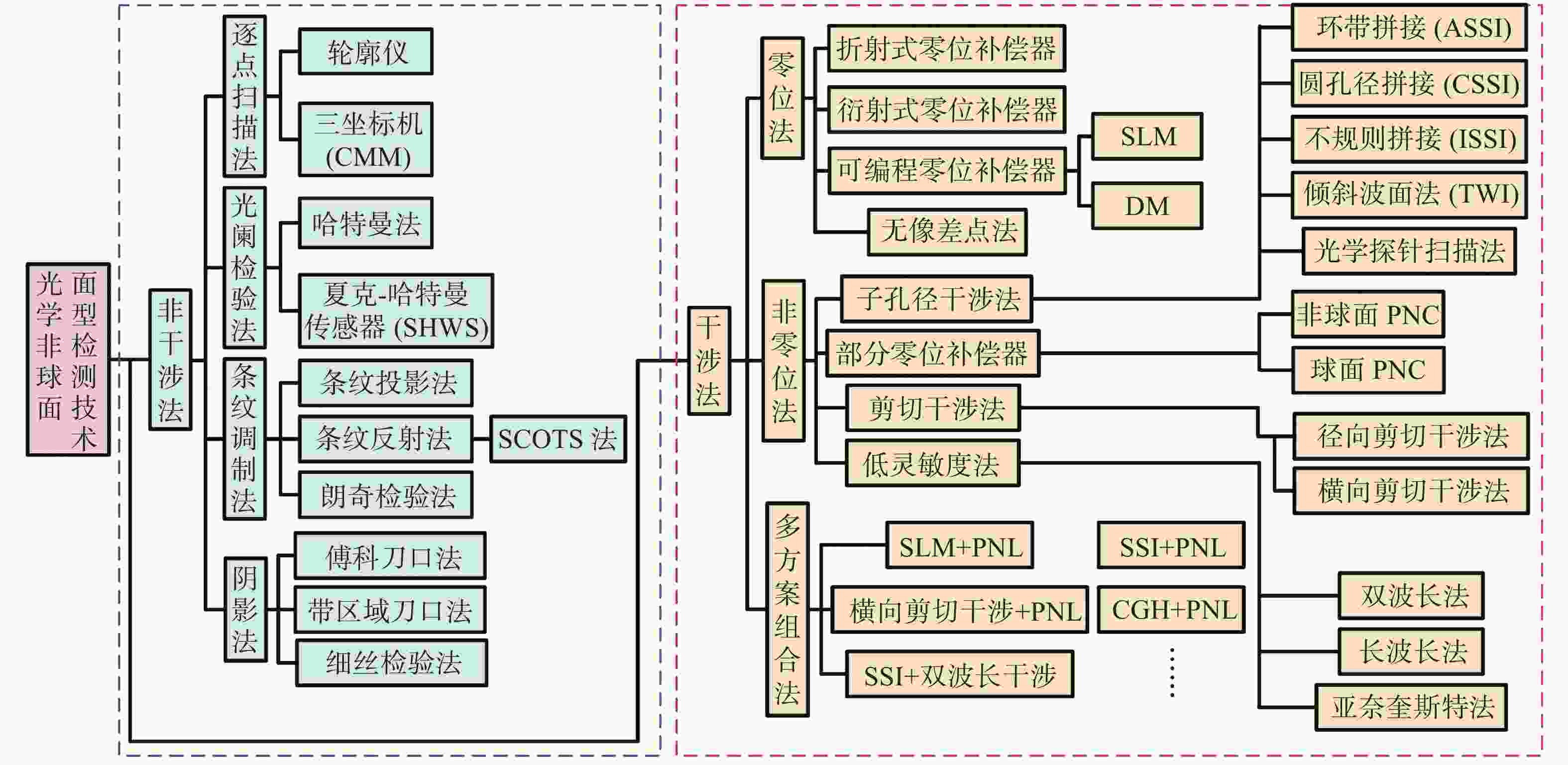
-
摘要: 非球面光学元件，特别是其中的自由曲面元件，在设计自由度上相比于球面具有很大的优势，基于非球面构建的光学系统能够以简单的光机结构实现复杂的设计目的。面型检测技术是保障光学非球面加工精度的关键，针对不同种类的非球面以及非球面加工的不同阶段对检测指标要求的多样性，现已发展出了种类繁多的检测方法。本文回顾了非球面光学元件面型检测技术的发展历程，分非干涉法与干涉法两大类整理了常用的检测技术，介绍了各自的技术指标与适用条件、研究进展与应用情况。本文重点讨论了基于干涉方法的非球面精密检测技术，举例说明了非零位与零位两条技术路线下各检测方法的基本原理、光路结构与检测能力，对比分析了各方法的优缺点与适用范围，介绍了一些配套算法以及检测光路的精密调节方法。Abstract: Optical Systems using aspheric components (especially for free-form ones) have remarkable advantages over traditional spherical systems in that they can satisfy complicated requirements with simple optical-mechanical structures relying on abundant optional design parameters. Surface testing is an essential process for ensuring accuracy in manufacturing. Therefore, plenty of testing methods have been developed to meet varying testing demands of different types of surfaces at different stages in manufacturing. This paper summarizes the history of aspheric surface testing technology, classifies available techniques by whether they use interferometry, then introduces corresponding technical indexes, applicable conditions, research progress and applications. This paper highlights the high-precision interferometric methods, basic principles, optical layout and testing performances of every measurement method classified into Null and Non-null testing. The pros and cons of each method are compared, relative algorithms are introduced and precise adjustment methods are discussed.
-
Key words:
- aspheric surface testing /
- free-form surface testing /
- interferometry /
- null testing /
- non-null testing
-
1. 引 言
非球面光学元件，顾名思义即包含无法用球面方程描述的表面的光学元件[1-2]。这类元件凭借其更多的设计自由度，不仅能够更有效地校正各种像差，还可以同时满足一些理论上相互制约的设计需求。例如在成像系统的设计中，通过引入非球面元件，可以显著增大系统的拉格朗日-赫姆霍兹不变量(Lagrange-Helmholtz Invariant)[3]，从而使得设计结果能够同时满足大视场和高分辨的要求。从另一个角度讲，针对同样的性能指标，采用非球面元件的设计往往需要的元件数量更少，因此更容易实现系统的小型化，这对于在载荷尺寸、重量方面有严苛限制的空间光学系统具有重要的意义，例如对地遥感系统常用的离轴三反消像散(Three-Mirror Anastigmat, TMA)[4]结构，其所包含的“一主二次”3片反射镜目前一般均采用非球面。
光学非球面的研究起步很早，最早的记载可以追溯到17世纪[2]，然而受限于工艺水平，其真正走向实际应用则要等到20世纪后半叶[5]。在民用领域，第一款采用非球面镜片的商业级摄影镜头是德国Leica公司在1966年推出的MOKTILX50mmF112；而在军用领域，采用非球面镜片的美军AN/PVS系列头盔夜视镜也是60年代之后才开始列装。在兴起伊始，非球面元件的成本仍然较高，其应用也局限于军用以及少数高端民品，直到20世纪90年代起光学玻璃的模压加工以及光学塑料的注塑成型工艺被广泛引入到非球面的生产中，光学非球面的价格才逐渐走向“白菜化”。与之同时，基于计算机数控技术(Computer Numerical Control,CNC)的单点金刚石车削(Single Point Diamond Turning, SPDT)[6]、磁流变抛光(Magnetorheological Finishing, MRF)[7]以及离子束抛光(Ion Beam Figuring, IBF)[8]等现代精密加工技术的提出，使得加工面型精度达到nm级的非球面成为了可能[5]。例如美国Thorlabs公司目前在售的“衍射极限非球面透镜”采用了美国QED公司的MRF技术，其面型均方根(Root Mean Square, RMS)值优于55 nm；国防科技大学的廖文林等人利用IBF技术加工的有效口径为380 mm抛物面[9]，面型RMS值达到了4.03 nm。
面型检测技术是保障非球面加工质量的手段，也是保障非球面光学系统能否正常工作的关键。诸如欧洲南方天文台(ESO)的新技术望远镜(New Technology Telescope, NTT)与美国航空航天局(NASA)的哈勃(Hubble)空间望远镜等资金充裕、专家云集的大科学装置，都曾因非球面镜片加工过程中面型检测的小失误，最终系统成像质量与设计目标相去甚远，只能通过后续“打补丁”来实现装置的正常工作，造成了巨大的损失[10]。随着业界对于非球面加工精度要求的不断提高以及极大口径非球面或是不规则形状自由曲面加工需求的出现，缺乏与之匹配的面型检测技术愈发成为制约该领域进一步发展的主要瓶颈。
本文回顾了非球面光学元件面型检测技术的发展历程，分类梳理了已有的各类检测方法，分析对比了各自的技术特点与适用范围、研究进展与应用情况，并展望了各技术方案的发展趋势。
2. 非球面光学元件面型检测技术分类
经过多年发展，非球面光学元件面型检测技术具备了明显的体系化特点。针对不同种类(材料、对称性、尺寸、曲率以及相对于最佳拟合球的偏离量等)的待测面型以及加工过程中不同阶段对检测精度、灵敏度、动态范围等指标的不同要求，对应有不同的检测方法[11-14]。
由于光学干涉法在检测原理、流程与检测精度等方面与其他方法有明显的区别，本文以是否基于干涉原理将所有检测方法分为非干涉法与干涉法两类，各自包含的技术路线与具体技术方案如图1所示。
非干涉法主要包括：逐点扫描法、光阑检验法、条纹调制法与阴影法这4条技术路线。逐点扫描法利用轮廓仪[15]或者三坐标机[16-17](Coordinate Measuring Machine, CMM)直接测量待测面上离散点的矢高并通过拟合得到面型数据，大多数轮廓仪或CMM采用的机械探针与待测面直接接触，因此属于有损检测；另外的部分装置采用了基于干涉原理的光学探针，可以进行非接触式测量，但应归入干涉法的范畴。光阑检验法又称哈特曼(Hartman)检验法[18-20]，包括早期的Hartman光阑检验法与20世纪70年代提出的Shack-Hartman法，该方法通过探测器上光斑的横向偏移量计算出波前斜率，进而利用波前重构算法得到反映待测面型的重构波面。条纹调制法利用投影到待测面上的条纹光作为载频，通过分析待测面引入的条纹畸变求出待测面型，其又可以分为结构光法[21-23](漫反射、镜面反射)和Ronchi检验法[24-25]。阴影法是一种经典的面型检测方法，包括傅科(Foucault)刀口法[26]与由其改进而来的区域刀口法和细丝法等。
图 1 光学非球面面型检测技术分类Figure 1. Classification of optical aspheric surface testing technology非干涉法各具体方案之间差异较大，但亦不乏一些共同特点。相比于后续介绍的干涉法，非干涉法普遍具备较好的通用性，但检测精度相对较低，一般在μm量级(部分方法可以达到亚μm级精度)，因此多用于低精度的模压、注塑非球面或去除法加工高精度非球面过程中的研磨与粗抛光阶段。非干涉法各具体方案的原理特点、发展现状与业界应用情况见本文第3节。
干涉法是一类具备nm级检测精度的精密测试方法。采用干涉法检测非球面的关键问题在于如何解决由于非球面法线像差(由非球面与参考球面的偏离而产生)导致的干涉条纹增密问题，由此引申出两条主要的技术路线：零位检测与非零位检测。
其中零位检测利用补偿器将入射到待测面上的测试光波由球面波转化为对应待测面标称面型对应的非球面波，因而当不存在面型偏差时干涉场对应零条纹。常见的零位补偿器包括传统的折(反)射式补偿器[27-28]，基于计算全息(Computer Generated Hologram, CGH)的衍射式补偿器[29-31]以及基于可变形反射镜(Deformable Mirror, DM)[32-39]或空间光调制器(Spatial Light Modifier, SLM)[40-44]的可编程(自适应)补偿器[41]，此外针对圆锥曲面还可以采用无像差点法进行零位检测。
非零位检测则仅采用一些手段将干涉场中的条纹增密降低到不影响干涉图解调的程度，并通过算法消除由不完全补偿法线像差引入的系统误差。实现非零位检测的方法多样，常用方法可归纳为以下4条技术路线，分别是：部分零位补偿器法、子孔径干涉法、剪切干涉法与低灵敏度法。其中，部分零位补偿器(Partial Null Compensator, PNC)[45]法与零位检测中的补偿器法类似，只是这里的补偿器不完全补偿非球面的法线像差，故而即使待测非球面完全理想，干涉场中依然存在条纹。子孔径干涉法除环带拼接(ASSI)[46-48]、圆孔径拼接(CSSI)[49-51]以及不规则孔径拼接(ISSI)[52]等子孔径拼接干涉法以外，还包括一种运用微透镜阵列进行波面分割的倾斜波前法(Tilted Wave Interferometry, TWI)[53-54]以及采用光学探针的逐点扫描法。其中TWI法在检测过程中无需移动待测面，因此也无需利用相邻区域的重叠部分进行拼接；而采用光学探针的CMM或轮廓仪的每一个测量点可以视为一个很小的子孔径。子孔径干涉法的共同特点是将待测面分为多个子区域，使得子区域的干涉条纹密度降低到能够解调的程度。剪切干涉法[55-58]采用自干涉的剪切干涉装置取代传统的泰曼-格林(Twyman-Green)或菲索(Fizeau)干涉装置，可以通过降低剪切率(自干涉的两个波面的偏离程度)来降低条纹密度，常用的剪切干涉法有横向剪切干涉与径向剪切干涉两种。低灵敏度法主要包括长波长法[59]、双(多)波长法[60]以及亚奈奎斯特(Sub-Nyquist)法(又称欠采样法)[61]等，这类方法都是通过降低系统的灵敏度来换取动态范围的提高，从而使干涉图得以解调。
干涉法的检测精度一般高于非干涉法，且均属于非接触检测，避免了检测过程中对待测面的损伤，因此可以用于去除法加工非球面的精抛光阶段的检测，但干涉法对待测面的材料与粗糙度等方面存在限制，对测试环境的要求更高，实施起来较为困难。在干涉法中，零位检测的精度相对更高，但非球面度大或是形状特别复杂的非球面的零位检测较难实现；非零位检测的精度需要通过严格的回程误差(Retrace Error)[62]校正来保证，因此算法复杂度更高，但其优势在于具备一定的通用性。有些情况下，多种技术组合使用可以兼取各自的优势。此外，干涉法的高精度需要建立在对检测系统的精密调节上。以上内容的详细介绍见本文第4节。
3. 非干涉检测技术
3.1 逐点扫描法
逐点扫描法是一种各领域通用的三维形貌检测方法，基于此类方法的检测装置主要包括CMM[16]与轮廓仪(Profiler)[15]，两者的基本原理类似，但一般来说CMM能够检测更大尺寸的待测面。逐点扫描法的工作模式是采用一根“探针”，按照一定的扫描路径逐点测量非球面的矢高，最后将矢高数据拟合得到面型分布。该方法通用性好，能够检测一些大口径、大曲率与大非球面度(非球面相对参考球面偏离的程度)的待测面，但由于需要扫描，检测速度慢，利用散点数据拟合面型时存在较大误差(主要包括扫描过程引入的位移误差与采样点稀疏造成的拟合误差)。
传统的探针为机械探针，与待测面有接触，因此其属于有损检测，只能用于检测精抛光之前的毛胚非球面。该类方法的检测精度大多在μm量级，少部分高端设备在量程范围内可以实现亚μm级精度。例如图2(a)所示，英国泰勒-霍普森(Taylor Hobson)公司生产的Talysurf系列轮廓仪，检测口径为60~120 mm，检测重复性约0.12 μm (RMS，满足2σ原则)；如图2(b)所示，德国蔡司(ZEISS)公司的XENOS系列CMM，检测口径约1 m，检测精度约0.3 μm (RMS)。
目前来看，传统的接触式逐点扫描法在非球面去除法加工初期仍具备较好的实用性，但其未来发展空间已不大。近年来冠以“Profiler”或“CMM”之名的新设备往往采用的是非接触式的“光学探针”，而不少“探针”实际上是小型干涉装置，因此逐点扫描法未来有望与子孔径拼接干涉法结合使用，以同时实现高精度与高通用性。
3.2 光阑检验法
光阑检验法[65]主要包括Hartman方法及其改进而来的Shack-Hartman方法[18-20]。如图3(a)所示，早期的Hartman法通常将一个由许多小光阑组成的阵列(称为Hartman光阑)放在靠近待测面的位置，位于待测非球面最佳拟合球(即最接近非球面的球面)曲率中心附近的点光源发出的光线经其采样后由待测面反射回到光源附近的像面。当待测面存在面型偏差时，其反射到像面上的光斑将偏离理想位置(如图3(b)所示)，此时记录其上各个光斑与理想位置的偏移量，可计算得到该条光线的斜率，最后通过波前重构算法恢复得到反映面型偏差的波面信息。作为一种斜率检测方法，Hartman法的波前重构算法与结构光法类似，包括梯形积分法、索斯韦尔算法[65]等。
图 3 Hartman法及Shack-Hartman法示意图Figure 3. Schematic diagrams of the Hartman & Shack-Hartman tests1971年，Shack R V等人改进了传统的Hartman方法[18]，采用微透镜阵列替代了原来的光阑阵列，改善了CCD像面上光斑的会聚度，从而能够更准确地定位各采样点的中心坐标，提高了检测精度。基于此的夏克-哈特曼波前传感器(Shack-Hartman Wavefront Sensor, SHWS)可以很方便地用于检测各类非球面，其检测光路模型如图3(c)所示。
Shack-Hartman法属于一种简单可行的非接触式检测方法，由于可以一次性测得整个面的面型，其检测精度一般略高于传统的接触式逐点扫描方案。20世纪90年代，美国Sandia国家实验室的Neal D R等人首先将SHWS用于研磨至抛光阶段的非球面检测[66]；2002年，中国科学院成都光电技术研究所（简称成都光电所）姜文汉团队利用SHWS检测了一块口径为630 mm的非球面，检测精度(参照零位干涉法的检测结果，下同) PV值约为90 nm，RMS值约为13 nm[67]；2013年，新加坡南洋理工大学Guo W团队利用SHWS检测了由空间光调制器(Space Light Modulator, SLM)模拟的复杂自由曲面(尺寸8~14 mm)，采用其提出的自适应光斑中心定位算法后，RMS精度最高达到27 nm[68]。
Hartman方法的主要问题是受光阑或微透镜的口径限制，无法检测大非球面度待测面引入的大畸变波前(检测动态范围小)，同时微透镜的尺寸也限制了采样密度，横向分辨率较低，这些因素限制了其应用范围。
3.3 条纹调制法
条纹调制法主要包括基于结构光的方法与朗奇(Ronchi)检验法。
结构光方法的原理是将某种结构光(大多是余弦条纹光)投影到待测非球面上，而受待测面调制的条纹光就携带了待测面的面型信息，对其进行解调即可求得待测面的面型。根据投影方法与待测面反射特性的不同，结构光方法可以分为条纹投影法(Fringe Projection Method, FPM)与条纹反射法(Fringe Reflection Method, FRM)两种[14]。其中FPM法一般采用投影仪产生条纹光，经粗糙待测面调制后通过漫反射被相机接收(如图4(a))；而FRM法则大多采用LCD屏幕产生条纹光，经光滑待测面调制后通过镜面反射被相机接收[21](如图4(b))，后者有时又称相位偏折法(Phase Measuring Deflectometry, PMD)[69]。
两种结构光方法中与非球面检测相关的研究与应用主要集中在PMD上[22]。2008年，四川大学苏显瑜等人采用PMD方法检测了一块口径400 mm、顶点曲率半径为500 mm的抛物面，与接触式CMM的检测结果偏差PV值约为3.5 μm[70]；2010年，Arizona大学的Su P团队提出了一种称为“软件可调试光学检测系统”(Software Configurable Optical Test System, SCOTS)的高精度PMD检测系统(光路实拍见图5(a))[71-72]，该团队利用SCOTS检测了GMT望远镜其中一片口径为8.4 m的离轴非球面子镜，在完成误差校正后与干涉法检测结果偏差RMS值仅约为25 nm。在工业界应用方面，德国3D-shape公司推出了一种用于检测眼镜片的PMD设备(如图5(b))，该设备对3 mm口径渐近式非球面镜片的检测精度(RMS)达到了20 nm[21]。
与Hartman方法相比，PMD方法不受光阑或微透镜的口径限制，因此动态范围相对较高，但PMD方法也存在制约其发展的问题。例如，PMD方法需要精确标定LCD屏、待测面与相机之间的坐标关系[23]，同时条纹光对待测面的调制不仅与面型起伏(即矢高或曲率的梯度)有关，还与其矢高的绝对量有关系，因此存在一个“高度-梯度”的二义性问题，上述这些因素使得PMD方法实现高精度比较困难。虽然Arizona大学的SCOTS方法可以实现几十nm的RMS精度，但其需要经过复杂的定标过程，复现难度高，国内中国科学院长春光学精密机械与物理研究所（简称长春光机所）某团队尝试搭建SCOTS系统检测一块口径821.65 mm的离轴抛物面，但检测结果的PV精度仅能达到143.65 nm[73]，考虑到其所测非球面的口径仅有前例中GMT子镜的约1/10，检测精度明显下降。
基于Ronchi光栅的Ronchi检验法是另一种条纹调制法。如图6所示，Ronchi检验法将一块线光栅(Ronchi光栅)放置在靠近待测非球面最佳拟合球曲率中心附近的位置，位于曲率中心的点光源发出的光锥经Ronchi光栅加载条纹后入射到待测面上，经其反射后的畸变条纹叠加到Ronchi光栅上形成莫尔(Moire)条纹，通过对该Moire条纹进行解调分析即可得到待测面型信息。
Ronchi检验法是一种传统方法，近年来新的研究与应用较少，主要原因是该方法相比于后续兴起的Hartman法和结构光法不存在明显的优势点。首先，根据墨西哥学者Malacara D的研究[65]，Ronchi检验法可以视为一维的Hartman检验法[74]，但由于待测面型偏差往往不对称，因此需要进行两个方向上的Ronchi检验，这增加了检测系统的复杂度；其次，Ronchi检验法的物理原理决定了光栅与待测面之间的距离需为泰伯距离(Talbot Distance)，方能获得较好的条纹锐度，这限制了检测系统的布局；最后，Ronchi检验法作为一种双通系统，受Ronchi光栅的尺寸等因素限制，系统的动态范围不如结构光法。
基于此，非球面Ronchi检验法的发展方向主要集中在实现便捷的二维定量检测与扩展动态范围这两个方面。在2007~2012年间，四川大学和成都光电所的一些团队对此进行了研究[24-25]，提出采用透明LCD屏幕替代实体的Ronchi光栅，从而可以方便地改变线光栅方向以实现二维检测，改变线光栅频率以扩展动态范围。
3.4 阴影法
包括Foucault刀口法及其改进方法在内的阴影法是另一种传统的非球面面型检测方法[65]。刀口法实际上是一种曲率检测法，其原理是利用刀口遮拦(切割)一部分入射光束，当待测面各点曲率相等(理想球面)时反射光斑中的阴影区域与遮拦区域一致，反之则不一致，通过分析阴影区域的形状分布，可以计算出待测面各点曲率分布。
经典的刀口法检测装置如图7所示。为了提高对非球面检测的灵敏度，有些系统在经典Foucault装置外引入了一个部分环带区域通光的光阑或是不透明细丝，称为“带区刀口法”与“细丝法”。
阴影法的优点是灵敏度较好，适合于检测大口径、小曲率的待测面，但其缺点是实现数字化定量检测比较困难。2011年，南京理工大学朱日宏团队提出一种数字化刀口仪[26]，建立起了像素级的阴影分布与曲率分布的映射关系，其检测灵敏度可与干涉法媲美，但由于对刀口精确定位难度大，其检测重复性较差。
由于高灵敏度的干涉法现已非常成熟，阴影法的应用空间已受到很大挤压，目前国内仅有少数单位还在采用阴影法，多数采用的是轮廓仪结合干涉法的检测体系。
4. 干涉检测技术
4.1 零位检测
在采用干涉方法检测非球面时，利用补偿器将测试光波从标准球面波转变为与非球面法线像差对应的非球面波，使得当非球面不存在面型偏差时，测试光沿非球面各点法线方向入射，此时干涉场中应不存在条纹，这种检测方法就是零位检测法。零位检测的实现思路目前主要有折射式和衍射式以及可编程式3种，其中折射式采用透镜(组)作为补偿器，衍射式采用CGH作为补偿器而可编程式采用SLM或DM等自适应器件充当补偿器。
此外，当待测面为二次圆锥曲面(椭球面、双曲面与抛物面)，可以利用无像差点法实现零位检测，图8(a)、图8(b)分别给出了利用无像差点法检测凹、凸抛物面的光路模型(中心遮拦)，其中图8(b)检测凸面时采用的辅助球面又称Hindle球。无遮拦的方案可以参考Malacara D所著《光学车间检验》第3版12.4~12.5章节[65]，这里不再展开。
图 8 无像差点法检测抛物面光路模型Figure 8. Schematic diagrams of testing paraboloids using aberration-free point method4.1.1 折射式零位法
由透镜或透镜组充当补偿器以实现对非球面的零位检测是干涉法中最传统的技术方案。经典的零位补偿器有多尔(Dall)补偿器[65]和奥夫纳(Offner)补偿器[27-28]等，其光路模型如图9所示(为作图方便放大了补偿镜的尺寸)。
Dall补偿器是最简单的折射式补偿器，仅含一片平凸镜，由Dall H E于1947年提出用于凹抛物面的检测[69]。其设计原理是根据三级像差理论利用单透镜的像差(主要是球差)去平衡非球面法线像差，检测光路模型如图9(a)所示。Dall补偿器的主要问题是单透镜的设计自由度很少导致其只能平衡一些非球面度较小的低阶非球面，同时其残余波像差的PV值一般仍有300 nm左右，按照当今的标准已属于非零位补偿的范畴(一般认为补偿残差PV大于1/20λ，本文所有λ=632.8 nm)，在不进行误差校正的情况下检测精度较低。
图 9 折射式补偿器零位检测光路模型Figure 9. Schematic diagrams of null test by the refractive compensatorOffner补偿器是最经典的折射式补偿器，包含了一片补偿镜和一片场镜，由Offner A于1963年提出[28]。Offner补偿器的设计原理同样是利用补偿镜的球差来平衡非球面法线像差(三阶)，其不同之处在于使用了一片置于待测面最佳拟合球曲率中心附近的场镜，主要用于平衡非球面的五阶球差。在Offner本人提出的光路(如图9(b)所示)中，场镜的位置由两对物像共轭关系确定，即：补偿镜与场镜把干涉仪焦点(O1)成像到最佳拟合球曲率中心(O3)处，场景把补偿镜(O2)成像到待测面(O4)上。然而，这种布局方式并非最理想的选择，尤其对于大非球面的待测面而言，场镜的位置需要重新讨论以尽可能多地消除高阶像差。
除去上述两种补偿器外，经典的折(反)射式零位补偿器还有谢弗(Shafer)补偿器以及反射式Offner补偿器等，由于其设计理论的相似性这里不再逐一介绍。
此类补偿器的特点是利用补偿镜(组)的球差去平衡非球面法线像差，一般只能用于非球面度不太大的旋转对称非球面的检测之中。针对大非球面度的待测面，由于法线像差的曲线不再与补偿镜的球差曲线实现很好的匹配，因此会有较大的补偿残差，这便是后续介绍的“部分零位补偿器”的设计逻辑；而针对非旋转对称的自由曲面，则需要采用后续介绍的“衍射式零位补偿器”。
4.1.2 衍射式零位法
衍射式零位补偿法采用衍射光学元件(Diffraction Optical Element, DOE)作为补偿器，其中最常用的DOE补偿器是计算全息(Computer Generated Hologram, CGH)板。CGH由美国IBM公司的Lohmann A W等人于1967年提出[75]，它通过计算的方式模拟了传统光学全息中的“干涉记录”过程，从而可以随心所欲地得到各种全息图样。CGH从原理与外观上都可以看作是一种变周期的特殊光栅，由于充当补偿器作用的仅是其中一个衍射级次，为了避免混叠CGH会引入一定量的载频以分离各级次，包括存在中心遮拦的离焦载频和无中心遮拦的倾斜载频，图10为两者的示意图。
CGH充当零位补偿器这一方法建立在标量衍射条件下各衍射级次的几何光线模型之上。
如图11所示，某曲率中心位于O点的标准球面波经过CGH零位补偿后，变换为与待测非球面面型对应的非球面光波。根据几何光学中经典的费马原理(Fermat principle)，若要满足上述变换条件，则图中路径OA-AB-BC与路径OP-PQ-QR应满足等光程条件。设CGH折射率为n，厚度为d，用于补偿的衍射级次为m，测试光波数为k并以轴上B点为0相位点，则Q点的相位值φ(Q)可以表示为：
φ(Q)=mk(OA+nAB+BC−OP−nPQ−QR). (1) 由于CGH后方的光线均沿非球面上对应点法线入射，避免了传统的非球面光线追迹中的迭代问题。因此，即使对于那些处于离轴状态的非球面或复杂自由曲面，通过反向建模的方式也很容易求出非球面与CGH上对应点的空间距离，从而根据式(1)算出CGH的相位分布
φ 。然而，由连续的相位分布获得如图10所示的台阶形式的CGH还需要经过量化与编码的过程，这个过程就是产生干扰级次的主要原因，在载频的作用下通过设置在曲率中心O点的小孔光阑滤除干扰级次，以免其进入干涉系统之中。CGH充当零位补偿器引入非球面干涉检测中的先行者是美国Arizona大学的Wyant J C，他于1971年提出可以在马赫-曾德(Mach-Zehnder)干涉装置中引入CGH来检测非球面反射镜[76](如图12所示)，此后，他又在杂散级次分析[77]、制版误差分析[78]以及在不同干涉光路中引入CGH方面做了大量的研究[79]。受到当时CGH制作工艺限制与理论体系尚不完善的影响，早期的研究者并没有系统地讨论精度问题，通常只与采用零位补偿镜的检测结果进行比较：例如Wyant曾采用CGH检测一块口径为0.69 m的离轴非球面，检测结果与采用零位补偿镜的检测结果相比，PV值偏差约为90 nm[79]。80年代中后期，E-Beam电子束曝光技术[80]逐步取代早期的光学照相法成为CGH生产的主流工艺，CGH的刻蚀精度和线宽限制有了质的改善，目前CGH制版过程引入的系统误差(RMS)已经可以控制在1 nm以内。
90年代以后，同样是Arizona大学的Burge J H成为了该领域的引领者，其于1994年提出利用氧化铬的热化学方法在曲面基底上加工CGH[81]，这种曲面CGH被其称为CGH测试板(CGH test plate)，适用于大非球面度凸非球面的检测，如图13所示。Burge教授及其弟子Zhao C Y、Zhou P等人在CGH的设计方法与误差分析[30, 82-84]等方面做了大量的工作，此外，他还利用CGH并结合其他检测手段，承担了NST[85]、LSST[86]和GMT[29]等大型天文望远镜的检测任务，其中3.4 m口径的LSST次镜的理论误差(检测精度)可以达到13 nm (RMS)。
此外，德国Stuttgart大学Reichelt S团队[87]以及德国Erlangen-Nurnberg大学Beyerlein等人[88]提出复用单块CGH编码两组图样，并称这种CGH为Twin-CGH。Twin-CGH的特点是：除测试光波外还会产生一束会聚到待测非球面顶点位置的衍射光作为参考光，其原理与菲涅耳波带板(Fresnel Zone Plate)干涉仪类似，故而Burge J H又将其称为CGH波带板(CGH zone plate)。从上述描述和图14可以看出，CGH波带板法是一种共光路干涉方法，无需参考波面的特点使其一定程度上解决了CGH衍射效率低、难以与参考光的光强进行匹配的问题；同时由于共模抑制的作用，气流与震动等环境因素的干扰可以得到很大程度的削弱。针对Twin-CGH与CGH波带板法，南京理工大学朱日宏团队[89]、成都光电所邢廷文团队[90]以及俄罗斯国家科学院Poleshchuk A G等人[91]也进行了研究，主要的研究方向是利用CGH波带板法实现非球面的绝对检验。除此之外，长春光机所多个团队专注于CGH的制版工艺以及大口径、离轴非球面以及自由曲面的检测[92-93]，为我国的空间探测领域做出了重要的贡献。
CGH零位补偿法的优点是补偿能力强，理论上针对任何待测面均可实现零位补偿，通常作为检验其他方法检测精度的标准。但CGH也存在以下几点局限性：第一，通用性不好，CGH与待测非球面之间是一一对应的关系；第二，掩模材料与E-beam光刻加工成本较高；第三，针对大非球面度待测面设计的CGH刻线往往很密，加工难度大；第四，对于低反面的检测(例如常见的非镀膜玻璃或石英表面)，振幅型CGH的衍射效率可能不足，探测器接收的测试光强度弱，而相位型CGH需要经过二次加工(离子刻蚀)，会引入额外的系统误差(主要是刻蚀深度的影响)。
该方法未来的研究方向主要包括以下两个方面：其一是对适用于复杂离轴面或是自由曲面的非对称CGH设计原理与加工方法的研究；其二是对进一步提高检测精度的研究，包括对系统中衍射鬼像、投影畸变等主要误差源进行标定或消除以及对非球面绝对检验方面的研究。
4.1.3 可编程零位法
可编程(自适应)补偿法是21世纪以来研究领域热门的非球面干涉检测技术方案[41]，其采用的DM[32-39]与SLM[40-44, 94]等自适应补偿器兼具自由度极高和通用性强的优点。DM与SLM的区别在于DM是由微机电系统(Micro-Electro-Mechanical System, MEMS)驱动的微透镜或微反射镜阵列，通过镜片的形态变化直接产生对应于待测镜的非球面波前，按原理可以归入折射式补偿器；而SLM，以最常用的液晶空间光调制器(LC-SLM)为例，则是利用电控信号下液晶分子的偏转，从而改变其折射率以实现相位调制，因其原理与相位型CGH有类似之处，有时会将其归入衍射式补偿器。
最早将DM用于非球面检测的是德国Stuttgart大学的Pruss C团队。该团队在2004年采用了一块直径为25 mm、分辨率为170 μm，由电极驱动的薄膜反射镜(Membrane Mirror)阵列，结合两个4f系统(起到了类似于Offner补偿镜中场镜的作用，将薄膜透镜成像于待测面)，检测了一块凸非球面，检测精度(RMS)优于1/20λ[95]。
DM补偿器常用来与其他方案组合使用，以提高检测精度或拓展动态范围。2014年，美国Rochester大学Fuerschbach K团队结合了DM补偿器和传统Offner补偿镜，检测了用于远红外系统的一块自由曲面反射镜[96]，其光路布局如图15(a)所示；2016年，清华大学的Huang L与Arionza大学Kim D W团队结合了DM补偿器和结构光PDM技术检测了一块尺寸为120 mm×80 mm的自由曲面，为了验证检测精度，该团队针对另一块同样大小的反射面与ZYGO干涉仪的检测结果进行了交叉验证，两者结果偏差PV值为101.36 nm，RMS值为18.07 nm[38]，其光路布局如图15(b)；2020年，安徽大学张磊团队结合了级联的两块DM(分别为高频Tweeter DM与低频Wooter DM)与部分零位镜(图中PNO)，扩大了传统DM系统的动态范围，使其能够检测面型PV偏差达80 μm的自由曲面，该团队利用一块轮廓为椭圆(长短轴分别为24.6 mm和18.8 mm)的离轴抛物面对系统精度进行了交叉验证，与ZYGO干涉仪的检测结果偏差RMS值仅为4.68 nm[35]，其方案模型如图15(c)所示。
相比于DM补偿器，基于衍射原理的SLM补偿器的优势在于其分辨率更高[42]：例如Thorlabs公司在售的基于硅基液晶技术(LCoS)的Exulus空间光调制器的分辨率就达到了3.74 μm，而研究领域早在2003年就提出了分辨率为1.8 μm的SLM[97]，与通过E-beam技术加工的实体CGH已相差无几，与之相比，DM的分辨率普遍在几十到几百μm之间，但SLM也存在系统误差相对较大且难以分析的缺点(SLM的非线性效应导致)[32]。2021年，北京科技大学Hu Y团队基于HOLOEYE公司8 μm分辨率SLM搭建了非球面偏振移相干涉检测系统，其光路模型如图16[43]所示。对于同一块10 mm圆形口径非球面，该系统测得PV值为2.906λ，RMS值为0.652λ，而ZYGO干涉仪测得PV值为2.941λ，RMS值为0.710λ，考虑到该待测面尺寸与误差均与图15(c)中基于DM的检测系统所选待测面类似，因此在某种意义上可以对SLM检测精度相对DM较低提供佐证。
虽然具备高自由度与高通用性的优点，但自适应补偿器带来的成本问题与系统误差分析问题制约了这类方法从实验室走向实际应用。随着MEMS技术的进步与相关研究的不断深入，这类方法有着很好的发展前景。
4.2 非零位检测
非零位检测法，顾名思义即为不完全补偿非球面像差的干涉检测方法。相比于零位法，非零位法无需提供与待测非球面形状完全对应的测试光波而只需通过一些方式让干涉图能够解调，因此，实现起来相对容易，同时具备一定的通用性。根据干涉图解调的方式，非零位法的具体实现方案可以分为：部分零位补偿器法、子孔径干涉法、剪切干涉法以及低灵敏度法。
非零位法的关键在于消除“非零位”引入的系统误差。由于大部分干涉检测系统为双通光路，当非球面法线像差没有完全被补偿时，由非球面反射的光线便会在第二次通过系统光路时偏离设计路径，故而由此引入的系统误差又被称为“回程误差”(Retrace Error, RE)[62]。
回程误差的校正算法主要有“黑盒”与“白盒”两类[46]，前者不依赖于干涉系统结构参数，但校正精度一般；后者则建立在对干涉系统进行精确建模的基础上，但校正精度较高。常用的具体算法包括“黑盒”中的基于零位近似的两倍关系法[98-99]以及“白盒”中的逆向迭代优化法 (Iterative Reverse Optimization, IRO)[100-101]、理论参考波面法(Theoretical Reference Wavefront, TRW)[102]等。各算法的简单对比如表1所示。
表 1 常用回程误差校正算法对比Table 1. Comparison of common RE calibration algorithms方法 理论 条件 精度 速度 GDI 小畸变近似理论 黑盒 较低 较快 TRW 参考波面替代理论 白盒 一般 较快 IRO 系统函数的不变性 白盒 高 较慢 表1中IRO算法在精确建模的前提下拥有相对更高的校正精度，应用广泛，因此这里简单介绍其原理。设以某种正交多项式(例如单位圆域上的Zernike多项式)表征的非球面面型偏差E(矩阵形式)，同时设非零位检测系统像面波前W如式(2)所示，其中Zj、Z'j为多项式系数，而Uj为多项式矩阵。
{E=J∑j=1Zj⋅UjW=J∑j=1Z′j⋅Uj. (2) 从E到W存在一种由检测系统决定的映射关系，本文称其为系统函数，记为F。对于采用正交多项式表征的情况，F可以直接作用到多项式系数上，即：
[Z′1,⋯,Z′y]=F([Z1,⋯,ZJ]). (3) 对系统进行精确建模，记模型中的面型偏差与像面波前分别为Em、Wm，实测像面波前为Wt，而待测面型Et则是求解目标。参照式(3)，模型与实测的两组面型与波前数据均可通过系统函数F建立联系，即：
{[Ztm1,⋯,Z′mJ]=F([Zm1,⋯,ZmJ])[Z′t1,⋯,Z′tJ]=F([Zt1,⋯,ZtJ]). (4) 由于F未知，式(4)需要采用迭代方法进行求解，即通过对模型面型Em的不断迭代，使得模型像面波前Wm不断逼近实测像面波前Wt，当残差小于阈值时，此时的模型面型
E∗m 即为迭代求得的待测面型Et。Zemax为代表的光学设计软件常用的迭代方法是一种阻尼最小二乘法(Levenberg-Marquarat)，其评价函数如式(5)所示，其中ωj为第j项Zernike多项式的权重因子。O([Zt1,⋯,ZtJ])=min(J∑j=1ω2j(Z′mj−Z′tj)2). (5) IRO算法的主要流程如图17所示。
4.2.1 部分零位补偿器法
早期的Dall补偿镜(单透镜)仅能对很少一部分抛物面实现零位补偿，但若将设计要求从完全补偿非球面法线像差改变为降低干涉场中的条纹密度到能解调的程度，单透镜的补偿范围将会得到极大的扩展，此时设计所得的单透镜可以称其为部分零位补偿器(Partial Null Compensator, PNC)。随着学界对PNC引入回程误差及其消除方法方面研究的深入[100]，基于PNC的非球面非零位干涉方法的检测精度已可与零位法匹配，而PNC的形式也从单透镜向多样化发展。
在理论研究阶段，2003年，北京理工大学的Liu H等人分析了PNC设计中探测器像面处波前斜率的约束条件，提出每条干涉条纹至少需要4.35个像素点进行采样(对应波前斜率0.23λ/pixel)并分析了PNC球差与非球面法线像差的匹配关系[102]；2007年，美国Arizona大学Sullivan J J等人讨论了基于PNC的光路对准、回程误差校正、探测器波前斜率以及光线遮拦等问题并提出了针对不同非球面度凸非球面(8 mm口径、7 mm顶焦距)的两片式PNC补偿方案[103]。
2009年起浙江大学杨甬英团队系统性地研究了基于球面单透镜PNC的非零位检测系统[104]，讨论了包括PNC的设计约束控制、初始结构选择、优化求解方法、回程误差校正以及干涉系统的构建等方面的问题[46, 100, 104-105]，提出了鲁棒性强、精度高的IRO回程误差校正算法[100]，并针对常规的5~500 mm口径、不同F数的抛物面建立了由5种单透镜PNC覆盖的补偿数据库[46]。该团队利用100 mm口径，F/2.4的抛物面与ZYGO干涉仪(采用无像差点法)进行了交叉验证(单透镜PNC非零位检测光路如图18所示)，两者偏差RMS值小于1/100λ。
2018年，国防科技大学陈善勇团队提出了具有很大补偿范围的平凸非球面PNC单透镜(High order Even Asphere, HOEA)，可以用于补偿大非球面度的高次非球面。该团队利用一块口径为268 mm、非球面度约为40λ的椭球面与ZYGO干涉仪(采用Offner零位补偿器)进行了交叉验证(非球面PNC非零位检测光路如图19所示)，两者偏差PV值为0.012λ，RMS偏差为0.004λ[106]，达到了零位法的检测精度。
2018年，南京理工大学高志山团队利用小数值孔径球面反射镜倾斜入射主要引入像散的特点，提出了基于像散补偿原理的反射式PNC。该团队利用一块口径为44 mm、顶点曲率半径为500 mm、离轴量为80 mm、圆锥系数为−0.25的离轴椭球面与ZYGO干涉仪(采用CGH零位法)进行了交叉验证(反射式PNC非零位检测光路如图20所示)，利用其提出的IRO结合高频回溯的算法进行回程误差校正后，两者偏差PV值为0.011λ，RMS值为0.002λ，也达到了零位法的检测精度[107]。
基于PNC的非零位检测方法在检测光路装调正确并且回程误差得到良好校正的情况下拥有可靠的检测精度，但受限于PNC的口径与补偿能力，其对于大口径或大非球面度待测面的检测能力有限。PNC技术的发展方向是与4.2.2中所述子孔径方法结合以扩大其动态范围。
4.2.2 子孔径干涉法
子孔径干涉法的思路在于将待测面划分为多个小区域(子孔径)进行检测，由于子孔径的非球面度远低于整个待测面，因此检测难度也容易得多。最终在解调得到所有子孔径的波前信息后，采用不同的方式合成得到待测面型。
子孔径的合成方式主要有拼接法与几何法两种，拼接法的应用场景是各子孔径之间带有不同的系统误差(因平移、旋转检测系统导致的)，因此需要利用相邻子孔径重叠区域的数据，通过算法进行拼接，其对应的检测方法一般称为子孔径拼接干涉法(Sub-aperture Stitching Interferometry, SSI)；而几何法应用于各子孔径系统误差分布一致的情况，一个典型的例子是倾斜波前干涉法(Tilted Wave Interferometry, TWI)。其中SSI法根据子孔径轮廓的不同，又可以细分为环带子孔径拼接(Annular Sub-aperture Stitching Interferometry, ASSI)、圆形域子孔径拼接(Circular Sub-aperture Stitching Interferometry, CSSI)和任意不规则区域子孔径拼接(Irregular Sub-aperture Stitching Interferometry, ISSI)等。此外，子孔径干涉法作为一种非零位检测方法同样需要对回程误差进行校正。
ASSI方法最早由Arizona大学Liu Y M等人于20世纪80年代提出[108]。如图21所示，该方法是将待测非球面沿孔径方向划分为多个环带，然后改变待测面与补偿器之间的轴向位置使得相应环带对应到干涉场中的条纹密度低于采样的极限。ASSI方法的优势在于待测面只需要进行轴向(一维)的移动，系统误差相对较小，同时基于正交的Annular Zernike多项式环形域的数据拼接也较为方便。ASSI方法的局限性同样显而易见，各子孔径同心使其一般只能用于检测旋转对称的凹非球面。
ASSI近年来的研究主要集中于算法研究，例如成都光电所伍凡团队研究了基于Annular Zernike正交多项式的拼接算法，降低了拟合求解过程中的病态误差[109]；浙江大学杨甬英团队提出了结合PNC与ASSI技术的检测体系，通过对环带划分与误差校正的研究，实现了与ZYGO干涉仪检测结果偏差PV值小于30 nm的精度(对口径100 mm，F/1.2的抛物面)[46]；长春光机所张学军团队则提出了基于三角剖分法的子孔径拼接算法，并将其应用到了小曲率凸非球面的检测中(口径310 mm，F/30的凸双曲面)[110]。
在产品方面，ZYGO公司的Verifire系列干涉仪(如图22)采用了ASSI的环带子孔径划分方式，但其采用几何法合成待测波面而未进行拼接，该系列干涉仪可以用于检测旋转对称非球面。
CSSI方法最早由Arizona大学Wyant J C于20世纪80年代提出，用于对大口径平面或非球面的面型检测[112]。如图23所示，该方法所采用的子孔径轮廓为圆形，其需要旋转多轴工作台，改变干涉系统与待测面的空间位置关系以实现各个子孔径区域条纹密度的最小化。
相比于ASSI，CSSI的自由度更多，因而可以用于离轴非球面或是自由曲面的检测，但系统误差的分析难度也提高了。CSSI领域近年的研究进展如下：2013年，长春光机所张学军团队利用CSSI方法检测了一块口径达1450 mm的离轴抛物面镜，误差校正后检测精度达到了PV值 0.031λ，RMS值0.005λ[49]；2015年，国防科技大学陈善勇团队提出采用的90个CSSI子孔径区域检测一块口径为88 mm的大曲率凸非球面[113]；2015年，浙江大学杨甬英团队将CSSI发展为子孔径轮廓可以选择任意形状的ISSI，检测PV精度约达到1/10λ[52]。
在产品方面，基于CSSI技术的主要有QED公司于21世纪初推出的MRF系统配套的干涉装置，2009年，QED公司提出了基于Risely棱镜的可变零位器(Variable Optical Null, VON)，并将其引入CSSI系统中(如图24所示)，可以检测非球面度达1000λ的待测面[41]，该CSSI干涉仪作为QED公司MRF精密抛光设备的一部分，可加工精度达1/50λ(RMS)的精密非球面。
这里简单介绍SSI法普遍采用的重叠区域波面拼接算法。假设整个待测面被划分为N个子孔径，每个子孔径的测得波面Wi可以表示为误差波面Wei与实际波面Wti之和，即。
Wi(x,y)=Wei(x,y)+Wti(x,y)=Ai+Bix+Ciy+Di(x2+y2)+Wti(x,y). (6) 其中Wei主要包含活塞差(Ai)、两个方向上的倾斜(Bi、Ci)以及离焦(Di)，恰好对应Zernike多项式的前4项，本文将其记作一个行向量Ei的形式，称为误差向量，即：
Ei=[Ai,Bi,Ci,Di]T. (7) 在两相邻子孔径m、n的重叠区域σj内，两者的实际波面Wtm、Wtn相等，由于各子孔径采样期间检测系统的运动，误差波面Wem、Wen并不相等，定义子孔径m、n之间的波面偏差ΔWj与相对误差向量ΔEj为：
{ΔWj(x,y)=Wm(x,y)−Wn(x,y)ΔEj=Em−En. (8) 利用σj内各点波面偏差ΔWj，以式(9)所示的评价函数，进行最小二乘拟合，即可得到相对误差向量ΔEj的最佳估计，从而实现Wn与Wm的拼接。由此遍历所有重叠区域，即可得到拼接后的完整波面。一般对拼接后的完整波面还会再进行一次Zernike多项式拟合，并将前4项作为整体的误差波面予以消除。
O(ΔEj)=min[∑σj(ΔWj(x,y)−MjΔEj)2],Mj=[1,x,y,x2+y2],(x,y)∈σj. (9) 图25给出了上述重叠区域拼接算法的一个仿真示例，在不考虑其他误差与噪声的情况下，拼接精度(PV)达到了10−12λ。
TWI法最早由德国Stuttgart大学Osten W团队于2007年提出[53]。区别于SSI法通过扫描的方式获取子孔径，TWI法引入了与Shack-Hartman传感器中类似的微透镜阵列并利用其对准直光束分割产生了多个轴外点光源，这些轴外点光源具有不同的倾斜角度以匹配待测非球面的各个子孔径，如图26(a)所示。此外，TWI法还利用一块掩模板以防止邻近点光源产生串扰并通过移动掩模实现全口径采样，如图26(b)所示。掩模位于不同位置时得到的干涉条纹如图26(c)所示。不难看出，TWI法相比于传统SSI方法的最大优势是检测时整个系统无需进行运动，从而显著降低了系统误差的校正难度。
2008年，Osten W团队搭建了基于TWI法的非球面检测样机，可用于检测非球面度为900 μm、最大斜率为10°的非球面，该团队利用一块自身面型精度达到1/20λ的球面镜测试了该样机的检测精度，结果表明其PV精度达到约0.13λ[114]；2014年，Osten W团队将TWI法拓展到了检测非旋转对称的自由曲面，以一块像散差达到1 mm的面型验证了其检测不确定度达到1/20λ (PV值)[54]；2019年，Osten W团队改进了TWI系统回程误差校正方法，通过消除非旋转对称的系统误差，即使存在较大环境扰动，系统残差依然可以控制在10 nm以内(RMS值)[115]。
3.1节在介绍逐点扫描法的时候提到，目前轮廓仪或CMM的探针开始采用基于干涉原理的光学探针[116]，这种方法应归入干涉方法，同时其检测原理又与SI方法有类似之处，故将其放在这里介绍。例如Taylor Hobson公司的Lupho Scan“轮廓仪”(图27(a))，采用了米勒(Miller)干涉装置(图27(b))充当光学探针并使用两个参考传感器(图27(c))保证了扫描拼接精度。该设备可以检测最大直径为420 mm、最大非球面度为800 μm的各类非球面，其对光滑面的检测精度(重复性)达到了25 nm (2σ)。同时由于其采用了1530~1610 nm近红外多波长光源，因此能够检测部分粗糙面和透明面(部分材料在该波段的透射/反射特性会发生明显变化)等传统干涉法难以检测的表面类型，其对粗糙度Ra达到1 μm的待测面依然可以保证250 nm (RMS, 2σ)的检测精度，因此该设备可以应用于从铣磨到精抛光的整个加工流程中。
此外，美国Arizona大学的Burge J H团队基于检测新太阳望远镜(NTT)和大麦哲伦望远镜(GMT)的大口径非球面子镜的需求，在2009年研发了一种采用全光纤干涉装置作为“光学探针”的摆臂式光学三坐标测量机(Swing-arm Optical Coordinate Measuring Machine, SOC-CMM)[117-120]，如图28(a)所示。该设备采用激光跟踪仪作为定位装置，从而保证了扫描精度，其对口径达1.4 m，非球面度达300 μm的离轴凸抛物面的检测精度达到了9 nm (RMS)。2011年，该团队为此设备额外增加了一个光学探针(如图28(b)所示，进一步校正了检测过程中的方位误差[119]。
相比于PNC方法，子孔径干涉法的优点是能检测形状更复杂、非球面度更大、口径更大的待测面，但其缺点在于检测精度受限于拼接精度，回程误差校正算法也更为复杂。总体上来说，由于SSI方法兼具优良的通用性与较好的检测精度，是目前不少成熟的商业化检测设备所采用的技术路线。
4.2.3 剪切干涉法
剪切干涉[121](Shearing Interferometry, SI)是一种典型的自干涉技术，其干涉场由两个(或数个)包含待测面信息的波前相互叠加产生而无需引入传统意义上的参考光。通常来说，SI系统中参与干涉的各波前在系统中的路径完全一致，因而其又属于完全共光路干涉(而Fizeau干涉系统中测试光比参考光多出一段光程，故称“部分共光路”)。根据参与干涉的波前相互叠加的形式(如图29所示)，剪切干涉又可以分为横向剪切干涉(Lateral Shearing Interferometry, LSI)、径向剪切干涉(Radial Shearing Interferometry, RSI)、旋转剪切干涉与翻转剪切干涉等，其中常用的是LSI与RSI两类。
LSI系统中干涉场的条纹密度不仅与待测波前有关，还和各波前之间的横向偏移量有关，因而通过控制各波前在探测器像面上的横向偏移量，可以有效抑制非球面法线像差带来的条纹增密问题，这便是LSI系统实现非球面非零位检测的机理所在。
2020年，浙江大学杨甬英团队将单透镜PNC非零位检测系统中的干涉装置由传统的Twyman-Green式替换为四波前横向剪切(即同时实现两个方向上的横向剪切)干涉系统(Quadra Wave Lateral Shearing Interferometer, QWLSI)[57, 122]，如图30所示。PNC与QWLSI两种非零位技术的结合提升了系统对于大曲率、大非球面度面型的补偿能力：例如对于100 mm口径的凹抛物面，单透镜PNC所能补偿的最小曲率半径由193 mm(对应非球面度26.72 μm)下降到了139 mm(对应非球面度70.46 μm)；与此同时，基于完全共光路与自干涉的特点，该方法对震动、气流等环境扰动的灵敏度极低，无需工作在气浮平台上。
RSI系统中参与干涉的两个波前形状一致但具有不同径向缩放比例。根据产生缩放方式的不同，RSI可分为雅敏(Jamin)式、马赫-曾德(Mach-Zehnder)式、波带板式与环形RSI，其中完全共光路的环形RSI是目前主流的RSI系统结构(如图31(a)所示)。RSI系统无载频时两波前共心，但为了使干涉图能够解调，往往需要附加倾斜载频，此时不再共心，其干涉场如图31(b)、31(c)所示。与LSI类似的是，RSI系统干涉条纹的密度除了由待测波前决定外还受剪切比(即两个波前缩放系数之比)的影响，因此，可以通过控制剪切比将RSI系统的条纹密度降低至探测器采样限制以内。
RSI系统用于非球面检测的研究尚不成熟。2008年，南京理工大学高志山团队曾利用环形RSI系统检测人眼角膜(非球面)地形图，但并未给出定量的检测结果与误差分析[123]；2019年，西安工业大学刘缠牢团队采用环形RSI系统检测了某块参数未知的非球面，但其未考虑倾斜载频等主要系统误差的影响，检测精度较低，仅有μm量级[56]。
对比两种剪切干涉方法，相较于QWLSI系统，环形RSI系统无论从光路结构还是重构算法(需要迭代计算)[121]上都较为复杂，精度亦不如前者，因而前者的实用性更高。总的来说，剪切干涉技术在非球面检测领域应用的较少，但基于其完全共光路的结构特点，值得进一步研究，特别是其中的横向剪切干涉。其未来发展方向不仅局限于图30，其可与PNC结合以提高非零位系统的动态范围，还可与其他检测技术结合，发挥其完全共光路的优势，用以解决传统干涉系统中光强匹配、环境扰动等方面的问题。
4.2.4 低灵敏度法
低灵敏度法泛指通过降低检测系统灵敏度以实现非零位检测的一类方法，包括双波长法、长波长法以及亚奈奎斯特法等。
其中双波长法与长波长法都是通过降低系统光源的等效波长从而降低干涉场条纹密度。这类方法很少单独使用而是作为其他方法中的一种技术手段，以提高检测范围。例如前文提到的Lupho Scan“轮廓仪”就结合了多波长(1530~1610 nm)、长波长与子孔径拼接干涉技术。
而亚奈奎斯特法(Sub Nyquist Interferometry, SNI)[61]是一种特殊的非零位干涉方法，由Greivenkamp J E于1987年提出[124]。该方法利用高密度条纹产生的“低频赝像”恢复出超过探测器Nyquist采样定律限制的高频信息，可检具有较大非球面度的待测面，但其需要采用特殊的稀疏阵列探测器和特殊的回程误差校正方法。美国ESDI公司曾推出过基于SNI方法的Dimetior AS干涉仪，其装置实物与检测结果如图32所示。
图 32 基于SNI法的Dimetior AS干涉仪Figure 32. Dimetior AS interferometer based on the SNI method这类方法由于牺牲了灵敏度，因此检测精度相对较低，其中SNI法还存在横向分辨率较低的问题。
4.3 干涉检测中的精密装调技术
干涉系统的精密装调是保障干涉检测精度的关键。在采用补偿器(PNC、CGH)的非球面干涉检测系统中，干涉仪、补偿器与待测非球面三者的位姿失调会在检测结果中引入倾斜、离焦、慧差、球差等初级像差以及大量不可预知的高阶像差[93]，这些像差将成为重要的系统误差源而影响系统的检测精度。因此，这里以PNC以及CGH作为补偿器的检测光路为例，介绍非球面干涉检测中常用的精密装调技术。
4.3.1 基于PNC的非零位检测光路装调
如图33所示的光路中，需要精密调节以消除的参数包括PNC对于干涉仪的相对位姿(偏心、倾斜)以及待测非球面对于PNC与干涉仪的相对位姿(偏心、倾斜、轴向误差)。
对于PNC的位姿调节，一种常用且简单的方法是PNC反射光斑对准法[122]。具体来说如图34所示，首先用一块(负)十字叉丝替换参考镜，并将其调至光斑中心位置，然后利用CCD中的十字像与PNC前后两个表面反射像的相对位置，调节PNC的倾斜与偏心，直至三者共心。对于共心位置的判断可以利用图形学运算以达到像素级精度，对应到PNC的调节精度则因灵敏度的不同而有所不同，但一般能达到20 μm偏心、30''倾斜，对于大多数待测面而言，PNC实现这样的调节精度时引入的系统误差(RMS)小于1/100λ。
非球面对位姿误差的灵敏度往往更高，因此采用与PNC类似的方法(即把非球面反射光斑同样调至共心)仅能作为一种粗调手段。在粗调完毕后，沿轴向移动非球面至干涉场中出现条纹，然后调节非球面的偏心、倾斜与轴向位置，直到干涉场中条纹数目至3~5条，然后对干涉图进行解调，由解调得出的慧差与离焦数据进一步调节非球面的位姿。
4.3.2 基于CGH的零位检测光路装调
CGH对位姿误差的灵敏度一般大于PNC，同时由于不存在曲率不同的前后两表面，因而一般不能采用4.2.1中所述的反射光斑对准法。为了便于调整，在设计CGH时一般会加入两个区域，分别用于CGH与干涉仪以及待测非球面与CGH之间的对准，分别称为对准全息和基准全息。
如图35所示，经对准全息反射的某个衍射级次(对于图中这类环形布局的对准全息，为避免刻线密度过大一般为+3级)在理想位置形成自准直，以平行光入射到干涉系统中，因此可以解调这个波前用来调整CGH的位姿；而投射过基准全息的某个衍射级次则一般被设计为在待测面上某区域投影特定图样(例如十字线)，从而初步确定待测面的位置，而非球面的精调方法与基于PNC的系统类似，均是通过解调出的波面信息反馈调节位姿。
4.4 干涉检测技术总结与展望
4.1与4.2节介绍了目前常见的非球面干涉检测技术，其中基于CGH的零位补偿法、基于PNC的部分零位法以及子孔径拼接法(SSI)是目前得到广泛应用的方法。此外，基于DM或SLM的自适应补偿法、倾斜波前法(TWI)以及剪切干涉法等最新检测技术的研究工作也在不断推进中，表2从检测原理、检测通用性、检测精度、动态范围、检测效率5个方面对比了上述6种常用检测方法。
表 2 非球面常用干涉检测方法总结Table 2. Summary of widely used interferometric metrology methods of optics aspheric surfaces方法类别 检测原理 通用性 检测精度 动态范围 检测效率 CGH零位补偿法 衍射补偿器 差 高 较小 高 PNC部分补偿法 部分补偿、回程误差校正 较好 较高，取决于回程误差校正 较大 高 子孔径拼接法(SSI) 子孔径检测、拼接算法 好 较高，取决于回程误差校正 大 低 自适应补偿法 自适应补偿器 好 较高 较大 高 TWI倾斜波前法 倾斜子光束检测不同区域 较好 较高，取决于回程误差校正 较小 较高 剪切干涉法 剪切率调节系统动态范围 较好 较高，取决于回程误差校正 可调 高 对于每个方法未来的发展方向，前文在介绍时已做了简单分析与展望，主要包括提升各自应用场景所需求检测能力(如检测精度、动态范围、检测效率)，还包括提高检测系统的自动化水平与抗干扰能力以及降低成本等实用化方面需要考虑的因素。而达成上述目的的一个重要举措就是将多种检测技术融合，以兼取各自优势或消除其某方面的劣势。
引入部分零位补偿器(PNC)是最常见的组合思路。在零位检测领域，折衍射混合式补偿方案先采用简单透镜或反射镜补偿掉一部分像差(充当部分零位补偿器)，再由CGH补偿剩余像差，如此一来可以有效降低CGH的设计加工难度，提高检测系统的动态范围。在非零位检测领域，QED子孔径拼接干涉仪中采用的VON补偿器降低了每个子孔径干涉场内的条纹密度，减少了需要划分的子孔径数目，从而降低了拼接过程中引入的系统误差；而QWLSI横向剪切干涉技术与PNC的结合则显著提高了系统的动态范围。成熟的商业化检测设备有时则会结合多种检测技术，例如Hobson公司的Lupho Scan轮廓仪就基于Miller干涉装置采用了SSI技术、多波长(Multiple-Wavelengths, MW)与长波长技术(Long-Wavelength, LW)等，使其在检测精度、通用性、动态范围等方面都达到了较高的水平。未来，随着基于深度学习(Deep Learning, DL)的干涉图分析与系统装调技术应用到非球面检测系统中，实现无需人为干预的全自动化检测也是值得期待的。
5. 结束语
近年来，各种各样的非球面光学元件广泛应用于各个领域，非球面的面型检测技术必然需要形成一个完善的体系以适应不同的测试场景。本文对常见的干涉方法进行了分类整理，介绍了各方法的原理、技术特点、检测能力与适用范围、相关算法以及检测光路装调等方面的内容，并对各方法的未来发展进行了展望。
总的来看，非球面检测技术的发展存在通用化与高精度两个大的方向。其中通用化要求检测系统具备一定的通用性，即不对系统做出很大调整的情况下能够检测不同种类的非球面。由于其多见于工业化检测中，因此一般还附带着快速检测与自动化的要求(包括装调的自动化与干涉图判读的自动化)。而高精度则要求尽可能地提高检测精度从而用以(加工)检测面型误差为nm或是亚nm量级的超高精度非球面，补偿器的精度以及系统误差的校正精度成为了这方面发展的关键。在这个基础上，非干涉法中基于结构光的方法以及PNC结合子孔径拼接的方法是目前两种发展前景较好的通用化检测方法。为了应对高精度检测的要求，随着待测非球面面型的愈发复杂，基于CGH的零位检测法仍将是未来一段时间最为可靠的方案。
-
图 1 光学非球面面型检测技术分类
Figure 1. Classification of optical aspheric surface testing technology
图 3 Hartman法及Shack-Hartman法示意图
Figure 3. Schematic diagrams of the Hartman & Shack-Hartman tests
图 8 无像差点法检测抛物面光路模型
Figure 8. Schematic diagrams of testing paraboloids using aberration-free point method
图 9 折射式补偿器零位检测光路模型
Figure 9. Schematic diagrams of null test by the refractive compensator
图 32 基于SNI法的Dimetior AS干涉仪
Figure 32. Dimetior AS interferometer based on the SNI method
表 1 常用回程误差校正算法对比
Table 1. Comparison of common RE calibration algorithms
方法 理论 条件 精度 速度 GDI 小畸变近似理论 黑盒 较低 较快 TRW 参考波面替代理论 白盒 一般 较快 IRO 系统函数的不变性 白盒 高 较慢 
下载: 导出CSV
表 2 非球面常用干涉检测方法总结
Table 2. Summary of widely used interferometric metrology methods of optics aspheric surfaces
方法类别 检测原理 通用性 检测精度 动态范围 检测效率 CGH零位补偿法 衍射补偿器 差 高 较小 高 PNC部分补偿法 部分补偿、回程误差校正 较好 较高，取决于回程误差校正 较大 高 子孔径拼接法(SSI) 子孔径检测、拼接算法 好 较高，取决于回程误差校正 大 低 自适应补偿法 自适应补偿器 好 较高 较大 高 TWI倾斜波前法 倾斜子光束检测不同区域 较好 较高，取决于回程误差校正 较小 较高 剪切干涉法 剪切率调节系统动态范围 较好 较高，取决于回程误差校正 可调 高
下载: 导出CSV
-
[1] 潘君骅. 光学非球面的设计、加工与检验[M]. 苏州: 苏州大学出版社, 2004.PAN J H. The Design, Manufacture and Test of the Aspherical Optical Surfaces[M]. Suzhou: Soochow University Press, 2004. (in Chinese) [2] 舒朝濂. 现代光学制造技术[M]. 北京: 国防工业出版社, 2008.SHU CH L. Modern optics manufacturing technology[M]. Beijing: National Defense Industry Press, 2008. (in Chinese) [3] BORN M, WOLF E. Principles of Optics[M]. Cambridge: Cambridge University Press, 2019. [4] JU G, MA H C, GU ZH Y, et al. Experimental study on the extension of nodal aberration theory to pupil-offset off-axis three-mirror anastigmatic telescopes[J]. Journal of Astronomical Telescopes,Instruments,and Systems, 2019, 5(2): 029001. [5] 李池娟, 孙昌锋, 席喆, 等. 非球面光学零件的应用[J]. 激光与红外,2013,43(3):244-247. doi: 10.3969/j.issn.1001-5078.2013.03.003LI CH J, SUN CH F, XI ZH, et al. Application of optical aspheric element[J]. Laser &Infrared, 2013, 43(3): 244-247. (in Chinese) doi: 10.3969/j.issn.1001-5078.2013.03.003 [6] LI SH P, ZHANG Y. Application of single point diamond turning in infrared optics[C]. Proceedings of the 2016 International Symposium on Advances in Electrical, Electronics and Computer Engineering, ISAEECE, 2016: 12-19. [7] LUO CH, SHI F, TIAN Y, et al. A combination process of magnetorheological finishing and computer controlled optical surfacing on single-crystal silicon surface[J]. Proceedings of SPIE, 2019, 10838: 108380A. [8] KARABYN V, POLÁK J, PROCHÁSKA F, et al. Ion beam figuring with using einzel lens[J]. Proceedings of SPIE, 2019, 11385: 1138508. [9] LIAO W L, DAI Y F, NIE X Q, et al. Rapid fabrication technique for nanometer-precision aspherical surfaces[J]. Applied Optics, 2015, 54(7): 1629-1638. doi: 10.1364/AO.54.001629 [10] BURGE J H. Certification of null correctors for primary mirrors[J]. Proceedings of SPIE, 1994, 1994: 248-259. doi: 10.1117/12.167975 [11] 朱日宏, 孙越, 沈华. 光学自由曲面面形检测方法进展与展望[J]. 光学学报,2021,41(1):0112001. doi: 10.3788/AOS202141.0112001ZHU R H, SUN Y, SHEN H. Progress and prospect of optical freeform surface measurement[J]. Acta Optica Sinica, 2021, 41(1): 0112001. (in Chinese) doi: 10.3788/AOS202141.0112001 [12] 师途, 杨甬英, 张磊, 等. 非球面光学元件的面形检测技术[J]. 中国光学,2014,7(1):26-46.SHI T, YANG Y Y, ZHANG L, et al. Surface testing methods of aspheric optical elements[J]. Chinese Optics, 2014, 7(1): 26-46. (in Chinese) [13] 侯溪, 张帅, 胡小川, 等. 超高精度面形干涉检测技术进展[J]. 光电工程,2020,47(8):200209.HOU X, ZHANG SH, HU X CH, et al. The research progress of surface interferometric measurement with higher accuracy[J]. Opto-Electronic Engineering, 2020, 47(8): 200209. (in Chinese) [14] 张磊, 刘东, 师途, 等. 光学自由曲面面形检测技术[J]. 中国光学,2017,10(3):283-299. doi: 10.3788/co.20171003.0283ZHANG L, LIU D, SHI T, et al. Optical free-form surfaces testing technologies[J]. Chinese Optics, 2017, 10(3): 283-299. (in Chinese) doi: 10.3788/co.20171003.0283 [15] ADACHI M, MIKI H, NAKAI Y, et al. Optical precision profilometer using the differential method[J]. Optics Letters, 1987, 12(10): 792-794. doi: 10.1364/OL.12.000792 [16] FANG X ZH, FENG X G, ZHANG J Y. Development of a virtual model of five-axis coordinate measuring machine[J]. Proceedings of SPIE, 2019, 11343: 1134307. [17] 李昂, 王永刚, 邬志强, 等. 光学加工过程中高次非球面的三坐标测量数据处理[J]. 中国光学,2020,13(2):302-312. doi: 10.3788/co.20201302.0302LI A, WANG Y G, WU ZH Q, et al. Data processing of high-order aspheric surface measurements using CMM in optical fabrication[J]. Chinese Optics, 2020, 13(2): 302-312. (in Chinese) doi: 10.3788/co.20201302.0302 [18] SHACK R V, PLATT B C. Production and use of a lenticular hartmann screen[J]. Journal of the Optical Society of America, 1971, 61(5): 656-661. [19] 张金平, 张学军, 张忠玉, 等. Shack-Hartmann波前传感器检测大口径圆对称非球面反射镜[J]. 光学 精密工程,2012,20(3):492-498. doi: 10.3788/OPE.20122003.0492ZHANG J P, ZHANG X J, ZHANG ZH Y, et al. Test of rotationally symmetric aspheric surface using Shack-Hartmann wavefront sensor[J]. Optics and Precision Engineering, 2012, 20(3): 492-498. (in Chinese) doi: 10.3788/OPE.20122003.0492 [20] FURUKAWA Y, TAKAIE Y, MAEDA Y, et al. Development of one-shot aspheric measurement system with a Shack Hartmann sensor[J]. Applied Optics, 2016, 55(29): 8138-8144. doi: 10.1364/AO.55.008138 [21] HÄUSLER G, FABER C, OLESCH E, et al. Deflectometry vs. interferometry[J]. Proceedings of SPIE, 2013, 8788: 87881C. [22] 刘东, 严天亮, 王道档, 等. 条纹投影与相位偏折测量技术研究进展[J]. 红外与激光工程,2017,46(9):0917001. doi: 10.3788/IRLA201746.0917001LIU D, YAN T L, WANG D D, et al. Review of fringe-projection profilometry and phase measuring deflectometry[J]. Infrared and Laser Engineering, 2017, 46(9): 0917001. (in Chinese) doi: 10.3788/IRLA201746.0917001 [23] DENG X T, GAO N, ZHANG Z H. A calibration method for system parameters in direct phase measuring deflectometry[J]. Applied Sciences, 2019, 9(7): 1444. doi: 10.3390/app9071444 [24] 郭春凤, 苏显渝, 陈文静, 等. 一种新的非球面零朗奇检测法[J]. 光学学报,2012,32(8):0812002. doi: 10.3788/AOS201232.0812002GUO CH F, SU X Y, CHEN W J, et al. A new null ronchi test for aspheric surfaces[J]. Acta Optica Sinica, 2012, 32(8): 0812002. (in Chinese) doi: 10.3788/AOS201232.0812002 [25] 雷柏平, 伍凡, 陈强. 大口径非球面Ronchi光栅测量方法[J]. 光电工程,2007,34(4):140-144.LEI B P, WU F, CHEN Q. Measurement of large-aperture aspheric surfaces with Ronchi grating test method[J]. Opto-Electronic Engineering, 2007, 34(4): 140-144. (in Chinese) [26] 王小鹏, 朱日宏, 王雷, 等. 数字刀口仪定量检验非球面光学元件面形[J]. 光学学报,2011,31(1):0112008. doi: 10.3788/AOS201131.0112008WANG X P, ZHU R H, WANG L, et al. Digitized foucault tester for quantitative evaluation the surface of aspheric optical elements[J]. Acta Optica Sinica, 2011, 31(1): 0112008. (in Chinese) doi: 10.3788/AOS201131.0112008 [27] 陈旭, 刘伟奇, 康玉思, 等. Offner补偿器的结构设计与装调[J]. 光学 精密工程,2010,18(1):88-93.CHEN X, LIU W Q, KANG Y S, et al. Design and tolerance analysis of Offner compensator[J]. Optics and Precision Engineering, 2010, 18(1): 88-93. (in Chinese) [28] OFFNER A. A null corrector for paraboloidal mirrors[J]. Applied Optics, 1963, 2(2): 153-155. doi: 10.1364/AO.2.000153 [29] BURGE J H, KOT L B, MARTIN H M, et al. Design and analysis for interferometric measurements of the GMT primary mirror segments[J]. Proceedings of SPIE, 2006, 6273: 62730M. doi: 10.1117/12.672484 [30] COYLE L E, DUBIN M B, BURGE J H. Design and analysis of an alignment procedure using computer-generated holograms[J]. Optical Engineering, 2013, 52(8): 084104. doi: 10.1117/1.OE.52.8.084104 [31] 席庆奎, 朱日宏, 陈磊, 等. 计算全息用于非球面检测的方法[J]. 激光杂志,2004,25(6):67-69. doi: 10.3969/j.issn.0253-2743.2004.06.027XI Q K, ZHU R H, CHEN L, et al. Methods on testing an aspheric with a computer generated hologram[J]. Laser Journal, 2004, 25(6): 67-69. (in Chinese) doi: 10.3969/j.issn.0253-2743.2004.06.027 [32] HE Y W, HUANG L, HOU X, et al. Modeling near-null testing method of a freeform surface with a deformable mirror compensator[J]. Applied Optics, 2017, 56(33): 9132-9138. doi: 10.1364/AO.56.009132 [33] ZHANG L, ZHOU SH, LI D, et al. Model-based adaptive non-null interferometry for freeform surface metrology[J]. Chinese Optics Letters, 2018, 16(8): 081203. doi: 10.3788/COL201816.081203 [34] ZHANG L, ZHOU SH, LI J S, et al. Model calibration by multi-null constraint for an optical freeform surface adaptive interferometer[J]. Applied Optics, 2020, 59(3): 726-734. doi: 10.1364/AO.380965 [35] ZHANG L, LI C, HUANG X L, et al. Compact adaptive interferometer for unknown freeform surfaces with large departure[J]. Optics Express, 2020, 28(2): 1897-1913. doi: 10.1364/OE.380889 [36] XUE SH, CHEN SH Y, FAN ZH B, et al. Adaptive wavefront interferometry for unknown free-form surfaces[J]. Optics Express, 2018, 26(17): 21910-21928. doi: 10.1364/OE.26.021910 [37] ZHANG L, LI D, LIU Y, et al. Flexible interferometry for optical aspheric and free form surfaces[J]. Optical Review, 2017, 24(6): 677-685. doi: 10.1007/s10043-017-0363-6 [38] HUANG L, CHOI H, ZHAO W CH, et al. Adaptive interferometric null testing for unknown freeform optics metrology[J]. Optics Letters, 2016, 41(23): 5539-5542. doi: 10.1364/OL.41.005539 [39] GRAVES L R, CHOI H, ZHAO W CH, et al. Model-free deflectometry for freeform optics measurement using an iterative reconstruction technique[J]. Optics Letters, 2018, 43(9): 2110-2113. doi: 10.1364/OL.43.002110 [40] CHAUDHURI R, PAPA J, ROLLAND J P. System design of a single-shot reconfigurable null test using a spatial light modulator for freeform metrology[J]. Optics Letters, 2019, 44(8): 2000-2003. doi: 10.1364/OL.44.002000 [41] 陈善勇, 卢劲丰, 薛帅. 波面干涉测量中的可变像差补偿技术[J]. 激光与光电子学进展,2017,54(4):51-62.CHEN SH Y, LU J F, XUE SH. Variable aberration compensation techniques in wavefront interferometry[J]. Laser &Optoelectronics Progress, 2017, 54(4): 51-62. (in Chinese) [42] 马啸, 刘世杰, 张志刚, 等. 空间光调制器像素尺寸对非球面检测误差影响分析[J]. 中国激光,2017,44(1):0104002. doi: 10.3788/CJL201744.0104002MA X, LIU SH J, ZHANG ZH G, et al. Impact of spatial light modulator pixel pitch on the accuracy of aspheric testing[J]. Chinese Journal of Lasers, 2017, 44(1): 0104002. (in Chinese) doi: 10.3788/CJL201744.0104002 [43] HAO Q, NING Y, HU Y, et al. Simultaneous phase-shifting interferometer with a monitored spatial light modulator flexible reference mirror[J]. Applied Optics, 2021, 60(6): 1550-1557. doi: 10.1364/AO.414810 [44] HAO Q, NING Y, HU Y. Applications of wavefront modulation devices in aspheric and freeform measurement[J]. Proceedings of SPIE, 2018, 11053: 110530N. [45] 师途. 基于部分零位补偿透镜的非球面通用化检测技术研究[D]. 杭州: 浙江大学, 2017.SHI T. General interferometric aspheric testing with partial null lens[D]. Hangzhou: Zhejiang University, 2017. (in Chinese) [46] ZHANG L, TIAN CH, LIU D, et al. Non-null annular subaperture stitching interferometry for steep aspheric measurement[J]. Applied Optics, 2014, 53(25): 5755-5762. doi: 10.1364/AO.53.005755 [47] WEN Y F, CHENG H B, TAM H Y, et al. Modified stitching algorithm for annular subaperture stitching interferometry for aspheric surfaces[J]. Applied Optics, 2013, 52(23): 5686-5694. doi: 10.1364/AO.52.005686 [48] 张磊, 田超, 刘东, 等. 非球面非零位环形子孔径拼接干涉检测技术[J]. 光学学报,2014,34(8):0812003. doi: 10.3788/AOS201434.0812003ZHANG L, TIAN CH, LIU D, et al. Non-null annular subaperture stitching interferometry for aspheric test[J]. Acta Optica Sinica, 2014, 34(8): 0812003. (in Chinese) doi: 10.3788/AOS201434.0812003 [49] YAN L S, WANG X K, ZHENG L G, et al. Experimental study on subaperture testing with iterative triangulation algorithm[J]. Optics Express, 2013, 21(19): 22628-22644. doi: 10.1364/OE.21.022628 [50] 闫公敬, 张宪忠. 非零位凸非球面子孔径拼接检测技术研究[J]. 中国光学,2018,11(5):798-803. doi: 10.3788/co.20181105.0798YAN G J, ZHANG X ZH. Research on non-null convex aspherical sub-aperture stitching detection technology[J]. Chinese Optics, 2018, 11(5): 798-803. (in Chinese) doi: 10.3788/co.20181105.0798 [51] CHEN SH Y, DAI Y F, LI SH Y, et al. Calculation of subaperture aspheric departure in lattice design for subaperture stitching interferometry[J]. Optical Engineering, 2010, 49(2): 023601. doi: 10.1117/1.3314297 [52] ZHANG L, LIU D, SHI T, et al. Aspheric subaperture stitching based on system modeling[J]. Optics Express, 2015, 23(15): 19176-19188. doi: 10.1364/OE.23.019176 [53] GARBUSI E, PRUSS C, LIESENER J, et al. New technique for flexible and rapid measurement of precision aspheres[J]. Proceedings of SPIE, 2007, 6616: 61629. [54] BAER G, SCHINDLER J, PRUSS C, et al. Fast and flexible non-null testing of aspheres and free-form surfaces with the tilted-wave-interferometer[J]. International Journal of Optomechatronics, 2014, 8(4): 242-250. doi: 10.1080/15599612.2014.942925 [55] 刘璐. 径向剪切干涉误差综合分析[D]. 西安: 西安工业大学, 2019.LIU L. Comprehensive analysis of radial shear interference errors[D]. Xi'an: Xi'an Technological University, 2019. (in Chinese) [56] WANG M, ZHANG B, NIE S P, et al. Radial shearing interferometer for aspheric surface testing[J]. Proceedings of SPIE, 2002, 4927: 673-676. doi: 10.1117/12.471690 [57] ZHANG R, YANG Y Y, ZHAO H Y, et al. Non-Null testing of the aspheric surface using a quadriwave lateral shearing interferometer[J]. Applied Optics, 2020, 59(18): 5447-5456. doi: 10.1364/AO.391263 [58] 杨甬英, 凌曈. 新型共路干涉仪[M]. 杭州: 浙江大学出版社, 2020.YANG Y Y, LING T. Novel Common-Path Interferometers[M]. Hangzhou: Zhejiang Universisty Press, 2020. (in Chinese) [59] 贺俊, 陈磊. 使用红外干涉仪测量非球面面形[J]. 光学 精密工程,2010,18(1):69-74.HE J, CHEN L. Measurement of aspheric surfaces by infrared interferometer[J]. Optics and Precision Engineering, 2010, 18(1): 69-74. (in Chinese) [60] 杨甬英. 先进干涉检测技术与应用[M]. 杭州: 浙江大学出版社, 2017.YANG Y Y. Advanced Interferometry and Application[M]. Hangzhou: Zhejiang University Press, 2017. (in Chinese) [61] TAO W, VALERA J D, MOORE A J. High-speed, sub-Nyquist interferometry[J]. Optics Express, 2011, 19(11): 10111-10123. doi: 10.1364/OE.19.010111 [62] 刘东, 杨甬英, 田超, 等. 非球面非零位检测中的回程误差分析与校正[J]. 光学学报,2009,29(3):688-696. doi: 10.3788/AOS20092903.0688LIU D, YANG Y Y, TIAN CH, et al. Analysis and correction of retrace error for nonnull aspheric testing[J]. Acta Optica Sinica, 2009, 29(3): 688-696. (in Chinese) doi: 10.3788/AOS20092903.0688 [63] Taylor-Hobson, Inc. Taylsurf profiler[EB/OL]. [2021-08-31]. https://www.taylor-hobson.com/products/surface-profilers/optics-pgi/pgi-freeform. [64] ZEISS, Inc. XENOS[EB/OL]. [2021-08-31]. https://www.zeiss.com/metrology/products/systems/coordinate-measuring-machines/bridge-type-cmms/xenos.html. [65] MALACARA D. Optical Shop Testing[M]. 3rd ed. Hoboken: Wiley, 2007. [66] NEAL D R, ARMSTRONG D J, TURNER W T. Wavefront sensors for control and processing monitoring in optics manufacture[J]. Proceedings of SPIE, 1997, 2933: 211-220. [67] 饶学军, 凌宁, 王成, 等. 哈特曼-夏克传感器在非球面加工中的应用[J]. 光学学报,2002,22(4):491-494. doi: 10.3321/j.issn:0253-2239.2002.04.024RAO X J, LING N, WANG CH, et al. Application of hartmann-shack sensor in aspheric process[J]. Acta Optica Sinica, 2002, 22(4): 491-494. (in Chinese) doi: 10.3321/j.issn:0253-2239.2002.04.024 [68] GUO W J, ZHAO L P, TONG C S, et al. Adaptive centroid-finding algorithm for freeform surface measurements[J]. Applied Optics, 2013, 52(10): D75-D83. doi: 10.1364/AO.52.000D75 [69] KNAUER M C, KAMINSKI J, HAUSLER G. Phase measuring deflectometry: a new approach to measure specular free-form surfaces[J]. Proceedings of SPIE, 2004, 5457: 366-376. doi: 10.1117/12.545704 [70] TANG Y, SU X Y, LIU Y K, et al. 3D shape measurement of the aspheric mirror by advanced phase measuring deflectometry[J]. Optics Express, 2008, 16(19): 15090-15096. doi: 10.1364/OE.16.015090 [71] SU P, KHREISHI M, SU T Q, et al. Aspheric and freeform surfaces metrology with software configurable optical test system: a computerized reverse Hartmann test[J]. Optical Engineering, 2014, 53(3): 031305. [72] SU P, PARKS R E, WANG L R, et al. Software configurable optical test system: a computerized reverse Hartmann test[J]. Applied Optics, 2010, 49(23): 4404-4412. doi: 10.1364/AO.49.004404 [73] 袁婷. 基于条纹反射法的大口径非球面反射镜面形检测技术研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2016.YUAN T. Study on fringe-reflection optical surface shape measurement technology for large aspheric mirror[D]. Changchun: Changchun Institute of Optics, Fine Mehcanics and Physics, Chinese Academy of Sciences, 2016. (in Chinese) [74] CORNEJO-RODRIGUEZ A, CORDERO-DAVILA A, CARDONA-NUNEZ O. Ronchi and Hartman tests: a null Hartman test[J]. Proceedings of SPIE, 1990, 1319: 650. doi: 10.1117/12.34908 [75] BROWN B R, LOHMANN A W. Complex spatial filtering with binary masks[J]. Applied Optics, 1966, 5(6): 967-969. doi: 10.1364/AO.5.000967 [76] MACGOVERN A J, WYANT J C. Computer generated holograms for testing optical elements[J]. Applied Optics, 1971, 10(3): 619-624. doi: 10.1364/AO.10.000619 [77] ONO A, WYANT J C. Aspherical mirror testing using a CGH with small errors[J]. Applied Optics, 1985, 24(4): 560-563. doi: 10.1364/AO.24.000560 [78] ONO A, WYANT J C. Plotting errors measurement of CGH using an improved interferometric method[J]. Applied Optics, 1984, 23(21): 3905-3910. doi: 10.1364/AO.23.003905 [79] WYANT J C, O'NEILL P K. Computer generated hologram; null lens test of aspheric wavefronts[J]. Applied Optics, 1974, 13(12): 2762-2765. doi: 10.1364/AO.13.002762 [80] TAMURA H, ISHII Y. Computer-generated hologram fabricated by electron-beam lithography for noise reduction[J]. Optical Review, 2012, 19(2): 50-57. doi: 10.1007/s10043-012-0012-z [81] BURGE J H, ANDERSON D S. Full-aperture interferometric test of convex secondary mirrors using holographic test plates[J]. Proceedings of SPIE, 1994, 2199: 181-192. doi: 10.1117/12.176188 [82] ZHOU P, SHU Y, ZHAO CH Y, et al. Diffraction effects for interferometric measurements due to imaging aberrations[J]. Optics Express, 2012, 20(4): 4403-4418. doi: 10.1364/OE.20.004403 [83] CAI W R, ZHOU P, ZHAO CH Y, et al. Diffractive optics calibrator: measurement of etching variations for binary computer-generated holograms[J]. Applied Optics, 2014, 53(11): 2477-2486. doi: 10.1364/AO.53.002477 [84] CAI W R, ZHOU P, ZHAO CH Y, et al. Analysis of wavefront errors introduced by encoding computer-generated holograms[J]. Applied Optics, 2013, 52(34): 8324-8331. doi: 10.1364/AO.52.008324 [85] ZEHNDER R, BURGE J H, ZHAO CH Y. Use of computer generated holograms for alignment of complex null correctors[J]. Proceedings of SPIE, 2006, 6273: 62732S. doi: 10.1117/12.672139 [86] DUBIN M B, SU P, BURGE J H. Fizeau interferometer with spherical reference and CGH correction for measuring large convex aspheres[J]. Proceedings of SPIE, 2009, 7426: 74260S. doi: 10.1117/12.829053 [87] REICHELT S, PRUSS C, TIZIANI H J. Absolute interferometric test of aspheres by use of twin computer-generated holograms[J]. Applied Optics, 2003, 42(22): 4468-4479. doi: 10.1364/AO.42.004468 [88] BEYERLEIN M, LINDLEIN N, SCHWIDER J. Dual-wave-front computer-generated holograms for quasi-absolute testing of aspherics[J]. Applied Optics, 2002, 41(13): 2440-2447. doi: 10.1364/AO.41.002440 [89] 王成军. 双重计算全息图用于非球面绝对检验的研究[D]. 南京: 南京理工大学, 2008.WANG CH J. Research on dual CGH using for absolute test of aspherics[D]. Nanjing: Nanjing University of Science and Technology, 2008. (in Chinese) [90] 冯婕. 基于CGH高精度非球面检测技术研究[D]. 成都: 中国科学院研究生院(光电技术研究所), 2014.FENG J. Highly accuracy aspheric surface testing based on computer-generated hologram[D]. Chengdu: Institute of Optics and Electronics, Chinese Academy of Sciences, 2014. (in Chinese) [91] POLESHCHUK A G, NASYROV R K, ASFOUR J M. Combined computer-generated hologram for testing steep aspheric surfaces[J]. Optics Express, 2009, 17(7): 5420-5425. doi: 10.1364/OE.17.005420 [92] 李明. 基于CGH的非球面混合补偿检测及离轴光学系统装调的关键技术研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2015.LI M. Research on key technology of hybrid null testing of aspheric mirrorand off-axis optical system alignment based on CGH[D]. Changchun: Changchun Institute of Optics, Fine Mehcanics and Physics, Chinese Academy of Sciences, 2015. (in Chinese) [93] 高松涛. 超高精度非球面面形检测技术研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2014.GAO S T. Research on ultra-precise aspheric surface testing[D]. Changchun: Changchun Institute of Optics, Fine Mehcanics and Physics, Chinese Academy of Sciences, 2014. (in Chinese) [94] CAO ZH L, XUAN L, HU L F, et al. Investigation of optical testing with a phase-only liquid crystal spatial light modulator[J]. Optics Express, 2005, 13(4): 1059-1065. doi: 10.1364/OPEX.13.001059 [95] PRUSS C, TIZIANI H J. Dynamic null lens for aspheric testing using a membrane mirror[J]. Optics Communications, 2004, 233(1-3): 15-19. doi: 10.1016/j.optcom.2004.01.030 [96] FUERSCHBACH K, THOMPSON K P, ROLLAND J P. Interferometric measurement of a concave, φ-polynomial, Zernike mirror[J]. Optics Letters, 2014, 39(1): 18-21. doi: 10.1364/OL.39.000018 [97] HÄLLSTIG E, STIGWALL J, MARTIN T, et al. Fringing fields in a liquid crystal spatial light modulator for beam steering[J]. Journal of Modern Optics, 2004, 51(8): 1233-1247. doi: 10.1080/09500340408230419 [98] 师途, 臧仲明, 刘东, 等. 光学非球面面形非零位检测的回程误差校正[J]. 光学学报,2016,36(8):0812006. doi: 10.3788/AOS201636.0812006SHI T, ZANG ZH M, LIU D, et al. Retrace error correction for non-null testing of optical aspheric surface[J]. Acta Optica Sinica, 2016, 36(8): 0812006. (in Chinese) doi: 10.3788/AOS201636.0812006 [99] BEAR G, SCHINDLER J, PRUSS C, et al. Calibration of a non-null test interferometer for the measurement of aspheres and free-form surfaces[J]. Optics Express, 2014, 22(25): 31200-31211. doi: 10.1364/OE.22.031200 [100] SHI T, LIU D, ZHOU Y, H et al. Practical retrace error correction in non-null aspheric testing: a comparison[J]. Optics Communications, 2017, 383: 378-385. doi: 10.1016/j.optcom.2016.09.034 [101] 任王涛. 基于逆向迭代法对离轴非球面的面形检测[D]. 成都: 电子科技大学, 2020.REN W T. Surface shape detection of off-axis aspheric surface based on reverse iteration method[D]. Chengdu: University of Electronic Science and Technology of China, 2020. (in Chinese) [102] LIU H L, ZHU Q D, HAO Q, et al. Design of novel part-compensating lens used in aspheric testing[J]. Proceedings of SPIE, 2003, 5253: 480-484. doi: 10.1117/12.521761 [103] SULLIVAN J J, GREIVENKAMP J E. Design of partial nulls for testing of fast aspheric surfaces[J]. Proceedings of SPIE, 2007, 6671: 66710W. doi: 10.1117/12.734874 [104] 刘东, 杨甬英, 田超, 等. 用于非球面通用化检测的部分零位透镜[J]. 红外与激光工程,2009,38(2):322-325. doi: 10.3969/j.issn.1007-2276.2009.02.029LIU D, YANG Y Y, TIAN CH, et al. Partial null lens for general aspheric testing[J]. Infrared and Laser Engineering, 2009, 38(2): 322-325. (in Chinese) doi: 10.3969/j.issn.1007-2276.2009.02.029 [105] ZANG ZH M, XU ZH R, PENG SH J, et al. Non-null interferometers for irregular surface measurement with system modeling[J]. Measurement Science and Technology, 2021, 32(4): 045205. doi: 10.1088/1361-6501/abd11f [106] XUE SH, CHEN SH Y, TIE G P. Near-null interferometry using an aspheric null lens generating a broad range of variable spherical aberration for flexible test of aspheres[J]. Optics Express, 2018, 26(24): 31172-31189. doi: 10.1364/OE.26.031172 [107] DOU Y M, YUAN Q, GAO ZH SH, et al. Partial null astigmatism-compensated interferometry for a concave freeform Zernike mirror[J]. Journal of Optics, 2018, 20(6): 065702. doi: 10.1088/2040-8986/aac1db [108] LIU Y M, LAWRENCE G N, KOLIOPOULOS C L. Subaperture testing of aspheres with annular zones[J]. Applied Optics, 1988, 27(21): 4504-4513. doi: 10.1364/AO.27.004504 [109] HOU X, WU F, YANG L, et al. Experimental study on measurement of aspheric surface shape with complementary annular subaperture interferometric method[J]. Optics Express, 2007, 15(20): 12890-12899. doi: 10.1364/OE.15.012890 [110] 闫力松. 子孔径拼接干涉检测光学镜面算法的研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2015.YAN L S. Research on the algorithm testing optical mirror by subaperture stitching interferometry[D]. Changchun: Changchun Institute of Optics, Fine Mehcanics and Physics, Chinese Academy of Sciences, 2015. (in Chinese) [111] ZYGO, Inc. Verifire[EB/OL]. [2021-08-31]. https://www.zygo.com.cn/products/metrology-systems/laser-interferometers/verifire. [112] KIN C J, WYANT J C. Subaperture test of a large flat or a fast aspheric surface[J]. Journal of the Optical Society of America, 1981, 71(12): 1587. [113] CHEN SH Y, WU CH CH, TIE G P, et al. Stitching test of large flats by using two orthogonally arranged wavefront interferometers[J]. Applied Optics, 2017, 56(33): 9193-9198. doi: 10.1364/AO.56.009193 [114] GARBUSI E, PRUSS C, OSTEN W. Interferometer for precise and flexible asphere testing[J]. Optics Letters, 2008, 33(24): 2973-2975. doi: 10.1364/OL.33.002973 [115] SCHINDLER J, PRUSS C, OSTEN W. Simultaneous removal of nonrotationally symmetric errors in tilted wave interferometry[J]. Optical Engineering, 2019, 58(7): 074105. [116] MIKŠ A, NOVAK J. Noncontact interferometric optical probe for calibration of coordinate measuring machines[J]. Applied Optics, 2011, 50(5): 671-678. doi: 10.1364/AO.50.000671 [117] SU P, WANG Y H, OH C J, et al. Swing arm optical CMM: self calibration with dual probe shear test[J]. Proceedings of SPIE, 2011, 8126: 81260W. doi: 10.1117/12.894203 [118] WANG Y H, SU P, PARKS R E, et al. Swing arm optical coordinate-measuring machine: high precision measuring ground aspheric surfaces using a laser triangulation probe[J]. Optical Engineering, 2012, 51(7): 073603. doi: 10.1117/1.OE.51.7.073603 [119] SU P, OH C J, ZHAO CH Y, et al. Optical testing for meter size aspheric optics[J]. Proceedings of SPIE, 2012, 8466: 84660S. doi: 10.1117/12.930513 [120] SU P, PARKS R E, WANG Y H, et al. Swing-arm optical coordinate measuring machine: modal estimation of systematic errors from dual probe shear measurements[J]. Optical Engineering, 2012, 51(4): 043604. doi: 10.1117/1.OE.51.4.043604 [121] 凌曈. 基于多波前剪切干涉与光学层析技术三维折射率场重构研究[D]. 杭州: 浙江大学, 2016.LING T. Reconstruction of three-dimensional refractive index field based on multi-wave shearing interferometry and optical tomography[D] Hangzhou: Zhejiang University, 2016. (in Chinese) [122] 张锐. 基于随机编码混合光栅横向剪切干涉的波前检测技术关键参数与应用研究[D]. 杭州: 浙江大学, 2020.ZHANG R. Research on key parameters and application of wavefront metrology based on the randomly encoded hybrid grating lateral shearing interferometry[D]. Hangzhou: Zhejiang University, 2020. (in Chinese) [123] 邵锋. 角膜地形图测量装置的技术研究[D]. 南京: 南京理工大学, 2008.SHAO F. Research on testing equipment of corneal topography[D]. Nanjing: Nanjing University of Science and Technology, 2008. (in Chinese) [124] GREIVENKAMP J E. Sub-Nyquist interferometry[J]. Applied Optics, 1987, 26(24): 5245-5258. doi: 10.1364/AO.26.005245 期刊类型引用(31)
1. 唐卓睿，毛朝斌，张瀛怀，冯畅，丘敏艳，胡承，张鑫. 高次碳化硅非球面次镜CGH补偿面形检测技术. 红外与激光工程. 2025(02): 104-110 . 
百度学术2. 张旭，李世杰，刘丙才，田爱玲，梁海锋，蔡长龙. 凹非球面的非零位干涉检测技术. 中国光学(中英文). 2024(01): 140-149 . 百度学术3. 马霖，谭双龙，闫磊，马思宇，吴洪波，张新. 双面共体反射镜结构优化设计与分析. 应用光学. 2024(01): 45-53 . 百度学术4. 陈光宇，胡明勇，杨传龙，封志伟，徐剑锋，白茜，崔金龙. 高次凸非球面补偿检验方法研究. 量子电子学报. 2024(01): 57-66 . 百度学术5. 刁晓飞，范芯蕊，康岩辉. 高精度面形坐标测量方法研究进展与应用. 计量科学与技术. 2024(02): 101-110 . 百度学术6. 王龙飞，胡雨旺，张泽光，刘悦，薛常喜. 非球面光学元件的快速制造技术. 光电工程. 2024(01): 3-34 . 百度学术7. 刘斌，王孝坤，程强，刘忠凯，李凌众，蔡梦雪，张洛嘉，李文涵，王金成，张学军. 复杂曲面光学元件高精度面形检测技术概述. 南通大学学报(自然科学版). 2024(01): 1-27 . 百度学术8. 苏媛，田爱玲，王红军，刘丙才，朱学亮，王思淇，任柯鑫，张郁文. 同步环带子孔径干涉非球面检测方法. 光学学报. 2024(08): 264-272 . 百度学术9. 李春琦，黄启泰，任建锋. 计算全息图的高效编码方法. 激光与光电子学进展. 2024(08): 93-98 . 百度学术10. 李凌，张家福，陶鑫，于宗伟，李梦旭，王任远，陈西，崔程光，王向东. 高洁净度超光滑非球面的自动化干涉检测方法. 红外与激光工程. 2024(05): 103-112 . 百度学术11. 张郁文，刘丙才，王红军，田爱玲，任柯鑫，王凯. 同步相移横向剪切干涉中偏振器件的误差建模. 中国光学(中英文). 2024(03): 640-647 . 百度学术12. 陈建军，王琳琳，霍立民，匡翠方，毛磊，郑驰，尹禄. 正弦型中频面形误差对光学传递函数的影响. 中国光学(中英文). 2024(04): 725-732 . 百度学术13. 张海鑫，孟庆宇，王江南，刘美辰，李磊. 面向镜面面形可检测性的离轴三反光学系统设计方法. 红外与激光工程. 2024(10): 183-192 . 百度学术14. 王锦荣，叶建春，侯丽英，吴双娥，米成栋. 基于Zemax非球面单透镜的优化设计. 空间电子技术. 2024(05): 87-92 . 百度学术15. 闫烁，万嵩林，李瀚捷，韩宜池，牛振岐，吴珍，路晴，江国昌，沈鹏程，魏朝阳. 离轴非球面干涉测量中标记点最优排布求解与畸变误差校正方法（特邀）. 光学学报(网络版). 2024(03): 33-42 . 百度学术16. 卜和阳，田浩南，虞林瑶，张宇鹏. 红外成像系统异形非球面优化及冷反射分析. 红外. 2024(12): 7-18 . 百度学术17. 郝三峰，张建，杨建峰. F/0.78高次非球面零位补偿检测与投影畸变校正. 光子学报. 2023(02): 39-53 . 百度学术18. 吴翠红，于博. 高次非球面磨床动力学模态分析与加工验证. 制造技术与机床. 2023(04): 115-120+125 . 百度学术19. 陈善勇，薛帅，熊玉朋，彭小强，戴一帆. 面向制造的光学面形超精密测量技术研究进展. 激光与光电子学进展. 2023(03): 177-190 . 百度学术20. 朱德清，李扬，房建国，赵宏鑫. 离轴抛物面镜复合抛光技术研究. 航空精密制造技术. 2023(02): 9-12 . 百度学术21. 陈浩博，张力伟，孙文卿，陈宝华，曹召良，吴泉英. 基于主成分分析的白光干涉微观形貌测量算法. 中国光学(中英文). 2023(03): 637-644 . 百度学术22. 张家齐，郭艺博，张友建，张志华. 机载宽温条件下反射镜组件与粘接层设计. 中国光学(中英文). 2023(03): 578-586 . 百度学术23. 张鑫，张乐，宋驰，闫力松，尹小林，张斌智. 基于PSD评价及伪随机轨迹的单晶碳化硅表面粗糙度研究. 红外与激光工程. 2023(05): 407-413 . 百度学术24. 许宁晏，高志山，陈露，黄静，邹宇通，袁群. 应用自由曲面的紧凑型长焦手机镜头设计(特邀). 红外与激光工程. 2023(07): 71-80 . 百度学术25. 刘克，张孝天，钟慧，何飞，刘书豪，李艳秋. 四波前横向剪切干涉仪的关键技术研究. 光学学报. 2023(15): 255-265 . 百度学术26. 魏秀东，李柏霖，赵宇航，汤建方，张继，黄勇焕，许英朝. 基于自由曲面的聚焦型太阳模拟器设计. 中国光学(中英文). 2023(06): 1356-1364 . 百度学术27. 卜和阳，虞林瑶，田浩南，王健. 中波红外成像系统冷反射抑制. 中国光学(中英文). 2023(06): 1414-1423 . 百度学术28. 罗小葵，孙海洋，张宁，董书岳，马玉洋. 反射镜面形三坐标白光扫描检测精度研究. 航天返回与遥感. 2022(03): 51-59 . 百度学术29. 黄亚，王丰璞，李新南，陈哲，李博，徐晨，曹亭. 基于计算全息的大口径离轴非球面子镜的折衍混合补偿检测方法. 光学学报. 2022(12): 198-208 . 百度学术30. 范芯蕊，刁晓飞，吴剑威，康岩辉. 高精度轴对称非球面反射镜轮廓测量方法(特邀). 红外与激光工程. 2022(09): 124-131 . 百度学术31. 国成立，郑德康，朱德燕，杨晓飞，李元正，张健，赵烈烽. 混合型计算全息图检测低反射率非球面(特邀). 红外与激光工程. 2022(09): 107-113 . 百度学术其他类型引用(18)
-
下载:
下载:
百度学术
计量
- 文章访问数: 5359
- HTML全文浏览量: 2724
- PDF下载量: 1330
- 被引次数: 49
