变截面压弯椭球柱面反射镜优化设计

李桐; 王楠; 祝万钱; 任祖洋; 金利民; 薛松

doi:10.37188/CO.2021-0179

变截面压弯椭球柱面反射镜优化设计

doi: 10.37188/CO.2021-0179

李桐^{1, 2,},
王楠^{1, 3},
祝万钱^{1, 3},
任祖洋³,
金利民^{1, 3},
薛松^{1, 3, ,}

1.
中国科学院上海应用物理研究所, 上海201800
2.
中国科学院大学, 北京 100049
3.
中国科学院上海高等研究院, 上海201800

基金项目: 国家自然科学基金青年科学基金项目(No. 11805262)

详细信息

作者简介:
李　桐（1997—），男，江苏盐城人，博士研究生，2019年于中国民航大学获得学士学位，主要从事同步辐射光学工程方面的研究。E-mail: litong@sinap.ac.cn

薛　松（1962—） , 男, 吉林长春人, 研究员, 博士生导师, 1984年于东北大学获得学士学位, 主要从事同步辐射光学工程、精密机械和光谱仪器设计方面的研究。E-mail: xuesong@zjlab.org.cn

中图分类号: TH744;O434.1
计量
- 文章访问数: 796
- HTML全文浏览量: 500
- PDF下载量: 148
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-18
- 修回日期: 2021-11-22
- 录用日期: 2022-01-21
- 网络出版日期: 2022-01-27
- 刊出日期: 2022-05-20

Optimal design of variable cross-section compression-bending ellipsoidal cylindrical mirror

LI Tong^{1, 2
,},
WANG Nan^{1, 3},
ZHU Wan-Qian^{1, 3},
REN Zu-Yang³,
JIN Li-Min^{1, 3},
XUE Song^{1, 3
, ,}

1.
Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201800, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai 201800, China

Funds: Supported by National Natural Science Foundation of China(No. 11805262)

More Information

Corresponding author: xuesong@zjlab.org.cn

摘要

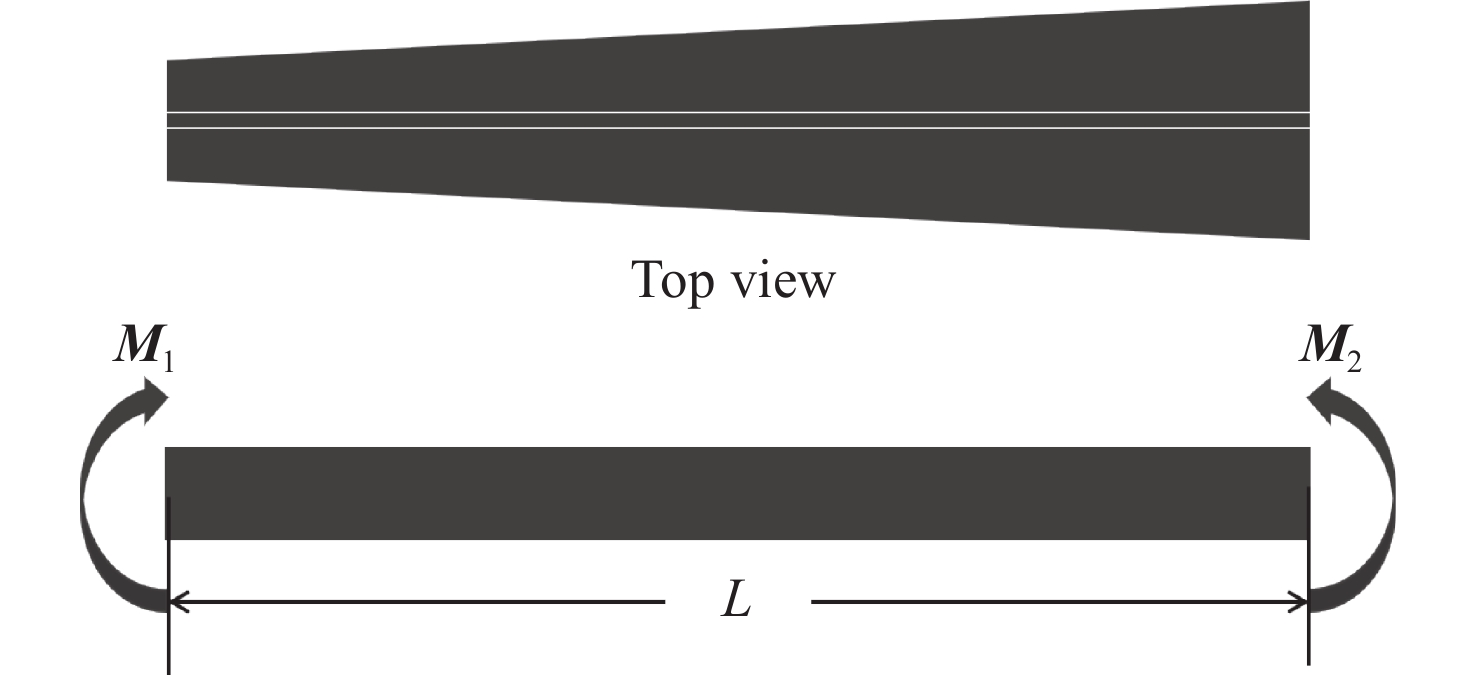
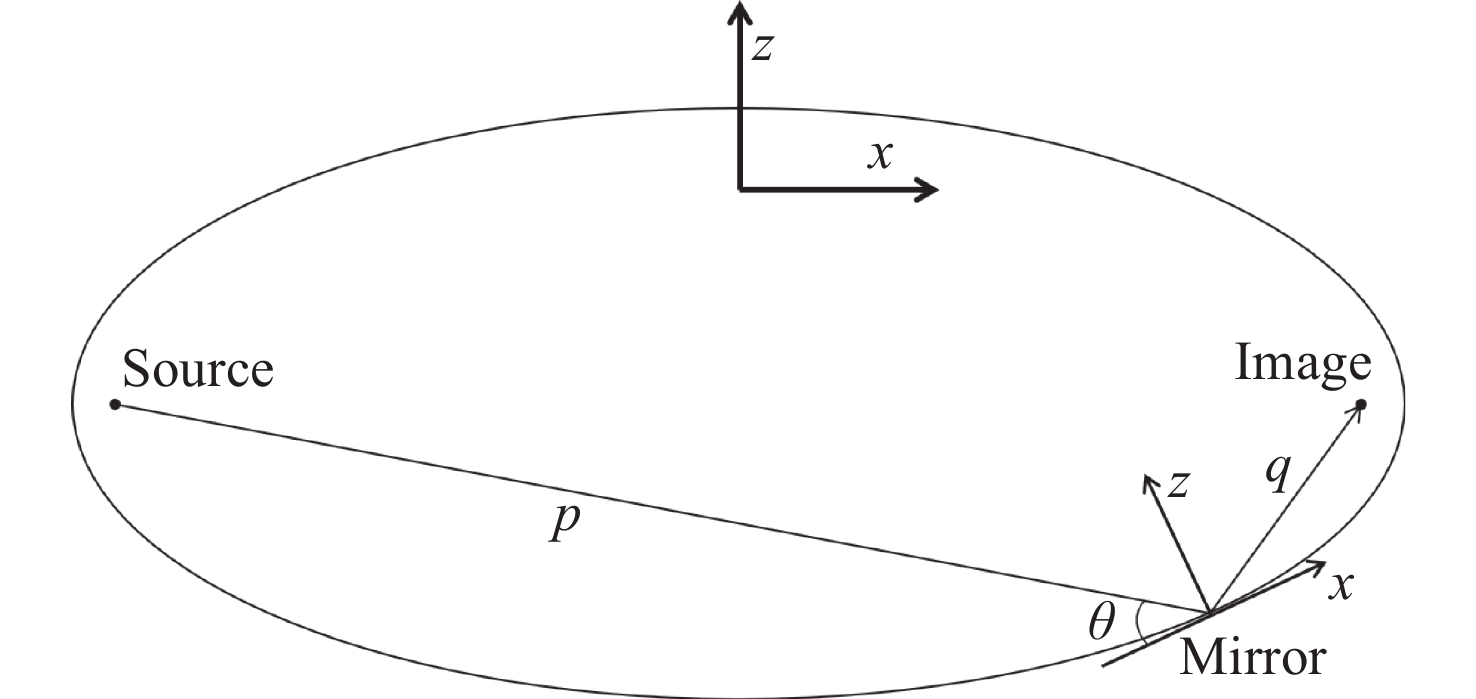
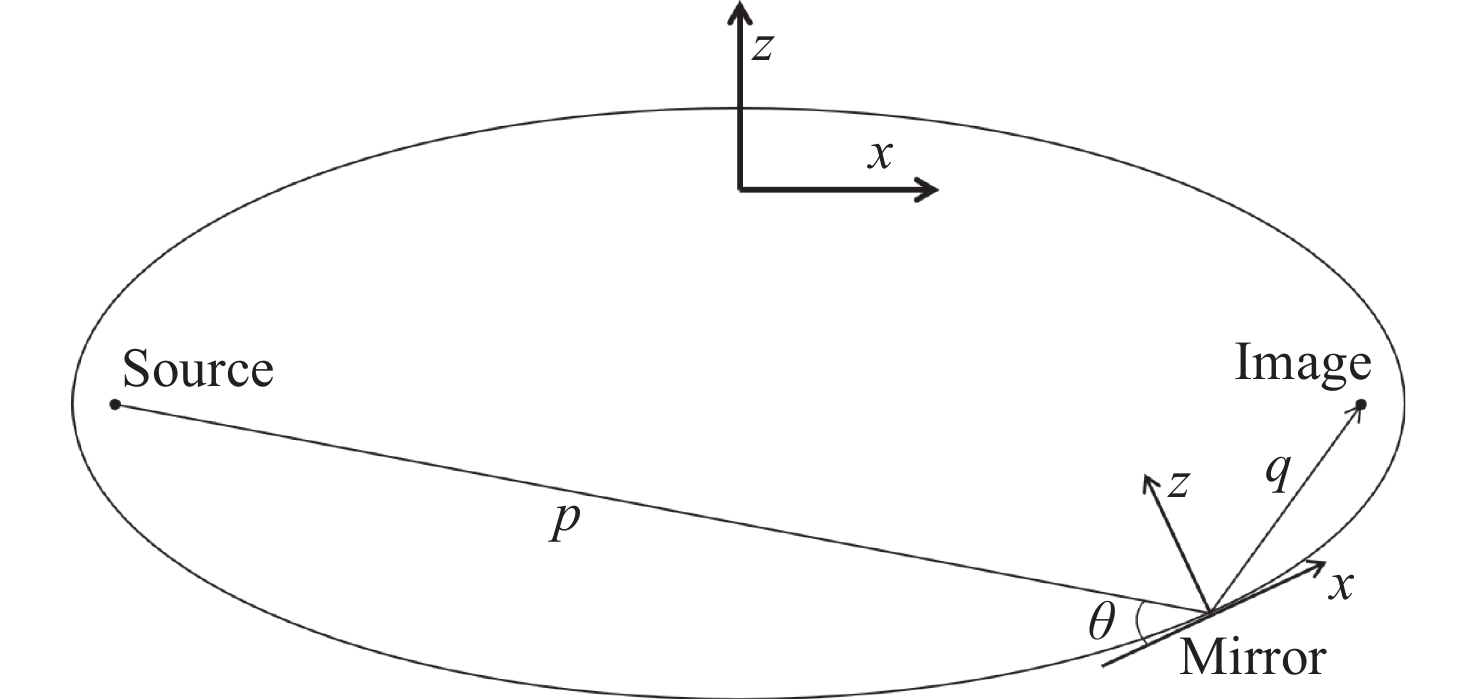
摘要: 根据同步辐射光束在建线站项目需要，提出变截面压弯椭球柱面反射镜方案。该方案基于变宽度压弯椭圆柱面聚焦镜设计理论，推导出变截面（带弧矢聚焦）反射镜镜面斜率误差的计算公式，并进行优化设计。本研究基于聚焦镜光学参数（物距$p$、像距$q$和掠入射角$\theta $）进行设计，最终借助有限元分析软件计算反射镜的设计误差。结果表明，在此需求下，反射镜两端最优宽度分别为49.5 mm和90.5 mm，对反射镜两端压弯弯矩进行计算、仿真、优化后，其斜率误差均方根值由~5.1368 μrad降低至~0.0636 μrad（取1 m长），接近系统误差（~0.0407 μrad），满足设计要求（<0.1 μrad）。
- 同步辐射 /
- 椭圆柱面镜 /
- 机械压弯 /
- 优化设计
Abstract: To meet the needs of the synchrotron radiation beamline station project under construction, a design scheme of variable cross-section bending ellipsoidal cylindrical mirror is proposed. In this scheme, the calculation formula of the slope error of the variable-section (with sagittal focus) mirror is deduced based on the design theory of variable-width bending ellipticalcylindrical focusing mirrors , and the design is optimized. This project is designed based on the optical parameters of the focusing lens (object distance p, image distance q and grazing incidence angle θ), and the design error of mirror is calculated by finite element analysis software. The results show that within the given requirements, the optimal widths at both ends of the mirror are 49.5 mm and 90.5 mm. After calculating, simulating and optimizing, the slope error RMS value of the bending moments at both ends of the mirror is reduced from ~5.1368 μrad to ~0.0636 μrad (at 1 m of length), close to the system error ~0.0407 μrad, meeting the design requirements.
- synchrotron radiation /
- elliptical cylindrical mirror /
- mechanical bending /
- optimized design

HTML全文

图 1 椭圆压弯聚焦原理图

Figure 1. Schematic diagram of elliptical bending focus

下载: 全尺寸图片幻灯片

图 2 压弯镜示意图

Figure 2. Schematic diagram of the bending mirror

下载: 全尺寸图片幻灯片

图 3 反射镜模型轴测图

Figure 3. Axonometric view of mirror model

下载: 全尺寸图片幻灯片

图 4 模型网格划分

Figure 4. Meshing results of the mirror model

下载: 全尺寸图片幻灯片

图 5 反射镜压弯面形及斜率分析

Figure 5. Analysis of the bending surface shape and slope of the mirror

下载: 全尺寸图片幻灯片

图 6 截面惯性矩示意图

Figure 6. Schematic diagram of the section moment of inertia

下载: 全尺寸图片幻灯片

图 7 反射镜各点处惯性矩

Figure 7. Moment of inertia at each point of the mirror

下载: 全尺寸图片幻灯片

表 1 反射镜设计参数

Table 1. Main indicators of the designed mirror

参数	指标
掠入射角/mrad	3.5
光源距离/m	5000
像点距离/m	2.5
反射镜尺寸	1200 mm(L)×50 mm(H)
有效光学长度	1000 mm
形状	梯形柱面镜
镜体材料	单晶硅
压弯斜率误差/μrad	<0.1
槽宽/弧矢半径	18 mm/R17.5 mm

下载: 导出CSV

表 2 用于仿真分析的材料属性

Table 2. Properties of the material used in the simulation analysis

材料	泊松比	杨氏模量/${\rm{GPa}}$	密度/${\rm{Kg} }\cdot{ {\rm{m} }^{-2}}$
Si	0.3	169	2330

下载: 导出CSV

表 3 本文计算的与初始公式计算的斜率误差对比

Table 3. Comparison of the slope errors calculated in this paper with that calculated by the initial formula

镜长/m	有效尺寸/m	系统斜率误差RMS/μrad	椭球镜斜率误差RMS/μrad
1.2	1.2	0.1025	6.2142
	1*	0.0407	5.1368
	0.8	0.0161	4.0643

下载: 导出CSV

表 4 修正前后斜率误差对比

Table 4. Comparison of the slope errors before and after correciton

有效尺寸/m	系统斜率误差RMS/μrad	修正前仿真误差RMS/μrad	修正后仿真误差RMS/μrad
1.2	0.1025	6.2142	0.1452
1*	0.0407	5.1368	0.0636
0.8	0.0161	4.0643	0.0271

下载: 导出CSV

参考文献(11)

[1]	吕清涛. 拉杆式压弯聚焦镜系统[D]. 北京: 中国科学院大学, 2010. LV Q T. Pull rod bending focusing lens system[D]. Beijing: University of Chinese Academy of Sciences, 2010. (in Chinese)
[2]	赵晨行, 卢启鹏, 宋源, 等. 自由电子激光光束线反射镜无应力夹持设计与分析[J]. 中国光学,2020,13(4):787-794. doi: 10.37188/CO.2019-0131 ZHAO CH H, LU Q P, SONG Y, et al. Design and analysis of stress-free clamping of mirrors used in free-electron laser beamlines[J]. Chinese Optics, 2020, 13(4): 787-794. (in Chinese) doi: 10.37188/CO.2019-0131
[3]	秦超. 同步辐射椭圆柱面压弯镜机构的研究[D]. 北京: 中国科学院大学, 2018. QIN CH. Research on synchrotron radiation elliptic cylinder mirror bender[D]. Beijing: University of Chinese Academy of Sciences, 2018. (in Chinese)
[4]	李明, 吴介立, 吴永前, 等. X射线反射镜研制技术的现状和发展[J]. 光电工程,2020,47(8):200205. LI M, WU J L, WU Y Q, et al. A review on the fabrication technology of X-ray reflector[J]. Opto-Electronic Engineering, 2020, 47(8): 200205. (in Chinese)
[5]	秦超, 薛松, 王楠, 等. 压弯椭圆柱面镜的有限元分析[J]. 核技术,2018,41(1):010101. doi: 10.11889/j.0253-3219.2018.hjs.41.010101 QIN CH, XUE S, WANG N, et al. The finite element analysis of the bent elliptical cylindrical mirror[J]. Nuclear Techniques, 2018, 41(1): 010101. (in Chinese) doi: 10.11889/j.0253-3219.2018.hjs.41.010101
[6]	程光宇, 黄智超, 王克逸, 等. 同步辐射聚焦镜压弯机构设计与面形误差分析[J]. 应用光学,2019,40(1):120-126. CHENG G Y, HUANG ZH CH, WANG K Y, et al. Design and surface shape error analysis of synchronous radiation focusing mirror bending mechanism[J]. Journal of Applied Optics, 2019, 40(1): 120-126. (in Chinese)
[7]	毛成文, 余笑寒, 肖体乔. 变宽度压弯椭圆柱面聚焦镜的光学参数可调性[J]. 核技术,2009,32(5):333-336. doi: 10.3321/j.issn:0253-3219.2009.05.003 MAO CH W, YU X H, XIAO T Q. Tunability of optical parameters of width-variable bent elliptical microfocus mirror[J]. Nuclear Techniques, 2009, 32(5): 333-336. (in Chinese) doi: 10.3321/j.issn:0253-3219.2009.05.003
[8]	ENG P J, RIVERS M L, YANG B X, et al. Micro-focusing 4-KeV to 65-KeV x-rays with bent Kirkpatrick-Baez mirrors[J]. Proceedings of SPIE, 1995, 2516: 41-51. doi: 10.1117/12.221682
[9]	MAO CH W, XI Z J, YU X H, et al. Design optimization of a tapered mirror for microfocusing optics[J]. Chinese Physics C, 2009, 33(8): 687-690. doi: 10.1088/1674-1137/33/8/017
[10]	ZHANG L, HUSTACHE R, HIGNETTE O, et al. Design optimization of a flexural hinge-based bender for X-ray optics[J]. Journal of Synchrotron Radiation, 1998, 5(3): 804-807. doi: 10.1107/S0909049597015288
[11]	周博文, 王楠, 祝万钱, 等. 等截面反射镜椭圆压弯机构变像距压弯[J]. 中国光学,2020,13(4):778-786. doi: 10.37188/CO.2019-0250 ZHOU B W, WANG N, ZHU W Q, et al. Variable image distance bending using an elliptical bending mechanism with a constant cross-section mirror[J]. Chinese Optics, 2020, 13(4): 778-786. (in Chinese) doi: 10.37188/CO.2019-0250