空间目标自适应光学图像椭圆部件检测

寇鹏; 智帅峰; 程耘; 刘永祥

doi:10.37188/CO.2021-0208

空间目标自适应光学图像椭圆部件检测

doi: 10.37188/CO.2021-0208

寇鹏^{1, 2,},
智帅峰^1,,
程耘^1,,
刘永祥^1, ,

1.
国防科技大学电子科学学院, 湖南长沙 410073
2.
西安卫星测控中心, 陕西西安 710600

基金项目: 国家自然科学基金（No. 61921001，No. 61801484）

详细信息

作者简介:
寇　鹏（1981—），男，河南洛阳人，博士研究生，西安卫星测控中心高级工程师，2003年于航天工程大学获得学士学位，2010年于国防科技大学获得硕士学位，主要从事空间目标探测与识别研究。E-mail：kou_810518@163.com

智帅峰（1992—），男，河南偃师人，博士，讲师，2011年于国防科技大学获得学士学位，2017年于国防科技大学获得硕士学位，2021年于英国帝国理工大学获得博士学位，主要从事三维机器人视觉，智能信号处理等方面的研究。E-mail：zhishuaifeng11@nudt.edu.cn

程　耘（1995—），男，重庆人，博士研究生，2018年于国防科技大学获得学士学位，主要从事阵列信号处理、电子对抗等方面的研究。E-mail：moraincy@126.com

刘永祥（1976—），男，河北唐山人，博士，教授，1999年于国防科技大学获得学士学位，2004年于国防科技大学获得博士学位，主要研究方向为雷达信号处理与目标识别。E-mail：lyx_bible@sina.com

中图分类号: TP391.4
计量
- 文章访问数: 1520
- HTML全文浏览量: 533
- PDF下载量: 191
- 被引次数: 0
出版历程
- 收稿日期: 2021-12-03
- 修回日期: 2022-01-04
- 录用日期: 2022-03-01
- 网络出版日期: 2022-03-01
- 刊出日期: 2022-05-20

Detection of elliptical components in adaptive optical image of space target

KOU Peng^{1, 2
,},
ZHI Shuai-feng^1
,,
CHENG Yun^1
,,
LIU Yong-xiang^{1
, ,}

1.
School of Electronic Science, University of Defense Science and Technology, Changsha 410073, China
2.
Xi’an Satellite Control Center, Xian 710600, China

Funds: Supported by National Natural Science Foundation of China (No. 61921001, No. 61801484)

More Information

Corresponding author: lyx_bible@sina.com

摘要

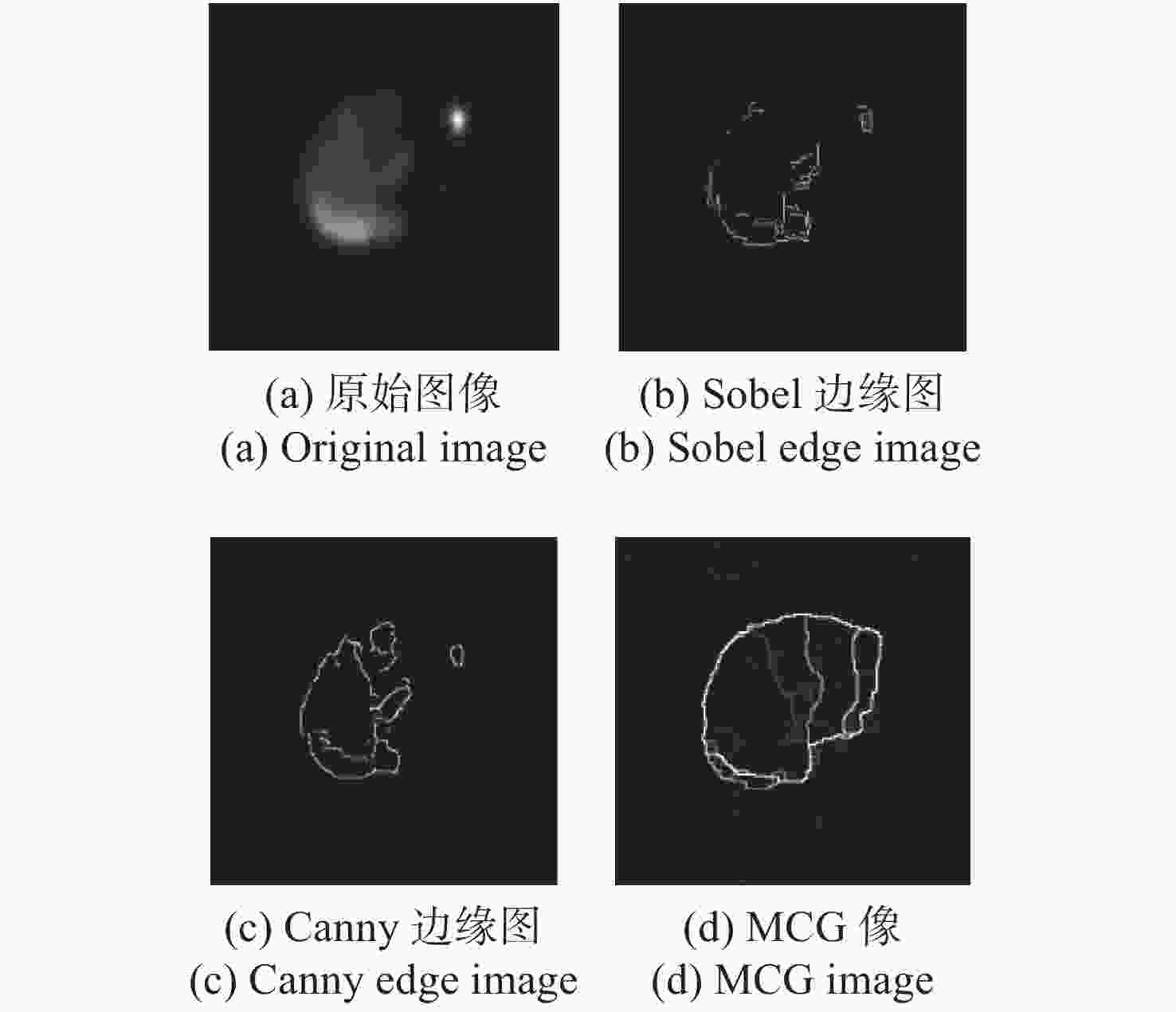
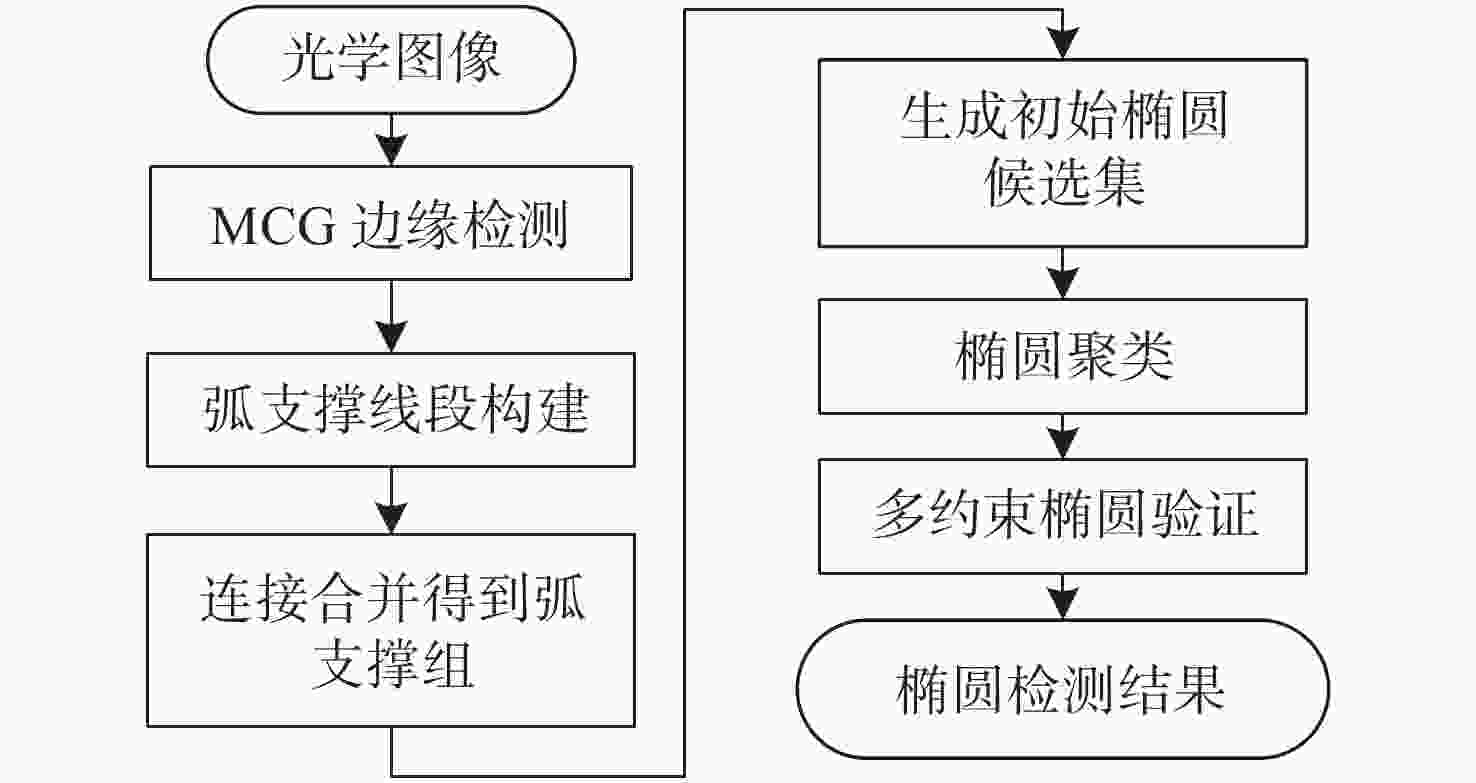
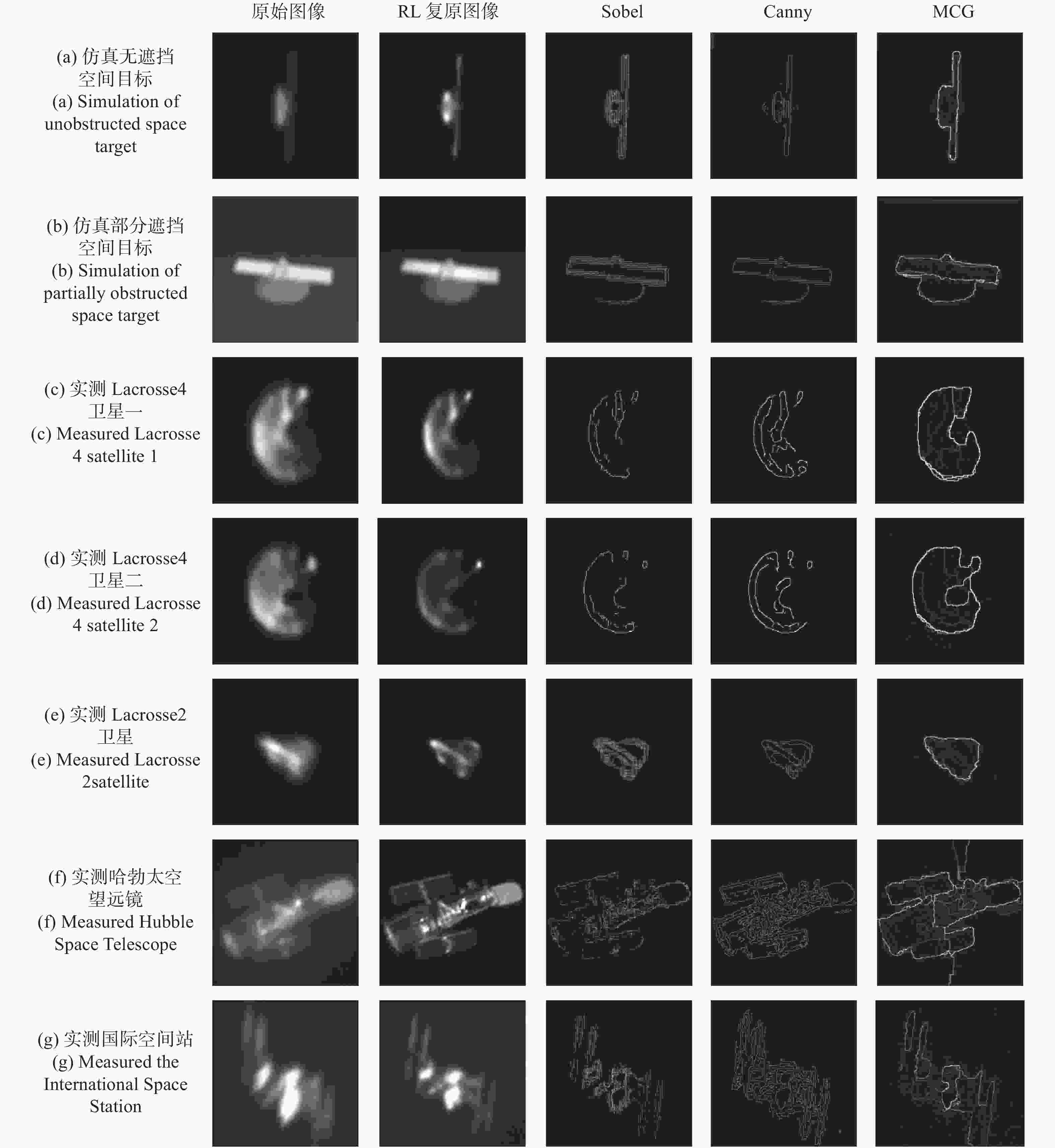
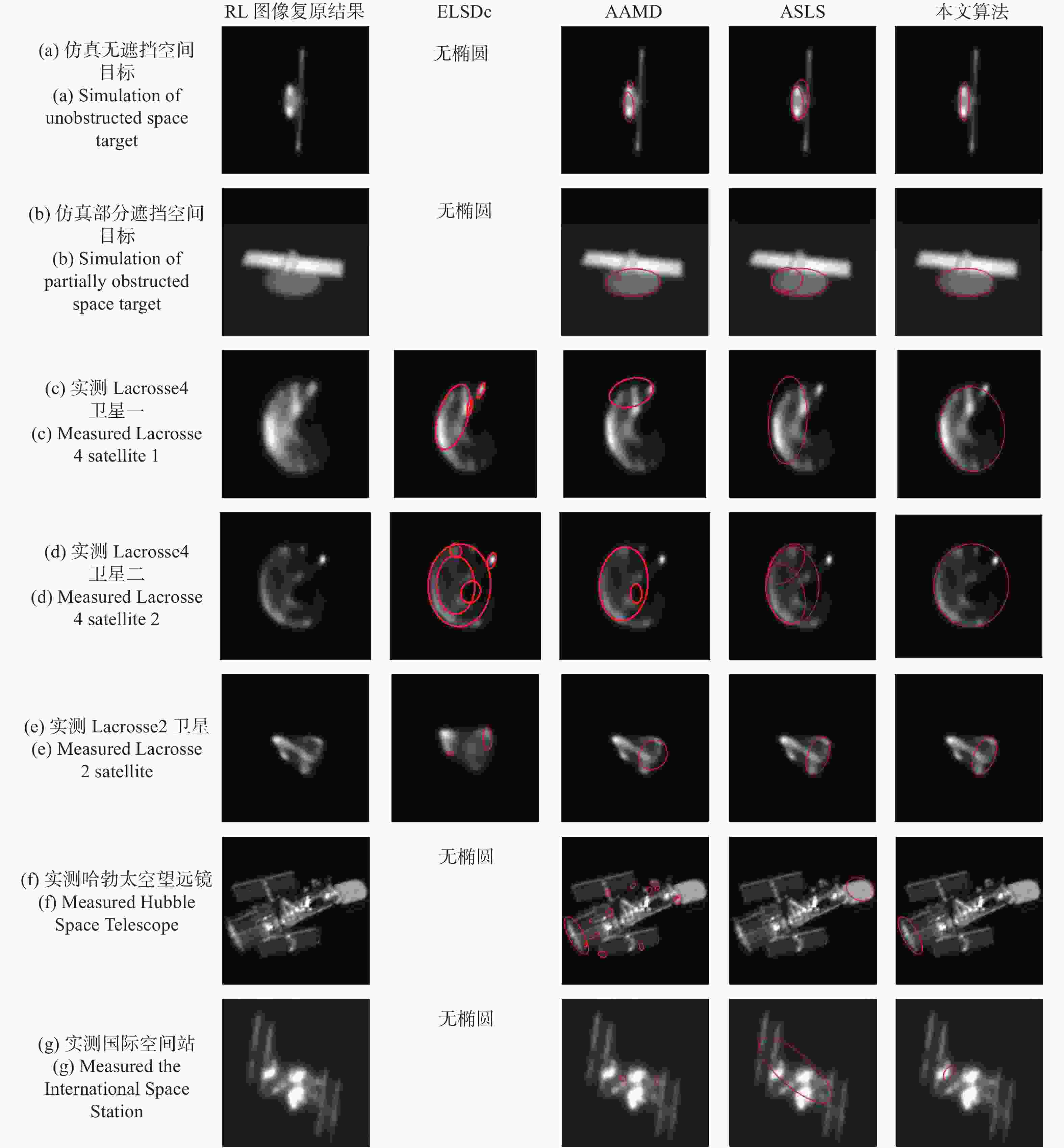
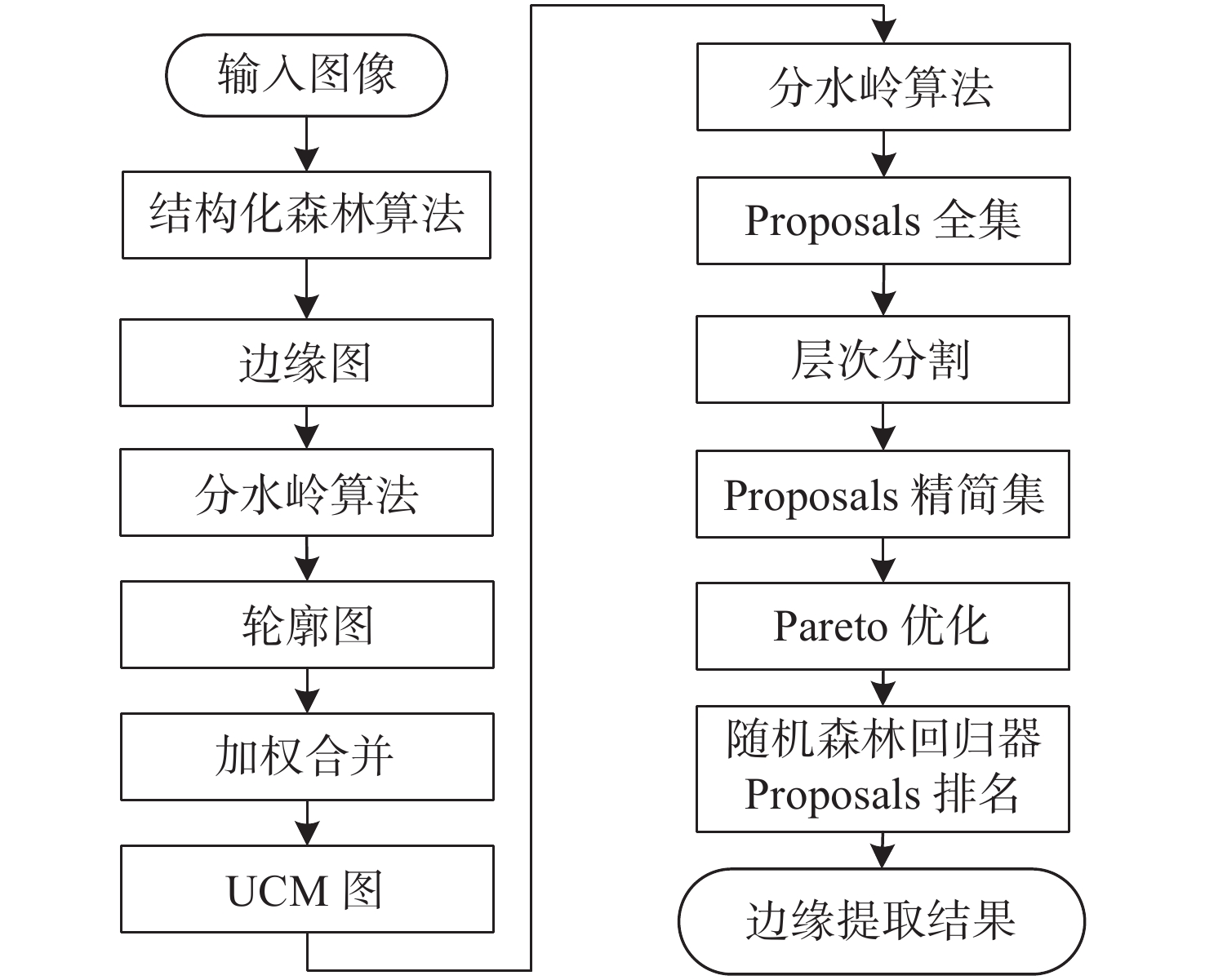
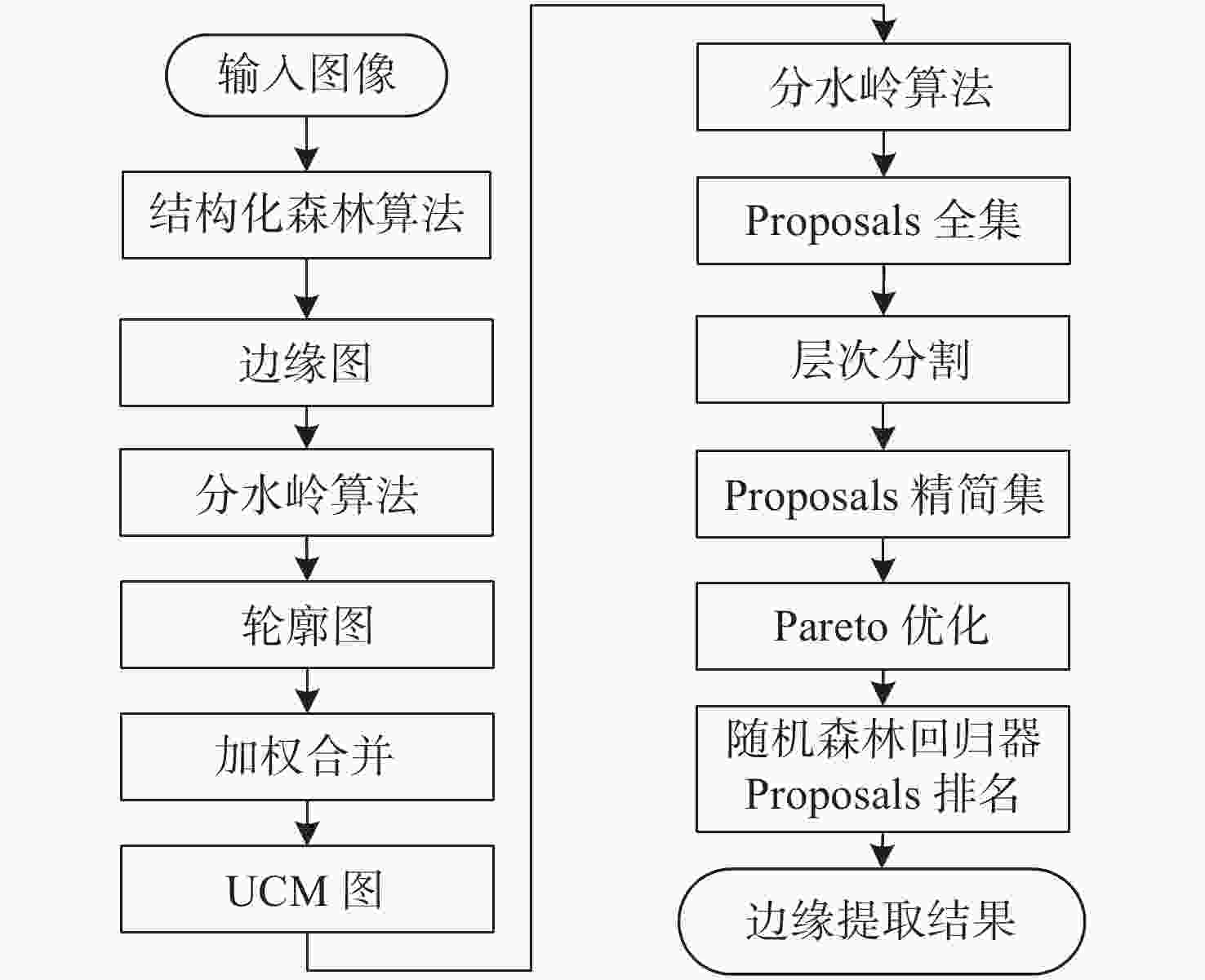
摘要: 为了识别空间目标的椭圆部件，提出了一种基于自适应光学图像的椭圆检测方法。首先，利用RL(Richardson-Lucy)方法对自适应光学图像进行复原，在此基础上，采用弧支撑线段(Arc-Support Line Segments, ASLS)方法对复原图像进行椭圆检测。针对ASLS算法使用的Canny边缘提取算法带来的“弧段过分割”和“语义信息差”等问题，提出了基于多尺度组合分组(Multiscale Combinatorial Grouping, MCG)边缘提取的解决方法。最后，针对ASLS算法使用优度指标等验证方法存在部分虚假椭圆的情况，综合利用多种几何指标进行约束，有效地消除了虚假椭圆。实验结果表明：椭圆中心点检测误差优于3 pixels，半长轴误差优于4 pixels，方向角误差优于3°。在重叠面积门限为0.65时，本文算法的准确率为85.7%、召回率为93.3%，F值指标为0.893，优于传统椭圆检测算法。
- 自适应光学图像 /
- 空间目标 /
- 椭圆部件检测 /
- 弧支撑线段 /
- 多尺度组合分组
Abstract: In order to identify the elliptical components of space target, an ellipse detection method based on adaptive optical image is proposed. Firstly, the RL(Richardson-Lucy) method is used to restore the adaptive optics image. Next, the Arc-Support Line Segments (ASLS) method is used to detect the ellipse of the restored image. To tackle the problems of “arc segment over segmentation” and “semantic information difference” caused by Canny edge extraction, an improved edge extraction algorithm based on Multiscale Combinatorial Grouping (MCG) is proposed. Finally, for some false ellipses produced by using verification methods such as goodness measurement, a variety of geometric constraint measurement are comprehensively used to effectively eliminate the false ellipse. The experimental results show that the detection error of ellipse center point, the semi-major axis error and the direction angle error are less than 3 pixels, 4 pixels and 3 degrees, respectively. When the overlap area threshold is 0.65, the accuracy rate of this algorithm is 85.7%, the recall rate is 93.3% and the F value is 0.893. Our method is better than the traditional ellipse detection algorithms.
- adaptive optical image /
- space target /
- elliptical part detection /
- arc-support segment /
- multiscale combinatorial grouping

HTML全文

图 1 MCG算法流程图

Figure 1. Flow chart of the MCG algorithm

下载: 全尺寸图片幻灯片

图 2 空间目标自适应光学原始和边缘图像

Figure 2. Adaptive optics original and edge images of space target

下载: 全尺寸图片幻灯片

图 3 椭圆参数定义

Figure 3. Definition of ellipse parameters

下载: 全尺寸图片幻灯片

图 4 改进ASLS算法流程

Figure 4. Flow chart of the improved ASLS algorithm

下载: 全尺寸图片幻灯片

图 5 两个弧支撑组生成候选椭圆

Figure 5. Candidate ellipse generated by two arc-support groups

下载: 全尺寸图片幻灯片

图 6 空间目标自适应光学复原图像边缘提取结果

Figure 6. Edge extraction results of adaptive optics restoration image of space targets

下载: 全尺寸图片幻灯片

图 7 空间目标自适应光学复原图像椭圆检测结果

Figure 7. Ellipse detection results of adaptive optics restored images of partial space targets

下载: 全尺寸图片幻灯片

图 8 重叠面积门限与检测指标关系

Figure 8. Relationship between overlapping area threshold and detection index

下载: 全尺寸图片幻灯片

表 1 仿真图像椭圆参数平均误差

Table 1. Average error of linear structure components for test

平均误差(像素)	中心 $ x $	中心 $ y $	方向角 $ \varphi $	半长轴 $ a $	半短轴 $ b $
ELSDc	40.10	37.81	47.26°	44.69	51.35
AAMD	2.84	10.13	10.33°	13.43	17.28
ASLS	2.57	5.08	2.11°	6.68	4.32
本文算法	1.73	2.14	2.27°	3.82	2.17

下载: 导出CSV

表 2 算法检测指标及平均耗时

Table 2. Average consumed times of those algorithms and the error detection rates

	ELSDc	AAMD	ASLS	本文算法
准确率(%)	28.6	51.7	69.1	85.7
召回率(%)	43.7	66.7	72.3	93.3
F值	0.466	0.641	0.707	0.893
平均耗时(s)	10.058	0.525	0.659	12.874

下载: 导出CSV

参考文献(24)

[1]	孙志伟, 刘伟奇, 吕博, 等. 大景深空间目标成像光学系统设计[J]. 液晶与显示,2021,36(11):1597-1604. doi: 10.37188/CJLCD.2021-0183 SUN ZH W, LIU W Q, LYU B, et al. Design of imaging optical system for space target with large depth of field[J]. Chinese Journal of Liquid Crystals and Displays, 2021, 36(11): 1597-1604. (in Chinese) doi: 10.37188/CJLCD.2021-0183
[2]	李正炜, 王建立, 吴元昊, 等. 基于单站地基望远镜的空间目标姿态估计方法[J]. 中国光学,2016,9(3):371-378. doi: 10.3788/CO.20160903.0371 LI ZH W, WANG J L, WU Y H, et al. Method of attitude estimation for space object based on single ground-based telescope[J]. Chinese Optics, 2016, 9(3): 371-378. (in Chinese) doi: 10.3788/CO.20160903.0371
[3]	张磊, 吴金灵, 刘仁虎, 等. 光学自由曲面自适应干涉检测研究新进展[J]. 中国光学,2021,14(2):227-244. doi: 10.37188/CO.2020-0126 ZHANG L, WU J L, LIU R H, et al. Research advances in adaptive interferometry for optical freeform surfaces[J]. Chinese Optics, 2021, 14(2): 227-244. (in Chinese) doi: 10.37188/CO.2020-0126
[4]	LU W, TAN J L. Detection of incomplete ellipse in images with strong noise by iterative randomized Hough transform (IRHT)[J]. Pattern Recognition, 2008, 41(4): 1268-1279. doi: 10.1016/j.patcog.2007.09.006
[5]	李娜, 王军, 董兴法, 等. 基于改进Hough变换的指针式仪表识别方法[J]. 液晶与显示,2021,36(8):1196-1203. doi: 10.37188/CJLCD.2020-0179 LI N, WANG J, DONG X F, et al. Pointer meter recognition method based on improved Hough transform[J]. Chinese Journal of Liquid Crystals and Displays, 2021, 36(8): 1196-1203. (in Chinese) doi: 10.37188/CJLCD.2020-0179
[6]	ARELLANO C, DAHYOT R. Robust ellipse detection with Gaussian mixture models[J]. Pattern Recognition, 2016, 58: 12-26. doi: 10.1016/j.patcog.2016.01.017
[7]	吴海滨, 魏喜盈, 刘美红, 等. 结合空洞卷积和迁移学习改进YOLOv4的X光安检危险品检测[J]. 中国光学,2021,14(6):1417-1425. doi: 10.37188/CO.2021-0078 WU H B, WEI X Y, LIU M H, et al. Improved YOLOv4 for dangerous goods detection in X-ray inspection combined with atrous convolution and transfer learning[J]. Chinese Optics, 2021, 14(6): 1417-1425. (in Chinese) doi: 10.37188/CO.2021-0078
[8]	YANG T, SRIHARI S N. Ellipse detection using sampling constraints[C]. Proceedings of the 2011 18th IEEE International Conference on Image Processing, IEEE, 2011: 1045-1048.
[9]	PĂTRĂUCEAN V, GURDJOS P, VON GIOI R G. Joint a Contrario ellipse and line detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(4): 788-802. doi: 10.1109/TPAMI.2016.2558150
[10]	CHEN S L, XIA R B, ZHAO J B, et al. A hybrid method for ellipse detection in industrial images[J]. Pattern Recognition, 2017, 68: 82-98. doi: 10.1016/j.patcog.2017.03.007
[11]	MENG C, LI ZH X, BAI X ZH, et al. Arc adjacency matrix-based fast ellipse detection[J]. IEEE Transactions on Image Processing, 2020, 29: 4406-4420. doi: 10.1109/TIP.2020.2967601
[12]	LU CH SH, XIA S Y, SHAO M, et al. Arc-support line segments revisited: an efficient high-quality ellipse detection[J]. IEEE Transactions on Image Processing, 2020, 29: 768-781. doi: 10.1109/TIP.2019.2934352
[13]	张帆, 韩树奎, 张立国, 等. Canny算法的GPU并行加速[J]. 中国光学,2017,10(6):737-743. doi: 10.3788/co.20171006.0737 ZHANG F, HAN SH K, ZHANG L G, et al. Parallel acceleration of Canny algorithm based on GPU[J]. Chinese Optics, 2017, 10(6): 737-743. (in Chinese) doi: 10.3788/co.20171006.0737
[14]	PONT-TUSET J, ARBELÁEZ P, BARRON J T, et al. Multiscale combinatorial grouping for image segmentation and object proposal generation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(1): 128-140. doi: 10.1109/TPAMI.2016.2537320
[15]	刘聪, 董文飞, 蒋克明, 等. 基于改进分水岭分割算法的致密荧光微滴识别[J]. 中国光学,2019,12(4):783-790. doi: 10.3788/co.20191204.0783 LIU C, DONG W F, JIANG K M, et al. Recognition of dense fluorescent droplets using an improved watershed segmentation algorithm[J]. Chinese Optics, 2019, 12(4): 783-790. (in Chinese) doi: 10.3788/co.20191204.0783
[16]	EVERINGHAM M, MULLER H, THOMAS B. Evaluating image segmentation algorithms using the Pareto front[C]. Proceedings of the 7th European Conference on Computer Vision, Springer, 2002: 34-48.
[17]	https://img2.baidu.com/it/u=1967449378,3214789687&fm=26&fmt=auto [OL].
[18]	赵云峰. 结合自适应核函数的Mean-shift改进算法[J]. 液晶与显示,2016,31(12):1143-1148. doi: 10.3788/YJYXS20163112.1143 ZHAO Y F. Improved mean-shift algorithm combined with adaptive kernel function[J]. Chinese Journal of Liquid Crystals and Displays, 2016, 31(12): 1143-1148. (in Chinese) doi: 10.3788/YJYXS20163112.1143
[19]	PRASAD D K, LEUNG M K H, QUEK C, et al. DEB: definite error bounded tangent estimator for digital curves[J]. IEEE Transactions on Image Processing, 2014, 23(10): 4297-4310. doi: 10.1109/TIP.2014.2346018
[20]	FISH D A, BRINICOMBE A M, PIKE E R, et al. Blind deconvolution by means of the Richardson-Lucy algorithm[J]. Journal of the Optical Society of America A, 1995, 12(1): 58-65. doi: 10.3969/j.issn.2095-1531.2011.05.017
[21]	http://www.astrospider.com/images/Lacrosse/051113_19stack.jpg [OL].
[22]	MATSON C L, BORELLI K, JEFFERIES S, et al. Fast and optimal multiframe blind deconvolution algorithm for high-resolution ground-based imaging of space objects[J]. Applied Optics, 2009, 48(1): A75-A92. doi: 10.1364/AO.48.000A75
[23]	https://gimg2.baidu.com/image_search/src=http%3A%2F%2Fwww.lunwenstudy.com%2Fuploads%2Fallimg%2F161014%2F14-161014104I5E7.png&refer=http%3A%2F%2Fwww.lunwenstudy.com&app=2002&size=f9999,10000&q=a80&n=0&g=0n&fmt=auto?sec=1652597051&t=c00e3ce939c8727f9f68d32e171e6747 [OL].
[24]	PĂTRĂUCEAN V, GURDJOS P, VON GIOI P G. A parameterless line segment and elliptical arc detector with enhanced ellipse fitting[C]. Proceedings of the 12th European Conference on Computer Vision, Springer, 2012: 572-585.