A new co-phasing detection technology of a segmented mirror based on broadband light
-
摘要:
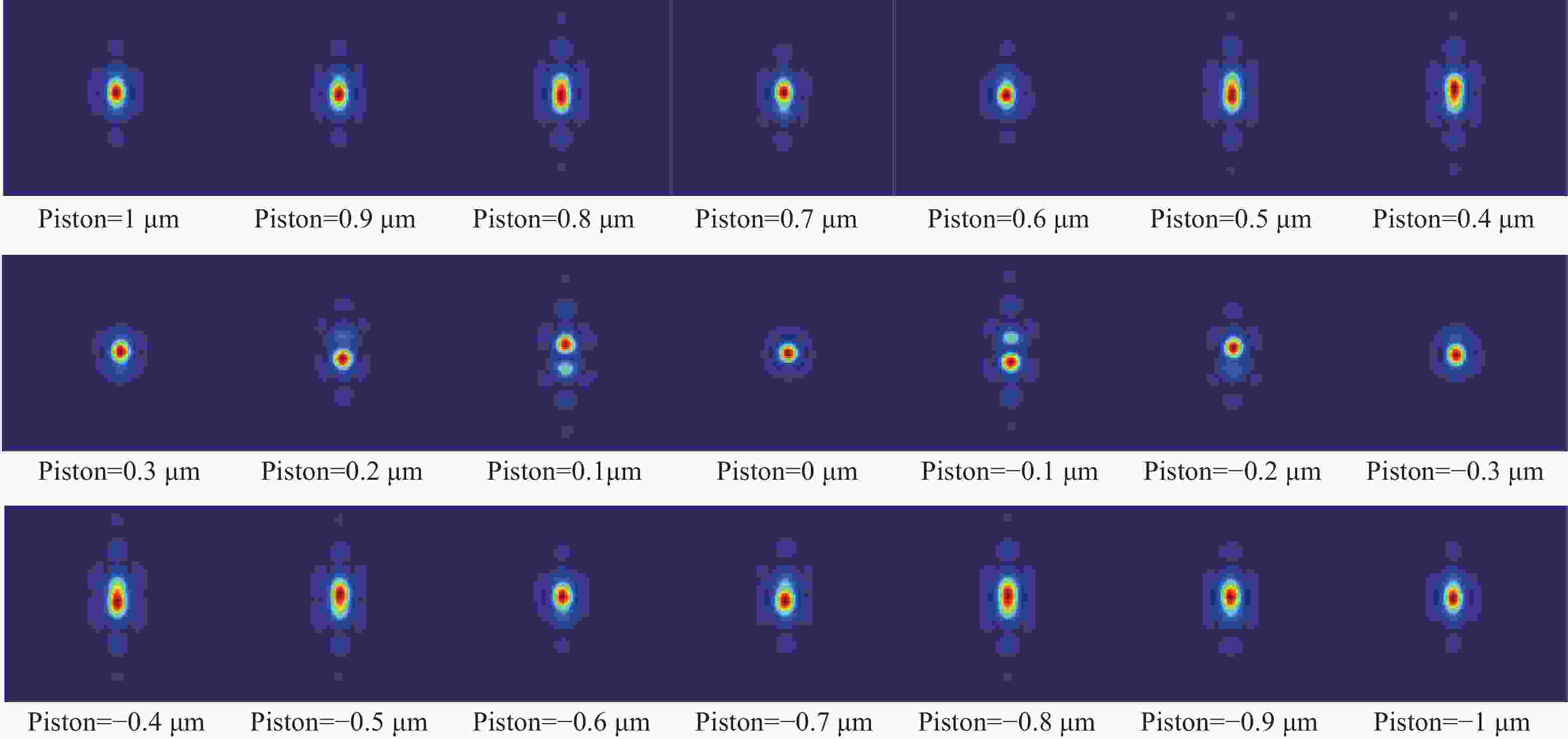
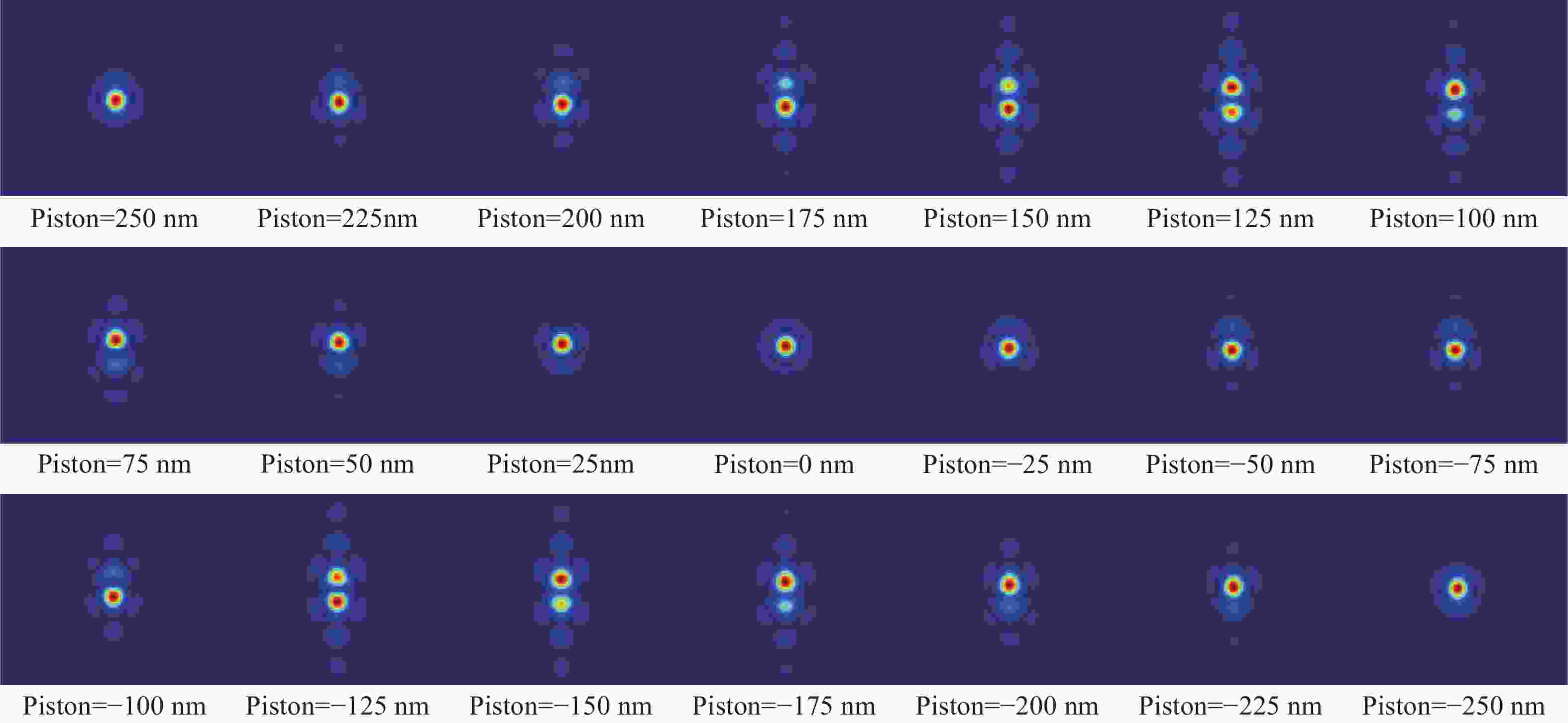
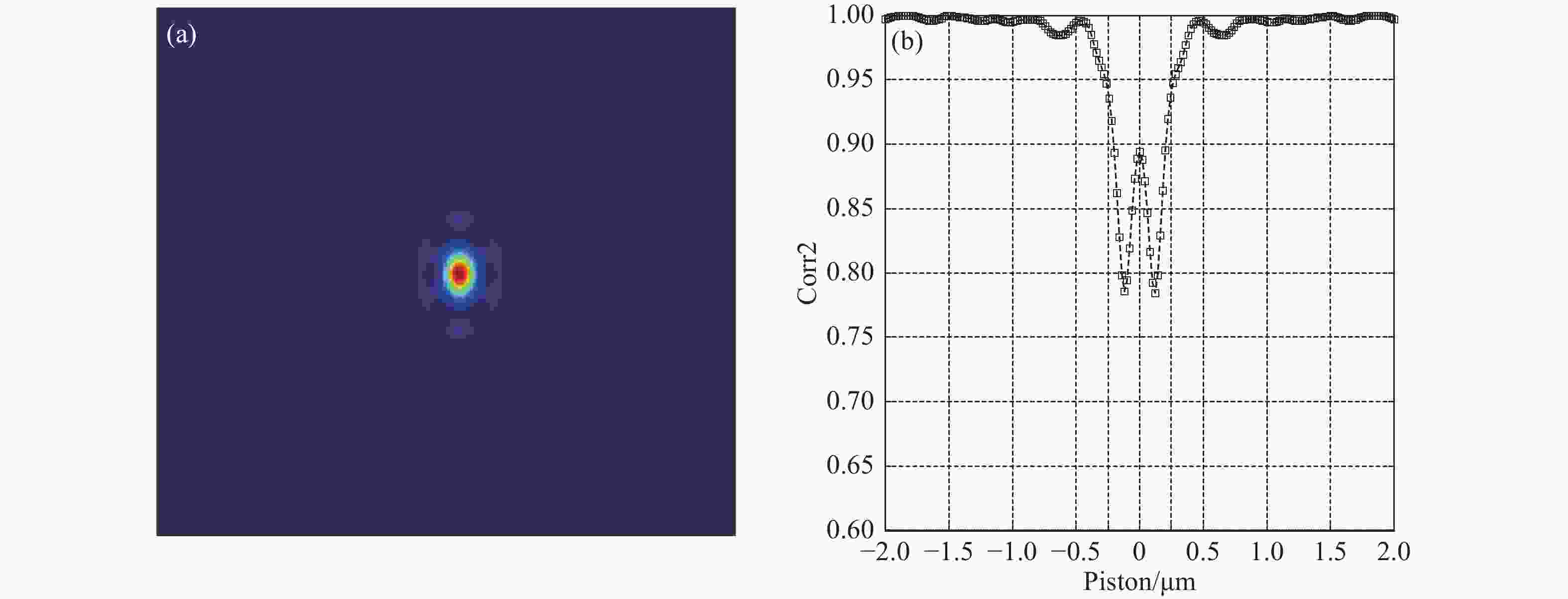
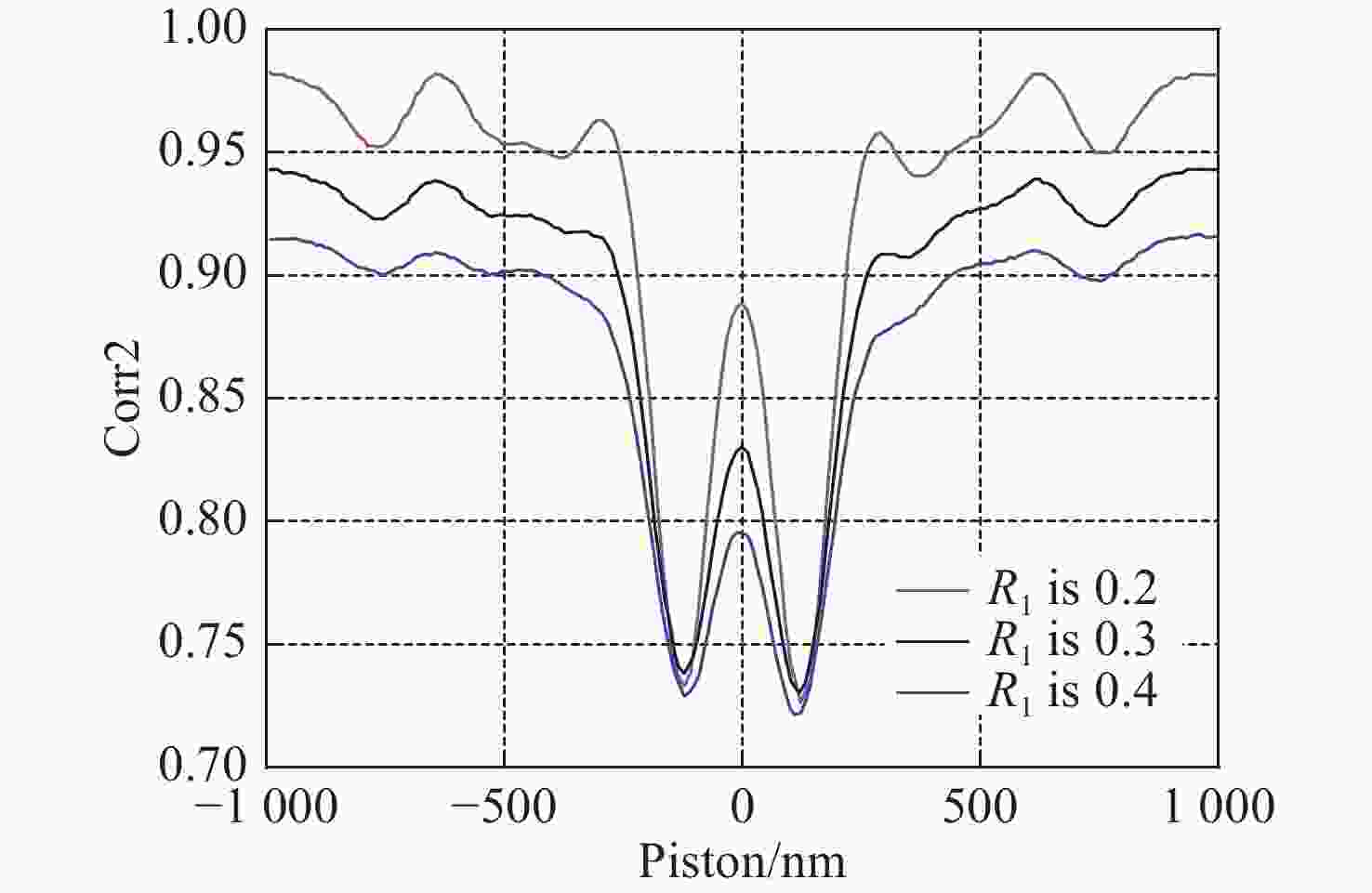
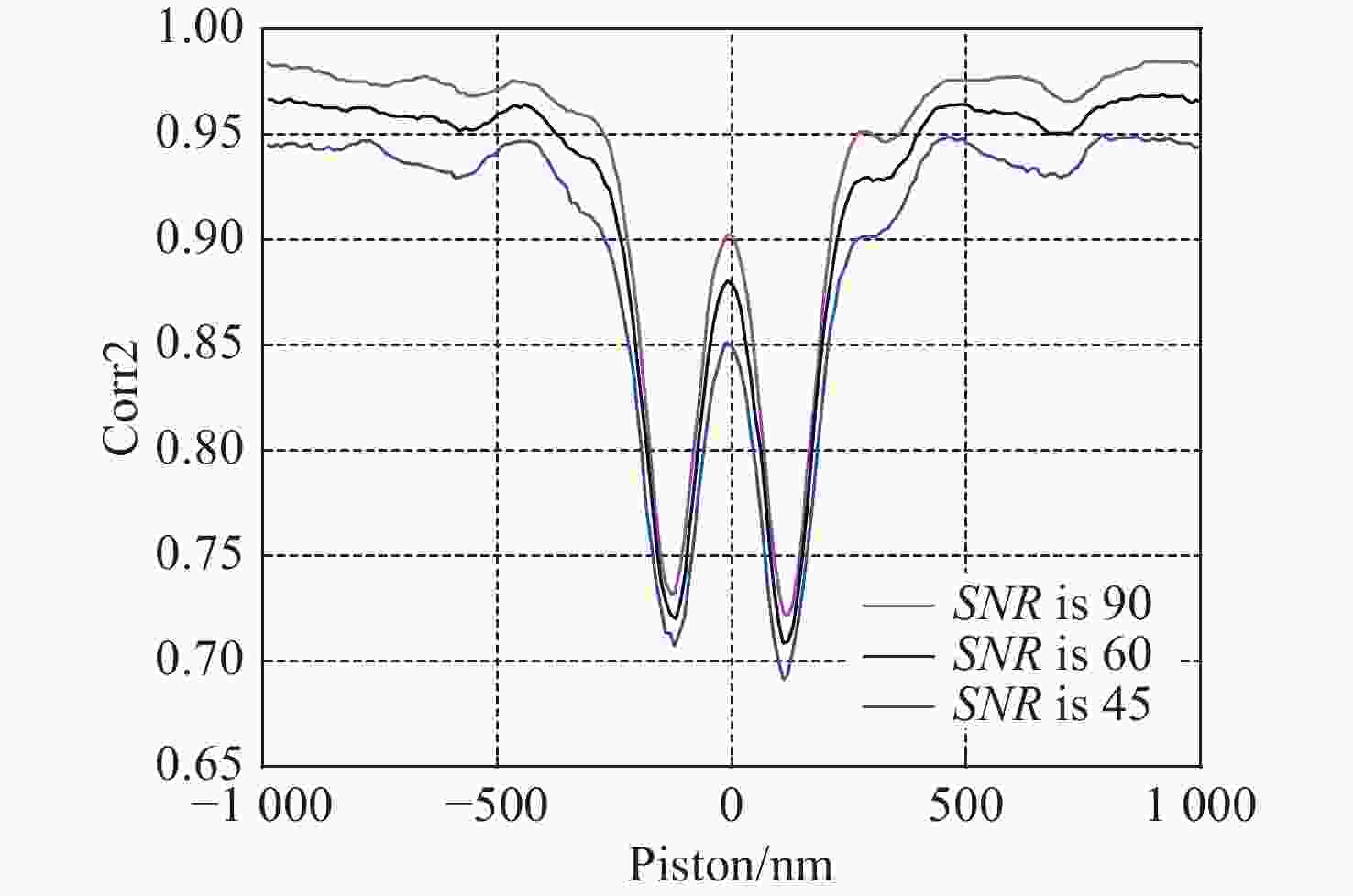
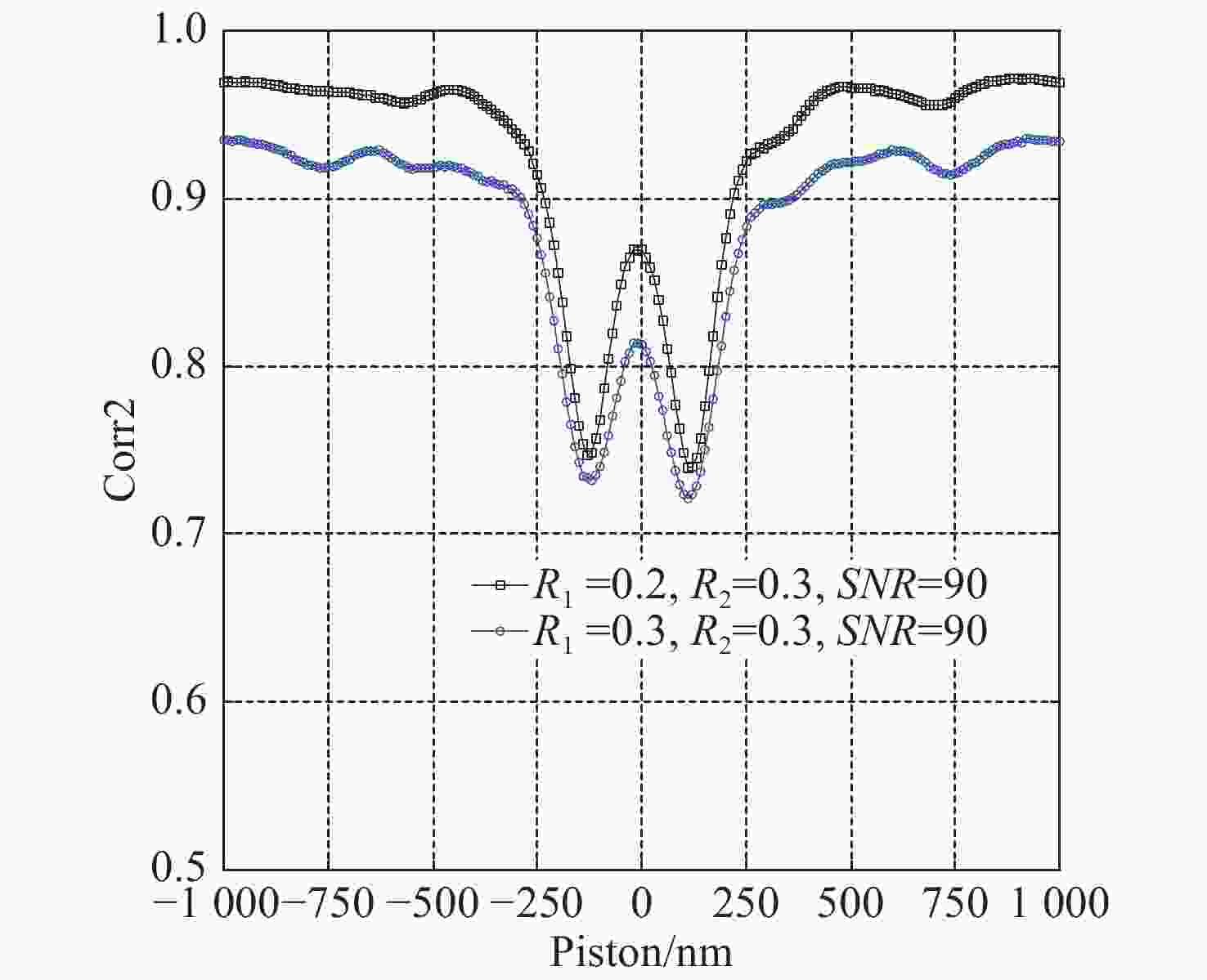
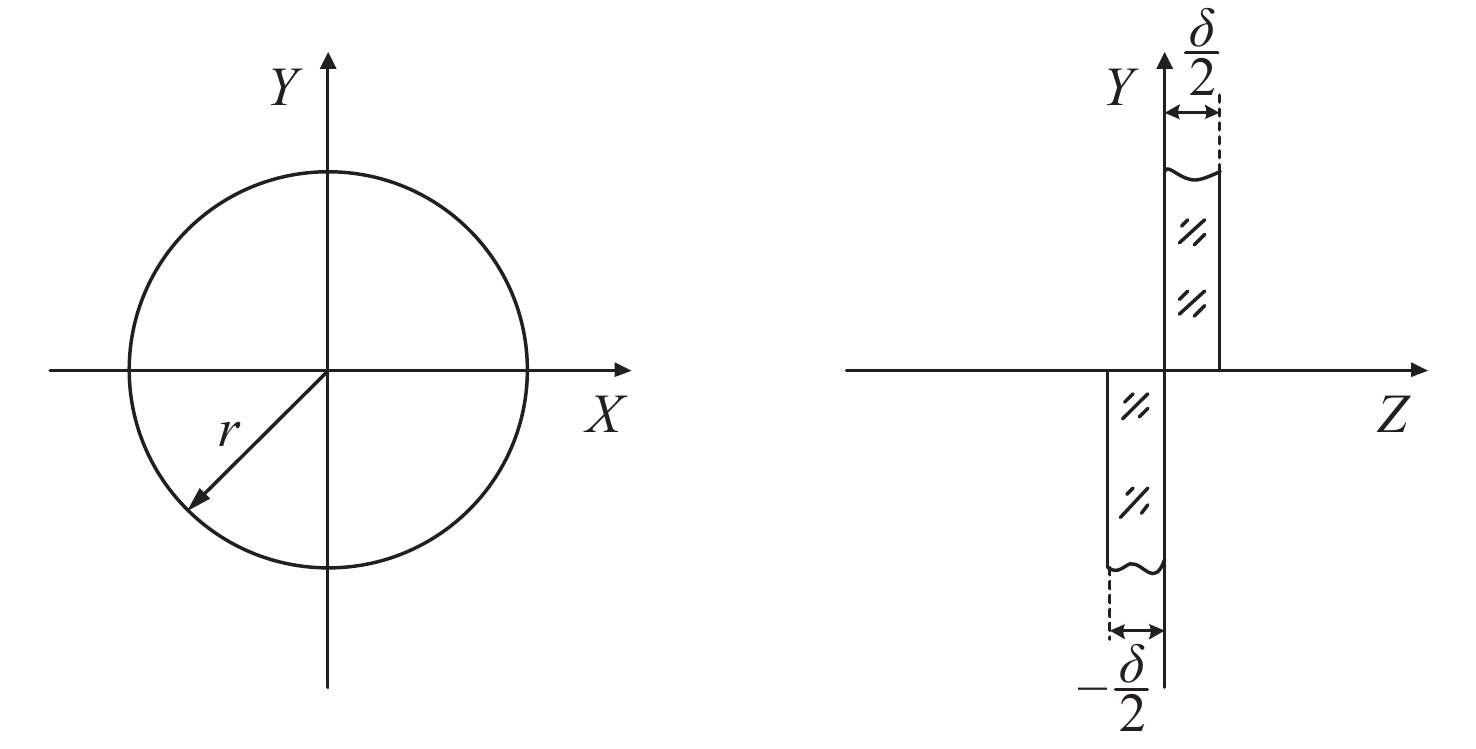
鉴于单块口径的光学望远镜不能无限增大，采用拼接镜技术才能造出10 m以上口径的光学望远镜，因此，拼接镜的共相检测技术成为了拼接过程和维持镜面质量的关键技术。针对目前最被接受的宽窄带夏克哈特曼法，本文提出使用宽波段（400~700 nm）光源的非相干性和相干性相结合方式实现250 nm粗共相，以及10 nm精共相，以此解决由于目标流量过低而引起测量时间过长的问题。即在粗共相时，以两个半圆孔的非相干衍射图样为模板，白光为光源，采用互相关算法计算互相关系数的值，通过设置合理的互相关系数阈值，以实现无限制的检测范围和0.25 μm 的检测精度；精共相时，以白光为光源、采用以一幅相干衍射图案（理想白光艾里斑）为模板的方式替代多幅不同平移误差下的相干衍射图案为模板方式，实现0.27 μm量程、0.01 μm以上精度的共相检测。对该共相方法进行了理论和仿真分析，结果表明：该新型共相检测方法的检测量程为无限量程，检测精度能达到 10 nm以上，该方法适用于拼接镜粗精共相的检测。
Abstract:Considering that the aperture of a monoblock telescope is limited in size, to build an aperture telescope that is greater than ten meters, the technology of segmented mirrors should be used. Therefore, the co-phasing detection technology of segmented mirrors has become the key technology in the segmented process and in maintaining the mirror quality. To solve the problem that the broadband method demands a long time consuming and the narrowband method has a small range in the most widely accepted broadband and narrowband shack Hartmann method, a new method is proposed combining the incoherent and coherent diffraction patterns of broadband light (400−700 nm) to realize coarse co-phasing of 250 nm precision and fine co-phasing of 10 nm precision. When a segmented mirror is coarse co-phasing, the incoherent diffraction pattern of two hale circular holes is used as a template and white light is used as the light source. The cross-correlation algorithm is used to calculate the value of cross-correlation coefficient, and then it can achieve the unlimited range and a detection precision of 0.25 μm by setting a reasonable threshold value for the cross-correlation coefficient. When segmented mirror is fine co-phasing, a disk pattern of white light instead of multiple coherent diffraction patterns with different piston errors is used as a template to achieve a range of 0.27 μm and a detection precision of 0.01 μm. The theoretical and simulation results show that the detection range is the range of actuator and the measurement accuracy is less than 10 nm. Both the theoretical analysis and simulation show that this method is suitable for the detection of a coarse and fine co-phasing of segmented mirror.
-
Key words:
- astronomical optics /
- telescopes /
- sub-aperture /
- phase measurement
-
1. 引 言
增大望远镜直径是获得更高分辨率的最有效途径，但是由于科学技术、制造成本、运输风险等因素，目前单块光学主镜的最大直径约为8.4 m。为了获取更大口径的望远镜，就需要采用其他方法，拼接镜技术应运而生。但为了保证拼接镜面的成像质量和望远镜的高分辨率，必须通过定量测量平移误差（piston）确定性调整拼接子镜。大口径望远镜拼接技术现已成为发达国家的重点研究课题，而实现拼接镜共相误差的高效率和高精度检测对于提高拼接镜的成像质量，促进拼接技术的发展具有重要的现实意义[1-7]。目前，检测拼接镜平移误差有很多种方法，如 PD法[8]、曲率传感器法[9-10]、夏克-哈特曼宽窄带法[11-14]、金字塔波前探测器法[15]、色散条纹传感器法[16]、色散瑞利干涉法[17]、双波长共相检测[18-20]、基于深度学习[21-22]等方法。但这些方法并不足够完善：如 PD 法耗时长，不适用于子镜过多的拼接镜检测；曲率传感器的检测量程小（为
$ \pm \lambda $ ）亦不适用于子镜过多的拼接镜检测；色散条纹干涉法存在相机靶面大和能量利用低的缺点，四棱锥波前探测器法的锥顶角加工难度大，存在$ 2{\text{π}} $ 模糊效应；双波长共相检测法存在能量利用率低、检测系统复杂的缺点；深度学习耗时长、鲁棒性差等。目前，应用最为广泛的共相检测技术为宽窄带夏克-哈特曼法。宽带夏克-哈特曼方法虽然有较大的检测量程，但在大量程检测时，所利用光能带宽很窄（10 nm 带宽），造成目标流量过低而使检测时间过长；且宽带夏克-哈特曼法检测精度较低。窄带夏克-哈特曼法检测精度高，但检测量程存在2π模糊现象，检测量程不能超过所检测准单色光的半个波长，且所利用光能带宽更窄（10 nm 带宽以下），也存在目标流量过低而使检测时间过长问题。并且，宽带检测方法需利用多幅不同平移误差下相干衍射图案（如 Keck 中宽波段光源检测中模板图案为 11 张）为模板，因而匹配时间长，且检测精度相对较低（30 nm 级）。基于此，本文提出一种新的拼接镜共相检测方法，即粗共相时，以 400~700 nm带宽白光为光源，基于两半圆孔的非相干衍射图案作为模板；精共相以白光为光源，以一幅相干衍射图案（白光艾里斑）代替多幅不同平移误差下的相干衍射图案为模板的新型共相检测方法。该方法目标流量大（300 nm 带宽），检测量程和时间均优于宽窄带夏克-哈特曼法，检测精度与宽窄带夏克-哈特曼法相当（10 nm 级），且检测系统可与宽窄带夏克-哈特曼法检测系统共用。
2. 基本原理
在拼接镜共相误差检测中，通过在拼接子镜间放置圆孔掩膜，并基于圆孔的夫朗和费衍射原理，通过放置圆孔的夫朗和费衍射图案随平移变化来计算两子镜间的平移误差。圆孔检测原理如图1所示，以圆孔的圆心为坐标原点，圆孔所在平面作为X-Y平面，圆孔的法线方向为Z轴建立坐标系，圆孔半径为 r ，平面Y=0将圆孔均分为上下两部分，X轴上半部分圆孔的平移误差为
$ \delta /2 $ ；X轴下半部分平移误差为$ - \delta /2 $ 。由图1可知：上下半圆孔的距离为$ \delta $ ，则波前的光程差为$ 2\delta $ 。
图 1 放置在子镜间的圆孔示意图Figure 1. Schematic diagram of circular hole placed between sub-mirrors假设光源为理想单色光，波长为
$ \lambda $ ，则像平面的强度为[23-24]：I(w,kδ)=f2(w,kδ)=[f(ρ,0)cos(kδ)+f(ρ,π/2)sin(kδ)]2, (1) 其中：
$k = {{2{\text{π}} } \mathord{\left/ {\vphantom {{2{\text{π}} } \lambda }} \right. } \lambda }$ ，$ {\boldsymbol{\rho }} $ 为孔平面极坐标，用$ (\rho ,\theta ) $ 表示；$ {\boldsymbol{w}} $ 为像平面极坐标,用$ (w,\psi ) $ 表示；$ (x,y) $ 为孔平面坐标，$ (\xi ,\eta ) $ 为像平面坐标。孔径平面的复振幅函数为$ f({\boldsymbol{\rho }},k\delta ) $ 。当光源是中心波长为
$ \lambda $ 、带宽为$ \Delta \lambda $ 的光源时，则该光源的相干长度$l={\lambda }^{2}/(2\cdot\Delta \lambda )$ ，且不满足${\lambda ^2}/\Delta \lambda \ll 1$ 时，此时$\Delta k= - \dfrac{{2{\text{π}} \Delta \lambda }}{{{\lambda ^2}}}$ 的值不能忽略，即$ \Delta k $ 对公式(1)中的三角函数值有很大影响。现假设
$ k $ 服从高斯分布，则：f(k)=1√2πσ2kexp[−(k−k0)22σ2k]. (2) 假设
$ \Delta k $ 是公式(2)的半波带宽，则可求出$ \Delta k = \sqrt {8\ln (2)} {\sigma _k} $ ，由于$\Delta \lambda \approx \dfrac{{2{\text{π}} \Delta k}}{{{k^2}}}$ ，根据$l = \dfrac{{{\lambda ^2}}}{{2\Delta \lambda }}$ 可得：l=π/Δk⇒σk=π√8ln21l=1.33l. (3) 把公式(2)带入公式(1)得[17]：
I(w,kδ)=α1f2(w;0)+α2f(w;0)f(w;π2)+α3f2(w;π2), (4) 其中：
${\alpha _1} = \dfrac{1}{2}\left[ {1 + \exp ( - 2\sigma _k^2{\delta ^2})\cos 2{k_0}\delta } \right],$ ${\alpha _2} = \exp ( - 2 \sigma _k^2{\delta ^2})\sin 2{k_0}\delta ,$ ${\alpha _3} = \dfrac{1}{2}\left[ {1 - \exp ( - 2\sigma _k^2{\delta ^2})\cos 2{k_0}\delta } \right].$ 由以上分析可知：宽窄带检测法分别是从公式(1)中的三角函数和公式(4)中的系数
${\alpha _1}, {\alpha _2}, {\alpha _3}$ 中提取相位信息。图2（彩图见期刊电子版）为在 400~700 nm 波段，不同平移误差下的两半圆孔衍射图案，此时该波段光源的相干长度值为l=0.552/(2×0.3)=0.504 µm。从图中可知：当平移误差在相干长度以内时，即在（−0.252 μm, 0.252 μm）以内时，衍射图案呈现相干性；当平移误差值在相干长度以外时，即平移>0.252 μm 或平移< −0.252 μm 时，衍射图案呈现非相干性。
图 2 在400~700 nm带宽下，平移误差从1 μm到−1 μm变化时的理论圆孔衍射图Figure 2. Theoretical circular diffraction patterns when piston error is varying from 1 μm to −1 μm at 400−700 nm bandwidth图3（彩图见期刊电子版）为平移误差在400~700 nm波段相干长度内的衍射图案，即平移误差从250 nm变化到−250 nm，21张两半圆孔衍射图案。从图中可以知：当平移误差在
$( - l/2, l/2)$ 以内时，衍射图案呈现相干性，且相干图案出现了重复，但白光理想艾里斑没有出现重复。
图 3 在400~700 nm带宽下，平移误差从250 nm到−250 nm变化时的理论圆孔衍射图Figure 3. Theoretical circular diffraction patterns when piston error is varying from 250 nm to −250 nm at 400−700 nm bandwidth3. 仿真分析
3.1 图像对比算法选取
通过理论仿真分析可知：在 400~700 nm 波段下，当拼接镜平移误差绝对值大于
$ l/2 $ 时，衍射图案呈现非相干性；当平移误差绝对值小于$ l/2 $ 时，衍射图案呈现相干性，虽然相干图案会重复出现，但白光理想艾里斑图案只出现了一次。因此，在平移误差的绝对值大于$ l/2 $ 时，可利用圆孔衍射图案非相干性来解算平移误差，当其绝对值小于$ l/2 $ 时，利用相干圆孔图案只出现一次白光理想艾里斑圆孔的性质来解算子镜平移误差。由于灰度匹配算法具有较好的精度和鲁棒性，且抗噪性能强，算法简单。因此选用基于灰度匹配算法来计算实时图与模板图案的相干性，通过两图案的互相关系数值的大小判别两图案相似程度，其公式如下：
Corr2=∑i∈N(xi−¯x)(yi−¯y)√∑i∈N(xi−¯x)2∑i∈N(yi−¯y)2, (5) 其中：
${\rm{Corr}}2$ 为互相关系数，$N$ 为图案像素点总数，$ {x_i} $ 为实时图案在$ i $ 点灰度值，$ \overline x $ 为实时图案灰度平均值，$ {y_i} $ 为模板图案在$ i $ 点的灰度值，$ \overline y $ 为模板图案灰度平均值。3.2 新型共相算法的仿真分析
由第二章分析可知：当平移误差绝对值大于
$ l/2 $ 时，衍射图案呈现非相干性，当平移误差绝对值小于$ l/2 $ 时，衍射图案呈现相干性。在实际平移误差检测时，可利用该性质求解，即选用两半圆孔的非相干衍射图案为模板，利用基于灰度匹配算法计算拼接子镜间两半圆孔衍射图案与模板图案之间的互相关系值；而当两子镜间的平移误差绝对值大于$ l/2 $ 时，衍射图案与模板图案的互相关系数值接近1，而当两子镜间的平移误差绝对值小于$ l/2 $ 时，子镜间的两半圆孔衍射图案呈现相干性，使得子镜间的两半圆孔衍射图案与模板图案的互相关系数值大幅下降。因此，可设定互相关系数的阈值，该阈值需小于平移误差为$ l/2 $ 时的互相关系数。当计算所得互相关系数小于该阈值时，圆孔衍射图案已经相干，即表明平移误差在一个相干长度以内，而此时只存在唯一的白光理想艾里斑。因此，采用白光理想艾里斑作为模板，以白光相干长度为量程，将检测精度设为步长，并利用互相关算法计算相邻子镜间圆孔衍射图案与模板图案之间的互相关系数。其中互相关系数对应的最大值平移误差为拼接镜平移误差值。以20 nm为步长，两圆孔平移误差扫描区间为（−2 μm，2 μm），可得到互相关系数仿真曲线，如图4（彩图见期刊电子版）所示。其中平移误差大于可见光相干长度时的模板图案为非相干圆孔衍射图案。从图4（b）中可知：当平移误差绝对值大于
$ l/2 $ 时，互相关系数值都大于0.95，而当平移误差绝对值小于$ l/2 $ 时，互相关系数值大幅下降，且所有的值都小于0. 95，因此设定阈值为0.9来判定平移误差的绝对值是否小于$ l/2 $ 。
图 4 平移误差大于可见光相干长度时的（a）模板图案和（b）互相关系数Corr2随拼接镜平移误差变化关系图Figure 4. (a) Template pattern and (b) Corr2 as a function of piston errors when piston error is greater than visible coherence length选用理想的圆孔艾里斑远场图案为模板图案，以 5 nm 为步长，圆孔平移误差扫描区间为（−250 nm，250 nm），可得到图5（彩图见期刊电子版）。从图5可知：在平移误差的绝对值小于
$ l/2 $ ，以及在平移误差为零时，所对应的互相关系数最大，即在实际检测中，以检测精度为步长，以相干长度为量程，扫描一圈，找到互相关系数最大值点，从而求出平移误差，检测精度为 10 nm。
图 5 平移误差在可见光相干长度以内时的（a）模板图案和（b）互相关系数Corr2随拼接镜平移误差变化关系图Figure 5. (a) Template pattern and (b) Corr2 as a function of piston errors when piston error is within the coherence length of visible light从图4和图5的仿真分析可知：该共相算法的检测量程为无限大，理论检测精度为10 nm以上，检测带宽为 300 nm。在实际检测平移误差时，首先需解耦平移误差与倾斜（tip/tilt）误差并实时对倾斜误差调节，而倾斜误差的检测方法与平移误差解耦过程以及控制方法都在文献[13−14]中有详细介绍。采用该新型共相检测方法检测平移误差时，选用400~700 nm波段光作为光源，选用该波段下的非相干两半圆孔衍射图案为模板，设定0.9为互相关系数的阈值，并以20 nm为步长进行扫描，当互相关系数的值小于0.9时，停止扫描。此时平移误差在相干长度以内，切换扫描模式。以白光理想艾里斑为模板，将白光的相干长度作为量程，检测精度作为步长进行扫描，即求得互相关系数最大值时对应的平移误差。该对应平移误差值，即为实际平移误差。
4. 误差分析
由于圆孔掩模与两拼接子镜间无法达到中心绝对对准，实际拼接镜工作时，就会产生一定的偏差；两拼接子镜需预留一定的间隙以防止因温度变化而使拼接子镜间相互挤压；而且拼接镜工作时探测光强会因相机产生的噪声起伏变化，这些误差都会对最终结果造成影响。因此，对拼接镜进行共相检测时还需要分析间隙误差、偏心误差和相机噪声的影响。
4.1 间隙误差对间隙精度影响分析
当在Y方向圆孔衍射存在0.2r的间隙误差时，此时该圆孔的孔径函数为：
t(x,y) = \left\{ \begin{gathered} 1,{x^2} + {y^2} \leqslant {r^2},y \geqslant 0.2r \\ {{\rm{e}}^{{\rm{j}}2k\delta }},{x^2} + {y^2} \leqslant {r^2},y \leqslant - 0.2r \\ 0,{x^2} + {y^2} > {r^2} \\ \end{gathered} \right.\quad. (6) 根据傅立叶光学理论，对间隙误差下的孔径函数进行傅立叶变换即可得到该处振幅函数，对振幅函数求平方可求得光强函数
$ I(x,y) $ ：I(x,y) = {U^2}(x,y) = \frac{1}{{{\lambda ^2}{\textit{z}^2}}}{(\wp t(x,y))^2}\quad, (7) 其中，
$\wp $ 的表示对函数t(x, y)进行傅立叶变换。由以上两式可依次求出在不同偏心距下的振幅，以及该偏心距下的光强。现定义：
{R}_1\text=\frac{{\varDelta }_{{\rm{space}}}}{{r}}\quad, 其中，r为圆孔半径，
${\varDelta }_{{\rm{space}}}$ 与r成正比例关系。如图6（彩图见期刊电子版）所示，互相关系数Corr2的值随着R1值的变大而减小。从图6（彩图见期刊电子版）可知：当互相关系数Corr2=0.9，R1分别为0.2、0.3时，对应的平移误差分别为220 nm和250 nm，均在相干长度±0.25 μm内；而当R1=0.4，互相关系数Corr2=0.9时，对应的平移误差为400 nm，大于相干长度，此时不能用本文方法检测。因此，使用本文方法检测时，间隙误差R1需小于0.3。
图 6 R1分别为0.2、0.3、0.4时，互相关系数Corr2值与平移误差关系图Figure 6. Corr2 as a function of piston errors when R1 is 0.2, 0.3 and 0.44.2 圆孔偏心误差对检测精度的影响分析
当圆孔衍射在Y方向存在0.2r偏心误差时，此时该圆孔的孔径函数为：
t(x,y) = \left\{ \begin{gathered} 1,{x^2} + {y^2} \leqslant {r^2},y \geqslant 0.2r \\ {{\rm{e}}^{{\rm{j}}2k\delta }},{x^2} + {y^2} \leqslant {r^2},y \leqslant 0.2r \\ 0,{x^2} + {y^2} > {r^2} \\ \end{gathered} \right.\quad. (8) 则圆孔下的振幅函数
$ U(x,y) $ 为：U(x,y) = \frac{1}{{{\rm{j}}\lambda \textit{z}}}\exp ({\rm{j}}k\textit{z}) \cdot \exp\left[{\rm{j}}\frac{k}{{2\textit{z}}}({x^2} + {y^2})\right] \cdot \wp t(x,y)\quad, (9) 其中：
\begin{split} \wp t(x,y) =& \iint\limits_\infty {t(x,y)\exp ( - {\rm{j}}2k[({f_x}x + {f_y}y)])}{\rm{d}}x{\rm{d}}y = \\ &\iint\limits_{\begin{subarray}{l} {x^2} + {y^2} \leqslant {r^2} \\ y \geqslant 0.2r \end{subarray} } {\exp [} - {\rm{j}}2k[({f_x}x +{f_y}y)]{\rm{d}}x{\rm{d}}y +\\ &\iint\limits_{\begin{subarray}{l} {x^2} + {y^2} \leqslant {r^2} \\ y < 0.2r \end{subarray}} {\exp [} - {\rm{j}}2k[({f_x}x + {f_y}y) + {\rm{j}}2k\delta ]{\rm{d}}x{\rm{d}}y , \\ \end{split} (10) 其中：
${f_x} = \dfrac{x}{{\lambda \textit{z}}},{f_y} = \dfrac{y}{{\lambda \textit{z}}}$ ，(x, y) 为圆孔的平面坐标。又：
\begin{split} &\iint\limits_{\begin{subarray}{l} {x^2} + {y^2} \leqslant {r^2} \\ y \geqslant 0.2r \end{subarray} } {\exp [} - {\rm{j}}2k[({f_x}x + {f_y}y)]{\rm{d}}x{\rm{d}}y = \\ &\frac{1}{{{\rm{j}}2k{f_y}}}\int\limits_{ - \tfrac{{2\sqrt 6 }}{5}r}^{\tfrac{{2\sqrt 6 }}{5}r} {[\exp } ( - {\rm{j}}2k{f_x}x)(\exp ( - {\rm{j}}2k{f_y}r/10) -\\ &\exp ( - {\rm{j}}2k{f_y}\sqrt {{r^2} - {x^2}} )]{\rm{d}}x \quad, \\ \end{split} (11) 同理可得：
\begin{split} &\iint\limits_{\begin{subarray}{l} {x^2} + {y^2} \leqslant {r^2} \\ y < 0.2r \end{subarray} } {\exp [} - {\rm{j}}2k[({f_x}x + {f_y}y) + {\rm{j}}2k\delta ]{\rm{d}}x{\rm{d}}y =\\ &\frac{{{{\rm{e}}^{{\rm{j}}2k\delta }}}}{{{\rm{j}}2k{f_x}}}\int\limits_{ - r}^{0.2r} {[\exp ( - {\rm{j}}2k{f_y}} y)(\exp({\rm{j}}2k{f_x}\sqrt {{r^2} - {y^2}} ) -\\ &\exp( - {\rm{j}}2k{f_x}\sqrt {{r^2} - {y^2}} ))]{\rm{d}}y \quad, \\ \end{split} (12) 则当存在偏心误差时，光强计算公式同式(7)。
现定义：
{R}_2\text=\frac{{\varDelta }_{{\rm{eccentric}}}}{{r}} \quad, 其中，
${\varDelta }_{{\rm{eccentric}}}$ 与r成正比例关系如图7（彩图见期刊电子版）所示，随着R2值的变大，互相关系数Corr2最小值整体递增。从图7可知：在互相关系数Corr2=0.9，R2分别为0.3、0.4时，平移误差都在相干长度±0.25 μm内；而当 R2=0.5时，互相关系数Corr2值均大于0.9，此时，无法获得圆孔衍射的相干图案，因此偏心误差值R2需小于0.4。
图 7 R2分别为0.3、0.4、0.5时，互相关系数Corr2值与平移误差关系图Figure 7. Corr2 as a function of piston errors when R2 is 0.3, 0.4 and 0.54.3 相机噪声对检测精度的影响分析
现定义SNR为：
S NR=\frac{{I}_{\max}-{I}_{{\rm{ave}}}}{\delta } \quad, (13) 其中：
${I_{\max}}$ 为信号光强峰值，${I}_{{\rm{ave}}}$ 为噪声均值，δ为标准差。如图8（彩图见期刊电子版）所示，随着SNR的变差，互相关系数Corr2整体递减。从图8可知：在互相关系数Corr2=0.9，SNR分别为90、60时，平移误差分别为 210 nm 和 220 nm，都在相干长度±0.25 μm内。而当R2=45时，平移误差为270 nm, 在相干长度±0.25 μm以外。因此噪声误差值 SNR 需大于60。
图 8 SNR分别为45、60、90时，互相关系数Corr2值与平移误差关系图Figure 8. Corr2 as a function of piston errors when SNR is 45, 60 and 904.4 同时存在多种误差检测精度的影响分析
在实际检测平移误差时，偏心误差、间隙误差和相机噪声等误差往往是同时存在的，因此，需分析存在多种误差时对检测精度的影响。如图9所示：在R2=0.3，SNR=90 时，互相关系数Corr2随着R1的增大而减小。由图9可知：在R1=0.2, R2=0.3，SNR=90 时，互相关系数Corr2为0.9时，平移误差为230 nm和−220 nm，都在相干长度±0.25 μm内。而当R1=0.3，R2=0.3，SNR=90时，平移误差为−290 nm和300 nm, 在相干长度±0.25 μm以外。因此，R1≤0.2，R2≤0.3，SNR≥90。
图 9 R1=0.2，R2=0.3，SNR=90和R1=0.3，R2=0.3，SNR=90时，互相关系数Corr2值与平移误差关系图Figure 9. Corr2 as a function of piston errors when R1=0.2, R2=0.3, SNR=90 and R1=0.3, R2=0.3, SNR=905. 结 论
本文针对所提的新型共相算法，理论分析了该新型共相检测的方法的合理性。通过仿真验证该新型共相算法性能，仿真中，实现了从微米级到10 nm级误差范围内的平移误差检测，同时利用理论和仿真分析了该新型共相算法中间隙误差、偏心误差以及噪声误差对检测精度和结果的影响，得到了该新型共相算法中的间隙误差R1值小于0.2、偏心误差R2值小于0.3以及噪声误差SNR值大于90时不会出现误检测。理论和仿真分析结果表明：该新型共相检测方法适合于拼接镜间共相的调节，且量程大、精度高、能量利用率高。
-
图 1 放置在子镜间的圆孔示意图
Figure 1. Schematic diagram of circular hole placed between sub-mirrors
图 2 在400~700 nm带宽下，平移误差从1 μm到−1 μm变化时的理论圆孔衍射图
Figure 2. Theoretical circular diffraction patterns when piston error is varying from 1 μm to −1 μm at 400−700 nm bandwidth
图 3 在400~700 nm带宽下，平移误差从250 nm到−250 nm变化时的理论圆孔衍射图
Figure 3. Theoretical circular diffraction patterns when piston error is varying from 250 nm to −250 nm at 400−700 nm bandwidth
图 4 平移误差大于可见光相干长度时的（a）模板图案和（b）互相关系数Corr2随拼接镜平移误差变化关系图
Figure 4. (a) Template pattern and (b) Corr2 as a function of piston errors when piston error is greater than visible coherence length
图 5 平移误差在可见光相干长度以内时的（a）模板图案和（b）互相关系数Corr2随拼接镜平移误差变化关系图
Figure 5. (a) Template pattern and (b) Corr2 as a function of piston errors when piston error is within the coherence length of visible light
图 6 R1分别为0.2、0.3、0.4时，互相关系数Corr2值与平移误差关系图
Figure 6. Corr2 as a function of piston errors when R1 is 0.2, 0.3 and 0.4
图 7 R2分别为0.3、0.4、0.5时，互相关系数Corr2值与平移误差关系图
Figure 7. Corr2 as a function of piston errors when R2 is 0.3, 0.4 and 0.5
图 8 SNR分别为45、60、90时，互相关系数Corr2值与平移误差关系图
Figure 8. Corr2 as a function of piston errors when SNR is 45, 60 and 90
-
[1] CHANAN G, TROY M. Strehl ratio and modulation transfer function for segmented mirror telescopes as functions of segment phase error[J]. Applied Optics, 1999, 38(31): 6642-6647. doi: 10.1364/AO.38.006642 [2] 徐抒岩, 张旭升, 范阔, 等. 大型光学系统波前检测中气流扰动的抑制[J]. 光学 精密工程,2020,28(1):80-89. doi: 10.3788/OPE.20202801.0080XU SH Y, ZHANG X SH, FAN K, et al. Suppression of airflow turbulence in wavefront measurement for large-aperture optical systems[J]. Optics and Precision Engineering, 2020, 28(1): 80-89. (in Chinese) doi: 10.3788/OPE.20202801.0080 [3] 范文强, 王志臣, 陈宝刚, 等. 地基大口径拼接镜面主动控制技术综述[J]. 中国光学,2020,13(6):1194-1208. doi: 10.37188/CO.2020-0032FAN W Q, WANG ZH C, CHEN B G, et al. Review of the active control technology of large aperture ground telescopes with segmented mirrors[J]. Chinese Optics, 2020, 13(6): 1194-1208. (in Chinese) doi: 10.37188/CO.2020-0032 [4] 周程灏, 王治乐, 朱峰. 大口径光学合成孔径成像技术发展现状[J]. 中国光学,2017,10(1):25-38. doi: 10.3788/co.20171001.0025ZHOU CH H, WANG ZH L, ZHU F. Review on optical synthetic aperture imaging technique[J]. Chinese Optics, 2017, 10(1): 25-38. (in Chinese) doi: 10.3788/co.20171001.0025 [5] 王丰璞, 李新南, 徐晨, 等. 大型光学红外望远镜拼接非球面子镜反衍补偿检测光路设计[J]. 中国光学,2021,14(5):1184-1193. doi: 10.37188/CO.2020-0218WANG F P, LI X N, XU CH, et al. Optical testing path design for LOT aspheric segmented mirrors with reflective-diffractive compensation[J]. Chinese Optics, 2021, 14(5): 1184-1193. (in Chinese) doi: 10.37188/CO.2020-0218 [6] 管雯璐, 谭逢富, 靖旭, 等. 基于环境温度反馈的卡塞格林望远镜自动调焦[J]. 光学 精密工程,2021,29(8):1832-1838. doi: 10.37188/OPE.20212908.1832GUAN W L, TAN F F, JING X, et al. Automatic focusing of Cassegrain telescope based on environmental temperature feedback[J]. Optics and Precision Engineering, 2021, 29(8): 1832-1838. (in Chinese) doi: 10.37188/OPE.20212908.1832 [7] 顾伯忠, 陈萌, 乐中宇. 大型望远镜主镜室碳纤维桁架单元的优化[J]. 光学 精密工程,2021,29(9):2116-2125. doi: 10.37188/OPE.20212909.2116GU B ZH, CHEN M, YUE ZH Y. Optimization of carbon fiber truss element for primary mirror chamber of large telescope[J]. Optics and Precision Engineering, 2021, 29(9): 2116-2125. (in Chinese) doi: 10.37188/OPE.20212909.2116 [8] ZHANG D, ZHANG X B, XU SH Y, et al. Simplified phase diversity algorithm based on a first-order Taylor expansion[J]. Applied Optics, 2016, 55(28): 7872-7877. doi: 10.1364/AO.55.007872 [9] ORLOV V G, CUEVAS S, GARFIAS F, et al. Co-phasing of segmented mirror telescopes with curvature sensing[J]. Proceedings of SPIE, 2000, 4004: 540-551. doi: 10.1117/12.393930 [10] CAO H F, ZHANG J X, YANG F, et al. Extending capture range for piston error in segmented primary mirror telescopes based on wavelet support vector machine with improved particle swarm optimization[J]. IEEE Access, 2020, 8: 111585-111597. doi: 10.1109/ACCESS.2020.3002901 [11] CHANAN G, TROY M, DEKENS F, et al. Phasing the mirror segments of the Keck telescopes: the broadband phasing algorithm[J]. Applied Optics, 1998, 37(1): 140-155. doi: 10.1364/AO.37.000140 [12] CHANAN G, OHARA C, TROY M. Phasing the mirror segments of the Keck telescopes II: the narrow-band phasing algorithm[J]. Applied Optics, 2000, 39(25): 4706-4714. doi: 10.1364/AO.39.004706 [13] LI X Y, YANG X, WANG SH Q, et al. The piston error recognition technique used in the modified Shack–Hartmann sensor[J]. Optics Communications, 2021, 501: 127388. doi: 10.1016/j.optcom.2021.127388 [14] 林旭东, 王建立, 刘欣悦, 等. 拼接镜主动光学共相实验[J]. 光学 精密工程,2010,18(7):1520-1528.LIN X D, WANG J L, LIU X Y, et al. Co-phase experiment of active optics for segmented-mirrors[J]. Optics and Precision Engineering, 2010, 18(7): 1520-1528. (in Chinese) [15] ESPOSITO S, PINNA E, TOZZI A, et al. Cophasing of segmented mirrors using the pyramid sensor[J]. Proceedings of SPIE, 2003, 5169: 72-78. doi: 10.1117/12.511507 [16] ZHANG Y F, XIAN H. Coarse co-phasing method based on slope of visibility-enhanced dispersed fringe pattern for segmented telescope[J]. Optics Communications, 2020, 459: 124998. doi: 10.1016/j.optcom.2019.124998 [17] ZHANG Y F, XIAN H. Piston sensing for a segmented mirror system via a digital dispersed fringe generated by wavelength tuning[J]. Optics Letters, 2020, 45(5): 1051-1054. doi: 10.1364/OL.385262 [18] LI B, YU W H, TANG J L, et al. Theory and experiment of phasing detection by use of two wavelengths[J]. Applied Optics, 2017, 56(1): 1-7. doi: 10.1364/AO.56.000001 [19] LI B, YU W H, CHEN M, et al. Co-phasing experiment of a segmented mirror using a combined broadband and two-wavelength algorithm[J]. Applied Optics, 2017, 56(32): 8871-8879. doi: 10.1364/AO.56.008871 [20] LI B, YU W H, CHEN M, et al. Co-focus experiment of segmented mirror[J]. Chinese Physics B, 2017, 26(6): 060706. doi: 10.1088/1674-1056/26/6/060706 [21] WANG Y R, JIANG F Y, JU G H, et al. Deep learning wavefront sensing for fine phasing of segmented mirrors[J]. Optics Express, 2021, 29(16): 25960-25978. doi: 10.1364/OE.434024 [22] MA X F, XIE Z L, MA H T, et al. Piston sensing for sparse aperture systems with broadband extended objects via a single convolutional neural network[J]. Optics and Lasers in Engineering, 2020, 128: 106005. doi: 10.1016/j.optlaseng.2020.106005 [23] 李斌, 吴建, 刘燕德, 等. 拼接镜主动共相实验研究[J]. 光子学报,2018,47(2):0212003.LI B, WU J, LIU Y D, et al. Co-phasing experiment of active optics for segmented mirror[J]. Acta Photonica Sinica, 2018, 47(2): 0212003. (in Chinese) [24] 李斌, 刘燕德, 谢锋云. 拼接镜新型粗共相检测方法[J]. 光学 精密工程,2018,26(11):2647-2653. doi: 10.3788/OPE.20182611.2647LI B, LIU Y D, XIE F Y. Coarse co-phasing detection of segmented mirrors[J]. Optics and Precision Engineering, 2018, 26(11): 2647-2653. (in Chinese) doi: 10.3788/OPE.20182611.2647 期刊类型引用(2)
1. 安其昌，吴小霞，刘欣悦，王勋，李洪文. 大口径环形分段光学系统基准构建方法. 中国光学(中英文). 2024(02): 390-397 . 
百度学术2. 李斌，刘银岭，杨阿坤，陈莫. 基于深度降噪卷积神经网络的宽波段共相检测研究. 中国光学(中英文). 2024(06): 1329-1339 . 百度学术其他类型引用(1)
-
下载:
下载:
百度学术
计量
- 文章访问数: 638
- HTML全文浏览量: 384
- PDF下载量: 116
- 被引次数: 3
