Review of physical implementation architecture in compressive spectral imaging system
-
摘要:
不同于传统点对点映射成像方式，计算光学成像通过将前端光学信号的物理调控与后端数字信号的计算处理联合起来，使图像信息获取更加高效。这种新型成像体制有望缓解传统成像技术框架下低制造成本与高性能指标间的矛盾，尤其在高维图像信息获取中呈现更显著优势。而物理器件支撑下的系统架构一直是计算光学成像发展的基石，本文针对压缩光谱成像这一子技术领域，介绍了现有可实现空间或光谱调制的光学器件，并以此为基础对多型压缩光谱成像系统架构进行了梳理、归纳，依据信息调制过程的差异，将其规整为单像素光谱成像、编码孔径光谱成像、空间-光谱双重编码光谱成像、微阵列型光谱成像与散射介质光谱成像等几类。重点阐述了多种系统架构的信息调制与采集原理，以及对光谱图像数据立方体的调制效应，并讨论了其中的共性问题。最后给出了面临的技术挑战，探讨了未来发展趋势。
Abstract:Different from the traditional point-to-point mapping imaging method, computational optical imaging combines the physical regulation of the front-end optical signal with the processing of the back-end digital signal to make the image information acquisition more efficient. This new imaging mechanism is expected to alleviate the contradiction between low manufacturing cost and high performance indicators under the framework of traditional imaging technology, especially in the acquisition of high-dimensional image information. Since the system architecture supported by physical devices is the cornerstone of computational optical imaging, aiming at the sub-technical field of compressive spectral imaging, in this paper, we introduce the existing optical devices that can realize spatial or spectral modulation. Based on this, the architecture of multi-type compressive spectral imaging system is sorted out and summarized, which can be categorized as single-pixel spectral imaging, coded aperture spectral imaging, spatial-spectral dual-coded spectral imaging, microarray spectral imaging and scattering medium spectral imaging, based on the information modulation process. We focus on the information modulation and acquisition principles of various system architectures and their modulation effects on the spatial-spectral data cube, and then analyze and explore the common issues. Finally, the technical challenges faced are given, and the future development trend is discussed.
-
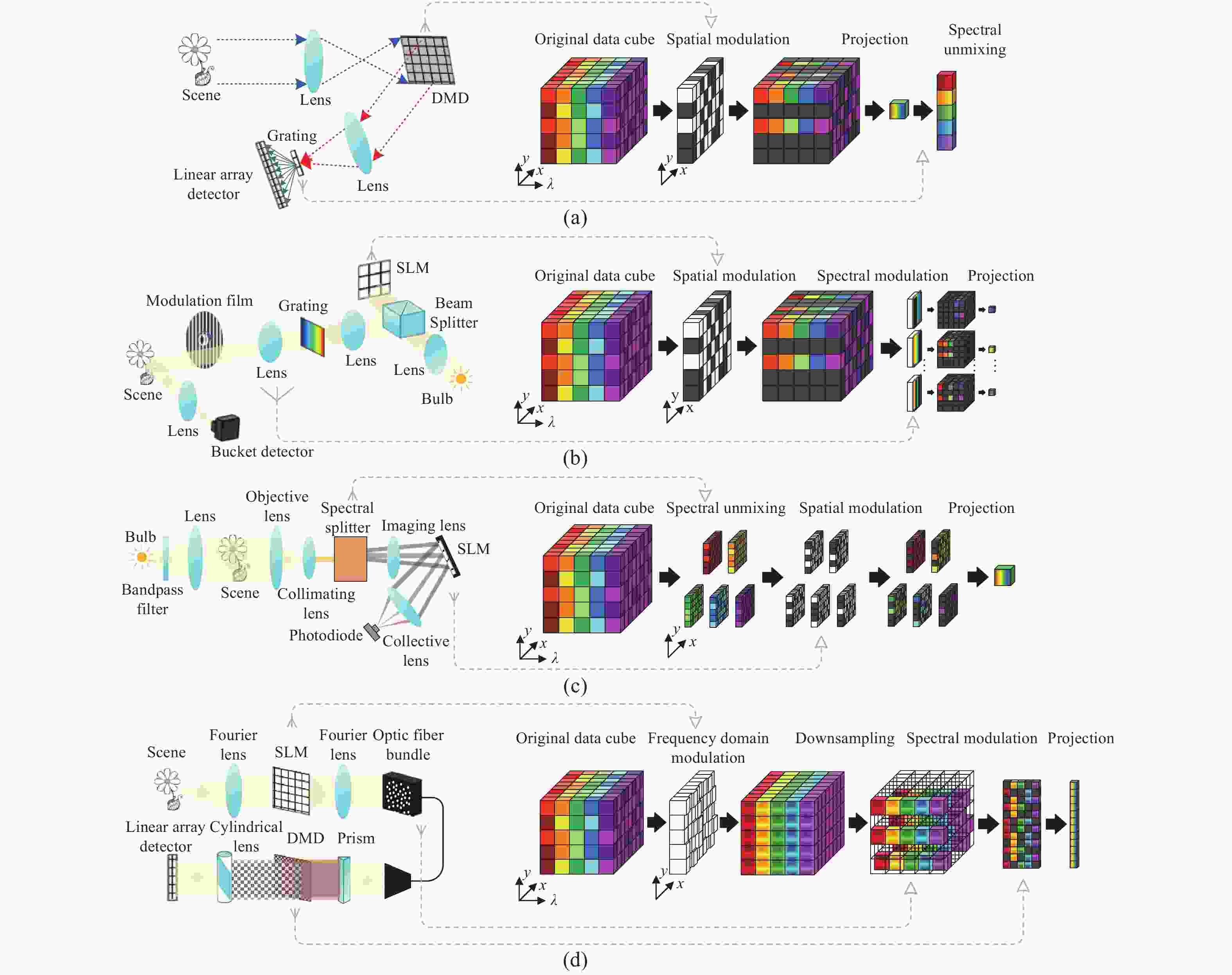
图 2 单像素光谱成像系统架构及相应的空间-光谱数据立方体调制过程：(a) 基于光谱仪的单像素光谱成像仪；(b) 空间-光谱调制单像素光谱成像仪；(c) 光谱分离单像素光谱成像仪；(d) 空间-光谱调制光谱成像仪
Figure 2. Single pixel spectral imaging system architecture and its corresponding spatial-spectral data cube modulation diagram. (a) Spectrometer-based single pixel spectral imager; (b) spatial-spectral modulation single-pixel spectral imager; (c) spectral unmixing single pixel spectral imager; (d) spatial-spectral modulation spectral imager
图 3 CASSI系统基本型式：(a) 单色散CASSI；(b) 双色散CASSI
Figure 3. Basic types of CASSI system. (a) SD-CASSI; (b) DD-CASSI
图 4 CASSI系统彩色编码孔径型式：(a) 彩色CASSI；(b) 压缩光谱图案式快照成像仪；(c) 基于变形镜的CSPSI
Figure 4. Colored coded aperture types of CASSI system. (a) C-CASSI; (b) CSPSI; (c) DM-based CSPSI
图 7 CASSI系统多帧互补采集型式：(a) 双相机CASSI；(b) 零级与一级衍射CASSI
Figure 7. Multi-frame complementary acquisition type of CASSI system. (a) Dual-camera CASSI; (b) 0th and 1st order diffraction CASSI
图 8 CASSI系统多帧阵列采集型式：(a) 图像倍增CASSI；(b) 透镜阵列CASSI
Figure 8. Multi-frame array acquisition type of CASSI system. (a) Image multiplier CASSI; (b) lenslet array CASSI
图 9 DCSI系统架构：(a) 双重编码孔径光谱成像仪；(b) 空间-光谱编码压缩成像仪
Figure 9. Architecture of DCSI System. (a) DCSI; (b) SSCSI
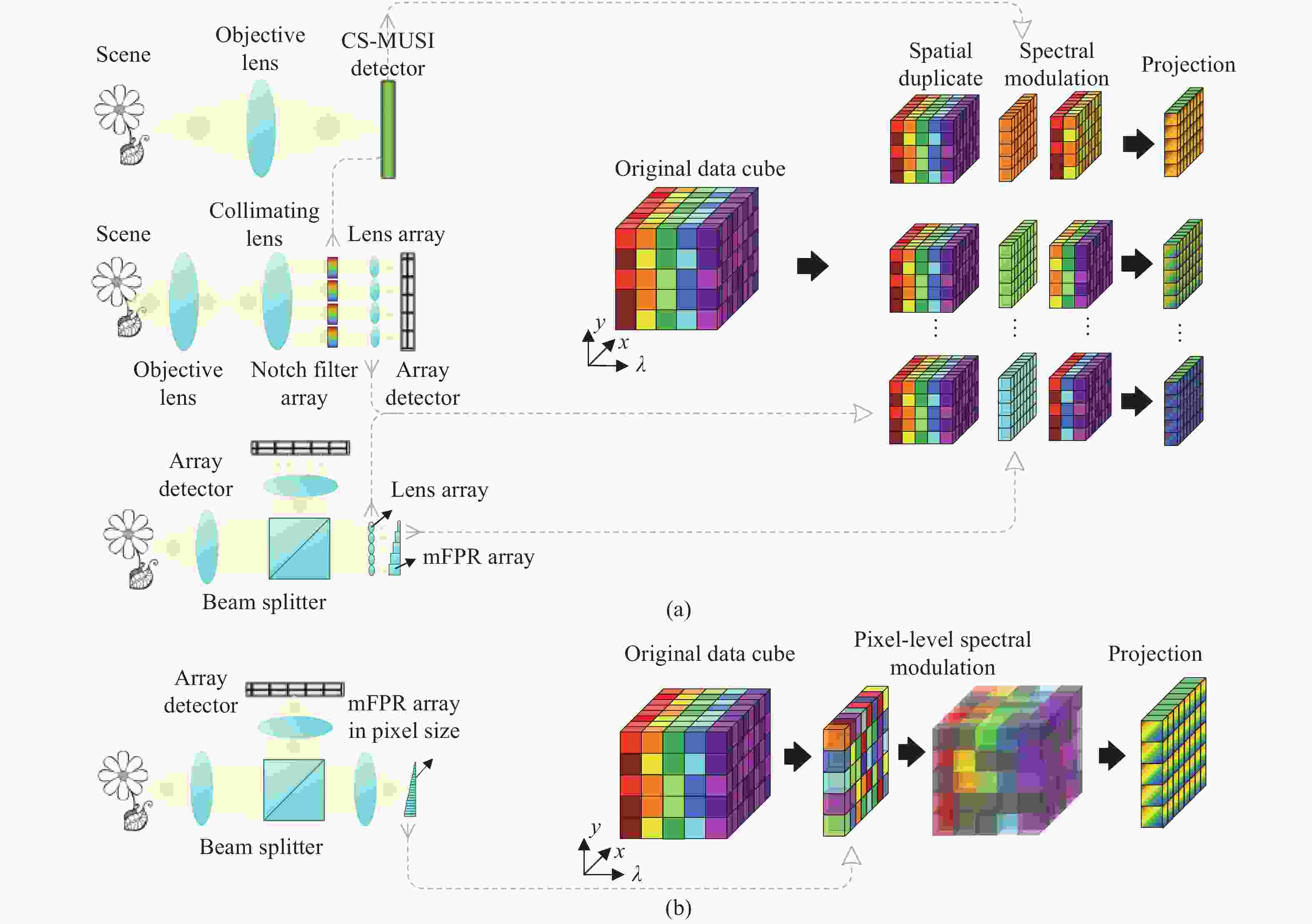
图 10 微阵列型光谱成像架构：(a) 左上为紧凑型超光谱成像仪，左中为陷波滤波器阵列光谱成像仪，左下为基于FPRA阵列的光谱成像仪；(b) 像素级FPRA阵列光谱成像仪
Figure 10. Architecture of microarray spectral imaging. (a) Top left is the MUSI，middle left is the notch filter array spectral imager， bottom left is FPRA-based spectral imager；(b) pixel-level FPRA-based spectral imager
表 1 各系统型式特征总结
Table 1. Summary of the characteristics of each system type
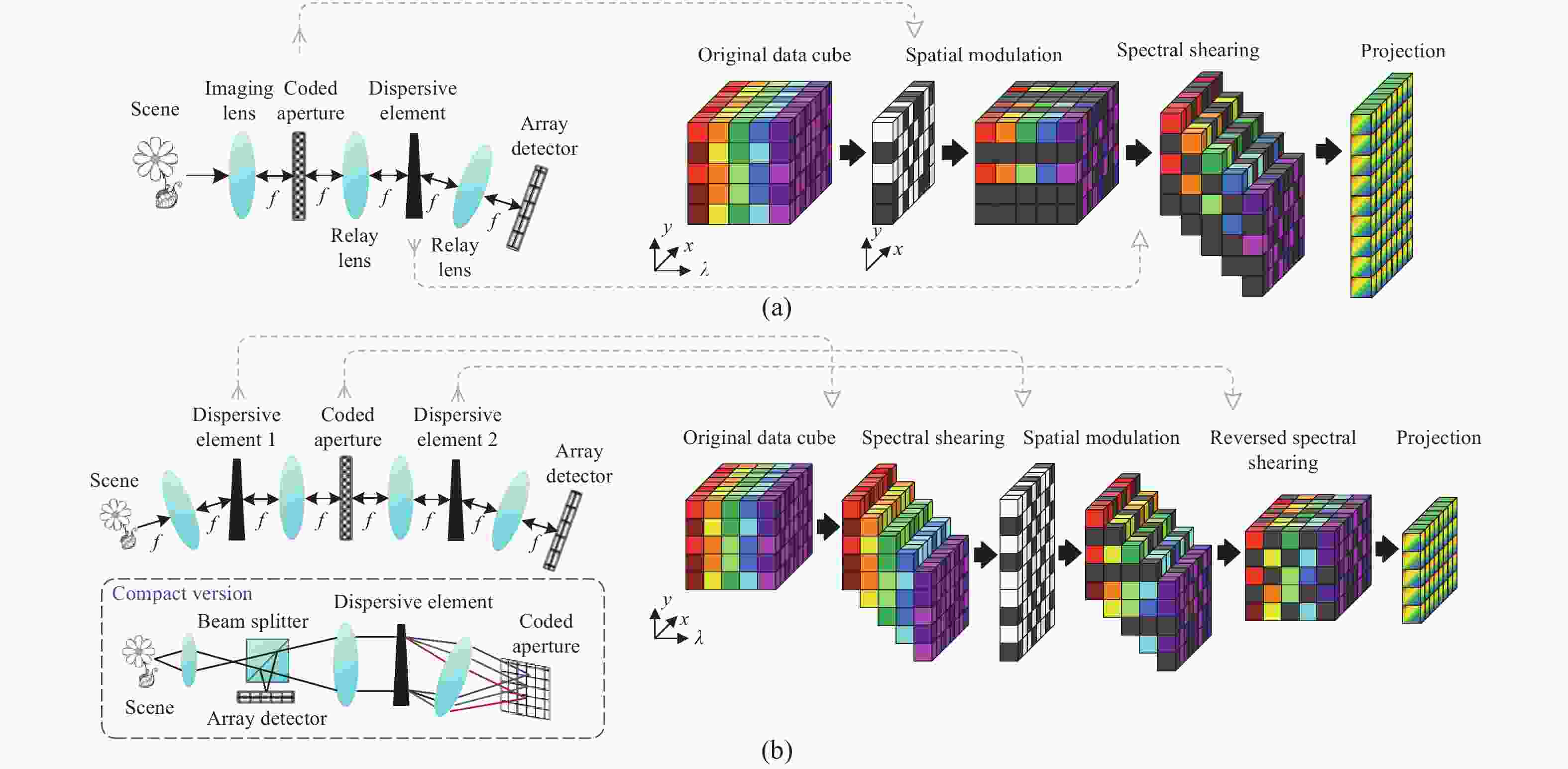
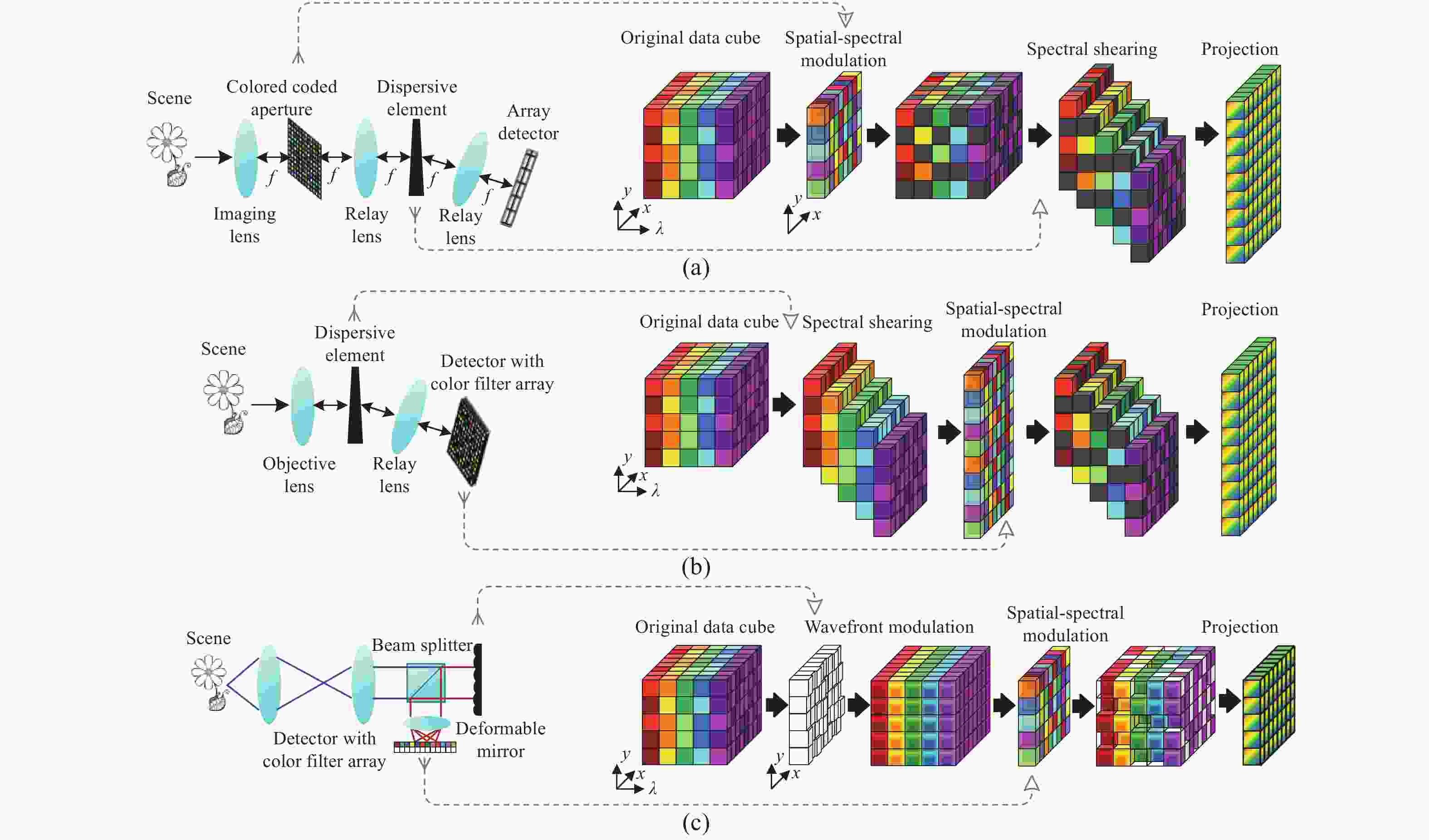
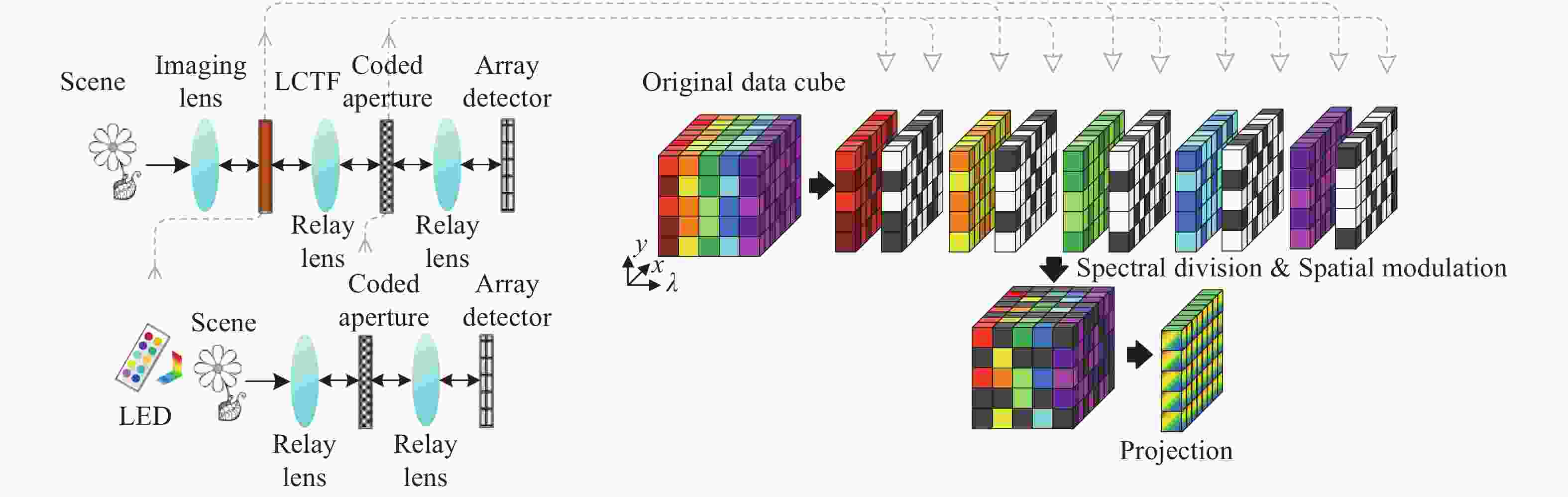
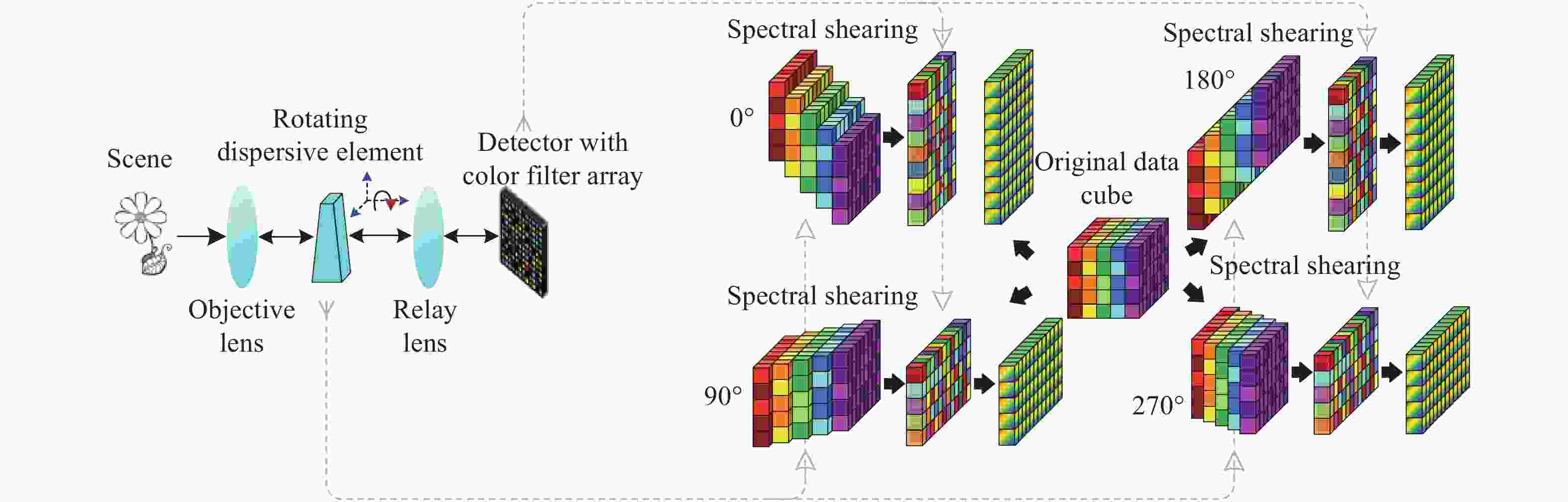
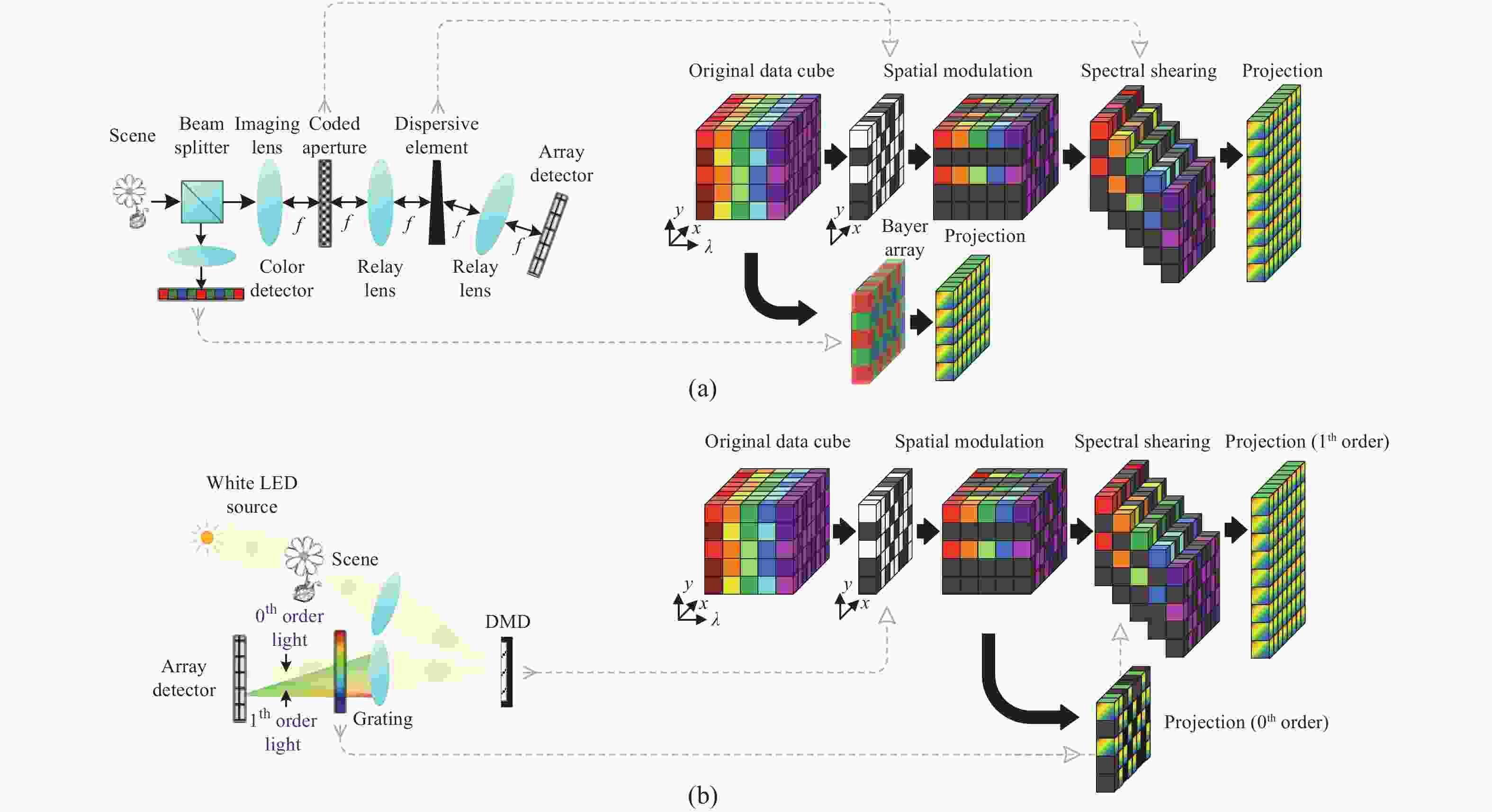
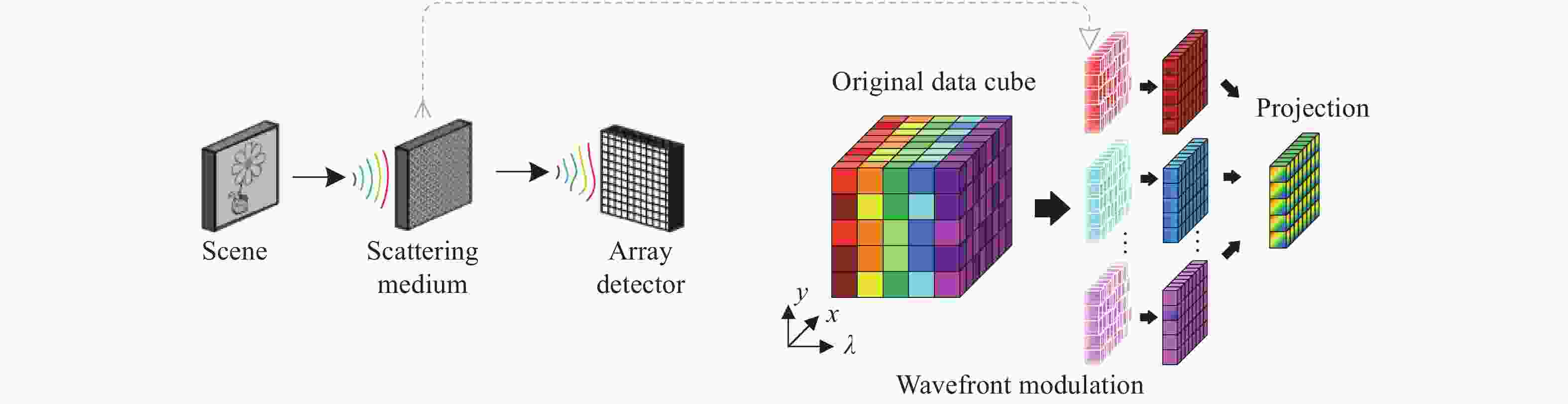
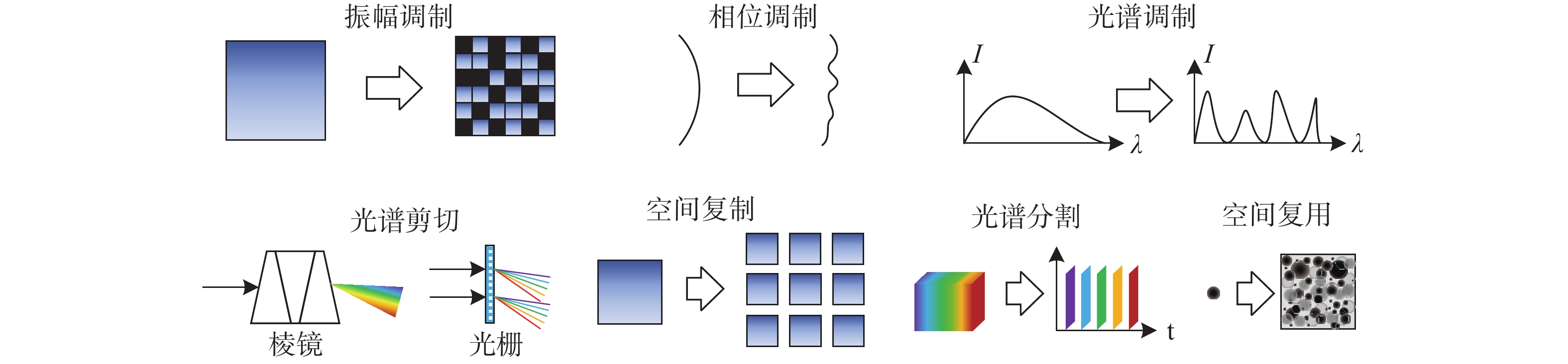
系统型式类别 系统名称 调制方式 物理器件 对应图表 单像素光谱成像 基于光谱仪的单像素光谱成像仪[6-11] 空间调制，光谱分离 DMD，色散元件 图2(a) 空间-光谱调制单像素光谱成像仪[12] 空间调制，光谱调制 DMD，衍射光栅，正弦调制转轮 图2(b) 光谱分离单像素光谱成像仪[13-14] 光谱分离，空间调制 光谱分离器，SLM 图2(c) 空间-光谱调制光谱成像仪[15] 空间调制，光谱调制 SLM+色散棱镜+DMD+柱状透镜 图2(d) 编码孔径光谱成像(基本型式) SD-CASSI [16-18] 空间调制，光谱剪切 光刻掩模板+色散棱镜 图3(a) DD-CASSI [19] 光谱剪切，空间调制，光谱逆剪切 色散棱镜+光刻掩模板+色散棱镜 图3(b) 编码孔径光谱成像(CCA型式) C-CASSI [23-30] 空间-光谱调制，光谱剪切 光谱滤波阵列+色散棱镜 图4(a) CSPSI [31-34] 光谱剪切，空间-光谱调制 色散棱镜+光谱滤波阵列 图4(b) DM-based CSPSI [36] 空间复用，空间-光谱调制 DM+光谱滤波阵列 图4(c) 编码孔径光谱成像(光谱分割型式) LCTF光谱分割型[37-38] 光谱分离，空间调制 LCTF+DMD 图5左上 LeSTI [39] LED+DMD 图5左下 编码孔径光谱成像(编码可调整型式) CAASI [40-44] 空间调制(时变)，光谱剪切 DMD(时变)/压电陶瓷，色散棱镜 / CSPSI [45] 光谱剪切(时变)，空间-光谱调制 色散棱镜(旋转)，光谱滤波阵列 图6 编码孔径光谱成像(多帧互补采集型式) Dual-camera CASSI [46,47] 通道1：空间调制，光谱剪切
通道2：空间-光谱调制(彩色相机)分束镜，光刻掩膜板，色散棱镜 图7(a) 0th and 1st order diffraction CASSI [48-50] 通道1(1st衍射光)：空间调制，光谱剪切；
通道2 (0th 衍射光)：无调制
(全色相机)DMD，衍射光栅 图7(b) 编码孔径光谱成像(多帧阵列采集型式) 图像倍增CASSI [52] 空间复制，空间调制，光谱剪切 图像倍增器，光刻掩模板，
色散棱镜图8(a) 透镜阵列CASSI [53] 空间复制，光谱剪切，空间调制，
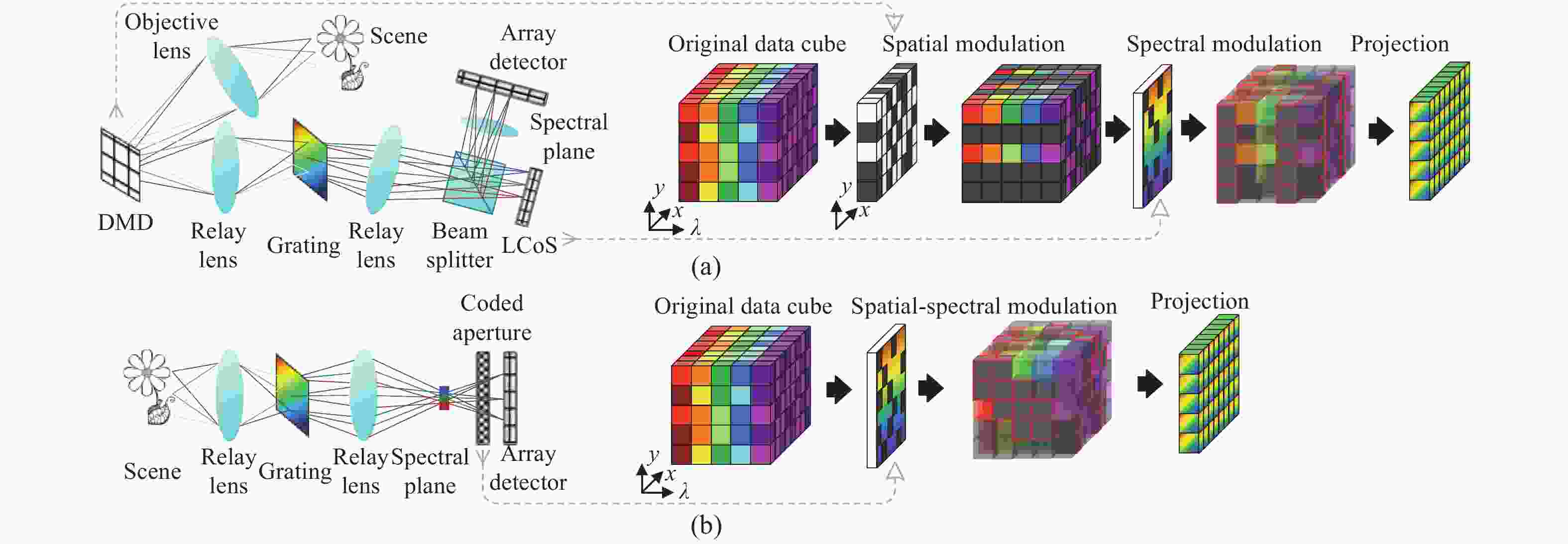
光谱逆剪切透镜阵列，色散棱镜，光刻掩模板，色散棱镜 图8(b) 空间-光谱双重编码光谱成像 DCSI [55-57] 空间调制+光谱调制 DMD+衍射光栅+LCoS 图9(a) SSCSI [58-61] 空间光谱混合调制 衍射光栅+光刻掩模板 图9(b) 微阵列型光谱成像 MUSI[62-64] 光谱调制(时间延展) LCC 图10(a)左上 陷波滤波器阵列光谱成像仪[65] 空间复制，光谱调制 陷波滤波器阵列，透镜阵列 图10(a)左中 FPRA阵列光谱成像仪[66] 空间复制，光谱调制 FPRA，透镜阵列 图10(a)左下 像素级FPRA阵列光谱成像仪[66] 空间-光谱调制(像素级) FPRA 图10(b) 散射介质光谱成像 散射介质光谱成像仪[67-72] 空间-光谱复用调制 散射介质/DFA 图11 
下载: 导出CSV
-
[1] 于磊. 成像光谱仪的发展与应用(特邀)[J]. 红外与激光工程,2022,51(1):20210940.YU L. Development and application of imaging spectrometer (Invited)[J]. Infrared and Laser Engineering, 2022, 51(1): 20210940. (in Chinese) [2] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. doi: 10.1109/TIT.2006.871582 [3] CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. doi: 10.1109/TIT.2005.862083 [4] CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. doi: 10.1109/MSP.2007.914731 [5] YUAN X, BRADY D J, KATSAGGELOS A K. Snapshot compressive imaging: theory, algorithms, and applications[J]. IEEE Signal Processing Magazine, 2021, 38(2): 65-88. doi: 10.1109/MSP.2020.3023869 [6] SUN T, KELLY K. Compressive sensing hyperspectral imager[C]. Proceedings of Computational Optical Sensing and Imaging, Optica Publishing Group, 2009: CTuA5. [7] LI CH B, SUN T, KELLY K F, et al. A compressive sensing and unmixing scheme for hyperspectral data processing[J]. IEEE Transactions on Image Processing, 2012, 21(3): 1200-1210. doi: 10.1109/TIP.2011.2167626 [8] MAGALHAES F, ARAÚJO F M, CORREIA M, et al. High-resolution hyperspectral single-pixel imaging system based on compressive sensing[J]. Optical Engineering, 2012, 51(7): 071406. doi: 10.1117/1.OE.51.7.071406 [9] CHENNING T, HUANZHENG Z, XUCHENG W, et al. Compressive single-pixel hyperspectral imaging using RGB sensors[J]. Optics Express, 2021, 29(7): 11207-11220. doi: 10.1364/OE.416388 [10] KRAVETS V, KONDRASHOV P, STERN A. Compressive ultraspectral imaging using multiscale structured illumination[J]. Applied Optics, 2019, 58(22): F32-F39. doi: 10.1364/AO.58.000F32 [11] GARCIA H, CORREA C V, ARGUELLO H. Optimized sensing matrix for single pixel multi-resolution compressive spectral imaging[J]. IEEE Transactions on Image Processing, 2020, 29: 4243-4253. doi: 10.1109/TIP.2020.2971150 [12] BIAN L H, SUO J L, SITU G H, et al. Multispectral imaging using a single bucket detector[J]. Scientific Reports, 2016, 6: 24752. doi: 10.1038/srep24752 [13] STARLING D J, STORER I, HOWLAND G A. Compressive sensing spectroscopy with a single pixel camera[J]. Applied Optics, 2016, 55(19): 5198-5202. doi: 10.1364/AO.55.005198 [14] LI Z W, SUO J L, HU X M, et al. Efficient single-pixel multispectral imaging via non-mechanical spatio-spectral modulation[J]. Scientific Reports, 2017, 7: 41435. doi: 10.1038/srep41435 [15] MARTÍN G, BIOUCAS-DIAS J M. Spatial-spectral hyperspectral image compressive sensing[C]. Proceedings of 2017 IEEE International Geoscience and Remote Sensing Symposium, IEEE, 2017: 3988-3991. [16] WAGADARIKAR A, JOHN R, WILLETT R, et al. Single disperser design for coded aperture snapshot spectral imaging[J]. Applied Optics, 2008, 47(10): B44-B51. doi: 10.1364/AO.47.000B44 [17] CAO X, YUE T, LIN X, et al. Computational snapshot multispectral cameras: toward dynamic capture of the spectral world[J]. IEEE Signal Processing Magazine, 2016, 33(5): 95-108. doi: 10.1109/MSP.2016.2582378 [18] HE J J, WU J M, LU ZH, et al. . Compressive hyperspectral imaging for snapshot multi-channel fluorescence microscopy[C]. Proceedings of Computational Optical Sensing and Imaging, Optica Publishing Group, 2018: CW2E. 5. [19] GEHM M E, JOHN R, BRADY D J, et al. Single-shot compressive spectral imaging with a dual-disperser architecture[J]. Optics Express, 2007, 15(21): 14013-14027. doi: 10.1364/OE.15.014013 [20] ZHAO ZH X, MENG Z Y, JU ZH Y, et al. . A compact dual-dispersion architecture for snapshot compressive spectral imaging[C]. Proceedings of 2021 Asia Communications and Photonics Conference, IEEE, 2021: 1-3. [21] RUEDA C H F, CALDERÓN G A R, FUENTES H A. Spectral selectivity in compressive spectral imaging based on grayscale coded apertures[C]. Proceedings of Symposium of Signals, Images and Artificial Vision, IEEE, 2013: 1-5. [22] DIAZ N, RUEDA H, ARGUELLO H. High-dynamic range compressive spectral imaging by adaptive filtering[C]. Proceedings of the 2015 3rd International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing, IEEE, 2015: 89-93. [23] RUEDA H, ARGUELLO H, ARCE G R. Experimental demonstration of a colored coded aperture-based compressive spectral imaging system[C]. Proceedings of Computational Optical Sensing and Imaging, Optica Publishing Group, 2014: CTu2C. 6. [24] ARGUELLO H, ARCE G R. Colored coded aperture design by concentration of measure in compressive spectral imaging[J]. IEEE Transactions on Image Processing, 2014, 23(4): 1896-1908. doi: 10.1109/TIP.2014.2310125 [25] RUEDA H, ARGUELLO H, ARCE G R. Compressive spectral imaging based on colored coded apertures[C]. Proceedings of 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, 2014: 7799-7803. [26] RUEDA H, ARGUELLO H, ARCE G R. DMD-based implementation of patterned optical filter arrays for compressive spectral imaging[J]. Journal of the Optical Society of America A, 2015, 32(1): 80-89. doi: 10.1364/JOSAA.32.000080 [27] RUEDA H, ARGUELLO H, ARCE G R. Colored coded aperture compressive spectral imaging: design and experimentation[C]. Proceedings of 2015 IEEE Global Conference on Signal and Information Processing, IEEE, 2015: 601-604. [28] RUEDA H, ARGUELLO H, ARCE G R. Compressive spectral testbed imaging system based on thin-film color-patterned filter arrays[J]. Applied Optics, 2016, 55(33): 9584-9593. doi: 10.1364/AO.55.009584 [29] GALVIS L, MOJICA E, ARGUELLO H, et al. Shifting colored coded aperture design for spectral imaging[J]. Applied Optics, 2019, 58(7): B28-B38. doi: 10.1364/AO.58.000B28 [30] PARADA-MAYORGA A, ARCE G R. Spectral super-resolution in colored coded aperture spectral imaging[J]. IEEE Transactions on Computational Imaging, 2016, 2(4): 440-455. doi: 10.1109/TCI.2016.2612943 [31] RUEDA H, LAU D, ARCE G R. RGB detectors on compressive snapshot multi-spectral imagers[C]. Proceedings of 2015 IEEE Global Conference on Signal and Information Processing, IEEE, 2015: 388-392. [32] CORREA C V, ARGUELLO H, ARCE G R. Compressive spectral imaging with colored-patterned detectors[C]. Proceedings of 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, 2014: 7789-7793. [33] CORREA C V, ARGUELLO H, ARCE G R. Snapshot colored compressive spectral imager[J]. Journal of the Optical Society of America A, 2015, 32(10): 1754-1763. doi: 10.1364/JOSAA.32.001754 [34] MEJÍA-MELGAREJO Y H, VILLARREAL-DULCEY O P, ARGUELLO-FUENTES H. Adjustable spatial resolution of compressive spectral images sensed by multispectral filter array-based sensors[J]. Revista Facultad de Ingeniería, 2016(78): 89-98. [35] MARQUEZ M, MEZA P, ARGUELLO H, et al. Compressive spectral imaging via deformable mirror and colored-mosaic detector[J]. Optics Express, 2019, 27(13): 17795-17808. doi: 10.1364/OE.27.017795 [36] MONAKHOVA K, YANNY K, WALLER L. Snapshot hyperspectral imaging using a random phase mask and spectral filter array[C]. Proceedings of Computational Optical Sensing and Imaging, Optica Publishing Group, 2020: JF2F. 4. [37] WANG X, ZHANG Y H, MA X, et al. Compressive spectral imaging system based on liquid crystal tunable filter[J]. Optics Express, 2018, 26(19): 25226-25243. doi: 10.1364/OE.26.025226 [38] XU C, XU T F, YAN G, et al. Super-resolution compressive spectral imaging via two-tone adaptive coding[J]. Photonics Research, 2020, 8(3): 395-411. doi: 10.1364/PRJ.377665 [39] MA X, YUAN X, FU CH, et al. LED-based compressive spectral-temporal imaging[J]. Optics Express, 2021, 29(7): 10698-10715. doi: 10.1364/OE.419888 [40] ARCE G R, BRADY D J, CARIN L, et al. Compressive coded aperture spectral imaging: an introduction[J]. IEEE Signal Processing Magazine, 2014, 31(1): 105-115. doi: 10.1109/MSP.2013.2278763 [41] KITTLE D, CHOI K, WAGADARIKAR A, et al. Multiframe image estimation for coded aperture snapshot spectral imagers[J]. Applied Optics, 2010, 49(36): 6824-6833. doi: 10.1364/AO.49.006824 [42] ARGUELLO H, ARCE G R. Code aperture optimization for spectrally agile compressive imaging[J]. Journal of the Optical Society of America A, 2011, 28(11): 2400-2413. doi: 10.1364/JOSAA.28.002400 [43] KITTLE D S, MARKS D L, BRADY D J. Design and fabrication of an ultraviolet-visible coded aperture snapshot spectral imager[J]. Optical Engineering, 2012, 51(7): 071403. doi: 10.1117/1.OE.51.7.071403 [44] WU Y H, MIRZA I O, ARCE G R, et al. Development of a digital-micromirror-device-based multishot snapshot spectral imaging system[J]. Optics Letters, 2011, 36(14): 2692-2694. doi: 10.1364/OL.36.002692 [45] CORREA C V, HINOJOSA C A A, ARCE G R, et al. Multiple snapshot colored compressive spectral imager[J]. Optical Engineering, 2017, 56(4): 041309. [46] WANG L ZH, XIONG ZH W, GAO H H, et al. Dual-camera design for coded aperture snapshot spectral imaging[J]. Applied Optics, 2015, 54(4): 848-858. doi: 10.1364/AO.54.000848 [47] WANG L ZH, XIONG ZH W, SHI G M, et al. . Compressive hyperspectral imaging with complementary RGB measurements[C]. Proceedings of 2016 Visual Communications and Image Processing, IEEE, 2016: 1-4. [48] ŽÍDEK K, DENK O, HLUBUČEK J, et al. Compact and robust hyperspectral camera based on compressed sensing[J]. Proceedings of the SPIE, 2016, 10151: 101510N. [49] HLUBUČEK J, LUKEŠ J, VÁCLAVÍK J, et al. Enhancement of CASSI by a zero-order image employing a single detector[J]. Applied Optics, 2021, 60(5): 1463-1469. doi: 10.1364/AO.414402 [50] SAITA Y, SHIMOYAMA D, TAKAHASHI R, et al. Single-shot compressive hyperspectral imaging with dispersed and undispersed light using a generally available grating[J]. Applied Optics, 2022, 61(5): 1106-1111. doi: 10.1364/AO.441568 [51] HLUBUČEK J, LUKEŠ J, VÁCLAVÍK J, et al. Differential coded aperture single-snapshot spectral imaging[J]. Optics Letters, 2022, 47(9): 2342-2345. doi: 10.1364/OL.454729 [52] JEON D S, CHOI I, KIM M H. Multisampling compressive video spectroscopy[J]. Computer Graphics Forum, 2016, 35(2): 467-477. doi: 10.1111/cgf.12847 [53] BLANCO G, PEREZ J, MONSALVE J, et al. . Single snapshot system for compressive covariance matrix estimation for hyperspectral imaging via lenslet array[C]. Proceedings of the 2021 XXIII Symposium on Image, Signal Processing and Artificial Vision, IEEE, 2021: 1-5. [54] MARQUEZ M, MONSALVE J, RUEDA H, et al. . Compressive spectral virtual multishot imager via lenslet array[C]. Proceedings of Optics and Photonics for Sensing the Environment, Optica Publishing Group, 2021: JW2A. 14. [55] AUGUST Y, VACHMAN C, RIVENSON Y, et al. . Compressive hyperspectral imaging by random separable projections in both the spatial and the spectral domains[J]. Applied Optics, 2013, 52(10): D46-D54. [56] STERN A, YITZHAK A, FARBER V, et al. . Hyperspectral compressive imaging[C]. Proceedings of the 2013 12th Workshop on Information Optics, IEEE, 2013: 1-3. [57] LIN X, WETZSTEIN G, LIU Y B, et al. Dual-coded compressive hyperspectral imaging[J]. Optics Letters, 2014, 39(7): 2044-2047. doi: 10.1364/OL.39.002044 [58] LIN X, LIU Y B, WU J M, et al. Spatial-spectral encoded compressive hyperspectral imaging[J]. ACM Transactions on Graphics, 2014, 33(6): 233. [59] WANG P, LI J, QI CH, et al. Input aperture restriction of the spatial spectral compressive spectral imager and a comprehensive solution for it[J]. Optics Express, 2021, 29(12): 17875-17889. doi: 10.1364/OE.422090 [60] SALAZAR E, PARADA A, ARCE G R. Spatial super-resolution reconstruction via SSCSI compressive spectral imagers[C]. Proceedings of Computational Optical Sensing and Imaging, Optica Publishing Group, 2018: CTu5D. 5. [61] SALAZAR E, PARADA-MAYORGA A, ARCE G R. Spectral zooming and resolution limits of spatial spectral compressive spectral imagers[J]. IEEE Transactions on Computational Imaging, 2019, 5(2): 165-179. doi: 10.1109/TCI.2019.2893596 [62] STERN A, AUGUST I Y, OIKNINE Y. Compressive gigavoxel spectral imaging[C]. Proceedings of Computational Optical Sensing and Imaging, Optica Publishing Group, 2016: CW5D. 1. [63] OIKNINE Y, AUGUST I, STERN A. Along-track scanning using a liquid crystal compressive hyperspectral imager[J]. Optics Express, 2016, 24(8): 8446-8457. doi: 10.1364/OE.24.008446 [64] AUGUST I, OIKNINE Y, ABULEIL M, et al. Miniature compressive ultra-spectral imaging system utilizing a single liquid crystal phase retarder[J]. Scientific Reports, 2016, 6: 23524. doi: 10.1038/srep23524 [65] ZHANG M Q, WANG L ZH, ZHANG L, et al. High light efficiency snapshot spectral imaging via spatial multiplexing and spectral mixing[J]. Optics Express, 2020, 28(14): 19837-19850. doi: 10.1364/OE.393173 [66] OIKNINE Y, AUGUST I, STERN A. Multi-aperture snapshot compressive hyperspectral camera[J]. Optics Letters, 2018, 43(20): 5042-5045. doi: 10.1364/OL.43.005042 [67] GOLUB M A, AVERBUCH A, NATHAN M, et al. Compressed sensing snapshot spectral imaging by a regular digital camera with an added optical diffuser[J]. Applied Optics, 2016, 55(3): 432-443. doi: 10.1364/AO.55.000432 [68] HAUSER J, GOLUB M A, AVERBUCH A, et al. Dual-camera snapshot spectral imaging with a pupil-domain optical diffuser and compressed sensing algorithms[J]. Applied Optics, 2020, 59(4): 1058-1070. doi: 10.1364/AO.380256 [69] HAUSER J, AVERBUCH A, NATHAN M, et al. Design of binary-phase diffusers for a compressed sensing snapshot spectral imaging system with two cameras[J]. Applied Optics, 2020, 59(26): 7853-7864. doi: 10.1364/AO.395541 [70] SAHOO S K, TANG D L, DANG C. Single-shot multispectral imaging with a monochromatic camera[J]. Optica, 2017, 4(10): 1209-1213. doi: 10.1364/OPTICA.4.001209 [71] WANG P, MENON R. Ultra-high-sensitivity color imaging via a transparent diffractive-filter array and computational optics[J]. Optica, 2015, 2(11): 933-939. doi: 10.1364/OPTICA.2.000933 [72] WANG P, MENON R. Computational multispectral video imaging [Invited][J]. Journal of the Optical Society of America A, 2018, 35(1): 189-199. doi: 10.1364/JOSAA.35.000189 [73] DUARTE M F, BARANIUK R G. Kronecker compressive sensing[J]. IEEE Transactions on Image Processing, 2012, 21(2): 494-504. doi: 10.1109/TIP.2011.2165289 [74] CAIAFA C F, CICHOCKI A. Multidimensional compressed sensing and their applications[J]. WIREs Data Mining and Knowledge Discovery, 2013, 3(6): 355-380. doi: 10.1002/widm.1108 [75] LU Y, WONG T T W, CHEN F, et al. Compressed ultrafast spectral-temporal photography[J]. Physical Review Letters, 2019, 122(19): 193904. doi: 10.1103/PhysRevLett.122.193904 [76] YANG CH SH, CAO F Y, QI D L, et al. Hyperspectrally compressed ultrafast photography[J]. Physical Review Letters, 2020, 124(2): 023902. doi: 10.1103/PhysRevLett.124.023902 [77] PARK J, FENG X H, LIANG R G, et al. Snapshot multidimensional photography through active optical mapping[J]. Nature Communications, 2020, 11(1): 5602. doi: 10.1038/s41467-020-19418-0 -
下载:
计量
- 文章访问数: 1671
- HTML全文浏览量: 470
- PDF下载量: 512
- 被引次数: 0
