Detection of large aperture flat mirror based on the differential optics transfer function method
-
摘要:
为了实现大口径平面镜的原位检测，本文基于差分传递函数结合瑞奇康芒检测架构，利用全息检测方法结合瑞奇康芒法，通过光瞳的遮拦编码实现大口径平面镜的面形检测。首先，对基于差分传递函数法的大口径平面镜检测基本原理进行了推导，并将现有的大口径波前与重建波前进行对比。最后，利用变形镜搭建了检测光路。本文方法所得到面形与输入面形相关性不低于70%。本文的研究成果对宇宙“首光”探测以及“一黑两暗三起源”等宇宙学基础命题的研究均有十分重要的意义。
Abstract:In order to realize the in-situ detection of large aperture plane mirrors, wavefront detection is achieved by a combination of the Ritchey-Common method and holographic detection through the differential transfer function, combined with the actual Ritchey-Common detection architecture, and through the occlusion code of the pupil. Firstly, the principle of large aperture plane mirror detection based on differential transfer function method is derived, and the existing large aperture wavefront is compared with the reconstructed wavefront. Finally, the detection light path is built by using deformable mirrors. The correlation between the surface shape obtained by this method and the input surface shape is not less than 70%. This paper is of great significance to the fundamental cosmological propositions such as the detection of the "first light" of the universe and the "one black, two dark and three origins".
-
图 1 孔径变分下的标准波前主成分分析结果
Figure 1. Principal component analysis results of standard wavefront
图 2 对彗差与像散混合波前的差分光学传递函数解算幅值（a）及相位（b）
Figure 2. (a) The amplitude and (b) phase calculated by the differential optical transfer function for the mixed wavefront of coma and astigmatism
图 3 孔径变分前（a）、后（b）焦斑能量分布
Figure 3. Energy distributions of the focal spot before (a) and after (b) aperture variation
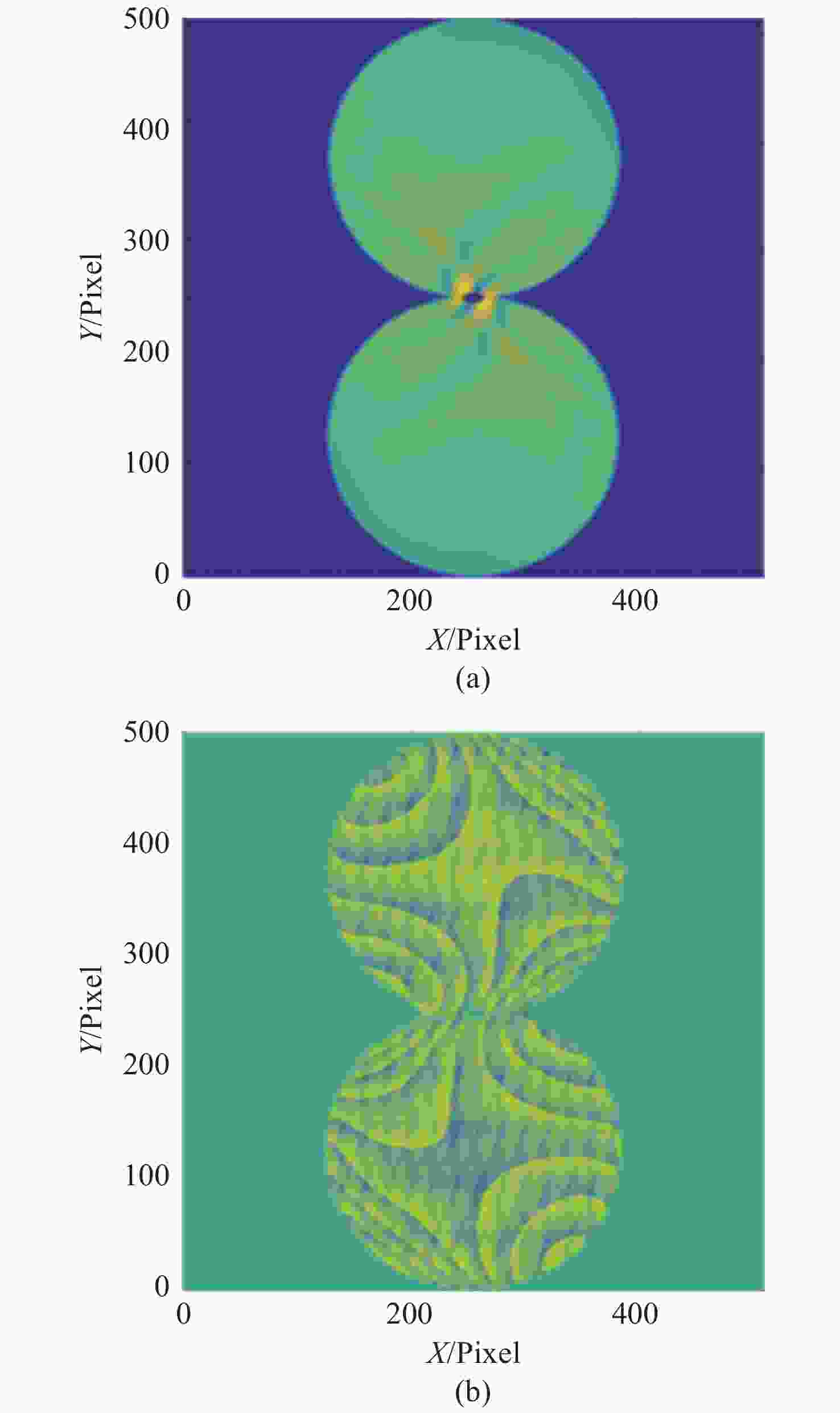
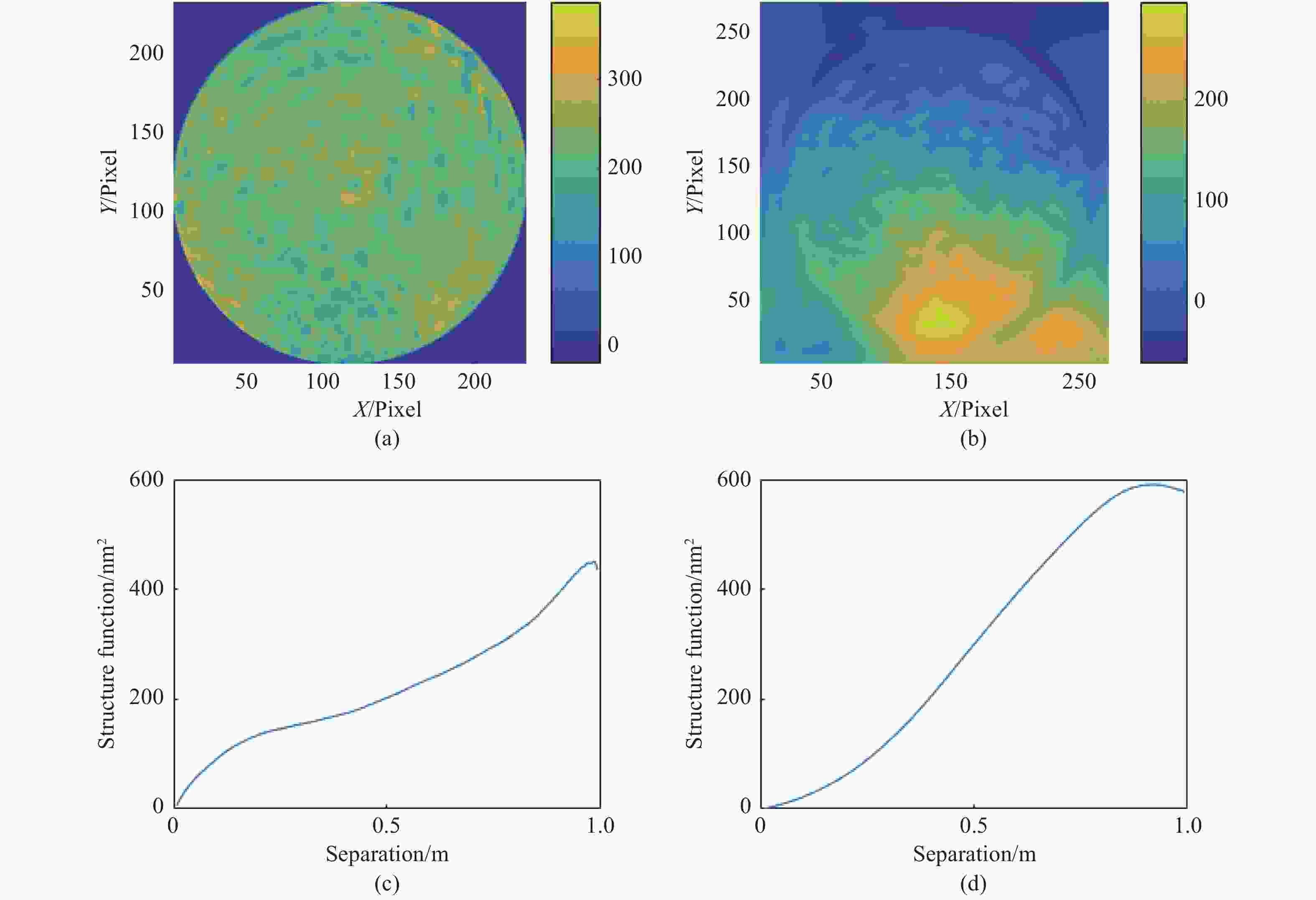
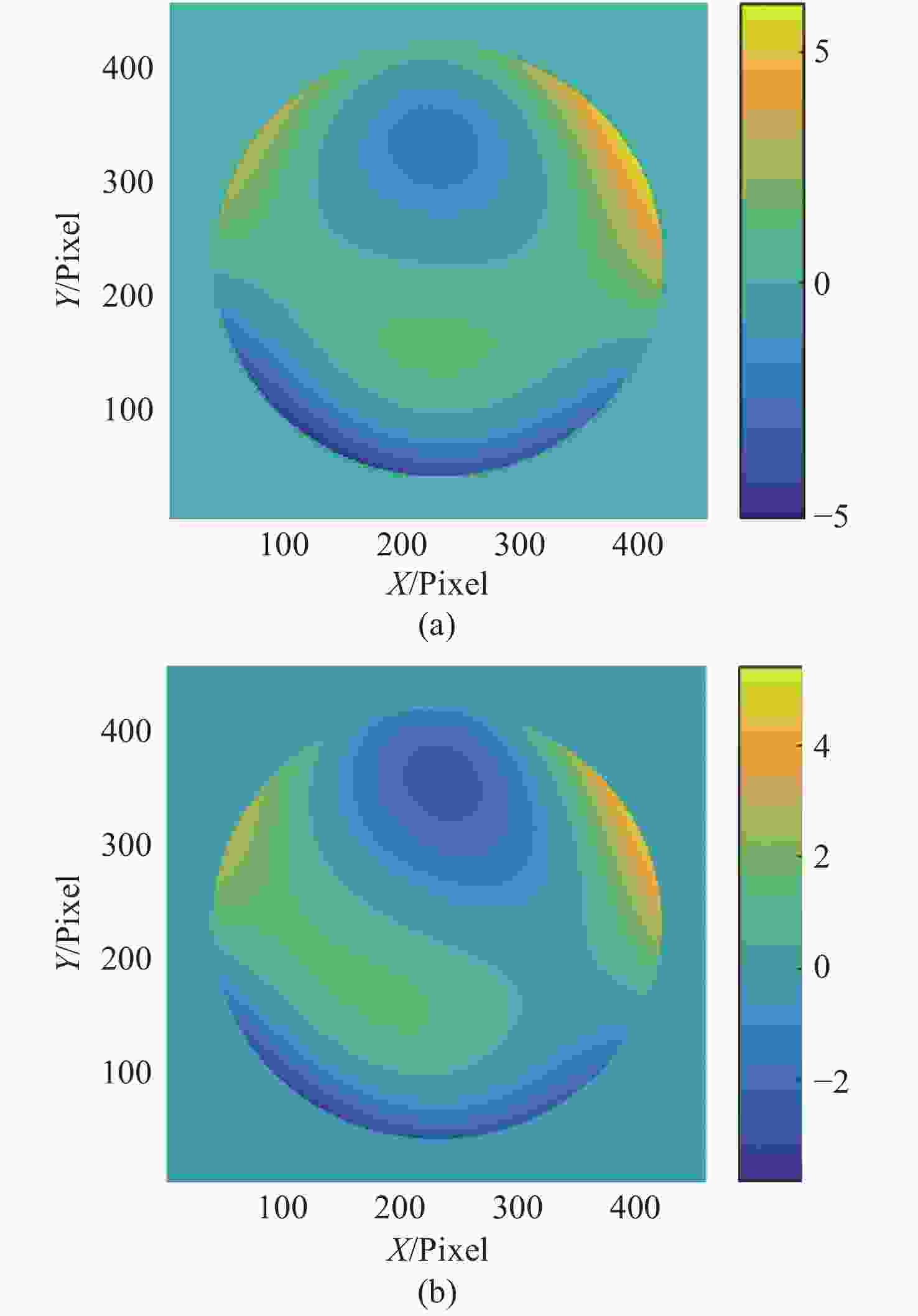
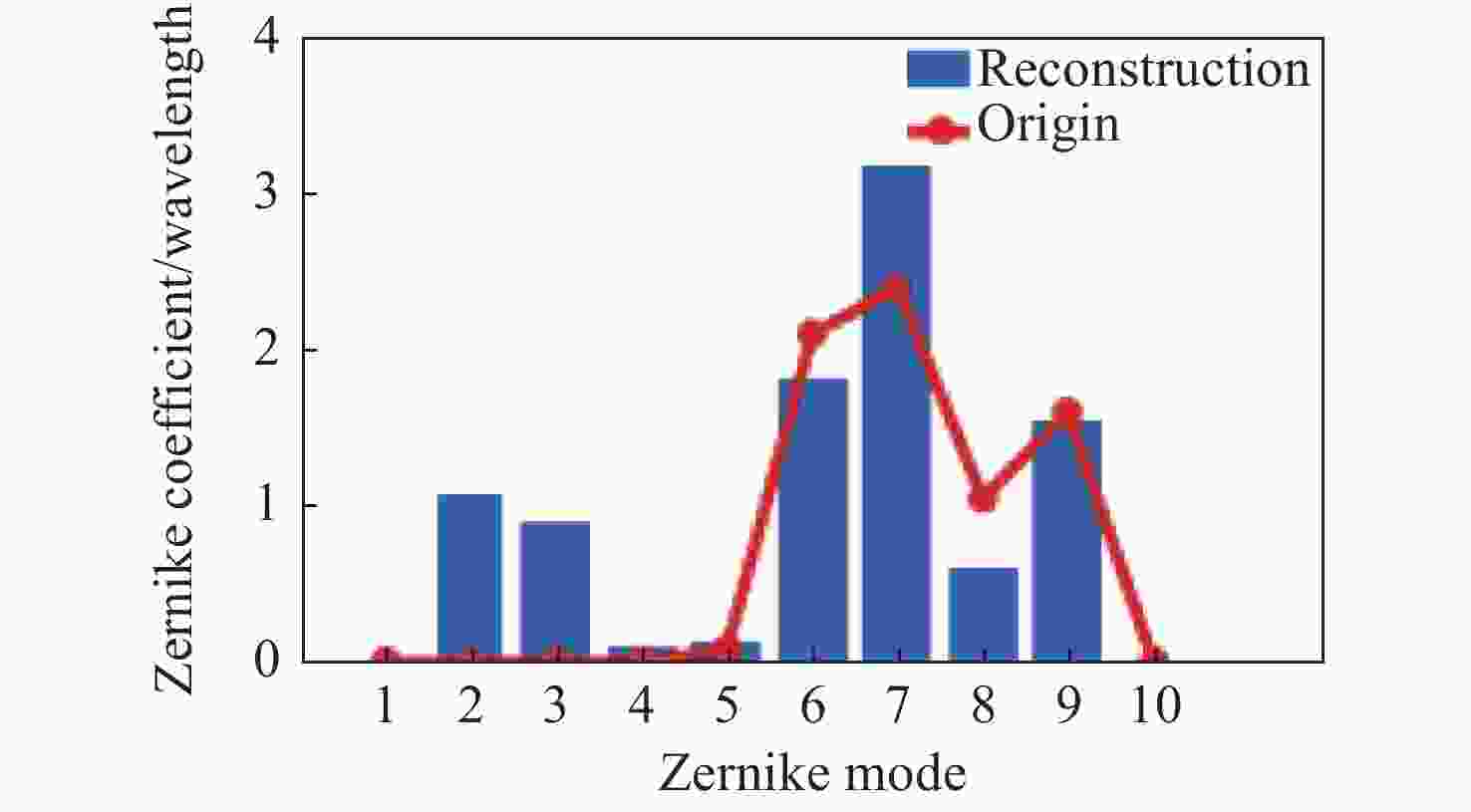
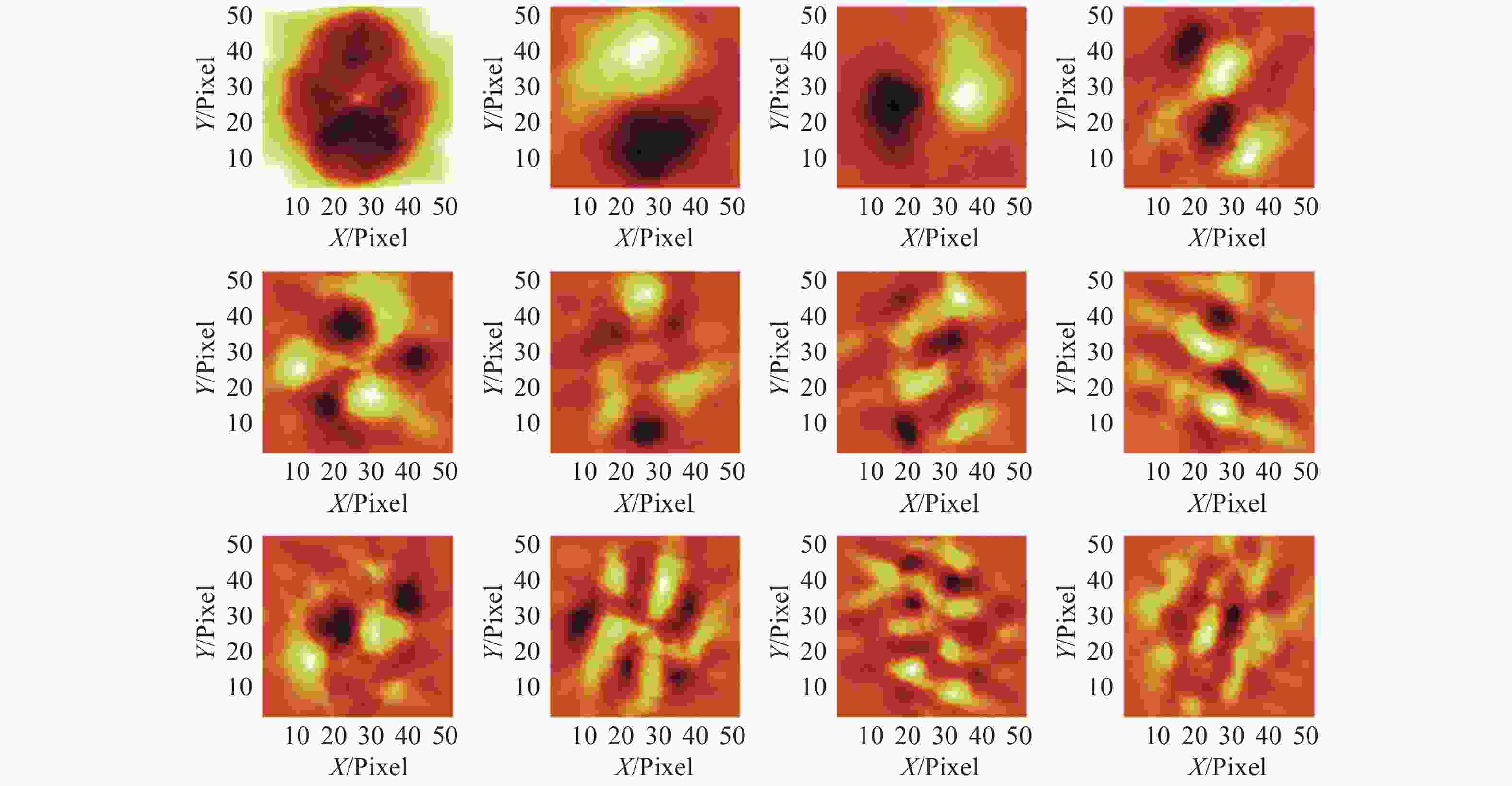
图 4 2 m级大口径反射镜面形差分光学传递函数解算结果。（a）原始波前；（b）恢复波前；（c）原始波前结构函数；（d）恢复波前结构函数
Figure 4. Differential optical transfer function solutions for a 2 m level large aperture mirror shape. (a) Original wavefront. (b) Recovered wavefront. (c) Original wavefront structure function. (d) Recovered wavefront structure function
图 5 原始波前与复原结果的互相关函数
Figure 5. Cross correlation function between the original wavefront and restoration′s result
图 6 基于全息瑞奇-康芒检测大口径平面镜离散孔径检测架构。（a）光瞳架构；（b）检测光路；（c）孔径变分解算过程
Figure 6. Large aperture planar mirror discrete aperture detection architecture based on holographic Ritchey-Common detection. (a) Pupil architecture. (b) Detection optical path. (c) Aperture variational calculation process
图 7 低阶像差组合的（a）原始波前与（b）重建波前
Figure 7. (a) Original wavefront and (b) reconstructed wavefront of low-order aberration combination
图 8 原始波前与重建波前对应的Zernike系数对比
Figure 8. Comparison of Zernike coefficients corresponding to the original wavefront and the reconstructed wavefront
-
[1] CUI X Q, ZHU Y T, LIANG M, et al. Introduction on Chinese 12m optical/infrared telescope (LOT)[J]. Proceedings of SPIE, 2018, 10700: 107001P. [2] BOUCHEZ A H, ANGELI G Z, ASHBY D S, et al. An overview and status of GMT active and adaptive optics[J]. Proceedings of SPIE, 2018, 10703: 107030W. [3] KORKIAKOSKI V, KELLER C U, DOELMAN N, et al. . High-order wavefront correction with a spatial light modulator: calibrations with dOTF method[C]. Proceedings of Adaptive Optics: Methods, Analysis and Applications 2013, Optica Publishing Group, 2013. [4] RODACK A T, KNIGHT J M, CODONA J L, et al. Adaptive optics self-calibration using differential OTF (dOTF)[J]. Proceedings of SPIE, 2015, 9605: 96052B. doi: 10.1117/12.2189583 [5] KIM D W, OH C J, LOWMAN A, et al. Manufacturing of super-polished large aspheric/freeform optics[J]. Proceedings of SPIE, 2016, 9912: 99120F. [6] STUHLINGER T W. Subaperture optical testing: experimental verification[J]. Proceedings of SPIE, 1986, 656: 118-127. doi: 10.1117/12.938467 [7] CHEN SH Y, DAI Y F, LI SH Y, et al. Error reductions for stitching test of large optical flats[J]. Optics &Laser Technology, 2012, 44(5): 1543-1550. [8] KIM C J. Polynomial fit of subaperture interferograms[J]. Proceedings of SPIE, 1983, 351: 28-41. doi: 10.1117/12.933909 [9] TROLINGER J D. The language of holography[J]. Light:Advanced Manufacturing, 2021, 2(4): 473-481. [10] ZHANG J W, DAI S Q, MA CH J, et al. A review of common-path off-axis digital holography: towards high stable optical instrument manufacturing[J]. Light:Advanced Manufacturing, 2021, 2(3): 333-349. [11] FRATZ M, SEYLER T, BERTZ A, et al. Digital holography in production: an overview[J]. Light:Advanced Manufacturing, 2021, 2(3): 283-295. [12] BONNET H, BIANCAT-MARCHET F, DIMMLER M, et al. Adaptive optics at the ESO ELT[J]. Proceedings of SPIE, 2018, 10703: 1070310. [13] WOLFE C R, DOWNIE J D, LAWSON J K. Measuring the spatial frequency transfer function of phase-measuring interferometers for laser optics[J]. Proceedings of SPIE, 1996, 2870: 553-557. doi: 10.1117/12.259943 [14] PARKS R E. Optical surface specification using the structure function[C]. Proceedings of Optical Fabrication and Testing 2010, Optica Publishing Group, 2010: OWE3. [15] SEO B J, NISSLY C, ANGELI G, et al. Analysis of normalized point source sensitivity as a performance metric for large telescopes[J]. Applied Optics, 2009, 48(31): 5997-6007. doi: 10.1364/AO.48.005997 [16] STOKES A J, DUNCAN B D, DIERKING M P, et al. Improving mid-frequency contrast in sparse aperture optical imaging systems based upon the Golay-9 array[J]. Optics Express, 2010, 18(5): 4417-4427. doi: 10.1364/OE.18.004417 [17] 孔小辉, 樊学武, 马臻, 等. 大口径平面镜的计算机辅助瑞奇-康芒检验[J]. 应用光学,2010,31(6):984-988. doi: 10.3969/j.issn.1002-2082.2010.06.023KONG X H, FAN X W, MA ZH, et al. Computer added Ritchey-Common test for large flat mirror measurement[J]. Journal of Applied Optics, 2010, 31(6): 984-988. (in Chinese) doi: 10.3969/j.issn.1002-2082.2010.06.023 [18] ZHU SH, ZHANG X H. Eliminating alignment error and analyzing Ritchey angle accuracy in Ritchey-Common test[J]. Optics Communications, 2013, 311: 368-374. doi: 10.1016/j.optcom.2013.08.024 [19] 刘一鸣, 李金鹏, 陈磊, 等. 采用单位激励影响矩阵数值计算的瑞奇-康芒检测技术[J]. 光学 精密工程,2018,26(4):771-777. doi: 10.3788/OPE.20182604.0771LIU Y M, LI J P, CHEN L, et al. Ritchey-Common interferometry using unit-excitation influence matrix's numerical calculation method[J]. Optics and Precision Engineering, 2018, 26(4): 771-777. (in Chinese) doi: 10.3788/OPE.20182604.0771 [20] 白晓泉, 郭良, 马宏财, 等. 离轴三反望远镜轴向与横向失调量像差耦合特性[J]. 中国光学(中英文),2022,15(4):747-760. doi: 10.37188/CO.2021-0164BAI X Q, GUO L, MA H C, et al. Aberration coupling characteristics of axial and lateral misalignments of off-axis three-mirror telescopes[J]. Chinese Optics, 2022, 15(4): 747-760. (in Chinese) doi: 10.37188/CO.2021-0164 [21] 冯维, 徐仕楠, 王恒辉, 等. 逐像素调制的高反光表面三维测量方法[J]. 中国光学,2022,15(3):488-497. doi: 10.37188/CO.2021-0220FENG W, XU SH N, WANG H H, et al. Three-dimensional measurement method of highly reflective surface based on per-pixel modulation[J]. Chinese Optics, 2022, 15(3): 488-497. (in Chinese) doi: 10.37188/CO.2021-0220 -
下载:
计量
- 文章访问数: 618
- HTML全文浏览量: 275
- PDF下载量: 191
- 被引次数: 0
