-
摘要:
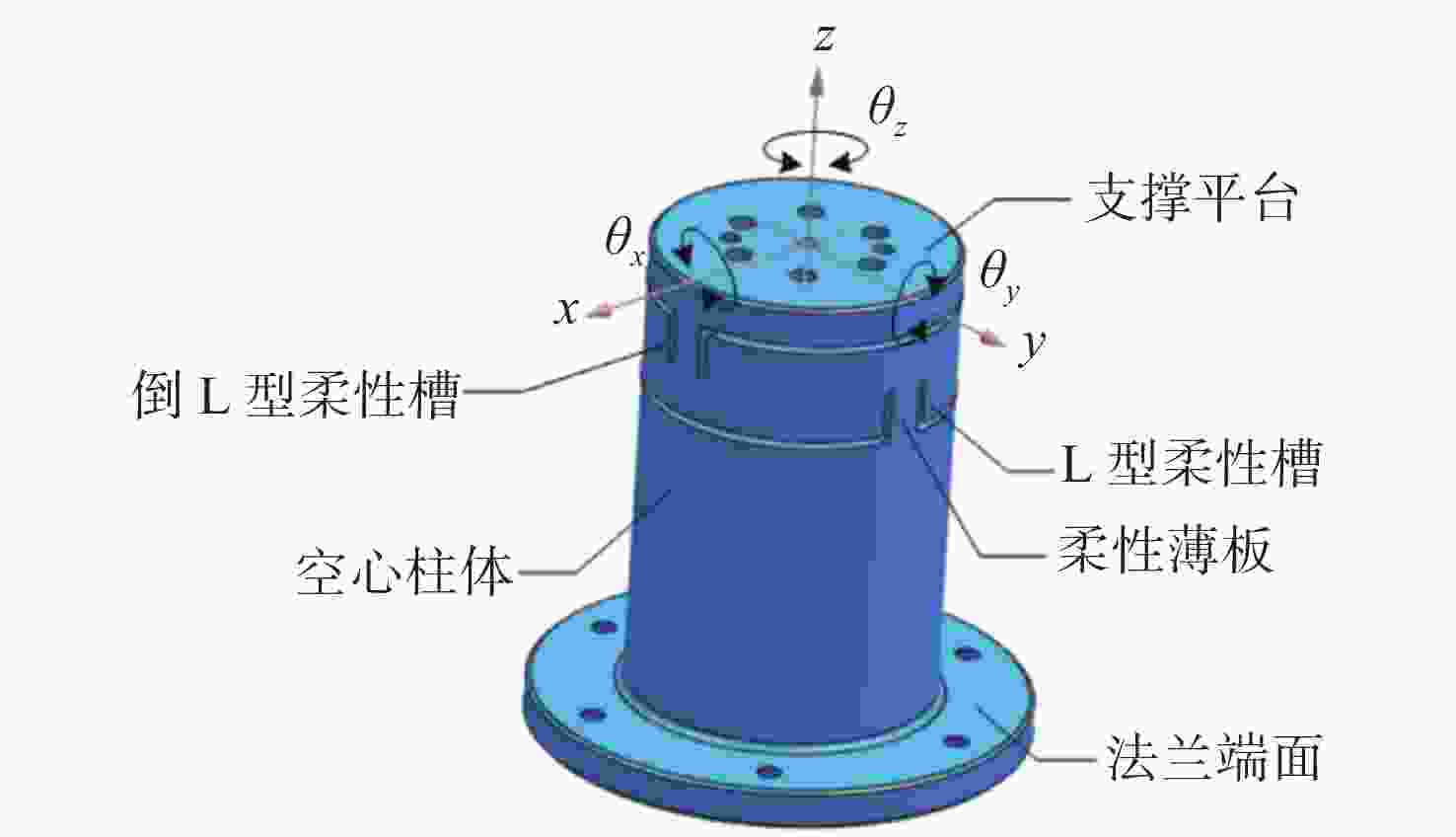
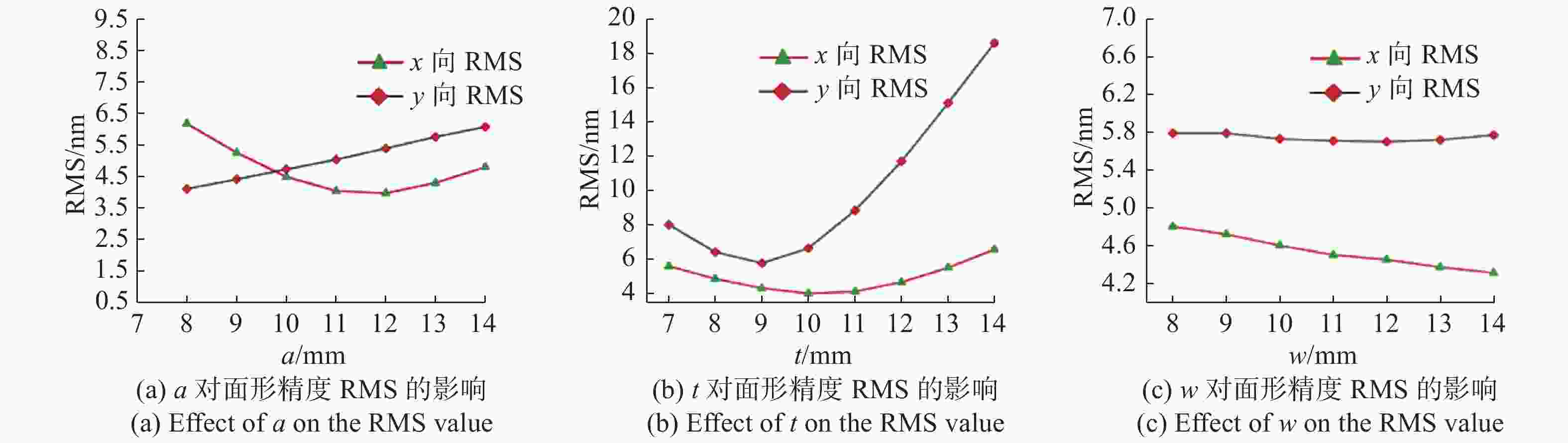
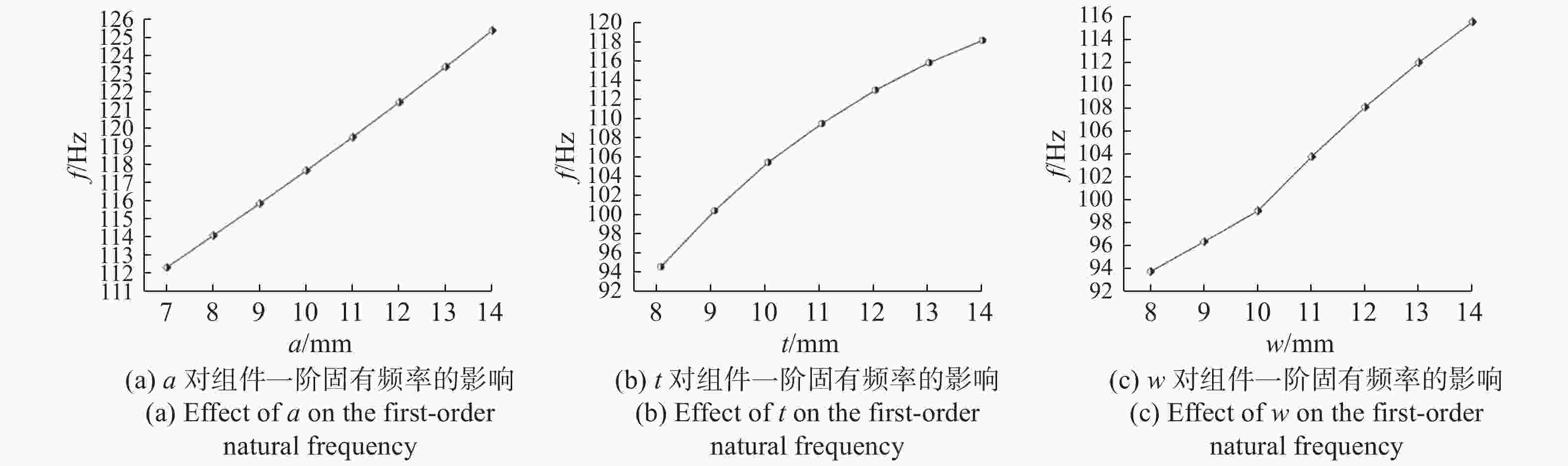
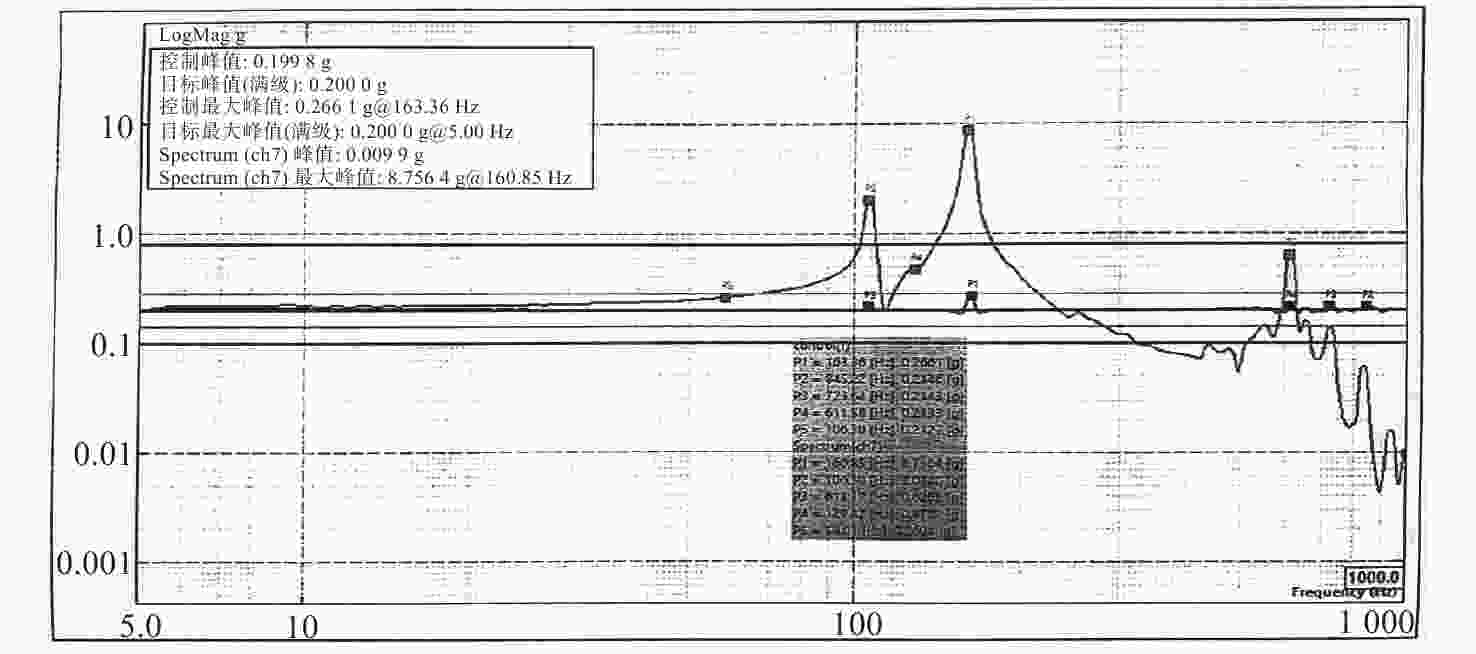
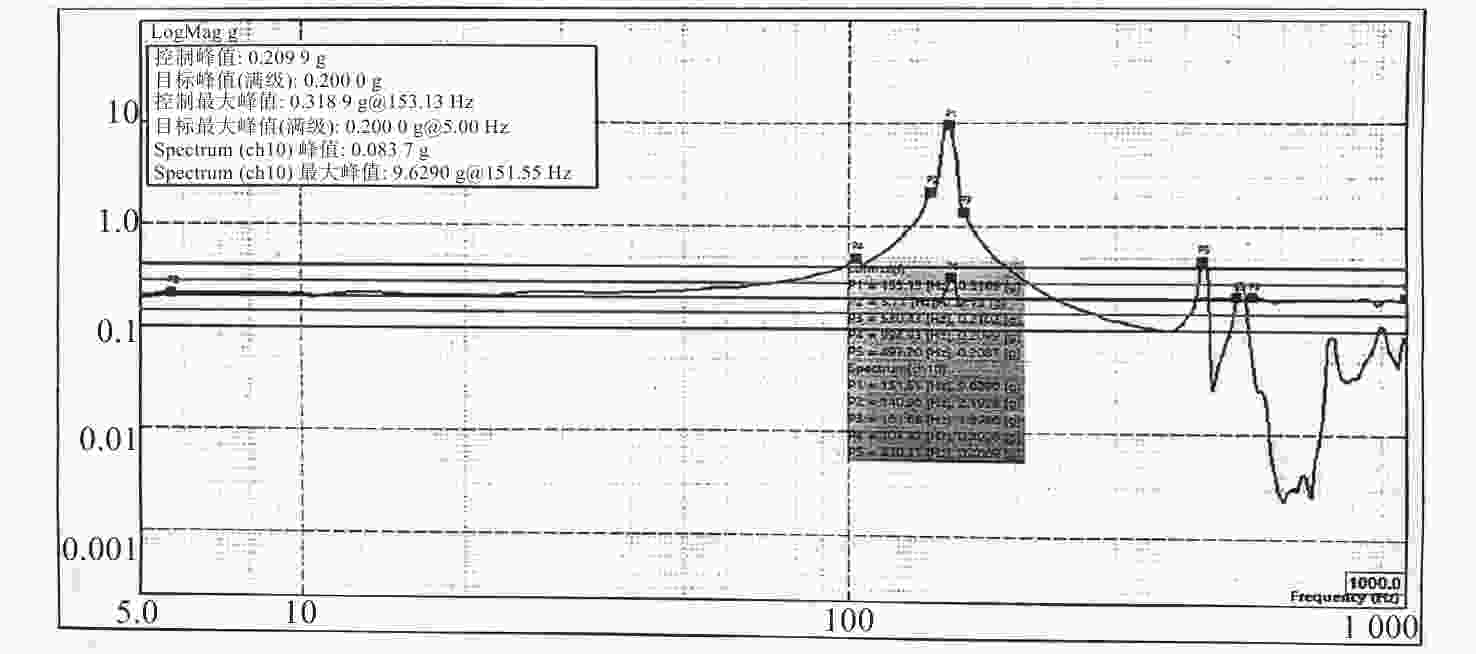
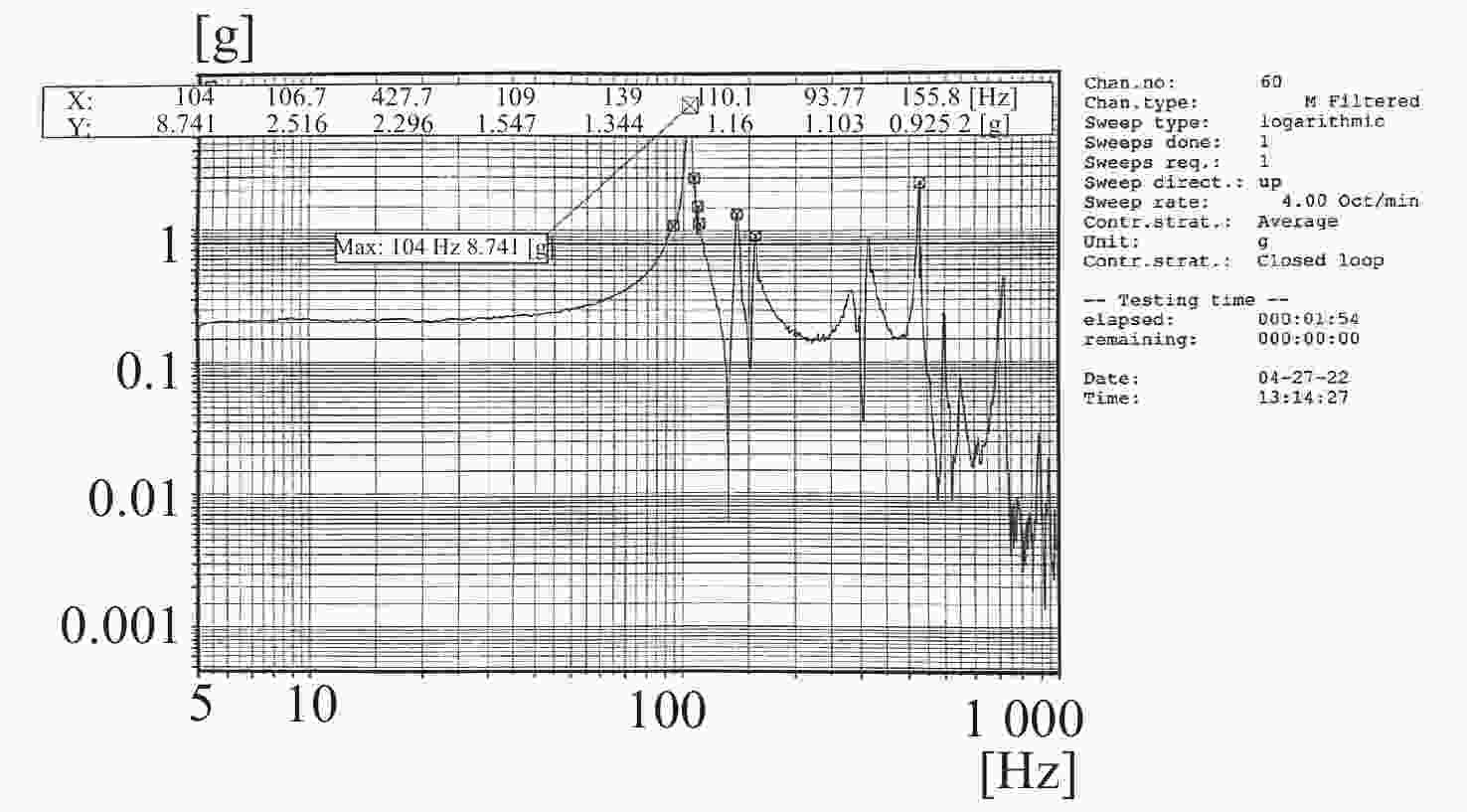
1.8 m×0.5 m口径的长条形主反射镜是某空间离轴三反光学系统的重要光学元件，其面形精度的好坏是决定光学系统在轨成像质量的关键。为保证主镜组件结构的稳定性、可靠性及反射镜的面形精度，提出一种适用于大尺寸长条形反射镜的双轴柔性支撑结构。首先，基于运动学等效原理提出双轴柔性支撑的初始结构，建立了柔性环节刚度数学模型并研究了其刚度特性。然后，对柔性支撑的安装位置进行了参数化研究并对柔性支撑的关键尺寸进行了优化设计。最后，确定了反射镜组件的最终设计方案。仿真与试验结果表明，反射镜组件一阶固有频率为104 Hz。
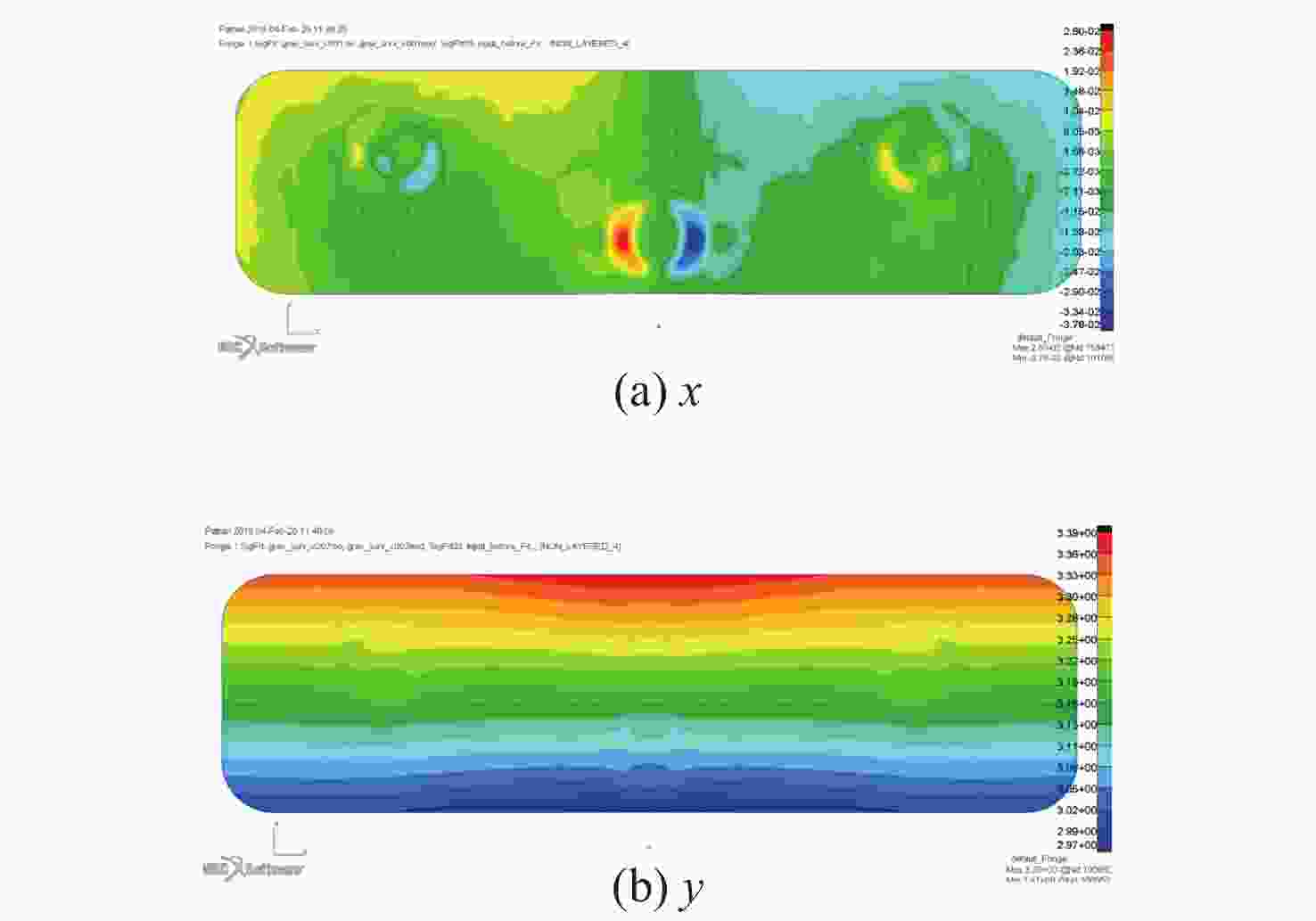
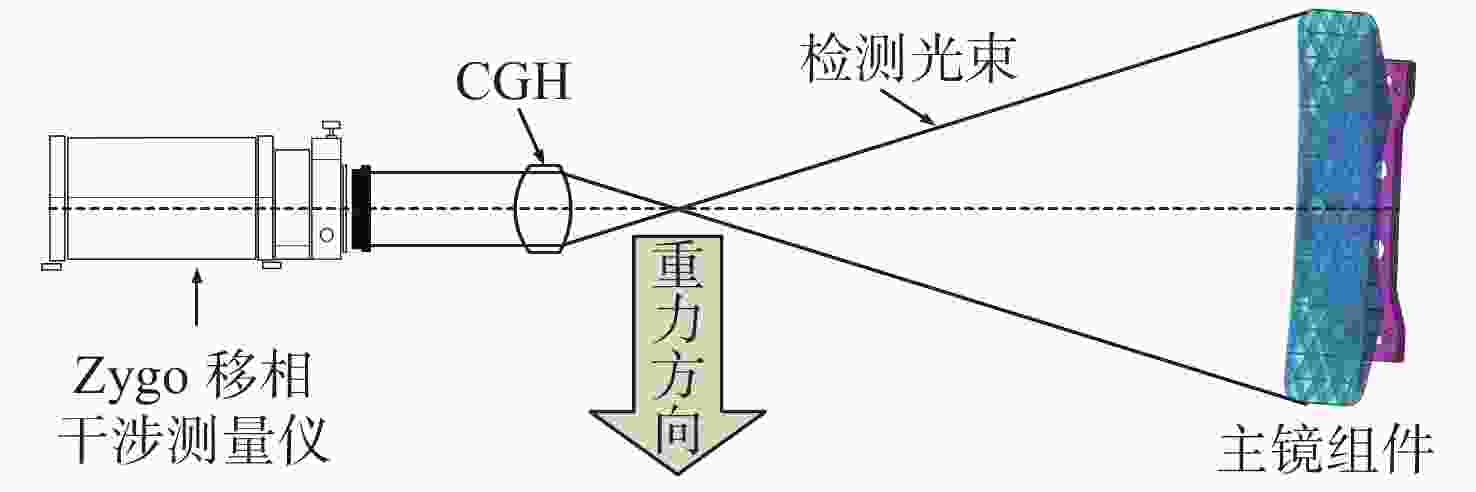
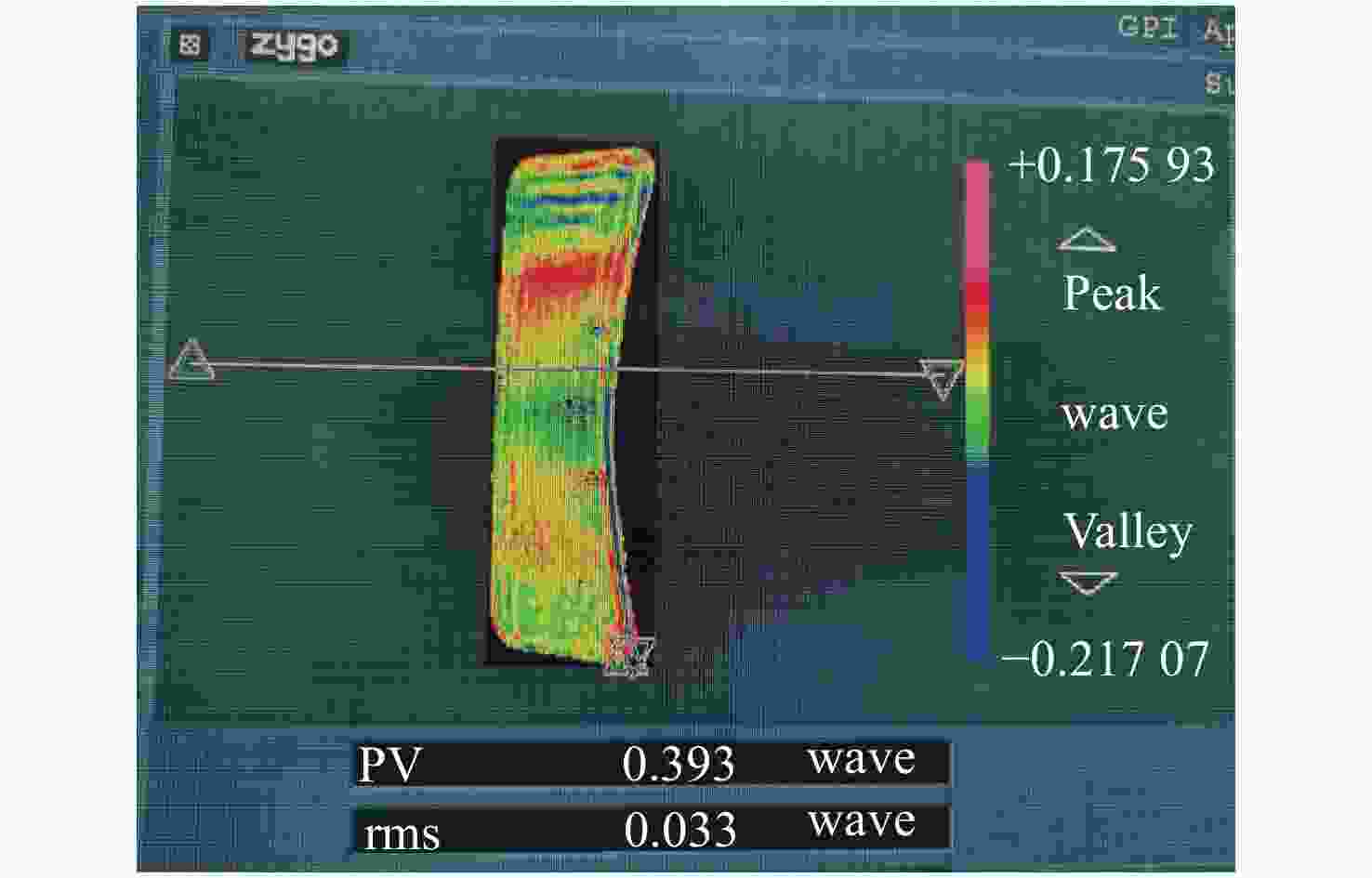
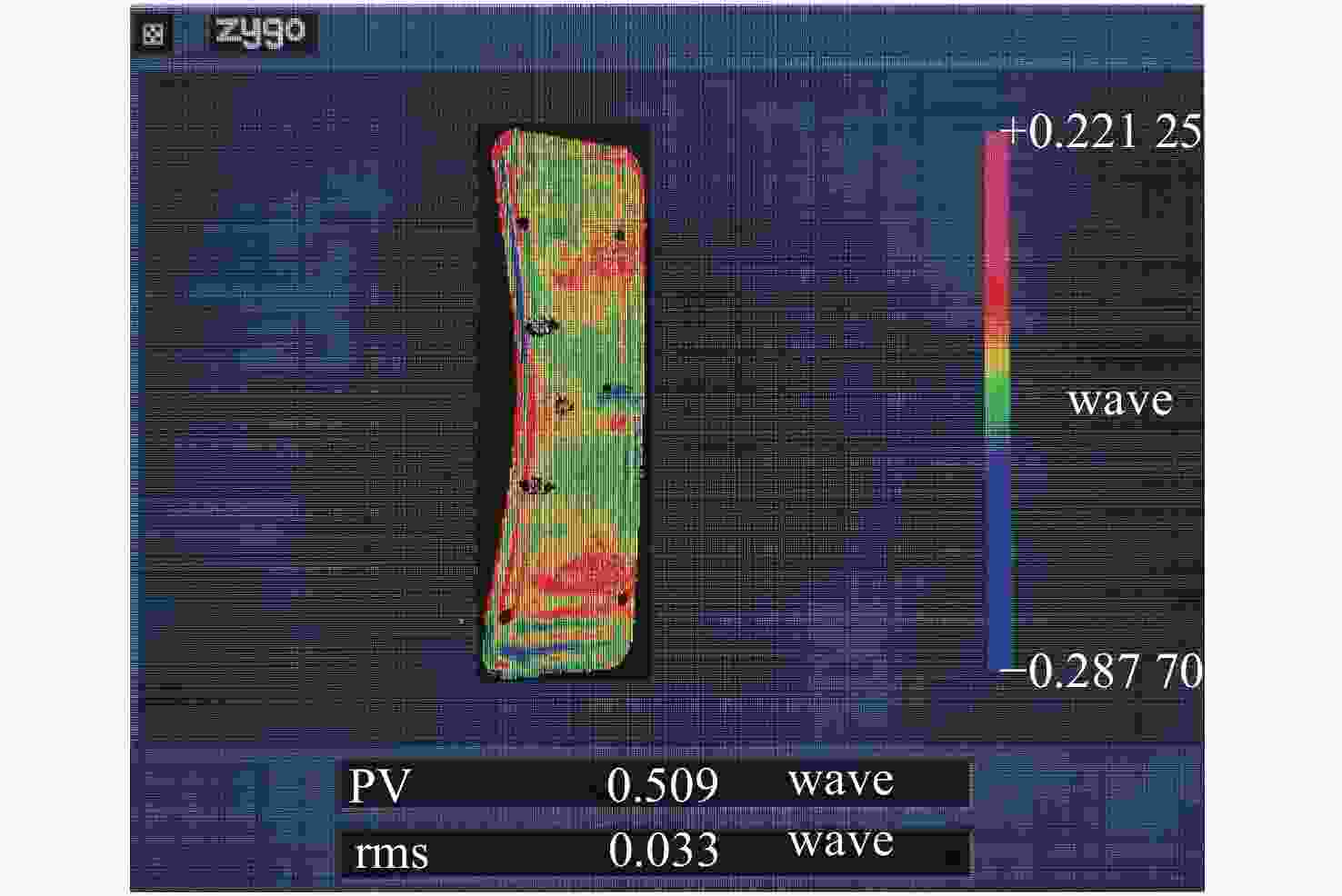
X /Y 两个光轴分别对径向施加1 G重力时面形精度RMS值分别为4.81 nm、6.09 nm，优于λ /50（λ =632.8 nm），均满足设计要求。组件正样动力学环境试验表明，反射镜组件的动力学特性良好，柔性支撑系统稳定可靠，与仿真结果一致。目前反射镜全口径面形精度已加工至λ /30 RMS，并在此精度下进行了自重0°/180°的±1 G面形检测试验，结果显示其稳定性良好。Abstract:The rectangular primary mirror with aperture of 1.8 m×0.5 m is the crucial component of an off-axis Three Mirror Anastigmat (TMA) space optical system. In order to guaranty the structural stability and reliability of the Primary Mirror Assembly (PMA) and the surface figure error (RMS value) of the mirror, a bi-axial flexural support has been proposed for the large-size rectangular mirror. First, based on the principle of kinematic equivalent, the initial structure of the bi-axial flexural support was designed and the analytical formula for stiffness and its characteristic was studied as well. Then the mounting position and the key dimensions of the flexural supports were studied and optimized. Finally, the final optimization design scheme of the PMA was determined. Experimental results indicate that the surface figure error (RMS value) of the PMA under 1 G gravity in
X andY directions are 4.81 nm and 6.09 nm respectively when the optical axis is placed horizontally, which are less thanλ /50 (λ =632.8 nm). The first-order natural frequency is 104 Hz, which can satisfy the design requirements. The dynamic tests have shown that the dynamic characteristics of the mirror assembly are good, and the flexural support system is stable and reliable. Now the mirror has been polished to have a surface figure better than λ/30 RMS. Zero Gravity optical testing has been performed under ±1 G respectively, which shows good coincidence with the analytical results. -
图 1 大尺寸长条形反射镜的支撑结构原理示意图
Figure 1. Schematic diagram of mounting structure of a rectangular mirror with large aperture
图 2 典型的反射镜约束方式。（a）“2-2-2”约束方式；（b）“3-2-1”约束方式
Figure 2. Typical constraints for a mirror. (a) 2-2-2 Constraint; (b) 3-2-1 Constraint
图 3 基于运动学等效原理的双轴柔性铰链
Figure 3. A bi-axial flexural hinge based on kinematic equivalence principle
图 6 kx与短直梁的高度a、厚度t、宽度w的关系图
Figure 6. Relationship between kx and height a, thickness t, width w of the short straight beam
图 11 ε1（a）和ε2（b）对RMS值的影响
Figure 11. Effect of ε1 (a) and ε2 (b) on the surface figure RMS
图 12 ε1（a）和ε2（b）对反射镜组件一阶固有频率的影响
Figure 12. Effect of ε1 (a) and ε2 (b) on the first-order natural frequency of PMA
图 14 不同θ1值1 G自重作用下的镜面变形(去除刚体位移)
Figure 14. Surface deformation at different θ1 values under 1 G gravity (removed rigid-body displacement)
图 15 θ2对RMS和一阶固有频率的影响
Figure 15. Effect of different θ2 values on the RMS and first-order natural frequency
图 16 柔性支撑的不同尺寸对面形精度的影响
Figure 16. Effect of different sizes of flexural support on the RMS value
图 17 柔性支撑不同尺寸对一阶固有频率的影响
Figure 17. Effect of different sizes of flexural supports on the first-order natural frequency
图 19 镜面在x、y向自重作用下的变形(去除刚体位移)
Figure 19. Surface deformation under 1 G gravity in x and y directions (rigid-body displacement removed)
图 25 反射镜非球面干涉检验原理图
Figure 25. Schematic diagram of mirror aspheric interferometry optical testing layout
图 26 反射镜0°方向的面形检测结果
Figure 26. The surface figure of the mirror tested in 0° direction
图 27 反射镜180°方向的面形检测结果
Figure 27. The surface figure of the mirror tested in 180° direction
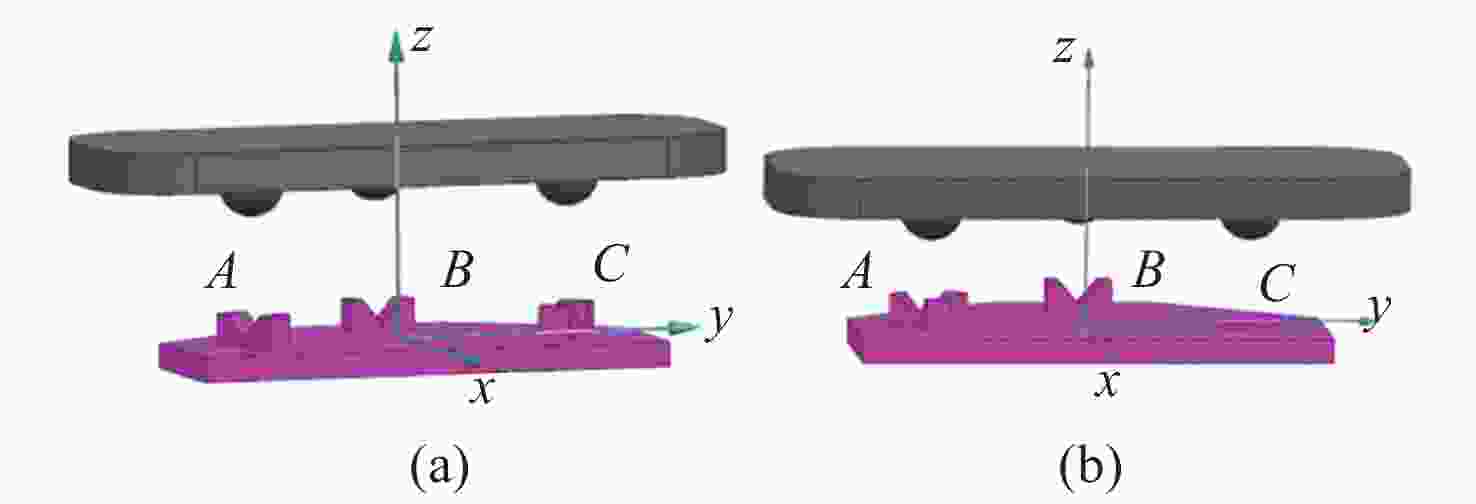
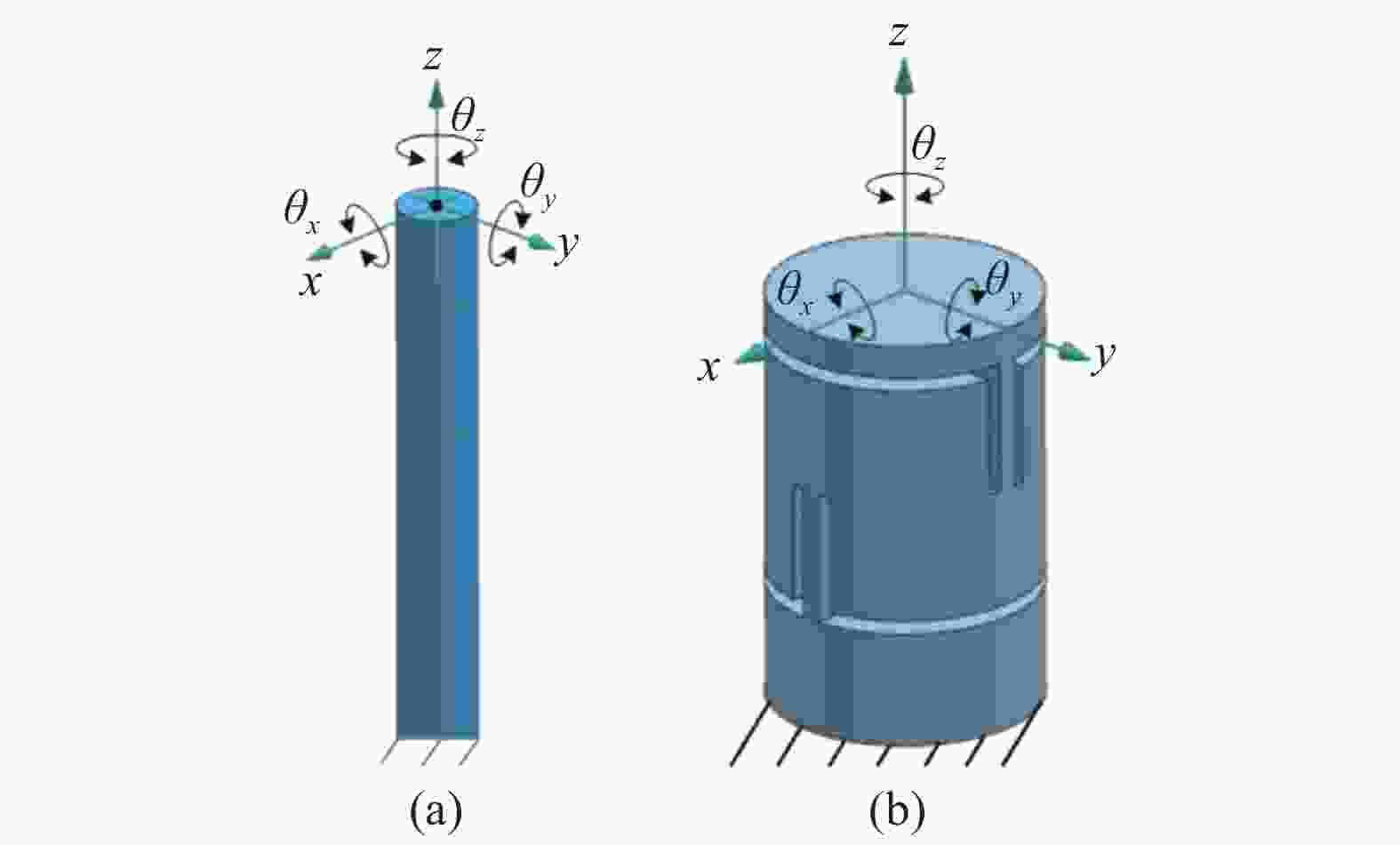
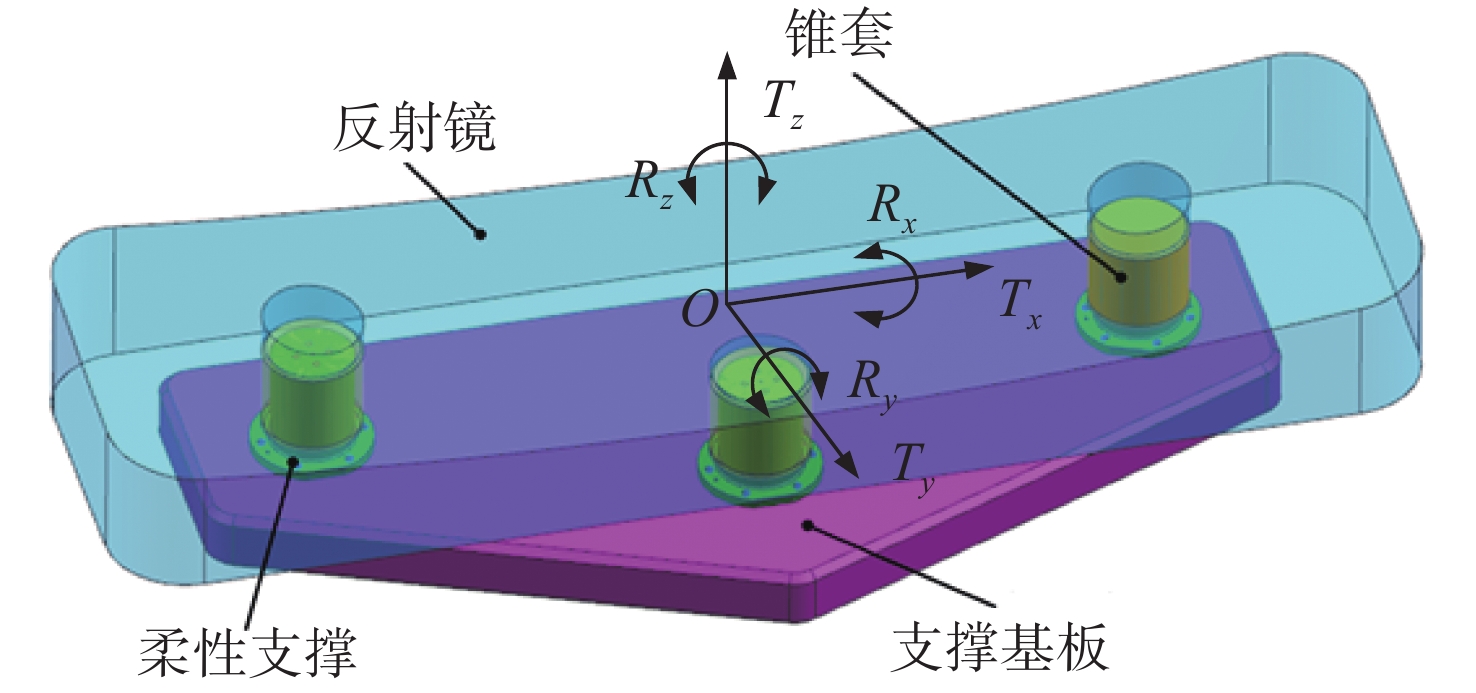
表 1 典型反射镜约束方式各支撑点的自由度
Table 1. Degree of freedom at each support point for mirror's typical constraints
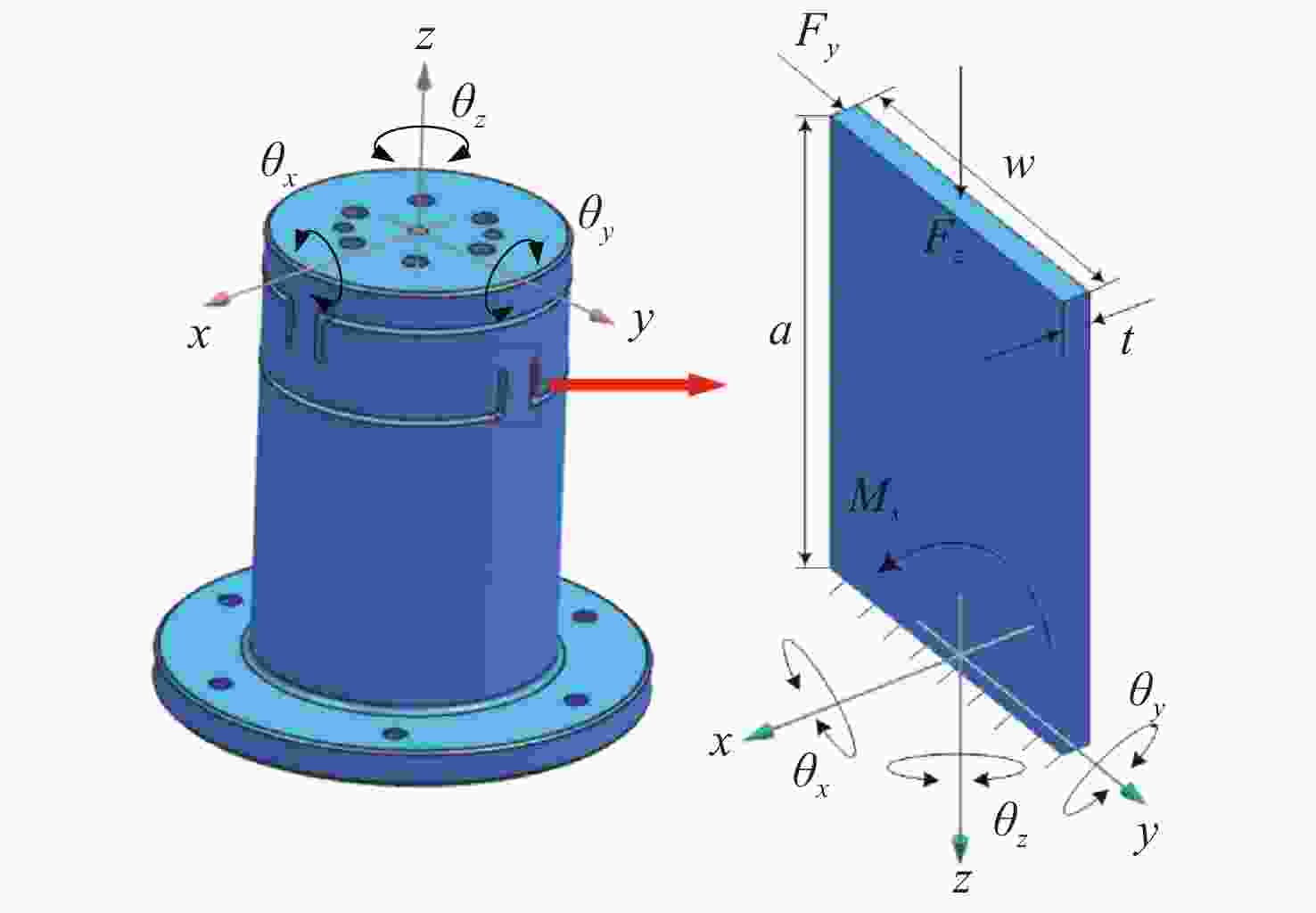
（a）“2-2-2”约束方式 支撑点 约束自由度 释放自由度 A Tx、Rx Ty、Tz、Ry、Rz B Ty、Ry Tx、Tz、Rx、Rz C Tz、Rz Tx、Ty、Rx、Ry （b）“3-2-1”约束方式 支撑点 约束自由度 释放自由度 A Tx、Ty、Tz Rx、Ry、Rz B Ty、Rz Tx、Ty、Tz、Rx C Rx Tx、Ty、Tz、Ry、Rz 
下载: 导出CSV
表 2 短直梁的尺寸初值
Table 2. Initial size values of the short straight beam
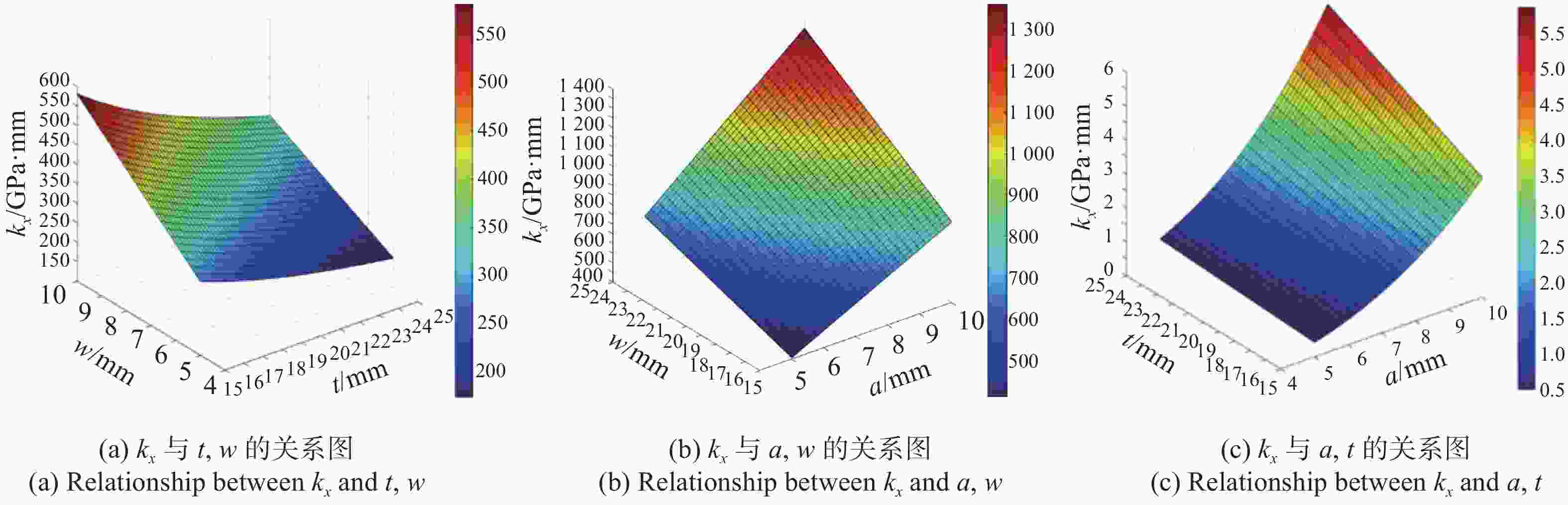
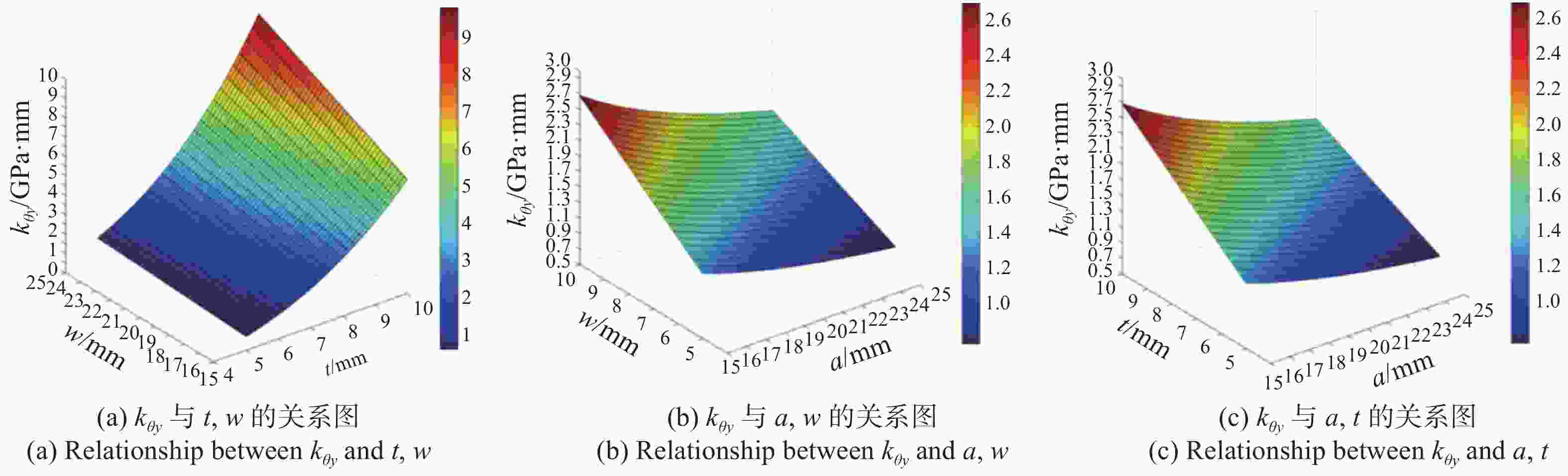
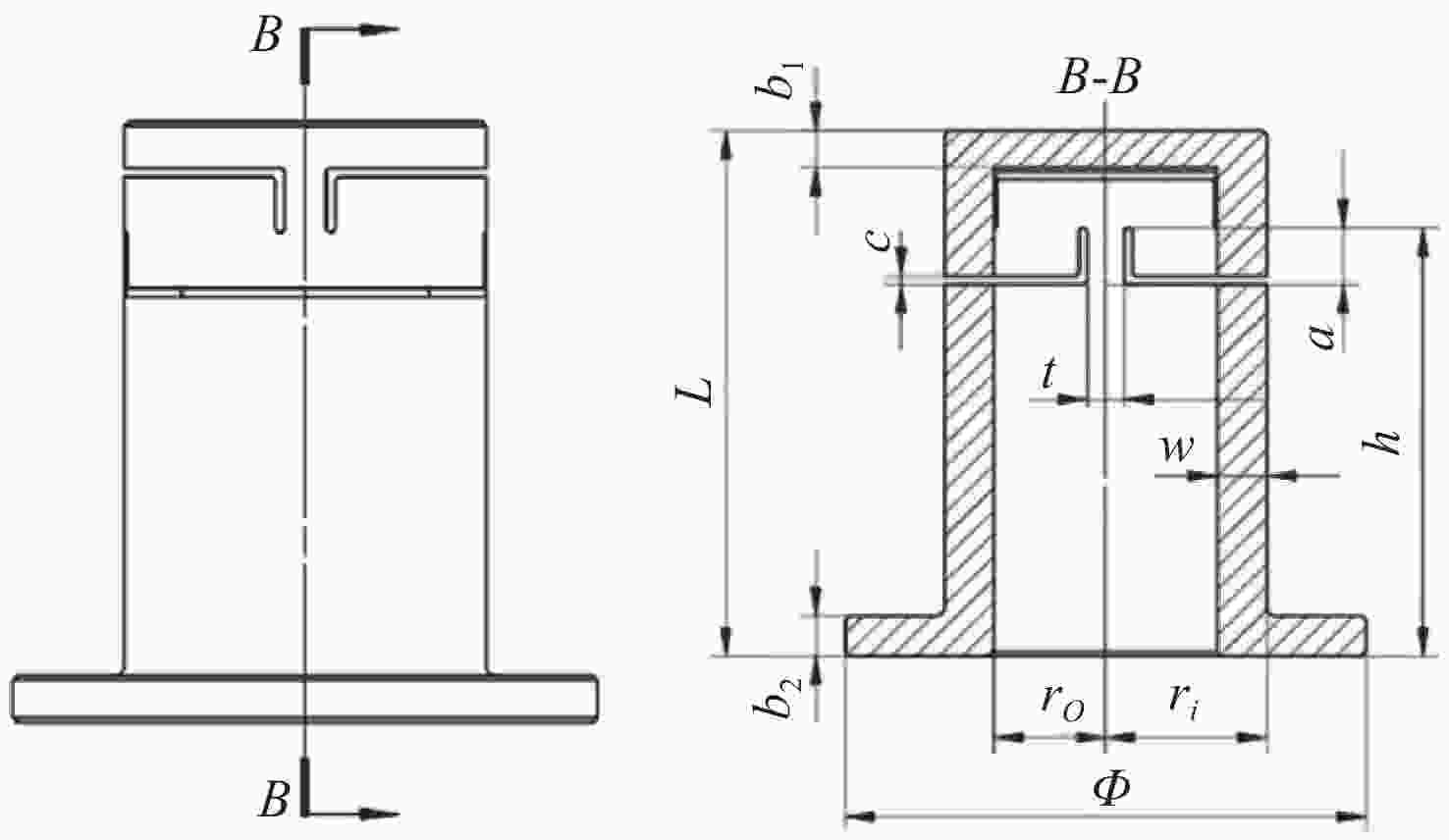
尺寸变量 初值/mm 尺寸范围/mm a 20 15~25 t 8 5~10 w 12 7~15
下载: 导出CSV
表 3 柔性支撑1在不同安装角度下的镜面面形值
Table 3. Surface figure error of flexural support No.1 at different mounting angles
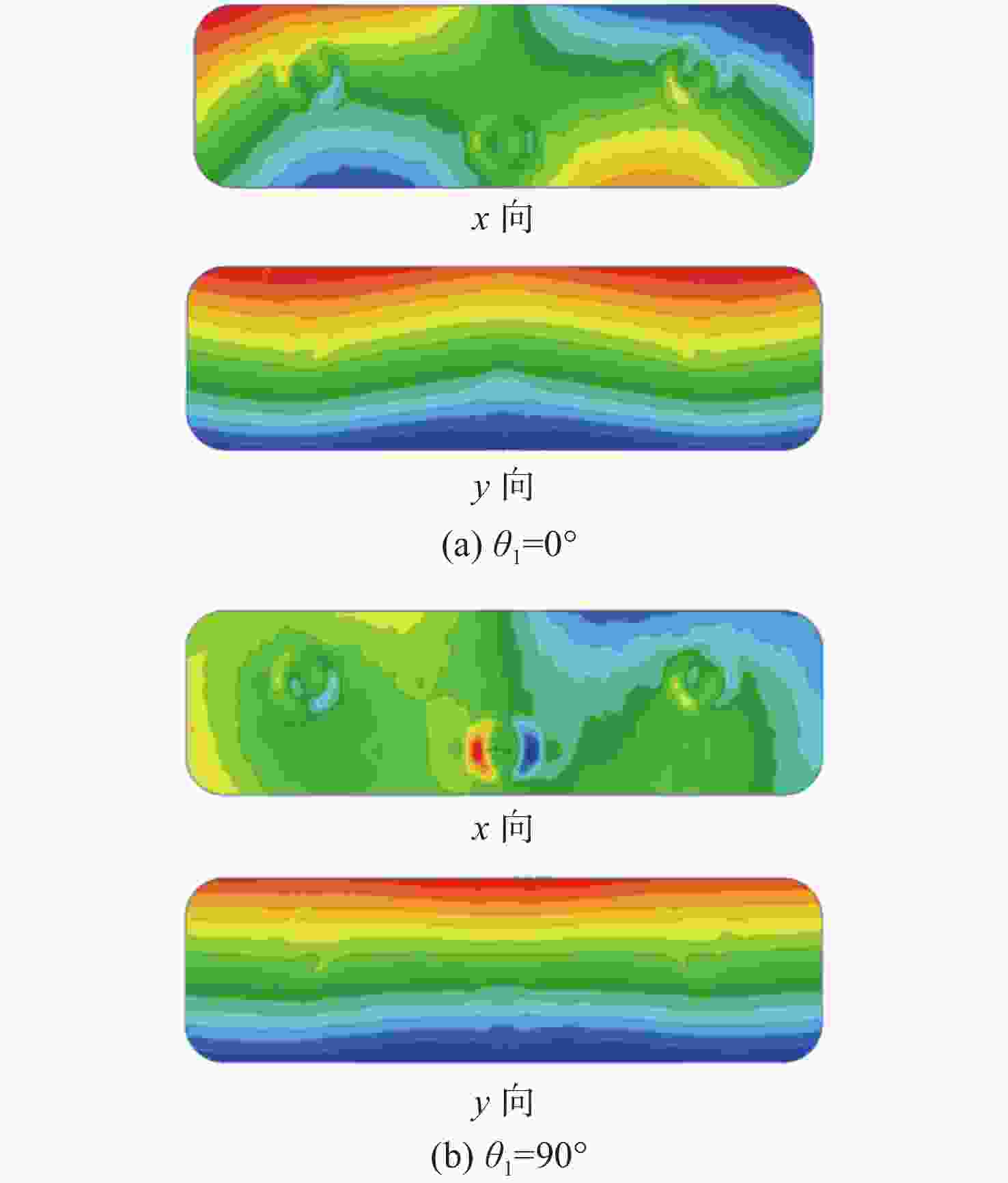
角度θ/° x向RMS/nm y向RMS/nm 一阶固有频率/Hz 0 10.1 28.5 108.75 90 3.97 5.34 106.36
下载: 导出CSV
-
[1] JI H R, ZHU ZH B, TAN H, et al. Design of a high-throughput telescope based on scanning an off-axis three-mirror anastigmat system[J]. Applied Optics, 2021, 60(10): 2817-2823. doi: 10.1364/AO.421998 [2] 李叶文, 李宗轩, 刘瑞婧, 等. 空间光学遥感器长条形反射镜集成优化设计[J]. 科学技术与工程,2019,19(35):375-381. doi: 10.3969/j.issn.1671-1815.2019.35.057LI Y W, LI Z X, LIU R J, et al. Integrated optimization design of rectangular mirror for space optical remote sensor[J]. Science Technology and Engineering, 2019, 19(35): 375-381. (in Chinese) doi: 10.3969/j.issn.1671-1815.2019.35.057 [3] 李宗轩, 陈雪, 张雷, 等. 大口径空间反射镜Cartwheel型柔性支撑设计[J]. 光学学报,2014,34(6):0622003. doi: 10.3788/AOS201434.0622003LI Z X, CHEN X, ZHANG L, et al. Design of Cartwheel flexural support for a large aperture space mirror[J]. Acta Optica Sinica, 2014, 34(6): 0622003. (in Chinese) doi: 10.3788/AOS201434.0622003 [4] 曲慧东, 魏加立, 董得义, 等. 长条形空间反射镜组件轻量化结构设计[J]. 红外与激光工程,2021,50(6):20200404. doi: 10.3788/IRLA20200404QU H D, WEI J L, DONG D Y, et al. Lightweight structural design of rectangular space mirror assembly[J]. Infrared and Laser Engineering, 2021, 50(6): 20200404. (in Chinese) doi: 10.3788/IRLA20200404 [5] KIHM H, YANG H S. Design optimization of a 1-m lightweight mirror for a space telescope[J]. Optical Engineering, 2013, 52(9): 091806. doi: 10.1117/1.OE.52.9.091806 [6] 朱俊青, 沙巍, 陈长征, 等. 空间长条形反射镜背部三支撑点的设置[J]. 光学 精密工程,2015,23(9):2562-2569. doi: 10.3788/OPE.20152309.2562ZHU J Q, SHA W, CHEN CH ZH, et al. Position layout of rear three point mounting for space rectangular mirror[J]. Optics and Precision Engineering, 2015, 23(9): 2562-2569. (in Chinese) doi: 10.3788/OPE.20152309.2562 [7] HUO T L, YU J J, ZHAO H ZH. Design of a kinematic flexure mount for precision instruments based on stiffness characteristics of flexural pivot[J]. Mechanism and Machine Theory, 2020, 150: 103868. doi: 10.1016/j.mechmachtheory.2020.103868 [8] 王朋朋, 辛宏伟, 朱俊青, 等. 长条反射镜及柔节的参数优化设计[J]. 红外与激光工程,2021,50(8):20200493. doi: 10.3788/IRLA20200493WANG P P, XIN H W, ZHU J Q, et al. Parametric optimization design of rectangular reflective mirror and flexible component[J]. Infrared and Laser Engineering, 2021, 50(8): 20200493. (in Chinese) doi: 10.3788/IRLA20200493 [9] 刘福贺, 程志峰, 石磊, 等. 长条形反射镜支撑结构设计与分析[J]. 红外与激光工程,2015,44(5):1512-1517. doi: 10.3969/j.issn.1007-2276.2015.05.021LIU F H, CHENG ZH F, SHI L, et al. Design and analysis of supporting structure for rectangular mirror[J]. Infrared and Laser Engineering, 2015, 44(5): 1512-1517. (in Chinese) doi: 10.3969/j.issn.1007-2276.2015.05.021 [10] 杨秋实, 张继友, 于建海, 等. 大口径空间反射镜支撑变形误差分析方法研究[J]. 航天返回与遥感,2020,41(3):60-70. doi: 10.3969/j.issn.1009-8518.2020.03.007YANG Q SH, ZHANG J Y, YU J H, et al. Research on error analysis of support deformation for large aperture space mirrors[J]. Spacecraft Recovery &Remote Sensing, 2020, 41(3): 60-70. (in Chinese) doi: 10.3969/j.issn.1009-8518.2020.03.007 [11] 刘小涵, 李双成, 李美萱, 等. 离轴三反光学系统主三反射镜支撑结构设计[J]. 红外与激光工程,2021,50(8):20210025. doi: 10.3788/IRLA20210025LIU X H, LI SH CH, LI M X, et al. Supporting structure design for primary and tertiary mirror of off-axis TMA system[J]. Infrared and Laser Engineering, 2021, 50(8): 20210025. (in Chinese) doi: 10.3788/IRLA20210025 [12] KRUIS J R C G. Design, analysis, testing and applications of two-body and three-body kinematic mounts[D]. Lausanne: École Polytechnique Fédérale de Lausanne, 2016. [13] HOWELL L L, MAGLEBY S P, OLSEN B M. 柔顺机构设计理论与实例[M]. 陈贵敏, 于靖军, 马洪波, 等译. 北京: 高等教育出版社, 2015.HOWELL L L, MAGLEBY S P, OLSEN B M. Handbook of Compliant Mechanisms[M]. CHEN G M, YU J J, MA H B, et al. , trans. Beijing: Higher Education Press, 2015. (in Chinese) [14] LI Z X, CHEN X, WANG SH J, et al. Optimal design of a Φ760 mm lightweight SiC mirror and the flexural mount for a space telescope[J]. Review of Scientific Instruments, 2017, 88(12): 125107. doi: 10.1063/1.4986042 -
下载:
计量
- 文章访问数: 594
- HTML全文浏览量: 433
- PDF下载量: 225
- 被引次数: 0
