Aligning method for point cloud prism boundaries of cultural relics based on normal vector and faceted index features
-
摘要:
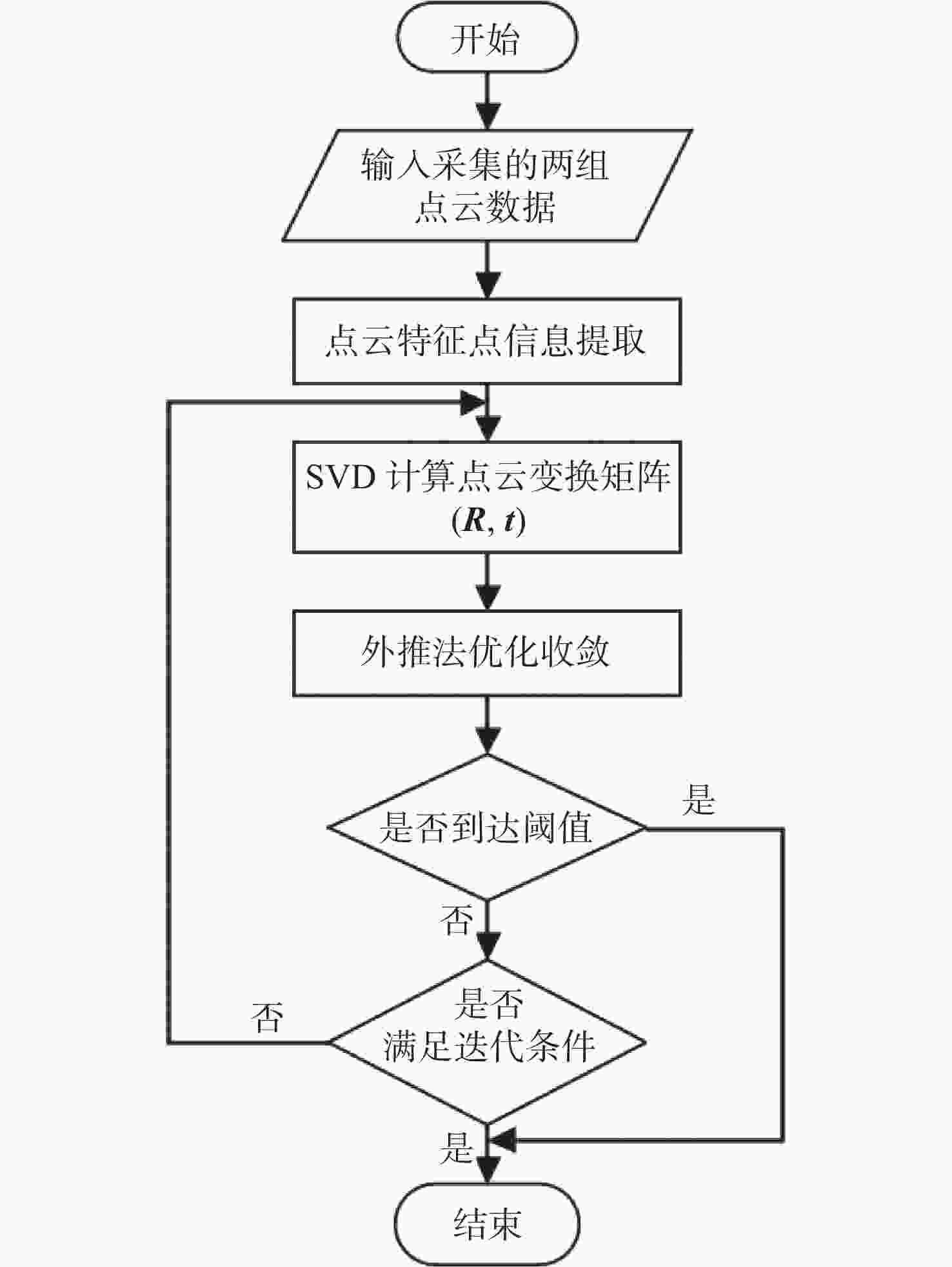
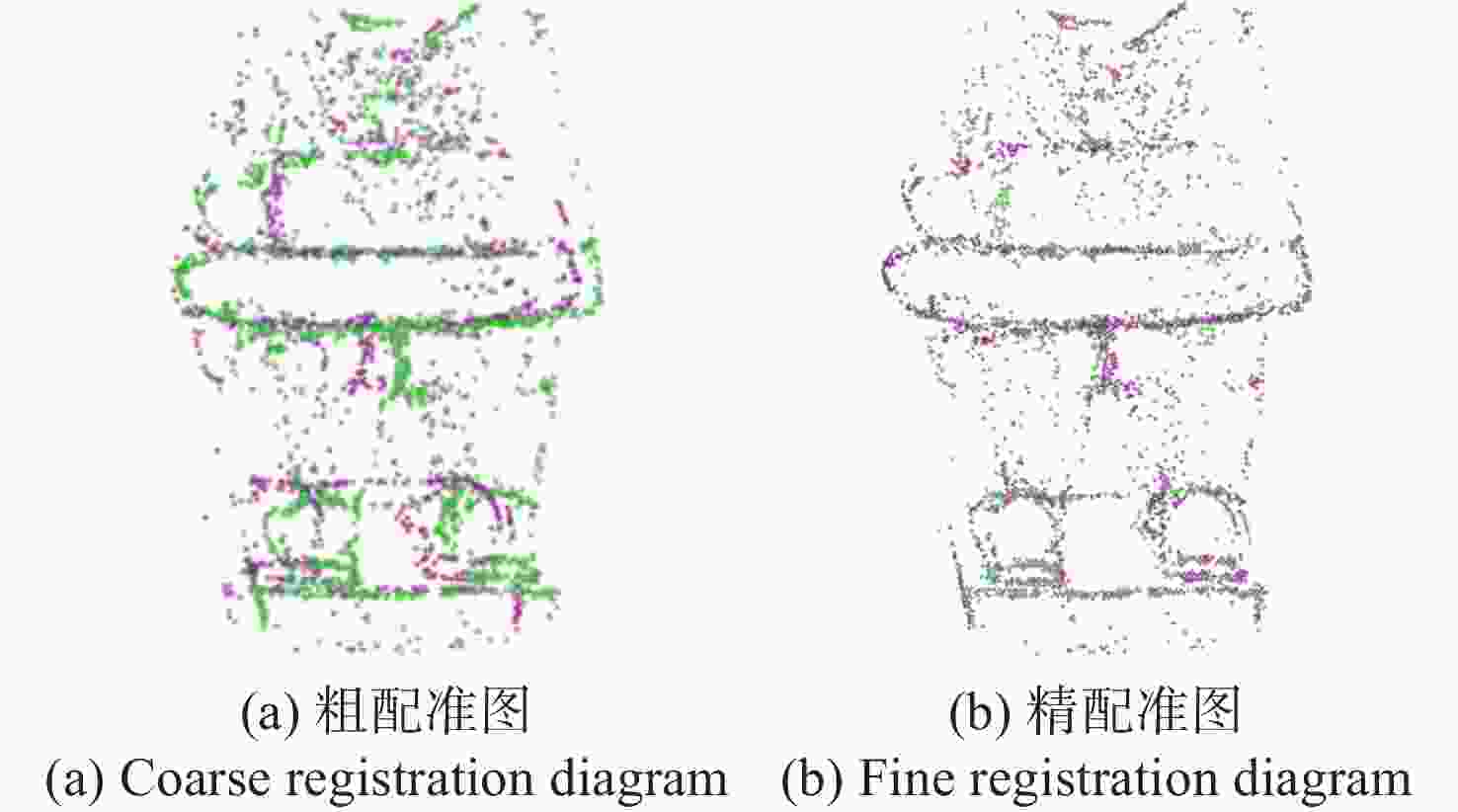
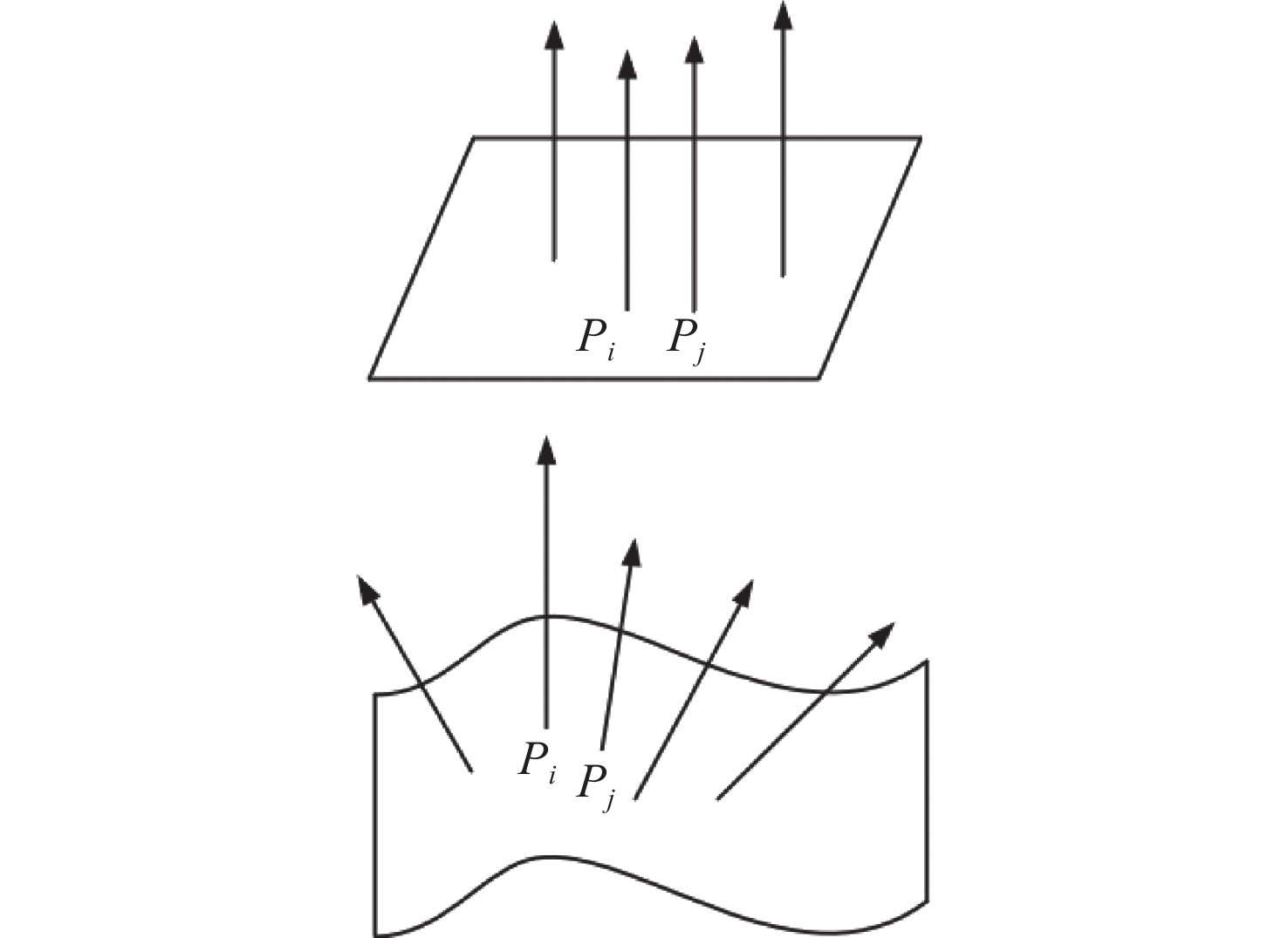
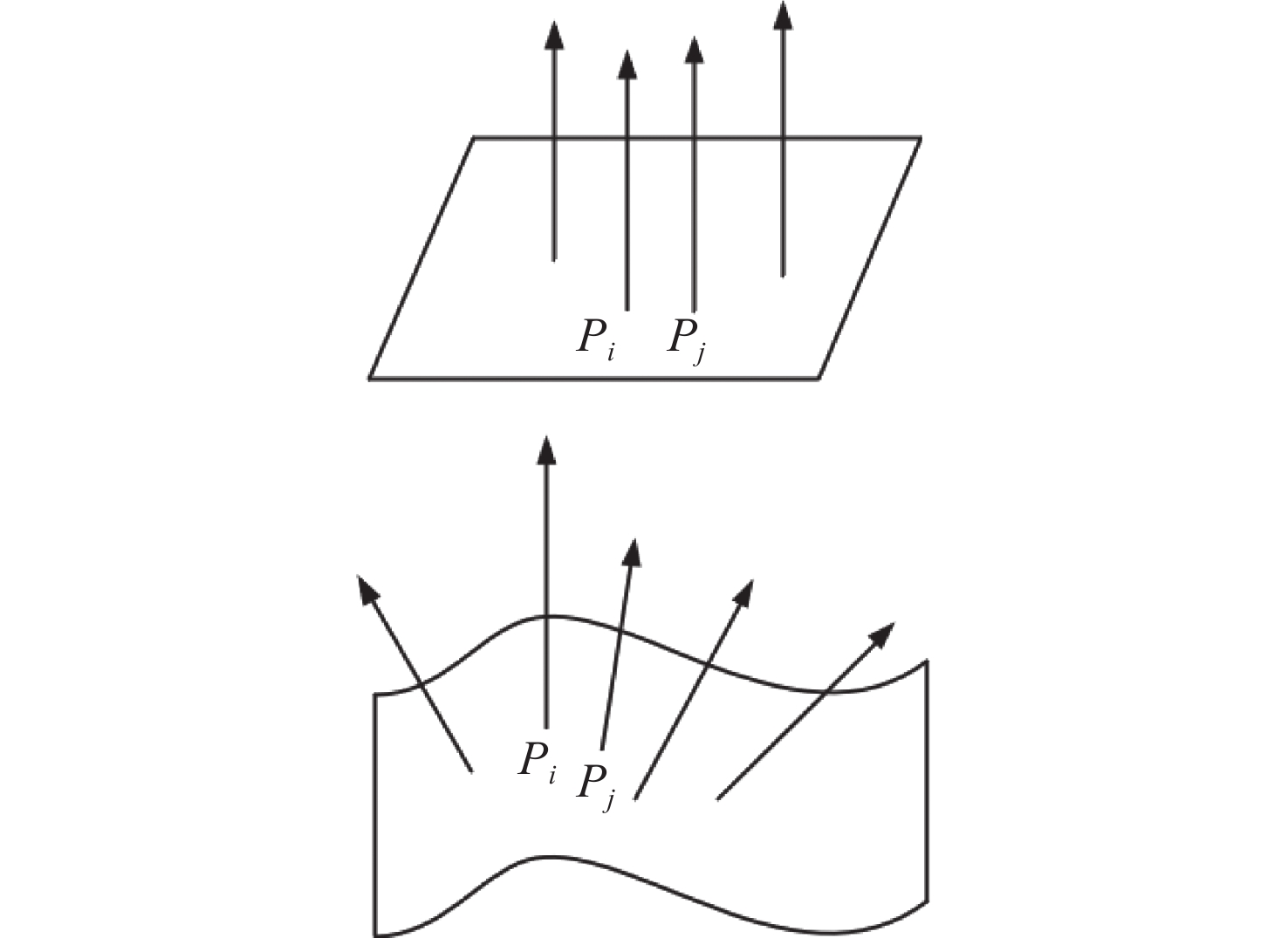
三维重建是文物信息保护常用的方法,其主要通过点云配准技术重组文物空间的点云信息,配准精度对文物复现有重要影响。针对文物表面复杂点云纹理特征配准存在精度低、鲁棒性差的问题,本文提出一种基于法向量夹角和面状指数特征的局域点云配准方法。首先,根据点云平面特性设定法向量夹角和协方差矩阵阈值,提取同时满足这两个特征的点云特征点;其次,采用K近邻搜索方法提取点云局域特征点集,通过刚性变换使两组点云质心位置重合,完成粗配准;最终,在两点云粗配准的基础上,根据迭代最近点ICP进行精配准。与传统ICP方法进行对比分析,结果显示本文方法的点云配准误差下降了3%,匹配耗时降低了50%,有效地提高了配准精度和效率,增强了点云配准的鲁棒性。
Abstract:Three-dimensional reconstruction is a common method for cultural relics information conservation, mainly through point cloud alignment technology to reorganize the spatial point cloud information of cultural relics, and its alignment accuracy has an important impact on cultural relics recovery. To address the problems of low accuracy and poor robustness in the alignment of complex point cloud texture features on the surface of cultural relics, this paper proposes a local point cloud alignment method based on normal vector angle and faceted index features. Firstly, the normal vector angle and covariance matrix thresholds are set according to the point cloud planar characteristics, and the point cloud feature points satisfying both features are extracted; secondly, the point cloud local feature point set is extracted by the K-nearest neighbor search methhod, and the two sets of point cloud center-of-mass positions are overlapped by rigid transformation for coarse alignment; finally, the nearest points are iterated based on ICP for fine alignment. By comparing with the traditional ICP, the point cloud alignment error of the proposed method reduces by 3% and the matching time reduces by 50%, which effectively improves the accuracy and efficiency of alignment and enhances the robustness of point cloud alignment.
-
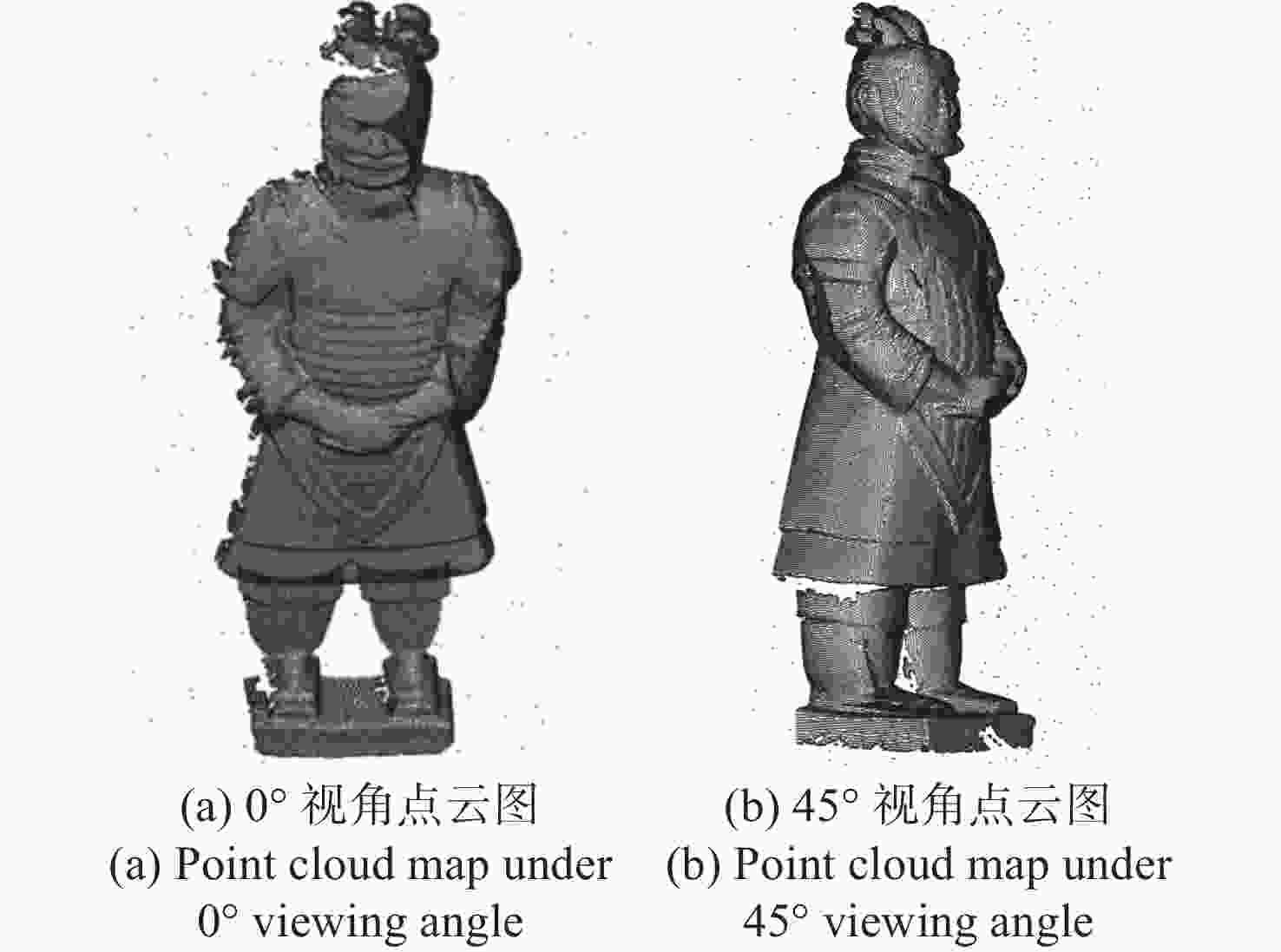
表 1 兵马俑点云配准过程实验数据分析
Table 1. Experimental data analysis of terracotta army point cloud registration process
方法 点云数目 特征点数 配准时间/s RMSE/mm 传统ICP 74320/
6677872322/66440 11.73 7.88 本文方法 6083/5723 6.22 4.73 -
[1] 肖宇强. 海外藏中国戏曲与民俗文物的“数字孪生”及数字化资源平台建设[J]. 文化遗产,2022(1):89-96. doi: 10.3969/j.issn.1674-0890.2022.01.012XIAO Y Q. Digital twin of Chinese opera and folklore relics in overseas collections and the construction of digital resource Platform[J]. Cultural Heritage, 2022(1): 89-96. (in Chinese) doi: 10.3969/j.issn.1674-0890.2022.01.012 [2] ALTUNTAS C. Point cloud acquisition techniques by using scanning LiDAR for 3D modelling and mobile measurement[J]. The International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences, 2022, XLIII-B2-2022: 967-972. doi: 10.5194/isprs-archives-XLIII-B2-2022-967-2022 [3] 史艳侠, 娄小平, 李伟仙. 线结构光点云粗拼接方法研究[J]. 电子测量与仪器学报,2018,32(6):12-16. doi: 10.13382/j.jemi.2018.06.003SHI Y X, LOU X P, LI W X. Coarse stitching of point structured cloud of line structured light research on unconstrained method of surface measurement[J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(6): 12-16. (in Chinese) doi: 10.13382/j.jemi.2018.06.003 [4] MEDDA D, ANOFFO Y M, PERRA C, et al. Automated point cloud acquisition system using multiple RGB-D cameras[J]. Proceedings of SPIE, 2020, 11353: 1135315. [5] TOSCHI I, FARELLA E M, WELPONER M, et al. Quality-based registration refinement of airborne LiDAR and photogrammetric point clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2021, 172: 160-170. doi: 10.1016/j.isprsjprs.2020.12.005 [6] 刘跃生, 陈新度, 吴磊, 等. 混合稀疏迭代最近点配准[J]. 光学 精密工程,2021,29(9):2255-2267. doi: 10.37188/OPE.20212909.2255LIU Y SH, CHEN X D, WU L, et al. Sparse mixture iterative closest point registration[J]. Optics and Precision Engineering, 2021, 29(9): 2255-2267. (in Chinese) doi: 10.37188/OPE.20212909.2255 [7] 林森, 张强. 应用邻域点信息描述与匹配的点云配准[J]. 光学 精密工程,2022,30(8):984-997. doi: 10.37188/OPE.20223008.0984LIN S, ZHANG Q. Point cloud registration using neighborhood point information description and matching[J]. Optics and Precision Engineering, 2022, 30(8): 984-997. (in Chinese) doi: 10.37188/OPE.20223008.0984 [8] FOTSING C, NZIENGAM N, BOBDA C. Large common plansets-4-points congruent sets for point cloud registration[J]. ISPRS International Journal of Geo-Information, 2020, 9(11): 647. doi: 10.3390/ijgi9110647 [9] SUN L, MANABE Y, YATA N. [Paper] double sparse representation for point cloud registration[J]. ITE Transactions on Media Technology and Applications, 2019, 7(3): 148-158. doi: 10.3169/mta.7.148 [10] JUNIOR E M O, SANTOS D R, MIOLA G A R. A new variant of the ICP algorithm for pairwise 3D point cloud registration[J]. American Academic Scientific Research Journal for Engineering,Technology,and Sciences, 2022, 85(1): 71-88. [11] KUÇAK R A, EROL S, EROL B. An experimental study of a new keypoint matching algorithm for automatic point cloud registration[J]. ISPRS International Journal of Geo-Information, 2021, 10(4): 204. doi: 10.3390/ijgi10040204 [12] BAUER P, HECKLER L, WORACK M, et al. Registration strategy of point clouds based on region-specific projections and virtual structures for robot-based inspection systems[J]. Measurement, 2021, 185: 109963. doi: 10.1016/j.measurement.2021.109963 [13] SUN W X, WANG J, JIN F X, et al. Datum feature extraction and deformation analysis method based on normal vector of point cloud[J]. International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences, 2018, XLII-3: 1601-1606. doi: 10.5194/isprs-archives-XLII-3-1601-2018 [14] FOORGINEJAD A, KHALILI K. Umbrella curvature: a new curvature estimation method for point clouds[J]. Procedia Technology, 2014, 12: 347-352. doi: 10.1016/j.protcy.2013.12.497 [15] 宁浩, 董秀军, 刘谦, 等. 利用点云法向量实现岩体结构面识别[J/OL]. 武汉大学学报(信息科学版), 1-13 [2022-06-07]. http://kns.cnki.net/kcms/detail/42.1676.tn.20211028.1541.027.html.NING H, DONG X J, LIU Q, et al. . Using point cloud normal vector to realize rock mass structural plane recognition[J/OL]. Geomatics and Information Science of Wuhan University, 1-13 [2022-06-07]. http://kns.cnki.net/kcms/detail/42.1676.tn.20211028.1541.027.html. (in Chinese) [16] 张溪溪, 纪小刚, 胡海涛, 等. 微型复杂曲面零件散乱点云特征点提取[J]. 机械设计与研究,2019,35(5):1-5,10. doi: 10.13952/j.cnki.jofmdr.2019.0263ZHANG X X, JI X G, HU H T, et al. Feature point extraction of scattered point cloud for complex micro-surface parts[J]. Machine Design &Research, 2019, 35(5): 1-5,10. (in Chinese) doi: 10.13952/j.cnki.jofmdr.2019.0263 [17] 赵夫群, 耿国华. 基于图像特征和奇异值分解的点云配准算法[J]. 激光与光电子学进展,2020,57(10):101101.ZHAO F Q, GENG G H. Point cloud registration algorithm based on image feature and singular value decomposition[J]. Laser &Optoelectronics Progress, 2020, 57(10): 101101. (in Chinese) [18] 谭国威, 伍吉仓. 基于FPFH特征的三维点云配准方法研究[J]. 工程勘察,2022,50(4):52-56. doi: 10.3969/j.issn.1000-1433.2022.4.gckc202204010TAN G W, WU J C. Research on 3D point cloud registration based on FPFH features[J]. Geotechnical Investigation &Surveying, 2022, 50(4): 52-56. (in Chinese) doi: 10.3969/j.issn.1000-1433.2022.4.gckc202204010 [19] 秦红星, 刘镇涛, 谭博元. 深度学习刚性点云配准前沿进展[J]. 中国图象图形学报,2022,27(2):329-348. doi: 10.11834/jig.210556QIN H X, LIU ZH T, TAN B Y. Review on deep learning rigid point cloud registration[J]. Journal of Image and Graphics, 2022, 27(2): 329-348. (in Chinese) doi: 10.11834/jig.210556 [20] ZHANG R ZH, LIU K. Research introduction of 3D measurement technology based on grating projection[J]. Proceedings of SPIE, 2021, 11887: 1188722. [21] MURTIYOSO A, GRUSSENMEYER P. Automatic point cloud noise masking in close range photogrammetry for buildings using AI-based semantic labelling[J]. The International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences, 2022, XLVI-2/W1-2022: 389-393. doi: 10.5194/isprs-archives-XLVI-2-W1-2022-389-2022 -





 下载:
下载: