Effect of atmospheric turbulence on the tracking accuracy of high-resolution remote sensing satellites
-
摘要:
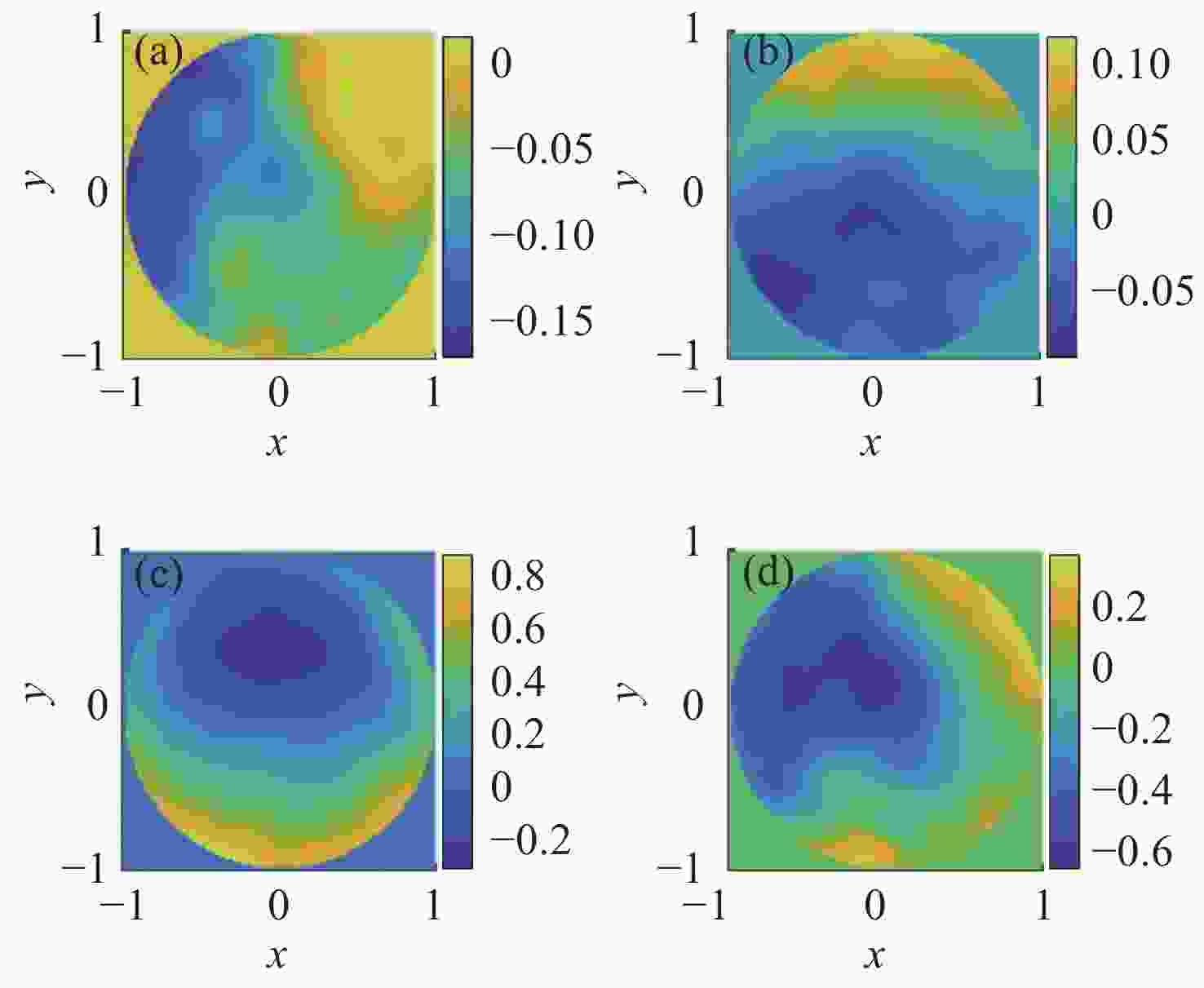
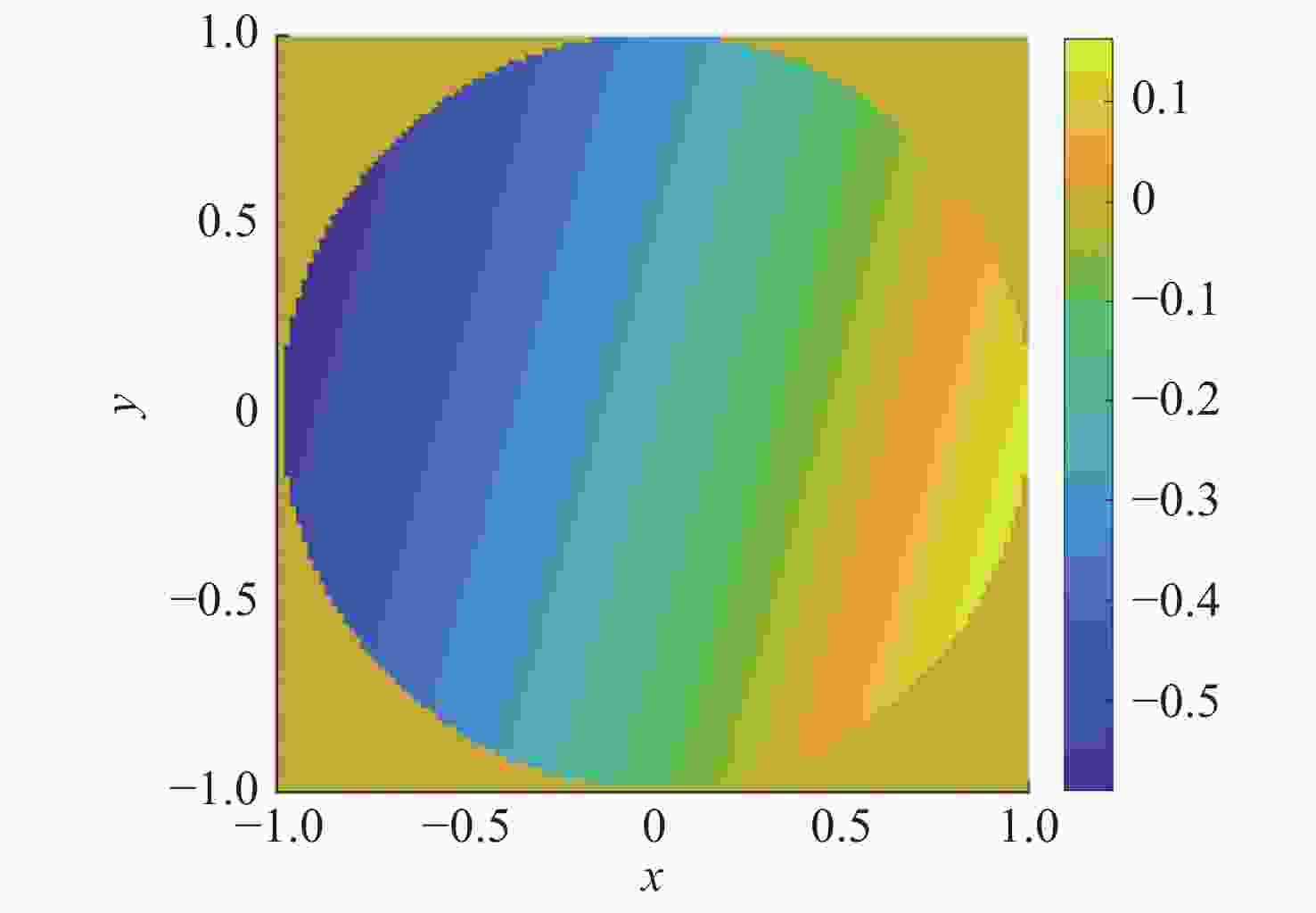
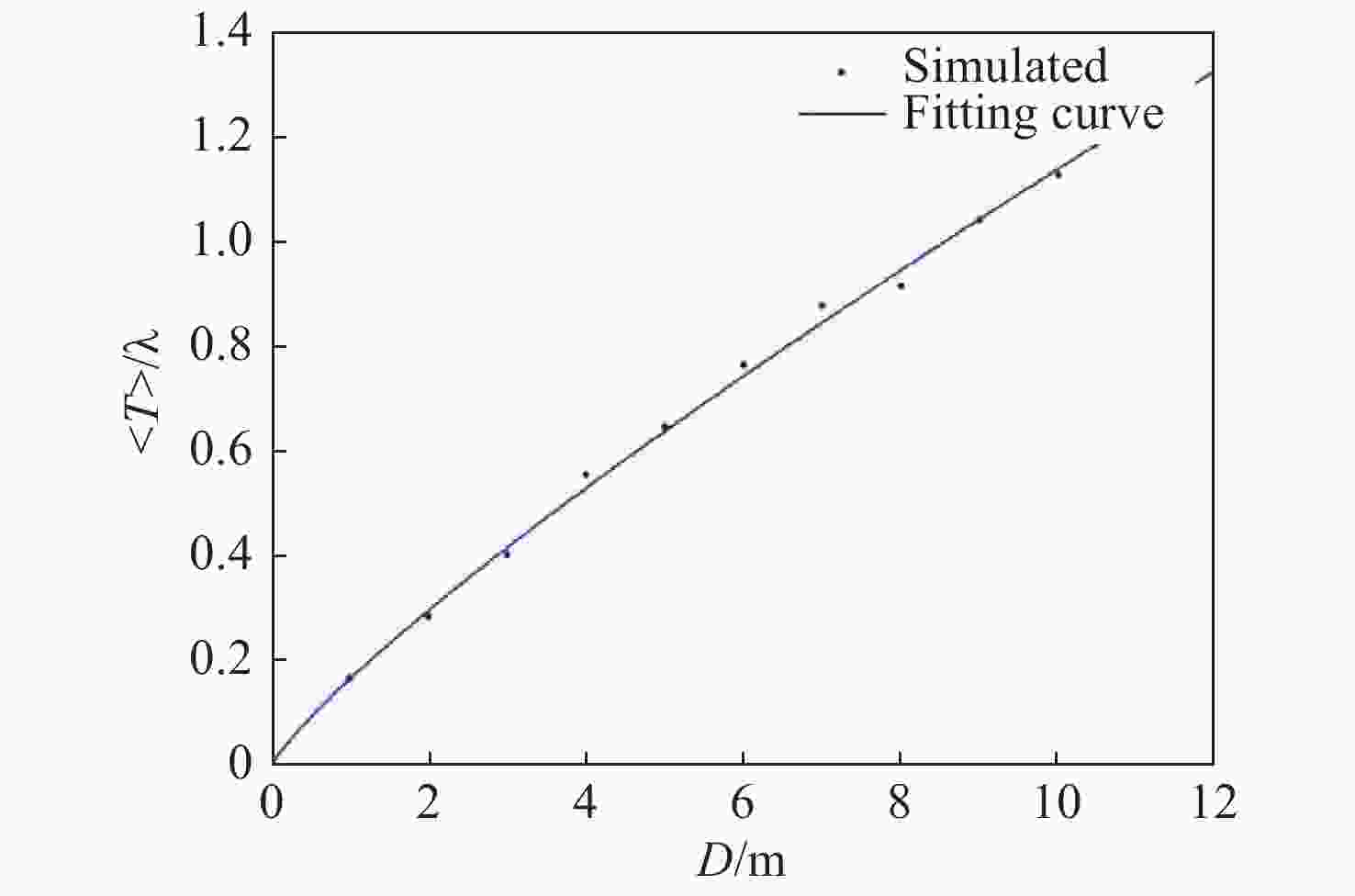
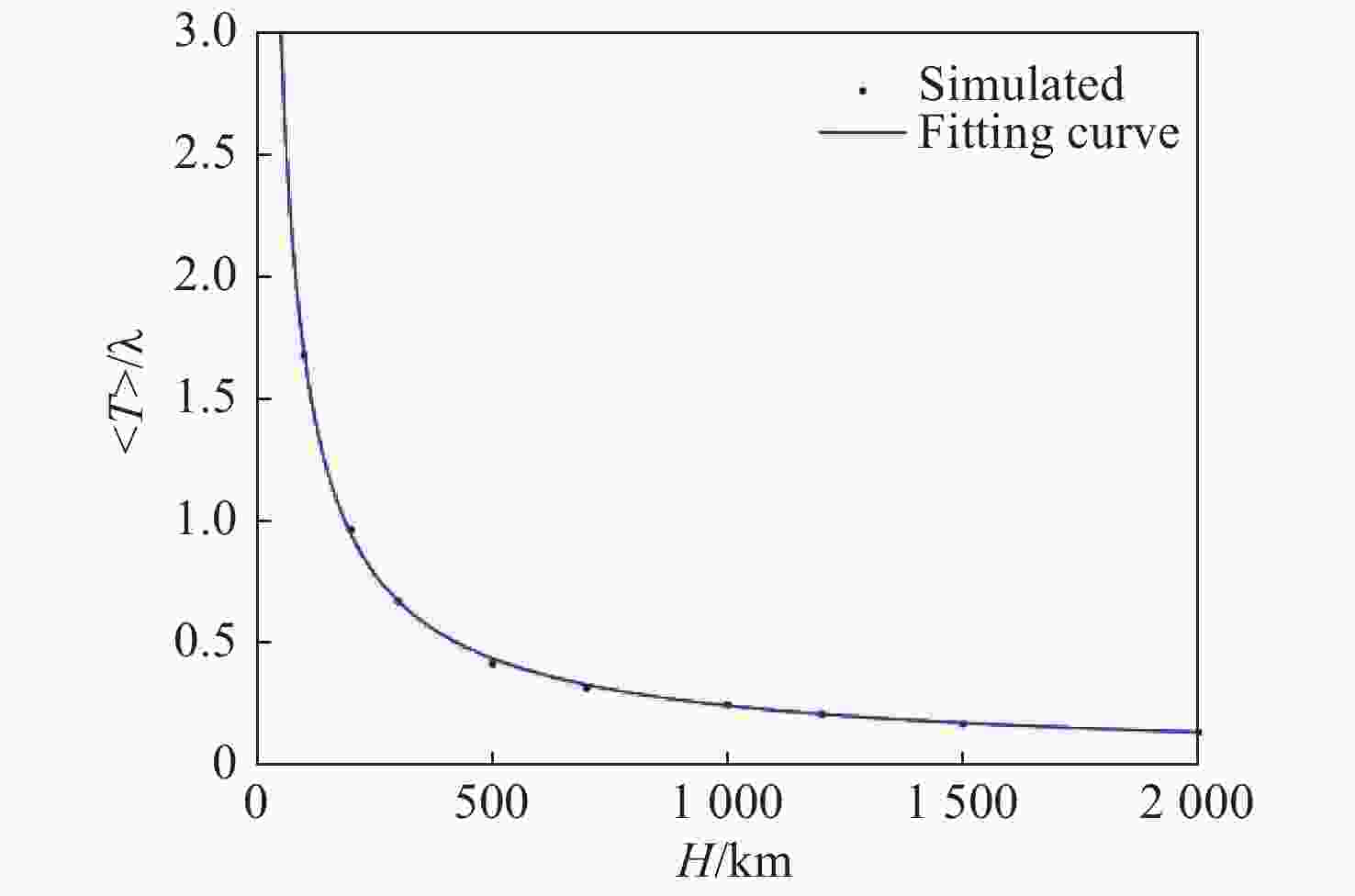
本文重点研究相机口径、大气湍流强度和卫星轨高对高分辨率遥感卫星定位精度的影响。首先，基于Kolmogorov湍流理论建立对地观测大气湍流模型和湍流模拟方法；然后，仿真分析了相机口径、卫星轨道高度和大气相干长度对卫星定位精度的影响规律，推导出湍流波前倾斜与相机口径、卫星轨道高度和大气相干长度的普适公式；最后，基于该普适公式，得出卫星对地观测时抖动量的理论计算公式。本论文的研究可为后续高分辨率遥感卫星的设计、分析和评估提供大气湍流影响的理论依据。
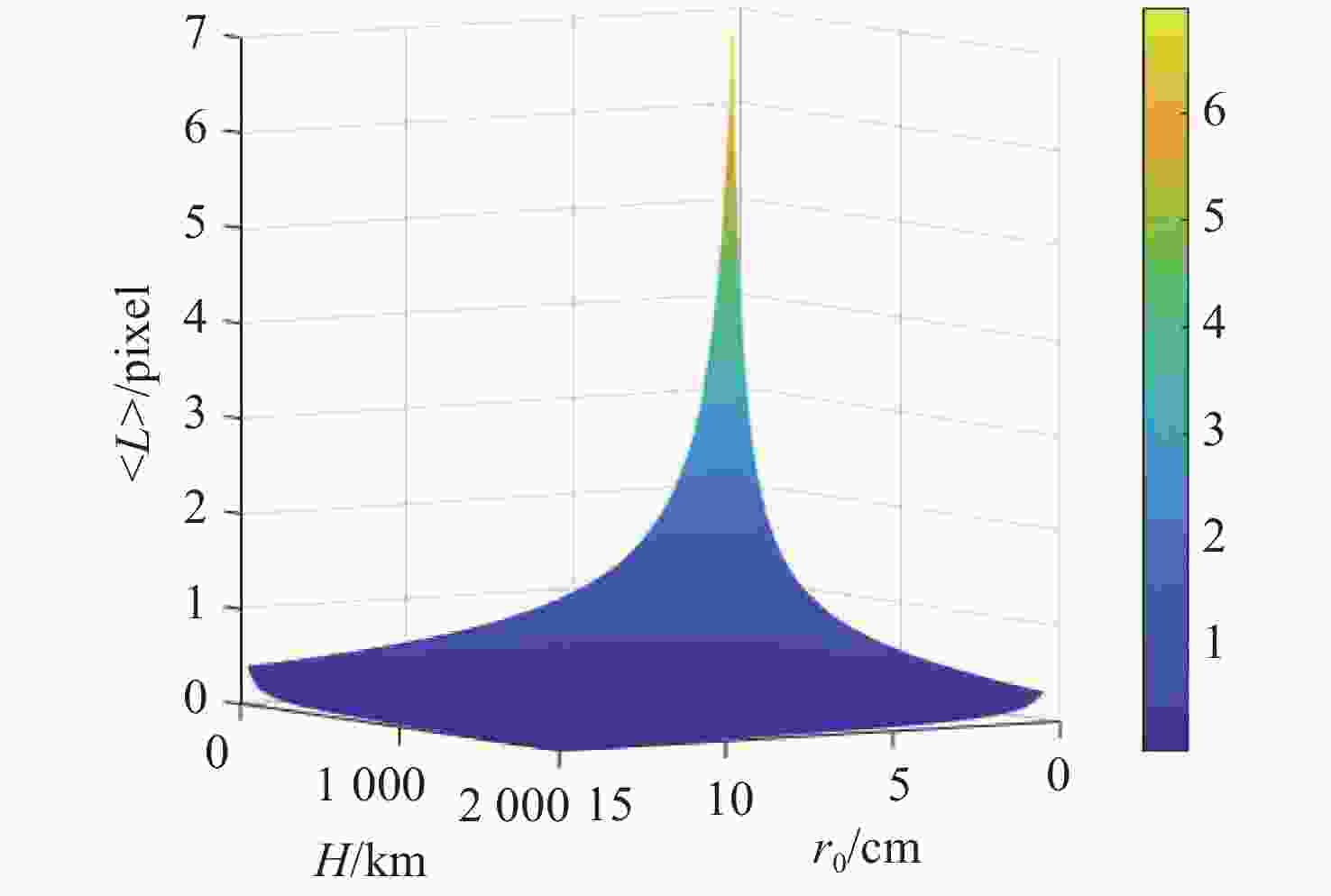
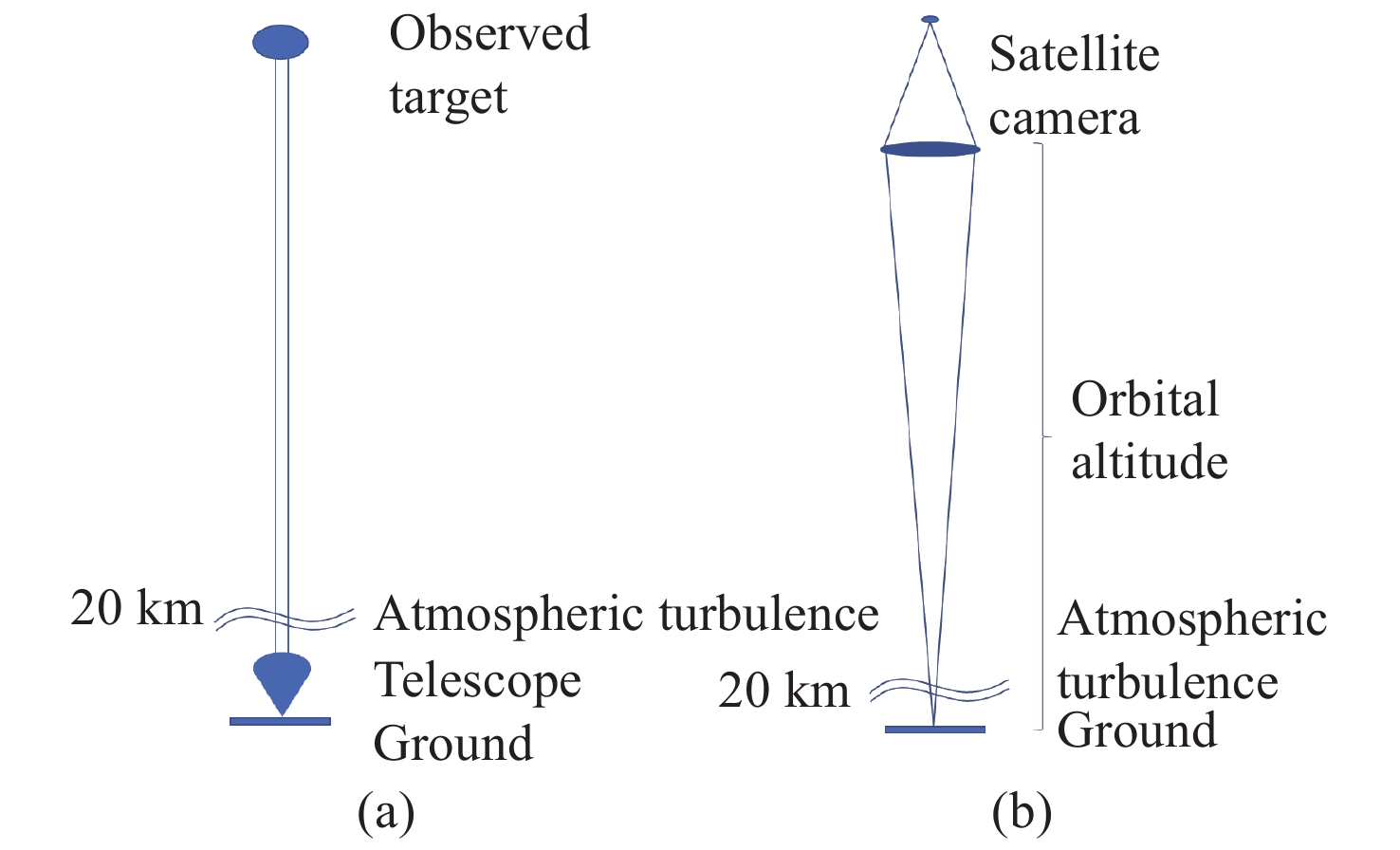
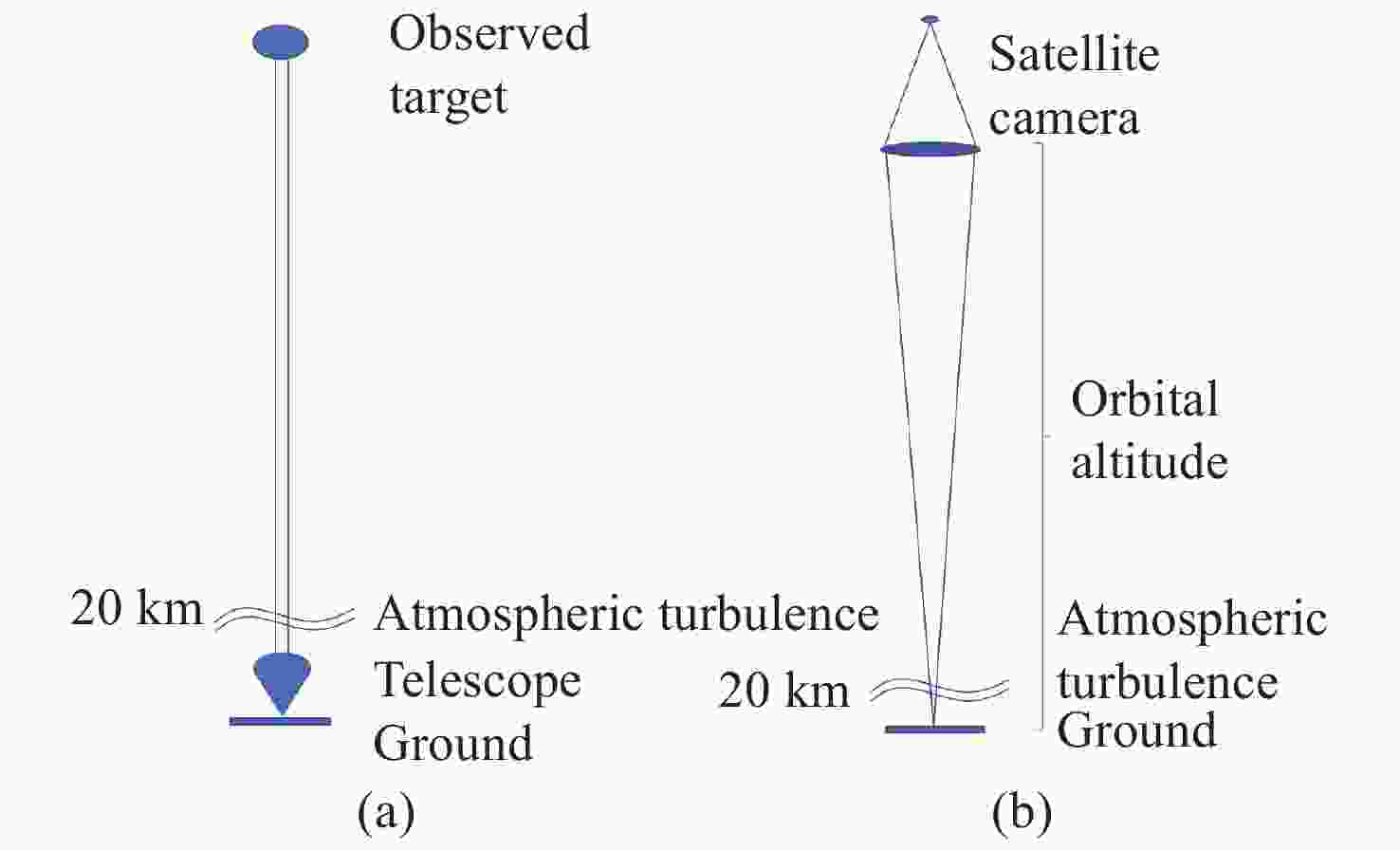
Abstract:We focuse on the effects of camera aperture, atmospheric turbulence intensity and satellite orbit height on the tracking and positioning accuracy of high-resolution remote sensing satellites. Firstly, we establish a turbulence model and turbulence simulation method based on Kolmogorov turbulence theory for observation of the Earth. Then, the influence of camera aperture, satellite orbit height and atmospheric coherence length on the positioning accuracy of the satellite is simulated and analyzed, and then a universal formula is deduced to calculate the tilt aberration of turbulence wavefront. Finally, based on this universal formula, a theoretical formula for calculating jitter is derived for Earth observation. This work can provide a theoretical basis of the influence of atmospheric turbulence for the design, analysis and evaluation of high-resolution remote sensing satellites.
-
图 1 （a）地对空成像示意图；（b）卫星对地成像示意图
Figure 1. Schematic diagrams of (a) ground-to-space imaging and (b) satellite-to-earth imaging
图 3 （a）第一层，（b）第二层，（c）第三层及（d）总的湍流波前畸变
Figure 3. (a) The first layer, (b) the second layer, (c) the third layer and (d) total distorted turbulents wavefronts
图 8 倾斜量随大气湍流强度和卫星轨高的变化关系
Figure 8. Variation of tilt with atmospheric turbulence intensity and satellite orbital height
图 10 不同参量值下的仿真与理论误差
Figure 10. Simulated and theoretical errors at different parameters
图 11 角度抖动量随轨高和大气相干长度的变化
Figure 11. Variation of angular jitter with satellite orbit height and atmospheric coherence length
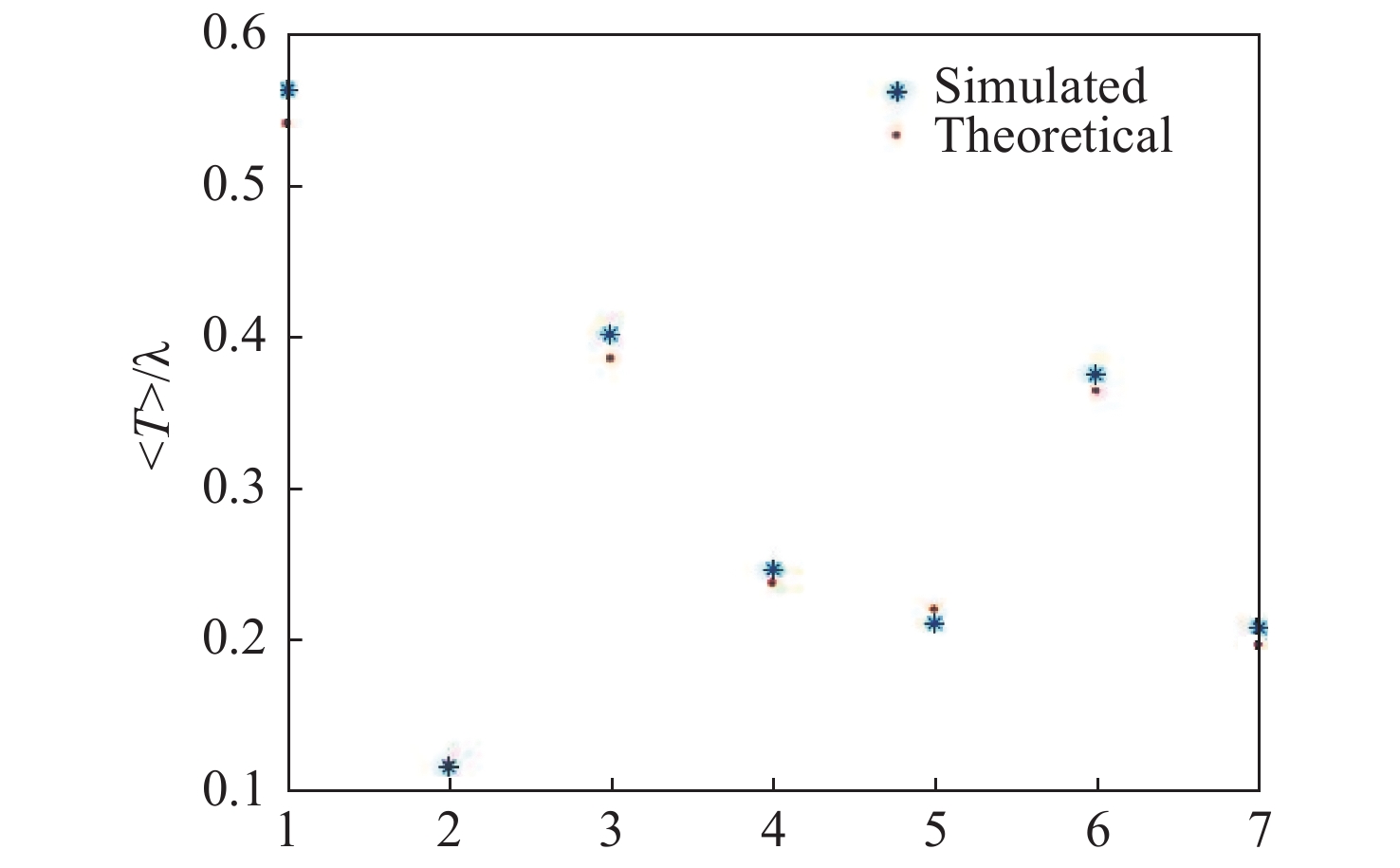
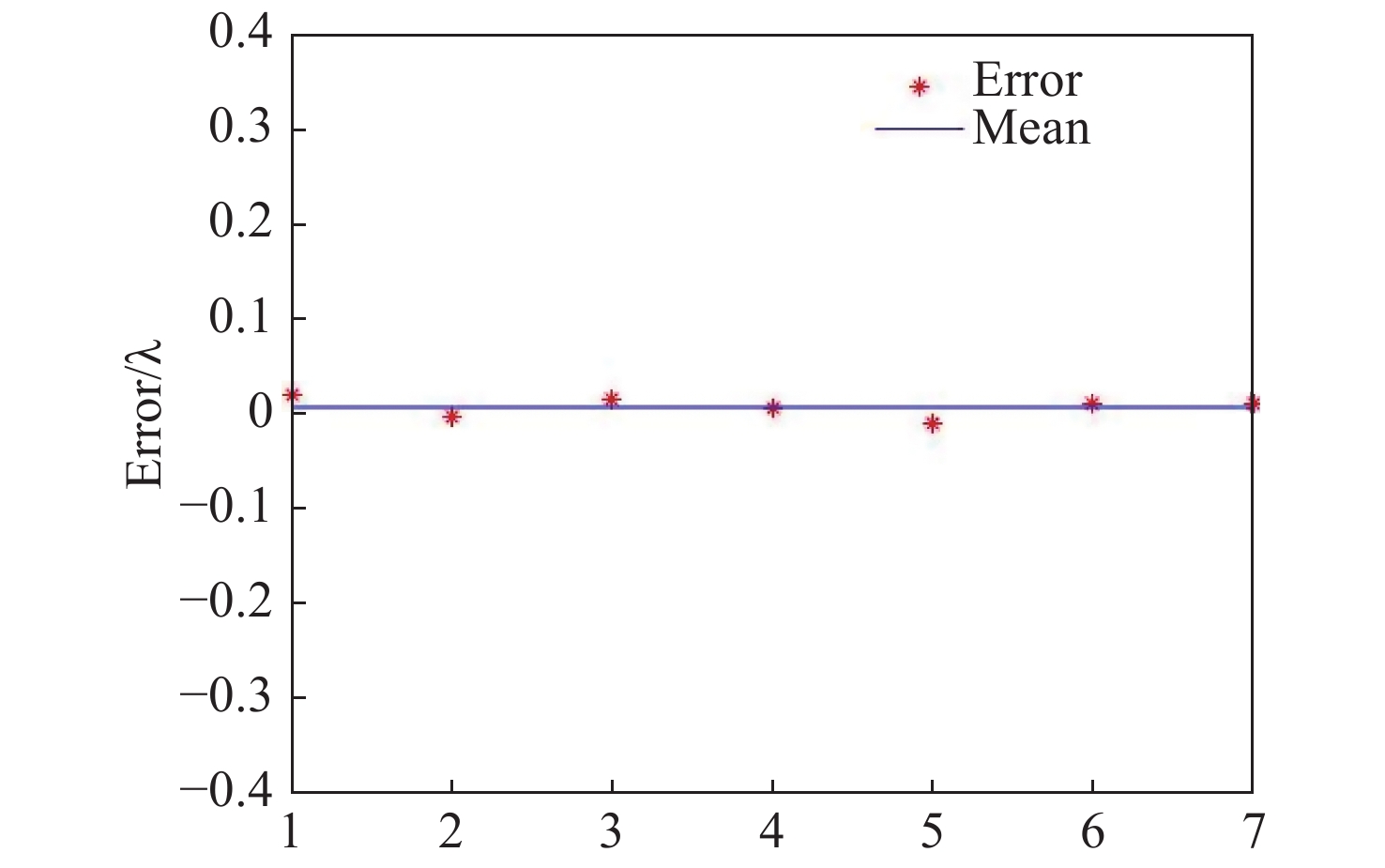
表 1 随机选取的变量
Table 1. Randomly selected variables
1 2 3 4 5 6 7 D(m) 2 2 4 4 6 8 10 H(km) 100 400 300 200 700 1200 800 r0(cm) 5.6 8.6 5.6 15 7 3 11.7 
下载: 导出CSV
-
[1] 高世杰, 吴佳彬, 刘永凯, 等. 微小卫星激光通信系统发展现状与趋势[J]. 中国光学,2020,13(6):1171-1181. doi: 10.37188/CO.2020-0033GAO SH J, WU J B, LIU Y K, et al. Development status and trend of micro-satellite laser communication systems[J]. Chinese Optics, 2020, 13(6): 1171-1181. (in Chinese) doi: 10.37188/CO.2020-0033 [2] SONG J K, LI Y Y, CHE D B, et al. Influence of turbulent atmosphere on the effect of coherent beam combining[J]. Chinese Optics, 2020, 13(4): 884-898. doi: 10.37188/CO.2019-0197 [3] 张景旭. 国外地基光电系统空间目标探测的进展[J]. 中国光学与应用光学,2009,2(1):10-16.ZHANG J X. Progress in foreign ground-based optoelectronic detecting system for space target detection[J]. Chinese Journal of Optics and Applied Optics, 2009, 2(1): 10-16. (in Chinese) [4] 周仁忠, 阎吉祥. 自适应光学理论[M]. 北京: 北京理工大学出版社, 1996.ZHOU R ZH, YAN J X. Theory of Adaptive Optics[M]. Beijing: Beijing Institute of Technology Press, 1996. (in Chinese) [5] RODDIER F. Adaptive Optics in Astronomy[M]. Cambridge: Cambridge University Press, 1999. [6] 王克, 钱桂山. 美国成像侦察卫星技术研究和体系分析[C]. 卫星通信技术研讨会论文集. 中国通信学会, 2004: 51-56WANG K, QIAN G SH. Technology research and system analysis of US imaging reconnaissance satellite[C]. Satellite Communication Technology Seminar, China Communication Society, 2004: 51-56. (in Chinese) [7] 喻际. 基于变形镜本征模式的无波前传感器自适应光学校正方法研究[D]. 北京: 北京理工大学, 2015.YU J. Wavefront sensorless adaptive optics correction method based on deformable mirror eigenmodes[D]. Beijing: Beijing Institute of Technology, 2015. (in Chinese) [8] 李俊. 传输型详查相机微小自适应光学系统研究[D]. 武汉: 华中科技大学, 2006.LI J. Study of the adaptive optic system in transmission type, high-resolution reconnaissance camera[D]. Wuhan: Huazhong University of Science and Technology, 2006. (in Chinese) [9] 张志伟, 马骏, 俞信. 微小型自适应光学系统及其在星载光学遥感器上的应用[J]. 红外与激光工程,2000,29(1):49-52. doi: 10.3969/j.issn.1007-2276.2000.01.013ZHANG ZH W, MA J, YU X. Micro adaptive optics and its application in air-borne optical remote sensor[J]. Infrared and Laser Engineering, 2000, 29(1): 49-52. (in Chinese) doi: 10.3969/j.issn.1007-2276.2000.01.013 [10] 邹皓, 李清瑶, 赵群, 等. 大气湍流参数对图像退化效果影响的研究[J]. 长春理工大学学报(自然科学版),2018,41(4):95-99.ZOU H, LI Q Y, ZHAO Q, et al. Research on influence of atmospheric turbulence parameters on image degradation[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2018, 41(4): 95-99. (in Chinese) [11] 管保柱, 陈海清, 叶嘉雄, 等. 星载自适应光学系统的双导星信标理论研究[J]. 激光技术,2004,28(6):613-615,624. doi: 10.3969/j.issn.1001-3806.2004.06.030GUAN B ZH, CHEN H Q, YE J X, et al. Model of beacon used in the air-borne adaptive optical system[J]. Laser Technology, 2004, 28(6): 613-615,624. (in Chinese) doi: 10.3969/j.issn.1001-3806.2004.06.030 [12] 李波, 王挺峰, 王弟男, 等. 激光大气传输湍流扰动仿真技术[J]. 中国光学,2012,5(3):289-295.LI B, WANG T F, WANG D N, et al. Simulation of laser beam propagation through turbulence[J]. Chinese Optics, 2012, 5(3): 289-295. (in Chinese) [13] 阎吉祥, 俞信. 大气湍流对遥感系统分辨力的影响[J]. 光学技术,2004,30(1):68-69. doi: 10.3321/j.issn:1002-1582.2004.01.032YAN J X, YU X. Effect of the turbulence on the image resolution of the remote sensing system[J]. Optical Technique, 2004, 30(1): 68-69. (in Chinese) doi: 10.3321/j.issn:1002-1582.2004.01.032 [14] 王仁礼, 郝振纯, 陈波, 等. 大气湍流对天基遥感系统地面分辨率的影响[J]. 测绘科学技术学报,2009,26(2):114-117. doi: 10.3969/j.issn.1673-6338.2009.02.010WANG R L, HAO ZH CH, CHEN B, et al. Effect of atmospheric turbulence on image ground-resolution of space-based remote sensing system[J]. Journal of Geomatics Science and Technology, 2009, 26(2): 114-117. (in Chinese) doi: 10.3969/j.issn.1673-6338.2009.02.010 [15] 陈欣欣, 苑克娥, 时东锋, 等. 大气湍流对空基光学成像系统影响的仿真研究[J]. 光学学报,2022,42(18):1801002. doi: 10.3788/AOS202242.1801002CHEN X X, YUAN K E, SHI D F, et al. Simulation study on effect of atmospheric turbulence on space-based optical imaging system[J]. Acta Optica Sinica, 2022, 42(18): 1801002. (in Chinese) doi: 10.3788/AOS202242.1801002 [16] 刘思臻, 任德清. 基于YAO软件的太阳地表层自适应光学系统的仿真[J]. 激光与光电子学进展,2017,54(9):090101.LIU S ZH, REN D Q. Simulation on solar ground-layer adaptive optics system based on YAO software[J]. Laser &Optoelectronics Progress, 2017, 54(9): 090101. (in Chinese) [17] HUFNAGEL R E. Variations of atmospheric turbulence[C]. Digest of Topical Meeting on Optical Propagation Through Turbulence, Washington, D.C. Optical Society of America, 1974. [18] 张逸新, 迟泽英. 光波在大气中的传输与成像[M]. 北京: 国防工业出版社, 1997.ZHANG Y X, CHI Z Y. Transmission and Imaging of Light Waves in the Atmosphere[M]. Beijing: National Defense Industry Press, 1997. (in Chinese) [19] NOLL R J. Zernike polynomials and atmospheric turbulence[J]. Journal of the Optical Society of America, 1976, 66(3): 207-211. doi: 10.1364/JOSA.66.000207 [20] 胡立发, 刘永军, 曹召良, 等. 液晶湍流模拟器的研制[C]. 中国科学院液晶相关研究学术研讨会, 中国物理学会, 2005.HU L F, LIU Y J, CAO ZH L, et al. . Development of liquid crystal turbulence simulator[C]. Chinese Academy of Sciences LCD Related Research Symposium, Chinese Physical Society, 2005. (in Chinese) -
下载:
点击查看大图
计量
- 文章访问数: 517
- HTML全文浏览量: 190
- PDF下载量: 282
- 被引次数: 0
