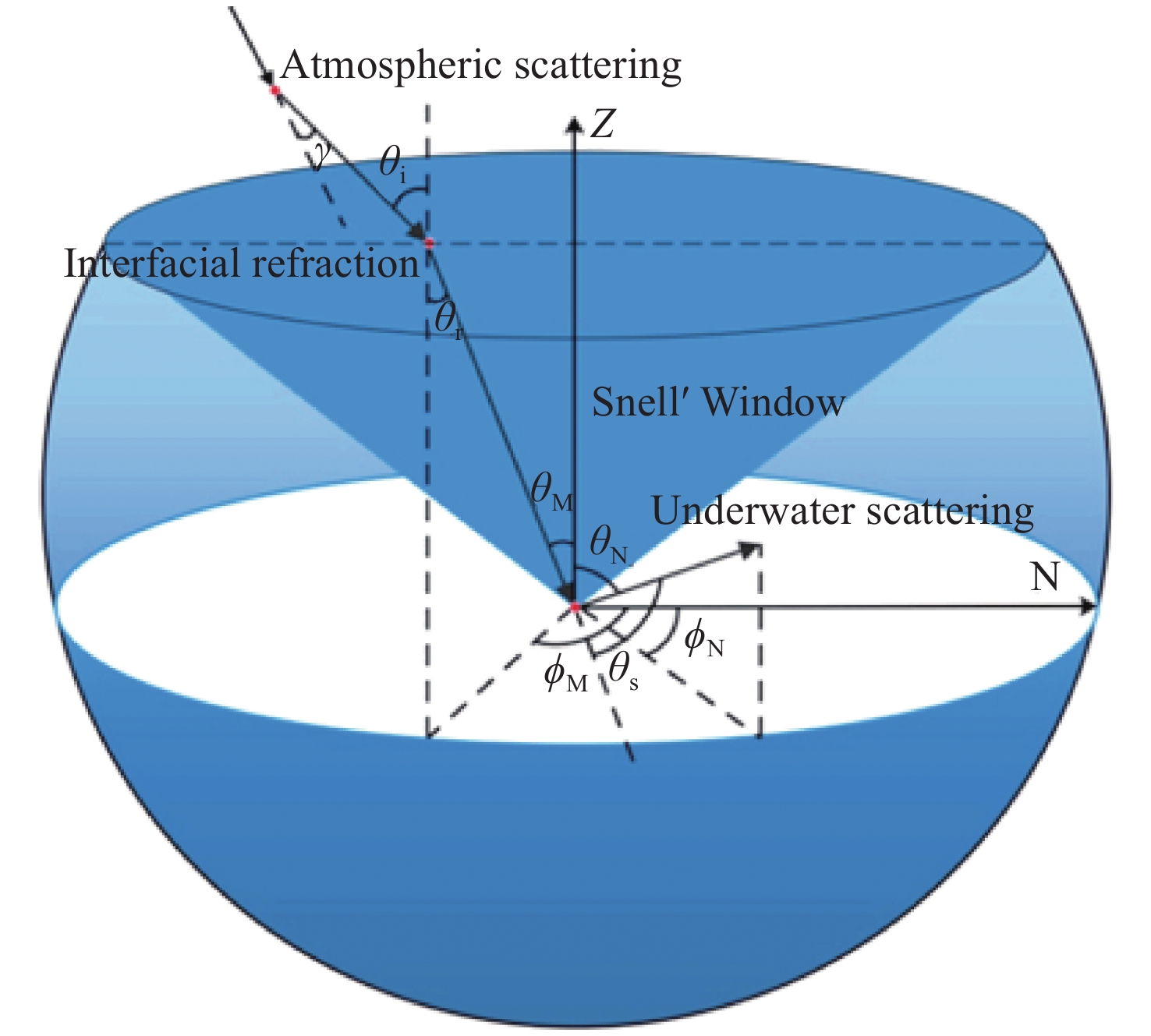
-
摘要:
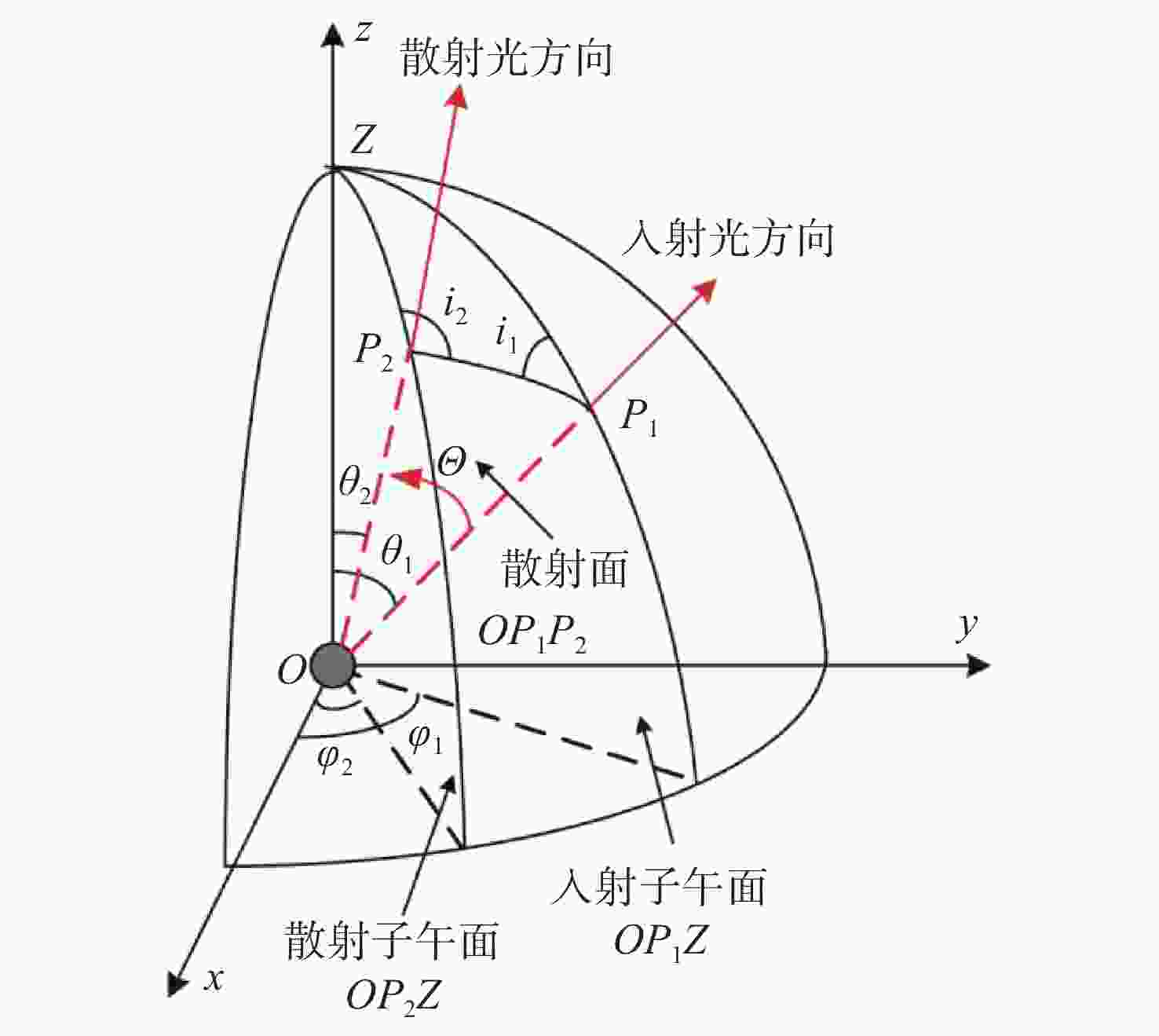
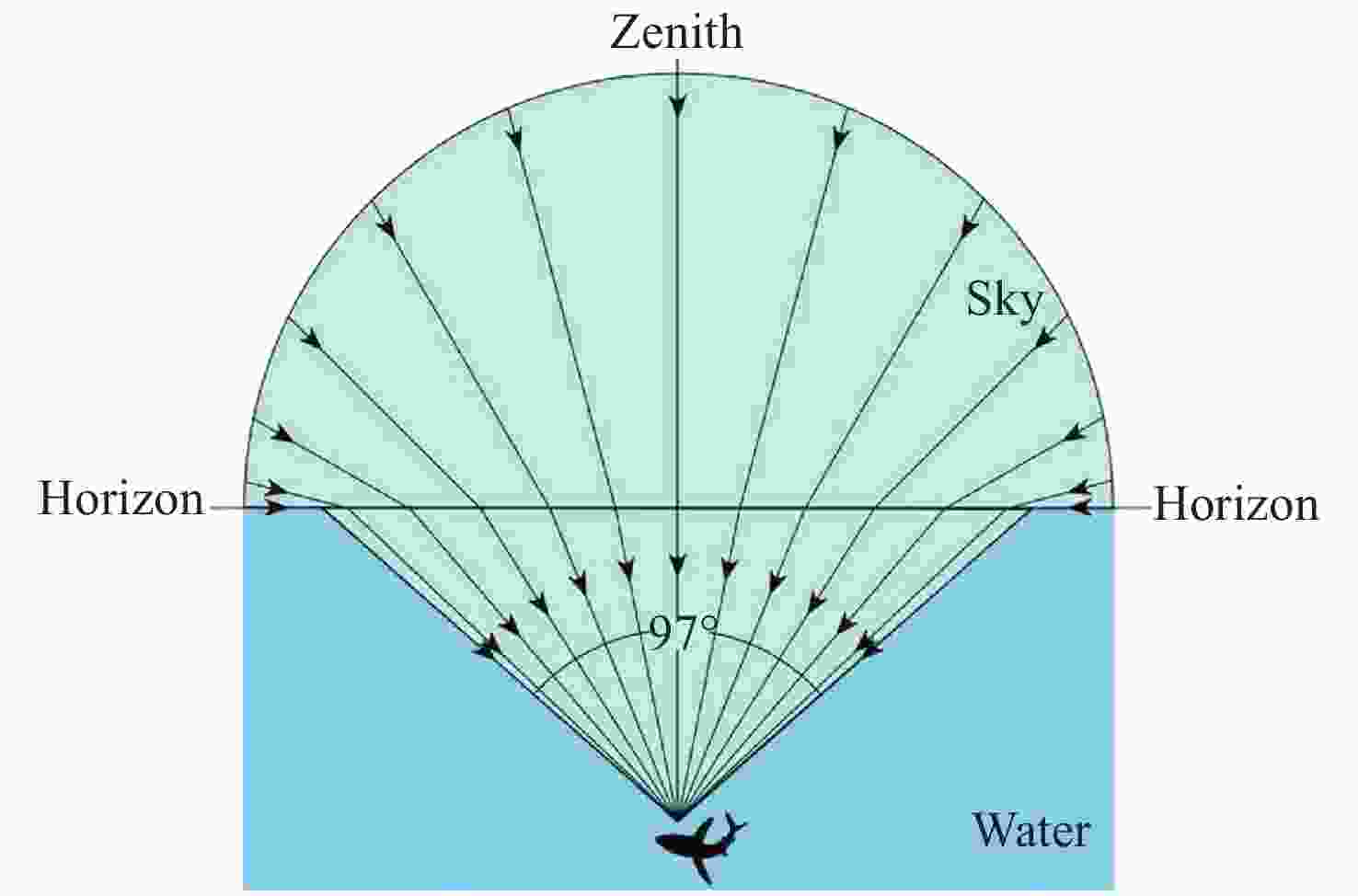
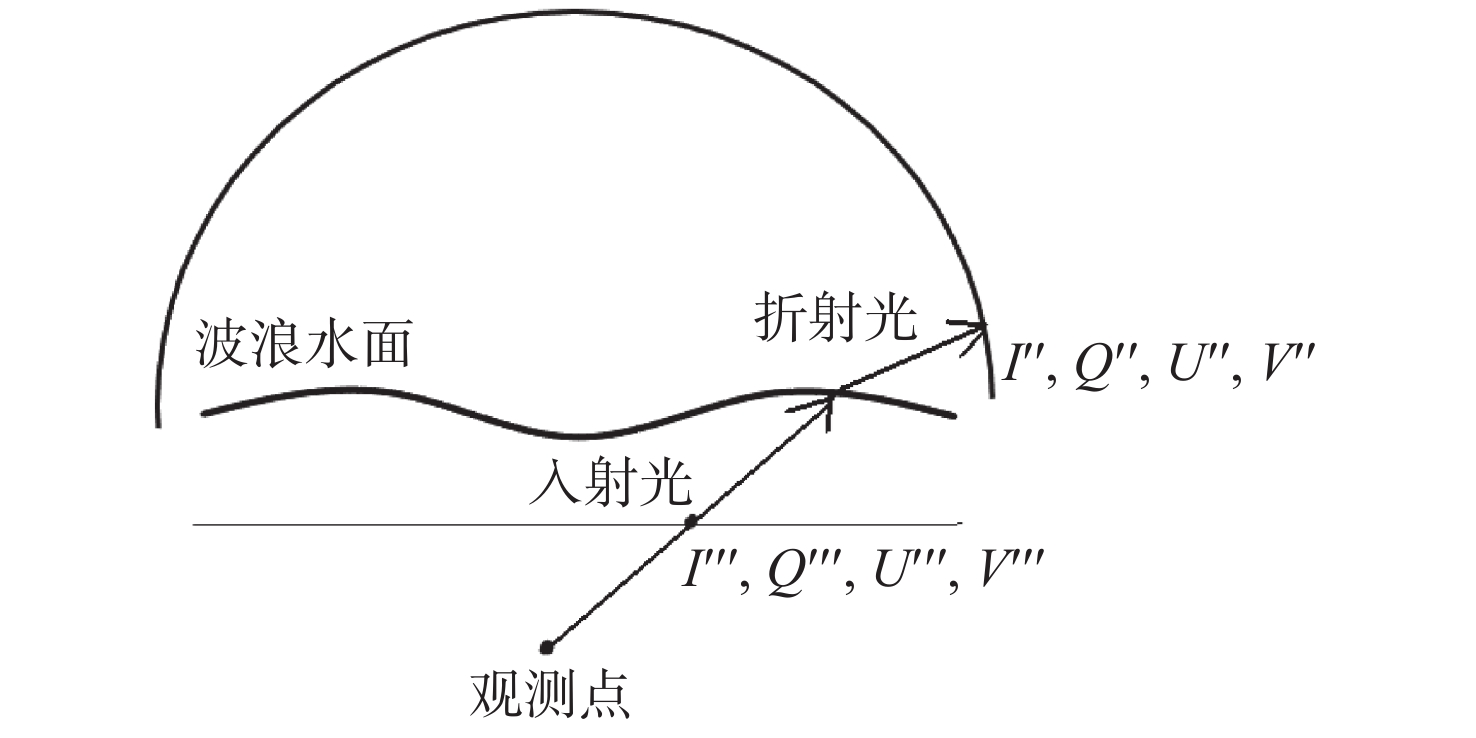
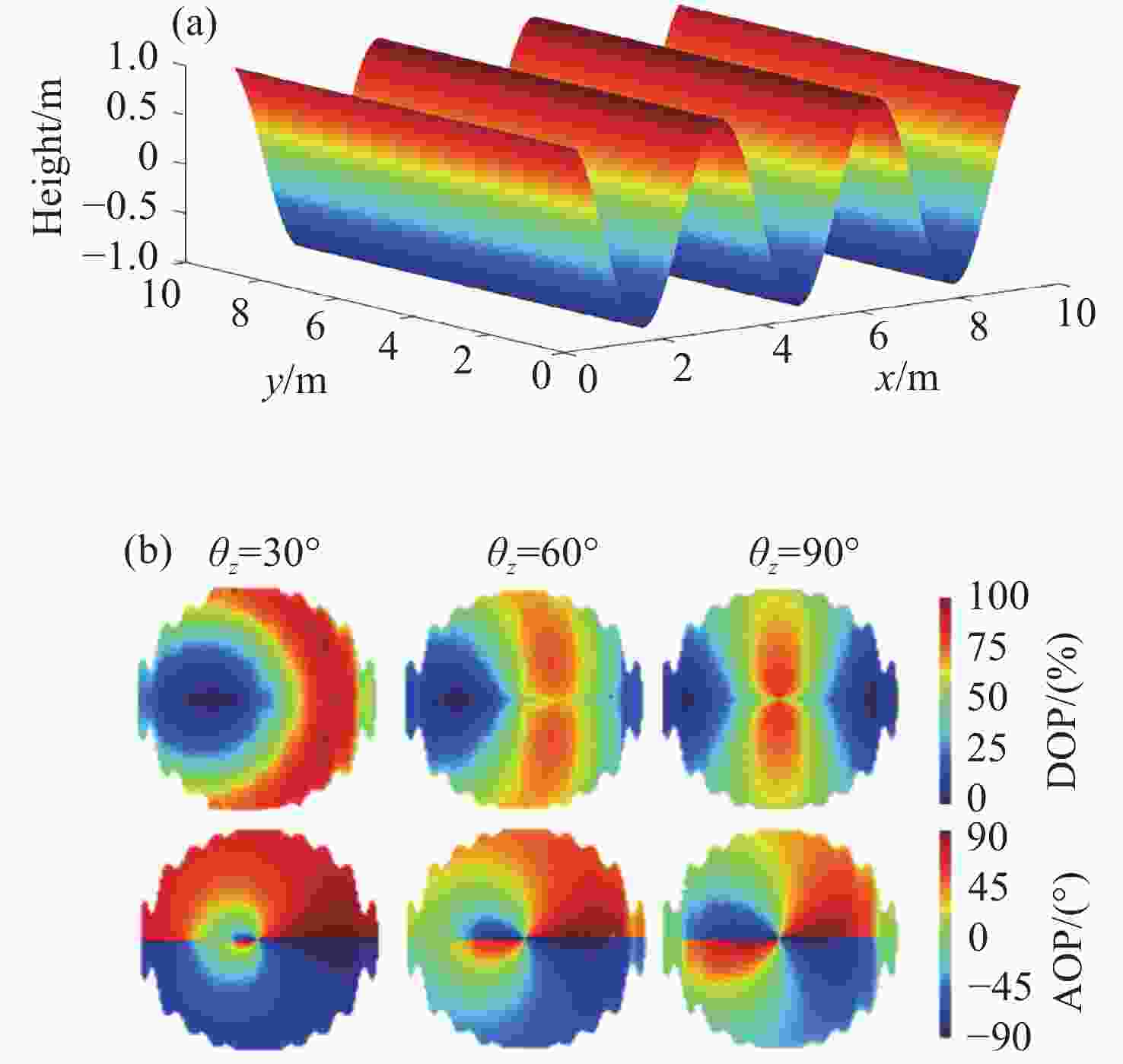
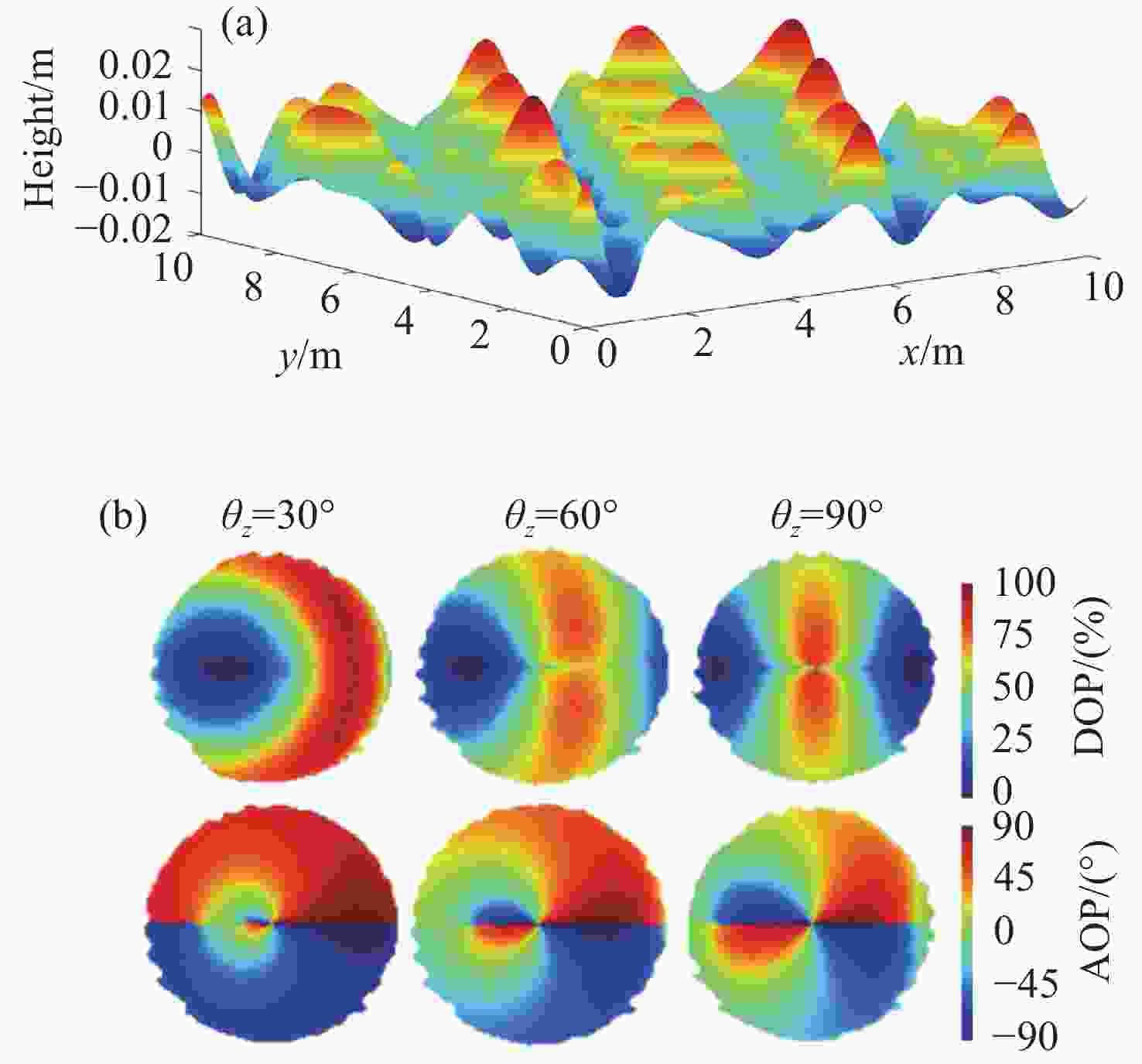
太阳光经大气散射与水面折射后会形成有一定分布特性的水下偏振光，利用水下偏振光的偏振分布模式可实现水下导航。本文提出了基于波浪水面下偏振光分布模式的气-水模型，可用于计算大气多次散射后波浪折射影响下水下偏振光的偏振分布模式。模拟并对比分析了平静水面、正弦波浪与随机波浪下，不同太阳高度角的水下偏振光的偏振度和偏振角的分布图像，并通过水下实验进行了验证。水下偏振光模式模拟结果与实测结果的对比表明，利用该模型可以准确表征典型波浪水面下的偏振光分布模式特性，为提高水下偏振导航在水面波动条件下的环境适应性提供理论模型基础。
Abstract:Underwater polarized light with certain distribution characteristics is formed when sunlight is scattered by the atmosphere and refracted by the surface of the water. The polarization distribution pattern of the underwater polarized light can be used in navigation. In this paper, an air-water model is proposed to calculate the polarization pattern of sky light under varying wave conditions and simulate the underwater polarization distribution pattern under the influence of wave refraction. Distribution images are simulated for underwater polarization degree and polarization angle in conditions with calm water, sinusoidal waves and random waves with different solar altitude angles. The results are verified using underwater experiments. The comparison of the polarization distribution pattern under the waves with that under the calm water show that the proposed model can accurately characterize the characteristics of the polarization distribution pattern under typical wave surfaces, providing a theoretical basis for improving the environmental adaptability of underwater polarization navigation under fluctuating water surface conditions.
-
Key words:
- underwater optics /
- refraction /
- fluctuating water surface /
- sky polarized light
-
图 5 太阳光在大气中发生单次Rayleigh散射的DOP和AOP分布，太阳天顶角分别为30°,60°,90°
Figure 5. The DOP and AOP distributions after single Rayleigh scattering of sunlight in the atmosphere. The zenith angles of the sun are 30°, 60°, and 90°, respectively
图 6 太阳光在大气中发生多次Rayleigh散射的DOP和AOP分布，太阳天顶角分别为30°,60°,90°
Figure 6. The DOP and AOP distributions after multiple Rayleigh scattering of sunlight in the atmosphere. The zenith angles of the sun are 30°, 60°, and 90°, respectively
图 7 大气多次散射光被平静水面折射到水中的DOP和AOP分布，太阳天顶角分别为30°,60°,90°
Figure 7. The distribution of DOP and AOP after multiple scattering of sunlight and refraction by calm water. The solar zenith angles are 30°, 60°, and 90°, respectively
图 8 （a）正弦波形水面波；（b）大气多次散射光被正弦形状的水面折射到水中的DOP和AOP分布，太阳天顶角分别为30°，60°，90°
Figure 8. (a) Sinusoidal surface waves; (b) the underwater distribution of DOP and AOP after multiple scattering of sunlight and refraction by sinusoidal surface waves. The solar zenith angles are 30°, 60°, and 90°, respectively
图 9 （a）随机波形水面波；（b）大气多次散射光被随机波形的水面折射到水中的DOP和AOP分布，太阳天顶角分别为30°，60°，90°
Figure 9. (a) Random surface wave; (b) the underwater distribution of DOP and AOP after multiple scattering of sunlight and refraction by random waveforms surface waves. The solar zenith angles are 30°, 60°, and 90°, respectively
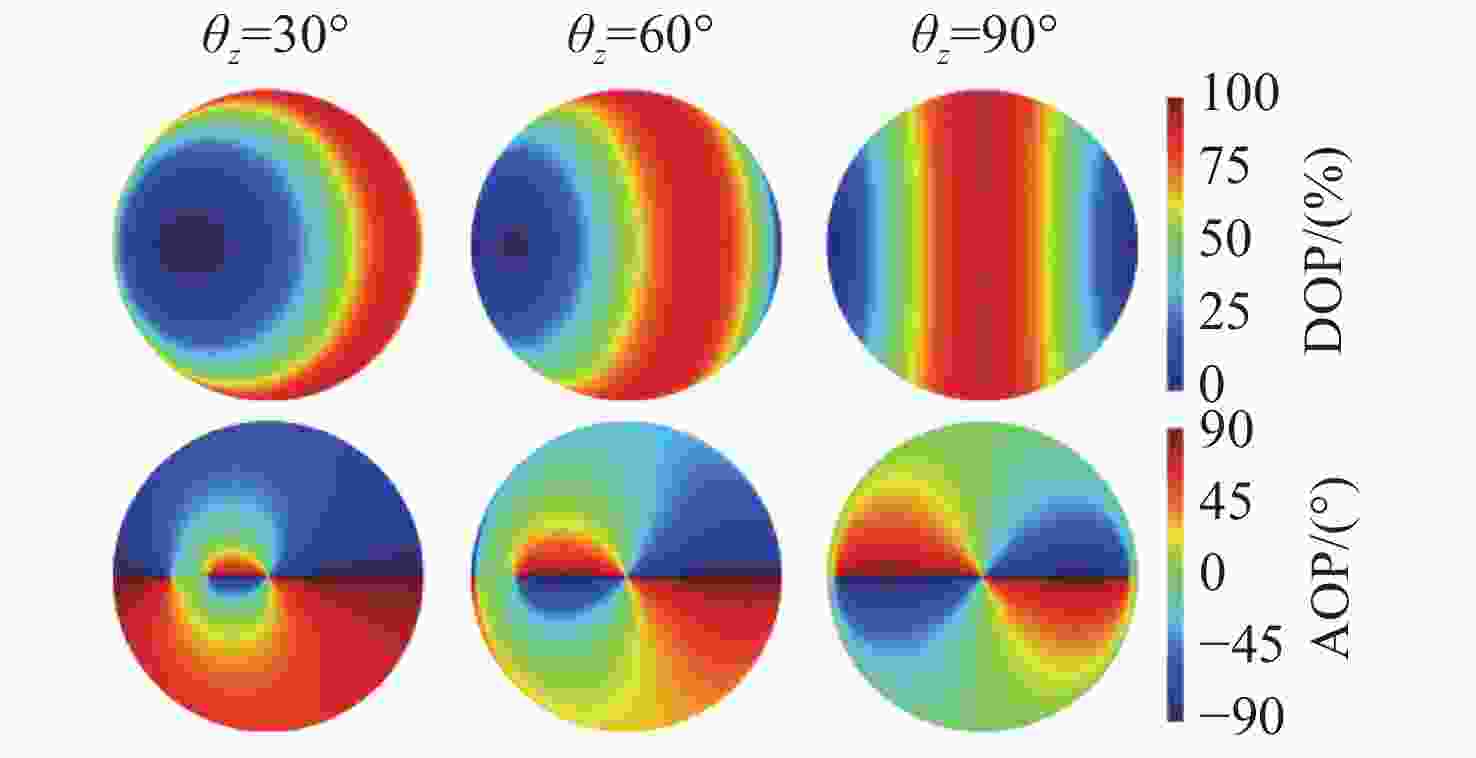
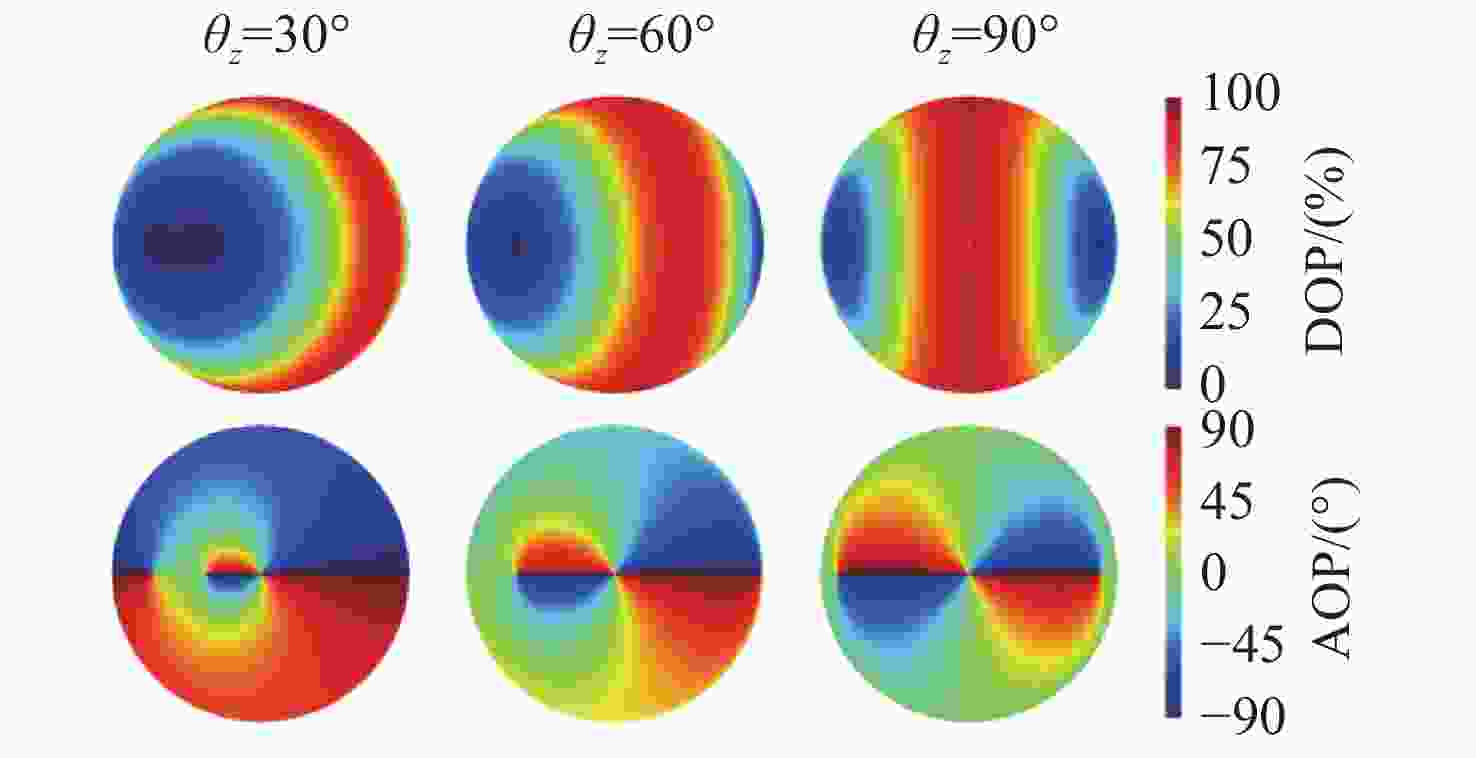
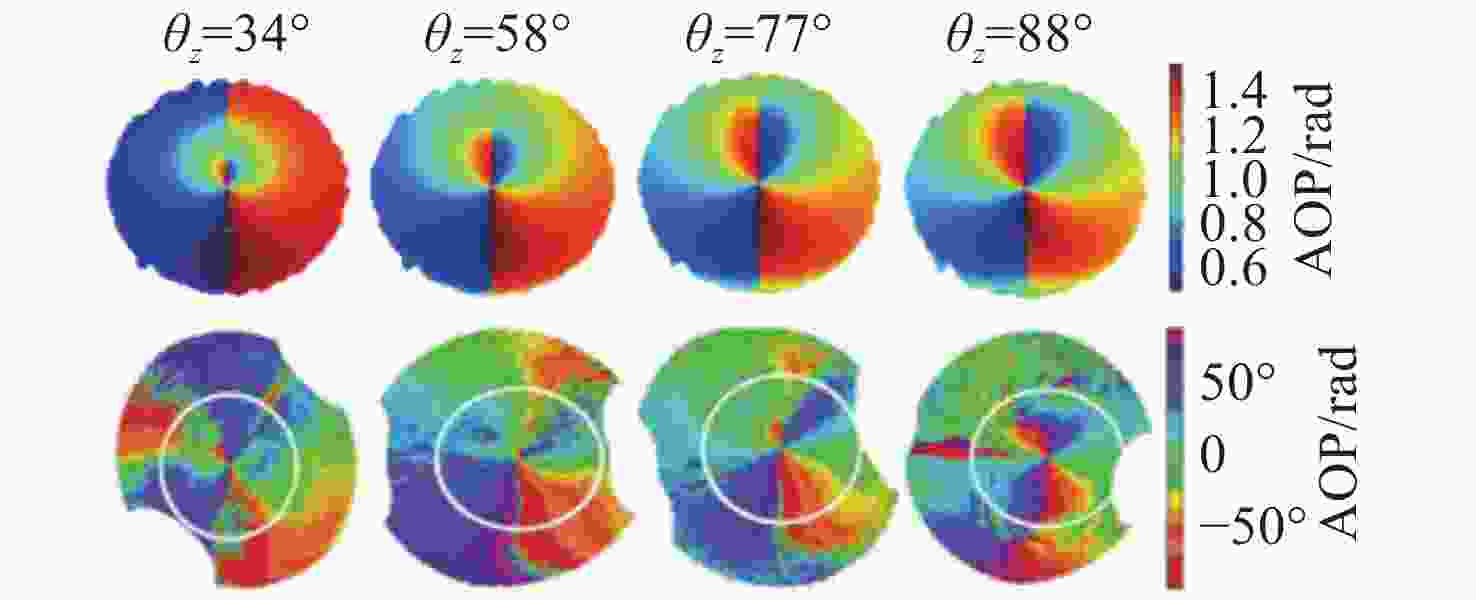
图 10 平静水面下的实测与模拟结果对比。(a)平静水面下的实测图片；(b)实测数据的DOP分布；(c)实测数据的AOP分布；(d) DOP模拟结果；(e) AOP模拟结果
Figure 10. Comparison of measured and simulated results under calm water. (a) Measured images under calm water; (b) DOP distribution of measured data; (c) AOP distribution of measured data; (d) results of DOP simulation; (e) results of AOP simulation
图 11 高度角为65.054°时平静水面下的实测结果、理想大气模拟结果、加入气溶胶后的模拟结果对比
Figure 11. Comparison of measured results under calm water, simulation results under ideal atmosphere, and simulation results with adding aerosols when zenith angle is 65.054°
-
[1] WATERMAN T H. Polarization of Marine Light Fields and Animal Orientation[M].//BLIZARD, MA. Ocean Optics IX, SPIE, 1988: 431-432. [2] CALABRESE G M, BRADY P C, GRUEV V, et al. Polarization signaling in swordtails alters female mate preference[J]. Proceedings of the National Academy of Sciences of the United States of America, 2014, 111(37): 13397-13402. doi: 10.1073/pnas.1321368111 [3] SHASHAR N, SABBAH S, CRONIN T W. Transmission of linearly polarized light in seawater: implications for polarization signaling[J]. Journal of Experimental Biology, 2004, 207(20): 3619-3628. doi: 10.1242/jeb.01187 [4] 褚金奎, 田连标, 成昊远, 等. 天空光主导的波浪水面下偏振分布模型仿真[J]. 光学学报,2020,40(20):2001002. doi: 10.3788/AOS202040.2001002CHU J K, TIAN L B, CHENG H Y, et al. Simulation of polarization distribution model under wavy water surfaces dominated by skylight[J]. Acta Optica Sinica, 2020, 40(20): 2001002. (in Chinese) doi: 10.3788/AOS202040.2001002 [5] LYNCH D K. Snell’s window in wavy water[J]. Applied Optics, 2015, 54(4): B8-B11. doi: 10.1364/AO.54.0000B8 [6] 刘镕滔, 柳稼航. 海底主动光学探测影像亮度校正与色彩恢复[J]. 中国光学(中英文),2022,15(4):689-702. doi: 10.37188/CO.2021-0211LIU R T, LIU J H. Brightness correction and color restoration of seabed image obtained by active optical detection[J]. Chinese Optics, 2022, 15(4): 689-702. (in Chinese) doi: 10.37188/CO.2021-0211 [7] WATERMAN T H. Polarization patterns in submarine illumination[J]. Science, 1954, 120(3127): 927-932. doi: 10.1126/science.120.3127.927 [8] HORVÁTH G, VARJÚ D. Underwater refraction-polarization patterns of skylight perceived by aquatic animals through Snell's window of the flat water surface[J]. Vision Research, 1995, 35(12): 1651-1666. doi: 10.1016/0042-6989(94)00254-J [9] 陈洁, 童奕澄, 肖达, 等. 大气气溶胶消光后向散射比反演方法研究[J]. 中国光学,2021,14(6):1305-1316. doi: 10.37188/CO.2021-0135CHEN J, TONG Y CH, XIAO D, et al. Retrieval methods for extinction-to-backscatter ratio of atmospheric aerosols[J]. Chinese Optics, 2021, 14(6): 1305-1316. (in Chinese) doi: 10.37188/CO.2021-0135 [10] 何大华, 李阳阳, 周少杰. 水下光场的迭代求解[J]. 中国光学,2022,15(2):297-305. doi: 10.37188/CO.2021-0162HE D H, LI Y Y, ZHOU SH J. Iterative solution of underwater scattering light field[J]. Chinese Optics, 2022, 15(2): 297-305. (in Chinese) doi: 10.37188/CO.2021-0162 [11] CHENG H Y, CHU J K, ZHANG R, et al. Underwater polarization patterns considering single Rayleigh scattering of water molecules[J]. International Journal of Remote Sensing, 2020, 41(13): 4947-4962. doi: 10.1080/01431161.2019.1685725 [12] CHENG H Y, CHU J K, ZHANG R, et al. Turbid underwater polarization patterns considering multiple Mie scattering of suspended particles[J]. Photogrammetric Engineering &Remote Sensing, 2020, 86(12): 737-743. [13] CHENG H Y, CHU J K, ZHANG R, et al. Real-time position and attitude estimation for homing and docking of an autonomous underwater vehicle based on bionic polarized optical guidance[J]. Journal of Ocean University of China, 2020, 19(5): 1042-1050. doi: 10.1007/s11802-020-4399-z [14] CHENG H Y, CHU J K, ZHANG R, et al. Simulation and measurement of the effect of various factors on underwater polarization patterns[J]. Optik, 2021, 237: 166637. doi: 10.1016/j.ijleo.2021.166637 [15] 田连标. 面向仿生导航系统的波浪水下偏振模式研究[D]. 大连: 大连理工大学, 2021.TIAN L B. Research on the underwater polarization patterns with wavy surface for bionic navigation systems[D]. Dalian: Dalian University of Technology, 2021. (in Chinese) [16] BHANDARI P, VOSS K J, LOGAN L, et al. The variation of the polarized downwelling radiance distribution with depth in the coastal and clear ocean[J]. Journal of Geophysical Research:Oceans, 2011, 116(C7): C00H10. [17] 胡帅, 高太长, 刘磊, 等. 偏振光在非球形气溶胶中传输特性的Monte Carlo仿真[J]. 物理学报,2015,64(9):094201. doi: 10.7498/aps.64.094201HU SH, GAO T CH, LIU L, et al. Simulation of radiation transfer properties of polarized light in non-spherical aerosol using Monte Carlo method[J]. Acta Physica Sinica, 2015, 64(9): 094201. (in Chinese) doi: 10.7498/aps.64.094201 [18] 郑茂琦, 马春翔, 王志波, 等. 基于海浪谱的海浪模拟的改进[J]. 系统仿真学报,2014,26(2):369-375. doi: 10.16182/j.cnki.joss.2014.02.002ZHENG M Q, MA CH X, WANG ZH B, et al. Improvement of wave simulation based on ocean wave spectrums[J]. Journal of System Simulation, 2014, 26(2): 369-375. (in Chinese) doi: 10.16182/j.cnki.joss.2014.02.002 -
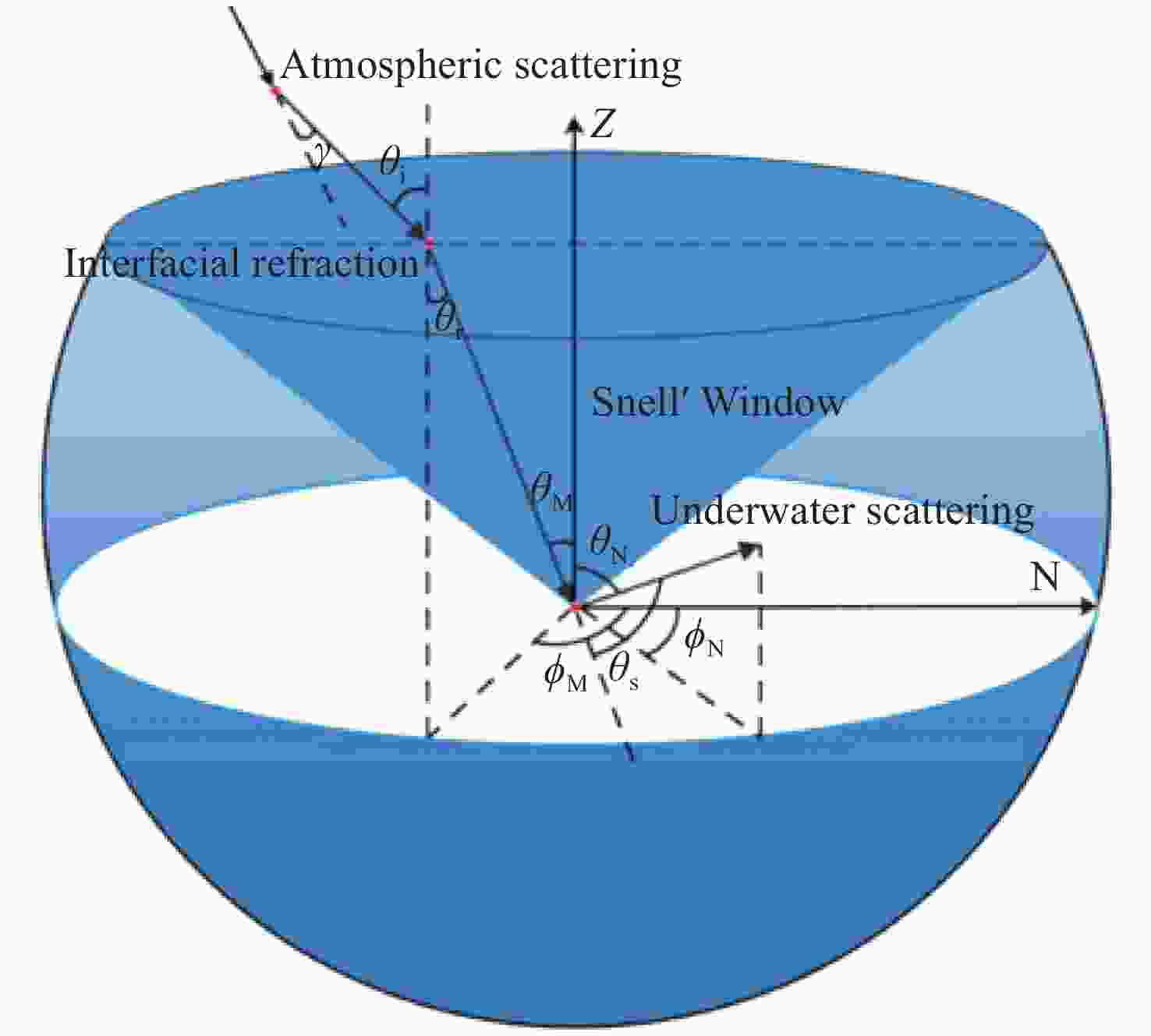
下载:
点击查看大图
计量
- 文章访问数: 311
- HTML全文浏览量: 203
- PDF下载量: 190
- 被引次数: 0
