A denoising method combining bitonic filtering and sine-cosine transform for shearography fringe pattern
-
摘要:
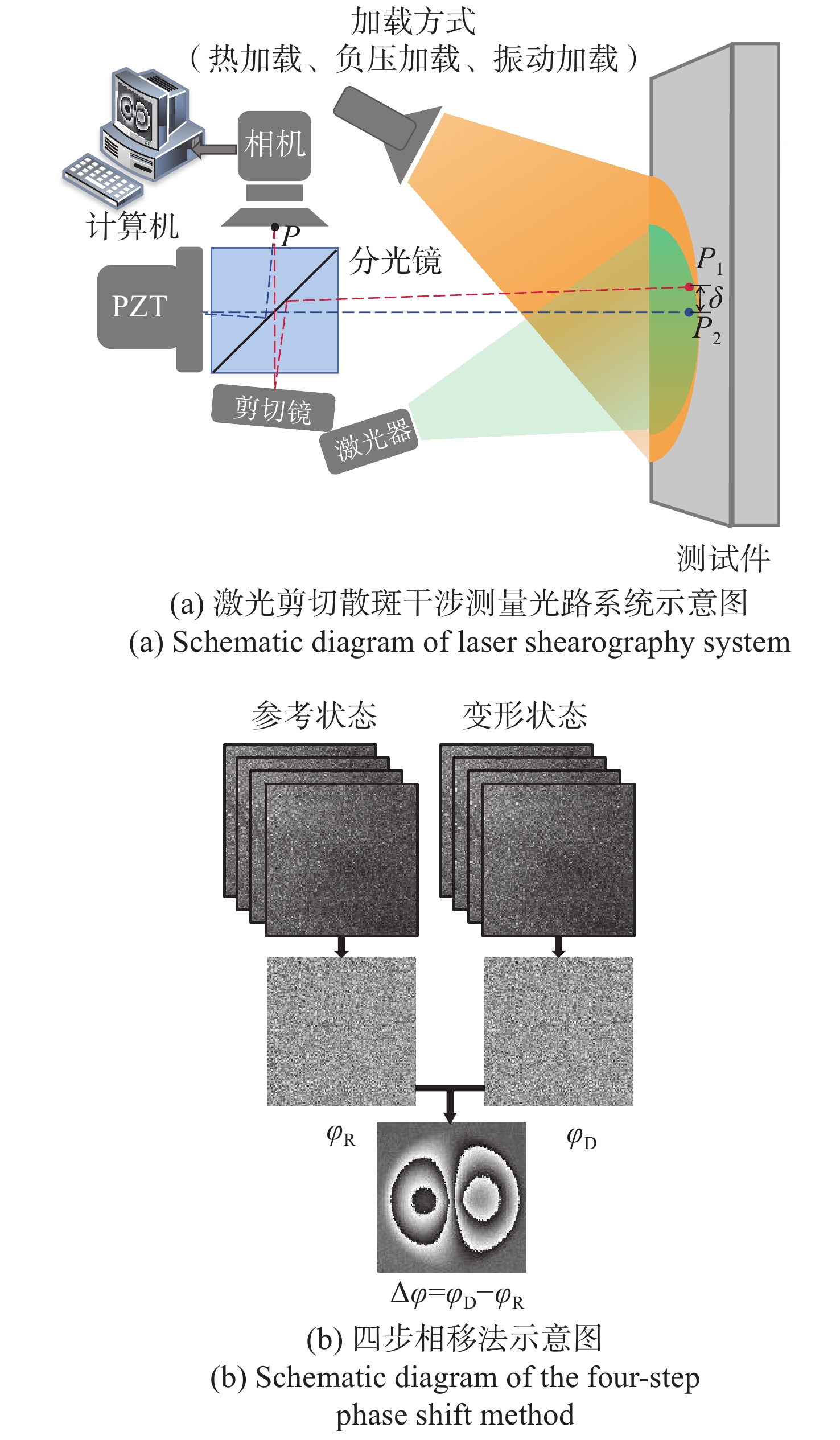
剪切散斑干涉是一种非接触式、全场高精度光学变形测量技术，由于环境等因素导致采集的散斑条纹图像存在大量随机噪声,进而影响测量精度。传统去噪方法在滤除噪声的同时，容易导致条纹边缘信息的丢失甚至破坏。针对该问题，本文提出基于正余弦变换和双调滤波相结合的剪切散斑干涉图像去噪方法。该方法首先对相位条纹图进行正余弦变换获得两幅图像，其次对这两幅图像分别运用双调滤波方法进行去噪，最后将滤波后的两幅图像合并为最终的相位条纹图。实验结果表明：经本文方法滤波后的相位图散斑抑制指数为0.999，平均保持指数为2.995，证明该方法较传统去噪方法能更好地改善相位图质量，且能较大程度地保留相位条纹的细节及边缘信息。
Abstract:Shearography is a non-contact, full-field, and high-precision optical deformation measurement technology. There is a lot of random noise in the acquired speckle fringe pattern caused by environmental factors, which affects the measurement accuracy. The traditional denoising methods easily cause the fringe information to be lost or even damaged while filtering out the noise. To solve this problem, we propose an image denoising method by combining sine and cosine transform and bitonic filtering. In this method, the phase fringe image is firstly obtained by sine and cosine transform. Secondly, the two images are denoised by the bitonic filtering method respectively. Finally, the filtered two images are merged into the final phase fringe image. Experimental results show that for the filtered phase pattern, the speckle suppression index is 0.999 and the average retention index is 2.995, which prove that the proposed method can improve the quality of the phase pattern better than the traditional denoising method, and can preserve the details and edge information of the phase fringes to a large extent.
-
Key words:
- shearography /
- interference /
- optical measurement /
- denoise /
- bitonic filtering
-
图 2 正余弦变换和双调滤波相结合的去噪方法
Figure 2. Denoising method based on bitonic filtering and sine-cosine transform
图 4 各种方法滤波后的相位图及其x轴处相位分布图
Figure 4. Phase maps after filtering and diagrams of phase distribution in x-axis
图 6 各滤波后的相位图及其x轴处相位分布图
Figure 6. Phase maps after filtering and corresponding phase distributions in x-axis
表 1 实验1中各滤波方法不同评价参数对比
Table 1. Comparison of evaluation parameters of different filtering methods in experiment 1
本文方法 正余弦中值 正余弦高斯 正余弦均值 原始图 ENL 3.338 3.327 3.324 3.329 3.124 SSI 0.999 1.001 1.002 1.002 1 SMPI 1.210 1.226 1.305 1.264 1 耗时(s) 11.36 0.79 0.58 0.89 - 
下载: 导出CSV
表 2 各滤波方法不同评价参数对比
Table 2. Comparison of evaluation parameters of different filtering methods
本文方法 正余弦中值 正余弦高斯 正余弦均值 原始图 ENL 10.236 9.586 10.052 10.059 9.368 SSI 0.957 0.989 0.965 0.965 1 SMPI 2.995 3.440 3.135 3.136 1 耗时(s) 9.76 0.41 0.25 0.24 -
下载: 导出CSV
-
[1] 程茶园, 林鑫, 葛丽, 等. 航天泡沫材料的声激励激光错位散斑检测[J]. 无损检测,2020,42(9):74-76.CHENG CH Y, LIN X, GE L, et al. Acoustic excitated laser shearography testing of aerospace foam materials[J]. Nondestructive Testing, 2020, 42(9): 74-76. (in Chinese) [2] 程茶园, 林鑫, 孙霖, 等. 自由装填式药柱包覆层黏接质量的错位散斑检测[J]. 无损检测,2021,43(8):58-61,66.CHENG CH Y, LIN X, SUN L, et al. Detection of the cladding bonding quality of free loading powder charge by shearography[J]. Nondestructive Testing, 2021, 43(8): 58-61,66. (in Chinese) [3] ANISIMOV A G, GROVES R M. Extreme shearography: Development of a high-speed shearography instrument for quantitative surface strain measurements during an impact event[J]. Optics and Lasers in Engineering, 2021, 140: 106502. doi: 10.1016/j.optlaseng.2020.106502 [4] YAN P ZH, LIU X W, DONG J T, et al. Robust dynamic phase-shifting common-path shearography using LCPG and pixelated micropolarizer array[J]. Optics and Lasers in Engineering, 2022, 153: 106997. doi: 10.1016/j.optlaseng.2022.106997 [5] 徐媛媛, 时刻, 王亚伟, 等. 相移干涉技术及相移获取方法研究进展[J]. 激光与光电子学进展,2018,55(2):020004.XU Y Y, SHI K, WANG Y W, et al. Research progresses of phase-shifting interferometry technology and phase shift extraction method[J]. Laser &Optoelectronics Progress, 2018, 55(2): 020004. (in Chinese) [6] HOSSEINI H, HESSAR F, MARVASTI F. Real-time impulse noise suppression from images using an efficient weighted-average filtering[J]. IEEE Signal Processing Letters, 2015, 22(8): 1050-1054. doi: 10.1109/LSP.2014.2381649 [7] JAYARAJ V, EBENEZER D. A new switching-based median filtering scheme and algorithm for removal of high-density salt and pepper noise in images[J]. EURASIP Journal on Advances in Signal Processing, 2010, 2010(1): 690218. doi: 10.1155/2010/690218 [8] ROBINSON D W, REID G T, DE GROOT P. Interferogram analysis: digital fringe pattern measurement techniques[J]. Physics Today, 1994, 47(8): 66. [9] AEBISCHER H A, WALDNER S. A simple and effective method for filtering speckle-interferometric phase fringe patterns[J]. Optics Communications, 1999, 162(4-6): 205-210. doi: 10.1016/S0030-4018(99)00116-9 [10] 蒋汉阳, 戴美玲, 苏志龙, 等. 基于散斑相位条纹方向的自适应正弦/余弦滤波[J]. 光学学报,2017,37(9):0910001. doi: 10.3788/AOS201737.0910001JIANG H Y, DAI M L, SU ZH L, et al. An adaptive sine/cosine filtering algorithm based on speckle phase fringe orientation[J]. Acta Optica Sinica, 2017, 37(9): 0910001. (in Chinese) doi: 10.3788/AOS201737.0910001 [11] 王智鑫, 胡烁陶, 夏振涛, 等. 基于正余弦变换和BM3D滤波的DSPI图像去噪方法[J]. 自动化与仪器仪表,2021(6):1-6,10.WANG ZH X, HU SH T, XIA ZH T, et al. DSPI image denoising method based on sine-cosine decomposition and BM3D filtering[J]. Automation &Instrumentation, 2021(6): 1-6,10. (in Chinese) [12] 王永红, 李骏睿, 孙建飞, 等. 散斑干涉相位条纹图的频域滤波处理[J]. 中国光学,2014,7(3):389-395.WANG Y H, LI J R, SUN J F, et al. Frequency domain filtering for phase fringe patterns of digital speckle pattern interferometry[J]. Chinese Optics, 2014, 7(3): 389-395. (in Chinese) [13] TREECE G. Morphology-based noise reduction: structural variation and thresholding in the bitonic filter[J]. IEEE Transactions on Image Processing, 2020, 29: 336-350. doi: 10.1109/TIP.2019.2932572 [14] TREECE G. The bitonic filter: linear filtering in an edge-preserving morphological framework[J]. IEEE Transactions on Image Processing, 2016, 25(11): 5199-5211. doi: 10.1109/TIP.2016.2605302 [15] KULKARNI R, RASTOGI P. Fringe denoising algorithms: a review[J]. Optics and Lasers in Engineering, 2020, 135: 106190. doi: 10.1016/j.optlaseng.2020.106190 -
下载:
计量
- 文章访问数: 394
- HTML全文浏览量: 163
- PDF下载量: 222
- 被引次数: 0
