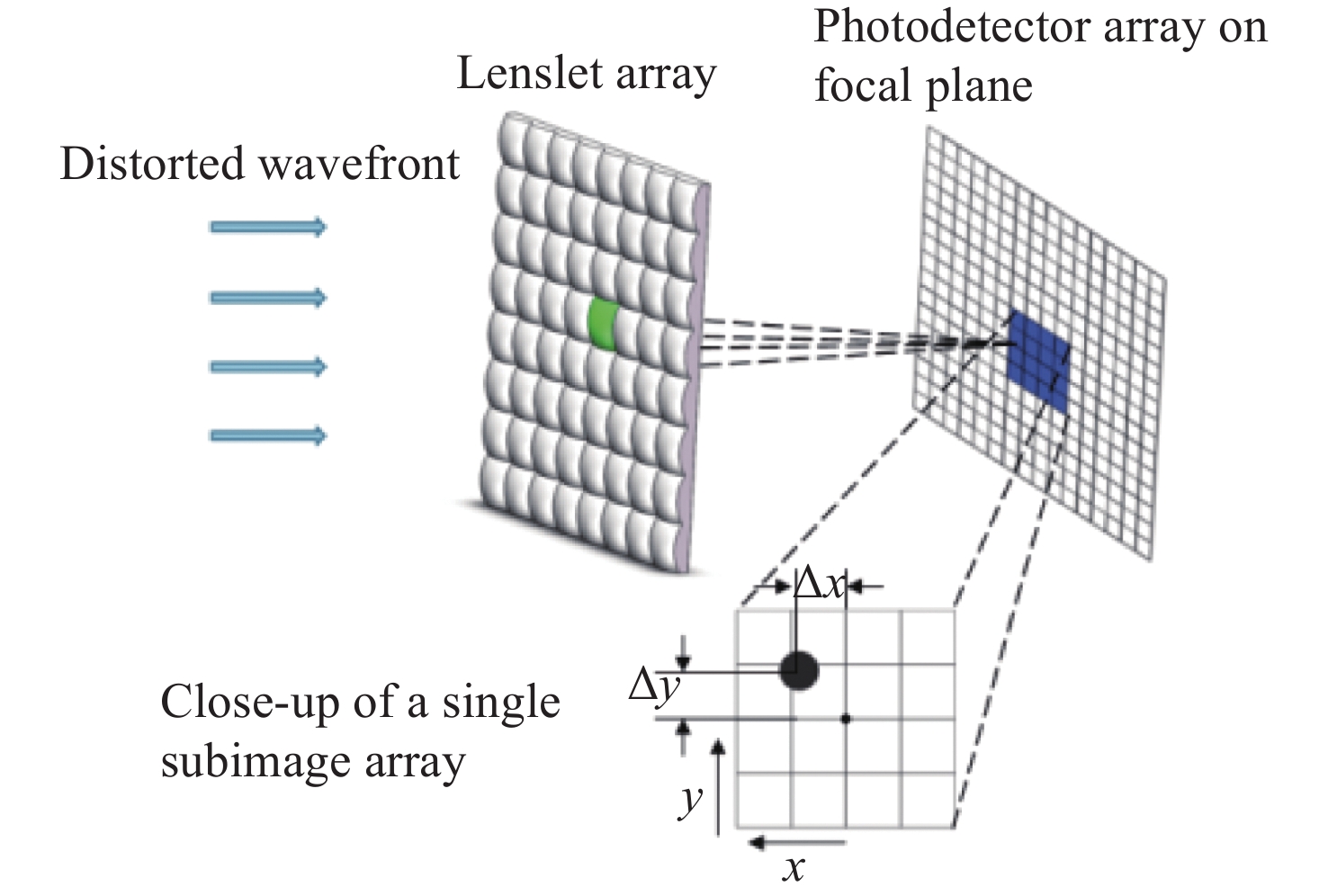
High-precision spherical wavefront calibration method for shack-hartmann wavefront sensor
-
摘要:
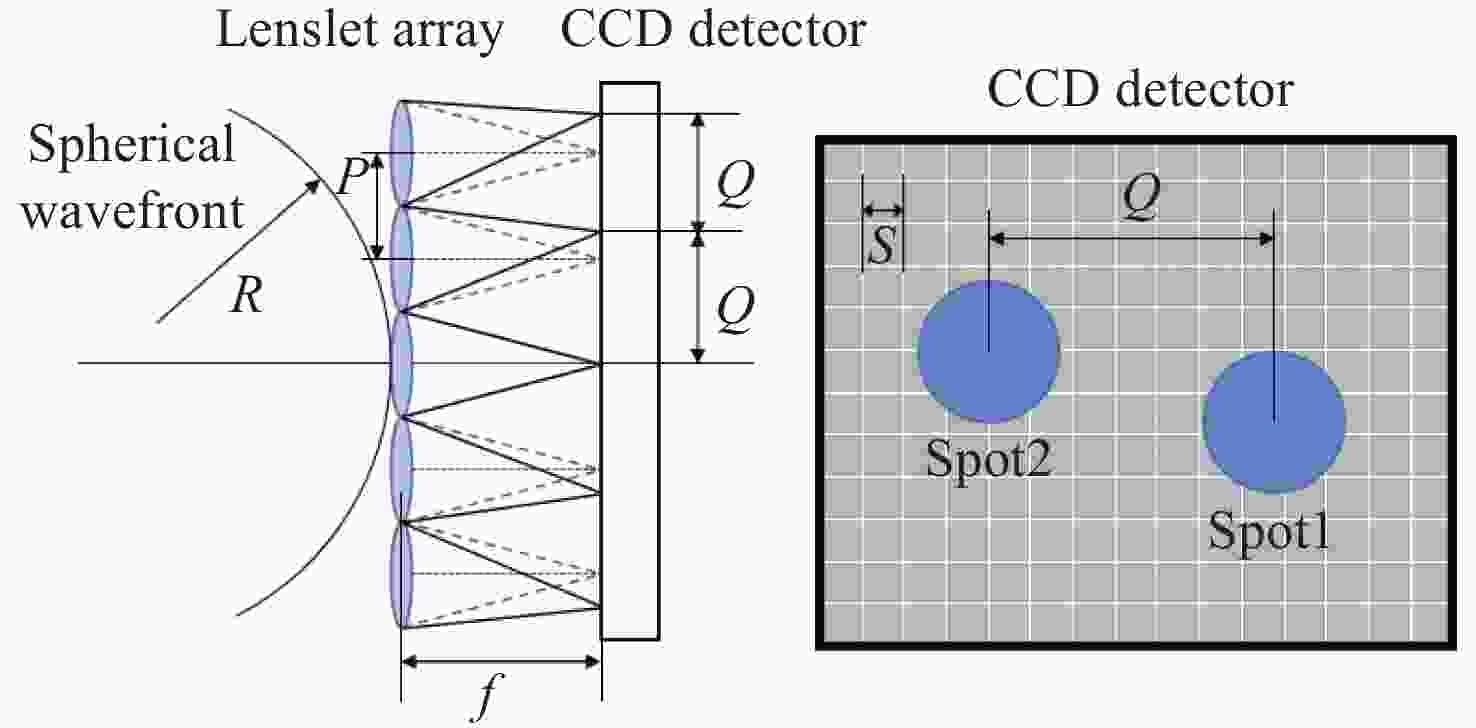
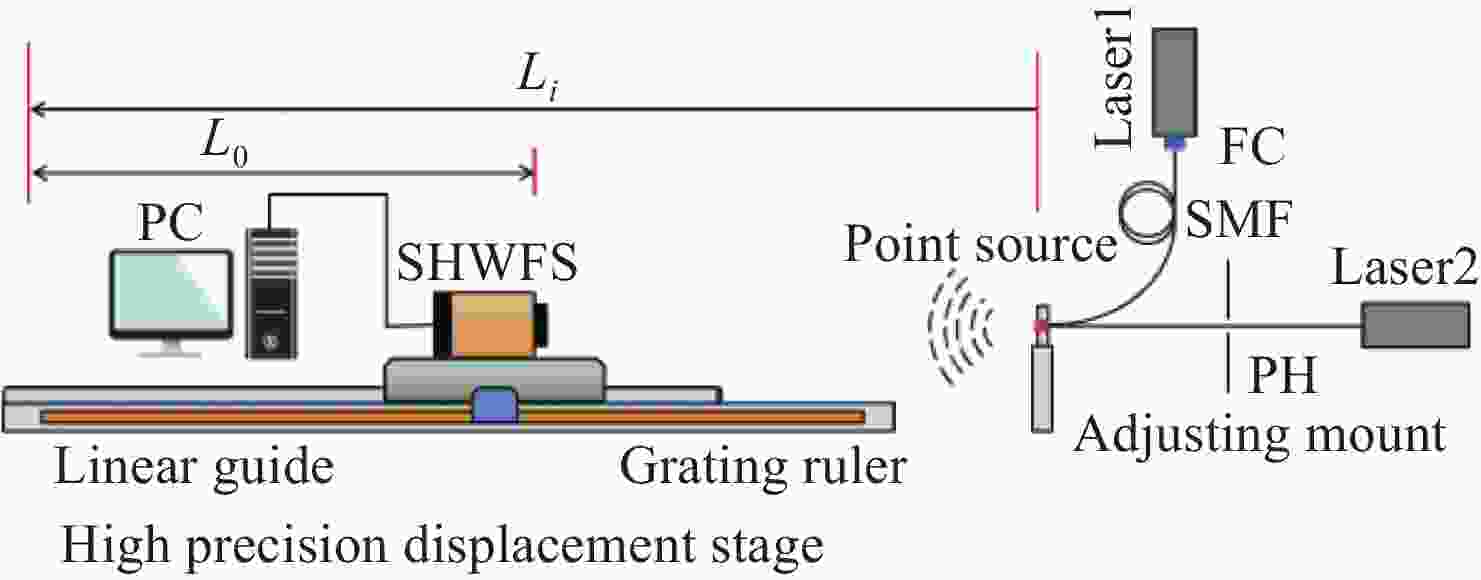
为解决哈特曼-夏克波前传感器传统标定方法存在的测量精度低、稳定性不足等问题，提出了一种基于球面波的哈特曼-夏克波前传感器高精度绝对标定方法。通过理论推导获取了球面波的高精度标定方法，结合搭建的球面波标定实验装置，对子孔径数为128×128的哈特曼-夏克波前传感器完成高精度标定。该方法计算得到了哈特曼-夏克波前传感器结构参数
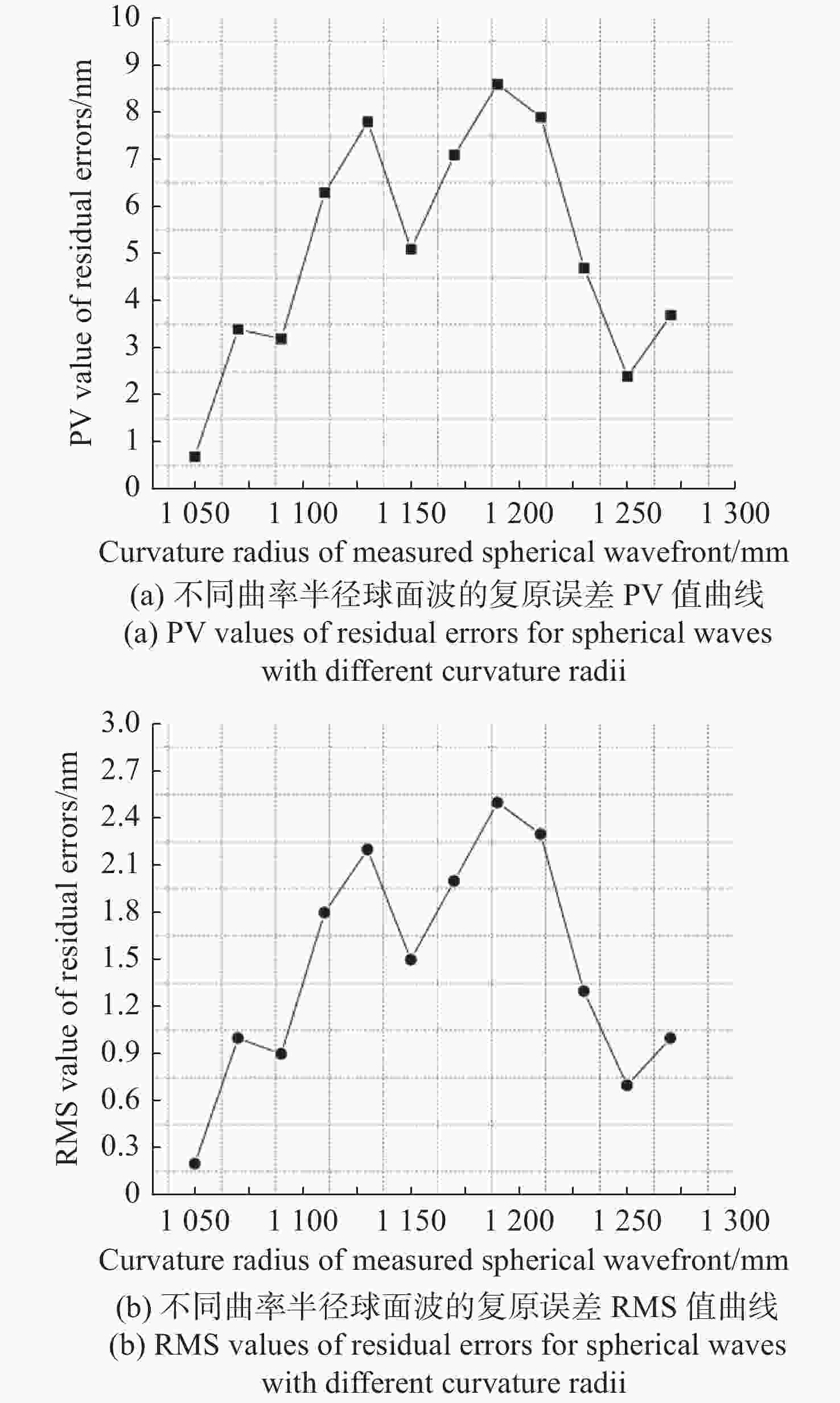
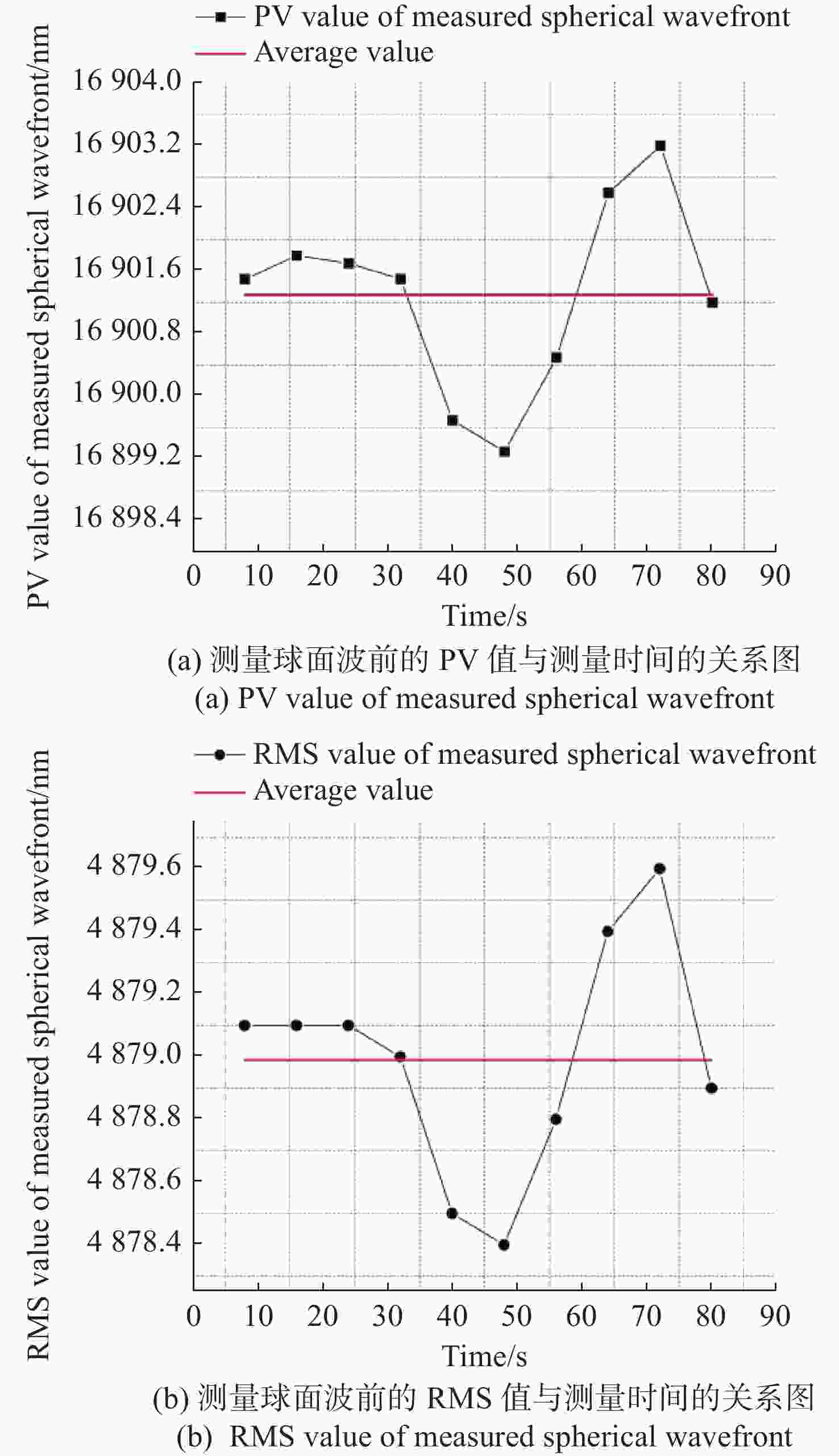
f ，w 以及L 0的精确值。对标定后的哈特曼-夏克波前传感器的测量精度进行测试，实验结果表明，经本文方法标定后的哈特曼-夏克波前传感器的波前复原精度达到了PV=1.376×10−2λ，RMS=4×10−3λ（λ=625 nm），重复性精度为PV=3.2×10−3λ，RMS=9.76×10−4λ（λ=625 nm）。该方法可以为大口径的SHWFS完成高精度标定，提升测量精度。-
关键词:
- 哈特曼-夏克波前传感器 /
- 绝对标定 /
- 球面波前
Abstract:To address the issues of low measurement accuracy and insufficient stability in traditional calibration methods for Shack-Hartmann wavefront sensors (SHWFS), we propose a high-precision absolute calibration method using spherical waves generated by sensor. A high-precision calibration method for spherical waves was obtained through theoretical derivation. Combined with the constructed spherical wave calibration experimental device, high-precision calibration was performed on the SHWFS with sub apertures of 128×128. The structural parameters of the SHWFS (
f ,w , andL 0) are calculated precisely. The measurement accuracy of the SHWFS is verified after calibration. The experimental results demonstrate that by using this method to calibrate the SHWFS, its wavefront recovery accuracy reaches a PV of 1.376×10−2λ and an RMS of 4×10−3λ (where λ=625 nm), respectively. Additionally, its repeatability accuracy reaches a PV of 3.2×10−3λ and an RMS of 9.76×10-4λ (where λ=625 nm), respectively. These findings suggest that this method is suitable for enhancing the measurement accuracy of high-precision calibration of SHWFS with large aperture. -
图 2 球面波前在SHWFS探测器上形成的光斑图
Figure 2. Spots pattern of a spherical wavefront on the plane of the SHWFS detector
图 3 高精度球面波标定装置原理图
Figure 3. Schematic diagram of the high-precision spherical wavefront calibration device
图 4 高精度球面波标定实物装置
Figure 4. Setup of the high-precision spherical wavefront calibration
图 5 不同曲率半径的球面波前复原误差
Figure 5. Residual errors for spherical waves with different curvature radii
图 6 重复性精度测试结果
Figure 6. Repeatability of wavefront measurements by the calibrated SHWFS
表 1 待标定的SHWFS的物理参数
Table 1. Parameters of the SHWFS to be calibrated
CCD相机 参数 微透镜阵列 参数 生产商 HIKROBOT 子孔径大小 0.1 mm×0.1 mm 型号 MV-CH250-90TM-M58S-NF 使用子孔径数 128×128 像素个数 5120×5120 焦距 2.4 mm 像素尺寸 2.5 μm x 2.5 μm 通光口径 Φ12.8 mm 
下载: 导出CSV
表 2 待标定的SHWFS的参数测量值
Table 2. Measured parameter values of the SHWFS to be calibrated
实验结果参数 f/mm $ {w}=\dfrac{{P}}{{S}} $ L0/mm 测量次数 1 2.402 39.960 1050.00 2 2.402 39.960 1050.00 3 2.402 39.960 1050.00 4 2.403 39.959 1050.00 5 2.402 39.960 1050.00 6 2.402 39.960 1050.00 7 2.403 39.959 1050.00 8 2.402 39.960 1050.00 9 2.401 39.961 1050.00 10 2.402 39.960 1050.00 均值 2.402 39.960 1050.00
下载: 导出CSV
-
[1] TYSON R K, FRAZIER B W. Principles of Adaptive Optics[M]. 5th ed. Boca Raton: CRC Press, 2022. [2] WEI K, LI M, CHEN SH Q, et al. First light for the sodium laser guide star adaptive optics system on the Lijiang 1.8m telescope[J]. Research in Astronomy and Astrophysics, 2016, 16(12): 183. doi: 10.1088/1674-4527/16/12/183 [3] SCHÄFER B, LÜBBECKE M, MANN K. Hartmann-Shack wave front measurements for real time determination of laser beam propagation parameters[J]. Review of Scientific Instruments, 2006, 77(5): 053103. doi: 10.1063/1.2198795 [4] SAKHAROV A M, BARYSHNIKOV N V, KARASIK V E, et al. A method for reconstructing the equation of the aspherical surface of mirrors in an explicit form using a device with a wavefront sensor[J]. Proceedings of SPIE, 2020, 11487: 114870B. [5] HE Y, DENG G H, WEI L, et al. Design of a compact, bimorph deformable mirror-based adaptive optics scanning laser ophthalmoscope[M]//LUO Q M, LI L Z, HARRISON D K, et al. Oxygen Transport to Tissue XXXVIII. Cham: Springer, 2016: 375-383. [6] 朱沁雨, 韩国庆, 彭建涛, 等. 双波长视网膜成像自适应光学系统的轴向色差补偿方法[J]. 中国光学,2022,15(1):79-89. doi: 10.37188/CO.EN.2021-0009ZHU Q Y, HAN G Q, PENG J T, et al. Longitudinal chromatic aberration compensation method for dual-wavelength retinal imaging adaptive optics systems[J]. Chinese Optics, 2022, 15(1): 79-89. (in Chinese). doi: 10.37188/CO.EN.2021-0009 [7] 王艳萍, 王茜蒨, 马冲. 哈特曼波前分析仪校准方法研究[J]. 中国激光,2015,42(1):0108003. doi: 10.3788/CJL201542.0108003WANG Y P, WANG Q Q, MA CH. Study on Hartmann wavefront analyzer calibration method[J]. Chinese Journal of Lasers, 2015, 42(1): 0108003. (in Chinese). doi: 10.3788/CJL201542.0108003 [8] ARTZNER G. On the absolute calibration of Shack-Hartmann sensors and UV laboratory wavefront measurements[J]. Pure and Applied Optics:Journal of the European Optical Society Part A, 1994, 3(2): 121-132. doi: 10.1088/0963-9659/3/2/005 [9] GREIVENKAMP J E, SMITH D G, GOODWIN E. Calibration issues with Shack-Hartmann sensors for metrology applications[J]. Proceedings of SPIE, 2004, 5252: 372-380. doi: 10.1117/12.513462 [10] CHERNYSHOV A, STERR U, RIEHLE F, et al. Calibration of a Shack–Hartmann sensor for absolute measurements of wavefronts[J]. Applied Optics, 2005, 44(30): 6419-6425. doi: 10.1364/AO.44.006419 [11] NIKITIN A N, GALAKTIONOV I, SHELDAKOVA J, et al. Absolute calibration of a Shack-Hartmann wavefront sensor for measurements of wavefronts[J]. Proceedings of SPIE, 2019, 10925: 109250K. [12] BAUTSCH J, SCHAKE M, EHRET G, et al. Traceable calibration of Shack–Hartmann wavefront sensors employing spherical wavefronts[J]. Optical Engineering, 2020, 59(8): 084104. [13] YANG J SH, WEI L, CHEN H L, et al. Absolute calibration of Hartmann-Shack wavefront sensor by spherical wavefronts[J]. Optics Communications, 2010, 283(6): 910-916. doi: 10.1016/j.optcom.2009.11.022 [14] 梁春, 沈建新, 童桂, 等. Hartmann-Shack传感器结构参量的自基准标定[J]. 光子学报,2009,38(4):780-784.LIANG CH, SHEN J X, TONG G, et al. A self-reference method for measuring Hartmann-shack wavefront sensor parameter[J]. Acta Photonica Sinica, 2009, 38(4): 780-784. (in Chinese). [15] 周晓斌, 栾亚东, 史雷蕾, 等. 基于已知球面波前的Hartmann-Shack传感器结构参量标定[J]. 应用光学,2015,36(6):909-912. doi: 10.5768/JAO201536.0603002ZHOU X B, LUAN Y D, SHI L L, et al. Structural parameters calibration of Hartmann-Shack sensor based on known spherical wavefront[J]. Journal of Applied Optics, 2015, 36(6): 909-912. (in Chinese). doi: 10.5768/JAO201536.0603002 [16] NIKITIN A N, GALAKTIONOV I, SHELDAKOVA J, et al. Calibration of a Shack-Hartmann wavefront sensor using spherical wavefronts from a point source[J]. Proceedings of SPIE, 2022, 11987: 119870J. [17] PLATT B C, SHACK R. History and principles of Shack-Hartmann wavefront sensing[J]. Journal of Refractive Surgery, 2001, 17(5): S573-S577. [18] BORN M, WOLF E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light[M]. 7th ed. Cambridge: Cambridge University Press, 1999. -
下载:
计量
- 文章访问数: 417
- HTML全文浏览量: 237
- PDF下载量: 125
- 被引次数: 0
