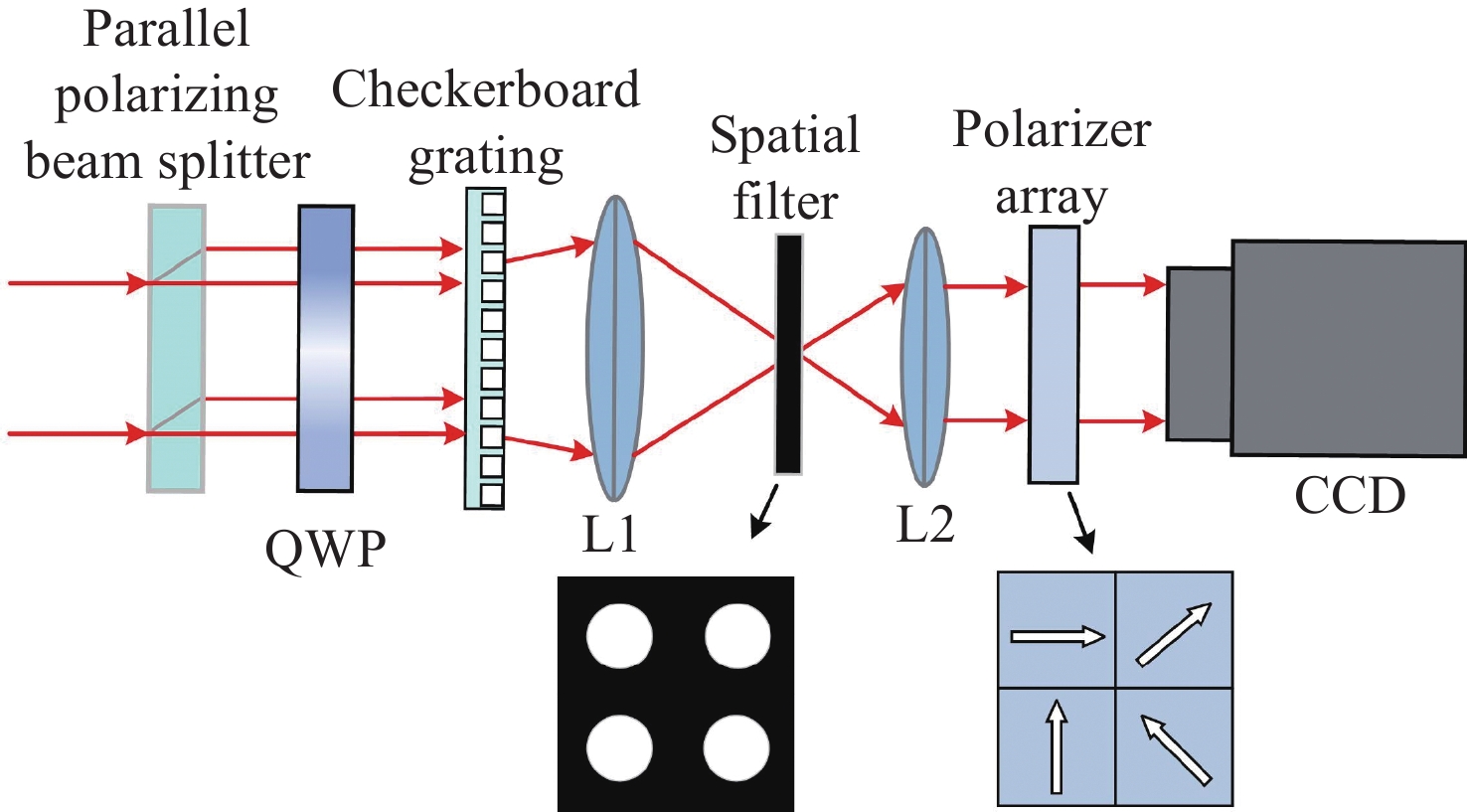
Error modeling of polarization devices in simultaneous phase-shifted lateral shearing interferometry
-
摘要:
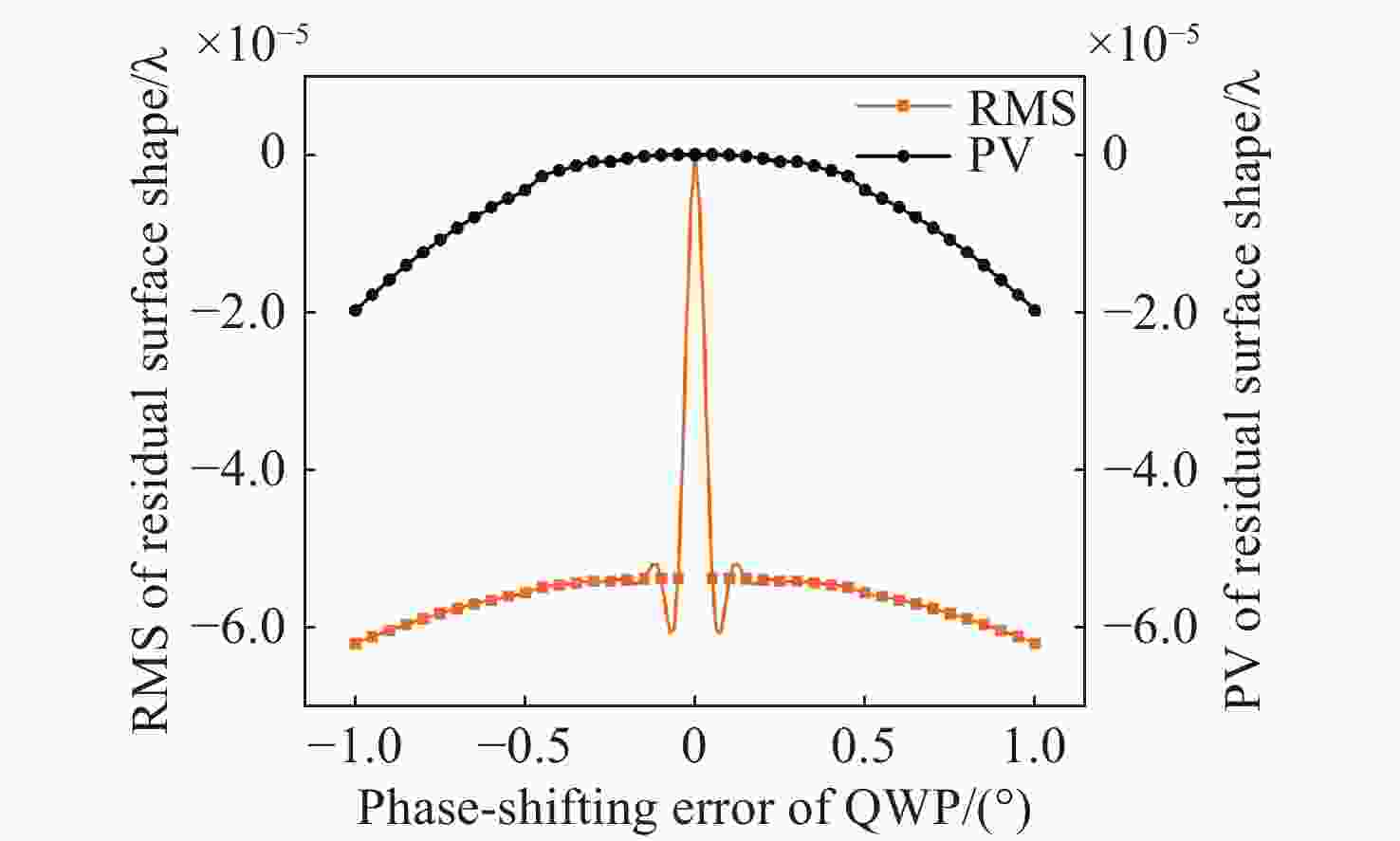
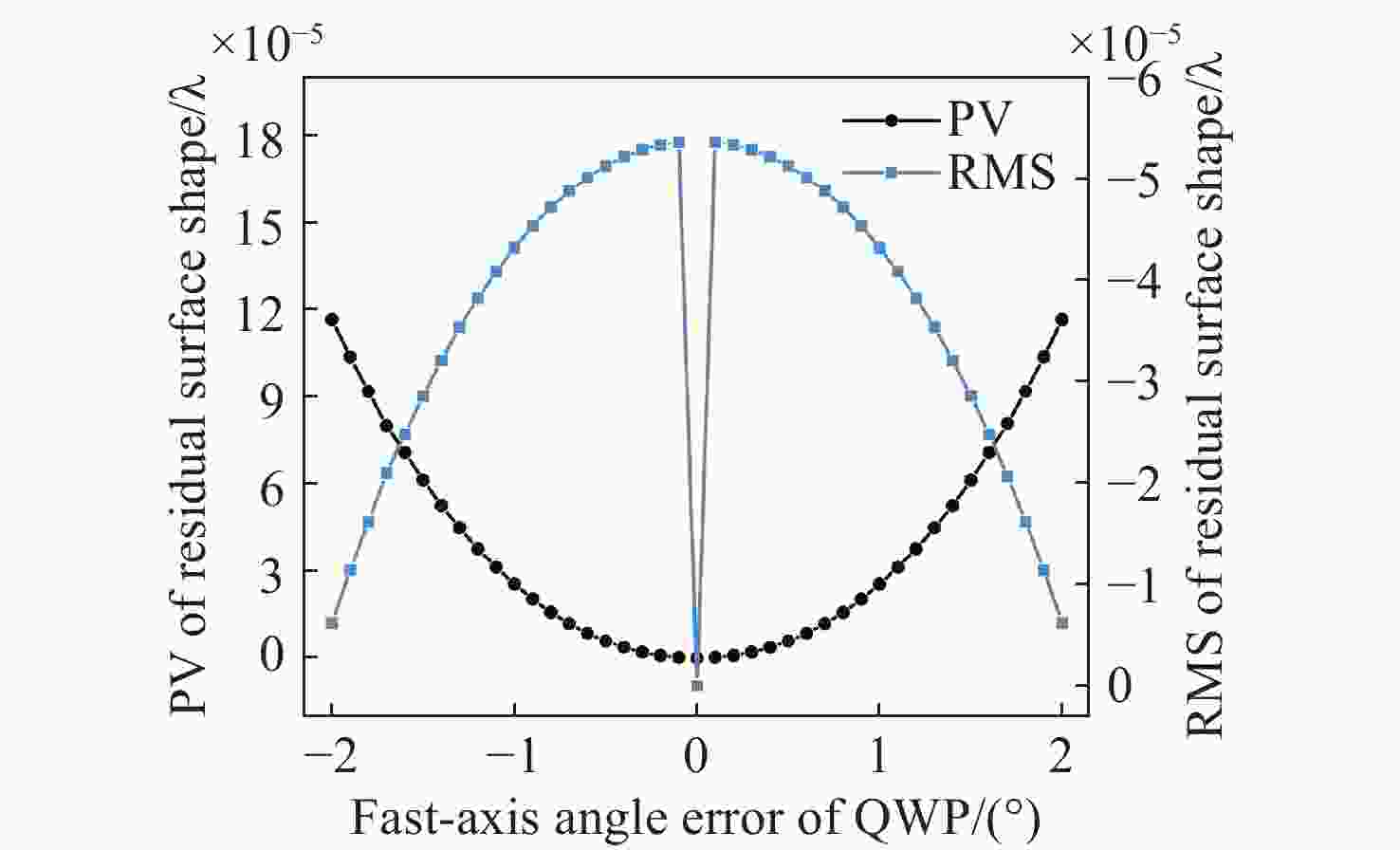
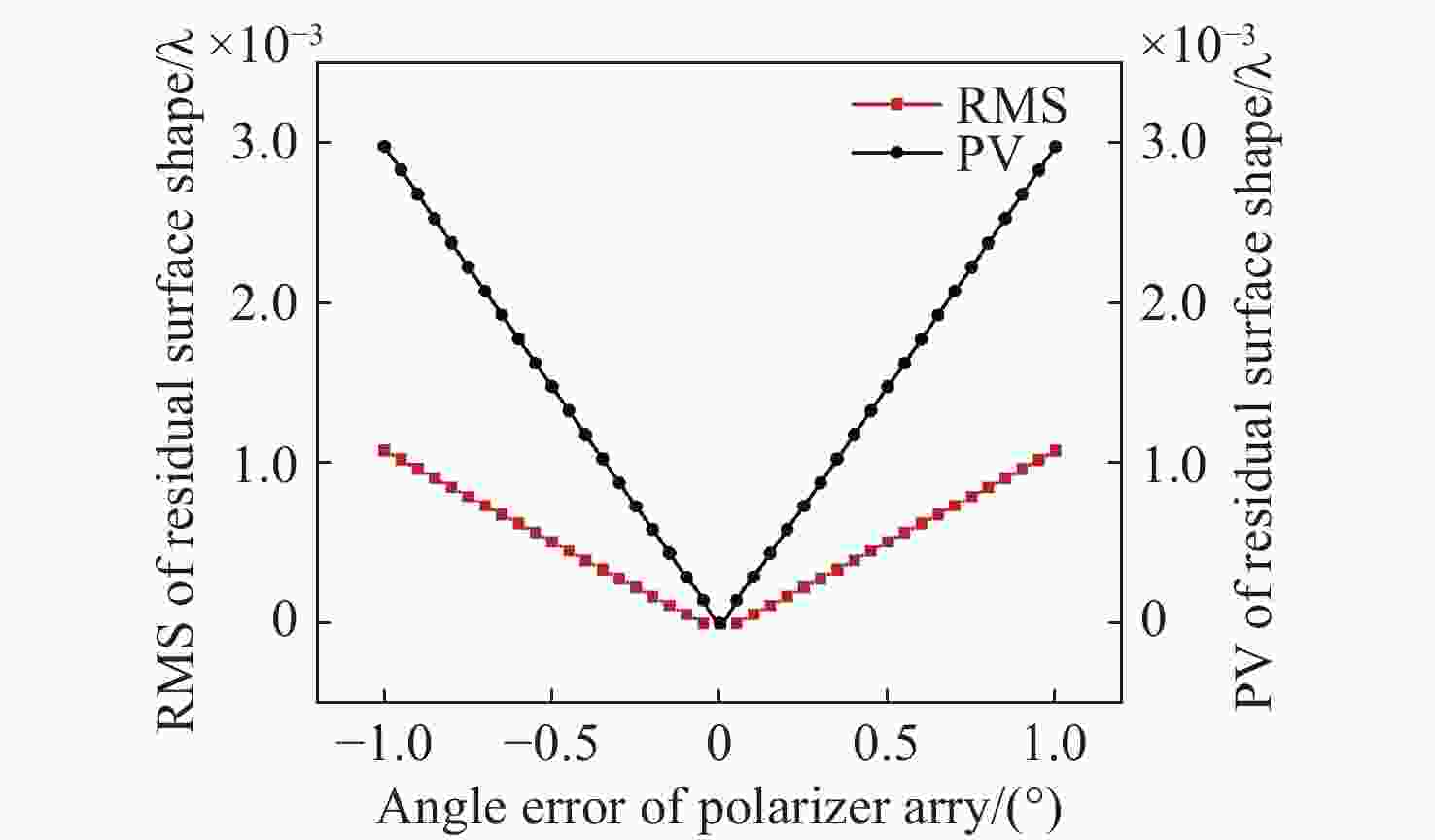
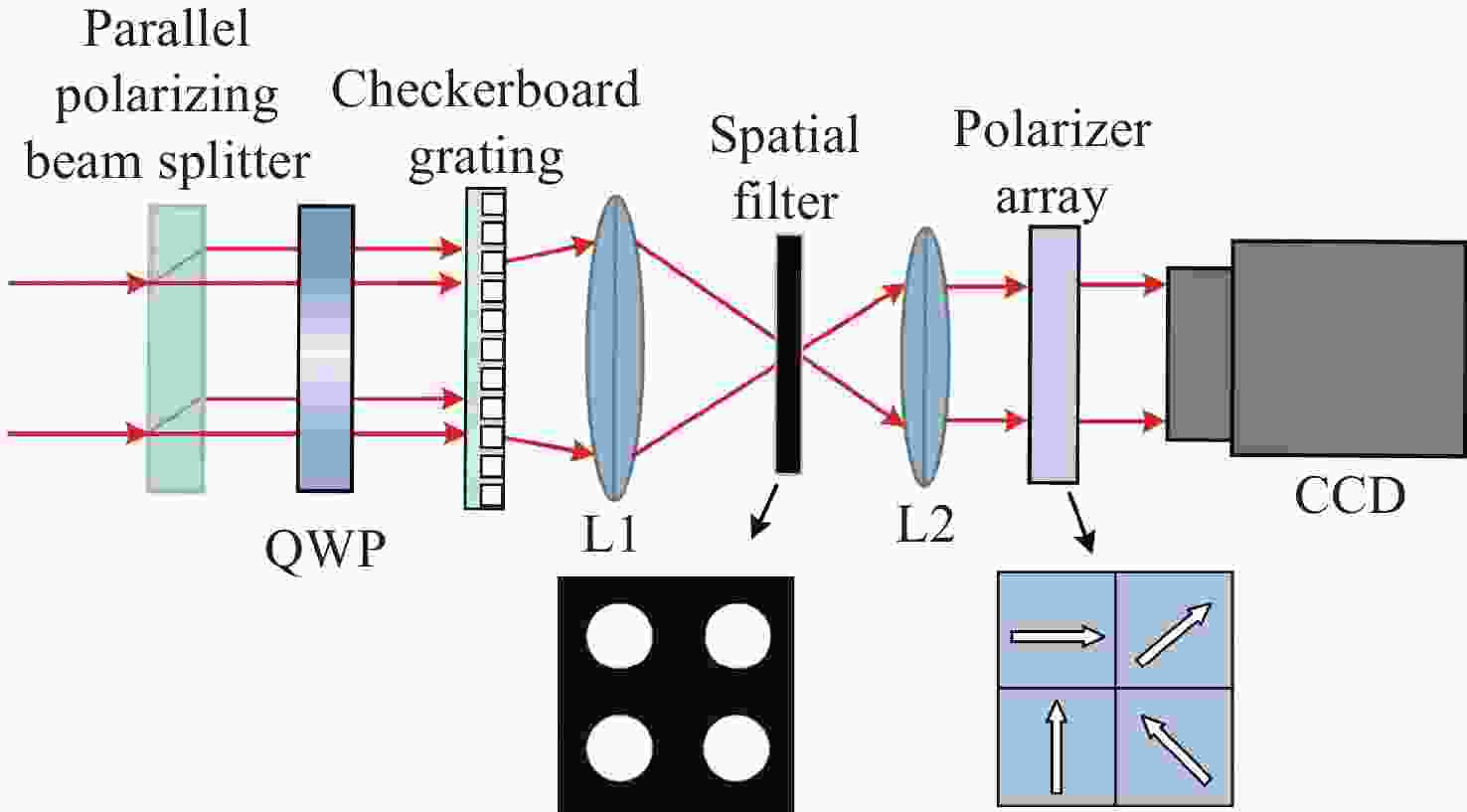
为了对同步相移横向剪切干涉系统中偏振器件的选型、装调以及误差补偿提供可靠的理论依据，本文根据琼斯矩阵原理，构建了系统中1/4波片和偏振片阵列误差对测量结果影响程度的误差模型，对四分之一波片的相位延迟误差、快轴方位角误差以及偏振片阵列透光轴方位角误差对测量结果的影响进行了定量分析。仿真结果表明：1/4波片的相位延迟误差在±1°以内时，波面测量误差为0.00002λ(PV)和0.000062λ(RMS)；1/4波片的调整精度在±2°以内时，波面测量误差为0.0001λ(PV)和0.00006λ(RMS)；偏振片阵列方位角误差在±1°以内时，测量误差为0.003λ(PV)和0.001λ(RMS)。根据仿真结果对测量系统中偏振元器件进行选型，同时选择两种不同精度的偏振元器件进行对比实验。实验结果的残差值与仿真结果的残差值的PV以及RMS值偏差均小于λ/20，可以在一定程度上验证模型的有效性。本文提出的数学模型可以为同步相移横向剪切干涉系统中偏振器件的选型提供可靠的理论依据。
Abstract:To provide a reliable theoretical basis for the selection, mounting, and error compensation of the polarization device in the synchronous phase-shift transverse shear interference system, based on the Jones matrix principle, we construct an error model reflecting the degree of influence of the errors of quarter-waveplate and polarizer array on the measurement results in the system. Then, we quantitatively analyze how the measurement results are influenced by the following factors: the phase delay error of quarter-waveplate, fast-axis azimuthal angle error, and transmission-axis azimuthal angle error of the polarizer array. The simulation results show that the wavefront measurement errors are 0.00002λ(PV) and 0.000062λ(RMS) when the phase delay error of the quarter-waveplate is within ±1°, 0.0001λ(PV) and 0.00006λ(RMS) when the adjustment accuracy of the quarter-waveplate is within ±2°, and 0.003λ(PV) and 0.001λ(RMS) when the azimuthal angle error of the polarizer array is within ±1°. According to the simulation results, the polarization components in the measurement system were selected. At the same time, two polarization components with different levels of accuracy were chosen for comparison experiments. The experimental results indicate the following conclusions: the deviations of the residual values of the experimental results from the residual values of the simulation results in terms of the PV and the RMS values are less than λ/20, and the validity of the model can be verified to a certain extent. The mathematical model proposed in this paper can provide a reliable theoretical basis for the selection of polarization devices in synchronous phase-shifted transverse shear interference systems.
-
图 1 同步相移横向剪切干涉原理图
Figure 1. Schematic diagram of simultaneous phase shift lateral shearing interferometry
图 2 重建面形残差随相位延迟误差变化曲线
Figure 2. Residual surface shape varying with waveplate phase delay error
图 3 重建面形残差随快轴方位角误差变化曲线
Figure 3. Residual surface shape varying with waveplate fast axis azimuth error
图 4 重建面形残差随偏振片阵列方位角误差变化曲线
Figure 4. Residual surface shape varying with polarizer array azimuth error
图 5 同步相移横向剪切干涉测量系统
Figure 5. Synchronous phase-shift transverse shear interferometry system
表 1 残差对比结果
Table 1. Comparative analysis of residual (Unit: λ)
PV RMS 实验结果残差 0.0058 0.0026 仿真结果残差 0.0040 0.0015 
下载: 导出CSV
-
[1] 侯溪, 张帅, 胡小川, 等. 超高精度面形干涉检测技术进展[J]. 光电工程,2020,47(8):200209.HOU X, ZHANG SH, HU X CH, et al. The research progress of surface interferometric measurement with higher accuracy[J]. Opto-Electronic Engineering, 2020, 47(8): 200209. (in Chinese). [2] 张梦瑶, 田爱玲, 王大森, 等. 基于逆向优化策略的面形绝对检测平移量研究[J]. 中国激光,2022,49(18):1804003.ZHANG M Y, TIAN A L, WANG D S, et al. Translation of surface shape absolute testing based on reverse optimization strategy[J]. Chinese Journal of Lasers, 2022, 49(18): 1804003. (in Chinese). [3] LIU X, GAO Y, CHANG M. A new lateral shearing interferometer for precision surface measurement[J]. Optics and Lasers in Engineering, 2009, 47(9): 926-934. doi: 10.1016/j.optlaseng.2009.03.019 [4] 谈宜东, 徐欣, 张书练. 激光干涉精密测量与应用[J]. 中国激光,2021,48(15):1504001. doi: 10.3788/CJL202148.1504001TAN Y D, XU X, ZHANG SH L. Precision measurement and applications of laser interferometry[J]. Chinese Journal of Lasers, 2021, 48(15): 1504001. (in Chinese). doi: 10.3788/CJL202148.1504001 [5] 梁子健, 杨甬英, 赵宏洋, 等. 非球面光学元件面型检测技术研究进展与最新应用[J]. 中国光学,2022,15(2):161-186.LIANG Z J, Yang Y Y, ZHAO H Y, et al. Advances in research and applications of optical aspheric surface metrology[J]. Chinese Optics, 2022, 15(2): 161-186. (in Chinese). [6] WANG S Q, LIU B C, WANG H J, et al. Improving the phase reconstruction accuracy of simultaneous phase-shifted lateral shearing interferometry using a polarization redundant sub-region interpolation method[J]. Optics Express, 2022, 30(19): 34297-34313. doi: 10.1364/OE.463534 [7] 师途, 杨甬英, 张磊, 等. 非球面光学元件的面形检测技术[J]. 中国光学,2014,7(1):26-46.SHI T, YANG Y Y, ZHANG L, et al. Surface testing methods of aspheric optical elements[J]. Chinese Optics, 2014, 7(1): 26-46. (in Chinese). [8] GU L Y, LIU L, HU SH Y, et al. Polarization phase-shifting lateral shearing interferometer with two polarization beam splitter plates[J]. Optical Review, 2017, 24(4): 600-604. doi: 10.1007/s10043-017-0351-x [9] ZHANG R, YANG Y Y, ZHAO H Y, et al. Non-null testing of the aspheric surface using a quadriwave lateral shearing interferometer[J]. Applied Optics, 2020, 59(18): 5447-5456. doi: 10.1364/AO.391263 [10] LI P, TANG F, WANG X ZH. Relationship between shear ratio and reconstruction accuracy in lateral shearing interferometry[J]. Optical Engineering, 2020, 59(3): 034113. [11] 徐春生. 同步移相抗振干涉的研究[D]. 南京理工大学, 2006.XU CH SH. Study on simultaneous phase-shifting anti-vibration interference[D]. Nanjing: Nanjing University of Science and Technology, 2006. (in Chinese). [12] 李杰, 唐锋, 王向朝, 等. 光栅横向剪切干涉仪及其系统误差分析[J]. 中国激光,2014,41(5):0508006. doi: 10.3788/CJL201441.0508006LI J, TANG F, WANG X ZH, et al. System errors analysis of grating lateral shearing interferometer[J]. Chinese Journal of Lasers, 2014, 41(5): 0508006. (in Chinese). doi: 10.3788/CJL201441.0508006 [13] MIAO X Y, MA J, YU Y F, et al. Modelling and correction for polarization errors of a 600 mm aperture dynamic Fizeau interferometer[J]. Optics Express, 2020, 28(22): 33355-33370. doi: 10.1364/OE.409983 [14] ZHU Y H, TIAN A L, WANG H J, et al. Analysis of the influence of simultaneous phase-shifting shearing interference polarizer[J]. Optical Engineering, 2022, 61(10): 104102. [15] 钱克矛, 伍小平. 利用位相光栅的实时偏振相移方法的误差分析[J]. 激光杂志,2000,21(6):17-20. doi: 10.3969/j.issn.0253-2743.2000.06.007QIAN K M, WU X P. A real-time polarization phase shifting method: error analysis[J]. Laser Journal, 2000, 21(6): 17-20. (in Chinese). doi: 10.3969/j.issn.0253-2743.2000.06.007 [16] WANG H J, WANG Z, TIAN A L, et al. Modeling and analysis of commonpath phase shifting shear system based on birefringent optical devices[J]. Journal of Nonlinear Optical Physics & Materials, 2008, 17(4): 503-510. [17] WANG D D, WANG CH, TIAN XB, et al. Snapshot phase-shifting lateral shearing interferometer[J]. Optics and Lasers in Engineering, 2020, 128: 106032. doi: 10.1016/j.optlaseng.2020.106032 [18] 左芬, 陈磊. 一种同步移相干涉测量系统的误差研究[J]. 光学技术,2009,35(4):536-540. doi: 10.3321/j.issn:1002-1582.2009.04.008ZUO F, CHEN L. Errors researching for a simultaneous phase shifting interferometer[J]. Optical Technique, 2009, 35(4): 536-540. (in Chinese). doi: 10.3321/j.issn:1002-1582.2009.04.008 [19] 蒋超, 郭仁慧, 张辉钦, 等. 基于四分之一波片的菲佐型同步移相干涉测量方法[J]. 激光与光电子学进展,2016,53(10):101203.JIANG CH, GUO R H, ZHANG H Q, et al. Method of Fizeau simultaneous phase-shifting interferometry based on quarter-wave plate[J]. Laser & Optoelectronics Progress, 2016, 53(10): 101203. (in Chinese). [20] ZHENG D H, CHEN L, LI J P, et al. Simultaneous phase-shifting interferometry: immune to azimuth error of fast-axes in retarder array[J]. Appl. Opt., 2015, 54(33): 9803-9808. doi: 10.1364/AO.54.009803 [21] MIAO X Y, YU Y F, LI A B, et al. Optical phase-shifting methods based on low coherence laser for large aperture Fizeau interferometer[J]. Optics and Lasers in Engineering, 2021, 140: 106513. doi: 10.1016/j.optlaseng.2020.106513 [22] LIU K, WANG J N, WANG H, et al. Wavefront reconstruction for multi-lateral shearing interferometry using difference Zernike polynomials fitting[J]. Optics and Lasers in Engineering, 2018, 106: 75-81. doi: 10.1016/j.optlaseng.2018.02.011 [23] 郑东晖, 李金鹏, 陈磊, 等. 空域移相偏振点衍射波前检测技术[J]. 物理学报,2016,65(11):114203. doi: 10.7498/aps.65.114203ZHENG D H, LI J P, CHEN L, et al. Spatial phase-shifting polarization point-piffraction interferometer for wavefront measurement[J]. Acta Physica Sinica, 2016, 65(11): 114203. (in Chinese). doi: 10.7498/aps.65.114203 -
下载:
计量
- 文章访问数: 298
- HTML全文浏览量: 124
- PDF下载量: 54
- 被引次数: 0
