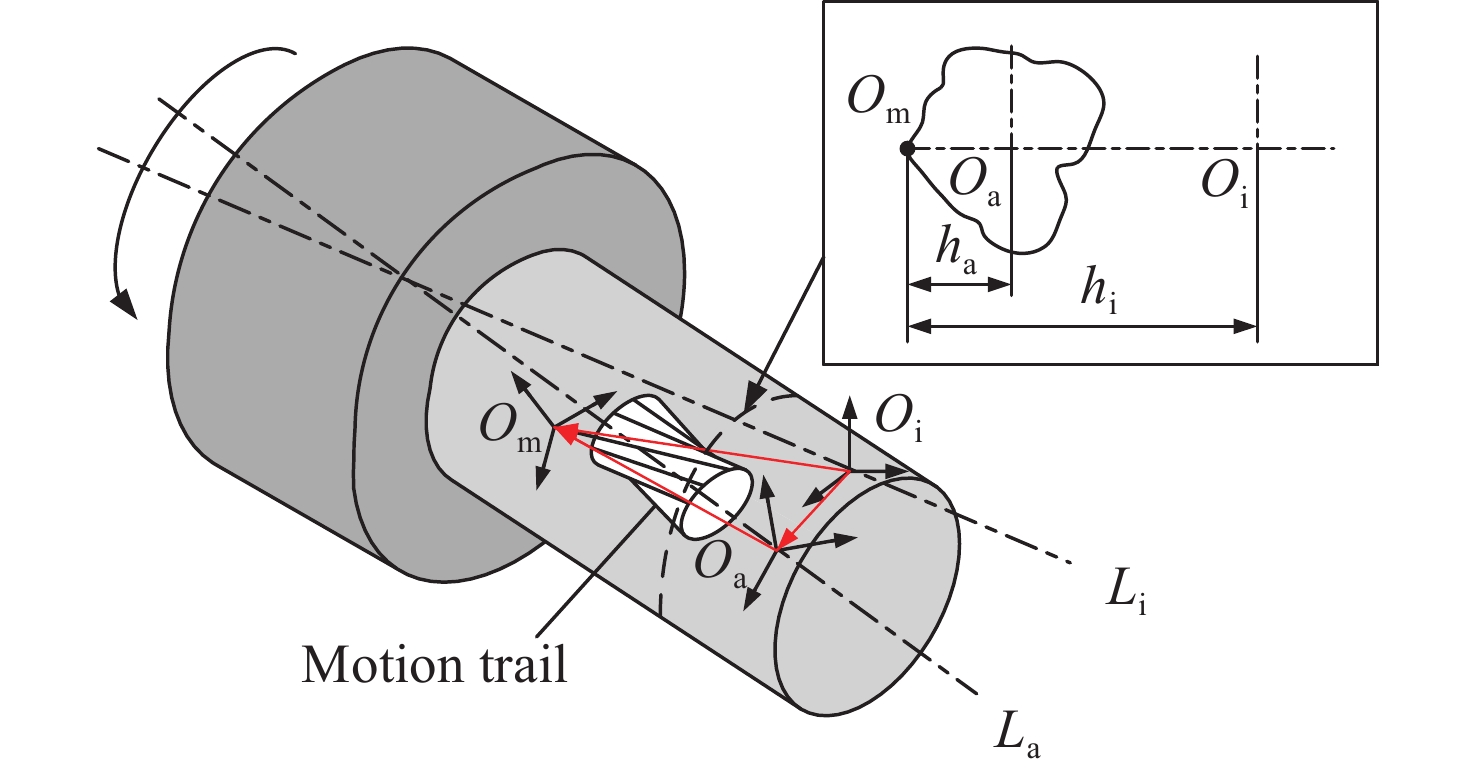
-
摘要:
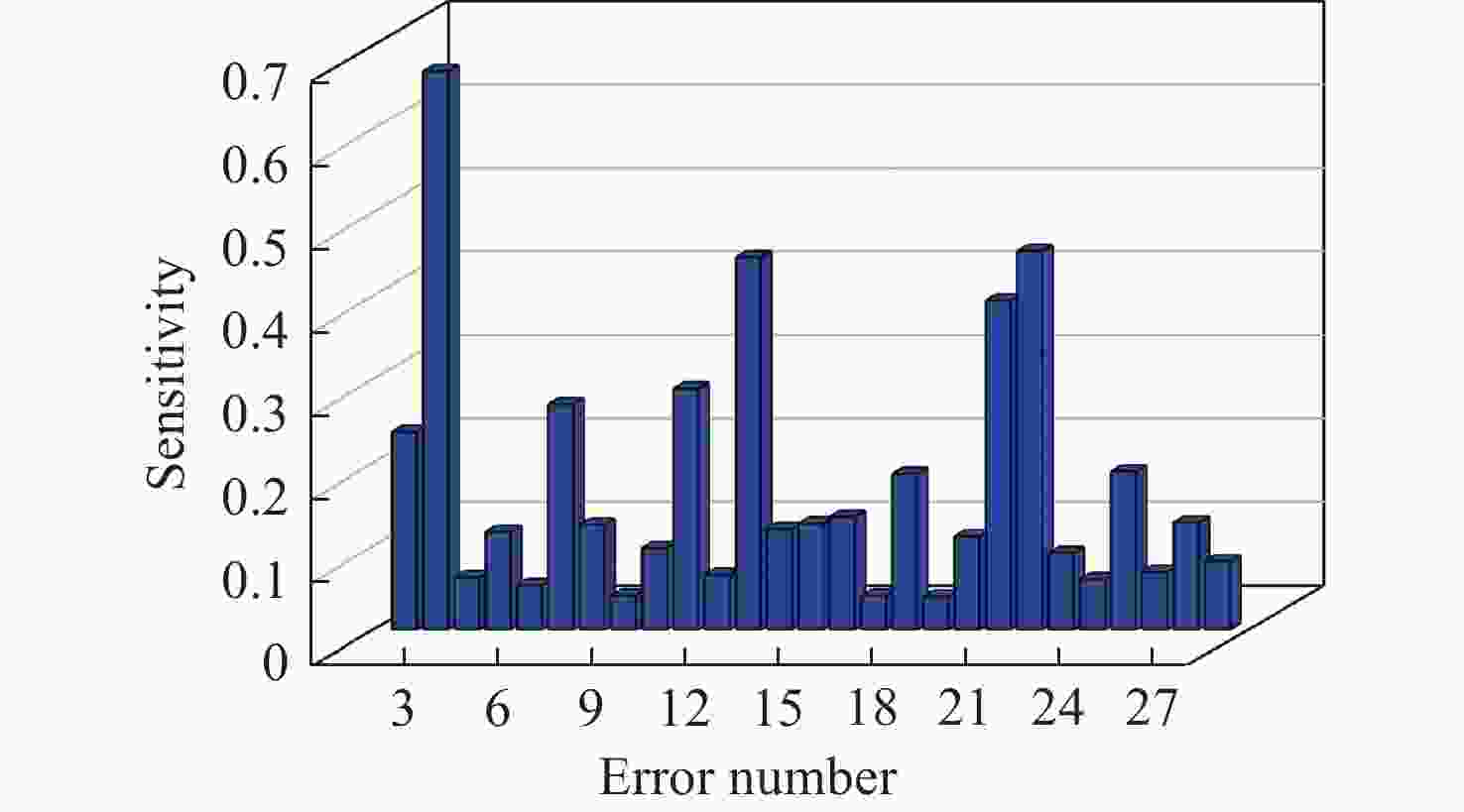
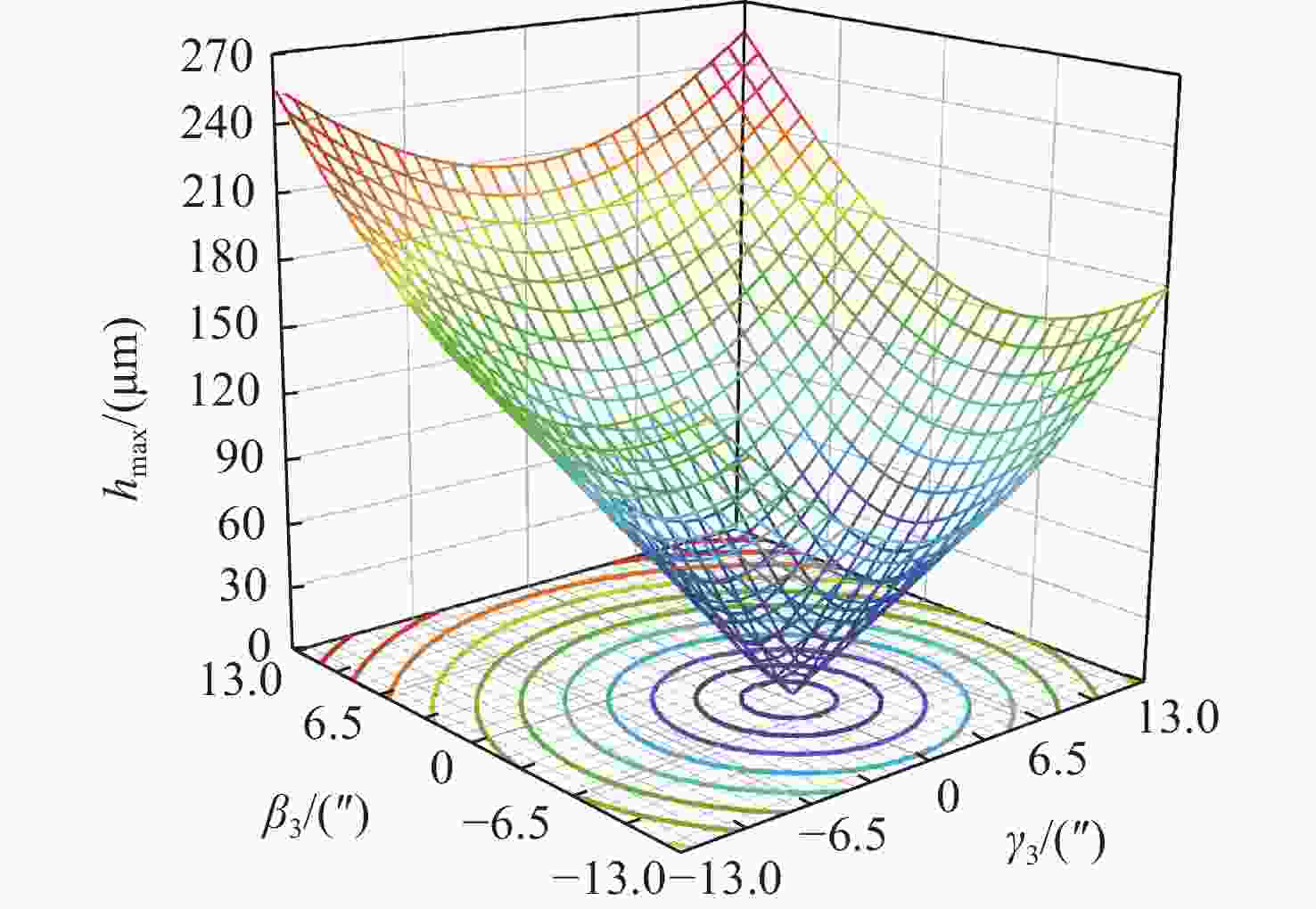
为提高光电经纬仪等二维转台的轴系运动精度,本文基于雅可比旋量理论建立了一种可考虑零件结构误差及其耦合放大效应的数学模型。针对“一端固定、一端游动”的轴系结构,提出了局部并联结构的分析方法。通过数值仿真分析,获得了各零件结构误差对轴系运动精度的影响以及最优的轴系装配方案。光学口径为650 mm的光电经纬仪的装调结果表明:装配优化后的轴系运动精度较优化前提高了32.1%。所构造的轴系运动精度模型及优化方法为指导光电经纬仪等二维转台的轴系装调以及公差设计提供了一定的理论根据。
Abstract:In order to improve the shafting motion accuracy of two-dimensional turntables such as photoelectric theodolites, we establish a mathematical model considering both the structural error of parts and the coupling amplification effect based on Jacobian-Torsor theory. Aiming at a shafting structure with one fixed end and one swimming, an analysis method of partial parallel structure was proposed. Through numerical simulation analysis, the impact of each part’s structural errors on the motion accuracy of the shafting and the optimal shafting assembly scheme were obtained. The results of assembly and adjustment of a photoelectric theodolite with an optical diameter of 650 mm show that assembly optimization improved the motion accuracy of the shaft system by 32.1%. The precision model and optimization method of shafting motion provide a theoretical basis for the shafting adjustment and tolerance design of two-dimensional turntables such as photoelectric theodolites.
-
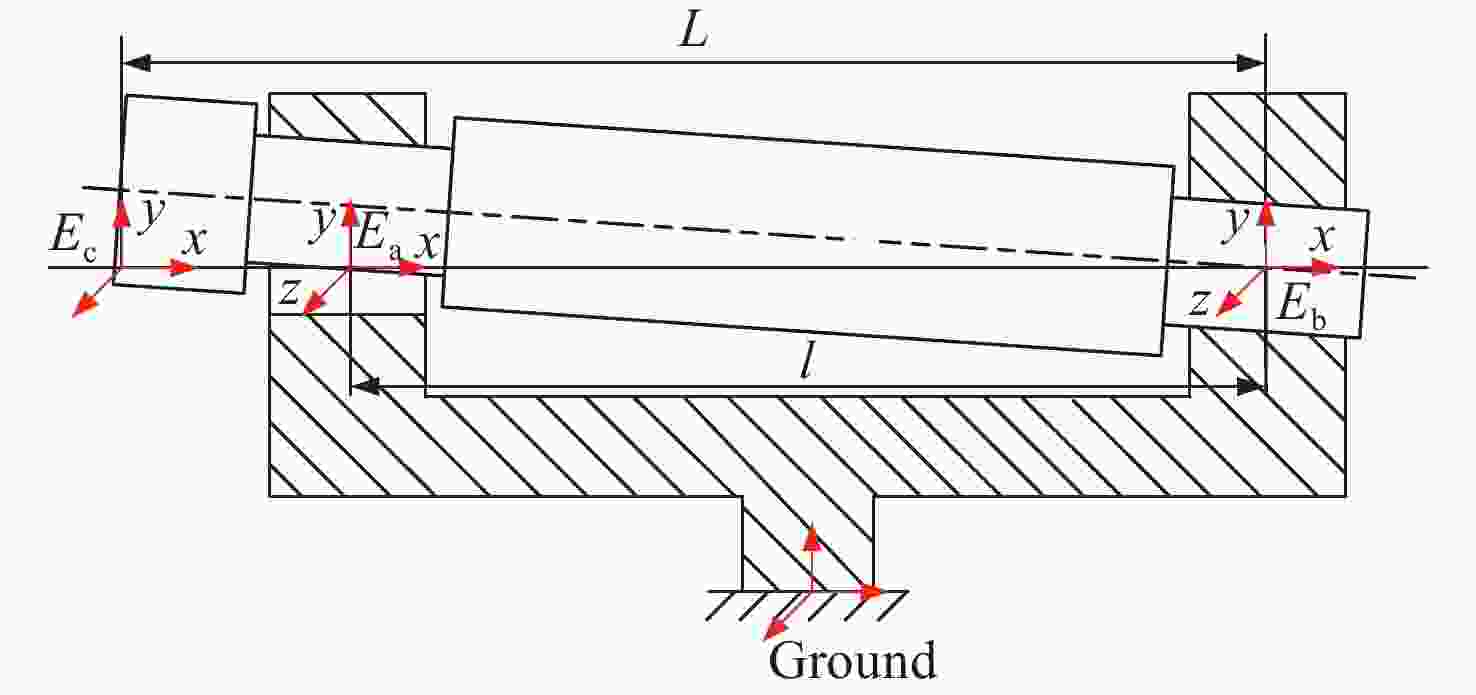
表 1 俯仰轴系几何误差及编号
Table 1. Geometric deviation items and numbers of elevation axle
零件名 坐标系 误差项 编号 固定端轴承 o1 δ(x), δ(y), δ(z), θ(y), θ(z) 1, 2, 3, 4, 5 固定端轴套 o2 δ(x), δ(y), δ(z), θ(y), θ(z) 6, 7, 8, 9, 10 固定端法兰 o3 δ(x), δ(y), δ(z), θ(y), θ(z) 11, 12, 13, 14, 15 游动端法兰 o4 δ(x), δ(y), δ(z), θ(y), θ(z) 16, 17, 18, 19, 20 游动端轴承 o5 δ(y), θ(z) 21, 22 游动端轴套 o6 δ(x), δ(y), δ(z), θ(y), θ(z) 23, 24, 25, 26, 27 表 2 轴系运动模型参数
Table 2. Shafting motion model parameters
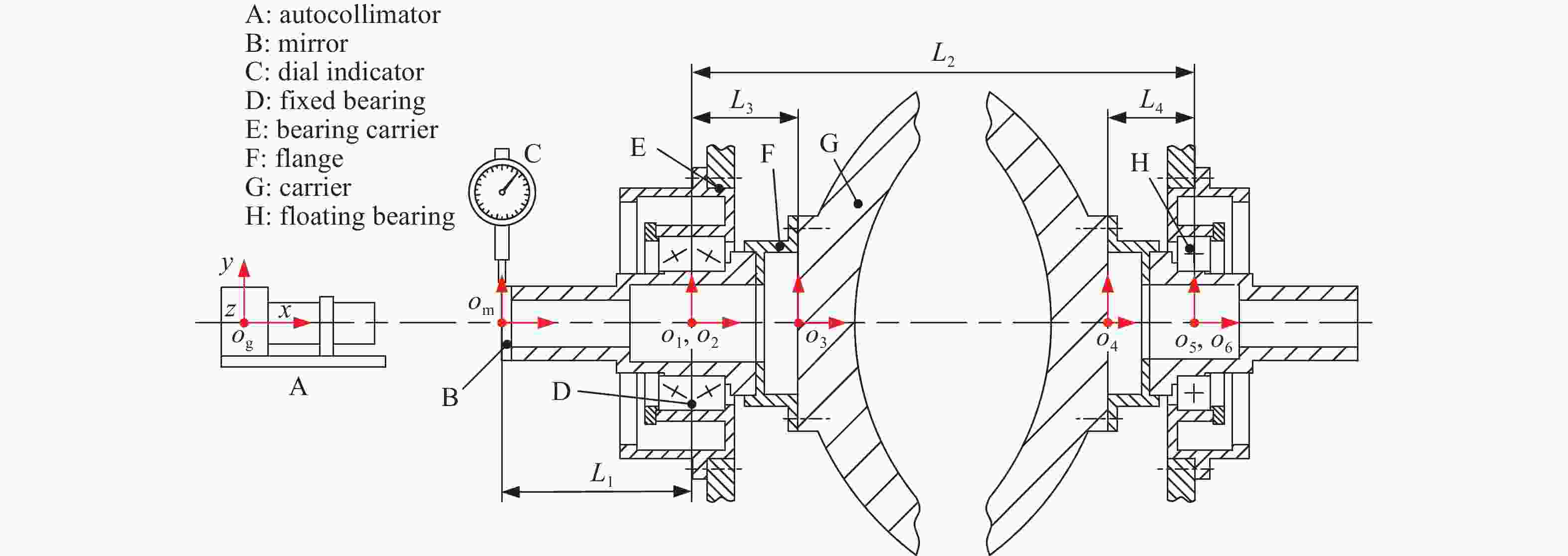
参数名 数值 E1 [±0.005, ±0.020, ±0.020, 0, ±9.696×10−6, ±9.696×10−6]T E2 [±0.005, ±0.005, ±0.005, 0, ±9.696×10−6, ±9.696×10−6]T E3 [±0.005, ±0.005, ±0.005, 0, ±9.696×10−6, ±9.696×10−6]T E4 [±0.010, ±0.010, ±0.010, 0, ±8.242×10−6, ±8.242×10−6]T E5 [0, ±0.010, ±0.010, 0, 0, 0]T E6 [±0.005, ±0.020, ±0.020, 0, ±9.696×10−6, ±9.696×10−6]T L1 250 mm L2 1100 mm L3 200 mm L4 150 mm 表 3 测量结果
Table 3. Measurement results
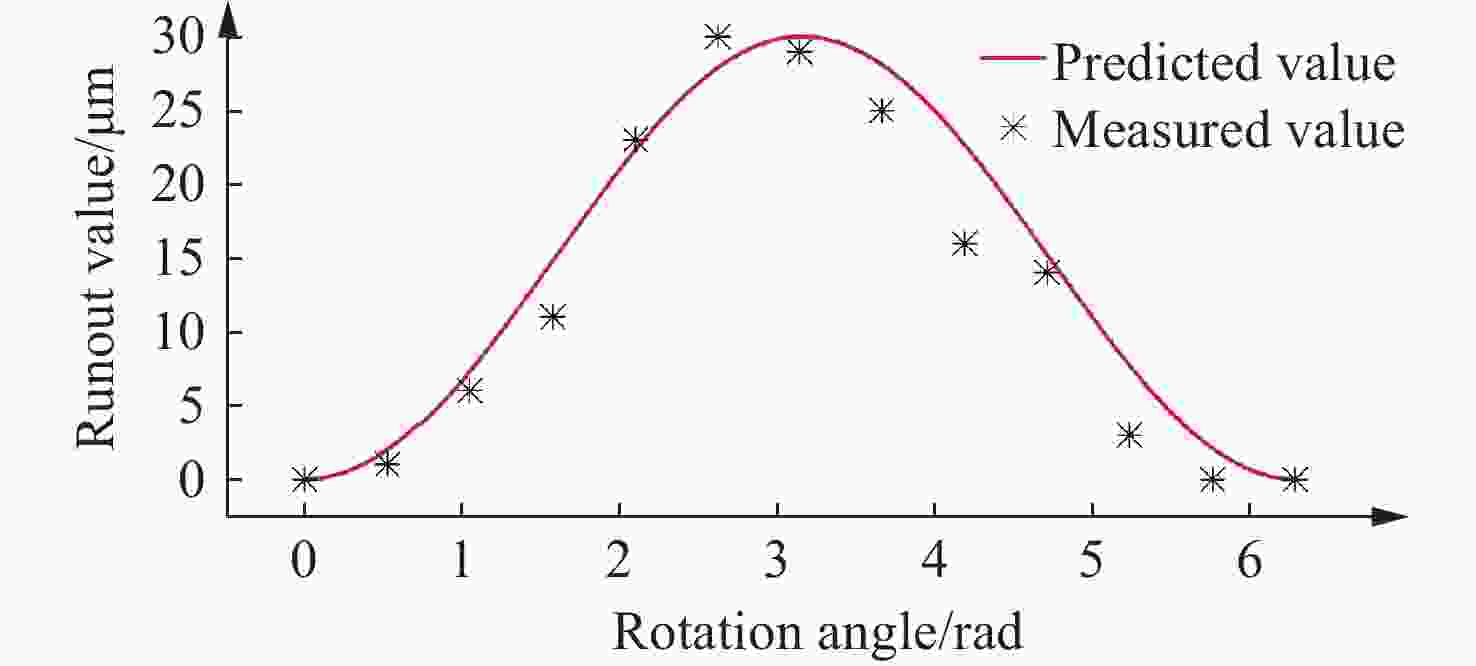
转角
/rad跳动量
/μm顺时针 逆时针 X/″ Y/″ $ \sqrt{X^{2}+Y^{2}} $ X/″ Y/″ $ \sqrt{X^{2}+Y^{2}} $ 0 0 0 0 0 0.5 0.2 0.54 0.52 4 1.7 1.5 2.27 1.9 0.8 2.06 1.05 3 2.2 1.7 2.78 3 1.5 3.35 1.57 5 2.8 1.6 3.22 3.3 1.2 3.51 2.09 2 2.3 0.3 2.32 2.6 −0.1 2.60 2.62 3 1.6 0.2 1.61 1.5 0.5 1.58 3.14 5 0.6 1.9 1.99 0.7 2.1 2.21 3.67 10 1.3 3.3 3.55 1 3.1 3.26 4.19 9 2.1 3.3 3.91 1.9 3 3.55 4.71 7 2.3 2 3.05 2.5 1.7 3.02 5.24 4 1.1 1 1.49 1 0.3 1.04 5.76 1 −0.1 −0.3 0.32 0.1 −0.1 0.14 6.28 1 0.4 −0.1 0.41 0.4 −0.1 0.42 -
[1] 胡一博, 孟立新, 白杨杨, 等. 空间激光通信粗跟踪等效复合控制技术[J]. 激光与光电子学进展,2023,60(9):0906004.HU Y B, MENG L X, BAI Y Y, et al. Coarse tracking equivalent compound control technology for space laser communication[J]. Laser & Optoelectronics Progress, 2023, 60(9): 0906004. (in Chinese). [2] 赵怀学, 刘波, 谢梅林, 等. 基于多视场拼接光电经纬仪的成像系统指向校正方法[J]. 光学学报,2022,42(6):0612002. doi: 10.3788/AOS202242.0612002ZHAO H X, LIU B, XIE M L, et al. Pointing calibration method for imaging systems of photoelectric theodolites with multi-field of view stitching[J]. Acta Optica Sinica, 2022, 42(6): 0612002. (in Chinese). doi: 10.3788/AOS202242.0612002 [3] 朱翠汝, 孙凤萤, 徐文清, 等. 研制二维直驱跟星转台测量夜晚整层大气透过率[J]. 光学学报,2021,41(16):1601002. doi: 10.3788/AOS202141.1601002ZHU C R, SUN F Y, XU W Q, et al. Developed two-dimensional direct-drive star-following turntable to measure whole-layer atmospheric transmittance at night[J]. Acta Optica Sinica, 2021, 41(16): 1601002. (in Chinese). doi: 10.3788/AOS202141.1601002 [4] FU Q, ZHAO F, ZHU R, et al. Research on the intersection angle measurement and positioning accuracy of a photoelectric theodolite[J]. Frontiers in Physics, 2023, 10: 1121050. doi: 10.3389/fphy.2022.1121050 [5] PAAR R, ROIć M, MARENDIć A, et al. Technological development and application of photo and video theodolites[J]. Applied Sciences, 2021, 11(9): 3893. doi: 10.3390/app11093893 [6] 于夫男, 徐抒岩. 应用于Φ300 mm平面反射镜的精密二维转台轴系设计[J]. 光学 精密工程,2020,28(5):1075-1082.YU F N, XU SH Y. Shafting design for precise two-dimensional turntable applied to Φ300 mm plane mirror[J]. Optics and Precision Engineering, 2020, 28(5): 1075-1082. (in Chinese). [7] LV T, RUAN P, JIANG K, et al. Modeling and analysis of fast steering mirror disturbance effects on the line of sight jitter for precision pointing and tracking system[J]. Mechanical Systems and Signal Processing, 2023, 188: 110002. doi: 10.1016/j.ymssp.2022.110002 [8] WU SH CH, TAN L Y, YU S Y, et al. Analysis and correction of axis error in periscope-type optical communication terminals[J]. Optics & Laser Technology, 2013, 46: 127-133. [9] ZHANG F R, RUAN P, HAN J F, et al. Analysis and correction of geometrical error-induced pointing errors of a space laser communication APT system[J]. International Journal of Optomechatronics, 2021, 15(1): 19-31. doi: 10.1080/15599612.2021.1895923 [10] ZHANG F R, RUAN P, HAN J F. Optical path pointing error and coaxiality analysis of APT system of space laser communication terminal[J]. Optica Applicata, 2021, 51(2): 203-222. [11] 李翔宇, 彭勃, 江波, 等. 基于角接触球轴承的小型经纬仪方位轴倾斜误差修正[J]. 红外与激光工程,2021,50(12):20210172. doi: 10.3788/IRLA20210172LI X Y, PENG B, JIANG B, et al. Tilt error correction of minitype theodolite's vertical shaft based on angular contact ball bearings[J]. Infrared and Laser Engineering, 2021, 50(12): 20210172. (in Chinese). doi: 10.3788/IRLA20210172 [12] 江波, 周泗忠, 姜凯, 等. 车载经纬仪的垂轴误差分析[J]. 红外与激光工程,2015,44(5):1623-1627.JIANG B, ZHOU S ZH, JIANG K, et al. Analysis of vertical axis error of vehicular theodolite[J]. Infrared and Laser Engineering, 2015, 44(5): 1623-1627. (in Chinese). [13] 江波, 梅超, 梁元庆, 等. 基于平面方程旋转变化方法的车载经纬仪测角误差修正[J]. 光学学报,2015,35(S1):s112002. doi: 10.3788/AOS201535.s112002JIANG B, MEI CH, LIANG Y Q, et al. Angle measurement error correction of vehicle-borne theodolite based on the rotation of plane equation[J]. Acta Optica Sinica, 2015, 35(S1): s112002. (in Chinese). doi: 10.3788/AOS201535.s112002 [14] 姜玉鑫, 孙建锋, 侯培培, 等. 基于Levenberg-Marquardt算法的旋转双棱镜指向偏差修正[J]. 中国激光,2023,50(6):0605001. doi: 10.3788/CJL220634JIANG Y X, SUN J F, HOU P P, et al. Correction of pointing deviation of Risley prisms based on Levenberg-Marquardt algorithm[J]. Chinese Journal of Lasers, 2023, 50(6): 0605001. (in Chinese). doi: 10.3788/CJL220634 [15] LAFOND P, LAPERRIERE L. Jacobian-based modeling of dispersions affecting pre-defined functional requirements of mechanical assemblies[C]. Proceedings of the 1999 IEEE International Symposium on Assembly and Task Planning, IEEE, 1999: 20-25. [16] 杨朝晖, 高天石, 李崇赫, 等. 基于新一代几何技术规范的装配误差建模[J/OL]. 计算机集成制造系统, 2022: 1-14. (2023-04-17) http://kns.cnki.net/kcms/detail/11.5946.TP.20221209.1431.001.html.YANG ZH H, GAO T SH, LI CH H, et al. Assembly error modeling based on geometrical product specifications (GPS)[J/OL]. Computer Integrated Manufacturing Systems, 2022: 1-14. (2023-04-17) http://kns.cnki.net/kcms/detail/11.5946.TP.20221209.1431.001.html. (in Chinese). [17] XI Y, GAO ZH Y, CHEN K, et al. Error propagation model using Jacobian-Torsor model weighting for assembly quality analysis on complex product[J]. Mathematics, 2022, 10(19): 3534. doi: 10.3390/math10193534 [18] CHEN H, JIN S, LI ZH M, et al. A solution of partial parallel connections for the unified Jacobian-Torsor model[J]. Mechanism and Machine Theory, 2015, 91: 39-49. doi: 10.1016/j.mechmachtheory.2015.03.012 [19] 戴宏玮, 陈琨, 于慧, 等. 雅可比旋量的装配体并联结构公差分析方法研究[J]. 西安交通大学学报,2022,56(5):156-165,222.DAI H W, CHEN K, YU H, et al. Tolerance analysis of partial parallel assemblies based on Jacobian-Torsor model[J]. Journal of Xi’an Jiaotong University, 2022, 56(5): 156-165,222. (in Chinese). -





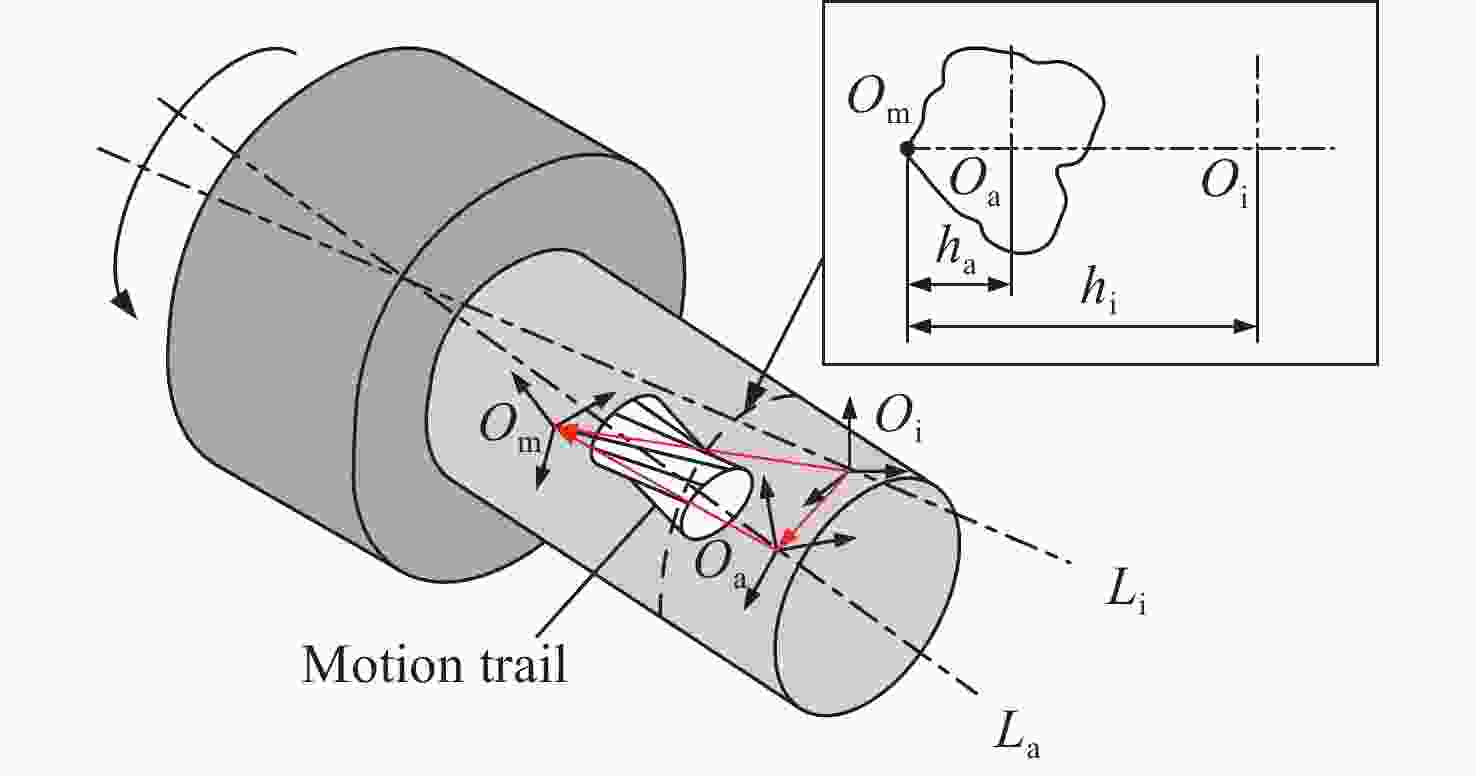
 下载:
下载: