-
摘要:
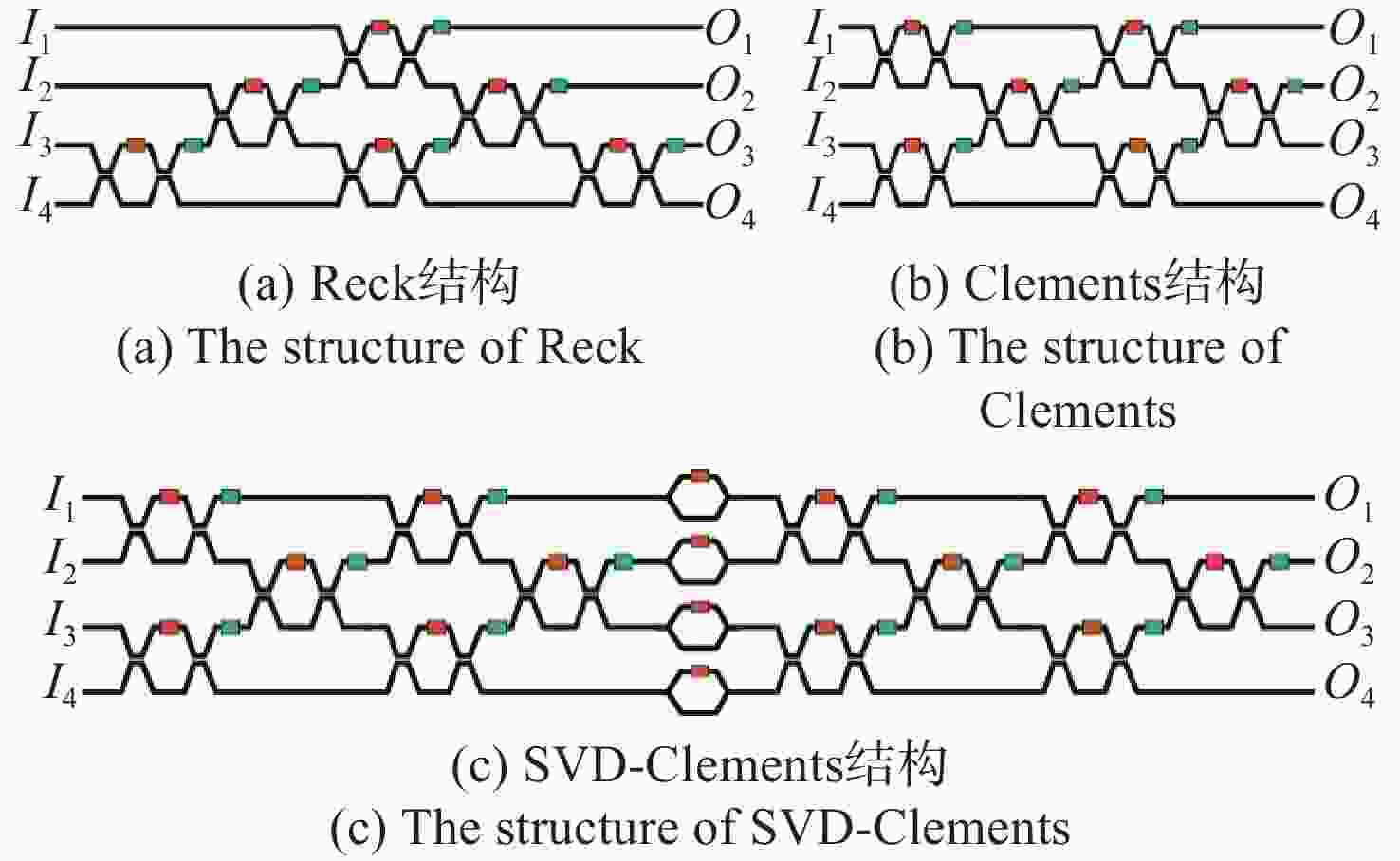
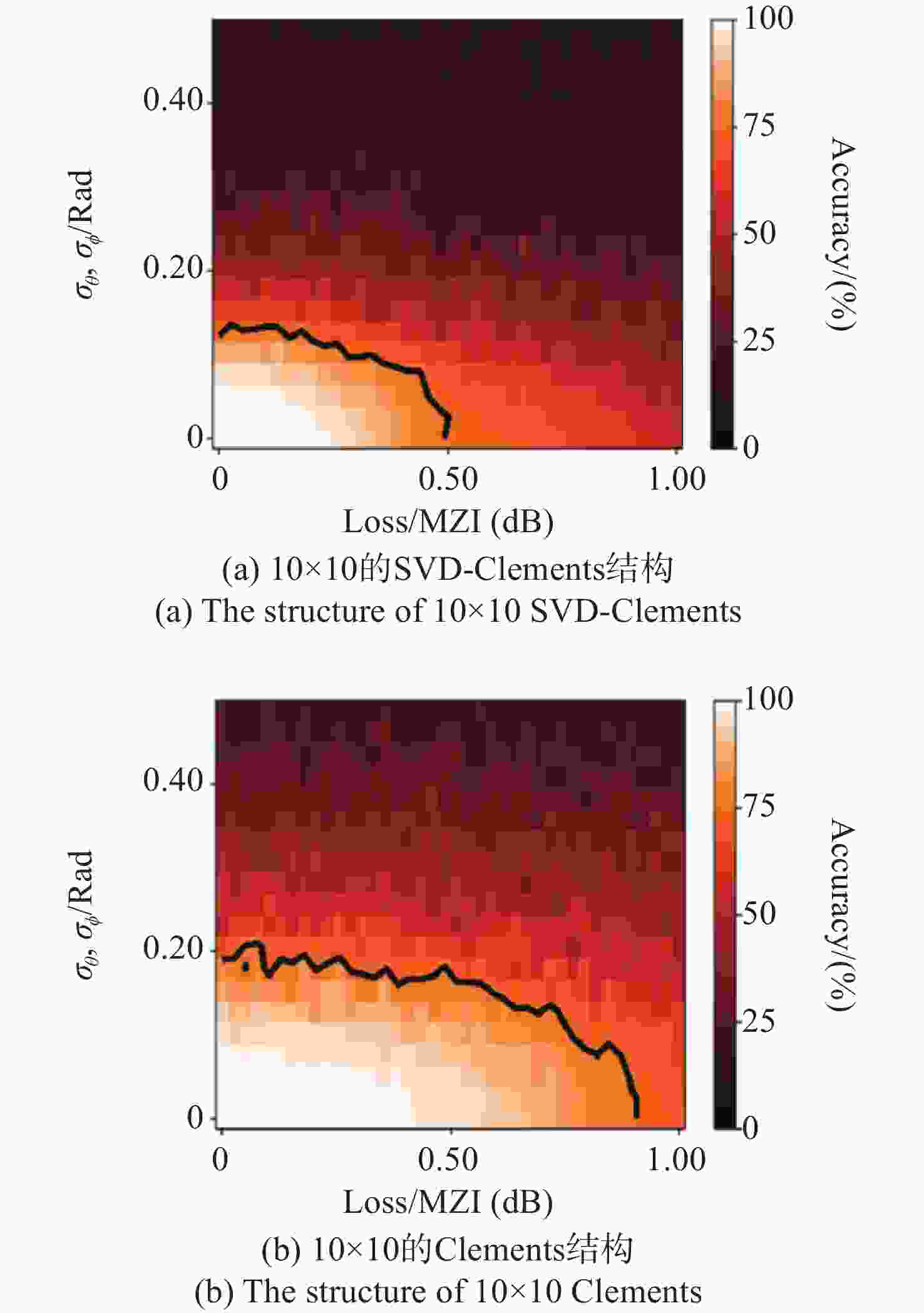
基于马赫-曾德尔干涉仪（Mach-Zehnder Interferometer, MZI）级联拓扑结构的线性光学处理器被证明是实现光学神经网络（Optical Neural Network, ONN）的重要途径，但还有不少实际问题有待解决。针对芯片制造、测试过程中可能导致的相位误差和插入损耗等问题，通过实验和理论仿真分析了几种基于MZI结构的可重构光学处理器。发现可以通过单个
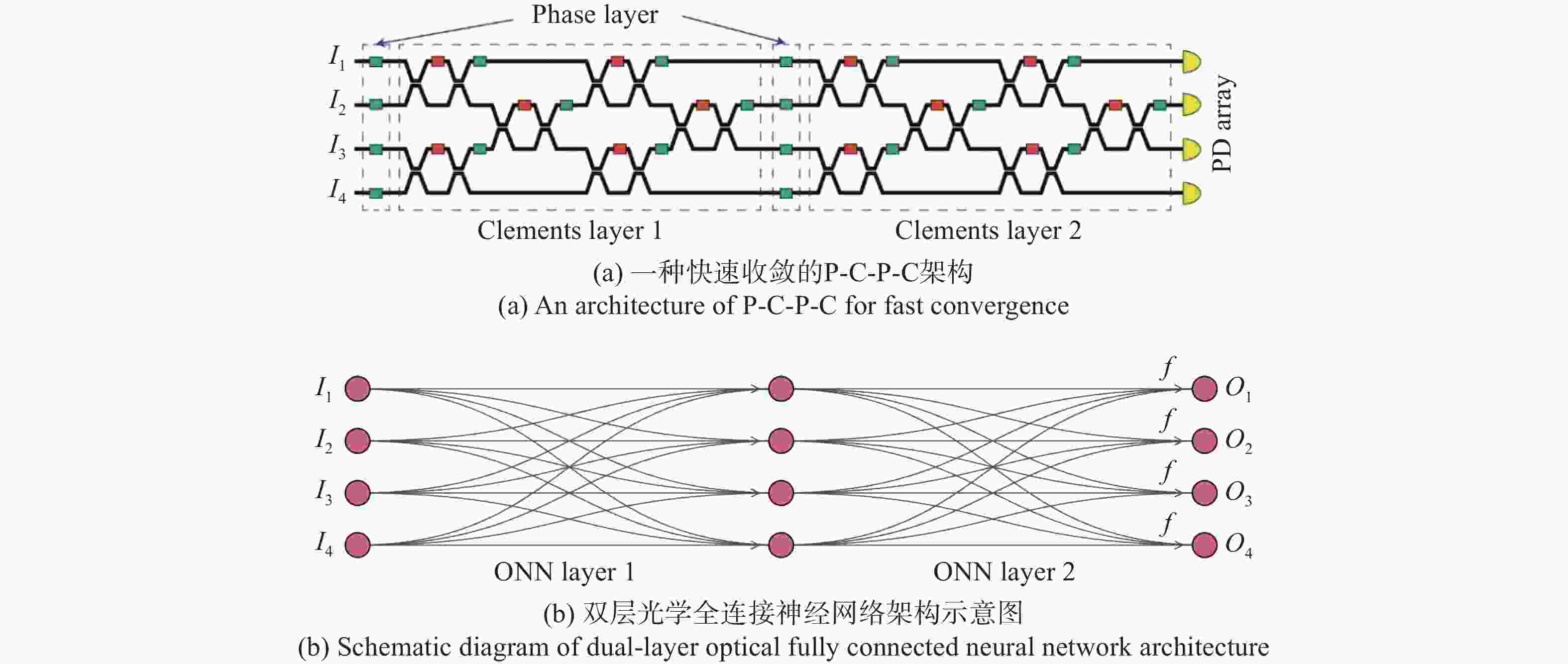
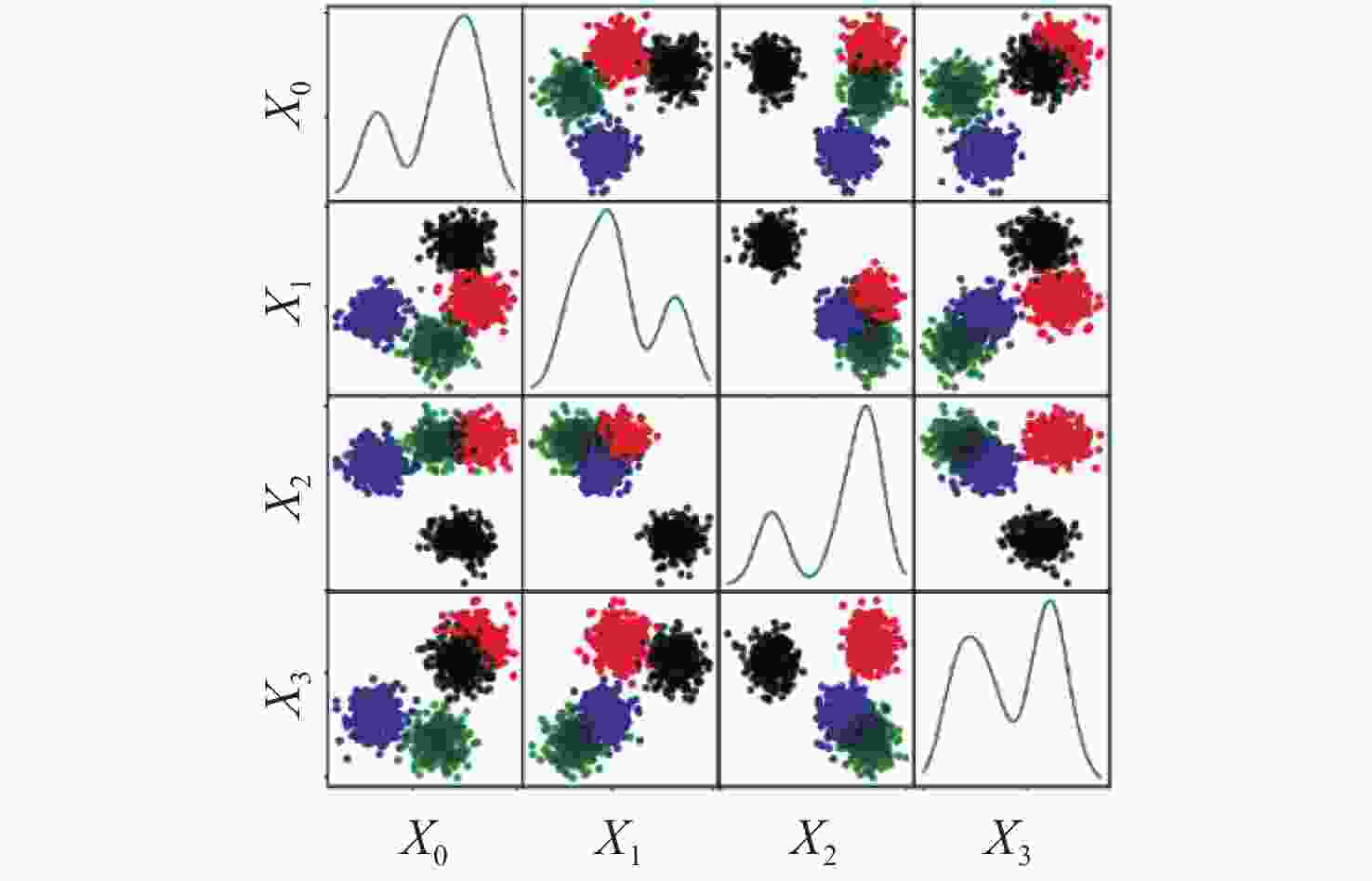
N ×N 的Clements阵列结构来实现任意酉矩阵的权重，构建稀疏连接的全复值光学神经网络，将光学深度大大降低，以实现较高的插入损耗鲁棒性。此外，对于多层光学神经网络来说，由于构建该任意酉矩阵的自由度有限，故在每一层Clements结构前面加一个相移器层，有助于将分类数据映射到更高的数据维度，能使神经网络更快速的收敛。Abstract:Linear optical processors based on the cascaded topology of Mach-Zehnder Interferometer (MZI) have been demonstrated to be an important way of implementing Optical Neural Networks (ONN), but several practical challenges still need resolution. Concerning issues arising from chip manufacturing and testing processes that could lead to phase errors and insertion losses, we conducted experiments and theoretical simulations for various reconfigurable optical processors. We found that the weights of any arbitrary unitary matrix can be realized through some single
N×N Clements units, that can substantially reduce the optical depth and enhance robustness against insertion losses. This approach allows for the construction of fully complex optical neural networks. Additionally, In multi-layer ONN, due to the limited degrees of freedom in constructing this arbitrary matrix, we introduced a phase-shift layer before each layer of the Clements unit. This design aids in mapping classification data to higher-dimensional spaces, facilitating faster neural network convergence. -
图 1 单个2×2 的MZI器件（a）结构示意图及（b）双端口输出功率响应曲线
Figure 1. (a) Structural diagram and (b) dual port output power response curves of single 2×2 MZI device
图 3 两种MZI阵列拓扑结构的插损与相位敏感性
Figure 3. Insertion-loss and phase sensitivity of two types of MZI array topologies
图 4 一种快速收敛的拓扑架构和对应的神经网络示意图
Figure 4. The rapidly converging topology architecture and the corresponding neural network diagram
图 5 多维聚类高斯分布数据的分类任务
Figure 5. Classification tasks for multidimensional clustering Gaussian-distribution data
图 6 两种双层光学神经网络芯片的训练过程
Figure 6. The training processes of two double-layer optical neural network chips
图 7 Iris数据在双层光学神经网络中的训练及分类结果
Figure 7. Training and classification results of Iris data in double-layer optical neural networks
表 1 第一层Clements结构中相移器的相位值
Table 1. The value of the phase shifter in the first layer Clements structure
MZI (1) (2) (3) (4) (5) (6) θ(rad) 1.354 2.518 1.683 2.614 2.614 6.248 φ(rad) 1.064 4.881 0.995 2.175 1.535 0.130 
下载: 导出CSV
表 2 第二层Clements结构中相移器的相位值
Table 2. The value of the phase shifter in the second layer Clements structure
MZI (1) (2) (3) (4) (5) (6) θ(rad) 0.393 1.452 0.270 0.505 5.662 1.250 φ(rad) 5.447 3.434 2.740 0.700 5.416 5.690
下载: 导出CSV
-
[1] 周治平, 许鹏飞, 董晓文. 硅基光电计算[J]. 中国激光,2020,47(6):0600001. doi: 10.3788/CJL202047.0600001ZHOU ZH P, XU P F, DONG X W. Computing on silicon photonic platform[J]. Chinese Journal of Lasers, 2020, 47(6): 0600001. (in Chinese) doi: 10.3788/CJL202047.0600001 [2] 王之江. 光计算技术进展[J]. 中国科学院院刊,1987,2(3):198-205.WANG ZH J. Progress in optical computing technology[J]. Bulletin of Chinese Academy of Sciences,1987,2(3):198-205. (in Chinese) [3] 周宏强, 黄玲玲, 王涌天. 深度学习算法及其在光学的应用[J]. 红外与激光工程,2019,48(12):1226004. doi: 10.3788/IRLA201948.1226004ZHOU H Q, HUANG L L, WANG Y T. Deep learning algorithm and its application in optics[J]. Infrared and Laser Engineering, 2019, 48(12): 1226004. (in Chinese). doi: 10.3788/IRLA201948.1226004 [4] FELDMANN J, YOUNGBLOOD N, WRIGHT C D, et al. All-optical spiking neurosynaptic networks with self-learning capabilities[J]. Nature, 2019, 569(7755): 208-214. doi: 10.1038/s41586-019-1157-8 [5] RÍOS C, YOUNGBLOOD N, CHENG Z G, et al. In-memory computing on a photonic platform[J]. Science Advances, 2019, 5(2): eaau5759. doi: 10.1126/sciadv.aau5759 [6] SHASTRI B J, TAIT A N, FERREIRA DE LIMA T, et al. Photonics for artificial intelligence and neuromorphic computing[J]. Nature Photonics, 2021, 15(2): 102-114. doi: 10.1038/s41566-020-00754-y [7] 谢意维, 张涛, 戴道锌. 智能化可重构硅光集成器件及芯片应用研究[J]. 中兴通讯技术,2020,26(2):64-69. doi: 10.12142/ZTETJ.202002009XIE Y W, ZHANG T, DAI D X. Applications of intelligent reconfigurable silicon photonic devices and circuits[J]. ZTE Technology Journal, 2020, 26(2): 64-69. (in Chinese). doi: 10.12142/ZTETJ.202002009 [8] 王俊, 杨晓飞. 光子芯片研究进展及展望[J]. 世界科学,2020(12):29-31.WANG J, YANG X F. Research progress and prospects of photonic chips[J]. World Science, 2020(12): 29-31. [9] CLEMENTS W R, HUMPHREYS P C, METCALF B J, et al. Optimal design for universal multiport interferometers[J]. Optica, 2016, 3(12): 1460-1465. doi: 10.1364/OPTICA.3.001460 [10] ZOU W W, MA B W, XU SH F, et al. Towards an intelligent photonic system[J]. China Information Sciences, 2020, 63(6): 160401. doi: 10.1007/s11432-020-2863-y [11] MARQUEZ B A, HUANG CH R, PRUCNAL P R, et al. Neuromorphic Silicon Photonics for Artificial Intelligence [M]//LOCKWOOD D J, PAVESI L. Silicon Photonics IV. Cham: Springer, 2021: 417-447. [12] 郑一臻, 戴键, 张天, 等. 基于异构光子神经网络的多模态特征融合[J]. 中国光学(中英文),2023,16(6):1343-1355. doi: 10.37188/CO.2023-0036ZHENG Y ZH, DAI J, ZHANG T, et al. Multimodal feature fusion based on heterogeneous optical neural networks[J]. Chinese Optics, 2023, 16(6): 1343-1355. (in Chinese). doi: 10.37188/CO.2023-0036 [13] GIAMOUGIANNIS G, TSAKYRIDIS A, MORALIS-PEGIOS M, et al. Universal linear optics revisited: new perspectives for neuromorphic computing with silicon photonics[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2023, 29(2): 6200116. [14] BANDYOPADHYAY S, HAMERLY R, ENGLUND D. Hardware error correction for programmable photonics[J]. Optica, 2021, 8(10): 1247-1255. doi: 10.1364/OPTICA.424052 [15] WILLIAMSON I A D, HUGHES T W, MINKOV M, et al. Reprogrammable electro-optic nonlinear activation functions for optical neural networks[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2020, 26(1): 7700412. [16] SPALL J, GUO X X, BARRETT T D, et al. Fully reconfigurable coherent optical vector–matrix multiplication[J]. Optics Letters, 2020, 45(20): 5752-5755. doi: 10.1364/OL.401675 [17] 谢锋, 朱硕隆, 张振荣. 分光比可调的光功率分束器的设计[J]. 中国光学(中英文),2023,16(5):1121-1128. doi: 10.37188/CO.2023-0038XIE F, ZHU SH L, ZHANG ZH R. Design of an optical power splitter with adjustable split ratio[J]. Chinese Optics, 2023, 16(5): 1121-1128. (in Chinese). doi: 10.37188/CO.2023-0038 [18] ZHANG H, GU M, JIANG X D, et al. An optical neural chip for implementing complex-valued neural network[J]. Nature Communications, 2021, 12(1): 457. doi: 10.1038/s41467-020-20719-7 [19] SHOKRANEH. F, NEZAMI M S, LIBOIRON-LADOUCEUR O. Theoretical and experimental analysis of a 44 recongurable MZI-based linear optical processor[J]. Journal of Lightwave Technology, 2021: 1. [20] SHOKRANEH F, GEOFFROY-GAGNON S, LIBOIRON-LADOUCEUR O. The diamond mesh, a phase-error- and loss-tolerant field-programmable MZI-based optical processor for optical neural networks[J]. Optics Express, 2020, 28(16): 23495-23508. doi: 10.1364/OE.395441 [21] TSAKYRIDIS A, GIAMOUGIANNIS G, TOTOVIC A, et al. Fidelity restorable universal linear optics[J]. Advanced Photonics Research, 2022, 3(10): 2200001. doi: 10.1002/adpr.202200001 [22] SHI Y, REN J Y, CHEN G Y, et al. Nonlinear germanium-silicon photodiode for activation and monitoring in photonic neuromorphic networks[J]. Nature Communications, 2022, 13(1): 6048. doi: 10.1038/s41467-022-33877-7 [23] SHAO R, ZHANG G, GONG X. Generalized robust training scheme using genetic algorithm for optical neural networks with imprecise components[J]. Photonics Research, 2022, 10(8): 1868-1876. doi: 10.1364/PRJ.449570 [24] HAMERLY R, BANDYOPADHYAY S, ENGLUND D. Asymptotically fault-tolerant programmable photonics[J]. Nature Communications, 2022, 13(1): 6831. doi: 10.1038/s41467-022-34308-3 [25] RECK M, ZEILINGER A, BERNSTEIN H J, et al. Experimental realization of any discrete unitary operator[J]. Physical Review Letters, 1994, 73(1): 58-61. doi: 10.1103/PhysRevLett.73.58 -
下载:
计量
- 文章访问数: 80
- HTML全文浏览量: 36
- PDF下载量: 16
- 被引次数: 0
