Effects of sinusoidal mid-spatial frequency surface errors on optical transfer function
-
摘要:
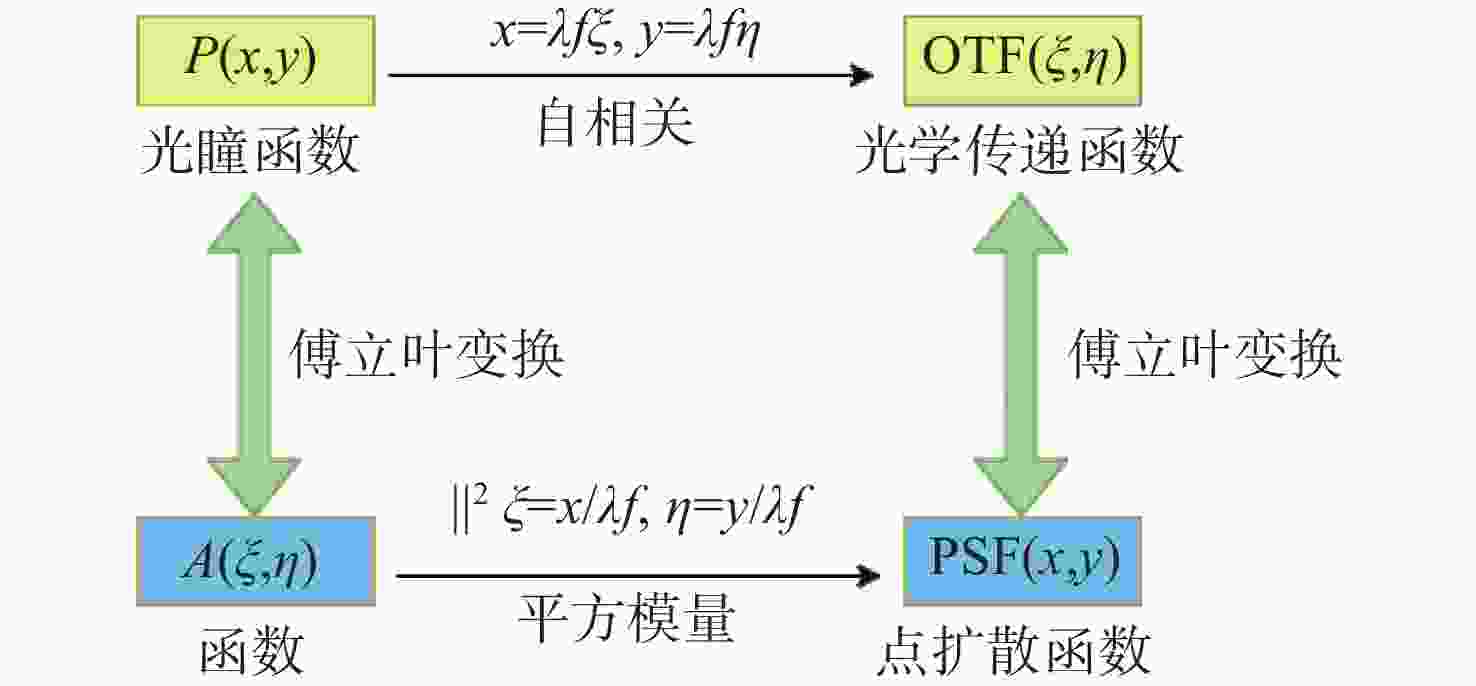
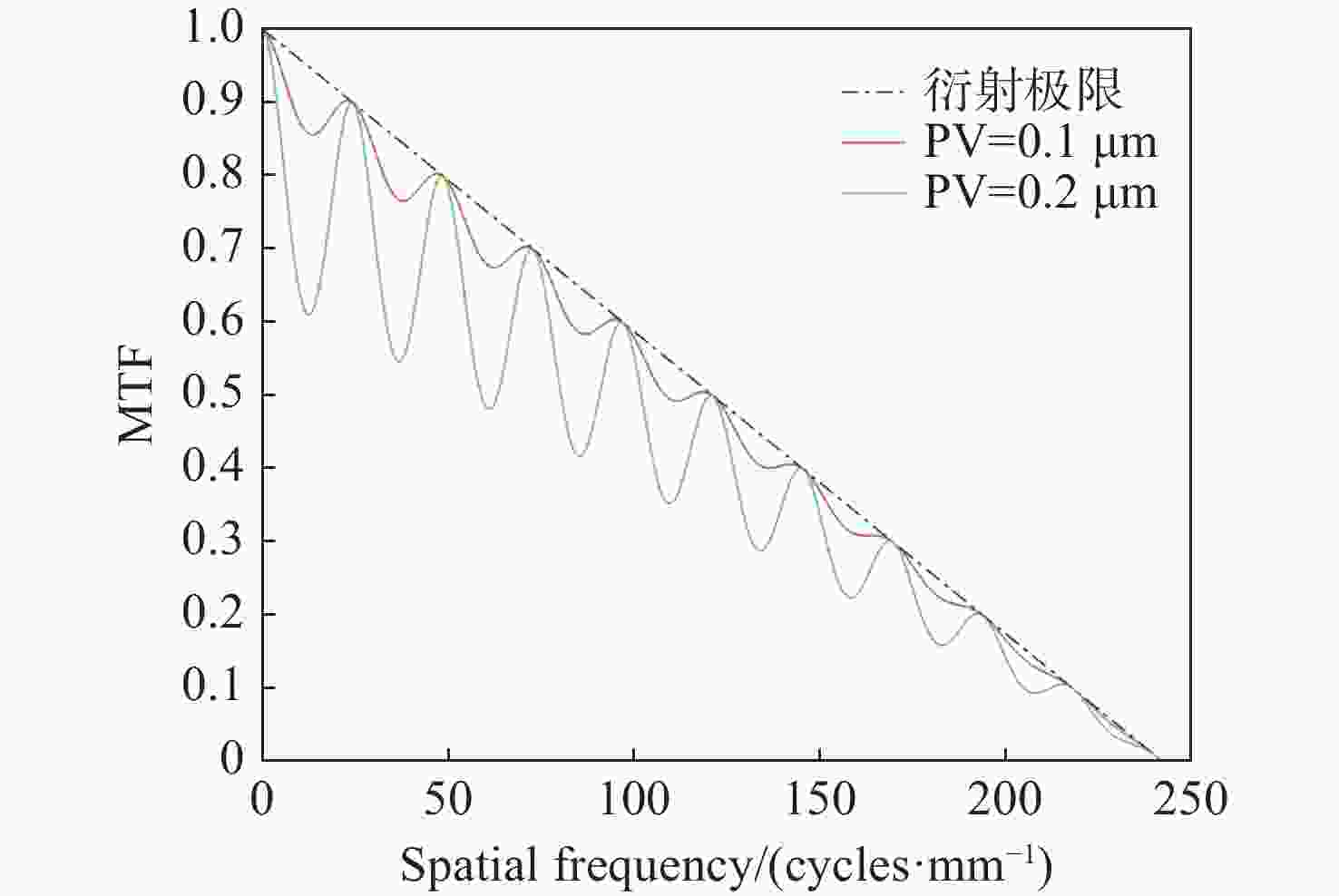
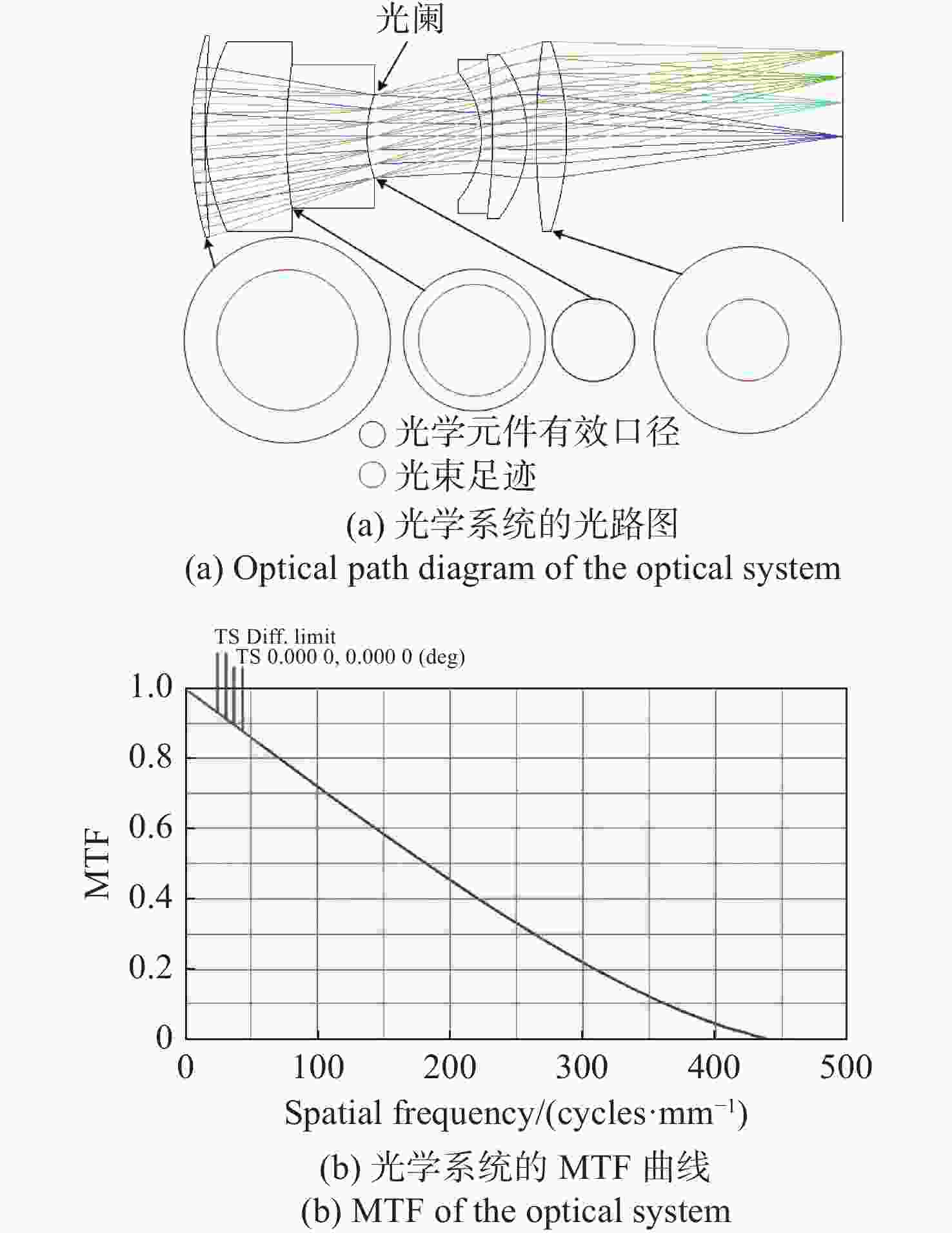
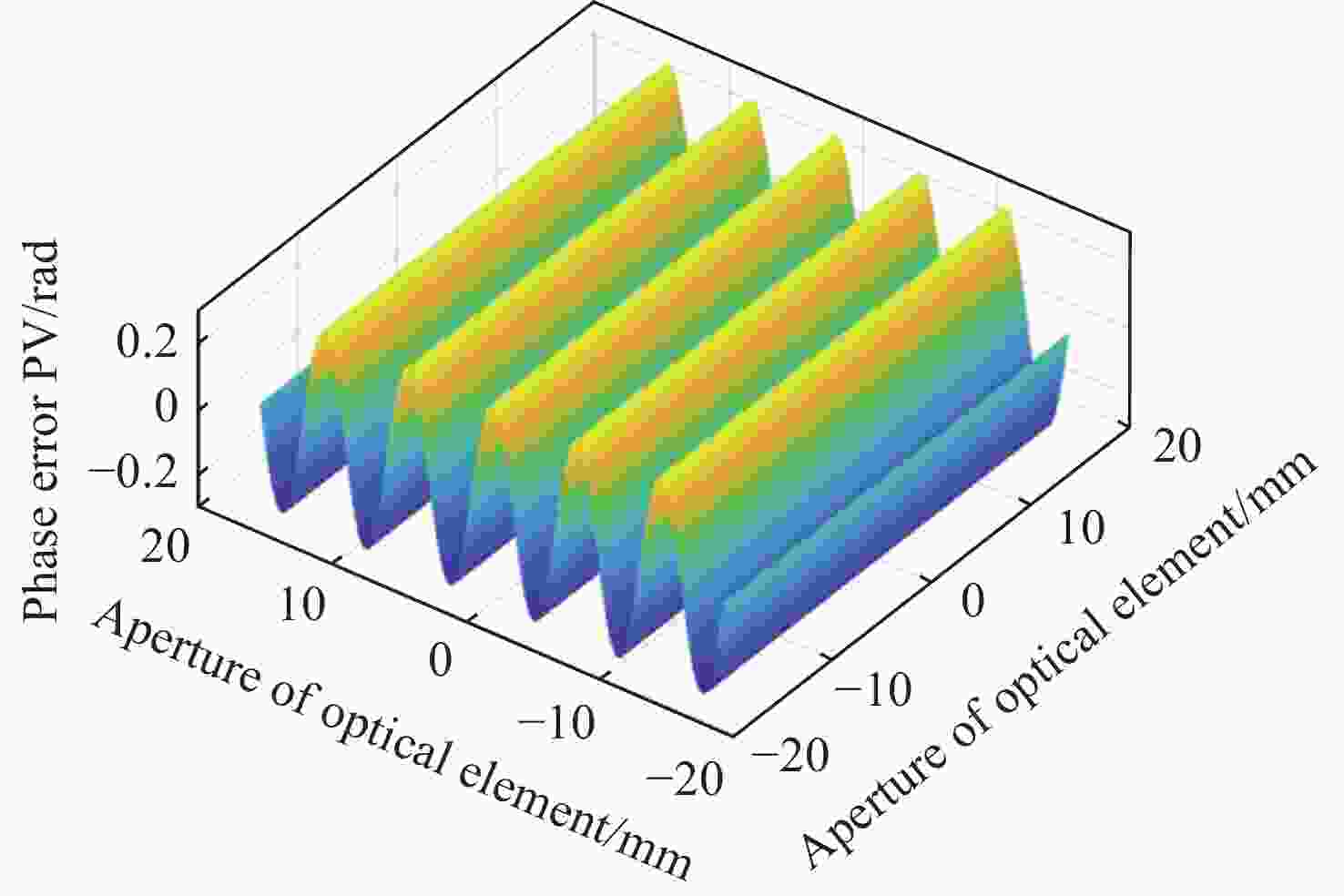
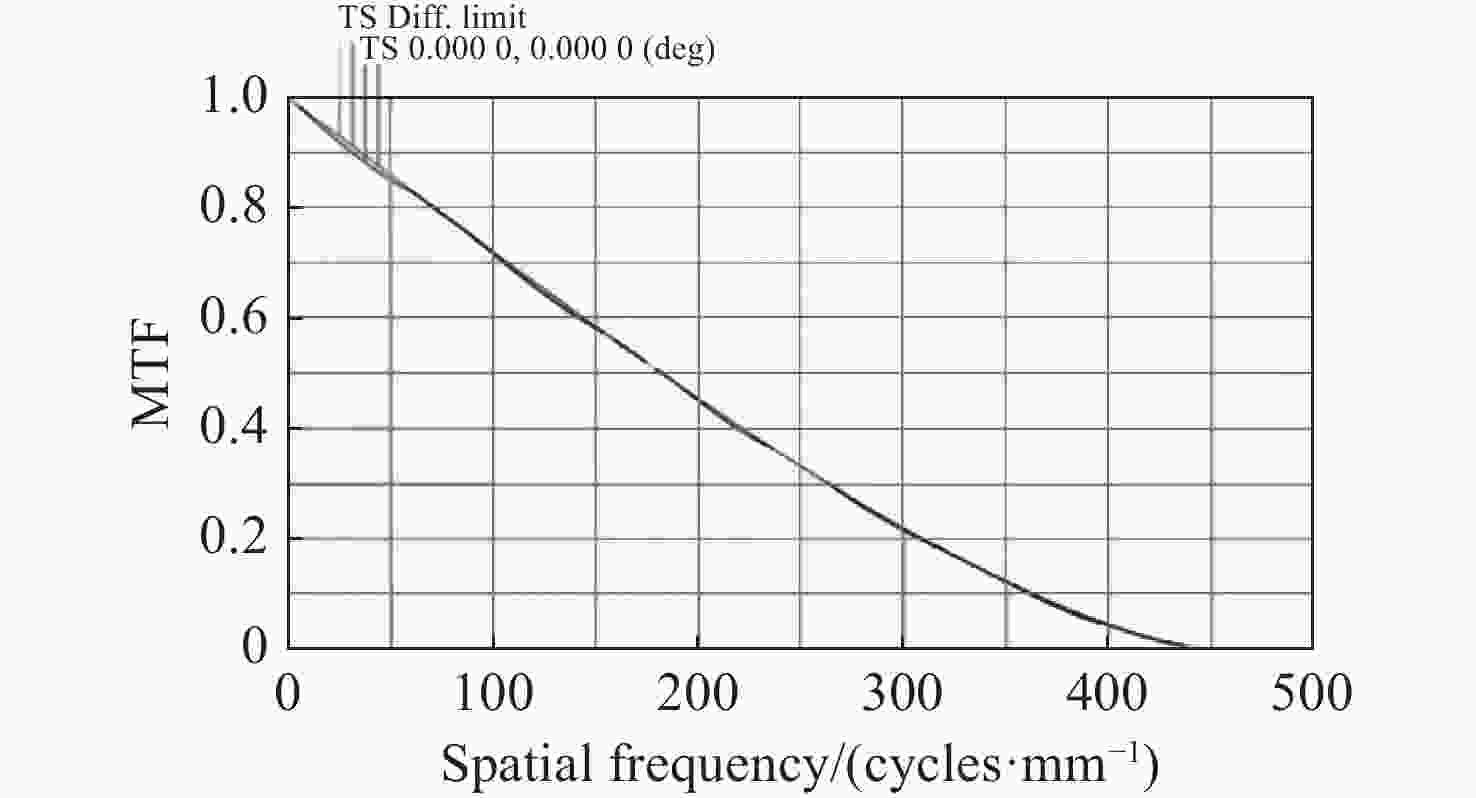
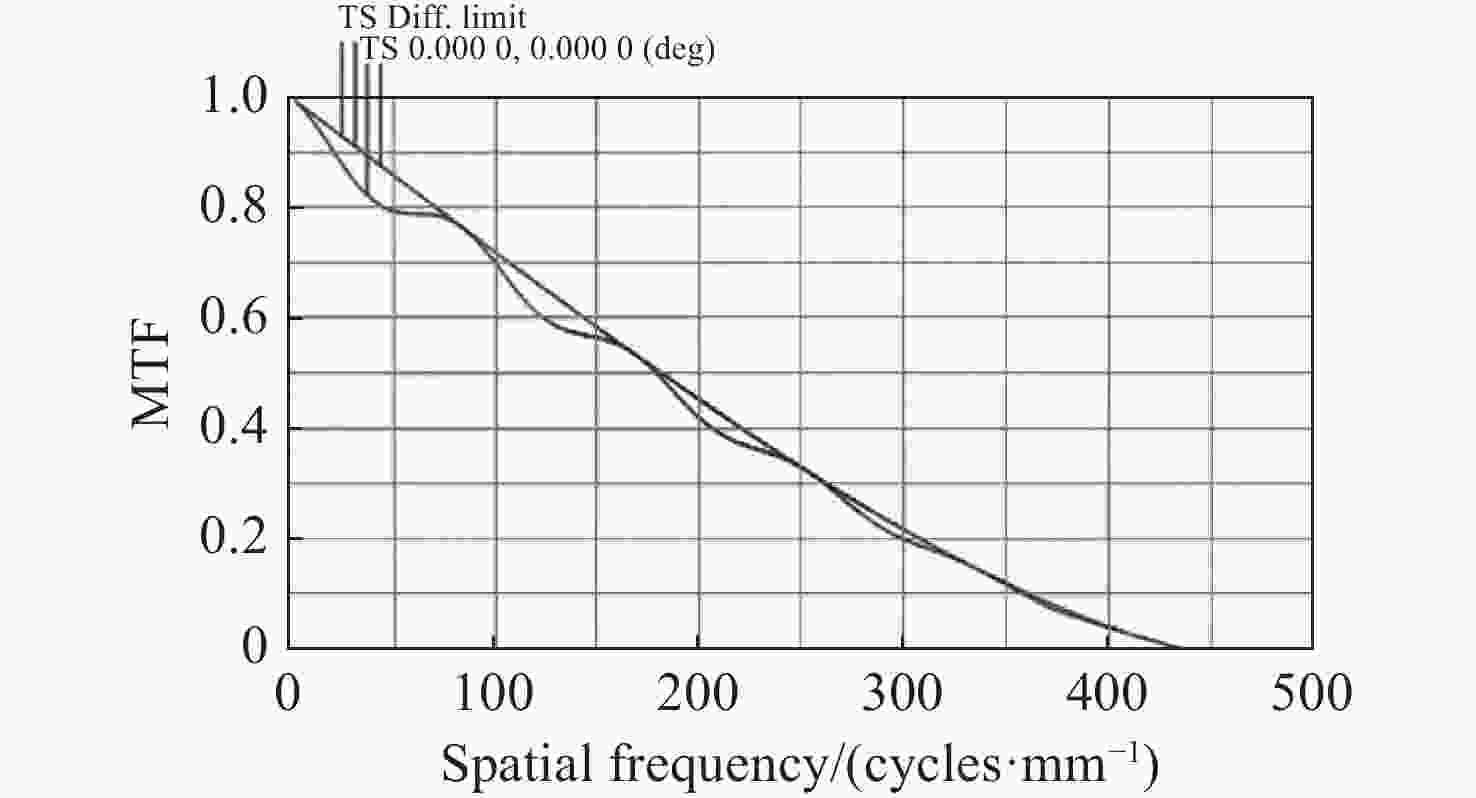
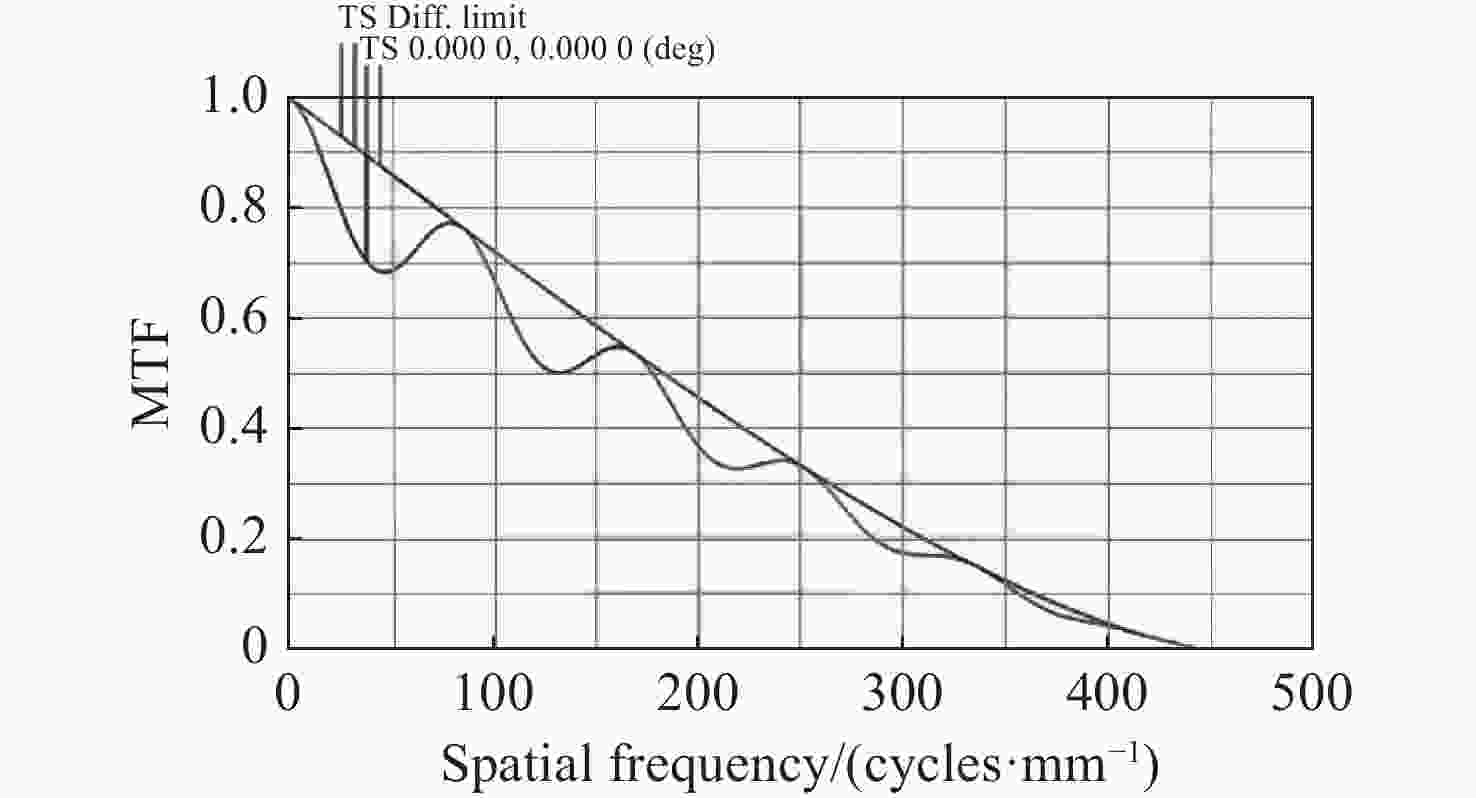
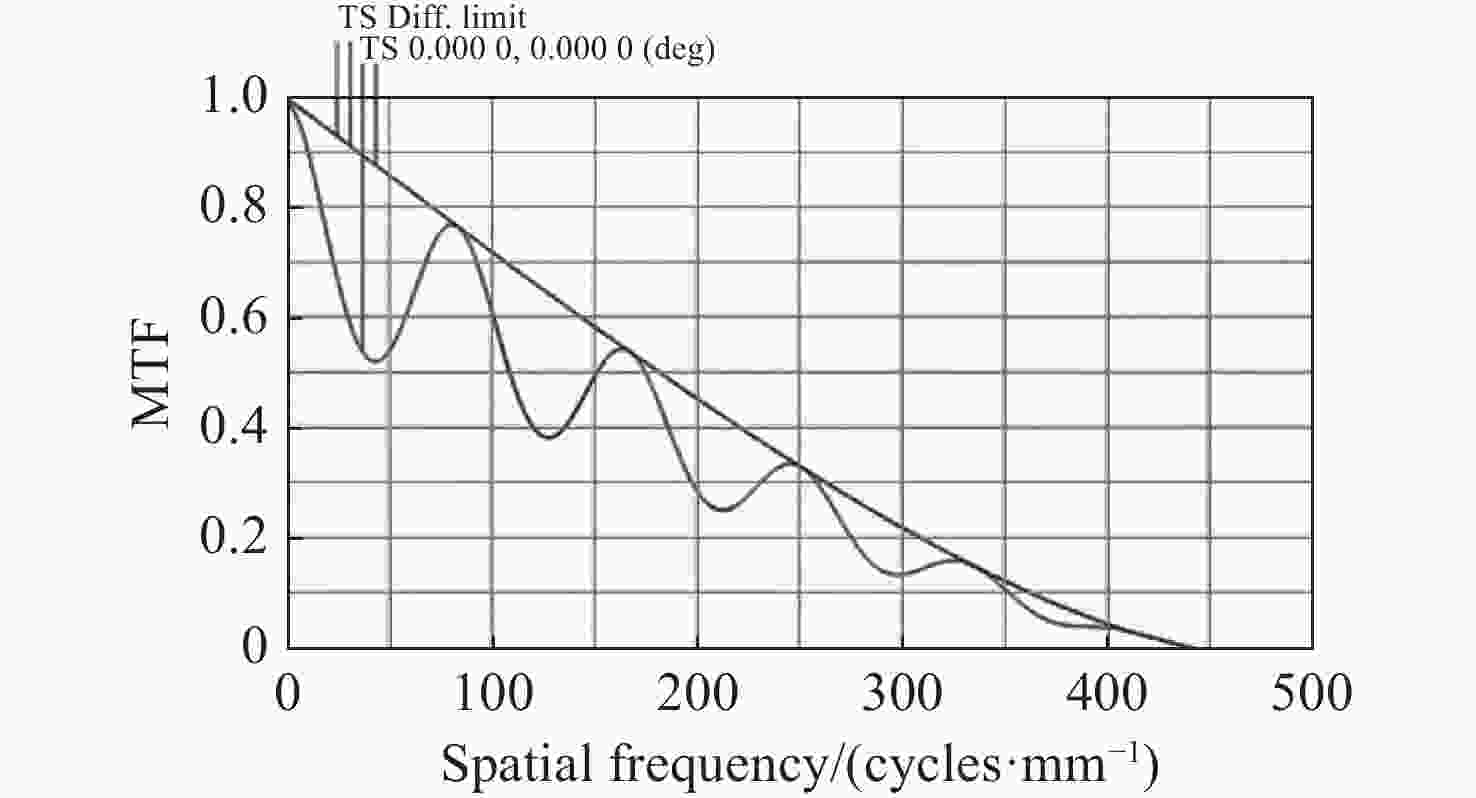
中频面形误差（MSFSE）会导致光学系统发生小角度散射，影响系统性能。为了在光学设计和光学加工中制定合理的中频面形误差公差，就中频面形误差对光学系统调制传递函数（MTF）的影响进行了量化研究。在衍射受限条件下，推导出正弦型中频面形误差对光学系统MTF的影响的表达式并对其进行分析，然后通过光学设计软件仿真验证理论推导结果。假设光学系统光瞳上带有正弦型中频面形误差，对光瞳函数进行傅立叶变换，然后平方得到点扩散函数（PSF），再对PSF进行傅立叶变换得到光学系统的光学传递函数（OTF），对OTF取模，即可得到中频误差影响下的MTF表达式。将该式与衍射受限条件下无中频误差的光学系统MTF进行对比，得到中频误差对光学系统MTF的量化影响。理论计算结果表明：正弦型中频误差会使光学系统的MTF在不同空间频率处产生不同的损失，损失值随空间频率呈周期性变化；峰谷值（PV）分别为0.030 μm、0.095 μm、0.159 μm和0.223 μm的中频面形误差，导致的光学系统MTF的最大损失比例分别为0.89%、8.80%、23.48%和43.31%；随着中频误差PV的增加，MTF的损失值呈非线性快速增加。软件仿真结果与理论计算结果吻合。
Abstract:Mid-spatial frequency surface errors (MSFSE) can cause small angle scattering in optical systems. In order to determine a reasonable tolerance for MSFSE in optical design and processing, this paper conducts a quantitative study on the impact of MSFSE on the modulation transfer function (MTF) of optical systems. Under diffraction-limited conditions, we derived an expression for the influence of MSFSE on the MTF of optical systems and analyzed it. Then, we verified the theoretical derivation results through optical design software simulation. Assuming that the optical system has a sinusoidal MSFSE on the pupil, we performed the Fourier transform on the pupil function and squared it to obtain the point spread function (PSF), and then performed the Fourier transform on the PSF to obtain the optical transfer function (OTF) of the optical system. By taking the OTF mode, the expression of MTF under the influence of MSFSE can be obtained. By comparing this expression of MTF with the MTF of an optical system without MSFSE under diffraction-limited conditions, the quantitative impact of MSFSE on the MTF of the optical system can be obtained. Theoretical calculation results indicate that sinusoidal MSFSE can lead to different losses of MTF at different spatial frequencies and that the changes in MTF losses are periodic. The maximum loss ratios of MTF in optical systems caused by sinusoidal MSFSE with peak-to-valley (PV) of 0.030 μm, 0.095 μm, 0.159 μm and 0.223 μm are 0.89 %, 8.80 %, 23.48 % and 43.31 %, respectively. The loss of MTF will increase nonlinearly with the increase of PV of MSFSE. The theoretical calculation results are consistent with the software simulation results.
-
图 2 光瞳函数、点扩散函数和光学传递函数的关系图
Figure 2. Relationship diagram of pupil function, point spread function, and optical transfer function
图 3 光学元件的中频误差对系统MTF的影响
Figure 3. The influence of mid-spatial frequency errors of optical components on system MTF
图 5 正弦型中频相位误差的3D示意图
Figure 5. 3D schematic diagram of sinusoidal mid-spatial frequency phase errors
图 6 中频误差为0.030 μm时双高斯光学系统的MTF
Figure 6. MTF of a double Gaussian optical system with a 0.030 μm MSFSE
图 7 中频误差为0.095 μm时双高斯光学系统的MTF
Figure 7. MTF of a double Gaussian optical system with a 0.095 μm MSFSE
图 8 中频误差为0.159 μm时双高斯光学系统的MTF
Figure 8. MTF of a double Gaussian optical system with a 0.159 μm MSFSE
图 9 中频误差为0.223 μm时双高斯光学系统的MTF
Figure 9. MTF of a double Gaussian optical system with a 0.223 μm MSFSE
表 1 仿真结果与理论计算结果对比
Table 1. Comparison between simulation results and calculation results
MSFSE PV/μm Calculation
resultSimulation
resultPercentage error 0.030 0.89% 0.86% 3.37% 0.095 8.80% 8.52% 3.18% 0.159 23.48% 22.16% 5.62% 0.223 43.31% 40.84% 5.70% 
下载: 导出CSV
-
[1] 张云进, 项华中, 王亚琼, 等. 渐进多焦点自由曲面镜片优化重构[J]. 光学 精密工程,2023,31(6):813-821. doi: 10.37188/OPE.20233106.0813ZHANG Y J, XIANG H ZH, WANG Y Q, et al. Optimization and reconstruction of progressive addition free-form surface lens[J]. Optics and Precision Engineering, 2023, 31(6): 813-821. (in Chinese). doi: 10.37188/OPE.20233106.0813 [2] 徐乐, 张春雷, 代雷, 等. 高精度非回转对称非球面加工方法研究[J]. 中国光学,2016,9(3):364-370. doi: 10.3788/co.20160903.0364XU L, ZHANG CH L, DAI L, et al. Research on manufacturing method of non-rotationally symmetrical aspheric surface with high accuracy[J]. Chinese Optics, 2016, 9(3): 364-370. (in Chinese). doi: 10.3788/co.20160903.0364 [3] 田杰文, 叶新, 方伟. 基于自由曲面的辐射定标光源设计[J]. 中国光学(中英文),2023,16(1):127-135. doi: 10.37188/CO.2022-0021TIAN J W, YE X, FANG W. Design of a radiometric calibration light source based on a freeform reflector[J]. Chinese Optics, 2023, 16(1): 127-135. (in Chinese). doi: 10.37188/CO.2022-0021 [4] DU CH Y, DAI Y F, GUAN CH L, et al. High efficiency removal of single point diamond turning marks on aluminum surface by combination of ion beam sputtering and smoothing polishing[J]. Optics Express, 2021, 29(3): 3738-3753. doi: 10.1364/OE.417537 [5] DENG Y H, HOU X, LI B CH, et al. Review on mid-spatial frequency error suppression in optical components manufacturing[J]. The International Journal of Advanced Manufacturing Technology, 2023, 126(11-12): 4827-4847. doi: 10.1007/s00170-023-11408-y [6] 安其昌, 张景旭, 杨飞, 等. 基于结构函数的大口径望远镜中频误差分配研究[J]. 光学 精密工程,2017,25(2):433-440. doi: 10.3788/OPE.20172502.0433AN Q CH, ZHANG J X, YANG F, et al. On middle frequency error distribution of large telescope based on structure function[J]. Optics and Precision Engineering, 2017, 25(2): 433-440. (in Chinese). doi: 10.3788/OPE.20172502.0433 [7] HONEYCUTT A, SCHMITZ T L. Surface location error and surface roughness for period-n milling bifurcations[J]. Journal of Manufacturing Science and Engineering, 2017, 139(6): 061010. doi: 10.1115/1.4035371 [8] 赵天骄, 乔彦峰, 孙宁, 等. 经纬仪主镜在支撑系统下的面形变化[J]. 中国光学,2017,10(4):477-483. doi: 10.3788/co.20171004.0477ZHAO T J, QIAO Y F, SUN N, et al. Surface deformation of theodolite primary mirror under the support system[J]. Chinese Optics, 2017, 10(4): 477-483. (in Chinese). doi: 10.3788/co.20171004.0477 [9] 梁子健, 杨甬英, 赵宏洋, 等. 非球面光学元件面型检测技术研究进展与最新应用[J]. 中国光学,2022,15(2):161-186. doi: 10.37188/CO.2021-0143LIANG Z J, YANG Y Y, ZHAO H Y, et al. Advances in research and applications of optical aspheric surface metrology[J]. Chinese Optics, 2022, 15(2): 161-186. (in Chinese). doi: 10.37188/CO.2021-0143 [10] AIKENS D M. Origin and evolution of the optics specifications for the National Ignition Facility[J]. Proceedings of SPIE, 1995, 2536: 2-12. doi: 10.1117/12.218410 [11] 曾雪锋. 光学表面频段误差对成像质量的影响研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2014.ZENG X F. Impact on image performance of surface spatial frequency[D]. Changchun: Changchun Institute of Optics and Fine Mechanics and Physics, Chinese Academy of Sciences, 2014. (in Chinese). [12] HARVEY J E. Total integrated scatter from surfaces with arbitrary roughness, correlation widths, and incident angles[J]. Optical Engineering, 2012, 51(1): 013402. doi: 10.1117/1.OE.51.1.013402 [13] LI L X, LI X CH, CHENG Q, et al. Optimized strategy to restrain the mid-spatial-frequency surface error in computer-controlled optical surfacing[J]. Results in Physics, 2020, 19: 103356. doi: 10.1016/j.rinp.2020.103356 [14] 曾雪锋, 张学军. 光学制造中频残差对光学调制传递函数的影响[J]. 激光与光电子学进展,2015,52(7):072202.ZENG X F, ZHANG X J. Impact of mid-spatial frequency errors in optical manufacturing on modulation transfer function[J]. Laser & Optoelectronics Progress, 2015, 52(7): 072202. (in Chinese). [15] XIE CH, REN J L, CHEN SH Y. Sub-aperture stitching method to measure aspherical mirror in phase retrieval[J]. Optical and Quantum Electronics, 2017, 49(11): 353. doi: 10.1007/s11082-017-1189-y [16] GOODMAN J W. Introduction to Fourier Optics[M]. San Francisco: McGraw-Hill Book Co., 1968. [17] TAMKIN J M, DALLAS W J, MILSTER T D. Theory of point-spread function artifacts due to structured mid-spatial frequency surface errors[J]. Applied Optics, 2010, 49(25): 4814-4824. doi: 10.1364/AO.49.004814 [18] TAMKIN J M, MILSTER T D, DALLAS W. Theory of modulation transfer function artifacts due to mid-spatial-frequency errors and its application to optical tolerancing[J]. Applied Optics, 2010, 49(25): 4825-4835. doi: 10.1364/AO.49.004825 -
下载:
计量
- 文章访问数: 379
- HTML全文浏览量: 186
- PDF下载量: 189
- 被引次数: 0
