Laser phase noise suppression method for a CO-OFDM-OQAM communication system with real-imaginary-alternate pilots
-
摘要:
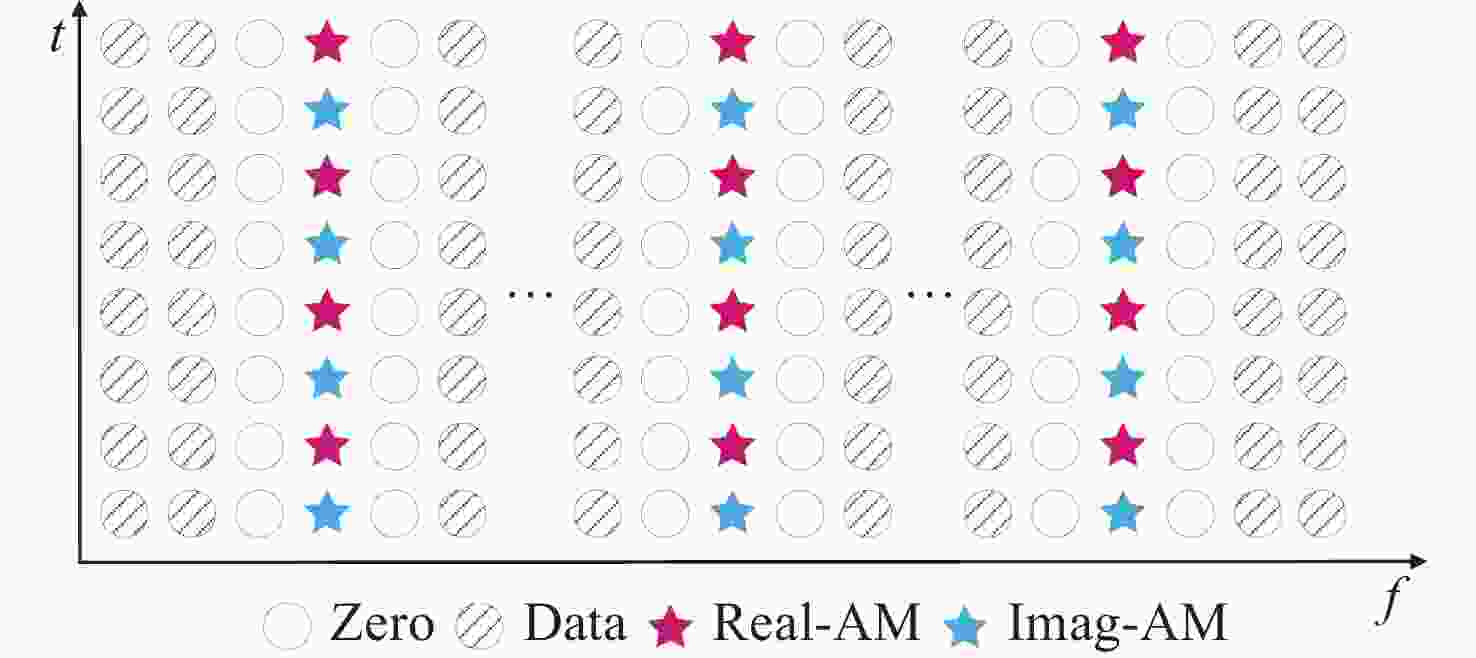
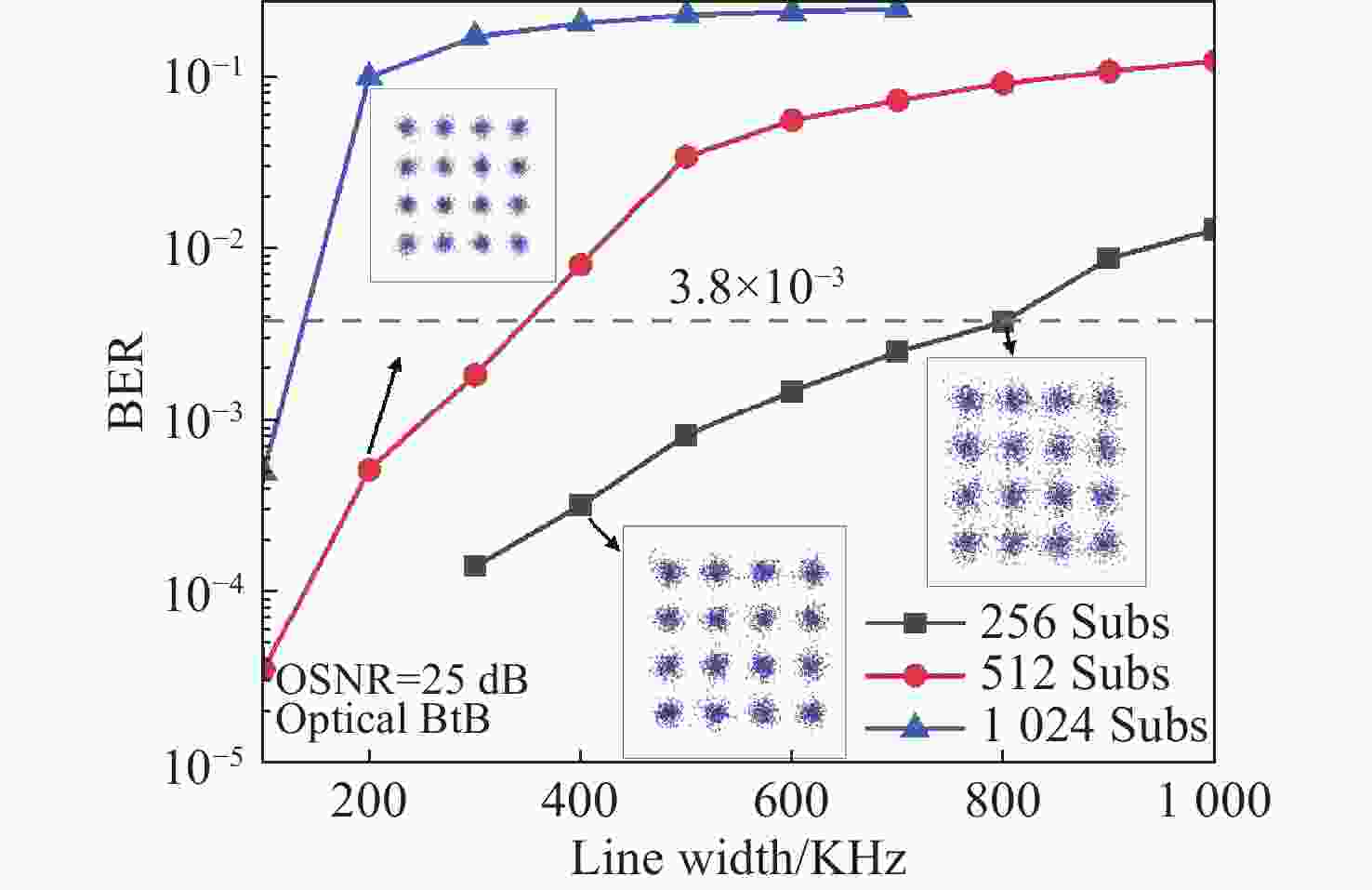
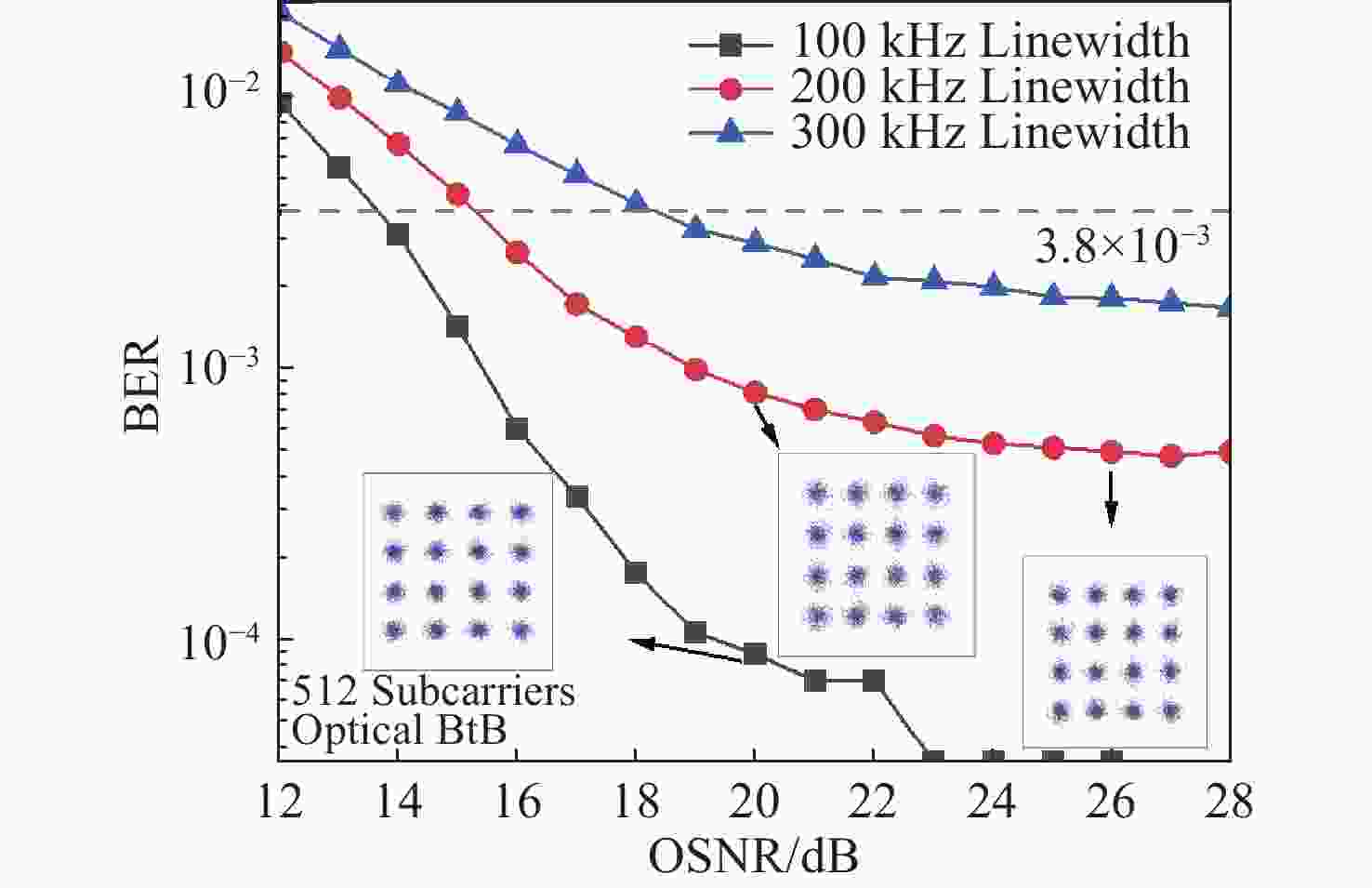
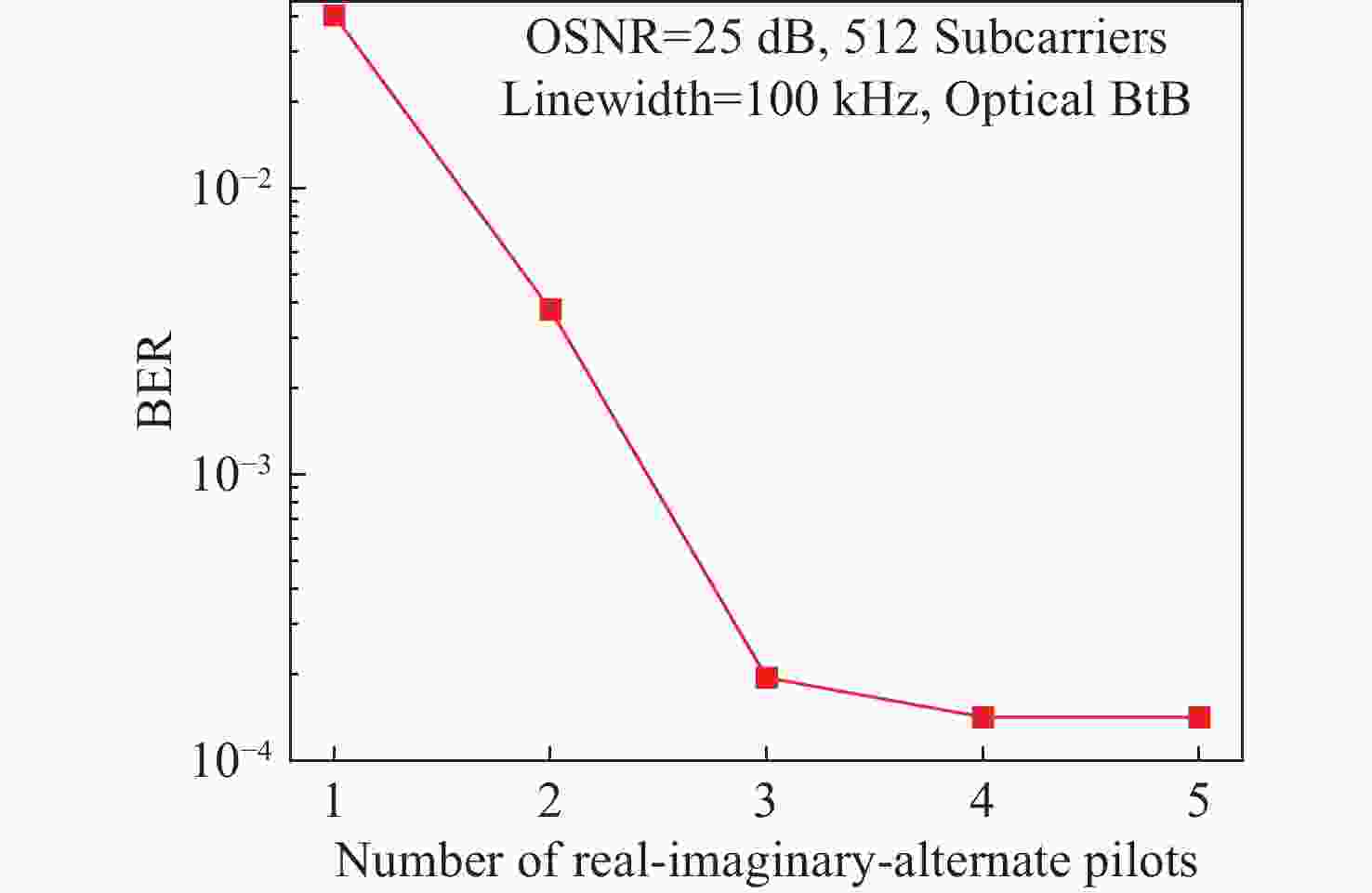
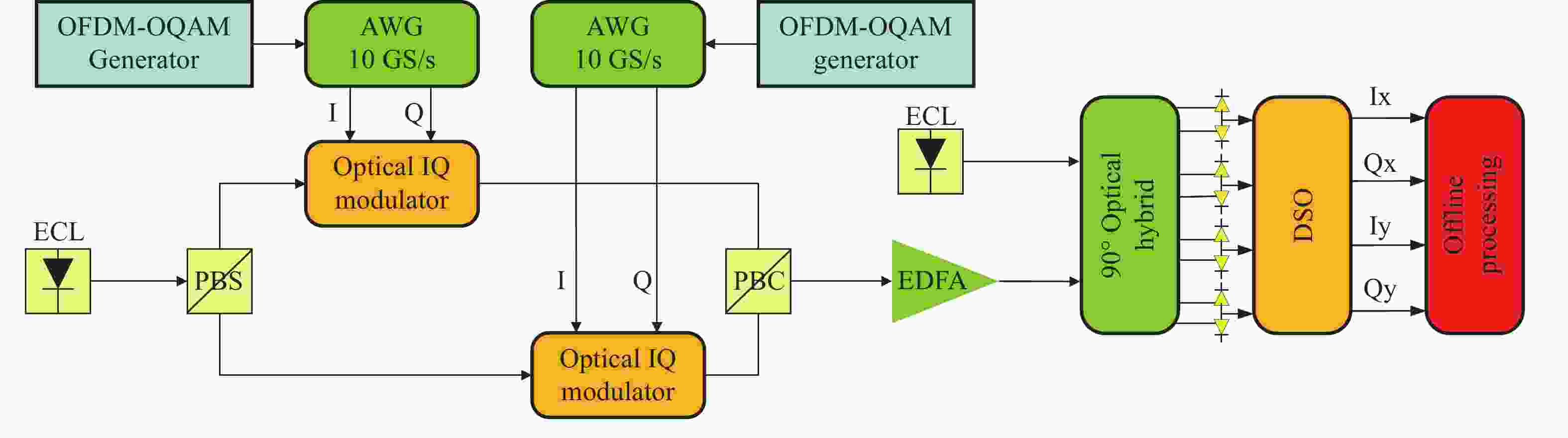
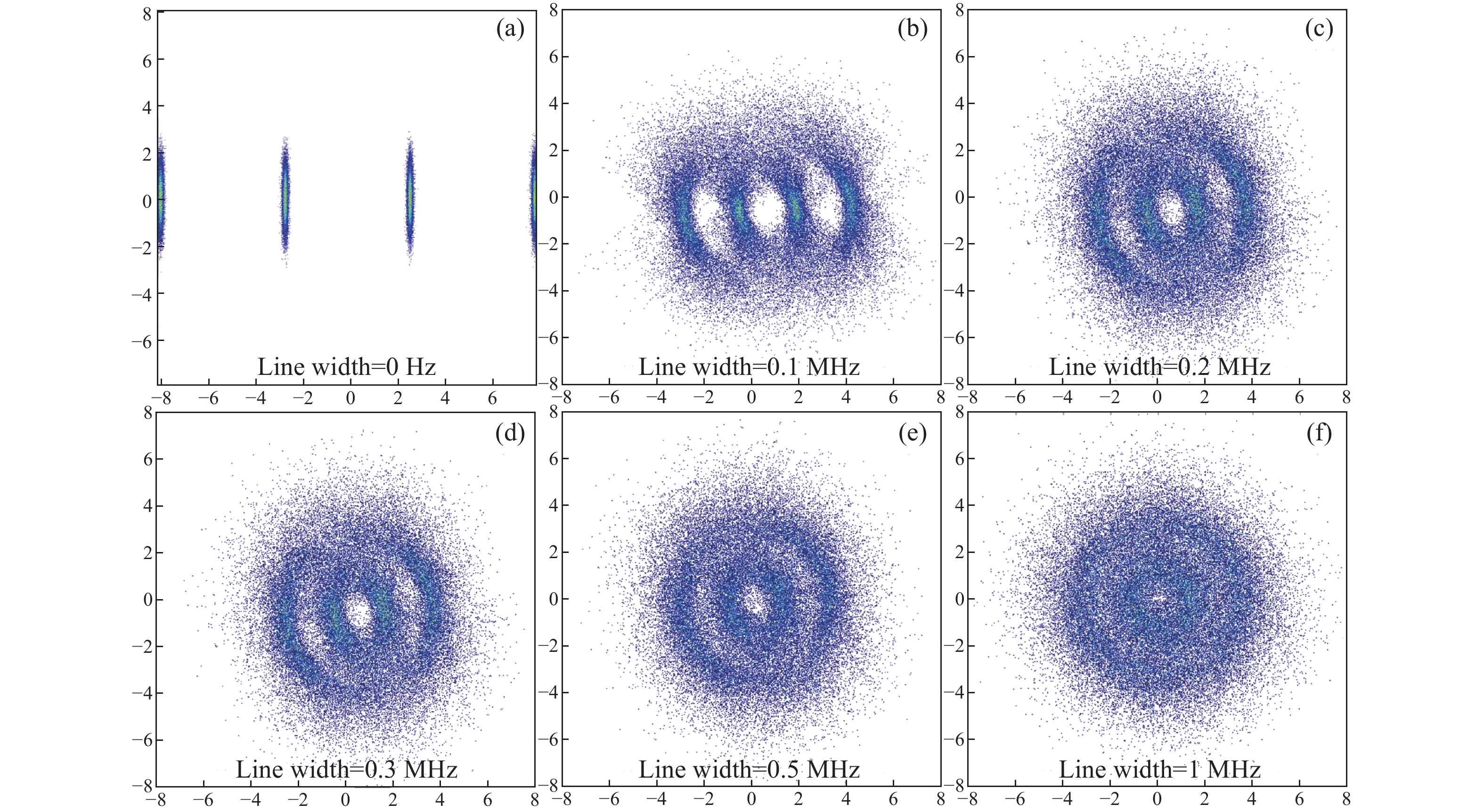
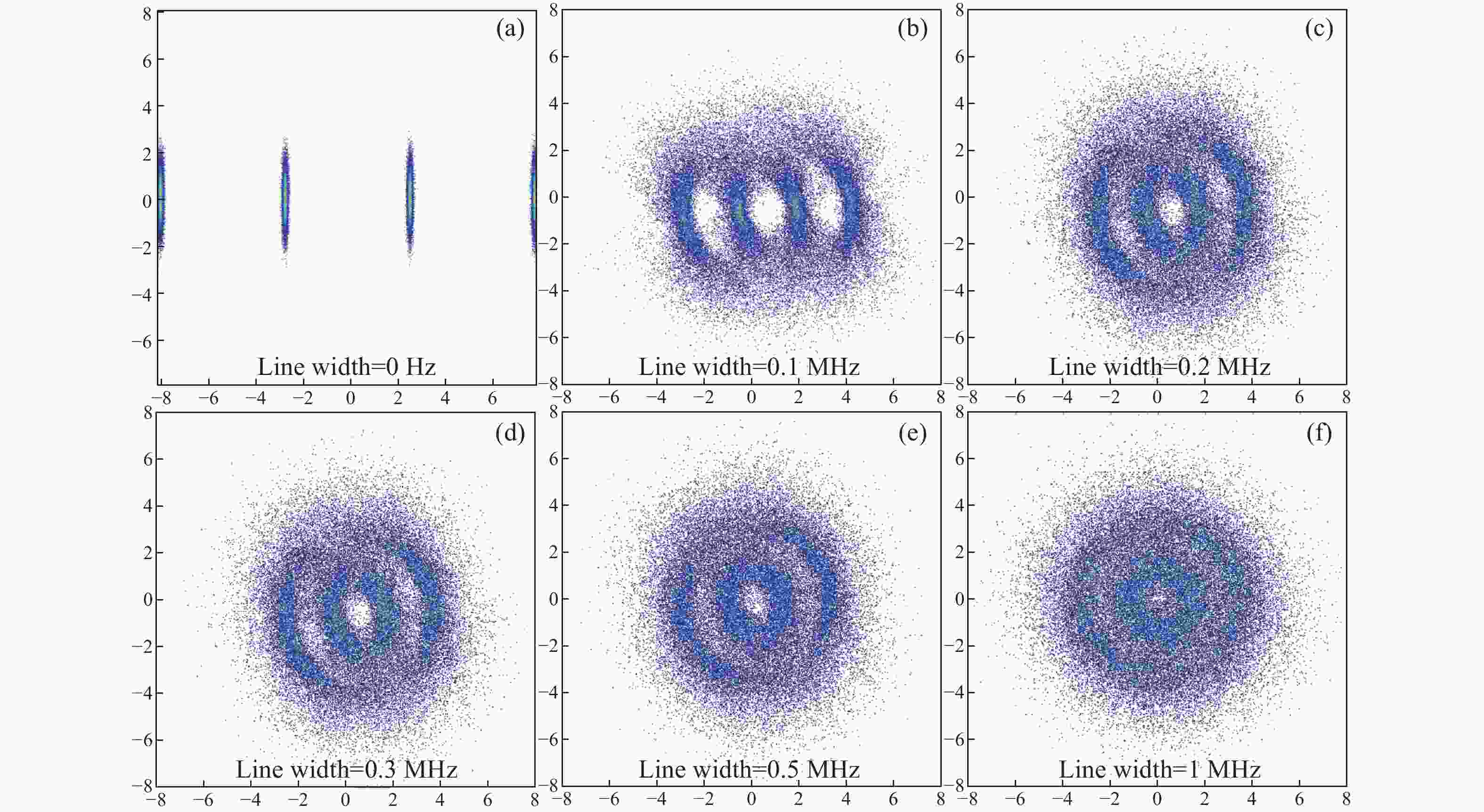
针对偏移正交幅度调制的相干光正交频分复用(CO-OFDM-OQAM)通信系统，本文提出了一种基于实虚交替导频的相位噪声抑制算法。该算法利用激光器相位噪声的性质和固有虚部干扰（IMI）系数的对称性规律设计全新的实虚交替导频，结合线性拟合，能够准确估计每个频域符号的公共相位误差（CPE）。由于是在频域进行补偿，与时域相位噪声抑制算法相比，计算复杂度大幅下降。搭建了有效速率为65 GBits/s的偏振复用CO-OFDM-OQAM系统的数值仿真平台，研究了不同激光器线宽和子载波个数下系统的传输性能，考察了所提方法对相位噪声的抑制效果。获得的结果证实：OSNR固定为25 dB，子载波总数分别为256、512和1024时，误码率达到FEC极限时所需要的线宽分别为801.1、349和138.4 kHz。对于使用16-QAM调制格式、子载波个数为256或512的系统，能较好补偿激光器的相位噪声，而且不会影响功率峰均比。
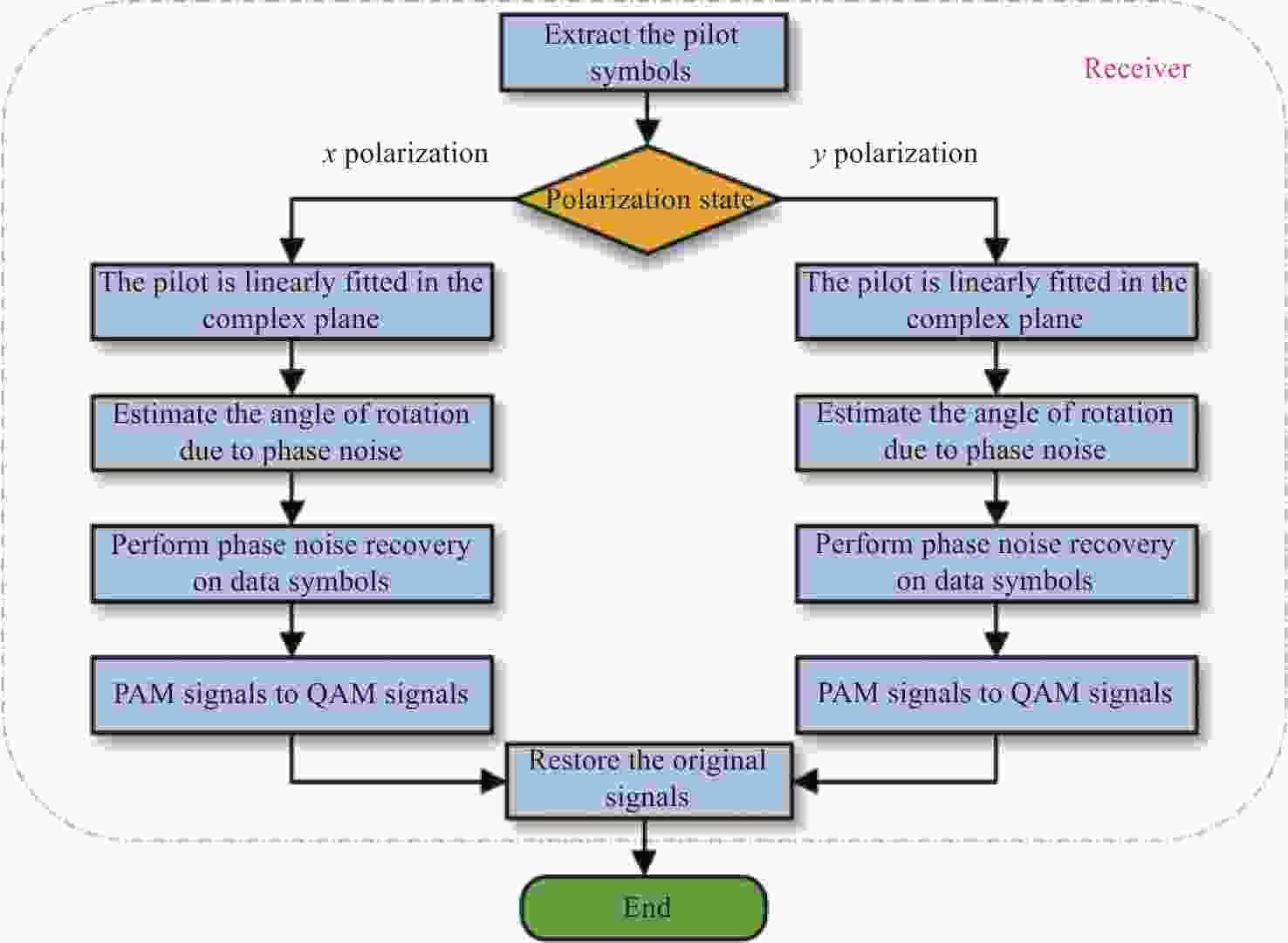
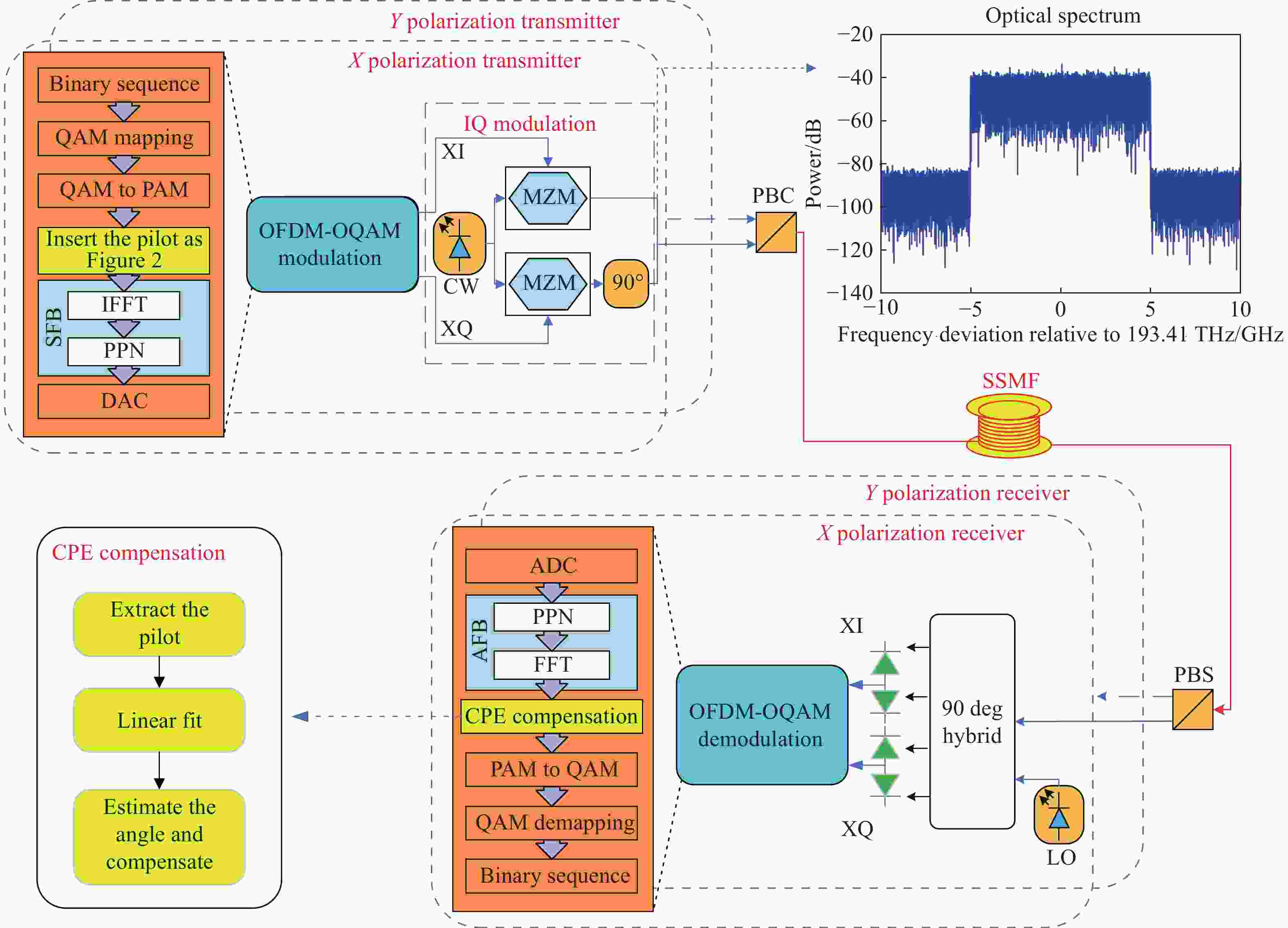
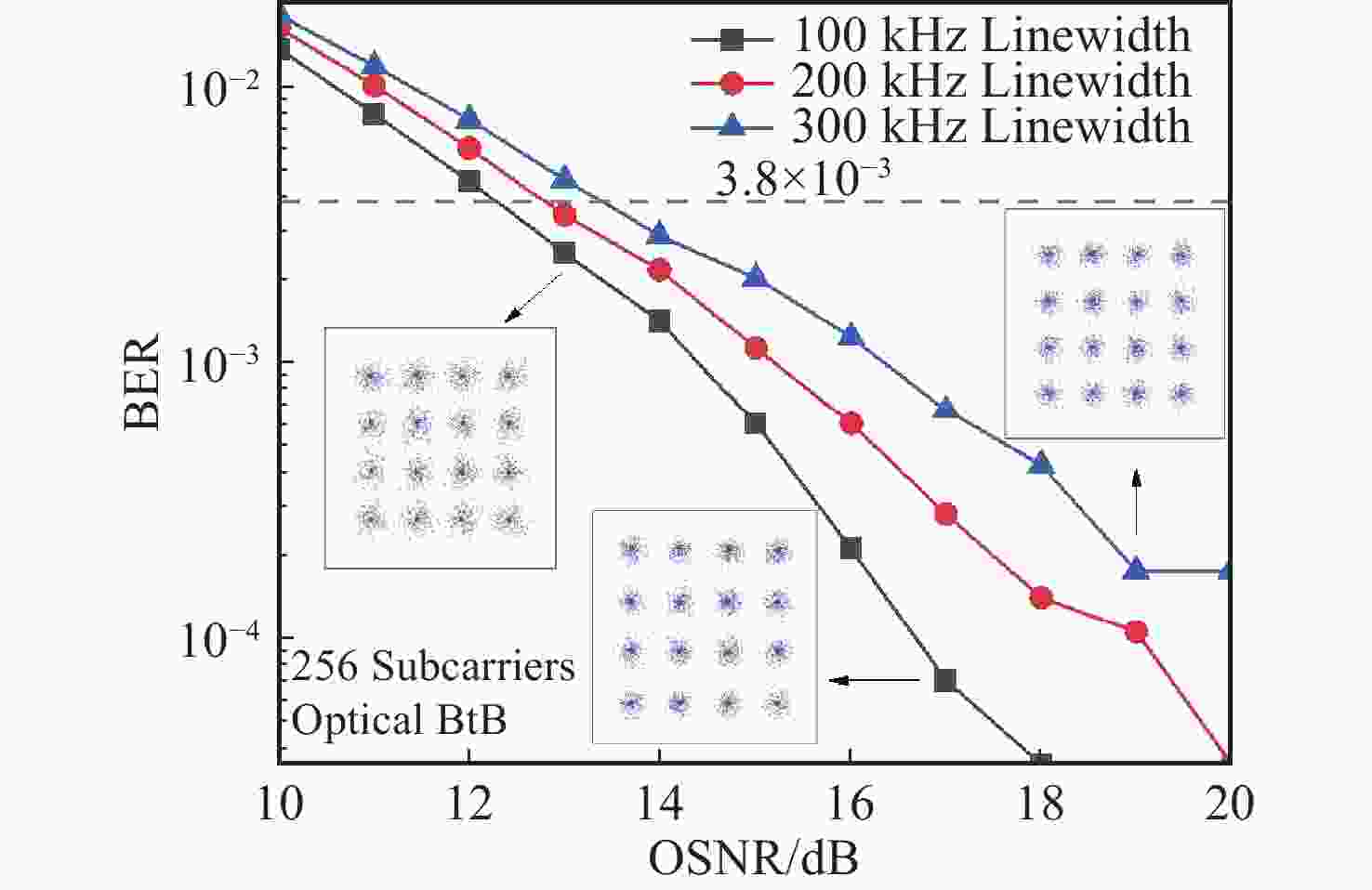
Abstract:A phase noise suppression algorithm based on real-imaginary-alternate pilots was proposed for a coherent optical orthogonal frequency division multiplexing communication system with offset quadrature amplitude modulation (CO-OFDM-OQAM). The algorithm uses the properties of laser phase noise and the intrinsic imaginary interference (IMI) symmetry law to design real-imaginary-alternate pilots. In combination with a linear fitting, it can accurately estimate the common phase error (CPE) for CO-OFDM-OQAM. As the compensation was performed in the frequency domain, the computational complexity was significantly reduced compared to the time-domain phase noise suppression algorithms. A numerical simulation platform was built for a polarization multiplexed CO-OFDM-OQAM system with an effective bit rate of 65 GBits/s. Through it, the transmission performance of the system with different laser linewidths and numbers of subcarriers was studied, and the suppression effect of the proposed method on phase noise was examined. The results obtained confirm that the linewidths required to reach the FEC limit for BER are equal to 801.1, 349, and 138.4 kHz for a fixed OSNR of 25 dB and a total number of subcarriers of 256, 512, and 1024, respectively. For the system using a 16-QAM modulation format with 256 or 512 subcarriers, it compensates well for the laser phase noise without affecting the power peak-to-average ratio.
-
图 1 OFDM-OQAM系统中信号受激光器线宽的影响。（a）线宽为0；（b）线宽为0.1 MHz；（c）线宽为0.2 MHz；（d）线宽为0.3 MHz；（e）线宽为0.5 MHz；（f）线宽为1 MHz
Figure 1. The effect of the laser linewidth on the signal in the OFDM-OQAM system. The line width is (a) 0; (b) 0.1 MHz; (c) 0.2 MHz; (d) 0.3 MHz; (e) 0.5 MHz; (f) 1 MHz
图 2 本文提出的相位噪声补偿方法导频结构图
Figure 2. Pilot structure diagram of the proposed phase noise compensation method
图 4 本文所提相位噪声补偿算法流程图
Figure 4. Flowchart of the proposed phase noise compensation algorithm
图 5 PDM CO-OFDM-OQAM系统原理示意图，插图显示了它的光谱和补偿流程
Figure 5. Schematic diagram of PDM CO-OFDM-OQAM system, with insets showing its optical spectra and compensation process
图 6 子载波数为256，光背靠背时，不同激光器线宽的误码率性能
Figure 6. The bit error rate performance of different laser linewidths with the subcarrier number 256 when light is back-to-back
图 8 OSNR为25 dB，光背靠背时，本方法在不同子载波数目下的误码率性能
Figure 8. The bit error rate performance for proposed method under different subcarrier numbers with OSNR 25 dB when light is back-to-back
图 7 子载波数为512，光背靠背时，不同激光器线宽的误码率性能
Figure 7. The bit error rate performance of different laser linewidths with subcarrier number 512 when light is back-to-back
图 9 不同导频组数目对误码率性能的影响
Figure 9. The influence of different pilot groups on bit error rate performance
图 10 本文方法的验证实验方案图。AWG代表任意波形发生器，I代表同相分量，Q代表正交分量，DSO代表高速数字存储示波器，ECL代表外腔激光器
Figure 10. Experimental scheme to validate the method proposed in this paper. Acronym key: AWG, Arbitrary Waveform Generator; I, In-phase; Q, quadrature; DSO, digital storage oscilloscope; ECL, External Cavity Laser.
-
[1] XIANG B Q, LI F. Joint cancellation of phase noise and clipping noise for OFDM[J]. IEEE Transactions on Vehicular Technology, 2023, 72(2): 1806-1814. doi: 10.1109/TVT.2022.3207622 [2] HU SH CH, KANG K, WANG H F, et al. Low complexity blind detection in OFDM systems with phase noise[J]. Digital Signal Processing, 2022, 129: 103638. doi: 10.1016/j.dsp.2022.103638 [3] 徐宪莹, 岳殿武. 可见光通信中正交频分复用调制技术[J]. 中国光学,2021,14(3):516-527. doi: 10.37188/CO.2020-0051XU X Y, YUE D W. Orthogonal frequency division multiplexing modulation techniques in visible light communication[J]. Chinese Optics, 2021, 14(3): 516-527. (in Chinese). doi: 10.37188/CO.2020-0051 [4] KESKIN M F, WYMEERSCH H, KOIVUNEN V. Monostatic sensing with OFDM under phase noise: from mitigation to exploitation[J]. IEEE Transactions on Signal Processing, 2023, 71: 1363-1378. doi: 10.1109/TSP.2023.3266976 [5] DODANE D, SANTACRUZ J P, BOURDERIONNET J, et al. Optical phase-locked loop phase noise in 5G mm-wave OFDM ARoF systems[J]. Optics Communications, 2023, 526: 128872. doi: 10.1016/j.optcom.2022.128872 [6] XUE ZH J, LI SH Y, LI J D, et al. OFDM radar and communication joint system using opto-electronic oscillator with phase noise degradation analysis and mitigation[J]. Journal of Lightwave Technology, 2022, 40(13): 4101-4109. doi: 10.1109/JLT.2022.3156573 [7] 管海军, 刘云清, 张凤晶. 基于数字相位恢复算法的正交相移键控自由空间相干光通信系统[J]. 中国光学,2019,12(5):1131-1138. doi: 10.3788/co.20191205.1131GUAN H J, LIU Y Q, ZHANG F J. Coherent free-space optical communication system with quadrature phase-shift keying modulation using a digital phase recovery algorithm[J]. Chinese Optics, 2019, 12(5): 1131-1138. (in Chinese). doi: 10.3788/co.20191205.1131 [8] SREEDHAR T V S, MEHTA N B. Inter-numerology interference in mixed numerology OFDM systems in time-varying fading channels with phase noise[J]. IEEE Transactions on Wireless Communications, 2023, 22(8): 5473-5485. doi: 10.1109/TWC.2023.3234363 [9] KESKIN M F, MARCUS C, ERIKSSON O, et al. On the impact of phase noise on monostatic sensing in OFDM ISAC systems[C]. 2023 IEEE Radar Conference (RadarConf23), IEEE, 2023: 1-6. [10] SREEDHAR T V S, MEHTA N B. Refined bounds for inter-carrier interference in OFDM due to time-varying channels and phase noise[J]. IEEE Wireless Communications Letters, 2022, 11(12): 2522-2526. doi: 10.1109/LWC.2022.3207322 [11] ALAGHBARI K A, LIM H S, AZIZ N H A, et al. Design and validation of the physical layer functions of FBMC/OQAM transceiver with improved residual phase error correction[J]. IEEE Access, 2022, 10: 97381-97393. doi: 10.1109/ACCESS.2022.3205405 [12] NGUYEN T H, LOUVEAUX J, GORZA S P, et al. Simple feedforward carrier phase estimation for optical FBMC/OQAM systems[J]. IEEE Photonics Technology Letters, 2016, 28(24): 2823-2826. doi: 10.1109/LPT.2016.2623946 [13] FICKERS J, GHAZISAEIDI A, SALSI M, et al. Multicarrier offset-QAM for Long-Haul coherent optical communications[J]. Journal of Lightwave Technology, 2014, 32(24): 4671-4678. doi: 10.1109/JLT.2014.2361617 [14] TANG H Y, XIANG M, FU S N, et al. Feed-forward carrier phase recovery for offset-QAM Nyquist WDM transmission[J]. Optics Express, 2015, 23(5): 6215-6227. doi: 10.1364/OE.23.006215 [15] LU J N, FU S N, TANG H Y, et al. Vertical blind phase search for low-complexity carrier phase recovery of offset-QAM Nyquist WDM transmission[J]. Optics Communications, 2017, 382: 212-218. doi: 10.1016/j.optcom.2016.07.083 [16] FANG X, ZHANG F. Phase noise estimation and suppression for PDM CO-OFDM/OQAM systems[J]. Journal of Lightwave Technology, 2017, 35(10): 1837-1846. doi: 10.1109/JLT.2017.2665464 [17] NGUYEN T T, LE S T, NISSEL R, et al. Pseudo-pilot coding based phase noise estimation for coherent optical FBMC-OQAM transmissions[J]. Journal of Lightwave Technology, 2018, 36(14): 2859-2867. doi: 10.1109/JLT.2018.2823335 [18] YOU B Y, YANG L, LUO F G, et al. Joint carrier frequency offset and phase noise estimation based on pseudo-pilot in CO-FBMC/OQAM system[J]. IEEE Photonics Journal, 2019, 11(1): 7201611. [19] NGUYEN T H, PEUCHERET C. Kalman filtering for carrier phase recovery in optical offset-QAM Nyquist WDM systems[J]. IEEE Photonics Technology Letters, 2017, 29(12): 1019-1022. doi: 10.1109/LPT.2017.2701907 [20] WANG X B, YANG L, LUO F G, et al. Adaptive EKF based estimation method for phase noise in CO-OFDM/OQAM system[J]. IEEE Access, 2020, 8: 204931-204940. doi: 10.1109/ACCESS.2020.3037312 -
下载:
计量
- 文章访问数: 253
- HTML全文浏览量: 128
- PDF下载量: 79
- 被引次数: 0
