-
摘要:
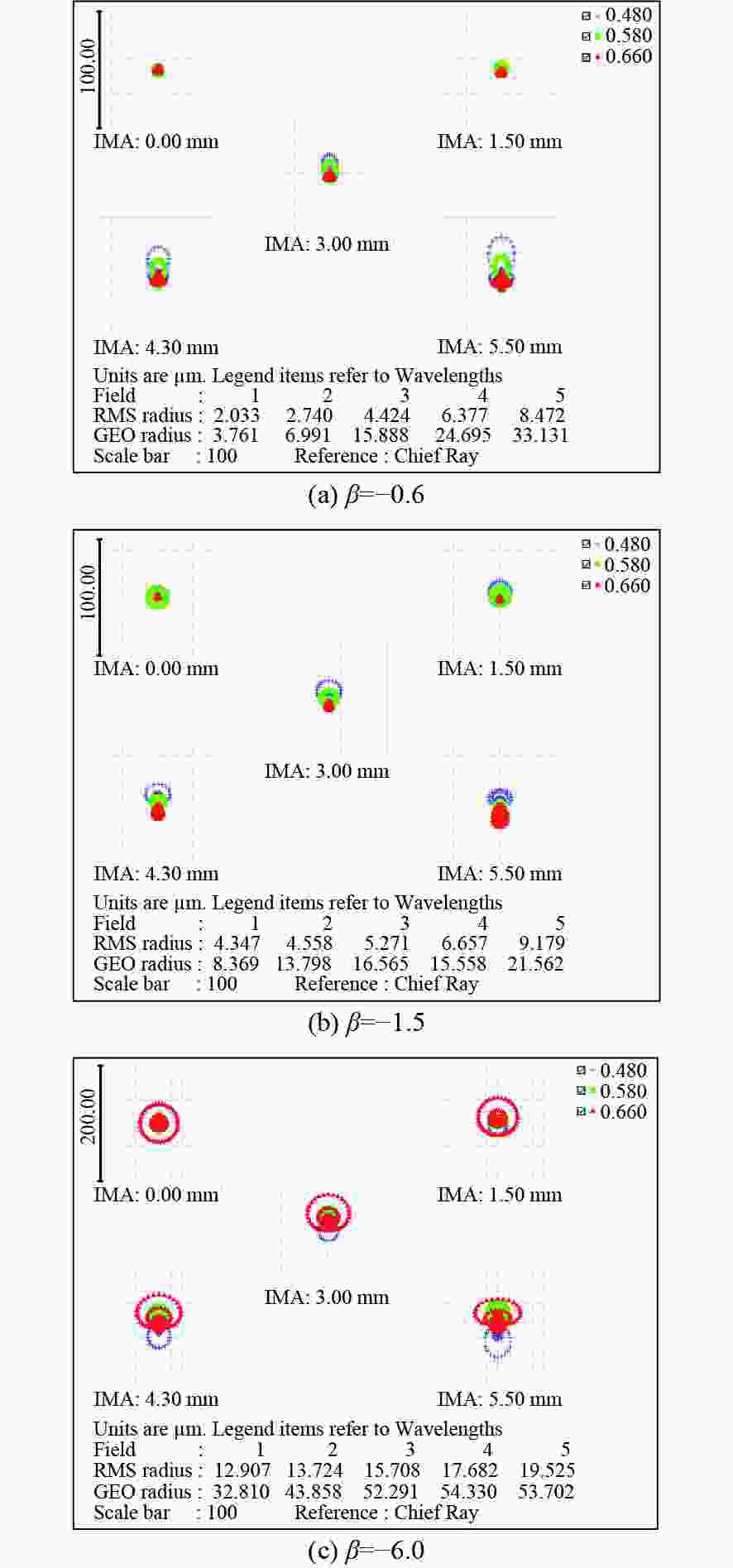
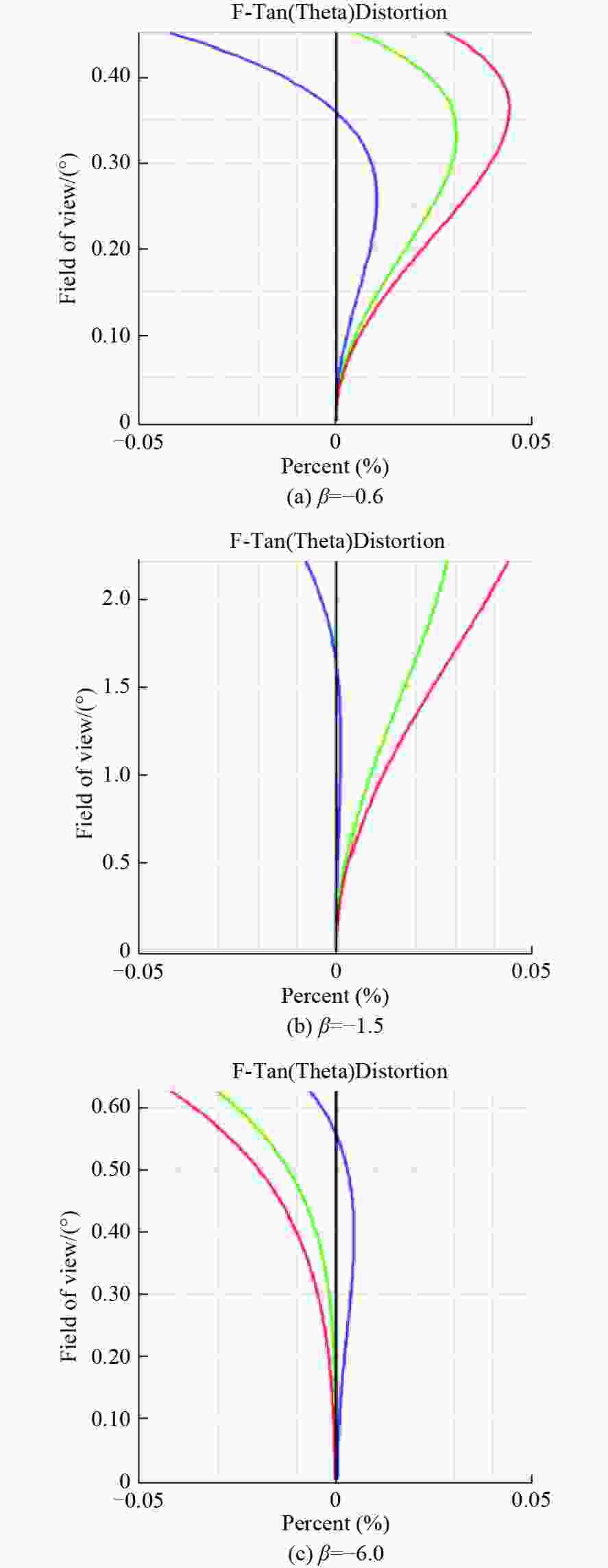
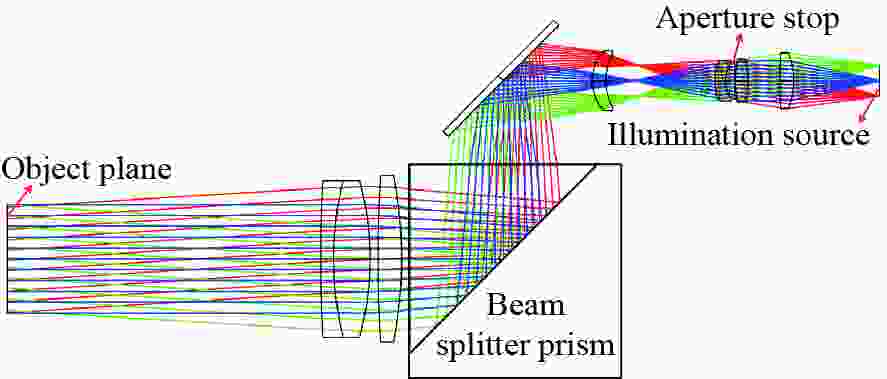
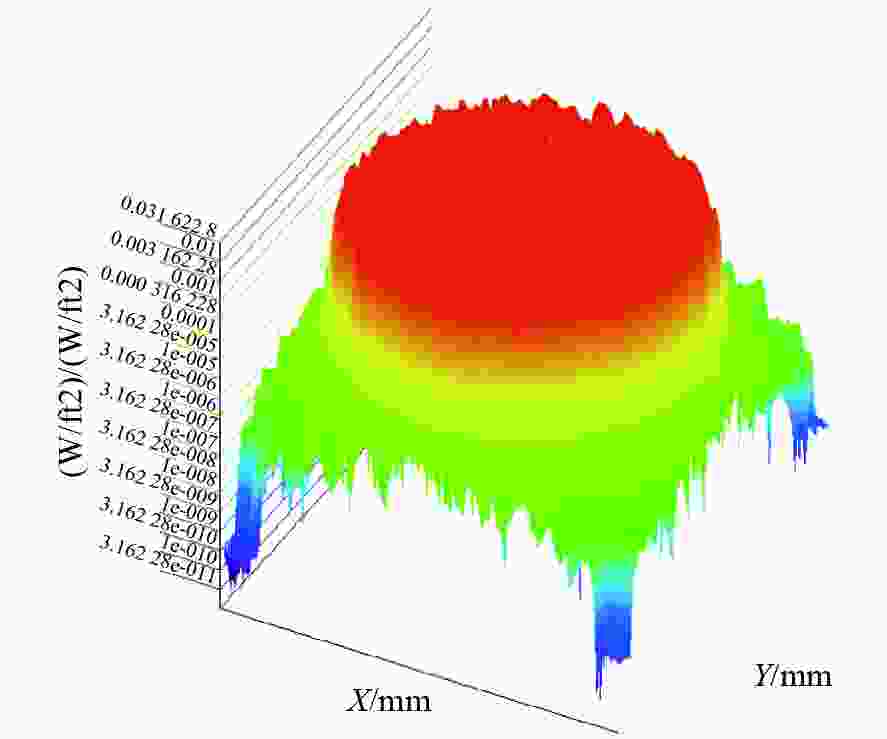
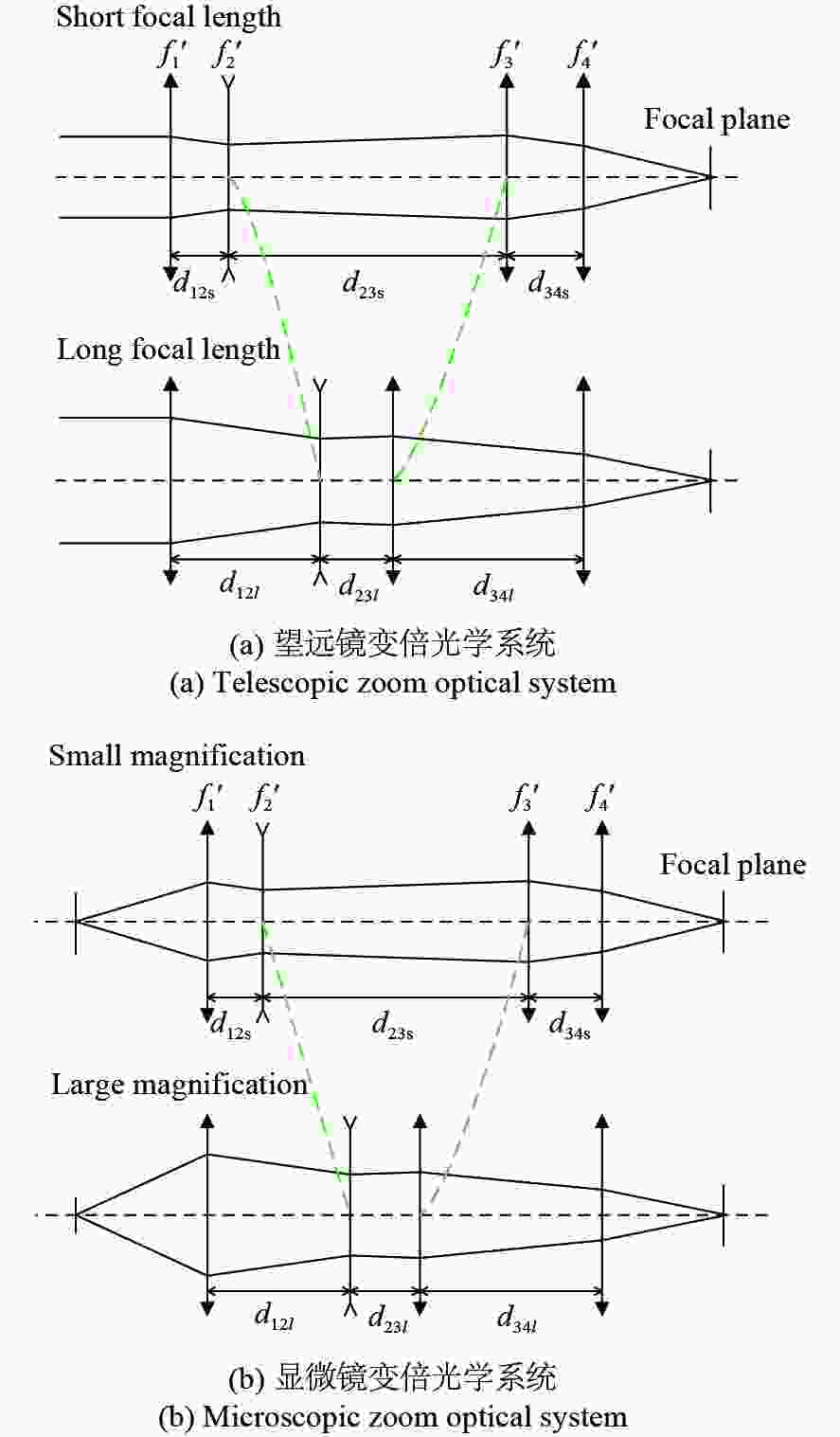
为了实现大靶面、大变倍比显微成像并解决同轴柯勒照明高集成度设计的问题，本文提出了一种基于同轴柯勒照明的大变倍比紧凑型显微镜光学系统设计方法。首先，对望远镜和显微镜连续变倍光学系统的成像原理进行了分析，并对正组补偿式变倍显微镜光学系统的设计原理进行了理论分析。然后，提出把前固定组分解为准直组和汇聚组，并在两镜组间设计分光镜，并通过共用透镜组实现同轴柯勒照明系统的紧凑型设计。最后，对大靶面连续变倍显微镜系统和与之匹配的同轴柯勒照明光学系统进行设计，设计结果表明显微成像光学系统的变倍比为10×，工作距离为60 mm，物方最高分辨率为1.75 µm，同轴照明均匀性为94.3%。该系统具有成像质量好、畸变小、变倍曲线平滑、体积小巧等特点，实验验证了该设计方法的可行性。
Abstract:In order to achieve a large image plane and large zoom ratio in microscopic imaging and solve the problem of the high integration of coaxial Kohler illumination, we propose a design method for a compact optical system with a large zoom ratio based on coaxial Kohler illumination. First, the imaging principle of the continuous zoom optical system of telescopes and microscopes is analyzed, and the design principle of the positive group compensation zoom microscope is analyzed theoretically. Then, the front fixed group is divided into a collimation group and a convergence group, and a beam splitter prism is designed between the two lens groups to achieve a compact coaxial Kohler illumination optical system by sharing lens groups. Finally, the continuous zoom microscope with a large image plane and the matched coaxial Kohler illumination optical system are designed. The design results show that the zoom ratio of the microscope optical system is 10×, the working distance is 60 mm, the highest resolution of the object side is 1.75 µm, and the coaxial illumination uniformity is 94.3%. The designed microscope has excellent imaging quality, minimal distortion, a smooth zoom curve, and a compact size, verifying the feasibility of the design method.
-
图 1 正组补偿变倍成像原理图
Figure 1. Imaging principle diagram of the positive group compensation zoom optical system
图 4 10×连续变倍显微镜二维结构图
Figure 4. 2D structural diagram of the 10× continuous zoom microscope
图 10 柯勒照明光学系统结构参数
Figure 10. Structural parameters of the Kohler illumination optical system
图 12 变倍显微镜总体光路图（β=−0.6）
Figure 12. Overall optical path diagram of the zoom microscope
表 1 变倍显微镜光学系统设计参数
Table 1. Design parameters of zoom microscope optical system
参数 数值 变倍比 10× 放大率 −0.6~−6.0 工作距/mm 60 工作波段/nm 480~660 相机分辨率/pixel 2448×2048 像素尺寸/µm 3.45×3.45 照明方式 同轴柯勒照明 
下载: 导出CSV
表 2 四组元的初始焦距
Table 2. Focal lengths of the four groups in the initial structure
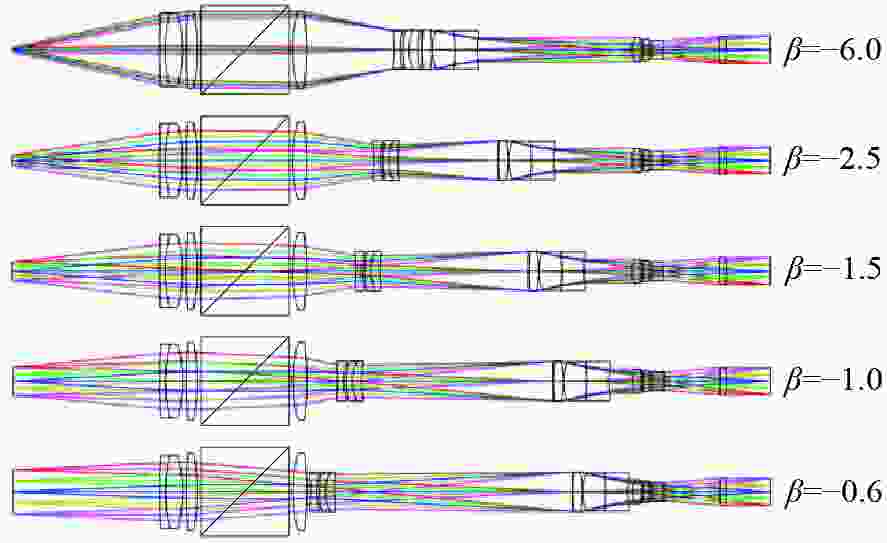
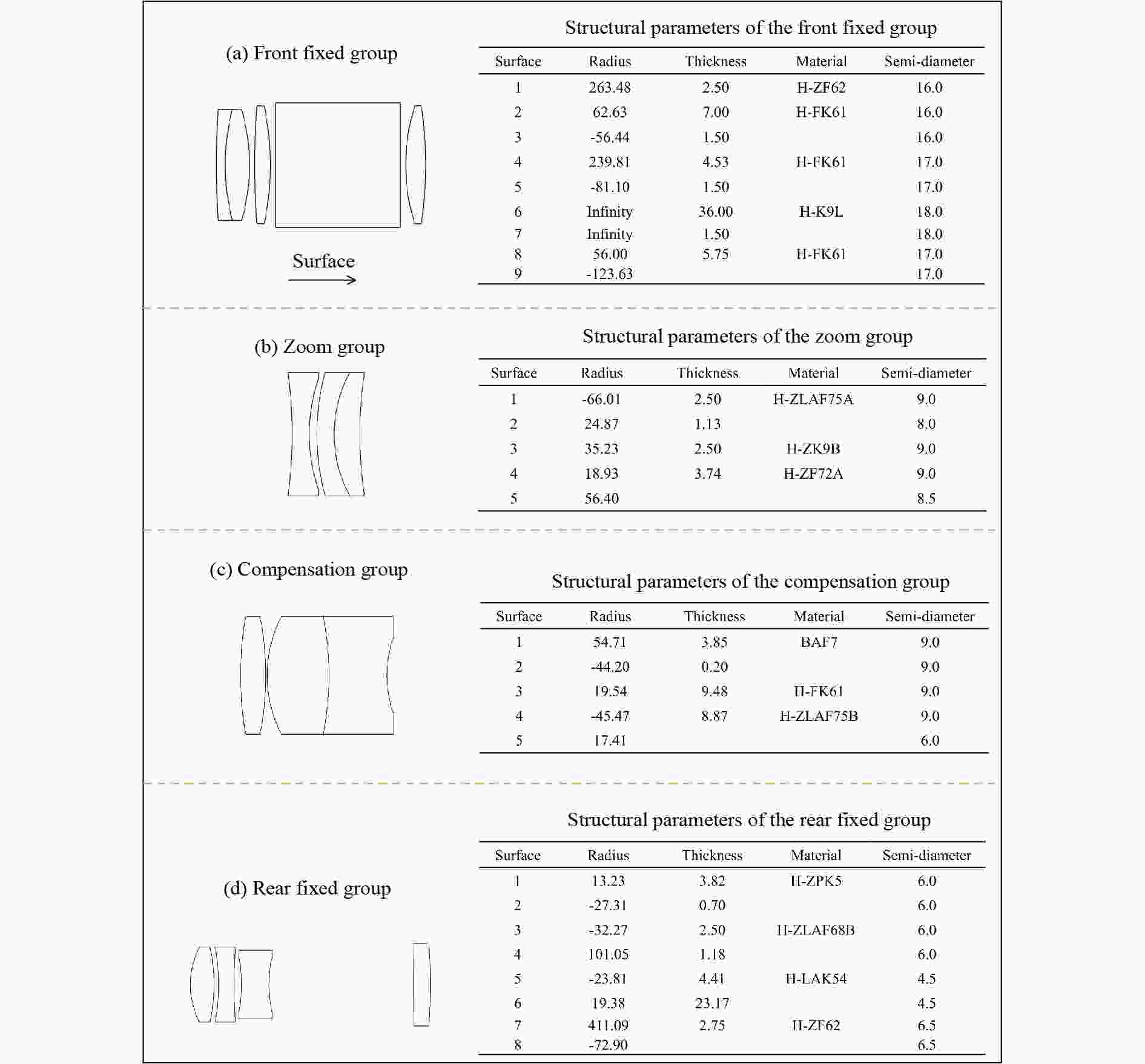
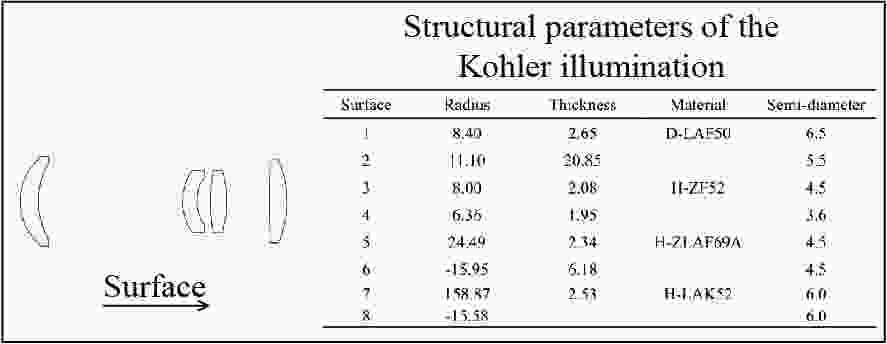
组元 前固定组 变焦组 补偿组 后固定组 焦距/mm 40.7 −29.3 54.4 1001.9
下载: 导出CSV
表 3 四组元之间的间距
Table 3. Spacing between the four groups
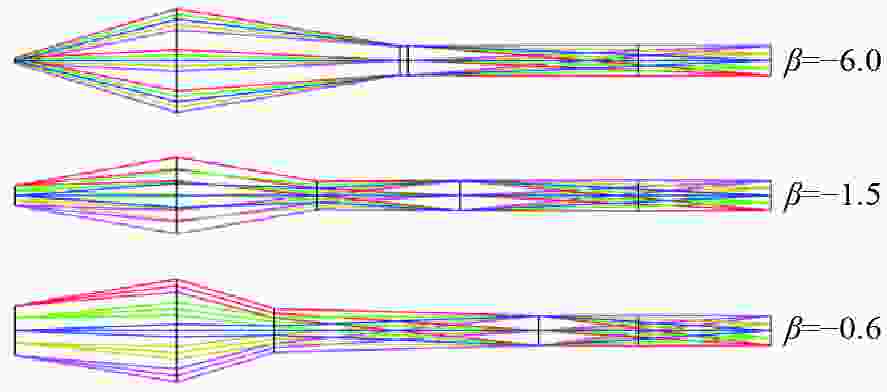
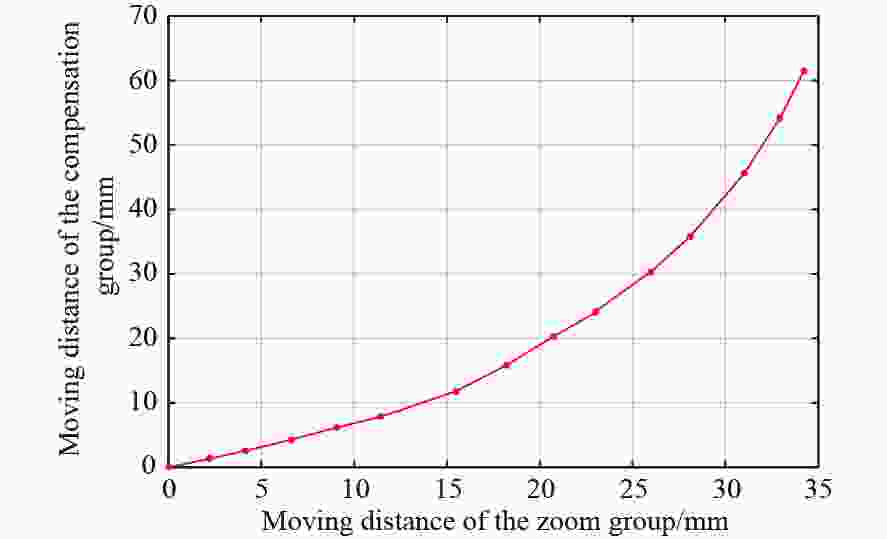
放大倍率β 组元距离 −l1/mm d12/mm d23/mm d34/mm l4ʹ/mm −0.6 60.0 36.02 98.06 36.75 49.17 −1.5 60.0 51.88 53.13 65.82 49.17 −6.0 60.0 82.53 3.20 85.10 49.17
下载: 导出CSV
表 4 变倍显微镜的物方分辨率
Table 4. Object-side resolution of the zoom microscope
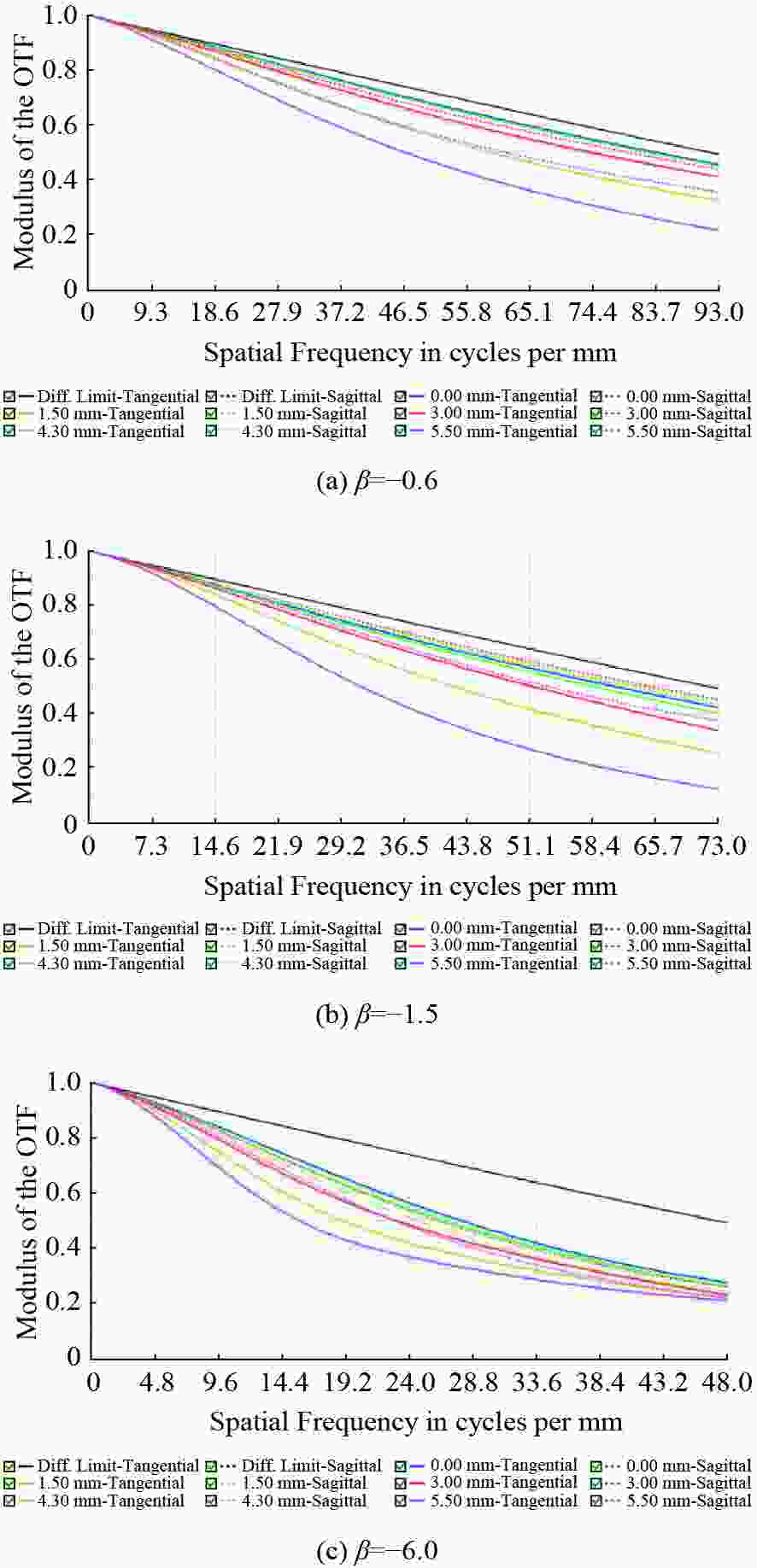
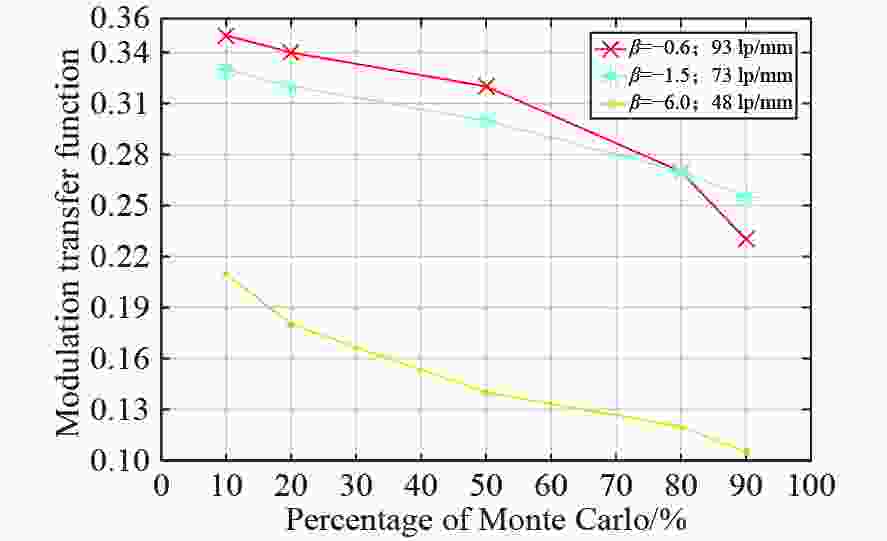
放大倍率 物方NA 物方分辨率 β=−0.6 0.038 9.0 µm β=−1.5 0.073 4.6 µm β=−6.0 0.192 1.75 µm
下载: 导出CSV
表 5 变倍显微镜公差分配表
Table 5. Tolerance distribution of the zoom microscope
公差项 数值 光圈/fringe ≤3 元件厚度/mm ±0.02 表面偏心/mm ±0.01 元件倾斜/(°) ±0.01 元件偏心/mm ±0.01 表面不规则度/fringe ≤0.3 折射率 ±0.001 阿贝数/% ±0.5
下载: 导出CSV
-
[1] ZHANG K, LI J CH, ZHANG X, et al. Design method of dual-band synchronous zoom optical system based on co-path zoom groups[J]. Optics and Lasers in Engineering, 2023, 170: 107791. doi: 10.1016/j.optlaseng.2023.107791 [2] FAN Z CH, WEI S L, ZHU ZH B, et al. Automatically retrieving an initial design of a double-sided telecentric zoom lens based on a particle swarm optimization[J]. Applied Optics, 2019, 58(27): 7379-7386. doi: 10.1364/AO.58.007379 [3] 张健, 罗天娇, 罗春华, 等. 30 mm~300 mm轻型变焦物镜光学系统设计[J]. 应用光学,2019,40(1):51-57.ZHANG J, LUO T J, LUO CH H, et al. Optical system design of 30 mm~300 mm light weight zoom objective[J]. Journal of Applied Optics, 2019, 40(1): 51-57. (in Chinese). [4] ZHANG K, LI J CH, SUN S, et al. Design method of dual-band synchronous zoom microscope optical system based on coaxial Kohler illumination[J]. Optics Express, 2023, 31(25): 41234-41251. doi: 10.1364/OE.505224 [5] 贺磊, 张建隆, 杨振. 6.5倍微小型可见光变焦光学系统设计[J]. 光学仪器,2019,41(2):46-52.HE L, ZHANG J L, YANG ZH. Design of a 6.5 times microscale continuous visible zoom optical system[J]. Optical Instruments, 2019, 41(2): 46-52. (in Chinese). [6] MIKŠ A, NOVÁK J. Paraxial imaging properties of double conjugate zoom lens system composed of three tunable-focus lenses[J]. Optics and Lasers in Engineering, 2014, 53: 86-89. doi: 10.1016/j.optlaseng.2013.08.018 [7] MIKŠ A, NOVÁK P. Paraxial design of four-component zoom lens with fixed position of optical center composed of members with variable focal length[J]. Optics Express, 2018, 26(20): 25611-25616. doi: 10.1364/OE.26.025611 [8] LIANG D, WANG X Y. Zoom optical system using tunable polymer lens[J]. Optics Communications, 2016, 371: 189-195. doi: 10.1016/j.optcom.2016.03.074 [9] 马海宽, 曹煊, 褚东志, 等. 应用于海洋监测的水下变焦镜头设计[J]. 激光与光电子学进展,2017,54(10):68-73.MA H K, CAO X, CHU D ZH, et al. Design of underwater zoom lens for marine monitoring[J]. Laser & Optoelectronics Progress, 2017, 54(10): 68-73. (in Chinese). [10] 张欣婷, 亢磊, 吴倩倩. 超高倍变焦光学系统设计[J]. 应用光学,2018,39(4):466-469.ZHANG X T, KANG L, WU Q Q. Design of ultra-high zoom optical system[J]. Journal of Applied Optics, 2018, 39(4): 466-469. (in Chinese). [11] FAN CH X, YANG B, LIU Y P, et al. Zoom lens with high zoom ratio design based on Gaussian bracket and particle swarm optimization[J]. Applied Optics, 2021, 60(11): 3217-3223. doi: 10.1364/AO.418970 [12] MIKŠ A, NOVÁK P. Double-sided telecentric zoom lens consisting of four tunable lenses with fixed distance between object and image plane[J]. Applied Optics, 2017, 56(25): 7020-7023. doi: 10.1364/AO.56.007020 [13] 闫晶, 刘英, 孙权, 等. 10倍中波红外连续变焦光学系统设计[J]. 激光与光电子学进展,2014,51(1):012201.YAN J, LIU Y, SUN Q, et al. Design of 10× MWIR continuous zoom optical system[J]. Laser & Optoelectronics Progress, 2014, 51(1): 012201. (in Chinese). [14] LIU Y P, YANG B, GU P X, et al. 50X five-group inner-focus zoom lens design with focus tunable lens using Gaussian brackets and lens modules[J]. Optics Express, 2020, 28(20): 29098-29111. doi: 10.1364/OE.404098 [15] 刘圆, 叶德茂, 王建楹, 等. 50 mm~1000 mm大变倍比变焦光学系统设计[J]. 应用光学,2020,41(6):1147-1152. doi: 10.5768/JAO202041.0601002LIU Y, YE D M, WANG J Y, et al. Design of 50 mm~1000 mm zoom optical system with high zoom ratio[J]. Journal of Applied Optics, 2020, 41(6): 1147-1152. (in Chinese). doi: 10.5768/JAO202041.0601002 [16] LEE S, CHOI M, LEE E, et al. Zoom lens design using liquid lens for laparoscope[J]. Optics Express, 2013, 21(2): 1751-1761. doi: 10.1364/OE.21.001751 [17] JO S H, PARK S C. Design and analysis of an 8x four-group zoom system using focus tunable lenses[J]. Optics Express, 2018, 26(10): 13370-13382. doi: 10.1364/OE.26.013370 [18] LI J CH, ZHANG K, DU J L, et al. Double-sided telecentric zoom optical system using adaptive liquid lenses[J]. Optics Express, 2023, 31(2): 2508-2522. doi: 10.1364/OE.479809 [19] ZHANG K, QU ZH, ZHONG X, et al. 40× zoom optical system design based on stable imaging principle of four groups[J]. Applied Optics, 2022, 61(6): 1516-1522. doi: 10.1364/AO.451726 [20] ZHANG K, ZHONG X, QU ZH, et al. Design method research of a radiation-resistant zoom lens[J]. Optics Communications, 2022, 509: 127881. doi: 10.1016/j.optcom.2021.127881 [21] 张坤, 曲正, 钟兴, 等. 30倍轻小型变焦光学系统设计[J]. 光学 精密工程,2022,30(11):1263-1271. doi: 10.37188/OPE.20223011.1263ZHANG K, QU ZH, ZHONG X, et al. Design of 30× zoom optical system with light weight and compact size[J]. Optics and Precision Engineering, 2022, 30(11): 1263-1271. (in Chinese). doi: 10.37188/OPE.20223011.1263 [22] 陈鲁, 李志强. 面板检测用显微镜光学系统设计[J]. 光学仪器,2021,43(1):42-48.CHEN L, LI ZH Q. Design of microscope optical system for panel inspection[J]. Optical Instruments, 2021, 43(1): 42-48. (in Chinese). [23] 王谭, 袁屹杰, 吴英春, 等. 连续变焦镜头凸轮曲线压力升角优化研究[J]. 电光与控制,2021,28(1):61-65.WANG T, YUAN Y J, WU Y CH, et al. Pressure angle optimization for cam curve of continuous zoom lens[J]. Electronics Optics & Control, 2021, 28(1): 61-65. (in Chinese). [24] LI J CH, ZHANG K, DU J L, et al. Design and theoretical analysis of the image-side telecentric zoom system using focus tunable lenses based on Gaussian brackets and lens modules[J]. Optics and Lasers in Engineering, 2023, 164: 107494. doi: 10.1016/j.optlaseng.2023.107494 -
下载:
计量
- 文章访问数: 257
- HTML全文浏览量: 130
- PDF下载量: 94
- 被引次数: 0
