-
摘要:
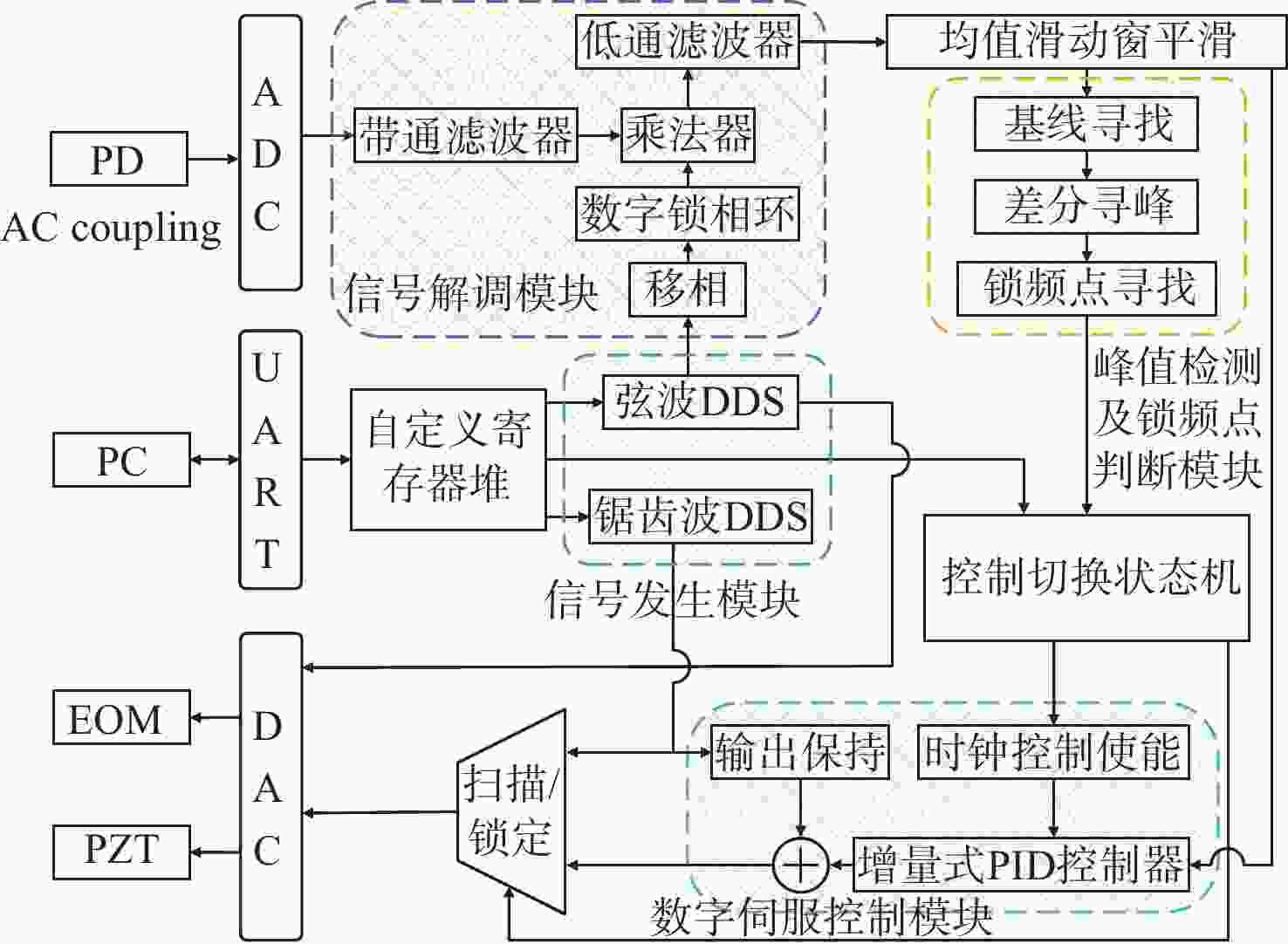
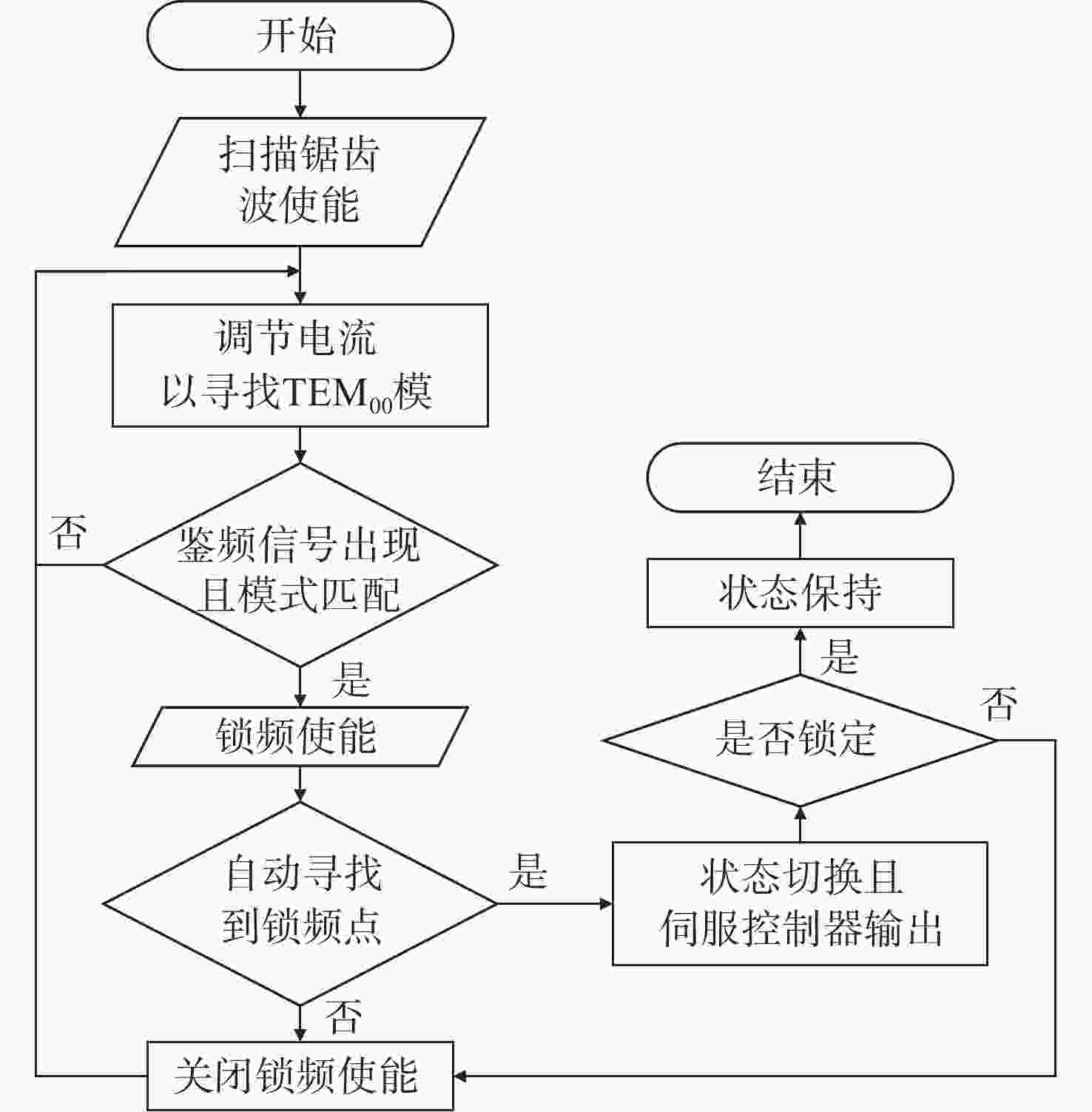
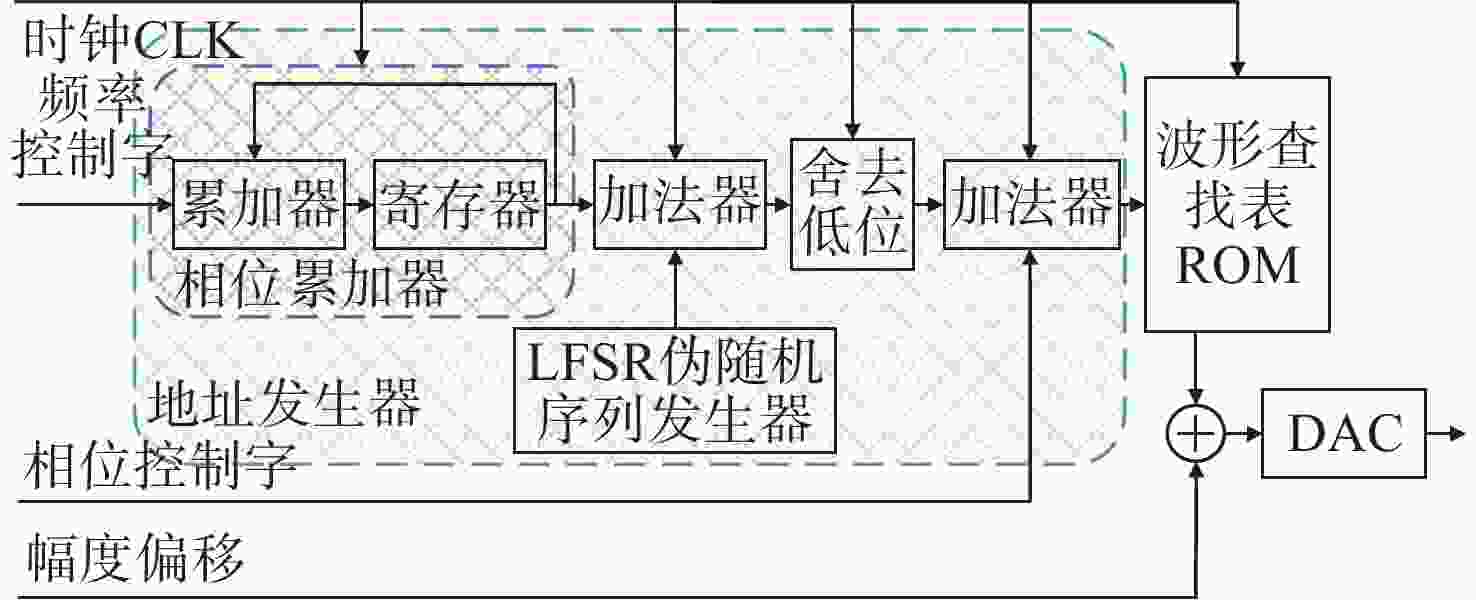
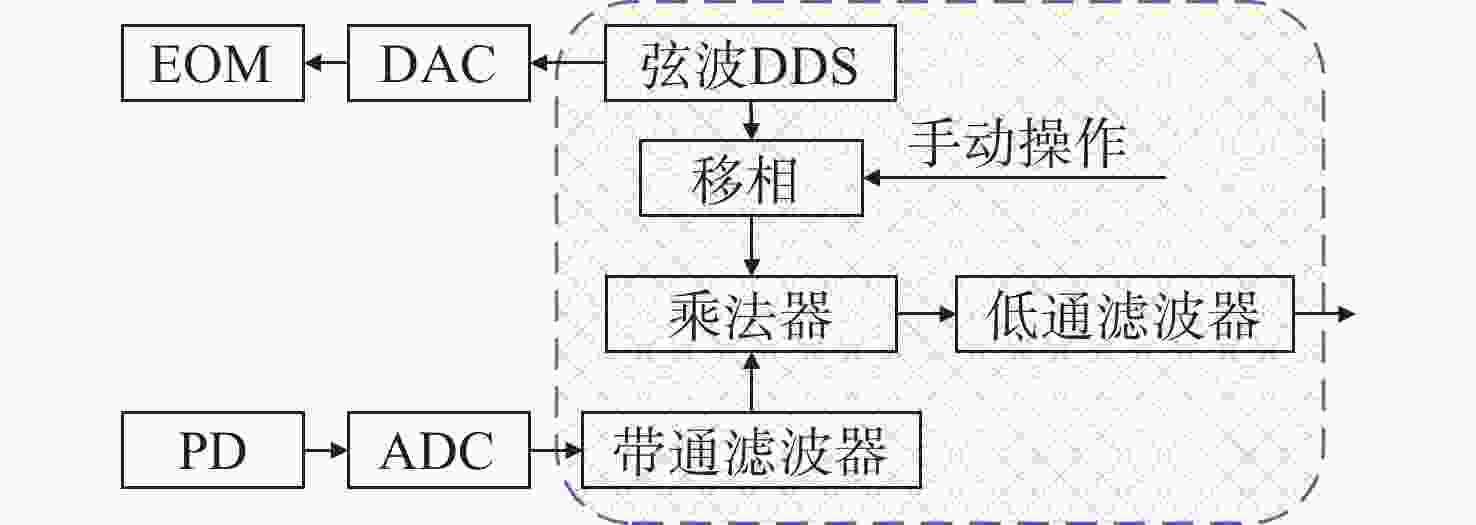
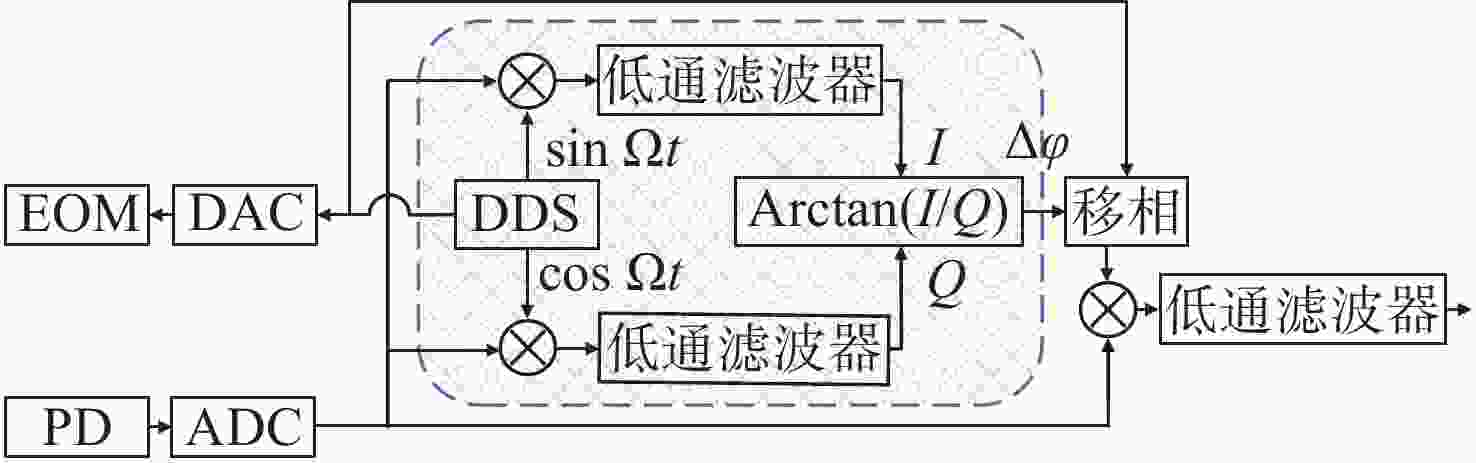
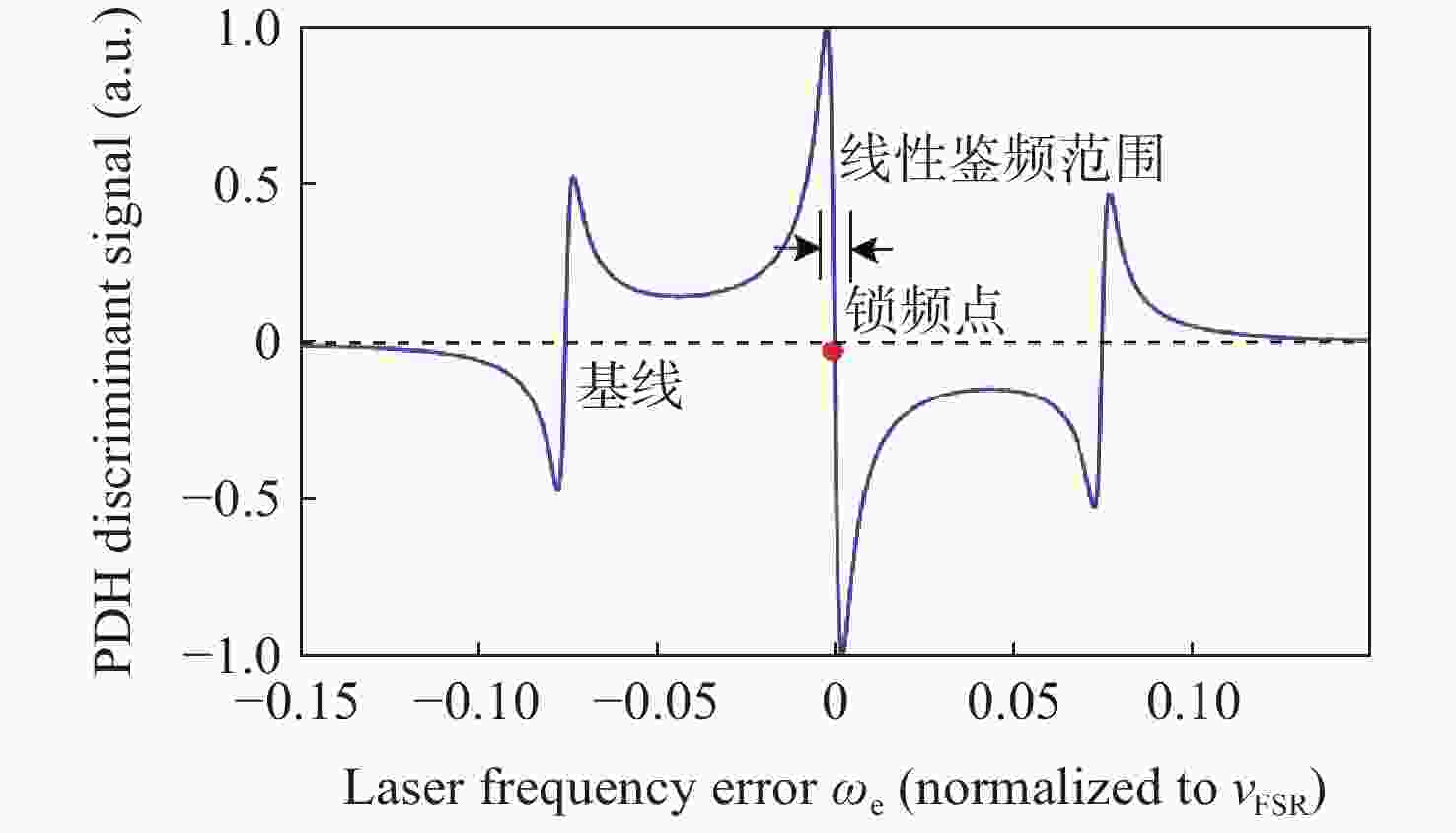
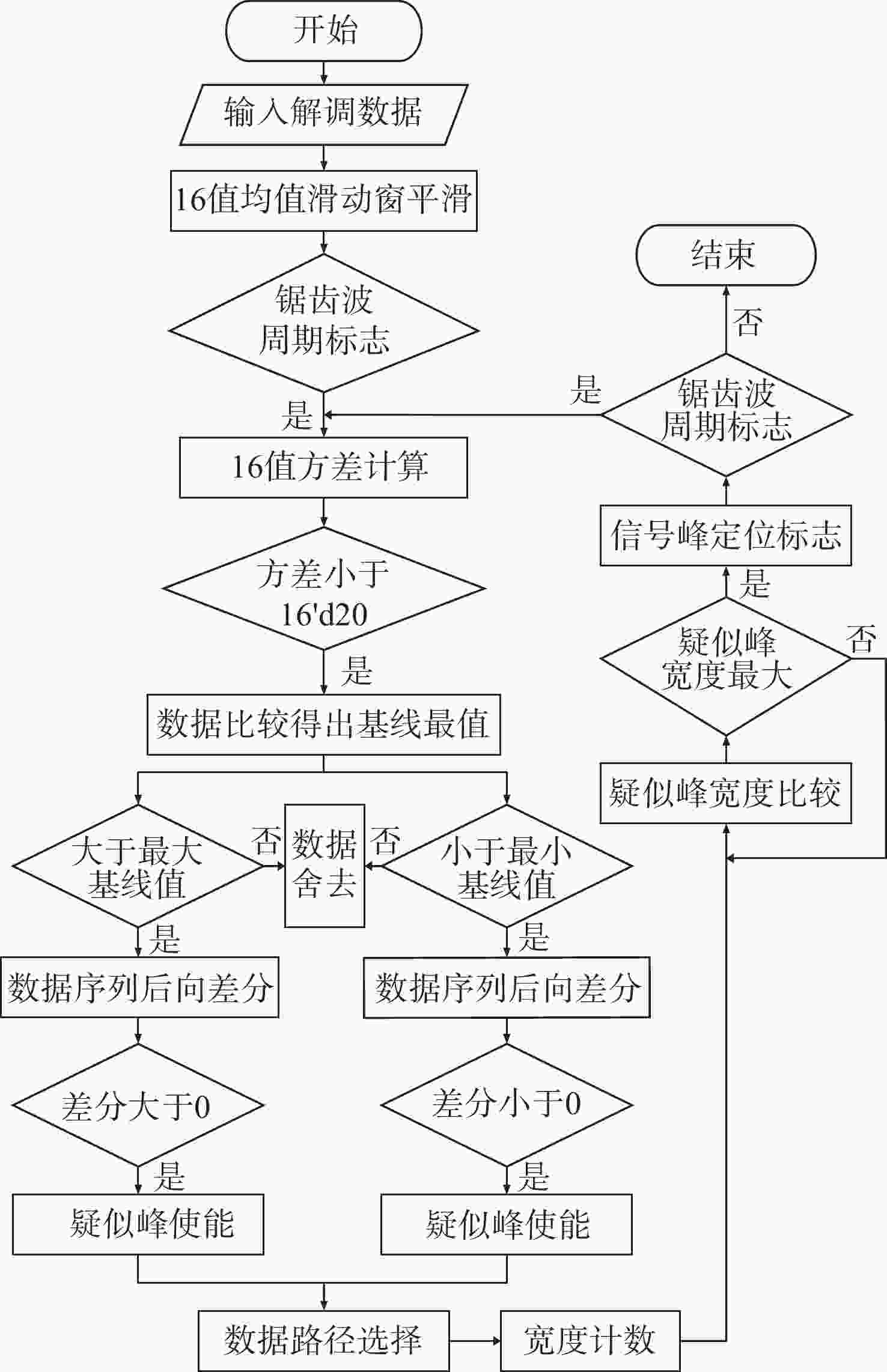
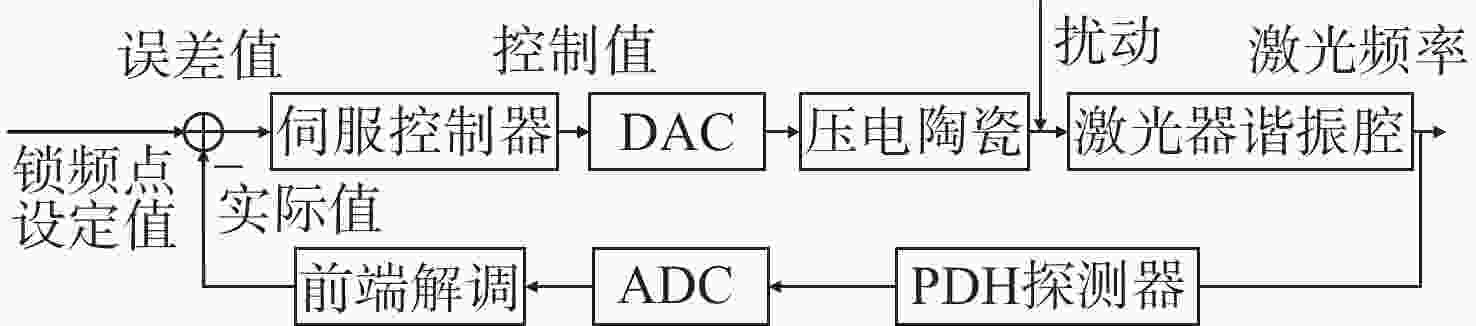
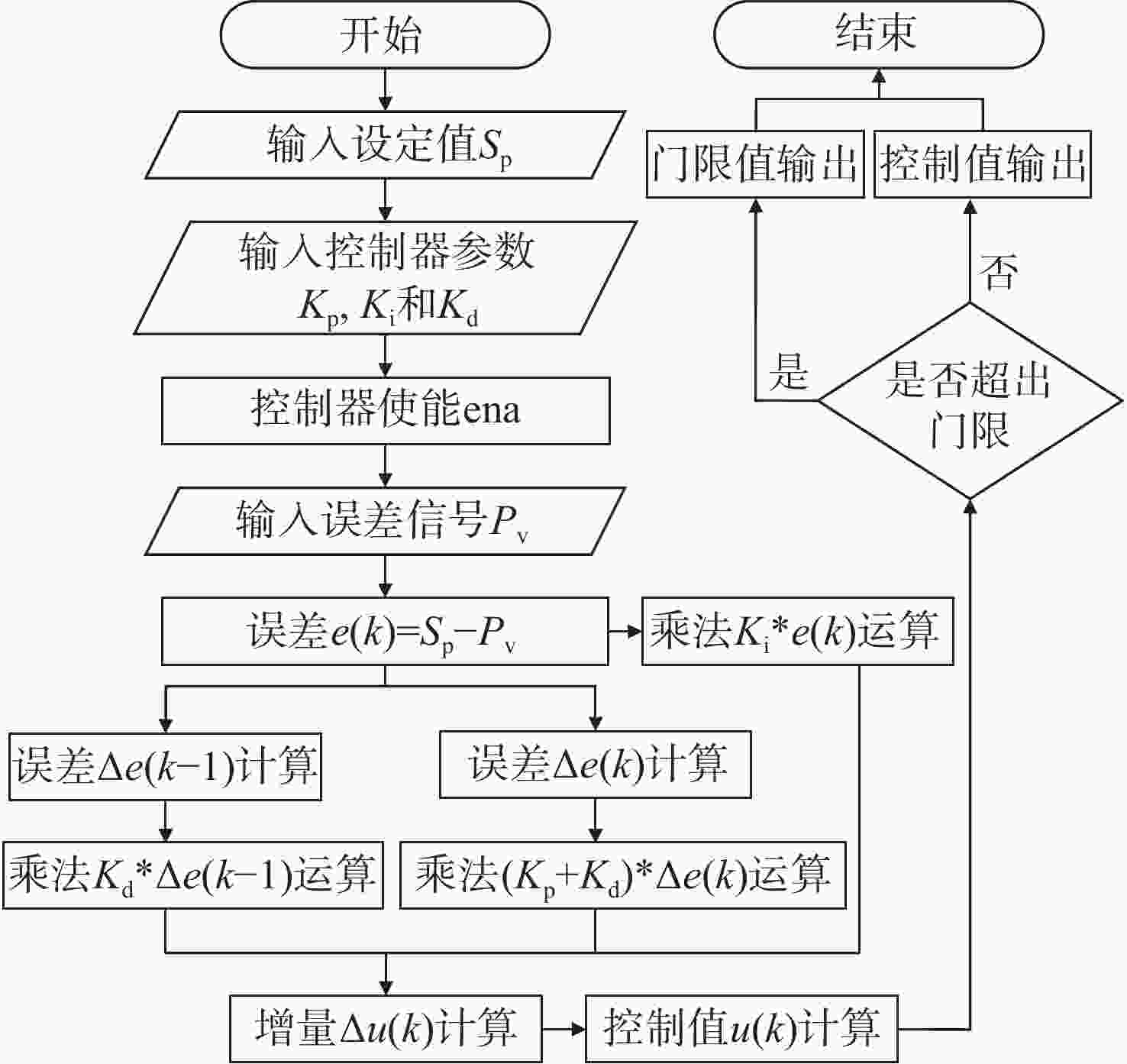
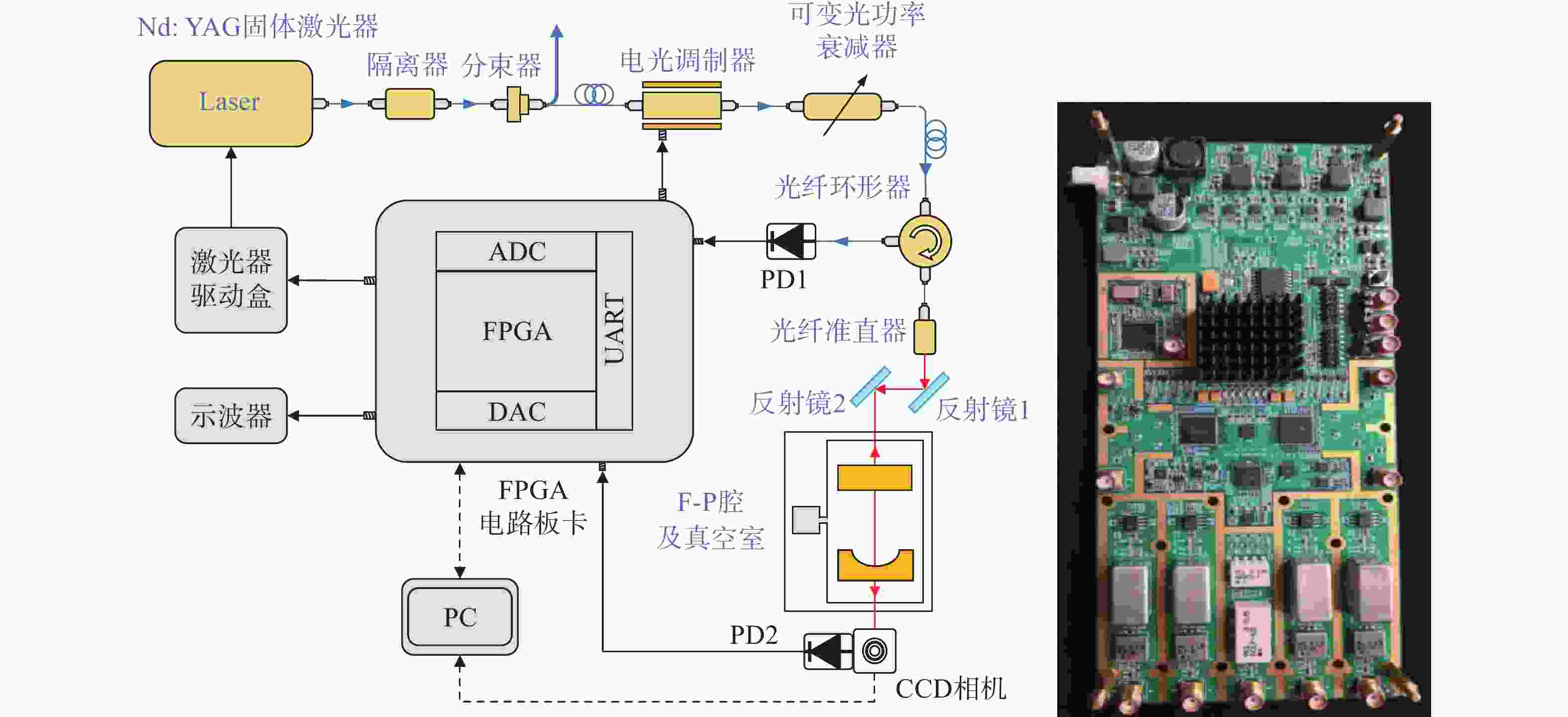
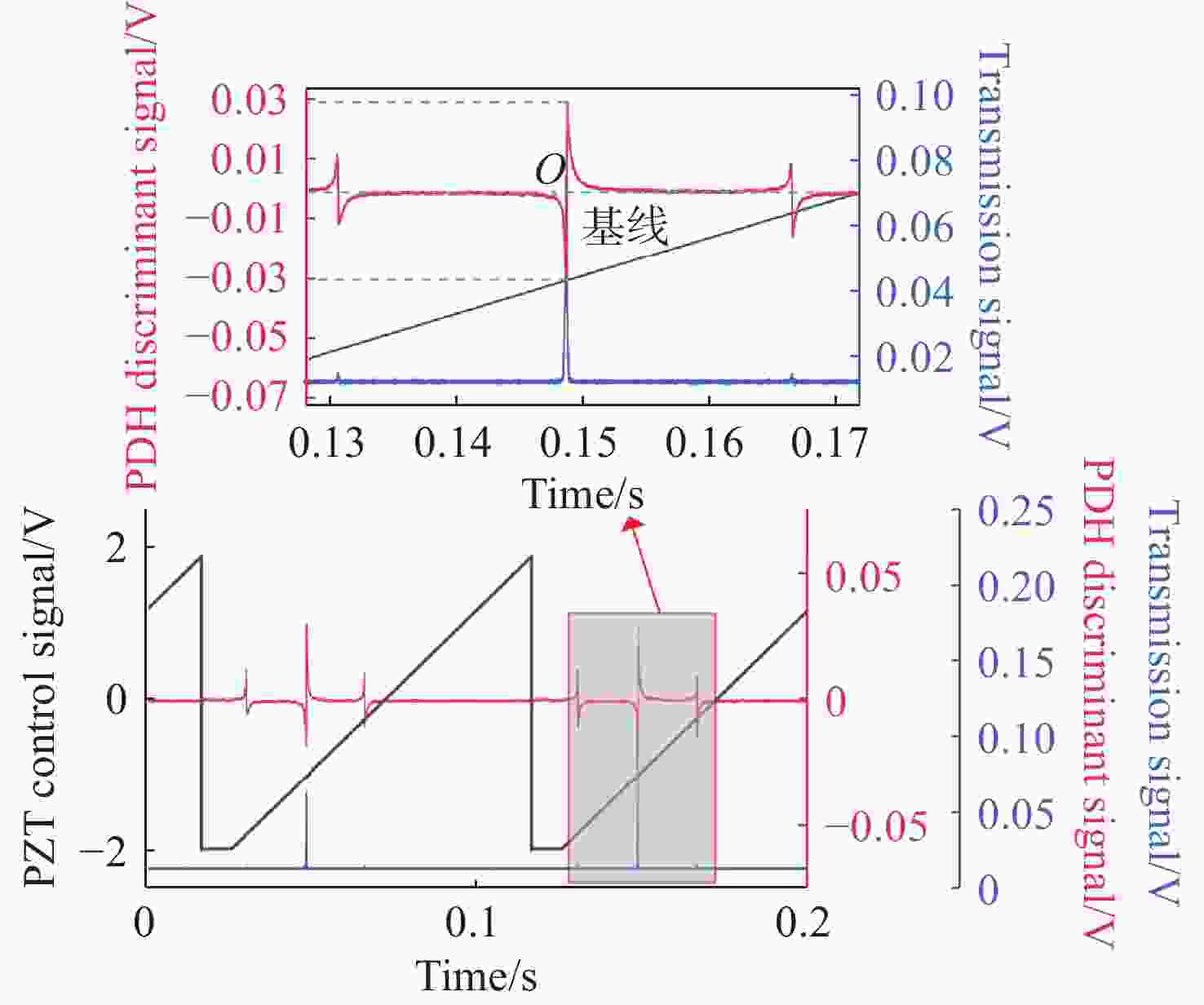
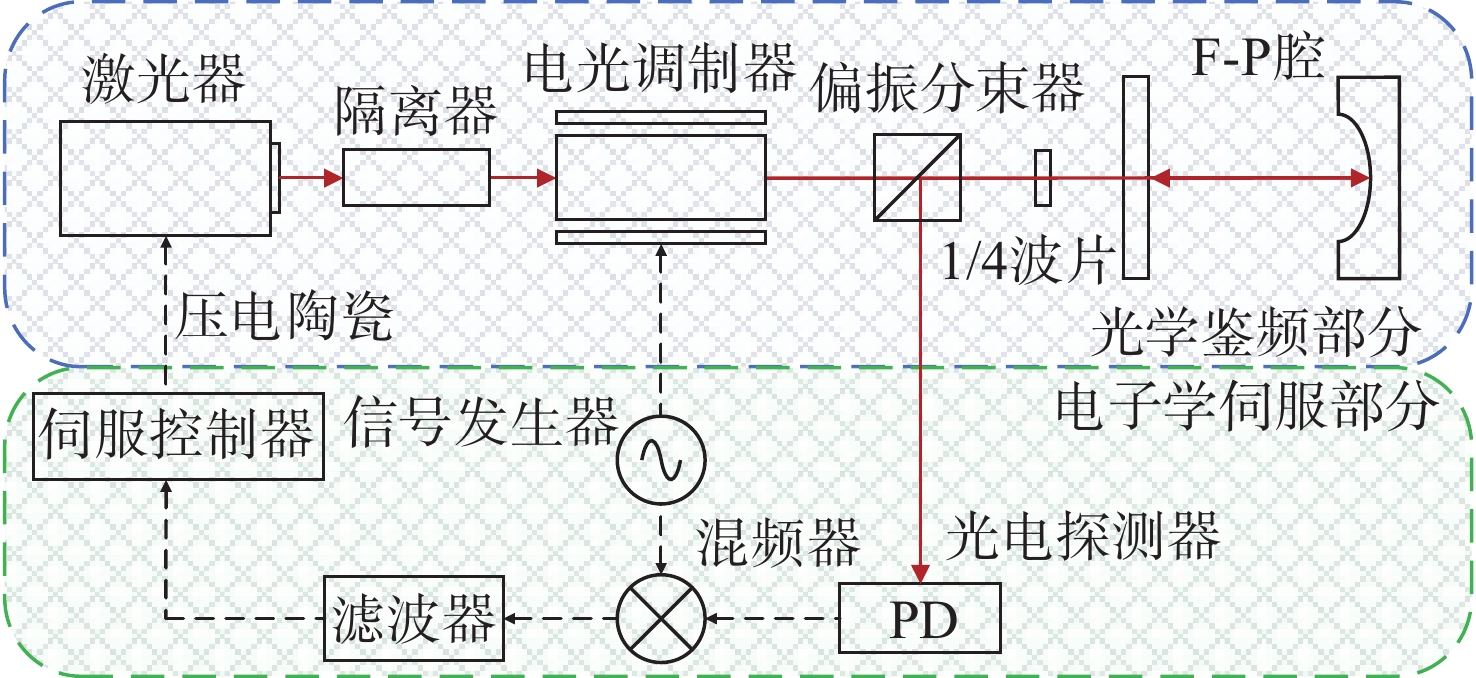
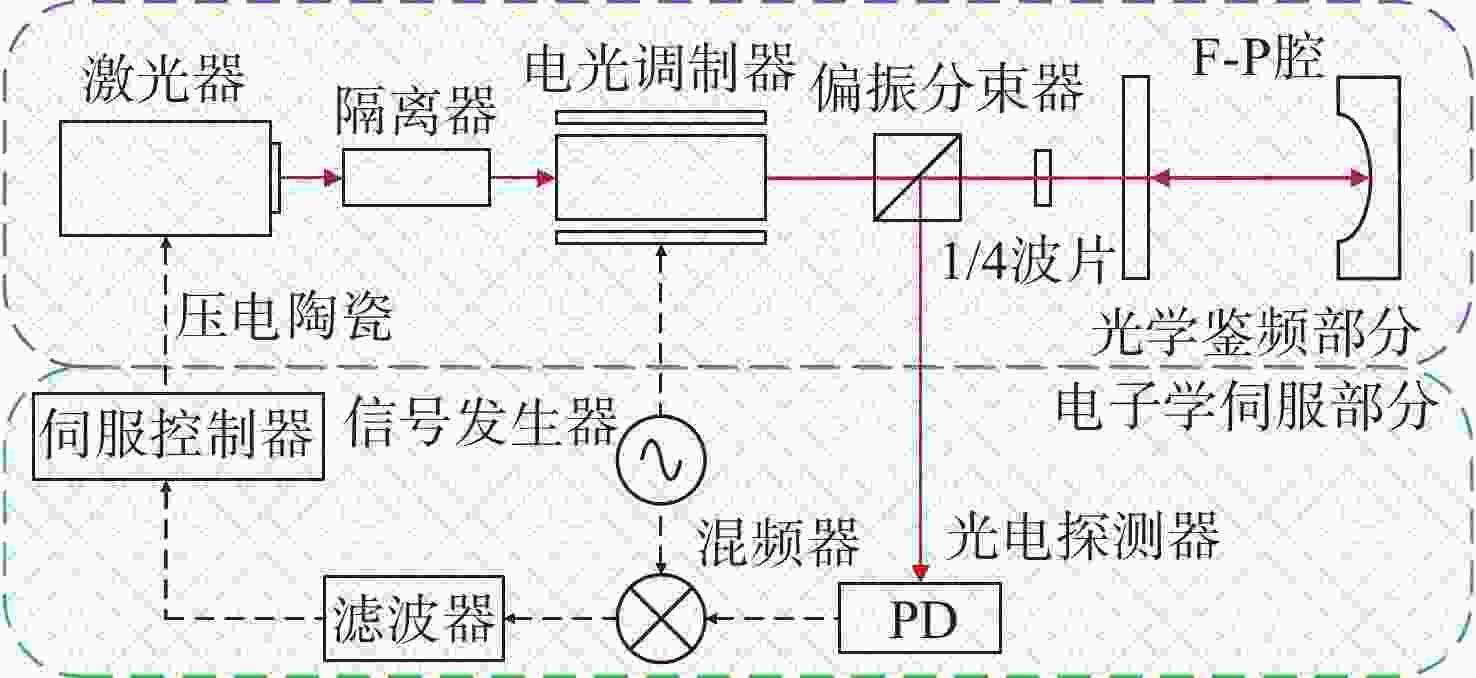
传统Pound-Drever-Hall（PDH）技术使用模拟器件来对激光器进行主动稳频，系统自身体积庞大，控制过程复杂，难以满足空间引力波探测等新型应用场景对稳频系统小型化和自动化的要求。本文在鉴频信号寻峰方面特别设计了一种基于后向差分的自动寻峰算法，可以有效减少稳频过程中的人为因素影响。该方法通过比较连续信号峰的时间宽度来完成信号主峰寻找以及控制状态切换，避免了常规阈值法的固有缺陷。且在此基础上设计搭建了一套基于现场可编程门阵列（FPGA）的数字稳频系统，该系统将稳频伺服反馈控制中的各分立部件全部数字化并集成到单块FPGA内，构建了以压电陶瓷为执行器的快速伺服反馈环路。稳频系统首先利用幅度解调方法在本地得出鉴频信号，再通过所设计的后向差分算法实现自动寻峰，最终在锁频点处开启伺服控制器，并利用增量式数字PID算法成功将商用Nd:YAG激光器频率锁定到精细度为
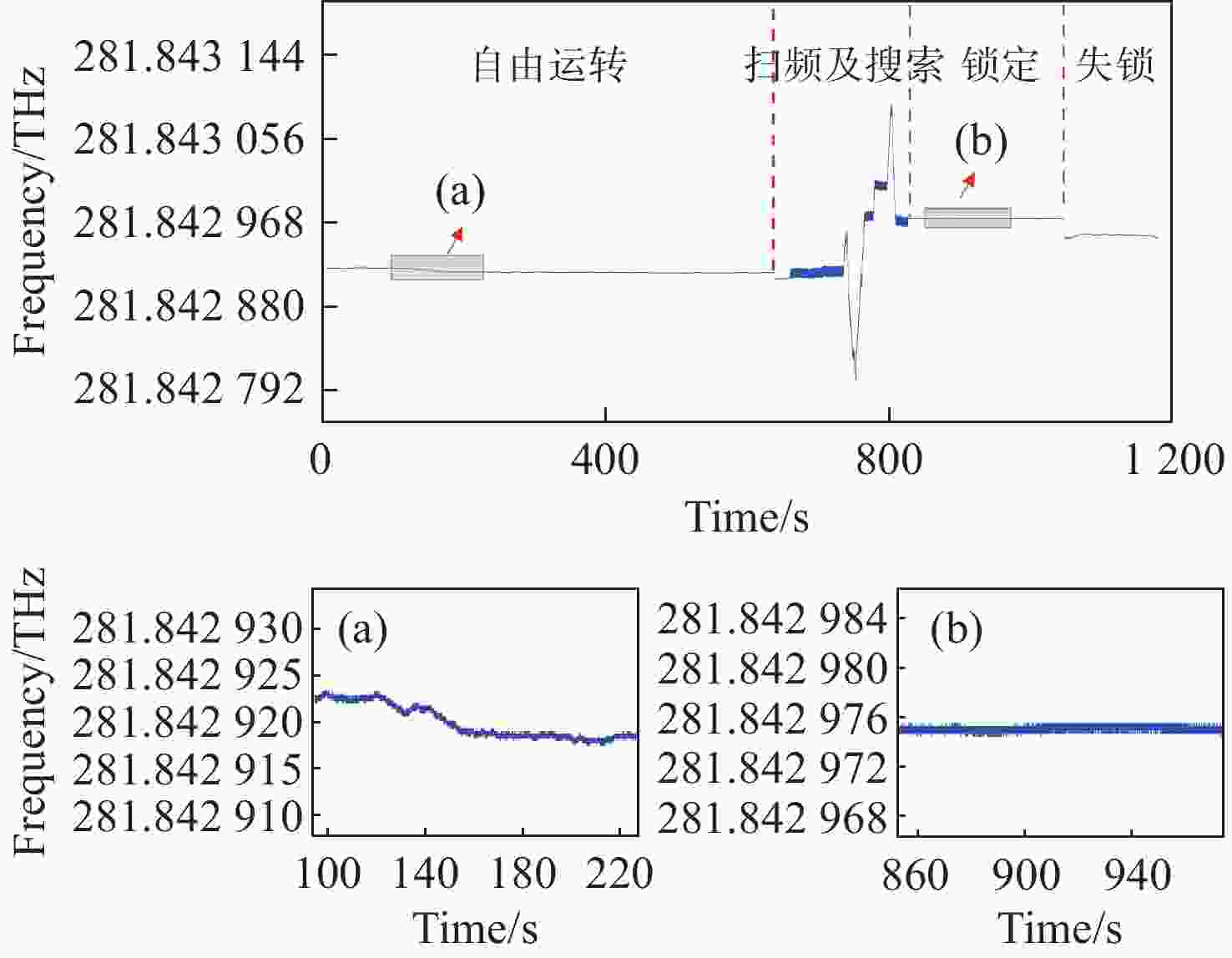
35000 的10 cm法布里-珀罗腔谐振峰频率上。功能测试实验中系统的锁频时长为半小时，波长计测量数据显示相对频率漂移小于2MHz。该结果验证了所设计的自动寻峰算法有效性，也表明FPGA是一种实现全数字化激光稳频控制的有效途径。-
关键词:
- 激光稳频 /
- Pound-Drever-Hall技术 /
- 自动寻峰 /
- FPGA
Abstract:The traditional Pound-Drever-Hall (PDH) technique utilizes analog devices to actively stabilize the frequency of lasers. However, this results in a bulky system and a rigid control process, making it difficult to meet the requirements of miniaturization and automation of the frequency stabilization system for new applications such as space gravitational wave detection. In this paper, an automatic peak-finding algorithm based on backward difference is specifically designed for frequency discrimination signal peak search, which effectively reduces human intervention in the frequency stabilization process. This method identifies the main signal peak and controls state switching by comparing the time width of consecutive signal peaks. Moreover, it avoids the inherent drawbacks of the conventional thresholding method. We have also designed and built a digital frequency stabilization system based on a field-programmable gate array (FPGA). This system digitizes and integrates the discrete components of the stabilization servo feedback control into a single FPGA, forming a fast servo feedback loop with a piezoelectric actuator. The digital frequency stabilization system first obtains the frequency discrimination signal locally through an amplitude demodulation, and then achieves automatic peak-finding through the designed backward difference algorithm. Finally, the servo controller is activated at the lock-in point, and an incremental digital PID algorithm is used to successfully lock the frequency of a commercial Nd:YAG laser to a resonance of a 10 cm Fabry-Pérot cavity with a finesse of
350000 . During functional testing, the system maintained frequency lock for half an hour, with a wavelength meter measurement showing a relative frequency drift of less than 2 MHz. This result validates the effectiveness of the designed automatic peak-finding algorithm and underscores the merits of FPGA as an effective approach for achieving comprehensive digital laser frequency stabilization control. -
图 1 PDH激光稳频技术原理图
Figure 1. Schematic of the PDH laser frequency stabilization technique
图 2 PDH数字稳频系统框图
Figure 2. Block diagram of the PDH digital frequency stabilization system
图 7 用MATLAB仿真的PDH鉴频信号
Figure 7. PDH discriminant signal simulated using MATLAB simulation
图 10 单环路的数字反馈控制框图
Figure 10. Block diagram of a single-loop digital feedback control system
图 12 数字稳频实验系统及FPGA硬件电路板
Figure 12. Digital frequency stabilization experimental system and FPGA hardware PCB
-
[1] 黄双林, 龚雪飞, 徐鹏, 等. 空间引力波探测——天文学的一个新窗口[J]. 中国科学: 物理学 力学 天文学,2017,47(1):010404.HUANG SH L, GONG X F, XU P, et al. Gravitational wave detection in space-a new window in astronomy[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2017, 47(1): 010404. (in Chinese). [2] LI R, WU Y L, RUI Y, et al. Absolute frequency measurement of 6Li D lines with khz-level uncertainty[J]. Physical Review Letters, 2020, 124(6): 063002. doi: 10.1103/PhysRevLett.124.063002 [3] LIU L, LÜ D SH, CHEN W B, et al. In-orbit operation of an atomic clock based on laser-cooled 87Rb atoms[J]. Nature Communications, 2018, 9(1): 2760. doi: 10.1038/s41467-018-05219-z [4] CORWIN K L, LU ZH T, HAND C F, et al. Frequency-stabilized diode laser with the Zeeman shift in an atomic vapor[J]. Applied Optics, 1998, 37(15): 3295-3298. doi: 10.1364/AO.37.003295 [5] 张沛, 王晨曦, 宋丽军, 等. 基于FPGA的半导体激光器稳频系统[J]. 量子光学学报,2024,30(1):95-104.ZHANG P, WANG CH X, SONG L J, et al. Frequency stabilization system of semiconductor laser based on FPGA[J]. Journal of Quantum Optics, 2024, 30(1): 95-104. (in Chinese). [6] 洪毅, 侯霞, 陈迪俊, 等. 基于Rb87调制转移光谱稳频技术研究[J]. 中国激光,2021,48(21):2101003.HONG Y, HOU X, CHEN D J, et al. Research on frequency stabilization technology of modulation transfer spectroscopy based on Rb87[J]. Chinese Journal of Lasers, 2021, 48(21): 2101003. (in Chinese). [7] BLACK E D. An introduction to Pound-Drever-Hall laser frequency stabilization[J]. American Journal of Physics, 2001, 69(1): 79-87. doi: 10.1119/1.1286663 [8] SHADDOCK D A, GRAY M B, MCCLELLAND D E. Frequency locking a laser to an optical cavity by use of spatial mode interference[J]. Optics Letters, 1999, 24(21): 1499-1501. doi: 10.1364/OL.24.001499 [9] MATEI D G, LEGERO T, HÄFNER S, et al. 1.5 μm lasers with sub-10 mHz linewidth[J]. Physical Review Letters, 2017, 118(26): 263202. [10] HERBERS S, HÄFNER S, DÖRSCHER S, et al. Transportable clock laser system with an instability of 1.6×10−16[J]. Optics Letters, 2022, 47(20): 5441-5444. doi: 10.1364/OL.470984 [11] JIAO D D, DENG X, GAO J, et al. Highly vibration-resistant sub-Hertz ultra-stable laser passing over 1700 km transport test[J]. Infrared Physics & Technology, 2023, 130: 104608. [12] GILLOT J, TETSING-TALLA S F, DENIS S, et al. Digital control of residual amplitude modulation at the 10−7 level for ultra-stable lasers[J]. Optics Express, 2022, 30(20): 35179-35188. doi: 10.1364/OE.465597 [13] ZEYEN M, AFFOLTER L, AHMED M A, et al. Pound-Drever-Hall locking scheme free from Trojan operating points[J]. Review of Scientific Instruments, 2023, 94(1): 013001. doi: 10.1063/5.0130508 [14] LUO Y X, LI H Y, YEH H C. Note: digital laser frequency auto-locking for inter-satellite laser ranging[J]. Review of Scientific Instruments, 2016, 87(5): 056105. doi: 10.1063/1.4950862 [15] 罗子人, 张敏, 靳刚, 等. 中国空间引力波探测“太极计划”及“太极1号”在轨测试[J]. 深空探测学报,2020,7(1):3-10.LUO Z R, ZHANG M, JIN G, et al. Introduction of Chinese space-borne gravitational wave detection program "Taiji" and "Taiji-1" satellite mission[J]. Journal of Deep Space Exploration, 2020, 7(1): 3-10. (in Chinese). [16] 吉经纬, 程鹤楠, 张镇, 等. 可搬运铷喷泉原子钟全自动激光稳频系统[J]. 光学学报,2020,40(22):2214002.JI J W, CHENG H N, ZHANG ZH, et al. Automatic laser frequency stabilization system for transportable 87Rb fountain clock[J]. Acta Optica Sinica, 2020, 40(22): 2214002. (in Chinese). [17] YAN CH ZH, SHI H S, YAO Y, et al. Automatic, long-term frequency-stabilized lasers with sub-hertz linewidth and 10−16 frequency instability[J]. Chinese Optics Letters, 2022, 20(7): 070201. doi: 10.3788/COL202220.070201 [18] GUO X Q, ZHANG L B, LIU J, et al. An automatic frequency stabilized laser with hertz-level linewidth[J]. Optics & Laser Technology, 2022, 145: 107498. [19] ZHANG F L, LIU K, LI Z Y, et al. Long-term digital frequency-stabilized laser source for large-scale passive laser gyroscopes[J]. Review of Scientific Instruments, 2020, 91(1): 013001. doi: 10.1063/1.5134928 [20] LEE S, LEE S B, PARK S E, et al. Compact modulation transfer spectroscopy module for highly stable laser frequency[J]. Optics and Lasers in Engineering, 2021, 146: 106698. doi: 10.1016/j.optlaseng.2021.106698 [21] LIU X, ZHAI Z H, LIU J L, et al. Parameter optimization of digital locking of an optical cavity[J]. Laser & Optoelectronics Progress, 2023, 60(15): 1536001. [22] LUDA M A, DRECHSLER M, SCHMIEGELOW C T, et al. Compact embedded device for lock-in measurements and experiment active control[J]. Review of Scientific Instruments, 2019, 90(2): 023106. doi: 10.1063/1.5080345 [23] YAN CH G, SUN J, LIU W Q. An efficient high SFDR PDDS using high-pass-shaped phase dithering[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2021, 29(11): 2003-2007. doi: 10.1109/TVLSI.2021.3114680 [24] HU J L, LIU SH, WU X, et al. Orthogonal demodulation pound-drever-hall technique for ultra-low detection limit pressure sensing[J]. Sensors, 2019, 19(14): 3223. doi: 10.3390/s19143223 [25] 严利平, 张哲伟, 谢建东, 等. 双调制深度大线性动态范围自适应PDH稳频方法[J]. 光学学报,2023,43(19):1907001.YAN L P, ZHANG ZH W, XIE J D, et al. Adaptive PDH frequency stabilization method with large linear dynamic range based on two modulation depths[J]. Acta Optica Sinica, 2023, 43(19): 1907001. (in Chinese). [26] BERSANETTI D, DIAZ J C, ALLOCCA A, et al. New algorithm for the Guided Lock technique for a high-Finesse optical cavity[J]. Astroparticle Physics, 2020, 117: 102405. doi: 10.1016/j.astropartphys.2019.102405 -
下载:
计量
- 文章访问数: 120
- HTML全文浏览量: 37
- PDF下载量: 17
- 被引次数: 0
