Structured light surface shape measurement method for highly reflective surfaces
-
摘要:
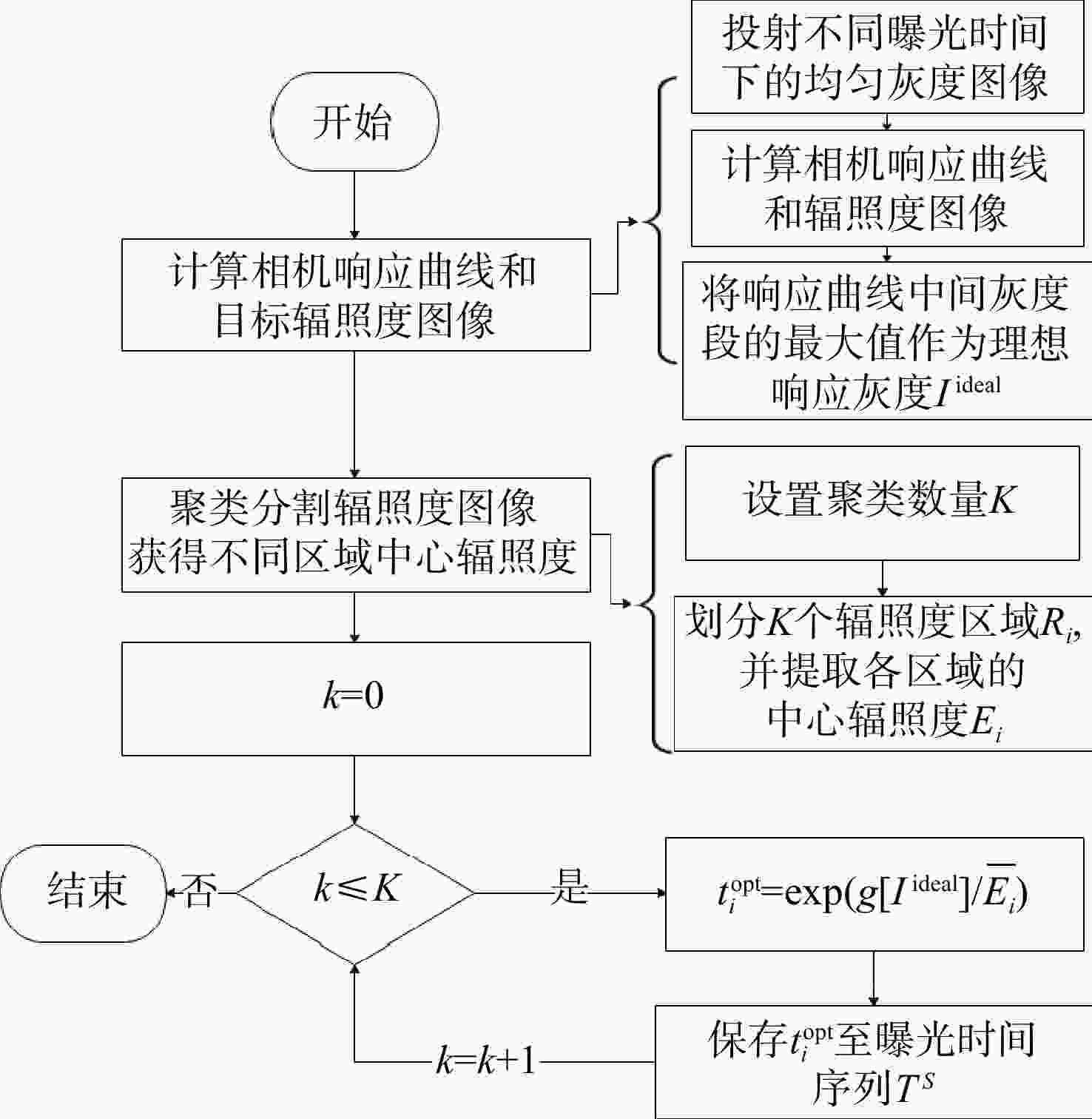
高反光表面复杂的反射性质会使面结构光测量时出现过度曝光和曝光不足的问题。为完整准确地重建被测表面，本文提出一种能根据被测表面反射强度预测曝光时间的多重曝光方法。首先，通过投射一系列不同曝光时间下的均匀灰度图像获得成像系统的相机响应曲线，同时计算得到能反映被测表面反射强度的辐照度图像。然后，通过模糊C均值聚类方法，自适应分割目标不同辐照度区域并获得各区域的中心辐照度，利用相机响应曲线预测不同反射区域的最优曝光时间。最后，结合多重曝光融合算法实现对高反光表面的三维重建。实验结果显示，所提方法能同时重建铝合金表面的强烈反光区域和过暗区域，重建误差小于0.5 mm，最大偏差降低了74.78%，标准偏差降低了48.96%。上述结果表明，所提方法能根据区域反射特性准确预测曝光时间，有效克服区域过曝和区域过暗带来的相位缺失和相位失真问题，完整准确地重建了高反光表面的不同反射区域。
Abstract:The complex reflective properties of highly reflective surfaces bring overexposure and underexposure problems to surface structured light technology. In order to reconstruct the measured surface completely and accurately, a multiple exposure method is proposed in this paper. The proposed method can predict the exposure time according to the reflective intensity of the measured surface. Firstly, the camera response curve of the imaging system is obtained by projecting a series of uniform gray images at different exposure times, and the irradiance image that can reflect the reflection intensity of the measured surface is calculated. Then, the fuzzy C-means clustering method is used to adaptively segment different irradiance regions of the target and obtain the central irradiance of each region. The optimal exposure time is predicted for different reflection regions based on the camera response curve. Finally, the 3D reconstruction of the highly reflective surface is realized by combining the multiple exposure fusion algorithm. The experimental results show that the proposed method can simultaneously reconstruct the strongly reflective area and the excessively dark area of the aluminum alloy surface, with a reconstruction error of less than 0.5 mm, the maximum deviation reduced by 74.78%, and the standard deviation reduced by 48.96%. The proposed method can correctly predict the exposure time according to regional reflection characteristics, effectively overcome the problems of phase loss and phase distortion caused by regional overexposure and regional darkness, and completely and accurately reconstruct different reflection regions of highly reflective surfaces.
-
Key words:
- highly reflective surface /
- structured light /
- multiple exposure /
- irradiance /
- clustering segmentation
-
图 3 不同曝光下捕获的条纹图像。（a）低曝光图像；（b）高曝光图像
Figure 3. Fringe images captured under different exposures. (a) Low exposure image; (b) high exposure image
图 4 铝合金金属板亮度分布。（a）相机捕获图像；（b）HDR合成图像
Figure 4. Luminance distribution on an aluminum alloy metal plate. (a) Camera captured image; (b) HDR composite image
图 7 基于辐照度分割的曝光时间预测算法
Figure 7. Exposure time prediction algorithm based on irradiance segmentation
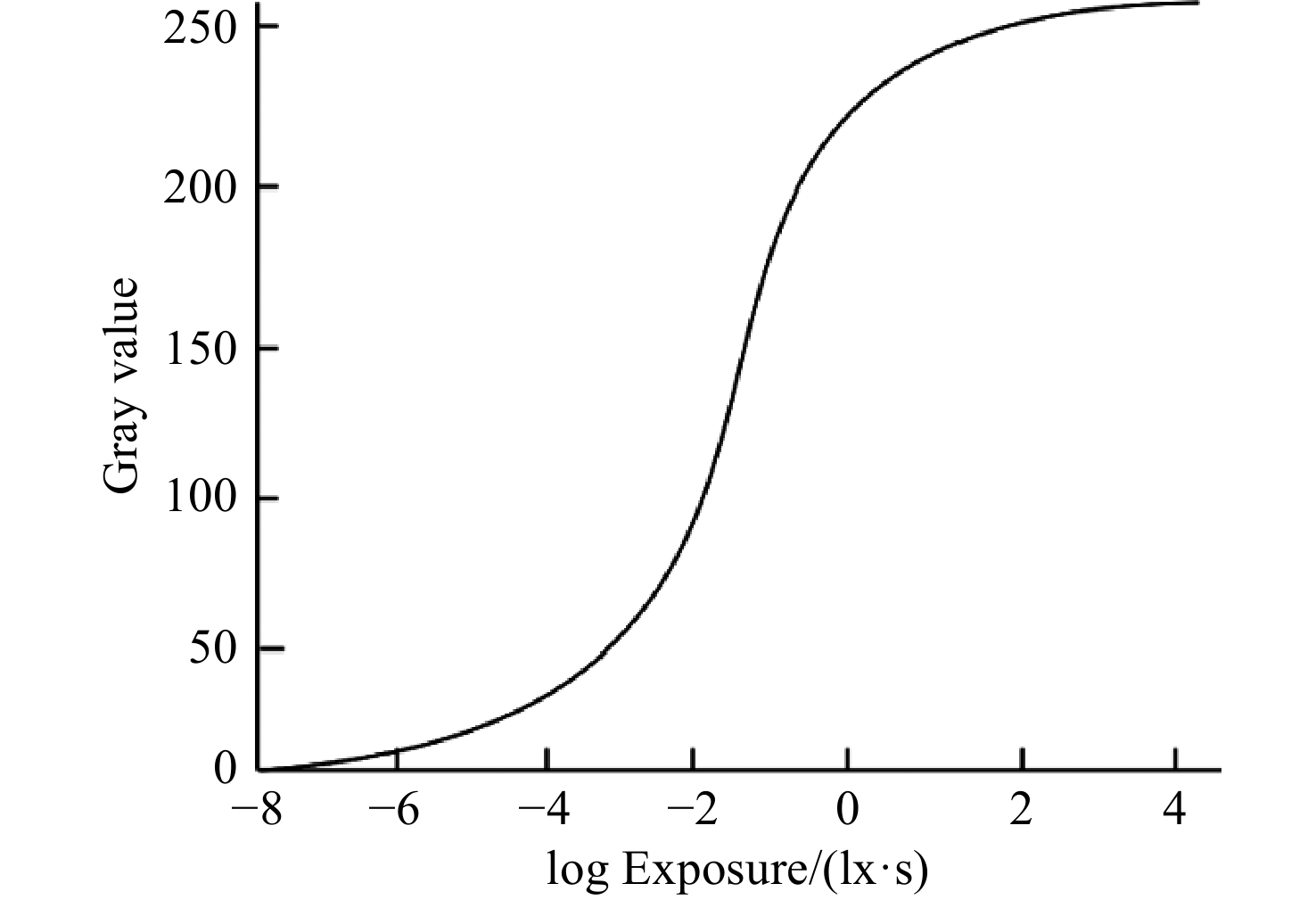
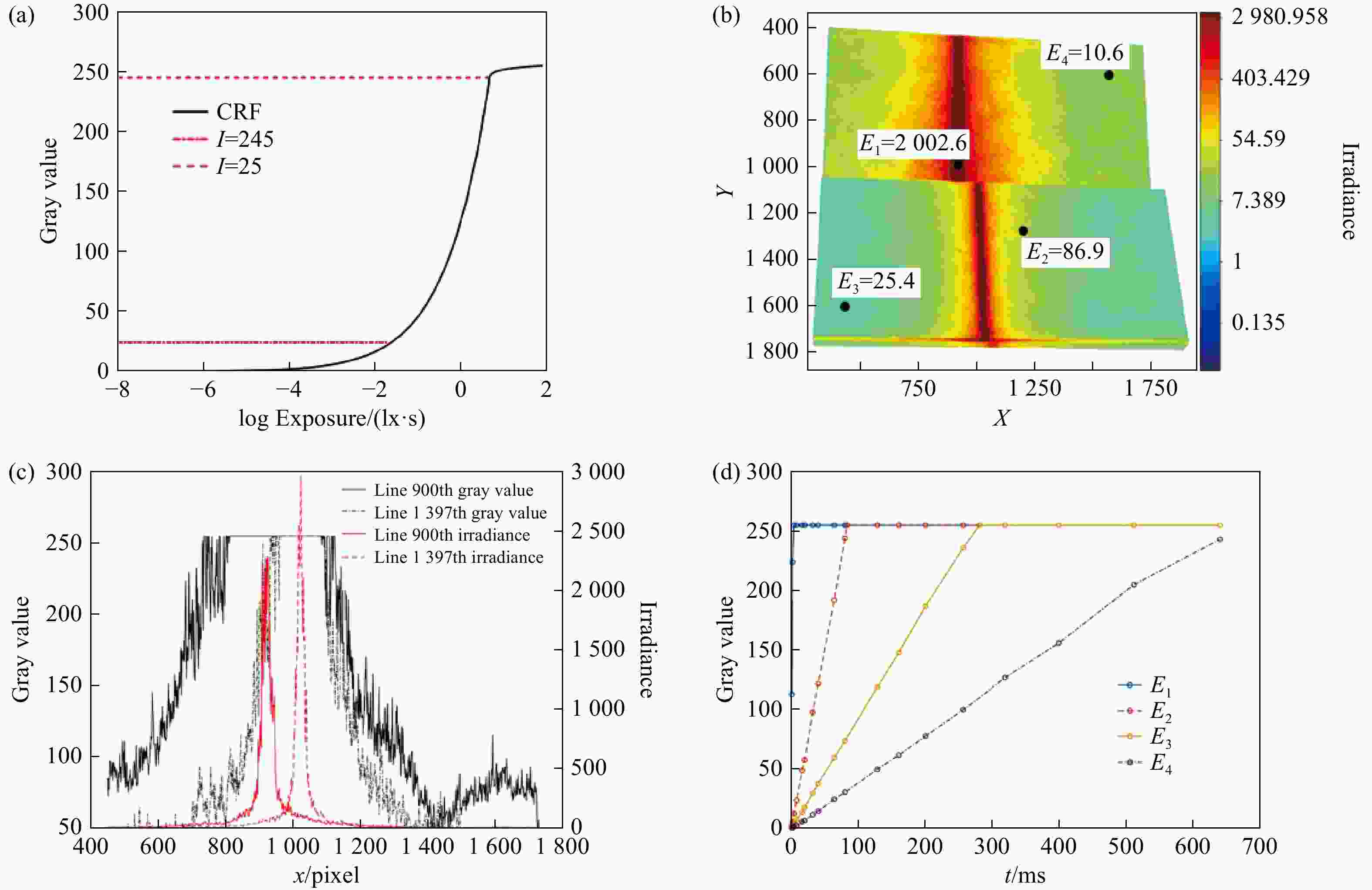
图 9 相机响应曲线和辐照度分布图像。(a)相机响应曲线；（b）辐照度图像；（c）灰度和辐照度在特定行的分布；（d）不同点的灰度变化曲线
Figure 9. Response curve of the camera and the irradiance distribution image. (a) Camera response curve; (b) irradiance image; (c) distribution curve of gray scale and irradiance in a specific line; (d) gray-scale variation curves of different points
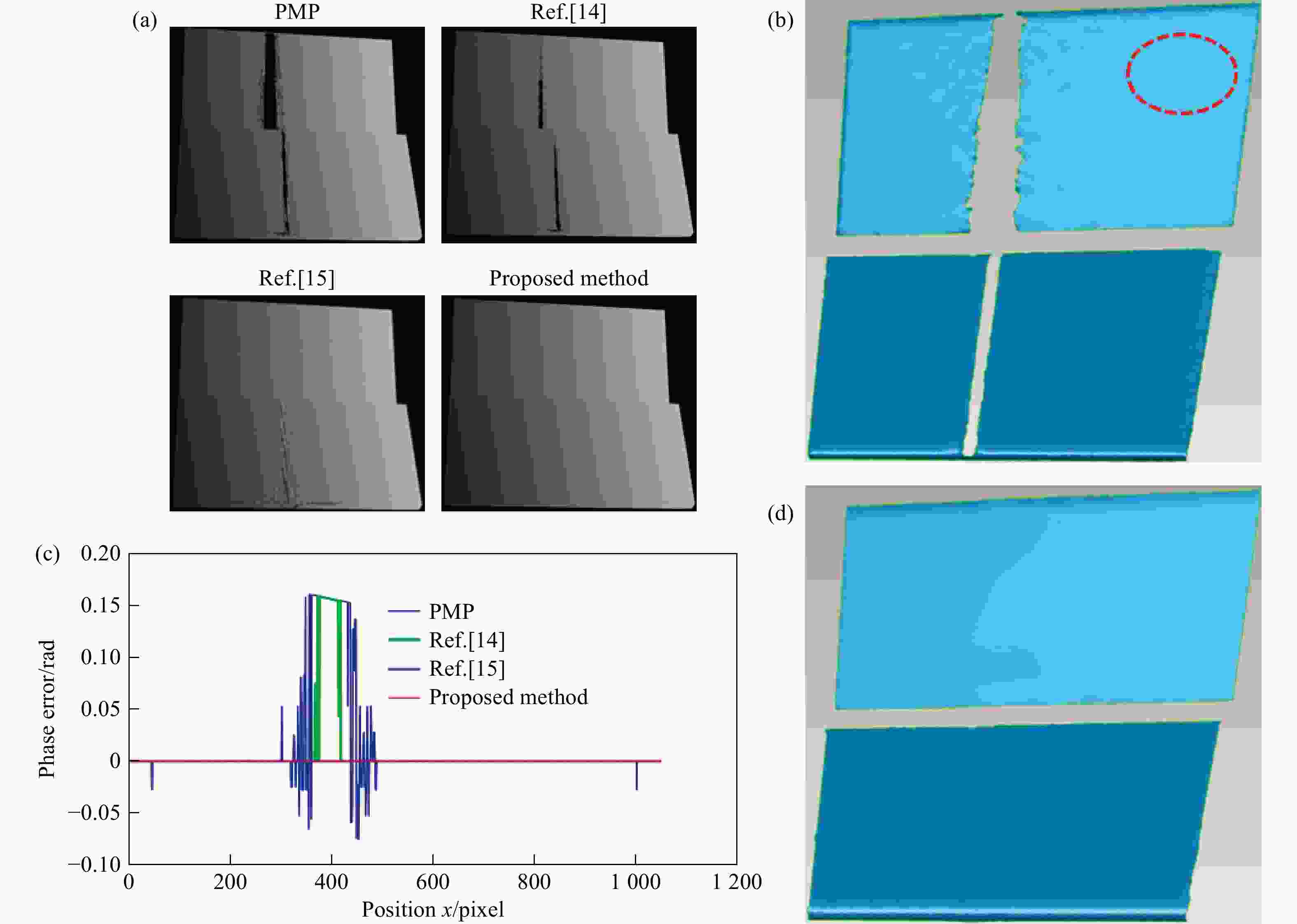
图 11 不同方法相位和点云处理结果。（a）不同方法获得的相位图片；（b）PMP方法的点云数据；（c）不同方法的第900行相位误差；（d）所提方法的点云数据重建结果
Figure 11. Phase and point cloud processing results of different methods. (a) Phase pictures obtained by different methods; (b) point cloud data of PMP method; (c) phase error of the 900th line obtained by different methods; (d) point cloud data of the proposed method
图 12 不同方法重建点云的偏差结果
Figure 12. Deviation results of point cloud reconstruction by different methods
图 13 （a）~（c）汽车刹车盘和（d）~（f）钣金件处理结果
Figure 13. Processing results of brake disc (a)−(c) and sheet metal workpiece (d)−(f)
表 1 本文FCM算法步骤
Table 1. The steps of the FCM algorithm in this paper
算法 1 高斯度量下的模糊C均值聚类算法 输入: 数据集 ${\mathbf{X}} = \{ {x_1},{x_2},\cdots,{x_L}\} $, 聚类数量 $K$, 最大迭代次数 $T = 50$,收敛阈值$\varepsilon = {10^{ - 6}}$, 正则化系数 $\gamma = 0.2$. 输出: 隶属度矩阵 $ {\boldsymbol{U}} = \{ {u_{ij}}\} $ #数据点${x_i}$对聚类中心${c_j}$的隶属度
聚类中心矩阵 $ {\boldsymbol{C}} = \{ {c_1},{c_2},...,{c_K}\} $.1：使用欧式距离度量下的模糊C均值聚类方法初始化隶属度矩阵${\boldsymbol{U}^{(o)}}$，聚类中心矩阵${\boldsymbol{C}^{(o)}}$, 和协方差矩阵$ {\boldsymbol{\Sigma }^{(o)}} $ 2：对于每一轮迭代，执行以下步骤直到收敛或达到最大迭代次数: a. 根据式(9)计算每个数据点到所有聚类中心的距离 b. 根据距离更新隶属度矩阵 ${\boldsymbol{U}}$：
${{\boldsymbol{u}}_{ij}} = - \Phi ({{\boldsymbol{x}}_j}|{{\boldsymbol{c}}_i},{{\boldsymbol{\Sigma}} _i})/2\gamma $
c. 更新聚类中心矩阵${\mathbf{C}}$：
$ {{\boldsymbol{c}}_i} = \displaystyle\sum\limits_{j = 1}^L {{{\boldsymbol{u}}_{ij}}{{\boldsymbol{x}}_j}} /\displaystyle\sum\limits_{j = 1}^L {{{\boldsymbol{u}}_{ij}}} $
d. 更新协方差矩阵$ {\boldsymbol{\Sigma }} $：
$ {{\boldsymbol{\Sigma}} _i} = \left[ {\displaystyle\sum\limits_{j = 1}^L {{{\boldsymbol{u}}_{ij}}{{({{\boldsymbol{x}}_j} - {{\boldsymbol{c}}_i})}^{\mathrm{T}}}} ({{\boldsymbol{x}}_j} - {{\boldsymbol{c}}_i})} \right]/\displaystyle\sum\limits_{j = 1}^L {{{\boldsymbol{u}}_{ij}}} $
e. 检测终止条件
计算聚类中心的变化量是否小于收敛阈值$\varepsilon $
如果变化量小于$\varepsilon $或得到最大迭代次数$T$，则停止迭代3：输出最终的聚类中心矩阵 ${\boldsymbol{C}}$ 和隶属度矩阵 ${\boldsymbol{U}}$ 
下载: 导出CSV
表 2 单目结构光系统的主要参数
Table 2. Main parameters of monocular structured light system
性能参数 参数值 相机分辨率 2448 （H）×2048（V）投影仪分辨率 1028 （H）×720（V）测量幅面大小/mm 400×300 标准测距/mm 630 曝光时间调节范围/ms 0~640 投射光源 蓝光LED
下载: 导出CSV
表 4 不同聚类数量获得的结果
Table 4. Results obtained by different clustering numbers
聚类
数量点云
数量最大偏差/
mm标准偏差/
mmRMS/
mm计算时间/
s3 532158 2.2817 0.0728 0.0839 53.08 4 574999 1.4990 0.0321 0.0532 85.47 5 604978 0.4789 0.0188 0.0332 130.81 6 656688 0.3612 0.0182 0.0303 201.33 7 680096 0.3010 0.0174 0.0293 294.54
下载: 导出CSV
-
[1] 刘泽隆, 李茂月, 卢新元, 等. 高动态范围条纹结构光在机检测技术及应用进展[J]. 中国光学(中英文),2024,17(1):1-18. doi: 10.37188/CO.2023-0068LIU Z L, LI M Y, LU X Y, et al. On-machine detection technology and application progress of high dynamic range fringe structured light[J]. Chinese Optics, 2024, 17(1): 1-18. (in Chinese). doi: 10.37188/CO.2023-0068 [2] 王中兴. 基于十六步相移技术的高精度三维重建系统[J]. 软件导刊,2021,20(5):108-113. doi: 10.11907/rjdk.201749WANG ZH X. Three-dimensional reconstruction system based on 16 step phase-shifting technology[J]. Software Guide, 2021, 20(5): 108-113. (in Chinese). doi: 10.11907/rjdk.201749 [3] 任明阳, 王立忠, 赵建博, 等. 复杂曲面零件面结构光扫描视点规划[J]. 中国光学(中英文),2023,16(1):113-126. doi: 10.37188/CO.2022-0026REN M Y, WANG L ZH, ZHAO J B, et al. Viewpoint planning of surface structured light scanning for complex surface parts[J]. Chinese Optics, 2023, 16(1): 113-126. (in Chinese). doi: 10.37188/CO.2022-0026 [4] 张宗华, 于瑾, 高楠, 等. 高反光表面三维形貌测量技术[J]. 红外与激光工程,2020,49(3):0303006. doi: 10.3788/IRLA202049.0303006ZHANG Z H, YU J, GAO N, et al. Three-dimensional shape measurement techniques of shiny surfaces[J]. Infrared and Laser Engineering, 2020, 49(3): 0303006. (in Chinese). doi: 10.3788/IRLA202049.0303006 [5] ZHAO H J, LI CH H, JIANG H ZH, et al. Simulation framework for fringe projection profilometry using ray tracing and light transport coefficient measurement[J]. Optics Express, 2022, 30(12): 22277-22291. doi: 10.1364/OE.461937 [6] JIANG H ZH, YAN Y J, LI X D, et al. Separation of interreflections based on parallel single-pixel imaging[J]. Optics Express, 2021, 29(16): 26150-26164. doi: 10.1364/OE.424777 [7] PALOUSEK D, OMASTA M, KOUTNY D, et al. Effect of matte coating on 3D optical measurement accuracy[J]. Optical Materials, 2015, 40: 1-9. doi: 10.1016/j.optmat.2014.11.020 [8] ZHU ZH M, ZHU W T, ZHOU F Q, et al. Three-dimensional measurement of fringe projection based on the camera response function of the polarization system[J]. Optical Engineering, 2021, 60(5): 055105. [9] LIU G H, LIU X Y, FENG Q Y. 3D shape measurement of objects with high dynamic range of surface reflectivity[J]. Applied Optics, 2011, 50(23): 4557-4565. doi: 10.1364/AO.50.004557 [10] RAO L, DA F P. High dynamic range 3D shape determination based on automatic exposure selection[J]. Journal of Visual Communication and Image Representation, 2018, 50: 217-226. doi: 10.1016/j.jvcir.2017.12.003 [11] LI SH X, DA F P, RAO L. Adaptive fringe projection technique for high-dynamic range three-dimensional shape measurement using binary search[J]. Optical Engineering, 2017, 56(9): 094111. [12] 冯建洋, 谌海云, 石础, 等. 基于结构光技术的高反射表面三维测量[J]. 激光与光电子学进展,2019,56(22):221202.FENG J Y, CHEN H Y, SHI CH, et al. Three-dimensional measurement of highly-reflective surface using structured light technique[J]. Laser & Optoelectronics Progress, 2019, 56(22): 221202. (in Chinese). [13] 冯维, 徐仕楠, 王恒辉, 等. 逐像素调制的高反光表面三维测量方法[J]. 中国光学,2022,15(3):488-497. doi: 10.37188/CO.2021-0220FENG W, XU SH N, WANG H H, et al. Three-dimensional measurement method of highly reflective surface based on per-pixel modulation[J]. Chinese Optics, 2022, 15(3): 488-497. (in Chinese). doi: 10.37188/CO.2021-0220 [14] 无锡图创智能科技有限公司. 不同反射率表面三维结构光测量的曝光值选择方法: 中国, 202111658669.6[P]. 2021-12-30.Wuxi Tuchuang Intelligent Technology Co. , Ltd. Exposure value selection method for measuring three-dimensional structured light on surfaces with different reflectivity: CN, 202111658669.6[P]. 2021-12-30. (in Chinese). [15] 李兆杰, 崔海华, 刘长毅, 等. 一种基于自动多次曝光面结构光的形貌测量方法[J]. 光学学报,2018,38(11):1112004. doi: 10.3788/AOS201838.1112004LI ZH J, CHUI H H, LIU CH Y, et al. A shape measurement method based on automatic multiple exposure surface structured light[J]. Acta Optica Sinica, 2018, 38(11): 1112004. (in Chinese). doi: 10.3788/AOS201838.1112004 [16] 李茂月, 刘泽隆, 赵伟翔, 等. 面结构光在机检测的叶片反光抑制技术[J]. 中国光学,2022,15(3):464-475. doi: 10.37188/CO.2021-0194LI M Y, LIU Z L, ZHAO W X, et al. Blade reflection suppression technology based on surface structured light on-machine detection[J]. Chinese Optics, 2022, 15(3): 464-475. (in Chinese). doi: 10.37188/CO.2021-0194 [17] LI Y X, JIANG H ZH, ZHAO H J, et al. Compressive parallel single-pixel imaging for efficient 3D shape measurement in the presence of strong interreflections by using a sampling Fourier strategy[J]. Optics Express, 2021, 29(16): 25032-25047. doi: 10.1364/OE.433118 [18] 詹瑜, 胡丹, 刘凯. 面向高反光区域的自适应结构光[J]. 光学学报,2022,42(16):1612001. doi: 10.3788/AOS202242.1612001ZHAN Y, HU D, LIU K. Adaptive structured light for high-reflective areas[J]. Acta Optica Sinica, 2022, 42(16): 1612001. (in Chinese). doi: 10.3788/AOS202242.1612001 [19] HUNTLEY J M, SALDNER H O. Shape measurement by temporal phase unwrapping: comparison of unwrapping algorithms[J]. Measurement Science and Technology, 1997, 8(9): 986-992. doi: 10.1088/0957-0233/8/9/005 [20] BATTIATO S, CASTORINA A, MANCUSO M. High dynamic range imaging for digital still camera: an overview[J]. Journal of Electronic Imaging, 2003, 12(3): 459-469. doi: 10.1117/1.1580829 [21] FENG SH J, ZHANG Y ZH, CHEN Q, et al. General solution for high dynamic range three-dimensional shape measurement using the fringe projection technique[J]. Optics and Lasers in Engineering, 2014, 59: 56-71. doi: 10.1016/j.optlaseng.2014.03.003 [22] JIA X H, LEI T, DU X G, et al. Robust self-sparse fuzzy clustering for image segmentation[J]. IEEE Access, 2020, 8: 146182-146195. doi: 10.1109/ACCESS.2020.3015270 -
下载:
计量
- 文章访问数: 151
- HTML全文浏览量: 169
- PDF下载量: 24
- 被引次数: 0
