改进AO优化算法的折反射全景镜头畸变参数估计

张越; 张宁; 徐熙平

doi:10.37188/CO.2024-0118

改进AO优化算法的折反射全景镜头畸变参数估计

doi: 10.37188/CO.2024-0118

长春理工大学光电工程学院, 吉林长春 130022

基金项目: 吉林省科技厅重点研发项目（产业关键核心技术攻关项目）（No. 20210201029GX）

详细信息

作者简介:
张越（1997—），男，吉林通化人，博士研究生，2019年于长春大学获得学士学位，2019年进入长春理工大学进行硕博连读，主要从事数字图像处理、群智能优化、视觉惯性导航方面的研究。E-mail：zycheney115@163.com

张宁（1979—），女，山东巨野人，工学博士，教授，博士生导师，2005年于中国矿业大学获得硕士学位，2013年于长春理工大学获得博士学位，主要从事光电检测与质量控制、图像目标模拟及识别方面的研究。E-mail：zhangning@cust.edu.cn

徐熙平（1969—），男，吉林桦甸人，工学博士，教授，博士生导师，分别于1993年、1999年在长春光学精密机械学院获得学士、硕士学位；2004年在长春理工大学获得博士学位，主要从事光电检测与质量控制、图像目标模拟及识别方面的研究。E-mail：xxp@cust.edu.cn

中图分类号: TP18;TP751
计量
- 文章访问数: 118
- HTML全文浏览量: 58
- PDF下载量: 11
- 被引次数: 0
出版历程
- 收稿日期: 2024-06-27
- 修回日期: 2024-07-23
- 录用日期: 2024-09-04
- 网络出版日期: 2024-09-25

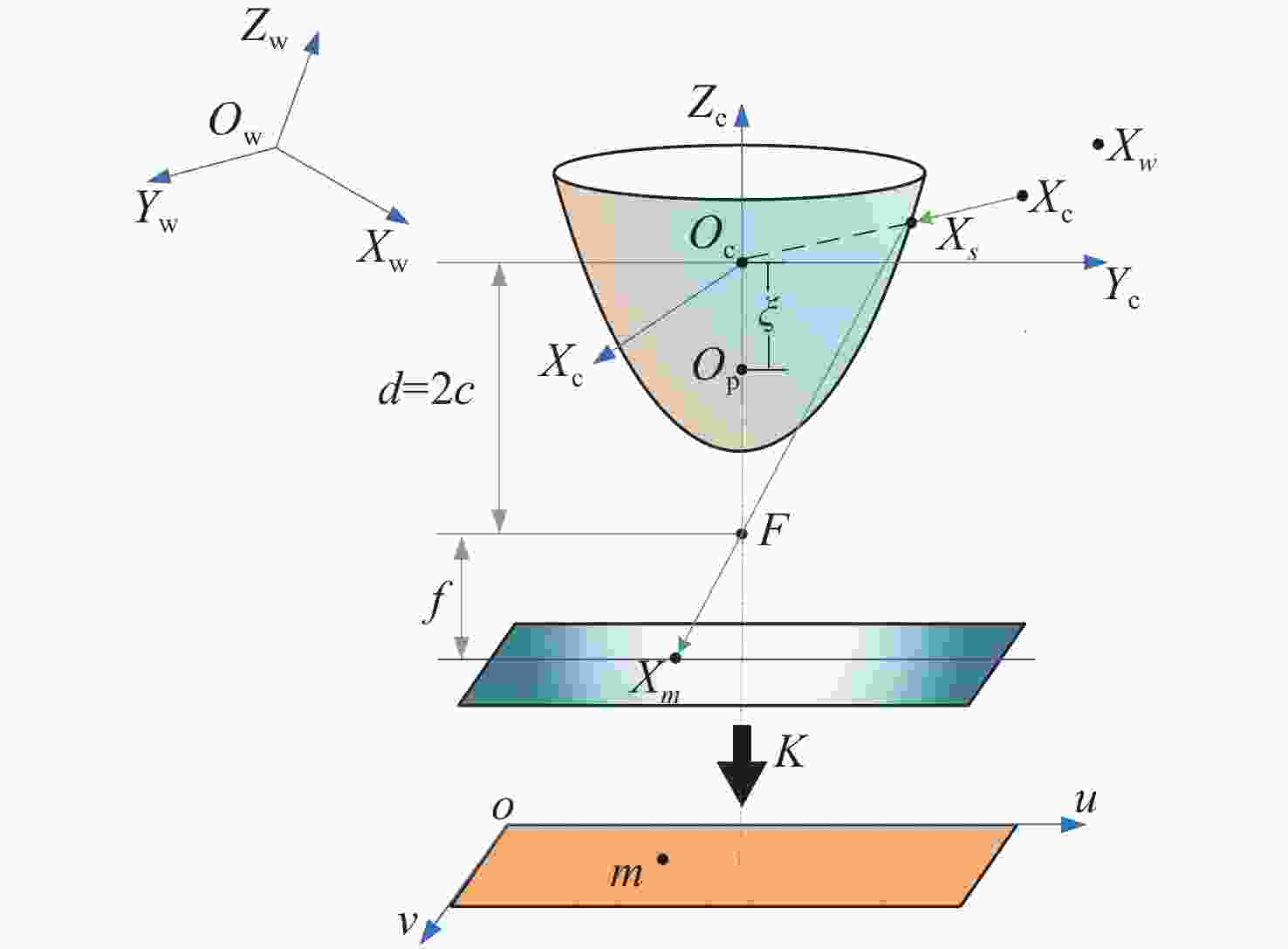
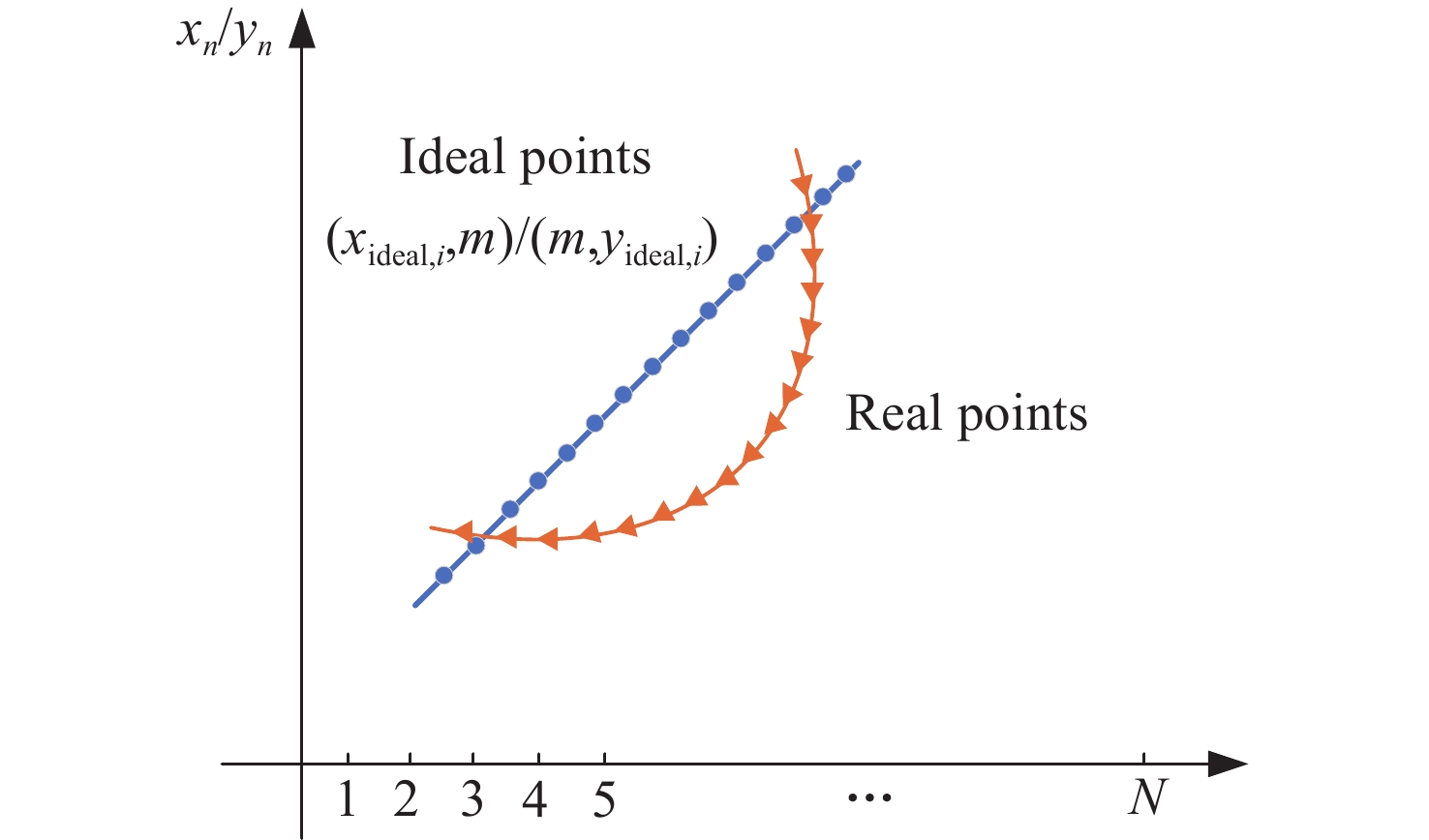
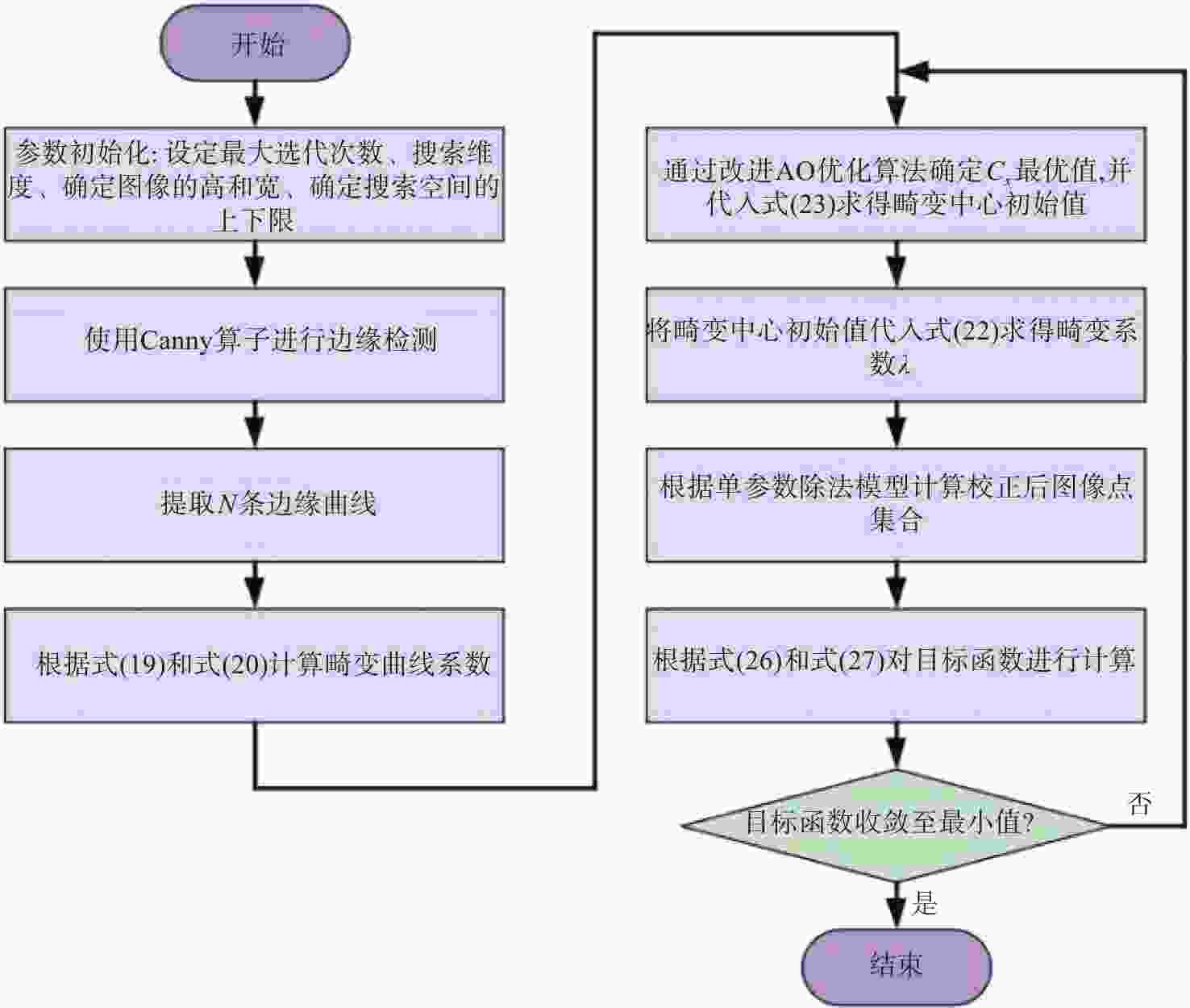
Improved AO Optimization Algorithm for Distortion Parameter Estimation of Catadioptric omnidirectional Lens

School of Optoelectronic Engineering, Changchun University of Science and Technology, Ji Lin Chang Chun 130022, China

Funds: Supported by Jilin Provincial Science and Technology Department Key R&D Projects (Industrial Key Core Technology Research Projects) (No. 20210201029GX)

More Information

Corresponding author: zhangning@cust.edu.cn; xxp@cust.edu.cn

摘要

摘要:
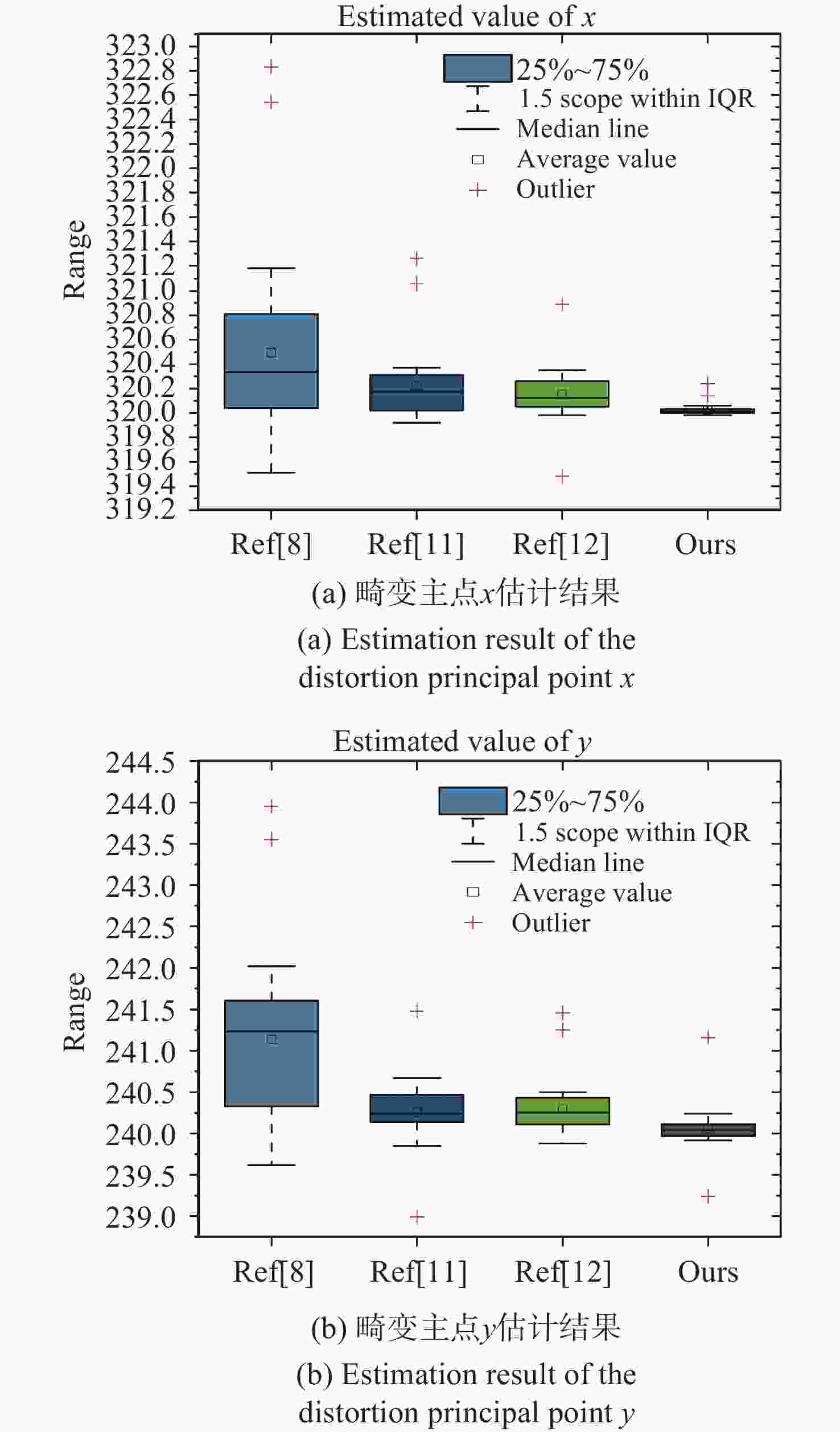
目的：针对现有镜头畸变参数估计方法存在精度低、易陷入局部最优解的问题，提出了一种基于改进天鹰优化算法的折反射全景相机镜头畸变参数方法。方法：首先通过融合混沌映射、自适应调节策略和通讯交流策略，增强了天鹰优化算法的寻优能力，解决了其收敛速度慢且容易陷入局部最优解的问题。其次，通过空间中直线对应的畸变边缘和单参数除法模型推导并确定畸变参数分布范围，然后构建包含畸变参数的优化目标函数。最后采用改进的天鹰优化算法对优化目标函数寻优求得最佳畸变参数。结果：经过对标准图库图像和全景图像的校正结果分析，本文提出的方法估计的主点误差在0.5 pixel以内，径向畸变系数误差在2.5%以内，能够有效地估计镜头畸变参数并实现全景图像畸变校正。结论：提高了视觉导航系统在环境感知任务下的图像质量，在工程应用中具有潜在价值。
- 折反射全景相机 /
- 天鹰优化算法 /
- 混沌映射 /
- 直线特征 /
- 畸变校正
Abstract:
Objetive
Aiming at the problems of low accuracy and easy to fall into local optimal solutions of the existing lens distortion parameter estimation methods, a catadioptric omnidirectional camera lens distortion parameter method based on the improved Aquila optimization (AO) algorithm is proposed.

Method
Firstly, the optimization ability of the Aquila optimization algorithm is enhanced by integrating chaotic mapping, adaptive adjustment strategy and population optimization strategy, which solves the problems of slow convergence speed and easy to fall into local optimal solutions. Secondly, the distribution range of distortion parameters is derived and determined by the corresponding distortion edges of straight lines in the space and the one parameter divisive model, and then the optimization objective function containing the distortion parameters is constructed. Finally, the improved Aquila optimization algorithm is used to find the best distortion parameters for the optimization objective function.
Result
After analyzing the correction results of standard gallery images and omnidirectional images, the method proposed in this paper estimates the main point error within 0.5 pixel and the radial aberration coefficient error within 2.5%, which is able to effectively estimate the lens aberration parameters and realize the omnidirectional image aberration correction.
Conclusion
It improves the image quality of the visual navigation system under the task of environment perception and is valuable in engineering applications.
- catadioptric omnidirectional camera /
- Aquila optimization algorithm /
- chaos map /
- linear features /
- distortion correction

HTML全文

图 1 折反射全景相机成像示意图

Figure 1. Catadioptric omnidirectional camera imaging schematic

下载: 全尺寸图片幻灯片

图 2 统一球面投影模型示意图

Figure 2. Unified Spherical Projection Model

下载: 全尺寸图片幻灯片

图 3 像点分布曲线

Figure 3. distribution curve of image point

下载: 全尺寸图片幻灯片

图 4 畸变参数求解流程图

Figure 4. Flowchart for solving distortion parameters

下载: 全尺寸图片幻灯片

图 5 基准函数图像和对比算法收敛曲线

Figure 5. Benchmark function image and comparison of algorithm convergence curves

下载: 全尺寸图片幻灯片

图 7 合成图像和其校正图像

Figure 7. Synthetic images and their corrected images

下载: 全尺寸图片幻灯片

图 6 畸变主点估计结果箱线图

Figure 6. Boxplot of the results of the distortion principal point estimation.

下载: 全尺寸图片幻灯片

图 8 噪声等级变化时的误差等级

Figure 8. Error level for sound level change

下载: 全尺寸图片幻灯片

图 9 两种折反射全景相机

Figure 9. Two types of catadioptric omnidirectional camera

下载: 全尺寸图片幻灯片

图 10 全景图像及其校正图像

Figure 10. Omnidirectional images and corrected images

下载: 全尺寸图片幻灯片

表 1 参数设定

Table 1. Parameter settings

算法	参数设置
GWO^[26]	a was linearly decreased from 2 to 0, rate=3
WOA^[27]	α decreased from 2 to 0, b=1
HHO^[28]	t=0
ALO^[29]	I ratio=10^ω, ω=[2,6]
AO^[18]	S=1.5, r₁ take a fixed index between 1 and 20, G₂ decreased from 2 to 0

下载: 导出CSV

表 2 基准测试函数

Table 2. Benchmark function

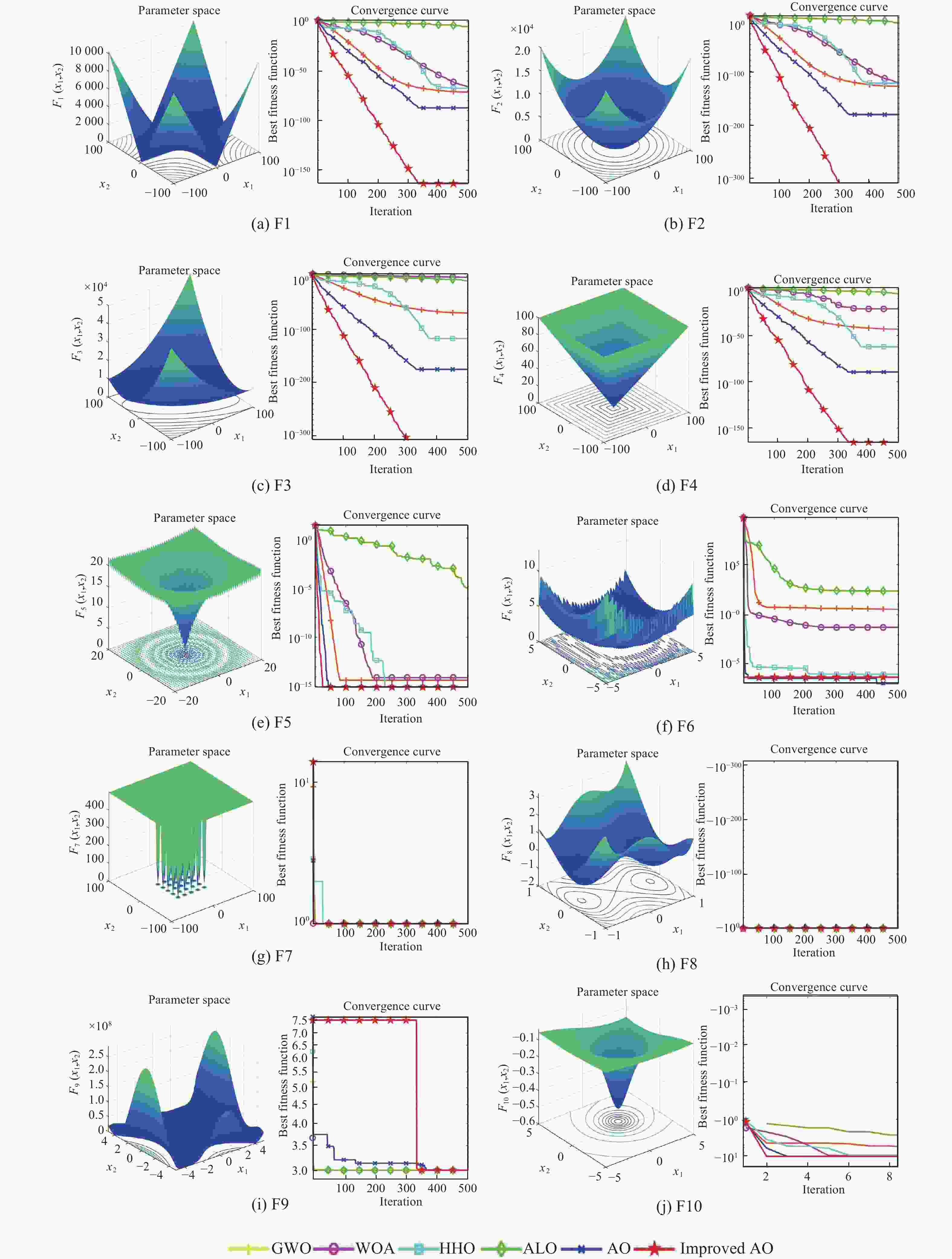
函数序号	函数名称	维度	范围	最优值
F1	Sphere	30	[−100,100]	0
F2	Schwefel 2.22	30	[−10,10]	0
F3	Schwefel 1.2	30	[−100,100]	0
F4	Schwefel 2.21	30	[−100,100]	0
F5	Ackley	10	[−32,32]	0
F6	Generalized Penalized	30	[−50,50]	0
F7	Shekel's Foxholes	2	[−65.536,65.536]	1
F8	Six-Hump Camel-Back	4	[−5,5]	−1.0316
F9	Goldstein-Price	2	[−2,2]	3
F10	Shekel's Family	4	[0,1]	−10.4028

下载: 导出CSV

表 3 不同算法对基准测试函数寻优结果

Table 3. Optimization results of different algorithms for benchmark functions

函数		GWO	WOA	HHO	ALO	AO	Improved AO
F1	AVG	1.40×10⁻¹²⁷	7.91×10⁻¹²¹	4.76×10⁻¹¹⁷	2.67×10⁻¹⁰	3.71×10⁻¹⁷⁴	3.95×10⁻³²³
	STD	6.08×10⁻¹²⁷	2.45×10⁻¹²⁰	2.21×10⁻¹¹⁶	1.24×10⁻¹⁰	0.00	0.00
	Best	5.36×10⁻¹³⁵	1.12×10⁻¹²⁷	2.56×10⁻¹²⁹	9.62×10⁻¹¹	9.38×10⁻¹⁸²	0.00
F2	AVG	2.31×10⁻⁷¹	4.86×10⁻⁶⁶	6.93×10⁻⁶⁵	1.94×10⁻⁵	7.45×10⁻⁸⁸	5.37×10⁻¹⁶⁶
	STD	6.58×10⁻⁷¹	2.58×10⁻⁶⁵	2.29×10⁻⁶⁴	4.16×10⁻⁵	2.29×10⁻⁸⁷	0.00
	Best	3.10×10⁻⁷⁴	6.20×10⁻⁷³	1.69×10⁻⁷⁵	5.99×10⁻⁶	4.82×10⁻⁹⁴	1.17×10⁻¹⁷⁴
F3	AVG	2.76×10⁻⁶⁷	1.17×10⁻²	2.11×10⁻¹⁰⁶	2.53×10⁻⁹	1.13×10⁻¹⁷⁰	0.00
	STD	6.84×10⁻⁶⁷	2.78×10⁻²	1.16×10⁻¹⁰⁵	1.27×10⁻⁹	0.00	0.00
	Best	1.91×10⁻⁷⁴	3.49×10⁻⁶	1.89×10⁻¹²³	3.96×10⁻¹⁰	5.12×10⁻¹⁸¹	0.00
F4	AVG	6.10×10⁻⁴⁴	2.27×10⁻⁹	2.90×10⁻⁵⁸	1.54×10⁻⁵	6.46×10⁻⁸⁸	8.25×10⁻¹⁶⁶
	STD	1.49×10⁻⁴³	7.34×10⁻⁹	1.11×10⁻⁵⁷	2.98×10⁻⁶	2.33×10⁻⁸⁷	0.00
	Best	1.01×10⁻⁴⁷	3.01×10⁻²⁵	1.68×10⁻⁶⁴	1.06×10⁻⁵	7.89×10⁻⁹⁵	2.23×10⁻¹⁸²
F5	AVG	4.00×10⁻¹⁵	2.46×10⁻¹⁵	4.44×10⁻¹⁶	5.49×10⁻²	4.44×10⁻¹⁶	4.44×10⁻¹⁶
	STD	0.00	2.02×10⁻¹⁵	0.00	3.01×10⁻¹	0.00	0.00
	Best	4.00×10⁻¹⁵	4.44×10⁻¹⁶	4.44×10⁻¹⁶	3.63×10⁻⁶	4.44×10⁻¹⁶	4.44×10⁻¹⁶
F6	AVG	3.00	3.39×10⁻²	4.18×10⁻⁷	2.16×10²	1.44×10⁻⁷	2.37×10⁻⁴
	STD	4.72×10⁻¹	3.06×10⁻²	6.39×10⁻⁷	1.72×10¹	2.16×10⁻⁷	4.32×10⁻⁴
	Best	2.08	9.24×10⁻³	1.19×10⁻¹¹	1.83×10²	4.47×10⁻¹¹	1.18×10⁻⁸
F7	AVG	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹
	STD	1.13×10⁻¹¹	8.48×10⁻¹⁵	1.04×10⁻¹⁵	2.31×10⁻¹⁶	8.48×10⁻¹¹	3.92×10⁻⁹
	Best	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹
F8	AVG	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03
	STD	1.01×10⁻⁹	7.23×10⁻¹⁵	4.25×10⁻¹⁶	8.87×10⁻¹⁵	5.38×10⁻⁶	2.44×10⁻⁴
	Best	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03
F9	AVG	2.99	3.00	2.98	2.98	3.00	3.00
	STD	1.71×10⁻⁷	1.00×10⁻⁹	3.01×10⁻¹⁴	4.99×10⁻¹⁴	3.24×10⁻⁴	6.16×10⁻¹⁵
	Best	2.99	3.00	2.98	2.98	3.00	3.00
F10	AVG	−1.02×10¹	−1.04×10¹	−6.86	−9.35	−1.04×10¹	−1.04×10¹
	STD	9.70×10⁻¹	8.75×10⁻⁷	2.55	2.15	5.73×10⁻⁵	3.22×10⁻²
	Best	−1.04×10¹	−1.04×10¹	−1.04×10¹	−1.04×10¹	−1.04×10¹	−1.04×10¹

下载: 导出CSV

表 4 Wilcoxon秩和检验结果

Table 4. Wilcoxon rank sum test result

对比算法	单峰函数	多峰函数	固定维数多峰函数
Improved AO vs. GWO	6.39×10⁻⁴	2.86×10⁻²	1.19×10⁻²
Improved AO vs. WOA	2.48×10⁻⁴	6.43×10⁻²	7.80×10⁻³
Improved AO vs. HHO	1.55×10⁻³	6.26×10⁻²	3.97×10⁻³
Improved AO vs. ALO	1.00×10⁻⁵	2.86×10⁻²	7.80×10⁻³
Improved AO vs. AO	9.58×10⁻³	7.62×10⁻²	5.69×10⁻²

下载: 导出CSV

表 5 改进AO算法种群数量（N）的敏感性分析

Table 5. Sensitivity analysis of the Improved AO for the number of population members (N)

函数	种群数量值
函数	100	200	300	400
F1	0.00	0.00	0.00	0.00
F2	5.13×10⁻¹⁶⁷	1.16×10⁻¹⁶⁷	7.23×10⁻¹⁷¹	3.09×10⁻¹⁷⁶
F3	0.00	0.00	0.00	0.00
F4	3.87×10⁻¹⁸¹	3.87×10⁻¹⁸⁷	5.83×10⁻¹⁹⁵	0.00
F5	4.44×10⁻¹⁶	4.44×10⁻¹⁶	3.45×10⁻¹⁸	1.12×10⁻²¹
F6	1.49×10⁻⁵	1.35×10⁻⁶	2.58×10⁻⁶	2.33×10⁻⁷
F7	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹
F8	−1.03	−1.03	−1.03	−1.03
F9	3.02	3.02	3.01	3.01
F10	−1.04×10⁻¹	−1.04×10⁻¹	−1.04×10⁻¹	−1.04×10⁻¹

下载: 导出CSV

表 6 改进AO算法迭代次数（T）的敏感性分析

Table 6. Sensitivity analysis of the Improved AO for the number of Iterations (T)

函数	最大迭代次数
函数	200	400	600	800
F1	1.68×10⁻²²⁵	0.00	0.00	0.00
F2	5.67×10⁻¹⁰⁸	3.64×10⁻¹⁴⁵	1.52×10⁻¹⁶⁷	6.26×10⁻¹⁷⁰
F3	2.28×10⁻²¹⁷	0.00	0.00	0.00
F4	5.91×10⁻¹⁰⁹	5.61×10⁻¹⁵⁹	5.85×10⁻¹⁶⁵	2.99×10⁻¹⁶⁸
F5	4.44×10⁻¹⁶	4.44×10⁻¹⁶	3.25×10⁻¹⁷	1.93×10⁻¹⁷
F6	3.93×10⁻⁵	1.79×10⁻⁵	1.45×10⁻⁶	9.95×10⁻⁷
F7	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹
F8	−1.03	−1.03	−1.03	−1.03
F9	3.01	3.01	3.01	3.01
F10	−1.04×10⁻¹	−1.04×10⁻¹	−1.04×10⁻¹	−1.04×10⁻¹

下载: 导出CSV

表 7 径向畸变参数估计结果

Table 7. Radial distortion parameter estimation results

序列	Ref [8]	Ref [11]	Ref [12]	Ours
(a)	−1.03×10⁻⁵	−1.01×10⁻⁵	−1.01×10⁻⁵	−1.01×10⁻⁵
(b)	−1.02×10⁻⁶	−1.02×10⁻⁶	−1.02×10⁻⁶	−1.02×10⁻⁶
(c)	−1.05×10⁻⁷	−0.96×10⁻⁷	−0.97×10⁻⁷	−1.02×10⁻⁷
(d)	−1.07×10⁻⁸	−1.04×10⁻⁸	−1.04×10⁻⁸	−1.02×10⁻⁸
(e)	−1.02×10⁻⁶	−1.03×10⁻⁶	−1.01×10⁻⁶	−1.01×10⁻⁶
(f)	−1.02×10⁻⁵	−1.01×10⁻⁵	−1.01×10⁻⁵	−1.01×10⁻⁵

下载: 导出CSV

表 8 畸变参数估计误差

Table 8. Estimation error of the distortion parameter

方法	D/(pixel)	R(%)
方法	D/(pixel)	(a)	(b)	(c)	(d)	(e)	(f)
Ref [8]	1.2412	3.2	2.8	5.1	7.0	2.5	2.3
Ref [11]	0.8430	1.5	2.8	4.6	4.3	3.0	1.5
Ref [12]	0.6762	1.2	2.6	3.2	4.3	1.3	1.2
Ours	0.4618	1.2	2.4	2.2	2.2	1.5	1.2

下载: 导出CSV

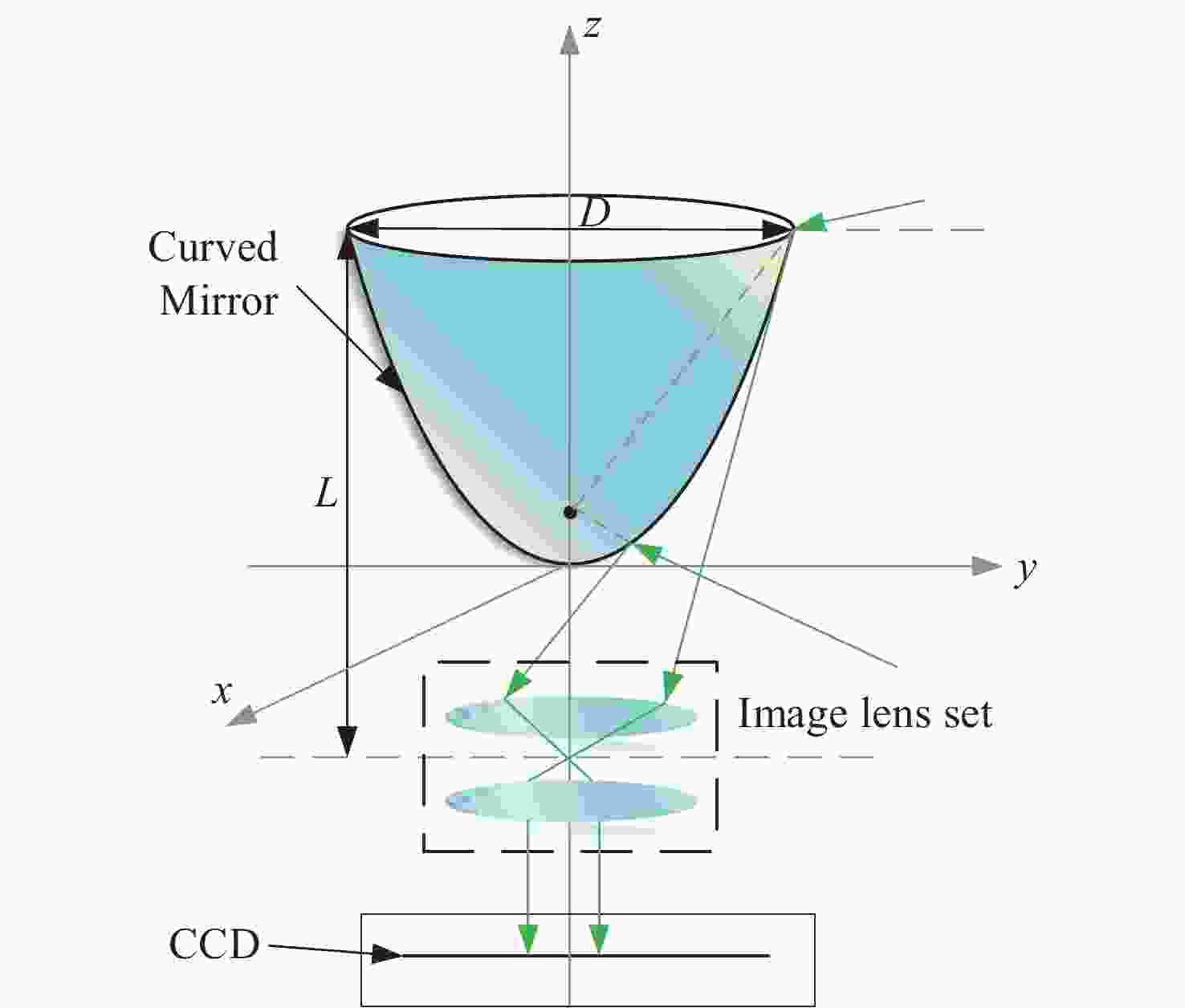
表 9 全景图像畸变参数估计结果

Table 9. Omnidirectional image distortion parameter estimation results

序列	图像大小	畸变参数	畸变中心
(a)	$2\;048 \times 1\;536$	2.2613×10⁻⁶	(1091.72,695.14)
(b)	$2\;048 \times 1\;536$	2.1983×10⁻⁶	(1095.62,692.57)
(c)	$2\;048 \times 1\;536$	2.3564×10⁻⁶	(1096.34,695.83)
(d)	$2\;048 \times 1\;536$	2.2083×10⁻⁶	(1094.61,696.53)
(e)	$4\;352 \times 3\;264$	3.2517×10⁻⁶	（517.86,382.15）
(f)	$4\;352 \times 3\;264$	2.8476×10⁻⁶	（516.43,380.93）

下载: 导出CSV

参考文献(30)

[1]	GONZALEZ-AGUILERA D, GOMEZ-LAHOZ J, RODRÍGUEZ-GONZÁLVEZ P. An automatic approach for radial lens distortion correction from a single image[J]. IEEE Sensors Journal, 2011, 11(4): 956-965. doi: 10.1109/JSEN.2010.2076403
[2]	BORN M, WOLF E. Electromagnetic theory of propagation, interference and diffraction of light[J]. Principles of Optics, 1980, 6: 327-329. (查阅网上资料, 未找到本条文献信息, 请确认) .
[3]	XIANG H T, TIAN L. Method for automatic georeferencing aerial remote sensing (RS) images from an unmanned aerial vehicle (UAV) platform[J]. Biosystems Engineering, 2011, 108(2): 104-113. doi: 10.1016/j.biosystemseng.2010.11.003
[4]	黄军辉, 王昭, 薛琦, 等. 基于有理函数式镜头畸变模型的摄像机标定[J]. 中国激光,2014,41(5):0508001. doi: 10.3788/CJL201441.0508001 HUANG J H, WANG ZH, XUE Q, et al. Calibration of camera with rational function lens distortion model[J]. Chinese Journal of Lasers, 2014, 41(5): 0508001. (in Chinese). doi: 10.3788/CJL201441.0508001
[5]	TSAI R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J]. IEEE Journal on Robotics and Automation, 1987, 3(4): 323-344. doi: 10.1109/JRA.1987.1087109
[6]	ZHANG ZH Y. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. doi: 10.1109/34.888718
[7]	WU F L, WEI H, WANG X J. Correction of image radial distortion based on division model[J]. Optical Engineering, 2017, 56(1): 013108. doi: 10.1117/1.OE.56.1.013108
[8]	ASARI K V, KUMAR S, RADHAKRISHNAN D. A new approach for nonlinear distortion correction in endoscopic images based on least squares estimation[J]. IEEE Transactions on Medical Imaging, 1999, 18(4): 345-354. doi: 10.1109/42.768843
[9]	DEVERNAY F, FAUGERAS O. Straight lines have to be straight: automatic calibration and removal of distortion from scenes of structured enviroments[J]. Machine Vision and Applications, 2001, 13(1): 14-24. doi: 10.1007/PL00013269
[10]	ALVAREZ L, GÓMEZ L, SENDRA J R. An algebraic approach to lens distortion by line rectification[J]. Journal of Mathematical Imaging and Vision, 2009, 35(1): 36-50. doi: 10.1007/s10851-009-0153-2
[11]	周前飞, 刘晶红. 航空变焦距镜头非线性畸变快速校正方法[J]. 光学学报,2015,35(4):0411001. doi: 10.3788/AOS201535.0411001 ZHOU Q F, LIU J H. Rapid nonlinear distortion correction of aerial optical zoom lens system[J]. Acta Optica Sinica, 2015, 35(4): 0411001. (in Chinese). doi: 10.3788/AOS201535.0411001
[12]	王平, 姚登银, 谯睿, 等. 基于双直线的镜头畸变参数估计方法[J]. 光学学报,2023,43(13):1315001. doi: 10.3788/AOS221724 WANG P, YAO D Y, QIAO R, et al. Estimation method of lens distortion parameters based on two lines[J]. Acta Optica Sinica, 2023, 43(13): 1315001. (in Chinese). doi: 10.3788/AOS221724
[13]	MICUSIK B, PAJDLA T. Estimation of omnidirectional camera model from epipolar geometry[C]. Proceedings of 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, IEEE, 2003.
[14]	曹立波, 夏家豪, 廖家才, 等. 基于3D空间球面的车载全景快速生成方法[J]. 中国公路学报,2020,33(1):153-162,171. doi: 10.3969/j.issn.1001-7372.2020.01.016 CAO L B, XIA J H, LIAO J C, et al. Fast generation methods of around view monitoring images for automobiles based on 3D space sphere[J]. China Journal of Highway and Transport, 2020, 33(1): 153-162,171. (in Chinese). doi: 10.3969/j.issn.1001-7372.2020.01.016
[15]	LIAO K, LIN CH Y, ZHAO Y, et al. OIDC-Net: omnidirectional image distortion correction via coarse-to-fine region attention[J]. IEEE Journal of Selected Topics in Signal Processing, 2020, 14(1): 222-231. doi: 10.1109/JSTSP.2019.2955017
[16]	FENG H, WANG W D, DENG J J, et al. SimFIR: a simple framework for fisheye image rectification with self-supervised representation learning[C]. Proceedings of 2023 IEEE/CVF International Conference on Computer Vision, IEEE, 2023: 12418-12427.
[17]	ARTIZZU C O, ALLIBERT G, DEMONCEAUX C. OMNI-CONV: generalization of the omnidirectional distortion-aware convolutions[J]. Journal of Imaging, 2023, 9(2): 29. doi: 10.3390/jimaging9020029
[18]	ABUALIGAH L, YOUSRI D, ABD ELAZIZ M, et al. Aquila optimizer: a novel meta-heuristic optimization algorithm[J]. Computers & Industrial Engineering, 2021, 157: 107250.
[19]	ZHANG Y, XU X P, ZHANG N, et al. Adaptive aquila optimizer combining niche thought with dispersed chaotic swarm[J]. Sensors, 2023, 23(2): 755. doi: 10.3390/s23020755
[20]	林之博, 刘媛华. 一种分片混沌贪婪振荡退火TSP优化算法[J]. 计算机应用研究,2021,38(8):2359-2364. LIN ZH B, LIU Y H. Divided chaotic oscillatory annealing TSP optimization algorithm based on greedy strategy[J]. Application Research of Computers, 2021, 38(8): 2359-2364. (in Chinese).
[21]	鲁英达, 张菁. 基于改进猎人猎物算法的VMD-KELM短期负荷预测[J]. 电气工程学报,2023,18(4):228-238. LU Y D, ZHANG J. VMD-KELM short-term load forecasting based on improved hunter-prey optimizer[J]. Journal of Electrical Engineering, 2023, 18(4): 228-238. (in Chinese).
[22]	张越, 张宁, 徐熙平, 等. 融合结构光的折反射全景单目视觉测距[J]. 光学精密工程,2024,32(4):490-503. doi: 10.37188/OPE.20243204.0490 ZHANG Y, ZHANG N, XU X P, et al. Catadioptric omnidirectional monocular visual distance measurement method integrating structured light[J]. Optics and Precision Engineering, 2024, 32(4): 490-503. (in Chinese). doi: 10.37188/OPE.20243204.0490
[23]	MEI C, RIVES P. Single view point omnidirectional camera calibration from planar grids[C]. Proceedings 2007 IEEE International Conference on Robotics and Automation, IEEE, 2007: 3945-3950.
[24]	STRAND R, HAYMAN E. Correcting radial distortion by circle fitting[C]. Proceedings of the British Machine Vision Conference 2005, BMVC, 2005: 2564-2570.
[25]	WANG A Q, QIU T SH, SHAO L T. A simple method of radial distortion correction with centre of distortion estimation[J]. Journal of Mathematical Imaging and Vision, 2009, 35(3): 165-172. doi: 10.1007/s10851-009-0162-1
[26]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007
[27]	MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008
[28]	HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris hawks optimization: algorithm and applications[J]. Future Generation Computer Systems, 2019, 97: 849-872. doi: 10.1016/j.future.2019.02.028
[29]	MIRJALILI S. The ant lion optimizer[J]. Advances in Engineering Software, 2015, 83: 80-98. doi: 10.1016/j.advengsoft.2015.01.010
[30]	BUKHARI F, DAILEY M N. Automatic radial distortion estimation from a single image[J]. Journal of Mathematical Imaging and Vision, 2013, 45(1): 31-45. doi: 10.1007/s10851-012-0342-2