相敏型光时域反射系统信噪比提升

王子豪; 刘志凯; 冯玉祥; 张成龙; 吕立冬

doi:10.37188/CO.2024-0122

相敏型光时域反射系统信噪比提升

doi: 10.37188/CO.2024-0122

cstr: 32171.14.CO.2024-0122

安徽工业大学电气与信息工程学院, 安徽马鞍山 243002

基金项目: 国家自然科学基金项目（No. 51977001）

详细信息

作者简介:
吕立冬（1982—），男，四川省邻水人，博士，副教授，硕士研究生导师，2005年获得西安工业大学学士学位，2009年获得中国科学院国家天文台南京天文光学技术研究所硕士学位，2012获得南京大学博士学位。主要研究方向为电力设备状态监测与诊断、分布式光纤传感、能源互联网等，现主要从事光纤传感技术及其在智能电网方面的研究。E-mail：lvlidong@ahut.edu.cn

中图分类号: TP212.9;TN212
计量
- 文章访问数: 103
- HTML全文浏览量: 21
- PDF下载量: 6
- 被引次数: 0
出版历程
- 收稿日期: 2024-07-02
- 录用日期: 2024-10-09
- 网络出版日期: 2024-11-28

Improvement of signal-to-noise ratio for phase-sensitive optical time-domain reflecting system

School of Electrical and Information Engineering, Anhui University of Technology, Maanshan 243002, China

Funds: Supported by National Natural Science Foundation of China (No. 51977001)

摘要

摘要:
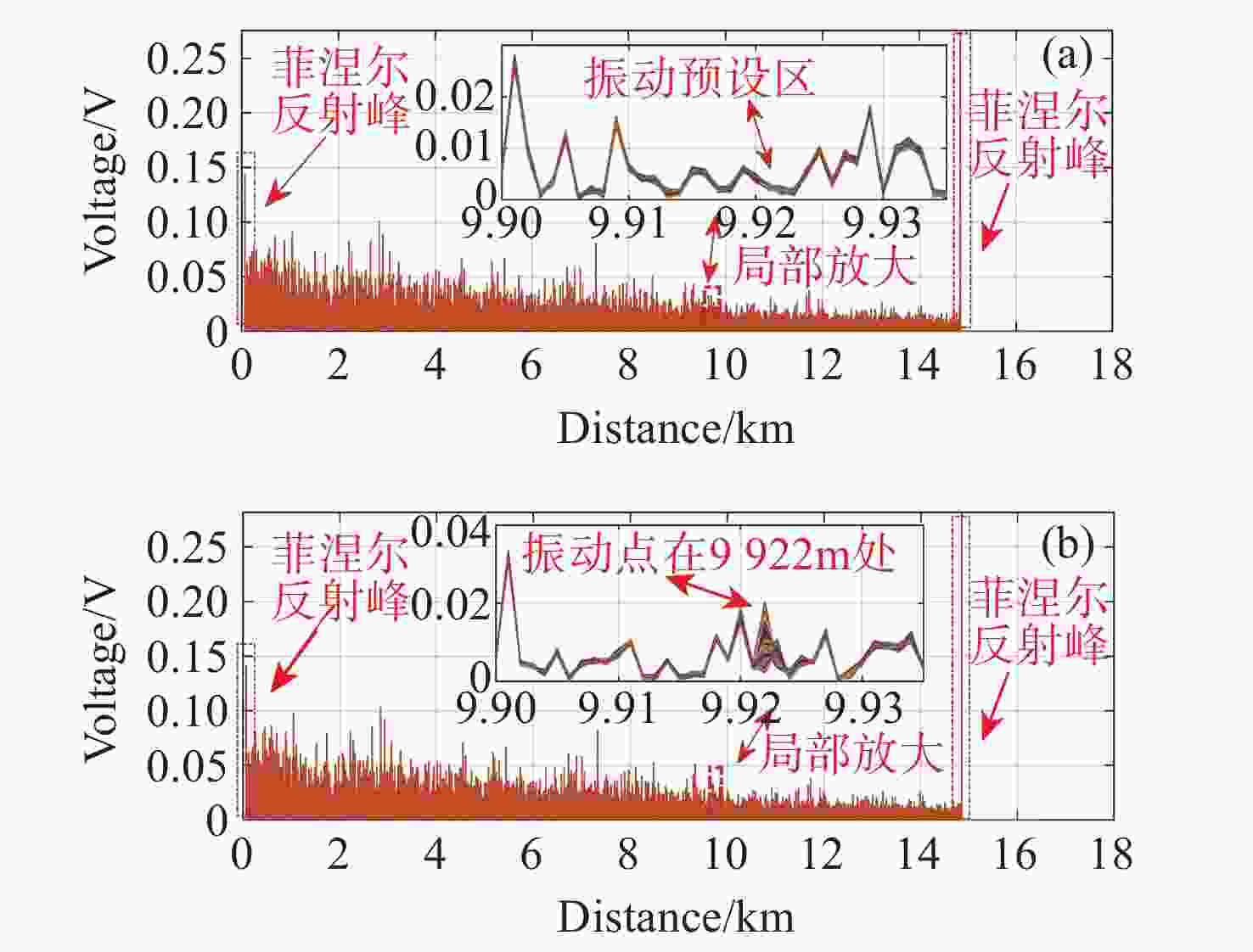
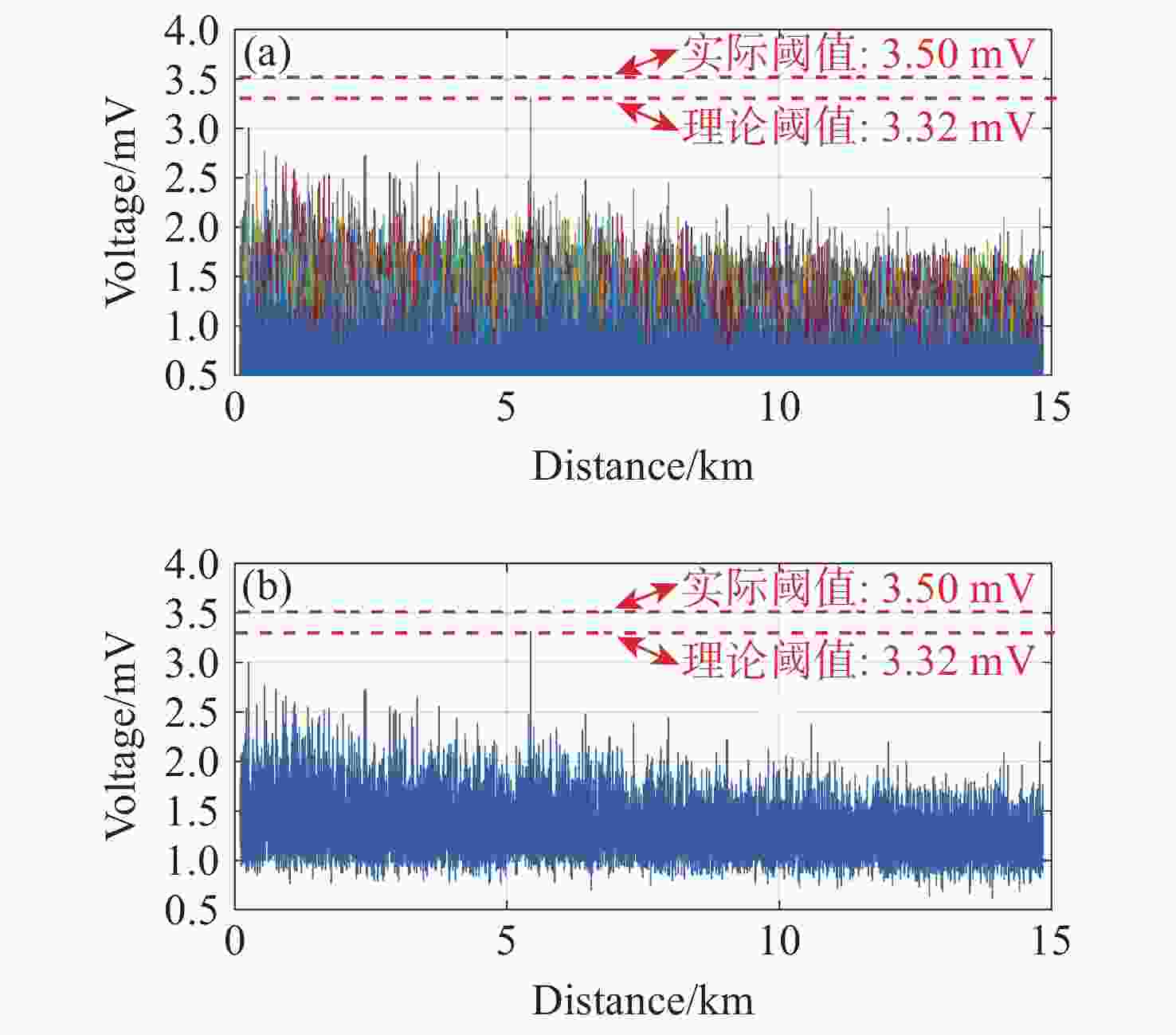
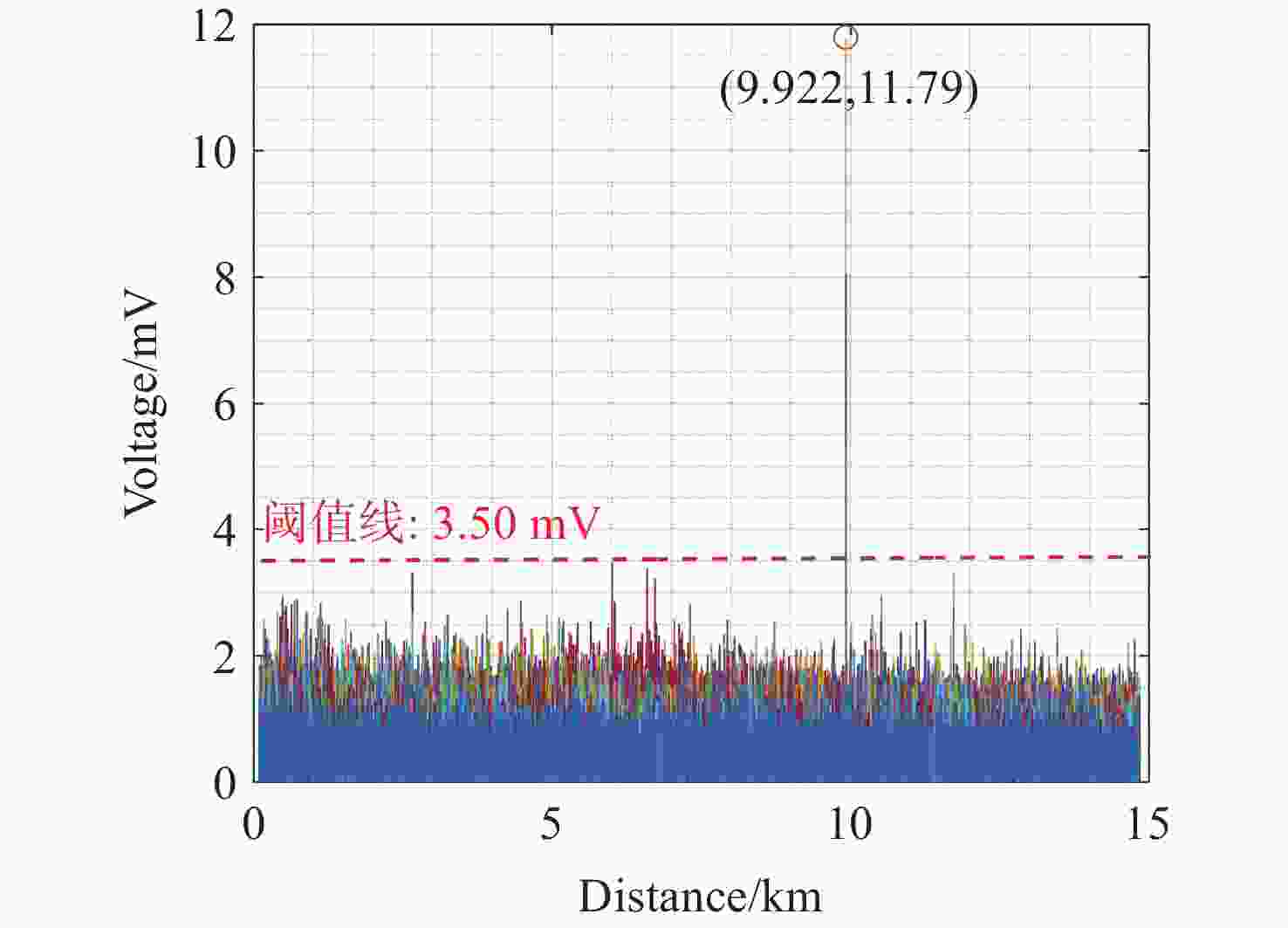
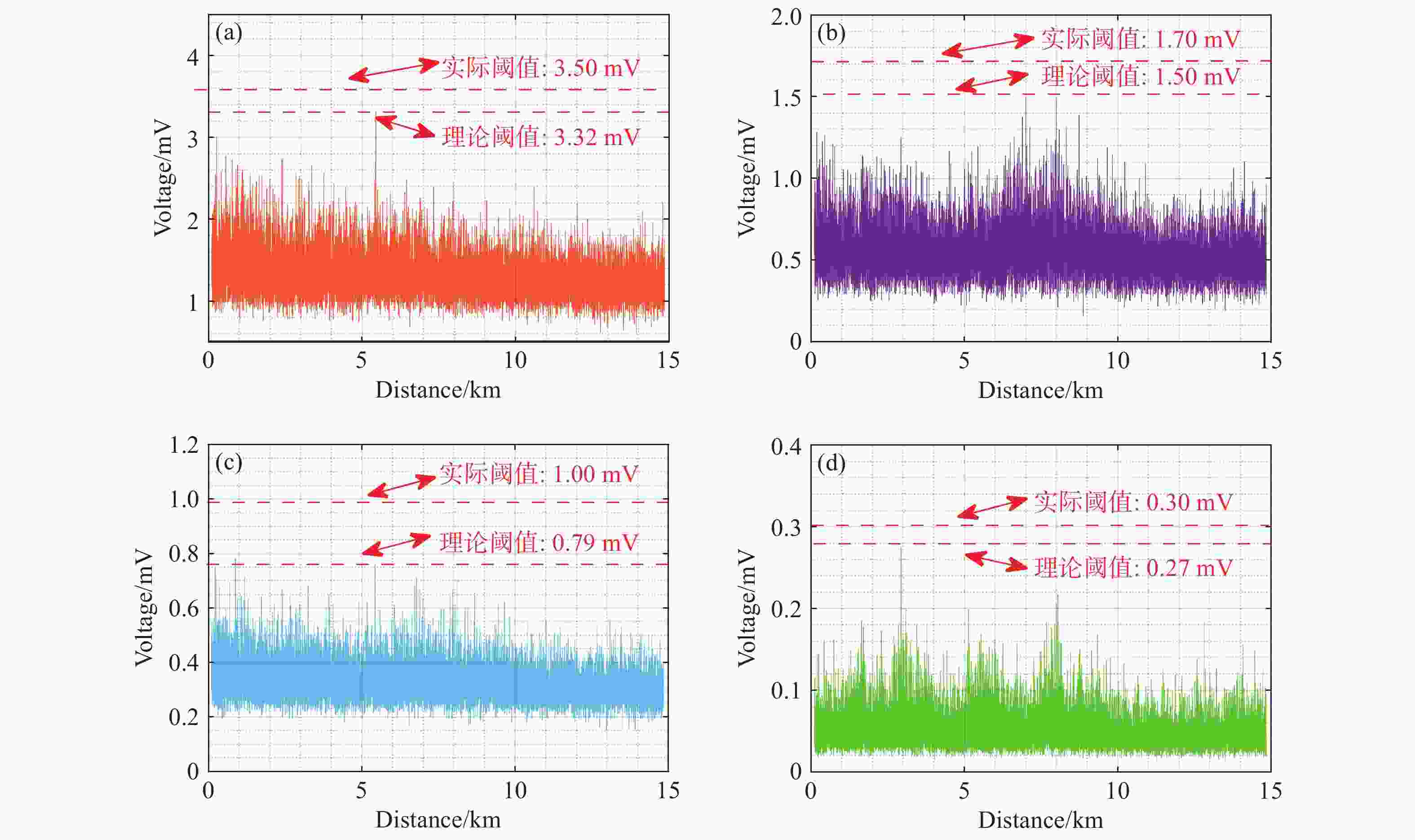
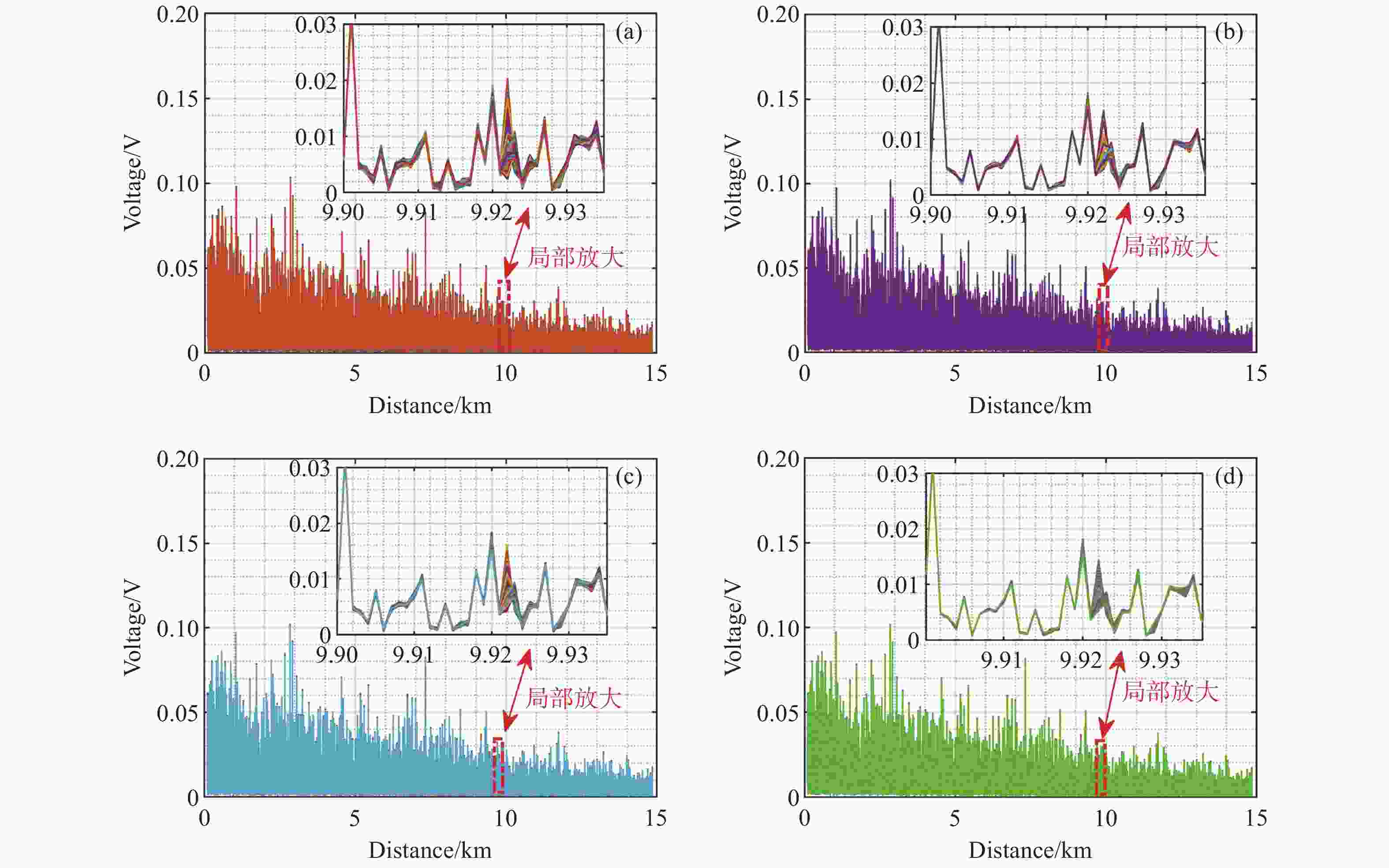
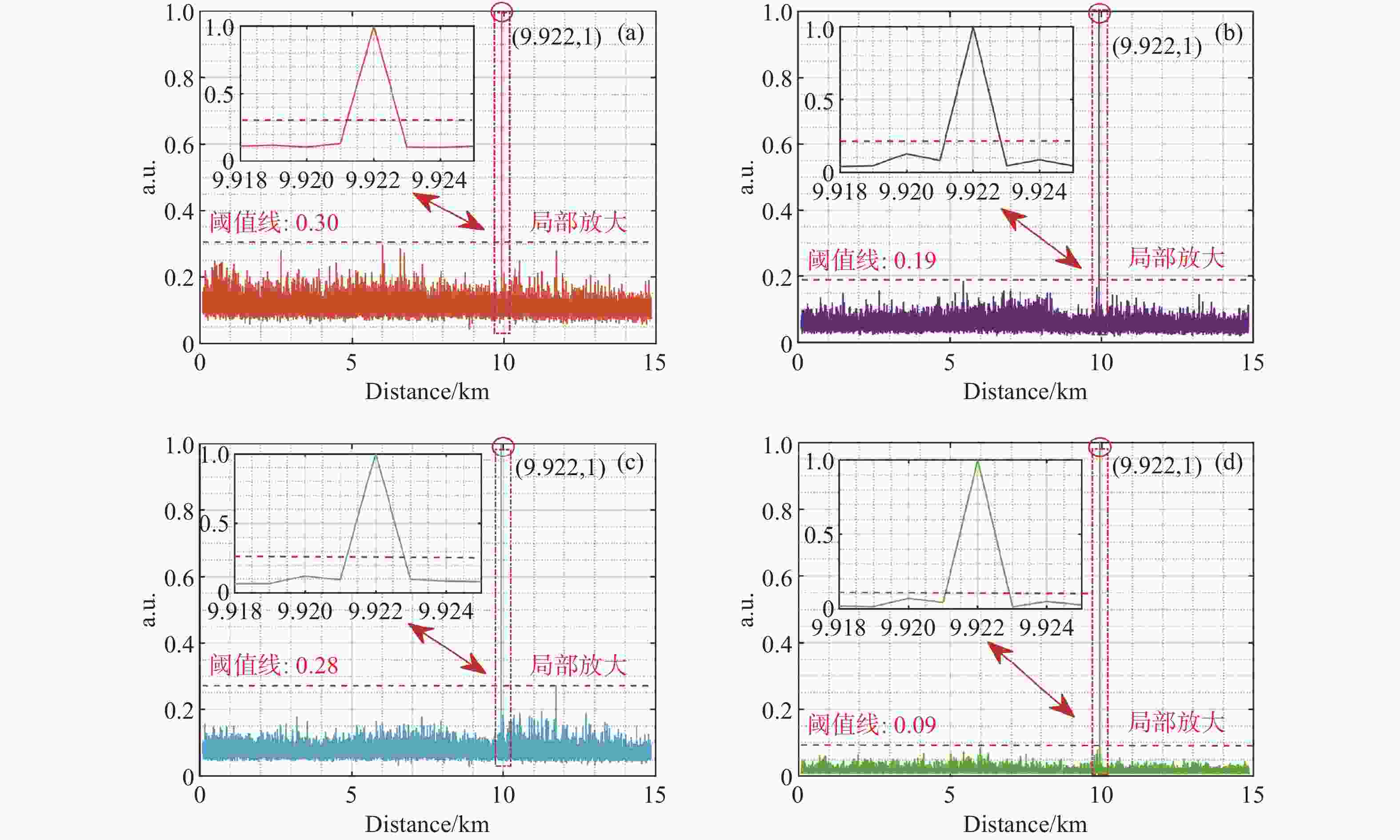
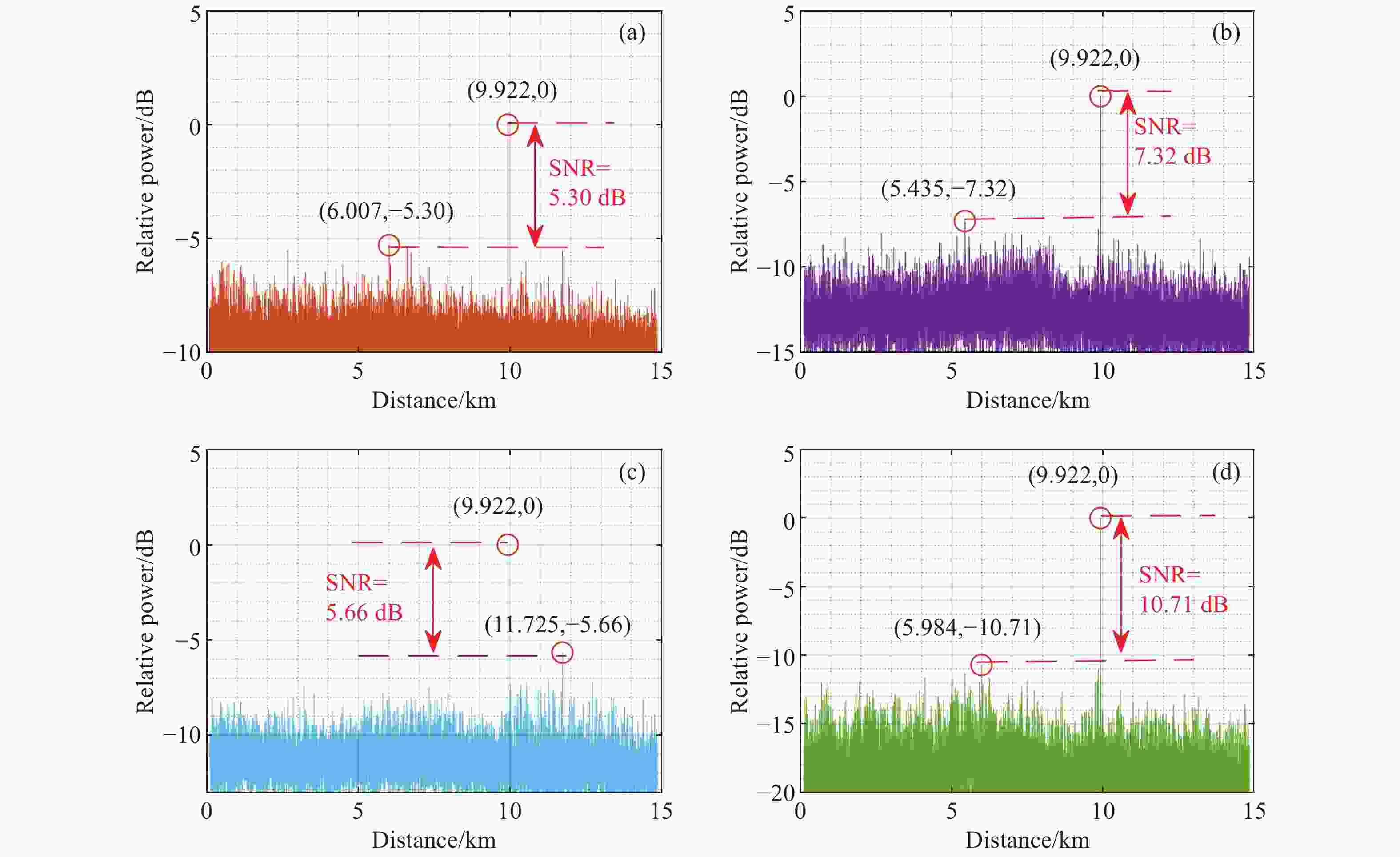
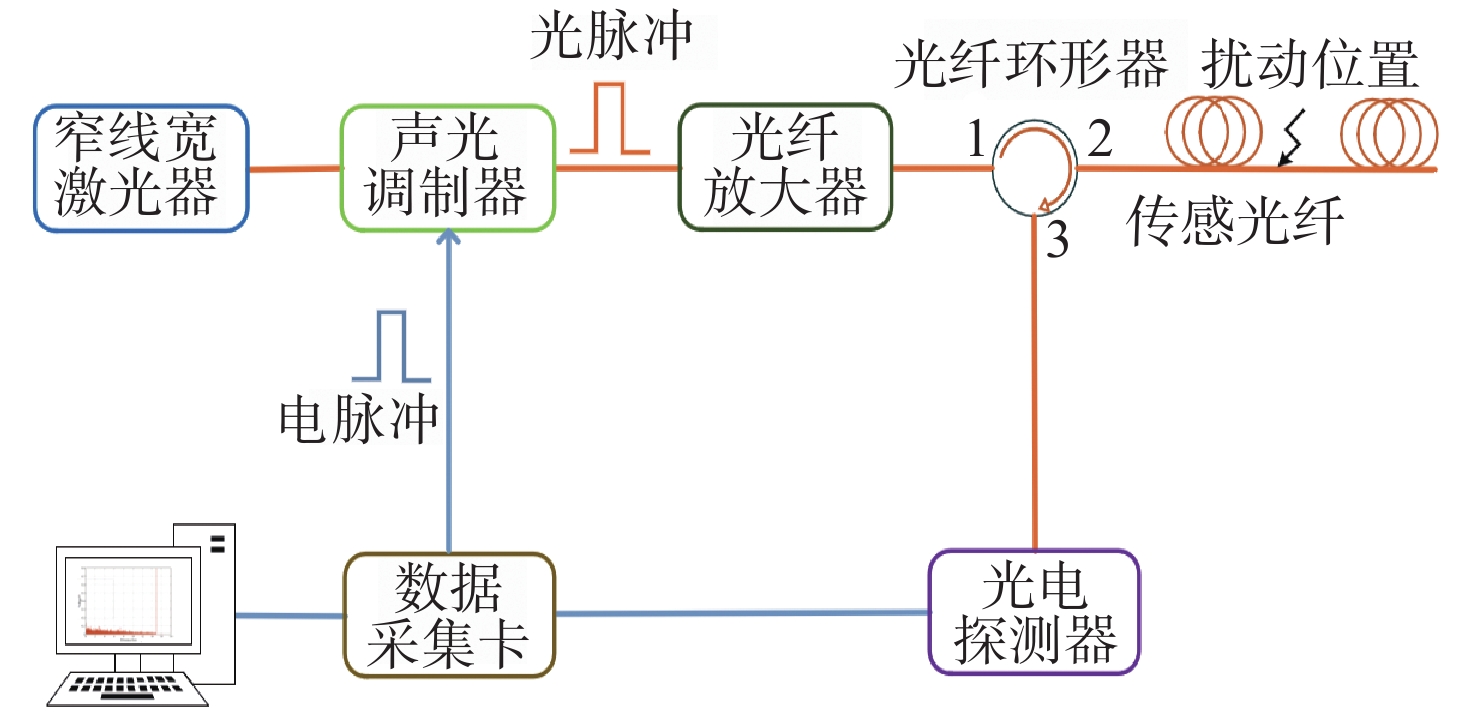
相位敏感型光时域反射系统（Φ-OTDR）的灵敏度受激光器的相位噪声、掺铒光纤放大器的自发辐射噪声、光电探测器的散粒噪声及热噪声等系统固有噪声和环境随机噪声的制约，因此，本文研究光时域反射数据的降噪算法，在不降低系统频率响应范围的条件下提高系统的信噪比。本文提出Savitzky-Golay平滑算法，选择固定长度的滑动窗口，对窗口内的光时域反射数据进行降噪处理，同时保持数据的采样频率，并搭建实验系统进行验证。实验结果显示：采用Savitzky-Golay平滑算法，系统的信噪比相对于原始信号逐差法的信噪比提高了5.41 dB，与常用的累加平均算法、滑动平均算法相比信噪比分别提升3.39 dB和5.05 dB。结果表明：Savitzky-Golay平滑算法可提高Φ-OTDR系统的灵敏度和准确度，使其能够精准的感知微小振动事件，以降低系统误报率。
- 相位敏感光时域反射仪 /
- Savitzky-Golay平滑算法 /
- 信噪比 /
- 阈值定位
Abstract:
The sensitivity of phase-sensitive optical time-domain reflecting (Φ-OTDR) system is limited by the intrinsic system noise such as the phase noise of the laser, the spontaneous emission noise of the erbium-doped fiber amplifier, and the shot noise and thermal noise of the photodetector, as well as the random noise in the environment. Therefore, the noise reduction algorithms based on the optical time-domain reflecting data is investigated to improve the signal-to-noise ratio (SNR) of the system without degrading the frequency response range. And the Savitzky-Golay smoothing algorithm is proposed by selecting a slidable window with fixed-length to process OTDR data for the SNR improvement, while maintaining the system sampling frequency, and then, the experimental system is built to demonstrate the results. The experimental results show that by using the Savitzky-Golay smoothing algorithm, the SNR of the system is improved by 5.41dB relative to that by difference method with the original data, and the SNR is improved by 3.39dB and 5.05dB respectively, compared to the commonly used cumulative averaging method and sliding averaging method. It is demonstrated that the Savitzky-Golay smoothing algorithm can improve the sensitivity and accuracy of the Φ-OTDR system, which helps to accurately sense weak vibration events and reduce false alarm rate.
- phase sensitive optical time domain reflectometer /
- Savitzky-Golay smoothing algorithm /
- SNR /
- threshold positioning

HTML全文

图 1 Φ-OTDR系统结构图

Figure 1. Schematic diagram of the Φ-OTDR system

下载: 全尺寸图片幻灯片

图 2 原始OTDR曲线。(a)未加载事件；(b)加载事件

Figure 2. Original OTDR traces.(a) no vibration event loaded; (b) loading vibration events

下载: 全尺寸图片幻灯片

图 3 无振动事件时的逐差曲线。(a)差值曲线；(b)峰值曲线

Figure 3. Differential traces in the absence of vibration events. (a) difference traces; (b) peak trace

下载: 全尺寸图片幻灯片

图 4 逐差法曲线

Figure 4. Traces by difference method

下载: 全尺寸图片幻灯片

图 5 不同算法无振动事件时的逐差峰值曲线。(a)原始曲线；(b)累加平均算法；(c)滑动平均算法；(d) S-G平滑算法

Figure 5. Differential peak traces of different algorithms without vibration events. (a) original trace; (b) cumulative average algorithm; (c) moving average algorithm; (d) S-G smoothing algorithm

下载: 全尺寸图片幻灯片

图 6 不同算法处理OTDR曲线。(a)原始曲线；(b)累加平均算法；(c)滑动平均算法；(d) S-G平滑算法

Figure 6. Different algorithms for processing OTDR traces. (a) original traces; (b) cumulative average algorithm; (c) moving average algorithm; (d) S-G smoothing algorithm

下载: 全尺寸图片幻灯片

图 7 不同算法归一化阈值定位。(a)原始曲线；(b)累加平均算法；(c)滑动平均算法；(d) S-G平滑算法

Figure 7. Different algorithms for normalized threshold localization. (a) original trace; (b) cumulative average algorithm; (c) moving average algorithm; (d) S-G smoothing algorithm

下载: 全尺寸图片幻灯片

图 8 不同算法的信噪比。(a)原始曲线；(b)累加平均算法；(c)滑动平均算法；(d) S-G平滑算法

Figure 8. Signal to noise ratio of different algorithms. (a) original trace; (b) cumulative average algorithm; (c) moving average algorithm; (d) S-G smoothing algorithm

下载: 全尺寸图片幻灯片

参考文献(26)

[1]	刘舒馨, 祝苒, 刘忠富. 分布式光纤传感器在地震监测中的应用综述[J]. 山西电子技术,2023(5):108-110. doi: 10.3969/j.issn.1674-4578.2023.05.036 LIU SH X, ZHU R, LIU ZH F. Application of distributed fiber optic sensor in seismic monitoring[J]. Shanxi Electronic Technology, 2023(5): 108-110. (in Chinese). doi: 10.3969/j.issn.1674-4578.2023.05.036
[2]	ELSHERIF M, SALIH A E, MUÑOZ M G, et al. Optical fiber sensors: working principle, applications, and limitations[J]. Advanced Photonics Research, 2022, 3(11): 2100371. doi: 10.1002/adpr.202100371
[3]	DUAN R. Real-time hotspot tracing and model analysis of a distributed optical fiber sensor integrated power transformer[J]. IEEE Access, 2022, 10: 57242-57254. doi: 10.1109/ACCESS.2022.3177844
[4]	江虹, 曾庆龙, 李家成. 基于VMD与MFE的光纤周界安防入侵事件识别[J]. 激光与红外,2023,53(7):1073-1080. doi: 10.3969/j.issn.1001-5078.2023.07.014 JIANG H, ZENG Q L, LI J CH. Intrusion event identification for fiber optic perimeter security based on VMD and MFE[J]. Laser & Infrared, 2023, 53(7): 1073-1080. (in Chinese). doi: 10.3969/j.issn.1001-5078.2023.07.014
[5]	CHAMOIN L, FARAHBAKHSH S, PONCELET M. An educational review on distributed optic fiber sensing based on Rayleigh backscattering for damage tracking and structural health monitoring[J]. Measurement Science and Technology, 2022, 33(12): 124008. doi: 10.1088/1361-6501/ac9152
[6]	ASHRY I, MAO Y, WANG B W, et al. A review of distributed fiber–optic sensing in the oil and gas industry[J]. Journal of Lightwave Technology, 2022, 40(5): 1407-1431. doi: 10.1109/JLT.2021.3135653
[7]	LIU SH Q, YU F H, HONG R, et al. Advances in phase-sensitive optical time-domain reflectometry[J]. Opto-Electronic Advances, 2022, 5(3): 200078. doi: 10.29026/oea.2022.200078
[8]	HEALEY P. Fading in heterodyne OTDR[J]. Electronics Letters, 1984, 20(1): 30-32. doi: 10.1049/el:19840022
[9]	SHATALIN S V, TRESCHIKOV V N, ROGERS A J. Interferometric optical time-domain reflectometry for distributed optical-fiber sensing[J]. Applied Optics, 1998, 37(24): 5600-5604. doi: 10.1364/AO.37.005600
[10]	LIAO Y H, LI K, GONG Y D. Research on the noise suppression by φ-OTDR[J]. Journal of Optics, 2024: 1-10. (查阅网上资料, 未找到对应的卷期页码信息, 请确认) .
[11]	SUN Y T, MA H ZH. Progress of Fiber Bragg Grating Sensors in state perception of electrical equipment[J]. Measurement, 2023, 222: 113691. doi: 10.1016/j.measurement.2023.113691
[12]	LU Y L, ZHU T, CHEN L, et al. Distributed vibration sensor based on coherent detection of phase-OTDR[J]. Journal of Lightwave Technology, 2010, 28(22): 3243-3249.
[13]	PAN ZH Q, LIANG K ZH, ZHOU J, et al. Interference-fading-free phase-demodulated OTDR system[J]. Proceedings of SPIE, 2012, 8421: 842129. doi: 10.1117/12.975656
[14]	ZHU T, XIAO X H, HE Q, et al. Enhancement of SNR and spatial resolution in φ-OTDR system by using two-dimensional edge detection method[J]. Journal of Lightwave Technology, 2013, 31(17): 2851-2856. doi: 10.1109/JLT.2013.2273553
[15]	CHEN D, LIU Q W, HE Z Y. Phase-detection distributed fiber-optic vibration sensor without fading-noise based on time-gated digital OFDR[J]. Optics Express, 2017, 25(7): 8315-8325. doi: 10.1364/OE.25.008315
[16]	CHEN D, LIU Q W, HE Z Y. High-fidelity distributed fiber-optic acoustic sensor with fading noise suppressed and sub-meter spatial resolution[J]. Optics Express, 2018, 26(13): 16138-16146. doi: 10.1364/OE.26.016138
[17]	CHEN W, MA X H, MA Q L, et al. Denoising method of the Φ-OTDR system based on EMD-PCC[J]. IEEE Sensors Journal, 2021, 21(10): 12113-12118. doi: 10.1109/JSEN.2020.3033674
[18]	杨文晨, 秦增光, 刘兆军, 等. 基于希尔伯特-黄变换的双马赫-曾德分布式光纤传感振动定位方法[J]. 中国光学,2021,14(6):1410-1416. doi: 10.37188/CO.2021-0065 YANG W CH, QIN Z G, LIU ZH J, et al. A Hilbert-Huang transform method for vibration localization based on a dual Mach-Zehnder distributed optical fiber sensor[J]. Chinese Optics, 2021, 14(6): 1410-1416. (in Chinese). doi: 10.37188/CO.2021-0065
[19]	LI T X, ZHANG F D, LIN J, et al. Fading noise suppression method of Φ-OTDR system based on GA-VMD algorithm[J]. IEEE Sensors Journal, 2023, 23(19): 22608-22619. doi: 10.1109/JSEN.2023.3306199
[20]	MARIE T F B, BIN Y, DEZHI H, et al. Principle and application state of fully distributed fiber optic vibration detection technology based on Φ-OTDR: a review[J]. IEEE Sensors Journal, 2021, 21(15): 16428-16442. doi: 10.1109/JSEN.2021.3081459
[21]	BAI X Y, LIU H ZH, LIN J, et al. SNR enhancement method for Φ-OTDR system based on Sdr SampEn-BiPSO-SVD algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 9502212.
[22]	潘冬阳, 南钢洋, 白雪. 基于高速信号采集系统累加平均算法研究[J]. 仪表技术与传感器,2021(8):122-125. doi: 10.3969/j.issn.1002-1841.2021.08.026 PAN D Y, NAN G Y, BAI X. Research on overlapping average algorithm based on high speed signal acquisition system[J]. Instrument Technique and Sensor, 2021(8): 122-125. (in Chinese). doi: 10.3969/j.issn.1002-1841.2021.08.026
[23]	NAKAJIMA I, MURAKI Y, ICHIMURA H, et al. Value and challenges of using the Savitzky-Golay method for ECG noise reduction[C]. Proceedings of 2022 International Conference on Electrical, Computer and Energy Technologies, IEEE, 2022: 1-5.
[24]	NIEDŹWIECKI M J, CIOŁEK M, GAŃCZA A, et al. Application of regularized Savitzky–Golay filters to identification of time-varying systems[J]. Automatica, 2021, 133: 109865. doi: 10.1016/j.automatica.2021.109865
[25]	JUAREZ J C, TAYLOR H F. Polarization discrimination in a phase-sensitive optical time-domain reflectometer intrusion-sensor system[J]. Optics Letters, 2005, 30(24): 3284-3286. doi: 10.1364/OL.30.003284
[26]	ZHOU ZH X, TIAN L, HAN Y SH, et al. Distributed vibration and temperature simultaneous sensing using one optical fiber[J]. Optics Communications, 2021, 487: 126801. doi: 10.1016/j.optcom.2021.126801