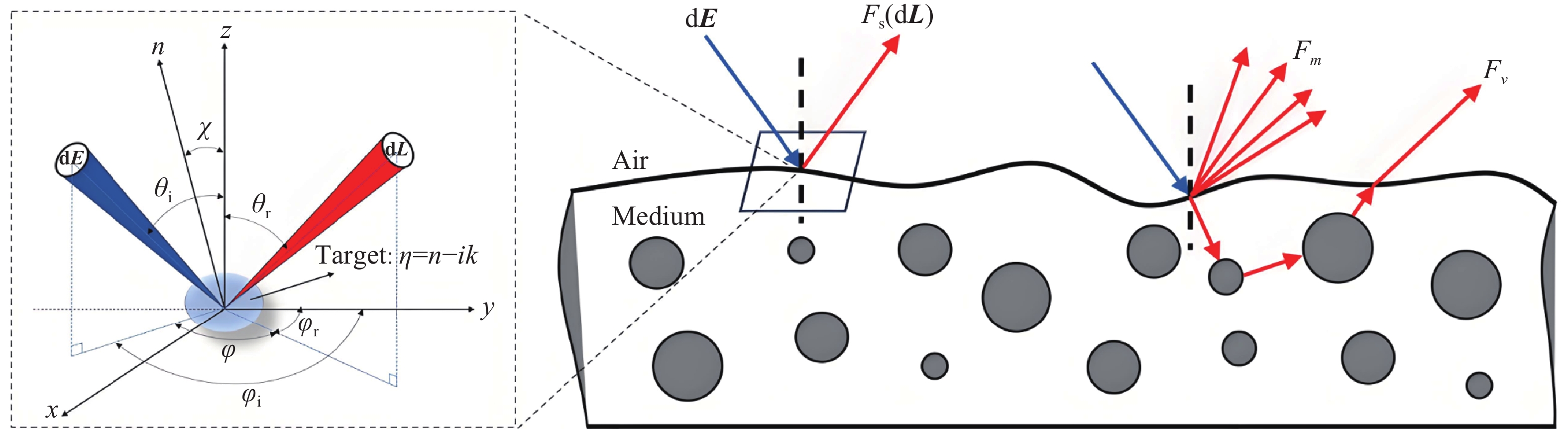
Visible polarization characteristics of airport ground material based on BPDF correction
-
摘要:
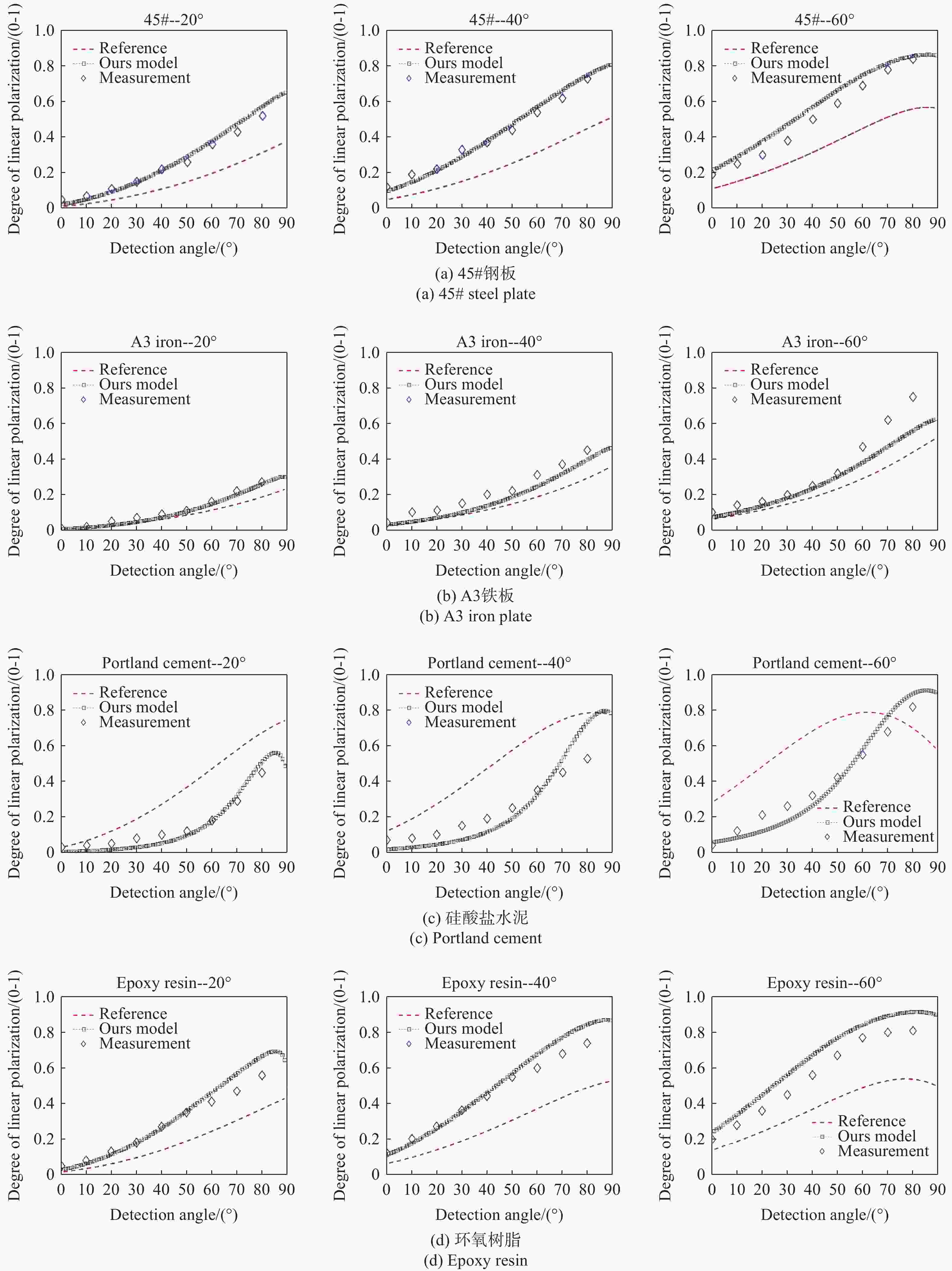
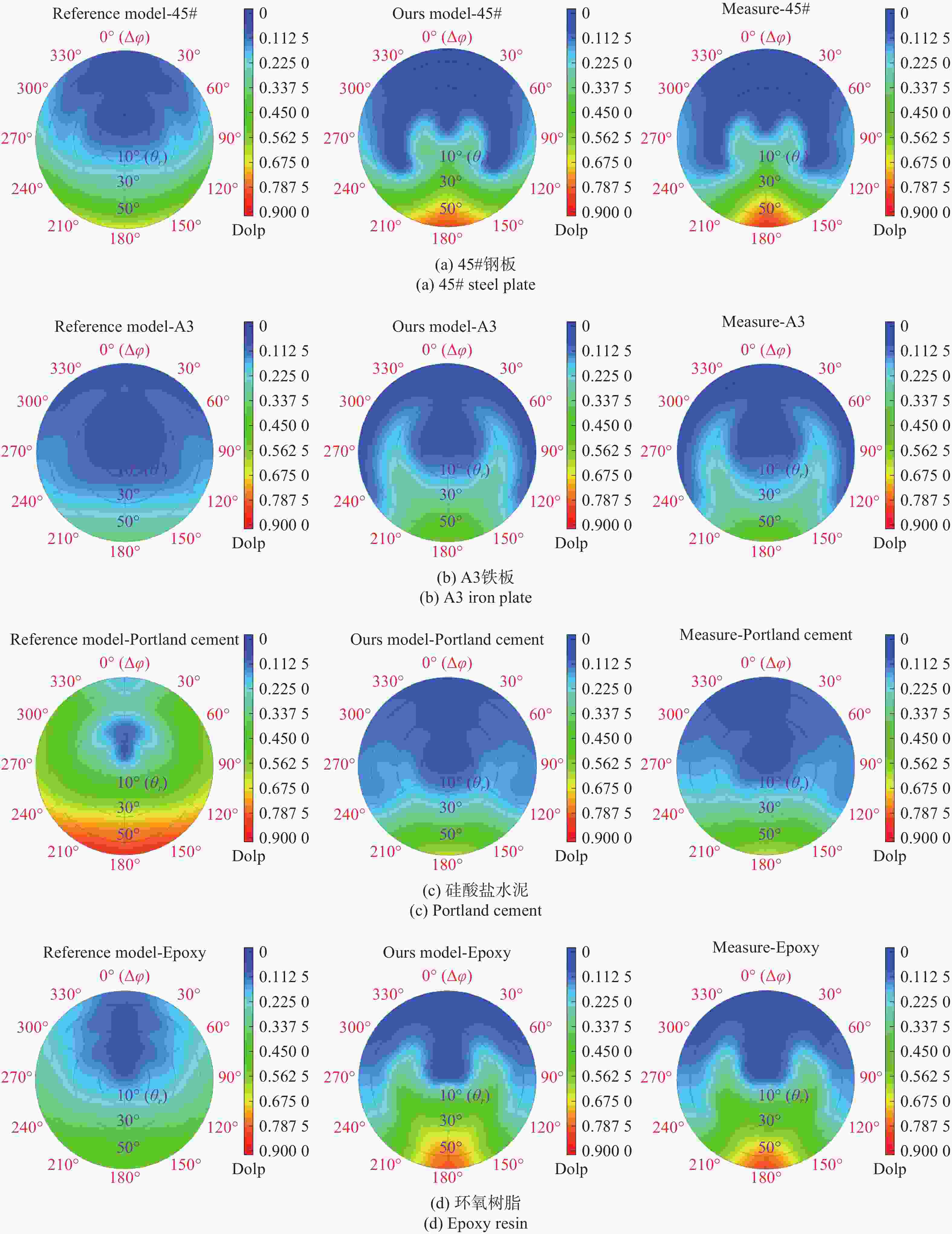
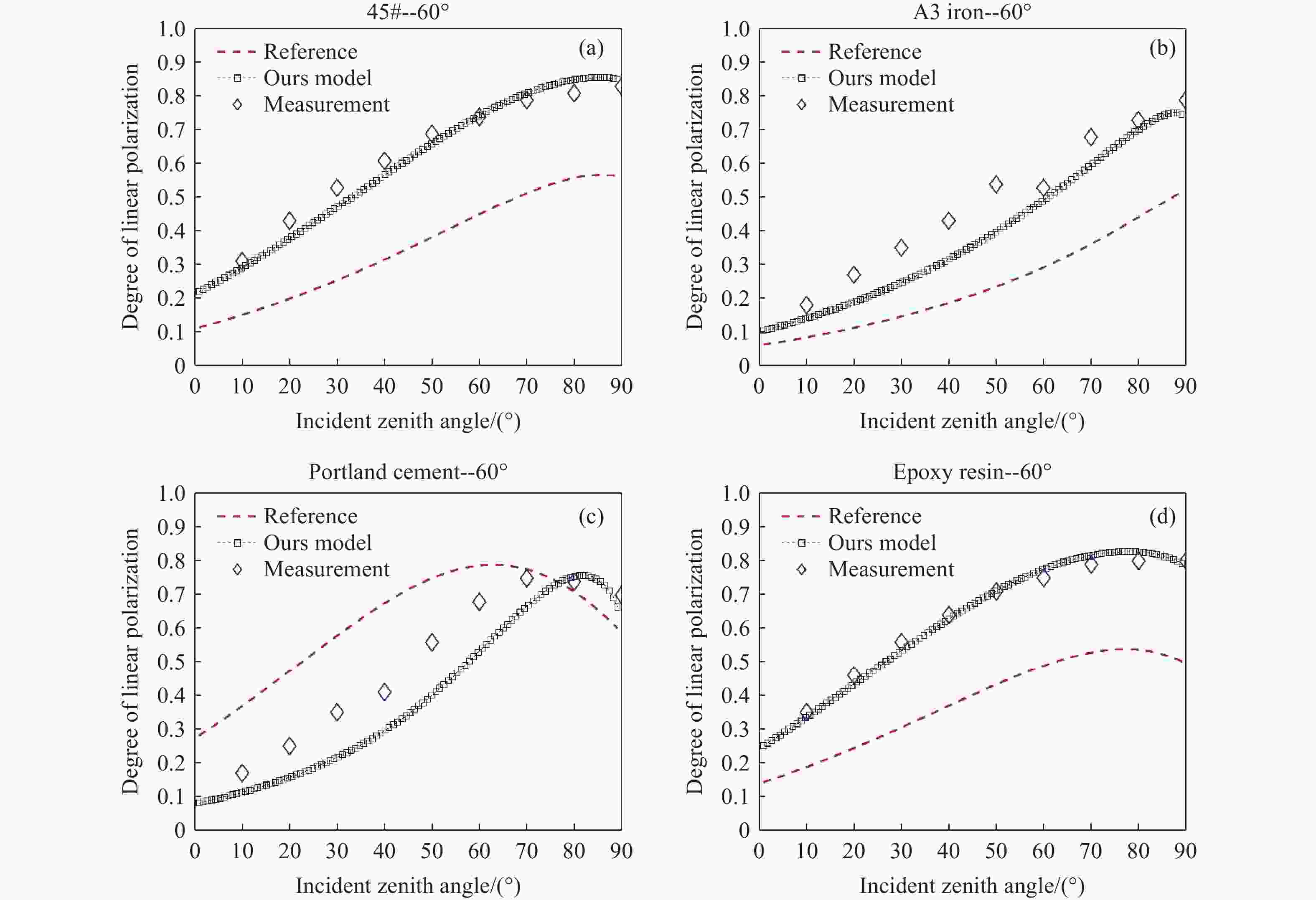
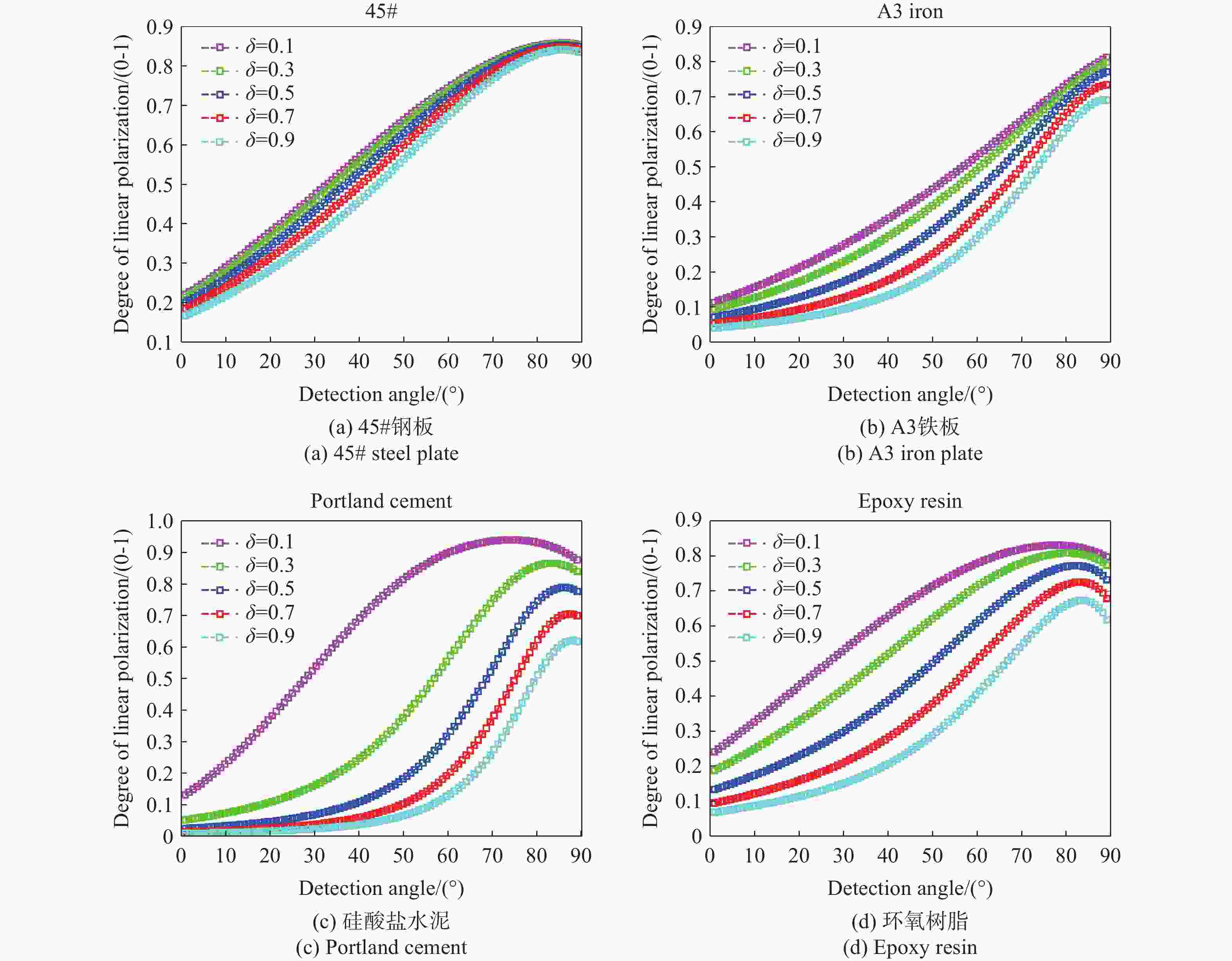
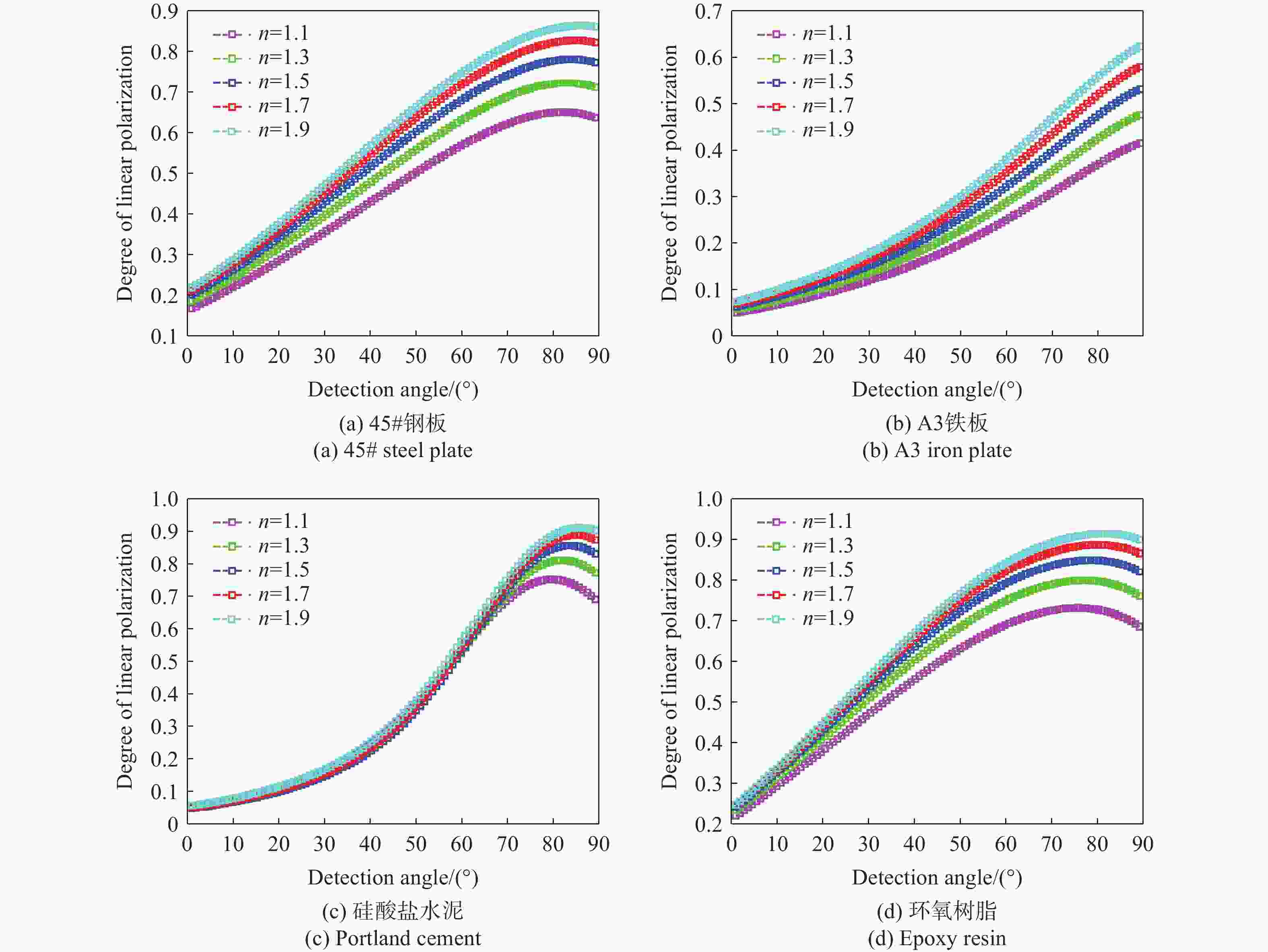
为研究典型机场地物材质的偏振特性，并为偏振成像仪器研制提供所需的理论模型，本文以P-G模型为基础，构建新的二向偏振分布函数(BPDF)模型。本文分析了当大角度光线入射时阴影遮蔽效应更严重的问题，创新性地提出将镜面反射点等效为三维球体的解决方案，并利用球面三角学公式对阴影遮蔽函数进行优化。同时，考虑到不同目标具有独特的色散特征，本研究引入色散模型代替受波长影响的传统二向反射分布函数(BRDF)参量，综合考虑漫反射、体散射，构建了新的BPDR模型。通过多角度BRDF实验，与基于动态TS算法的模型参量拟合，得到典型机场地物材质的线偏振度与模型六参量拟合结果。经过多组测试取均值，得到拟合参量中均方根粗糙度参量的测试值，验证了修正BPDF模型的有效性。在仿真分析阶段，以均方根误差(RMSE)作为精度评价指标，将修正BPDF模型、对照模型、实验结果三者进行对比，系统分析了探测角、方位角、入射角对偏振特性的影响。结果显示：4种实验目标在探测角变化时，修正模型的精度较对照模型分别提升了4.39%、4.00%、4.17%、5.26%，且在大探测角下的RMSE仍小于0.05，充分证明修正后模型可用于机场地物目标等粗糙材质的偏振特性研究。此外，通过仿真分析拟合参量对目标偏振特性的影响，发现线偏振度与折射率呈正比关系，而与表面粗糙程度呈反比关系。实验和仿真证明了修正BPDF模型的准确性，为机场地物目标的偏振特性研究提供了思路。
-
关键词:
- 偏振特性 /
- 镜面反射 /
- 色散 /
- 遮蔽效应 /
- 二向偏振分布函数(BPDF)
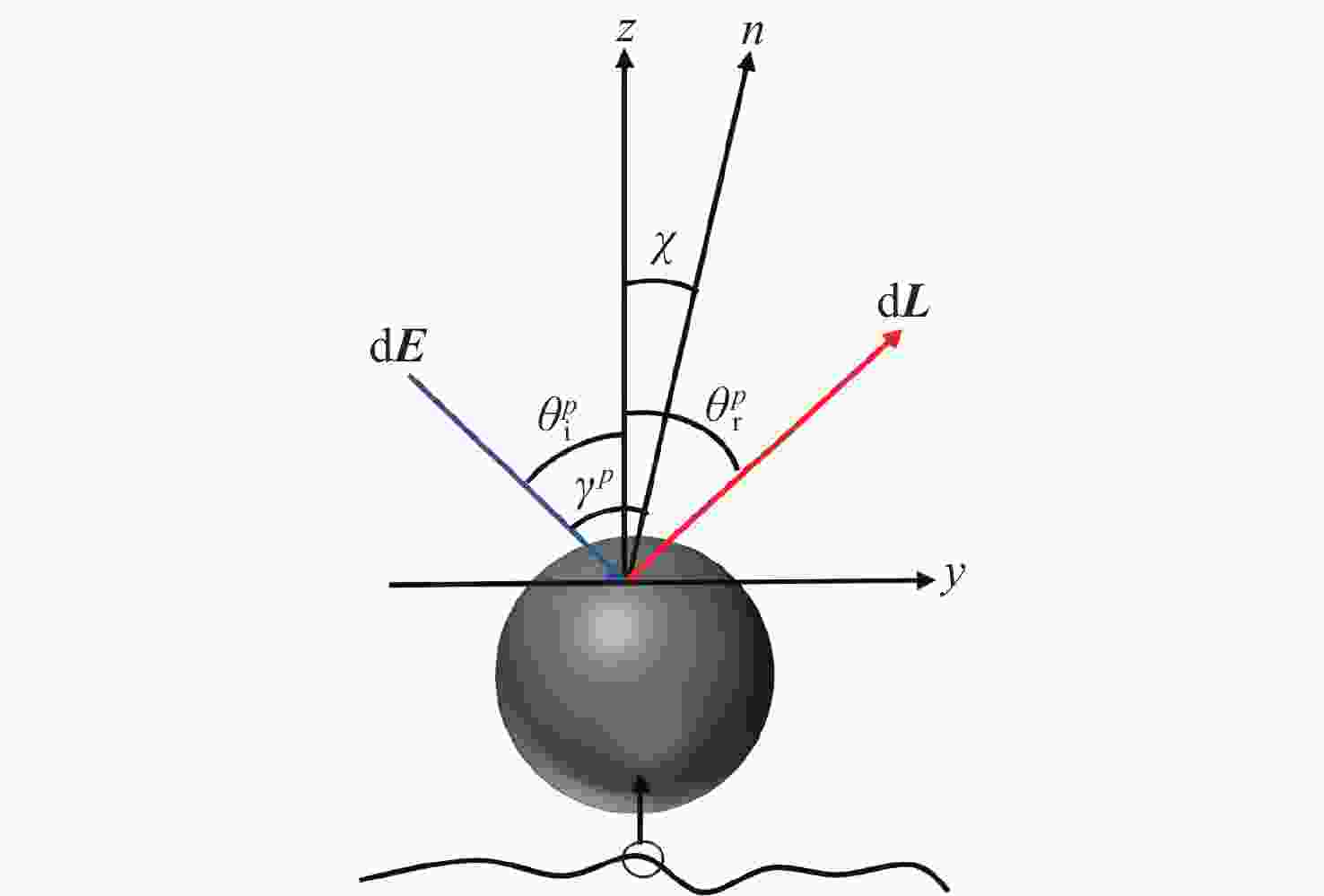
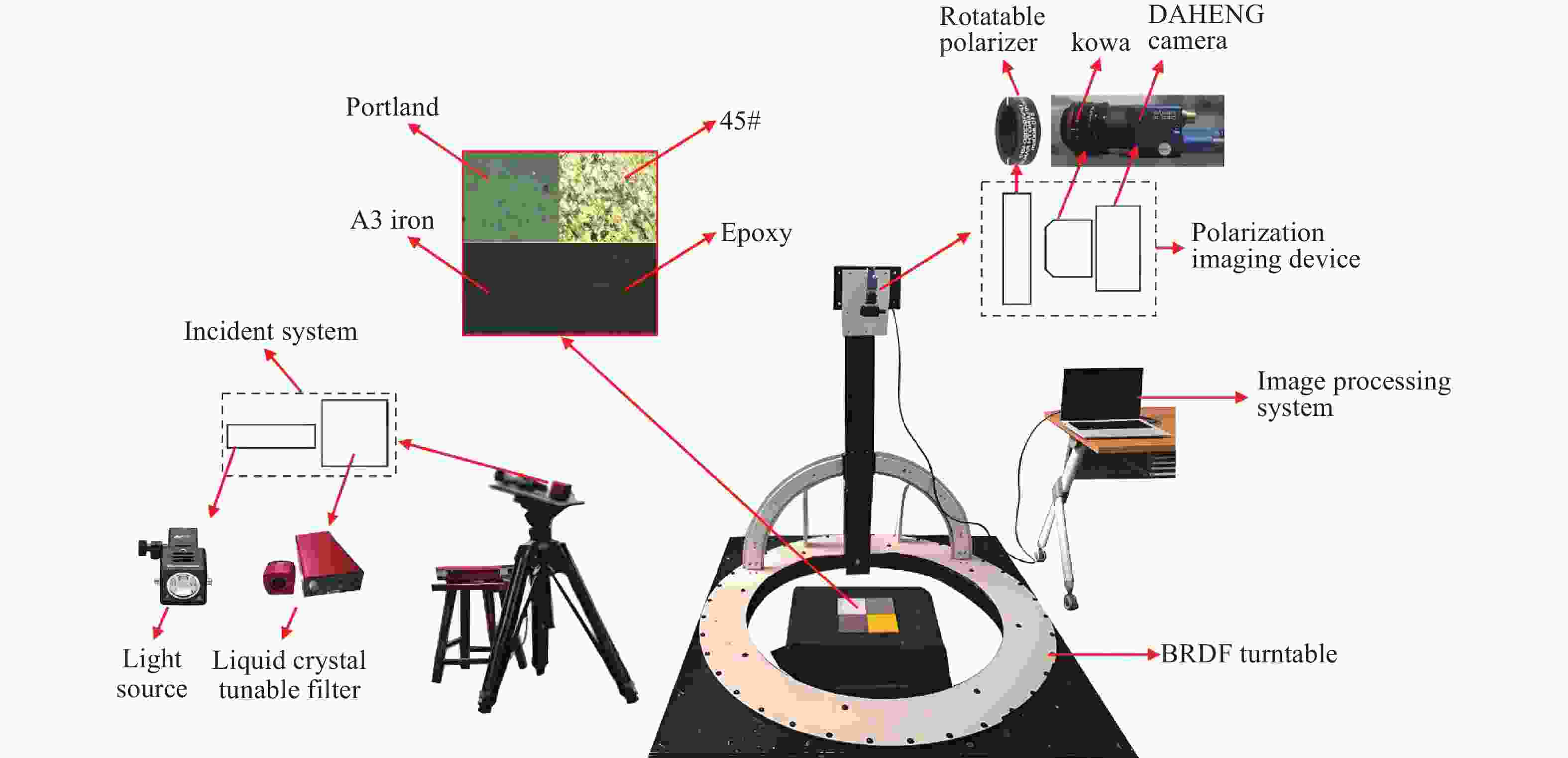
Abstract:This paper provides a theoretical model for studying typical airport ground materials’ polarization characteristics which is required for the development of polarization imaging instruments. First, serious shadow masking effects were analyzed based on the P-G model. These effects occur when light is incident at a large angle. Then, the shadow masking function was optimized using the spherical trigonometry formula. This optimization equates the specular reflection point to a three-dimensional sphere. Due to the unique dispersion characteristics of different targets, a new bidirectional polarization distribution function (BPDF) model was introduced to replace the traditional BRDF parameter affected by wavelength and body scattering. The new BPDF model integrates diffuse reflection and body scattering. In the experimental stage, the accuracy of the line polarization degree was calibrated. The line polarization degree of typical airport ground material was fitted with model parameters. This fitting was based on the dynamic TS algorithm through multi-angle BRDF experiments. The fitting model's six parameters were used to obtain the root mean square roughness parameter. This process verified the validity of the modified BPDF model. In the simulation stage, the root mean square error (RMSE) was used as the accuracy index. The modified BPDF model, control model, and experimental results were compared to analyze the effects of detection, azimuth, and incidence angles on polarization characteristics. The accuracies of the four experimental targets improved by 4.39%, 4.00%, 4.17%, and 5.26% compared with the control model. The RMSE was less than 0.05 for large detection angles. This allows the modified model to study polarization characteristics of rough materials like airport ground targets. Finally, the effect of fitting parameters on polarization characteristics was simulated. Results show that line polarization is positively related to the refractive index and inversely related to the surface roughness. The accuracy of the modified BPDF model is thus proved. This provides ideas for studying polarization characteristics of airport ground targets.
-
图 1 散射三分量的几何关系图
Figure 1. Geometric relationship between the three scattering components
图 6 相对方位角为180°，入射角分别为20°、40°、60°时，探测角与线偏振度的关系
Figure 6. Relationship between detection angle versus line polarization when the relative azimuth is 180° and incident angles are 20°, 40°, and 60°
图 7 入射角为60°下，
$2{\text{π }}$ 范围内线偏振度仿真结果（左侧为对照模型，中间为修正后BPDF模型，右侧为实验测量值）；Figure 7. Simulation results of line polarizability in the range of
$2{\text{π }}$ at an incidence angle of 60° (left: control model; middle: modified BPDF model; right: experimental measurements)
图 8 入射角和探测角均为60°时，修正模型与实验结果对比图
Figure 8. Comparison between the modified model and experimental results when incident angle and detection angle both are 60°
图 9 探测角为60°、相对方位角90°～270°范围内，入射角分别为10°、20°、30°、40°、50°、60°的仿真结果
Figure 9. Simulation results when incidence angles are 10°, 20°, 30°, 40°, 50°, and 60° in the range of detection angles of 60° and relative azimuth angles of 90° to 270°
图 10 相对方位角为180°、探测角为60°时，4种目标的入射角与线偏振度的关系。(a) 45#钢板；(b) A3铁板；(c) 硅酸盐水泥；(d) 环氧树脂
Figure 10. Relationship between incident zenith angle and DOLP for a range of relative azimuth angles of 180° and detection angles of 60°. (a) 45# steel plate; (b) A3 iron plate; (c) portland cement; (d) epoxy resin
图 11 均方根粗糙度
$\delta $ 分别为0.1，0.3，0.5，0.7和0.9时，4种材料的线偏振度随探测角的变化情况Figure 11. Relationship between DOLP of four targets and detection angle when
$\delta $ are 0.1, 0.3, 0.5, 0.7 and 0.9
图 12 当折射率n分别为1.1，1.3，1.5，1.7和1.9时，线偏振度随探测角的变化情况
Figure 12. Relationship between DOLP and detection angle for four kinds of objectives when n are 1.1, 1.3, 1.5, 1.7, and 1.9
表 1 DOLP标定结果
Table 1. DOLP calibration results
Polarized light (DOLP) Incident light (DOLP) Emerging light Maximum error (%) 0° 1 0.966 3.4% 45° 1 0.975 2.5% 90° 1 0.972 2.8% 135° 1 0.969 3.1% 
下载: 导出CSV
表 2 参量拟合结果
Table 2. Fitting results of parameters
材料 ${\varepsilon _{\text{i}}}$ ${\varepsilon _{\text{r}}}$ $\delta/\mu {\mathrm{m}}$ ${\delta ^*}/\mu {\mathrm{m}}$ ${{{k}}_{\rm{s}}}$ ${{{k}}_{\rm{m}}}$ ${{{k}}_{\rm{v}}}$ 45#钢板 4.56 −2.54 0.188 0.195 0.902 0.045 0.003 A3铁板 14.14 −9.55 0.302 0.306 0.521 0.334 0.015 硅酸盐水泥 1.37 1.48 0.318 0.328 0.311 0.327 0.009 环氧树脂 2.69 −1.62 0.120 0.122 0.773 0.202 0.031
下载: 导出CSV
表 3 探测角变化,目标仿真值与实测值的均方根误差
Table 3. Root mean square error of simulated and measured DOLP values of four targets for different detection angles
材料 RMSE1 RMSE2 精度提升/% 45#钢板 0.0634 0.0195 4.39% A3铁板 0.0514 0.0114 4.00% 硅酸盐水泥 0.0859 0.0442 4.17% 环氧树脂 0.0677 0.0151 5.26%
下载: 导出CSV
表 4 入射角变化,仿真值与实测值的均方根误差
Table 4. Root mean square error of simulated and measured DOLP values of four targets when incidence angle changes
材料 RMSE1 RMSE2 精度提升/% 45#钢板 0.0675 0.0214 4.61% A3铁板 0.0583 0.0148 4.35% 硅酸盐水泥 0.0573 0.0264 3.09% 环氧树脂 0.0681 0.0230 4.51%
下载: 导出CSV
-
[1] 付强, 战俊彤, 张肃, 等. 恶劣条件下多谱段偏振目视辅助光学成像技术[J]. 光学学报,2023,43(15):1511004. doi: 10.3788/AOS230961FU Q, ZHAN J T, ZHANG S, et al. Multispectral polarization visually assisted optical imaging technology under harsh conditions[J]. Acta Optica Sinica, 2023, 43(15): 1511004. (in Chinese). doi: 10.3788/AOS230961 [2] 段锦, 付强, 莫春和, 等. 国外偏振成像军事应用的研究进展(上)[J]. 红外技术,2014,36(3):190-195. doi: 10.11846/j.issn.1001_8891.201403003DUAN J, FU Q, MO CH H, et al. Review of polarization imaging technology for international military application I[J]. Infrared Technology, 2014, 36(3): 190-195. (in Chinese). doi: 10.11846/j.issn.1001_8891.201403003 [3] 胡浩丰, 黄一钊, 朱震, 等. 基于深度学习复杂环境的偏振成像技术研究进展(特邀)[J]. 红外与激光工程,2024,53(3):20240057. doi: 10.3788/IRLA20240057HU H F, HUANG Y Z, ZHU ZH, et al. Research progress on polarimetric imaging technology in complex environments based on deep learning[J]. Infrared and Laser Engineering, 2024, 53(3): 20240057. (in Chinese). doi: 10.3788/IRLA20240057 [4] WANG Y, SU Y Q, SUN X Y, et al. Principle and implementation of stokes vector polarization imaging technology[J]. Applied Sciences, 2022, 12(13): 6613. doi: 10.3390/app12136613 [5] ZHONG A Q, FU Q, HUANG D F, et al. Performance analysis of joint imaging system with polarized, infrared, and visible cameras for multi-sensor imaging[J]. Optik, 2023, 295: 171512. doi: 10.1016/j.ijleo.2023.171512 [6] 李淑军, 姜会林, 朱京平, 等. 偏振成像探测技术发展现状及关键技术[J]. 中国光学,2013,6(6):803-809.LI S J, JIANG H L, ZHU J P, et al. Development status and key technologies of polarization imaging detection[J]. Chinese Optics, 2013, 6(6): 803-809. (in Chinese). [7] 王佳林, 段锦, 付强, 等. 基于Mueller矩阵的偏振抑制反光方法[J]. 光学学报,2023,43(20):2012003. doi: 10.3788/AOS230572WANG J L, DUAN J, FU Q, et al. Polarization suppression reflection method based on Mueller matrix[J]. Acta Optica Sinica, 2023, 43(20): 2012003. (in Chinese). doi: 10.3788/AOS230572 [8] PRIEST R G, GEMER T A. Polarimetric BRDF in the microfacet model: theory and measurements[C]. Proceeding of 2000 Meeting of the Military Sensing Symposia Specialty Group on Passive Sensors, 2000, 1: 169-181. [9] 尚可, 晏磊, 张飞舟, 等. 从BRDF到BPDF: 遥感反演基础模型的演进初探[J]. 中国科学: 信息科学,2024,54(8):2001-2020. doi: 10.1360/SSI-2023-0193SHANG K, YAN L, ZHANG F ZH, et al. From BRDF to BPDF: a premilinary study on evolution of the basic remote sensing quantitative inversion model[J]. Scientia Sinica Informationis, 2024, 54(8): 2001-2020. (in Chinese). doi: 10.1360/SSI-2023-0193 [10] LIU S Y, LIN Y, YAN L, et al. Modeling bidirectional polarization distribution function of land surfaces using machine learning techniques[J]. Remote Sensing, 2020, 12(23): 3891. doi: 10.3390/rs12233891 [11] 白鹏涛, 孙兴伟, 董祉序, 等. 基于改进的微面元偏振BRDF模型的粗糙表面偏振反射特性分析[J]. 激光杂志,2022,43(8):24-29.BAI P T, SUN X W, DONG ZH X, et al. Analysis of rough surface polarization reflection characteristics based on improved micro-surface polarization BRDF model[J]. Laser Journal, 2022, 43(8): 24-29. (in Chinese). [12] 张潞, 樊金浩, 鲁宇轩, 等. 改进鲸鱼优化算法的壁面红外反射特性求解[J]. 中国光学(中英文),2024,17(3):595-604. doi: 10.37188/CO.2023-0095ZHANG L, FAN J H, LU Y X, et al. Infrared reflection characteristics of the wall solved by improved whale optimization algorithm[J]. China Optics, 2024, 17(3): 595-604. (in Chinese). doi: 10.37188/CO.2023-0095 [13] ZHAN H Y, VOELZ D G, KUPINSKI M. Parameter-based imaging from passive multispectral polarimetric measurements[J]. Optics Express, 2019, 27(20): 28832-28843. doi: 10.1364/OE.27.028832 [14] RENHORN I G E, BOREMAN G D, et al. Developing a generalized BRDF model from experimental data[J]. Optics Express, 2018, 26(13): 17099-17114. doi: 10.1364/OE.26.017099 [15] YANG M, XU W B, SUN ZH Y, et al. Degree of polarization modeling based on modified microfacet pBRDF model for material surface[J]. Optics Communications, 2019, 453: 124390. doi: 10.1016/j.optcom.2019.124390 [16] 刘卿, 战永红, 杨迪, 等. 粗糙表面偏振二向反射分布函数的影响参数及其反演[J]. 飞行器测控学报,2015,34(5):481-488.LIU Q, ZHAN Y H, YANG D, et al. Parameters of the polarimetric bidirectional reflectance distribution function of rough surfaces and parameter inversion[J]. Journal of Spacecraft TT & C Technology, 2015, 34(5): 481-488. (in Chinese). [17] RENHORN I G E, HALLBERG T, BOREMAN G D. Efficient polarimetric BRDF model[J]. Optics Express, 2015, 23(24): 31253-31273. doi: 10.1364/OE.23.031253 [18] 韦统方. BRDF优化统计建模及应用[D]. 西安: 西安电子科技大学, 2012.WEI T F. The optimized statistical modeling for BRDF and its application[D]. Xi’an: Xi'an University of Electronic Science and Technology, 2012. (in Chinese). [19] MINNAERT M. The reciprocity principle in lunar photometry[J]. Astrophysical Journal, 1941, 93: 403-410. doi: 10.1086/144279 [20] FU Q, LIU X W, WAMG L T, et al. Analysis of target surface polarization characteristics and inversion of complex refractive index based on three-component model optimization[J]. Optics & Laser Technology, 2023, 162: 109225. [21] 王安祥, 朱长军, 张晓军. 智能算法在晶体色散方程参量反演中的比较研究[J]. 光子学报,2015,44(03):34-41.WANG A X, ZHU CH J, ZHANG X J. Research on comparison of intelligent optimization algorithms in the parameters retrieval of crystal dispersion equation[J]. Acta Photonica Sinica, 2015, 44(03): 34-41. (in Chinese). [22] 王鑫. 基于多角度多光谱偏振遥感的地物目标识别研究[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2021.WANG X. Research on ground target recongnition based on multi-angle and multispectral polarimetric remote sensing[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2021. (in Chinese). [23] 王莉雅. 基于pBRDF模型的目标表面偏振特性分析[D]. 长春: 长春理工大学, 2022.WANG L Y. Polarization characteristics analysis of target surface based on pBRDF model[D]. Changchun: Changchun University of Science and Technology, 2022. (in Chinese). [24] 战俊彤, 邹宏扬, 张肃, 等. 基于pBRDF与动态TS算法的粗糙度测量装置及方法: 中国, 116448020A[P]. 2023-07-18.ZHAN J T, ZOU H Y, ZHANG S, et al. Roughness measuring device and method based on pBRDF and dynamic TS algorithm: CN, 116448020A[P]. 2023-07-18. (in Chinese). -
下载:
计量
- 文章访问数: 147
- HTML全文浏览量: 75
- PDF下载量: 7
- 被引次数: 0
